Степень числа. Квадрат и куб числа / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Степень числа. Квадрат и куб числа
Определение.
Степенью числа «» с натуральным показателем «», большим 1, называется произведение «» одинаковых множителей, каждый из которых равен числу «». |
Выражение «» читают так: » в степени » или » — ая степень числа «, и называют степенью. При этом в этой записи число «» называют основанием степени, а число «», которое показывает число множителей в произведении, — показателем степени.
Например, найдем значение следующих степеней:
24 = 2222 = 422 = 82 = 16;
3
Квадрат числа — это вторая степень числа. Квадрат числа записывают так: . Читают: » в квадрате» или » во второй степени».
Например, найдем квадрат чисел 4 и 8:
42 = 44 = 16;
82 = 88 = 64.
Куб числа — это третья степень числа. Куб числа записывают так: . Читают: » в кубе» или » в третей степени».
Например, найдем куб чисел 5 и 7:
53 = 555 = 255 = 125;
73 = 777 = 495 = 343;
Степенью числа «» с показателем = 1 является само это число, то есть .
Ноль в любой степени — это ноль, единица — это единица.
0n = 0;
1n = 1.
Действительно, т.к. степень можно расписать как произведение, то, если в основании находится ноль, то мы получим произведение n нолей, если единица — произведение n единиц.
Возведение числа в степень — это пятое арифметическое действие, поэтому стоит учитывать, что:
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом — остальные действия, в соответствии с порядком их выполнения.
Например, найдем значение выражения 642 — (3 + 2):
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:
642 — (3 + 2) = 616 — (3 + 2) = 616 — 5 = 96 — 5 = 91.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 652, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 656, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 687, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 774, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 866, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 590, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 918, Мерзляк, Полонский, Якир, Учебник
Номер 1195, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 173, Мерзляк, Полонский, Якир, Учебник
Номер 175, Мерзляк, Полонский, Якир, Учебник
Номер 352, Мерзляк, Полонский, Якир, Учебник
Номер 749, Мерзляк, Полонский, Якир, Учебник
Номер 750, Мерзляк, Полонский, Якир, Учебник
Задание 434, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 462, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1404, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1413, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 64, Мерзляк, Полонский, Якир, Учебник
Номер 129, Мерзляк, Полонский, Якир, Учебник
Номер 135, Мерзляк, Полонский, Якир, Учебник
Номер 140, Мерзляк, Полонский, Якир, Учебник
Номер 145, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 349, Мерзляк, Полонский, Якир, Учебник
Номер 564, Мерзляк, Полонский, Якир, Учебник
Номер 770, Мерзляк, Полонский, Якир, Учебник
| 1 | Множитель | ||
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
Решение задач по математике
ПРЕДИСЛОВИЕ
АРИФМЕТИЧЕСКИЕ И АЛГЕБРАИЧЕСКИЕ ЗАДАЧИ
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
КОМБИНАТОРНЫЕ И ТОПОЛОГИЧЕСКИЕ ЗАДАЧИ
ИГРОВЫЕ ГОЛОВОЛОМКИ
ГОЛОВОЛОМКИ С ДОМИНО
ГОЛОВОЛОМКИ СО СПИЧКАМИ
РАЗНЫЕ ГОЛОВОЛОМКИ
ОТВЕТЫ
101. Особое число. Какое число образовано из пяти последовательных цифр (идущих не
обязательно по порядку) так, что число, образованное первыми двумя цифрами, умноженное на
среднюю цифру, дает число, образованное последними двумя цифрами. (Например, если мы
возьмем число 12 896, то 12, умноженное на 8, дает 96. Но, к несчастью, 1, 2, 6, 8, 9
не являются последовательными цифрами, так что этот пример в качестве решения не
пригоден.)
Особое число. Какое число образовано из пяти последовательных цифр (идущих не
обязательно по порядку) так, что число, образованное первыми двумя цифрами, умноженное на
среднюю цифру, дает число, образованное последними двумя цифрами. (Например, если мы
возьмем число 12 896, то 12, умноженное на 8, дает 96. Но, к несчастью, 1, 2, 6, 8, 9
не являются последовательными цифрами, так что этот пример в качестве решения не
пригоден.)
|
|
102. Пять карточек. У меня пять карточек, на которых изображены цифры 1, 3, 5, 7 и 9. Как
расположить их в ряд таким образом, чтобы произведение числа, образованного первой парой
карточек, на число, образованное последней парой карточек, минус число, стоящее на средней
карточке, равнялось числу, составленному из повторений одной и той же цифры? Например (см.
рисунок), 31, умноженное на 79, минус 5 равно 2444; последнее число подошло бы нам, если бы
вместо 2 на первом месте стояло тоже число 4.
Как
расположить их в ряд таким образом, чтобы произведение числа, образованного первой парой
карточек, на число, образованное последней парой карточек, минус число, стоящее на средней
карточке, равнялось числу, составленному из повторений одной и той же цифры? Например (см.
рисунок), 31, умноженное на 79, минус 5 равно 2444; последнее число подошло бы нам, если бы
вместо 2 на первом месте стояло тоже число 4.
Очевидно, должно быть два решения, поскольку обе пары карточек — две первые и две последние — расположены совершенно симметрично.
103. Цифры и квадраты. Какой наименьший квадрат целого числа оканчивается наиболее длинной последовательностью одинаковых цифр?
Так, если бы наиболее длинная последовательность одинаковых цифр составила пять, то нам подошло бы число 24 677 777 (разумеется, если бы оно было наименьшим квадратом, но это неверно). Нуль не считается допустимой цифрой.
104. Две суммы. Можете ли вы расположить цифры 1, 2, 3, 4, 5, 7, 8, 9 двумя группами по
четыре цифры в каждой так, чтобы суммы чисел, составленных из цифр каждой группы, были
равны между собой?
Две суммы. Можете ли вы расположить цифры 1, 2, 3, 4, 5, 7, 8, 9 двумя группами по
четыре цифры в каждой так, чтобы суммы чисел, составленных из цифр каждой группы, были
равны между собой?
Очень просто получить ответ, заменив 9 на 6. Например, каждая из сумм двух групп чисел 1, 2, 7, 8 и 3, 4, 5, 6 равна 18. Но такая замена не допускается.
105. Повторяющаяся четверка цифр. Если мы умножим 64 253 на 365, то получим 23 452 345, где первые четыре цифры повторяются.
На какое наибольшее число нужно умножить 365, чтобы получить аналогичное произведение, содержащее восемь цифр, из которых первые четыре повторяются?
106. Легкое деление. Разделив число 8 101 265 822 784 на 8, вы убедитесь, что ответ можно получить, просто переставив 8 из начала в конец числа!
Не могли бы вы найти число, начинающееся с 7, которое можно разделить на 7 столь же простым способом?
107. Недоразумение. Один американский читатель попросил меня найти число, составленное
из любого количества цифр, для которого деление на 2 можно выполнить, переставив последнюю
цифру в начало. По-видимому, эта задача возникла у него после того, как он познакомился с
неправильно сформулированной предыдущей задачей. Если бы требовалось переставить в конец
первую цифру, то ответом служило бы число 315 789 473 684 210 526, а отсюда легко было бы
найти решение, начинающееся с любой цифры. Но если требуется переставить цифру из конца в
начало, то для делителя 2 решения нет. Однако существует решение для делителя 3. Не могли бы вы
его найти?
Один американский читатель попросил меня найти число, составленное
из любого количества цифр, для которого деление на 2 можно выполнить, переставив последнюю
цифру в начало. По-видимому, эта задача возникла у него после того, как он познакомился с
неправильно сформулированной предыдущей задачей. Если бы требовалось переставить в конец
первую цифру, то ответом служило бы число 315 789 473 684 210 526, а отсюда легко было бы
найти решение, начинающееся с любой цифры. Но если требуется переставить цифру из конца в
начало, то для делителя 2 решения нет. Однако существует решение для делителя 3. Не могли бы вы
его найти?
108. Две четверки. Меня постоянно спрашивают о старой головоломке «Четыре четверки».
Я опубликовал ее в 1899 г., но потом выяснил, что впервые она была опубликована в
первом томе журнала Knowlege за 1881 г. С тех пор к ней обращались различные авторы.
Формулируется головоломка так: «Найти все возможные числа, которые можно получить из
четырех четверок (не больше и не меньше) с помощью различных арифметических знаков. Например, число 17 можно представить в виде 4 4 + 4/4, число 50 — в виде 44 + 4 + и т.
д. Аналогичным образом можно записать все числа до 112 включительно, используя
лишь знаки сложения, вычитания, умножения, деления, квадратного корня, десятичной
точки7
и знака факториала (например, можно писать 4!, что означает всего лишь 1 2 3 4, или 24).
Число 113 уже нельзя представить в виде комбинации четырех четверок.
Например, число 17 можно представить в виде 4 4 + 4/4, число 50 — в виде 44 + 4 + и т.
д. Аналогичным образом можно записать все числа до 112 включительно, используя
лишь знаки сложения, вычитания, умножения, деления, квадратного корня, десятичной
точки7
и знака факториала (например, можно писать 4!, что означает всего лишь 1 2 3 4, или 24).
Число 113 уже нельзя представить в виде комбинации четырех четверок.
Необходимо выяснить, какие числа можно записать с помощью одной, двух и трех четверок. Большие трудности возникают из-за того, что некоторые числа нелегко поддаются такому представлению. Например, мне кажется, что лишь очень немногие смогут выразить 64 с помощью двух четверок. Сумеет ли это сделать читатель?
109. Две цифры. Напишите любое двузначное число (две различные цифры, отличные от
нуля), а затем выразите его, используя те же цифры, взятые в обратном порядке (в случае
необходимости разрешается использовать знаки арифметических действий). Например, число
45 = 5 9 подошло бы, если бы вместо 9 справа стояла цифра 4, а число 81 = (1 + 8)2 могло бы
служить решением задачи, если бы справа в показателе степени не появилась цифра
2.
Две цифры. Напишите любое двузначное число (две различные цифры, отличные от
нуля), а затем выразите его, используя те же цифры, взятые в обратном порядке (в случае
необходимости разрешается использовать знаки арифметических действий). Например, число
45 = 5 9 подошло бы, если бы вместо 9 справа стояла цифра 4, а число 81 = (1 + 8)2 могло бы
служить решением задачи, если бы справа в показателе степени не появилась цифра
2.
110. Цифровые совпадения. Если я перемножу две девятки и сложу 9 и 9, то получу 81 и 18 — два числа, состоящие из одинаковых цифр. Если я перемножу и сложу 2 и 47, то получу 94 и 49 — числа с одинаковыми цифрами, Если я перемножу и сложу 3 и 24, то получу 72 и 27 — два числа, состоящие из одинаковых цифр.
Можете ли вы найти два числа, перемножив и сложив которые вы получили бы два новых числа с тремя одинаковыми цифрами? Задача имеет два решения.
111. Квадраты-палиндромы. Вот любопытный предмет для исследований: найти
квадраты целых чисел, которые можно читать как обычным образом, так и справа налево.
Некоторые из них найти очень легко. Например, квадраты чисел 1, 11, 111 и 1111 равны
соответственно 1, 121, 12 321 и 1 234 321. Все получившиеся числа — палиндромы, и данное
правило применимо к любому числу единиц, не превосходящему 9. Однако существуют и
другие случаи, которые мы могли бы назвать нерегулярными. Например, 2642 = 69 696, а
22852 = 5 221 225.
Вот любопытный предмет для исследований: найти
квадраты целых чисел, которые можно читать как обычным образом, так и справа налево.
Некоторые из них найти очень легко. Например, квадраты чисел 1, 11, 111 и 1111 равны
соответственно 1, 121, 12 321 и 1 234 321. Все получившиеся числа — палиндромы, и данное
правило применимо к любому числу единиц, не превосходящему 9. Однако существуют и
другие случаи, которые мы могли бы назвать нерегулярными. Например, 2642 = 69 696, а
22852 = 5 221 225.
Во всех приведенных выше примерах число цифр было нечетным. Не мог бы читатель привести примеры с четным числом цифр?
112. Разложение на множители. На какие множители разлагается число 1 000 000 000 001? На этот вопрос легко ответить, зная кое-что о числах такого частного вида. Не менее легко указать два сомножителя, если между двумя единицами вставить не 11 нулей, а, например, 101 нуль,
Существует одно любопытное простое и красивое правило для всех подобных случаев. Не
сумеете ли вы найти его?
Не
сумеете ли вы найти его?
113. Два множителя. Найдите два целых числа, разность между которыми минимальна, а их произведение равно 1 234 567 890.
114. Деление на 11. Если девять цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 записаны в случайном порядке, например 412 539 768, то какова вероятность того, что получившееся число делится на 11? То число, которое я выписал, конечно, не делится на 11, но если в нем поменять местами 1 и 8, то оно будет делиться на 11.
115. Деление на 37. Мне хотелось бы узнать, делится ли число 49 129 308 213 на 37, и если нет, то чему равен остаток. Как мне это сделать, не выполняя деления? Оказывается, что при умелом подходе ответ на интересующий меня вопрос можно получить за несколько секунд.
116. Еще раз о делении на 37. Вот интересное развитие предыдущей головоломки. Девять цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 выписаны в случайном порядке, например 412 539 768. Какова вероятность того, что получившееся число делится без остатка на 37?
117. Задача о десяти цифрах. Расставьте все десять цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 в таком
порядке, чтобы получившееся число делилось на все числа от 2 до 18. Если, например, разместить
цифры в последовательности 1 274 953 680, то получившееся число будет делиться на 2, 3, 4, 5 и т.
д. до 16, но не разделится на 17.
Задача о десяти цифрах. Расставьте все десять цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 в таком
порядке, чтобы получившееся число делилось на все числа от 2 до 18. Если, например, разместить
цифры в последовательности 1 274 953 680, то получившееся число будет делиться на 2, 3, 4, 5 и т.
д. до 16, но не разделится на 17.
118. Тройки и семерки. Какое наименьшее число обладает тем свойством, что оно записывается только с помощью цифр 3 и 7 и что как оно, так и сумма его цифр делятся на 3 и 7? Например, 7 733 733 делится без остатка на 3 и на 7, но сумма его цифр (33) на 3 делится, а на 7 нет, поэтому оно не может служить решением задачи.
119. Извлечение корня. Однажды в разговоре с профессором Саймоном Грейтхедом,
человеком весьма эксцентричного склада ума, я как-то упомянул об извлечении кубического
корня.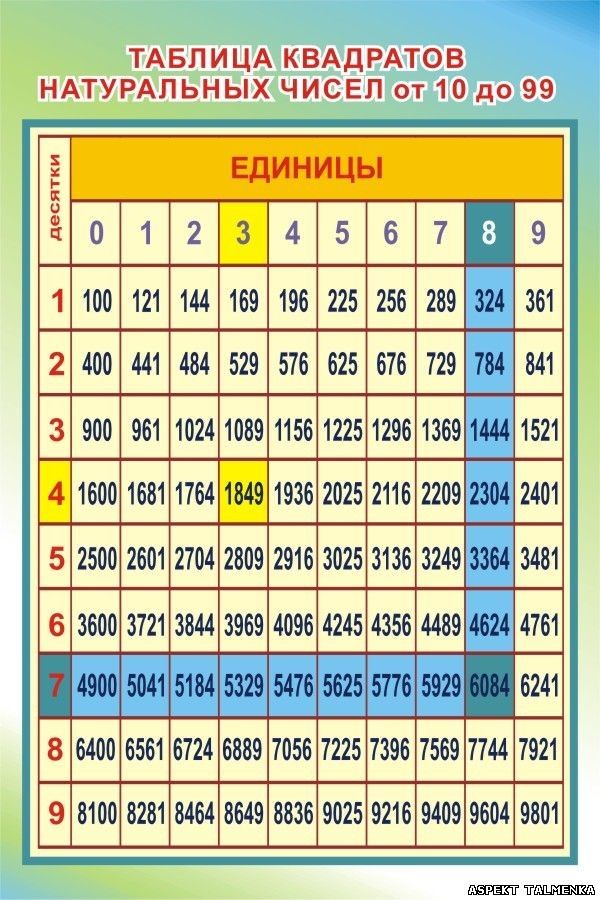
— Поразительно,— сказал профессор,— какое невежество проявляют люди в столь простом вопросе! Создается впечатление, что в извлечении корней со времен, когда единственными корнями были корни, извлекаемые с помощью лопат, вил и садового совка, мир никуда не продвинулся. Например, никто, кроме меня, до сих пор не обнаружил, что для извлечения кубического корня из какого-нибудь числа достаточно лишь найти сумму его цифр.
Извлечь кубический корень из 1 может всякий. Хотя этот пример и подкрепляет высказанное мной утверждение, он слишком тривиален, и мы его рассматривать не будем. Предположим, что требуется извлечь кубический корень из 512. Находим сумму цифр, равную 8, и ответ получен!
Я высказал предположение, что здесь мы имеем дело с исключительным случаем.
— Вовсе нет,— возразил профессор,— возьмем наугад другое число, скажем 4913. Сумма его цифр равна 17, а 17 в кубе равно 4913.
Я не осмелился возражать ученому, но попрошу читателей найти все остальные числа, у которых
кубический корень совпадает с суммой цифр. Этих чисел так мало, что их буквально можно
пересчитать по пальцам.
Этих чисел так мало, что их буквально можно
пересчитать по пальцам.
120. Необычный пример на деление. Вот довольно любопытная головоломка. Найдите наименьшее число, которое при последовательном делении на 45, 454, 4545 и 45 454 даст в остатке соответственно 4, 45, 454 и 4545. Быть может, найти такое число нелегко, зато, решая задачу, вы освежите свои познания в арифметике.
121. Три различные цифры. Профессор предложил студентам найти все числа, составленные из трех различных цифр, каждое из которых делится на квадрат суммы своих цифр. Так, в случае числа 112 сумма цифр равна 4, квадрат ее равен 16 и 112 делится на 16, но, к несчастью, 112 составлено не из трех различных цифр.
Сумеете ли вы найти все возможные решения задачи?
122. Цифры и кубы. Профессор Рэкбрейн попросил недавно своих молодых друзей найти все
пятизначные квадраты, у которых сумма чисел, образованных двумя первыми и двумя
последними цифрами, равна точному кубу. Так, если мы возьмем квадрат числа 141, равный
19 881, и прибавим 81 к 19, то получим 100 — число, не являющееся, к сожалению, точным
кубом.
Так, если мы возьмем квадрат числа 141, равный
19 881, и прибавим 81 к 19, то получим 100 — число, не являющееся, к сожалению, точным
кубом.
Сколько всего существует решений?
123. В обратном порядке. Какое девятизначное число, будучи умноженным на 123 456 789, даст произведение, у которого в девяти младших разрядах будут стоять цифры 9, 8, 7, 6, 5, 4, 3, 2, 1 (именно в таком порядке)?
124. Прогрессия. «Если из девяти цифр,— сказал профессор Рэкбрейн,— вы составите три числа 147, 258, 369, то обнаружите, что любое последующее отличается от предыдущего на 111 и что, следовательно, получилась арифметическая прогрессия».
Не смогли бы вы переставить девять цифр четырьмя способами так, чтобы в каждом случае три числа образовывали арифметическую прогрессию, а среднее число оставалось бы одним и тем же?
125. Составление целых чисел. Может ли читатель назвать сумму всех целых чисел,
составленных из четырех цифр 1, 2, 3, 4? Другими словами, требуется вычислить сумму таких
чисел, как 1234, 1423, 4312 и т. д. Разумеется, можно было бы выписать подряд все такие числа и
затем сложить их. Однако интереснее отыскать простое правило, с помощью которого можно найти
суммы чисел, составленных из четырех различных произвольно выбранных (отличных от нуля)
цифр.
Составление целых чисел. Может ли читатель назвать сумму всех целых чисел,
составленных из четырех цифр 1, 2, 3, 4? Другими словами, требуется вычислить сумму таких
чисел, как 1234, 1423, 4312 и т. д. Разумеется, можно было бы выписать подряд все такие числа и
затем сложить их. Однако интереснее отыскать простое правило, с помощью которого можно найти
суммы чисел, составленных из четырех различных произвольно выбранных (отличных от нуля)
цифр.
126. Суммирование чисел. Профессор Рэкбрейн хотел бы знать, чему равна сумма всех чисел, которые можно составить из девяти цифр (0 исключен), используя каждую цифру в каждом числе один и только один раз.
|
|
127. Цифровое квадрирование. Возьмите девять фишек с цифрами соответственно от 1 до 9
и расположите их в ряд, как показано на рисунке. Требуется, переставив пары фишек как можно
меньшее число раз, расположить их в таком порядке, чтобы цифры образовали квадрат
целого числа. В качестве примера приведем следующие шесть перестановок: (7 и 8
меняются местами), , , , , . В результате получается число 139 854 276, равное
квадрату числа 11 826. Однако задачу можно решить с помощью гораздо меньшего числа
перестановок.
Цифровое квадрирование. Возьмите девять фишек с цифрами соответственно от 1 до 9
и расположите их в ряд, как показано на рисунке. Требуется, переставив пары фишек как можно
меньшее число раз, расположить их в таком порядке, чтобы цифры образовали квадрат
целого числа. В качестве примера приведем следующие шесть перестановок: (7 и 8
меняются местами), , , , , . В результате получается число 139 854 276, равное
квадрату числа 11 826. Однако задачу можно решить с помощью гораздо меньшего числа
перестановок.
128. Цифры и квадраты. Одна из небольших рождественских головоломок профессора Рэкбрейна гласит следующее: чему равны наименьший и наибольший квадраты, содержащие все десять цифр от 0 до 9, причем каждую цифру — лишь по одному разу?
129. Цифровые квадраты. Очень хорошая головоломка состоит в том, чтобы найти число,
которое вместе со своим квадратом содержало бы по одному и только одному разу каждую из
девяти цифр, исключая нуль. Так, если бы квадрат числа 378 равнялся 152 694, то это число нам бы
подошло. Но на самом деле его квадрат равен 142 884, что дает нам две четверки и три восьмерки, а
6, 5 и 9 отсутствуют.
Так, если бы квадрат числа 378 равнялся 152 694, то это число нам бы
подошло. Но на самом деле его квадрат равен 142 884, что дает нам две четверки и три восьмерки, а
6, 5 и 9 отсутствуют.
Существует только два решения; их можно найти за четверть часа, если действовать правильно.
130. Отыскание квадрата. Даны шесть чисел: 4 784 887, 2 494 651, 8 595 087, 1 385 287, 9 042 451, 9 406 087. Известно, что три из них в сумме дают полный квадрат. Что это за числа?
Читатель, вероятно, не увидит другого пути, кроме утомительного метода проб и ошибок, и все же существует прямое решение задачи, использующее лишь простые арифметические соображения и не требующее извлечения квадратных корней.
131. Жонглирование цифрами. Составьте из десяти цифр три простейших арифметических
выражения, используя три из четырех арифметических действий — сложения, вычитания,
умножения и деления. (В записи выражений разрешается применять лишь знаки трех выбранных
арифметических действий. ) Поясним сказанное на примере. Рассмотрим три арифметических
выражения
) Поясним сказанное на примере. Рассмотрим три арифметических
выражения
Этот пример не может служить решением задачи, поскольку цифра 2 пропущена, а цифра 3 повторяется дважды.
132. Равные дроби. Можете ли вы составить три самые обычные дроби (скажем, что-нибудь вроде , , или ), используя каждую из девяти цифр по одному и только одному разу? Дроби можно образовывать одним из следующих способов:
Существует только пять решений, но пятое содержит некую «изюминку» — тонкость, которая, быть может, ускользнет от читателя.
133. Цифры и простые числа. Используя каждую из девяти цифр один и только один раз,
составить простые числа (числа, которые не делятся без остатка ни на какое целое число, кроме 1 и
самих себя), сумма которых была бы наименьшей.
|
|
Приведем пример. Четыре простых числа содержат все девять цифр по одному и только одному разу, их сумма равна 450, однако ее можно существенно уменьшить. Это совсем простая головоломка.
|
|
134. Еще раз о цифровых квадратах. Из девяти цифр многими различными способами
можно составить квадрат таким образом, чтобы числа, стоящие в первой и второй строках, в сумме
давали третью строку. Мы приводим три примера, в которых обнаруживается еще одна
закономерность: разность между второй суммой (819) и первой (657) равна разности между третьей
суммой (981) и второй (819). Составьте восемь квадратов (каждый из девяти цифр) так, чтобы
разность между соседними суммами была постоянной. Разумеется, эта разность будет отличаться от
162.
Еще раз о цифровых квадратах. Из девяти цифр многими различными способами
можно составить квадрат таким образом, чтобы числа, стоящие в первой и второй строках, в сумме
давали третью строку. Мы приводим три примера, в которых обнаруживается еще одна
закономерность: разность между второй суммой (819) и первой (657) равна разности между третьей
суммой (981) и второй (819). Составьте восемь квадратов (каждый из девяти цифр) так, чтобы
разность между соседними суммами была постоянной. Разумеется, эта разность будет отличаться от
162.
135. Девять цифр. Если 32 547 891 умножить на 6, использовав каждую из девяти
цифр один и только один раз, то получится произведение, равное 195 287 346 (также
содержащее девять цифр по одному и только одному разу). Не могли бы вы найти другое
число, обладающее тем же свойством при умножении на 6? Помните, что каждая из
девяти цифр должна появиться один и только один раз как в сомножителях, так и в
произведении.
136. Двадцать четыре. В одной книге было написано: «Запишите число 24 с помощью трех одинаковых цифр, отличных от 8. (Существуют два решения этой задачи.)»
Там же приводились два ответа: 22 + 2 = 24 и 33 — 3 = 24. Читатели, знакомые со старой головоломкой «Четыре четверки» и с другими головоломками такого рода, могут спросить, почему существует лишь два приведенных выше решения. Может быть, вы найдете больше?
|
|
137. Девять бочек. Сколькими способами можно разместить девять бочек в три яруса так,
чтобы числа, написанные на бочках, расположенных справа от любой из бочек или под ней, были
больше числа, написанного на самой бочке? Первым правильным размещением, которое придет вам
в голову, будет то, при котором в верхнем ряду стоит 123, в следующем 456 и внизу 789. На рисунке я привожу второе размещение. Сколькими способами можно разместить
бочки?
На рисунке я привожу второе размещение. Сколькими способами можно разместить
бочки?
138. Восемь карт. Полковник Крэкхэм во время завтрака положил на стол 8 перенумерованных карт (см. рисунок) и попросил своих юных друзей переложить их с помощью
|
|
возможно меньшего числа передвижений таким образом, чтобы суммы цифр, стоящих в двух столбцах, были равны. Можно ли это сделать?
139. Два числа. Можете ли вы найти два числа, составленные из одних единиц, которые при
сложении и умножении дают одинаковый результат? Конечно, 1 и 11 очень близки к решению, но
все же для решения не годятся, так как при сложении они дают 12, а при умножении — только
11.
140. Пример на умножение. Однажды за завтраком Крэкхэмы рассуждали о высоких материях, как вдруг Джордж попросил свою сестру Дору быстро перемножить
Сколько времени займет отыскание этого произведения у читателя?
141. Интересный сомножитель. Какое число обладает тем свойством, что если его умножить на 1, 2, 3, 4, 5 или 6, то в ответе появятся лишь те цифры, которые содержатся в записи исходного числа?
142. Сумма кубов. Числа 407 и 370 совпадают с суммой кубов своих цифр. Так, 4 в кубе равно 64, куб 0 равен 0, а куб 7 есть 343. Сложив 64, 0 и 343, вы получите 407. Аналогично куб числа 3 (27), прибавленный к кубу числа 7 (343), даст 370.
Не могли бы вы найти число, не содержащее нуля и обладающее тем же свойством? Разумеется, мы исключаем тривиальный случай числа, равного 1.
143. Одинокая семерка.
|
|
Эта головоломка, насколько я знаю, первый пример головоломки такого рода, в которой
известна лишь одна цифра. По-видимому, она имеет единственное решение, и, как это ни странно,
восстановить пропущенные цифры совсем нетрудно. Так, поскольку делитель, умноженный на 7,
дает три цифры, то мы заключаем, что первая цифра делителя равна 1. Затем можно
показать, что первая цифра делимого также равна 1. Поскольку две цифры делимого
сносятся вниз, предпоследняя цифра частного равна 0. Наконец, первая и последняя цифры
частного больше 7, поскольку в произведении с делителем они дают четыре цифры, и т.
д.
По-видимому, она имеет единственное решение, и, как это ни странно,
восстановить пропущенные цифры совсем нетрудно. Так, поскольку делитель, умноженный на 7,
дает три цифры, то мы заключаем, что первая цифра делителя равна 1. Затем можно
показать, что первая цифра делимого также равна 1. Поскольку две цифры делимого
сносятся вниз, предпоследняя цифра частного равна 0. Наконец, первая и последняя цифры
частного больше 7, поскольку в произведении с делителем они дают четыре цифры, и т.
д.
144. Совсем без цифр.
|
|
Вот головоломка, составленная мистером А. Корриганом, в которой не известно ни одной
цифры. Обратите внимание на запятую в частном. Благодаря тому что после запятой стоят четыре
цифры, головоломка решается неожиданно легко.
Корриганом, в которой не известно ни одной
цифры. Обратите внимание на запятую в частном. Благодаря тому что после запятой стоят четыре
цифры, головоломка решается неожиданно легко.
145. Простое умножение. Джордж Крэкхэм однажды за завтраком предложил следующую головоломку:
|
|
Джордж попросил поставить вместо звездочек все десять цифр в каждой строке так, чтобы при
умножении получился правильный ответ. Он сказал также, что 0 не должен стоять ни в начале, ни в
конце данных чисел.
Не сможет ли читатель найти ответ?
146. Полностью без цифр.
|
|
Вот еще одна хорошая головоломка. Условия ее таковы:
1. Никакая цифра не встречается дважды ни в одном ряду цифр, кроме делимого.
2. Если прибавить 2 к последней цифре частного, то получится предпоследняя цифра, а если 2 прибавить к третьей справа цифре частного, то получится четвертая справа цифра. Так, например, частное могло бы оканчиваться на 9742 или на 3186.
Нам удалось найти только одно решение.
147. Четные и нечетные.
|
|
В этой головоломке с делением каждая звездочка и буква стоит вместо цифры, причем буква О соответствует нечетной (1, 3, 5, 7 или 9), а буква Е — четной (2, 4, 6, 8 или 0) цифре.
Не смогли бы вы восстановить все цифры? Задача допускает шесть решений. Быть может, вы сумеете найти одно из них или даже все.
148. Деление.
|
|
Не могли бы вы восстановить данный пример на деление, не стирая семерки и не заменяя их
другими цифрами? Если вы попытаетесь решить задачу, считая, что все семерки заданы и других
нет, то вы приметесь тем самым за явно безнадежную работу, хотя доказательство этого факта
достаточно сложно. Задача решается сравнительно просто, если предположить, что любое
число семерок разрешается ставить на любое место в промежуточных результатах (хотя
вводить в делимое, делитель и частное другие семерки, кроме указанных в условии задачи,
запрещается).
Задача решается сравнительно просто, если предположить, что любое
число семерок разрешается ставить на любое место в промежуточных результатах (хотя
вводить в делимое, делитель и частное другие семерки, кроме указанных в условии задачи,
запрещается).
149. Без цифр.
|
|
Следует помнить, что головоломки, в которых цифры заменены звездочками, нельзя решить,
если нет дополнительных условий или не указано хотя бы одной цифры. Быть может, следующая
головоломка близка к идеалу, хотя в ней производятся два деления, связанные между собой тем
условием, что первое частное равно второму делимому. По-видимому, эта задача имеет лишь одно
решение.
По-видимому, эта задача имеет лишь одно
решение.
150. Действия с буквами. Существует много общего между теми головоломками, в которых следует восстановить арифметические действия по нескольким заданным цифрам и большому количеству звездочек, и теми, где каждая цифра заменена вполне определенной буквой, причем разным буквам соответствуют разные цифры. И те и другие головоломки решаются аналогично. Вот небольшой пример задач второго типа (вряд ли его можно назвать трудным):
|
|
Можете ли вы восстановить это деление? Каждая цифра заменена своей буквой.
7 В странах английского языка вместо привычной для нас десятичной запятой применяется десятичная точка. Причем, если целая часть числа равна нулю, то этот нуль иногда опускается, например, пишут не 0,5 а .5.— Прим. перев.
Cтраницы: ← предыдущая 1 2 3 4 следующая →
Население Кубы
Счетчик населения Кубы
11 374 816 | Численность населения |
5 720 936 | Численность мужского населения (50.3%) |
5 653 880 | Численность женского населения (49.7%) |
88 540 | Рождено в этом году |
201 | Рождено сегодня |
64 531 | Умерло в этом году |
146 | Умерло сегодня |
-11 878 | Мигрировало в этом году |
-27 | Мигрировало сегодня |
12 131 | Рост численности населения в этом году |
28 | Рост численности населения сегодня |
28-09-2022 13:44:30
Источник : Департамент по экономическим и социальным вопросам ООН: Отдел народонаселения .
Ежедневная статистика COVID-19
Уведомление касательно COVID-19!
Данные, представленные на этом сайте не отражают реальную миграционную картину, в связи с ограничением передвижения, введённым большинством стран мира из-за пандемии коронавирусной инфекции COVID-19.
Выберите странуАвстралияАвстрияАзербайджанАлбанияАлжирАмериканское СамоаАнгильяАнголаАндорраАнтигуа и БарбудаАргентинаАрменияАрубаАфганистанБагамские ОстроваБангладешБарбадосБахрейнБеларусьБелизБельгияБенинБермудские ОстроваБолгарияБоливияБосния и ГерцеговинаБотсванаБразилияБританские Виргинские ОстроваБрунейБуркина-ФасоБурундиБутанВануатуВеликобританияВенгрияВенесуэлаВиргинские Острова (США)Восточный ТиморВьетнамГабонГаитиГайанаГамбияГанаГваделупаГватемалаГвианаГвинеяГвинея-БисауГерманияГибралтарГондурасГонконгГренадаГренландияГрецияГрузияГуамДанияДжибутиДоминикаДоминиканская РеспубликаЕгипетЗамбияЗападная СахараЗимбабвеИзраильИндияИндонезияИорданияИракИранИрландияИсландияИспанияИталияЙеменКабо-ВердеКазахстанКаймановы ОстроваКамбоджаКамерунКанадаКатарКенияКипрКирибатиКитайКолумбияКоморские ОстроваКонго, Демократическая РеспубликаКосовоКоста-РикаКот-д’Ивуар (Берег слоновой кости)КубаКувейтКыргызстанКюрасаоЛаосЛатвияЛесотоЛиберияЛиванЛивияЛитваЛихтенштейнЛюксембургМаврикийМавританияМадагаскарМайоттаМакаоМалавиМалайзияМалиМальдивыМальтаМароккоМартиникаМаршалловы ОстроваМексикаМикронезияМозамбикМолдоваМонакоМонголияМонтсерратМьянмаНамибияНауруНепалНигерНигерияНидерландыНикарагуаНовая ЗеландияНовая КаледонияНорвегияНормандские острова (Джерси и Гернси)Объединенные Арабские ЭмиратыОманОстров МэнОстров Святой ЕленыОстрова КукаОстрова Уоллис и ФутунаПакистанПалауПалестинаПанамаПапуа — Новая ГвинеяПарагвайПеруПольшаПортугалияПуэрто-РикоРеспублика КонгоРеюньонРоссияРуандаРумынияСальвадорСамоаСан-МариноСан-Томе и ПринсипиСаудовская АравияСвазилендСеверная КореяСеверная МакедонияСеверные Марианские островаСейшельские островаСенегалСент-Винсент и ГренадиныСент-Киттс и НевисСент-ЛюсияСент-Пьер и МикелонСербияСингапурСинт-МартенСирияСловакияСловенияСоединенные Штаты Америки (США)Соломоновы ОстроваСомалиСуданСуринамСьерра-ЛеонеТаджикистанТаиландТайвань (Китайская Республика)ТанзанияТёркс и КайкосТогоТонгаТринидад и ТобагоТувалуТунисТуркменистанТурцияУгандаУзбекистанУкраинаУругвайФарерские ОстроваФиджиФилиппиныФинляндияФранцияФранцузская ПолинезияХорватияЦентральноафриканская РеспубликаЧадЧерногорияЧехияЧилиШвейцарияШвецияШри-ЛанкаЭквадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияЮжная КореяЮжно-Африканская РеспубликаЮжный СуданЯмайкаЯпония———————————————-Земля
Содержание
- Счетчик населения
- Население в 2022году
- Демография в 2021 году
- Плотность населения
- Религиозные убеждения
- Возрастно-половая пирамида
- Коэффициент демографической нагрузки
- Коэффициент детской нагрузки
- Коэффициент пенсионной нагрузки
- Продолжительность жизни
- Грамотность населения
- История населения
- Прогноз численности населения
Факты о населении Кубы
| Население на сегодняшний день |
| 11 374 789 |
| Рейтинг страны по населению |
84 (0. 14% от населения Земли) 14% от населения Земли) |
| Площадь |
| 110 860 км2 |
| Плотность населения |
| 102.6 на км2 |
| Соотношение полов |
| 1.01 (5 720 936 мужчин на 5 653 880 женщин) |
| Средний возраст |
| 41.1 |
| Ожидаемая продолжительность жизни |
| 77.7 (75.5 — мужчины, 80.1 — женщины) |
| Грамотность населения |
| 99.7 % |
(Число людей рассчитано Countrymeters (countrymeters.info) на основе последних данных, опубликованных отделом народонаселения ООН)
Население Кубы в 2022 году
В 2022 году численность населения Кубы увеличится на 16 362 человека и в конце года будет составлять 11 379 047 человек. Естественный прирост населения будет положительным и составит 32 384 человека. За весь год родится примерно 119 422 ребёнок и умрёт 87 038 человек. Если уровень внешней миграции останется на уровне прошлого года,
то в следствии миграционных причин численность населения изменится на -16 021 человек. То есть, суммарное количество людей, покидающих страну (эмигрантов) будет преобладать над количеством людей,
въезжающих в страну с целью долгосрочного пребывания (иммигрантов).
То есть, суммарное количество людей, покидающих страну (эмигрантов) будет преобладать над количеством людей,
въезжающих в страну с целью долгосрочного пребывания (иммигрантов).
Динамика изменения численности населения Кубы в 2022 году
Ниже представлены коэффициенты изменения численности населения Кубы, рассчитанные нами для 2022 года:
- Рождаемость: в среднем 327 детей в день (13.63 в час)
- Смертность: в среднем 238 человек в день (9.94 в час)
- Миграционный прирост населения: в среднем -44 человек в день (-1.83 в час)
Скорость прироста населения Кубы в 2022 году будет 45 человека в день.
Население Кубы 2021
Согласно нашей оценке, на конец 2021 года, население Кубы составляло 11 362 685 человек. За 2021 год население Кубы увеличилось приблизительно на 16 339 человек. Учитывая, что население Кубы в начале года оценивалось в 11 346 346 человек, годовой прирост составил 0. 14 %.
14 %.
Вот основные демографические показатели Кубы за 2021 год:
- Родившихся: 119 250 человек
- Умерших: 86 913 человек
- Естественный прирост населения: 32 337 человек
- Миграционный прирост населения: -15 998 человек
- Мужчин: 5 714 834 человека (по оценке на 31 декабря 2021 года)
- Женщин: 5 647 851 человек (по оценке на 31 декабря 2021 года)
Прирост населения 1952 — 2022
Плотность населения Кубы
Согласно данным Департамента Статистики Организации Объеденённых Наций, общая площадь Кубы составляет 110 860 квадратных километров.
Под общей площадью подразумевается площадь суши и площадь всех водных поверхностей государства в пределах международных границ.
Плотность населения считается как отношение общей численности населения, проживающей на данной территории, к общей площади этой территории.
Согласно нашим рассчётам на начало 2022 года население Кубы составляло приблизительно 11 362 685 человек.
Таким образом, плотность населения Кубы равна 102.5 человека на квадратный километр.
Религия на Кубе
| Религия | Количество последователей | Процент от общей численности населения |
|---|---|---|
| Христианство | 6 745 250 | 59.3 % |
| Нерелигиозные и атеисты | 2 616 201 | 23.0 % |
| Народные верования | 1 990 588 | 17.5 % |
| Индуизм | 22 750 | 0.2 % |
Источник: Pew Research Center. The Global Religious Landscape .
Количество последователей ( 28.09.2022 — Countrymeters.info ).
Распределение населения по возрастным группам
Согласно нашим расчётам, по состоянию на начало 2022 года, население Кубы имело следующее распределение по возрасту:
| 17.3 | 71.1 | 11.7 |
В абсолютных цифрах:
- 1 963 358 человек младше 15 лет (мужчин: 1 009 006 / женщин: 954 238)
- 8 074 892 человека старше 14 и младше 65 лет (мужчин: 4 045 116 / женщин: 4 029 776)
- 1 324 435 человек старше 64 лет (мужчин: 598 245 / женщин: 726 189)
Мы подготовили упрощенную модель возрастно- половой пирамиды, в которой представлены только три возрастные группы, данные о которых были приведены выше:
| мужчины | женщины | |||
Примечание: Масштаб пирамиды отличается от абсолютных значений, приведённых выше, поскольку в каждой возрастной группе содержится разное количество лет.
Как мы видим, возрастная пирамида Кубы имеет регрессивный или убывающий тип. Такой тип пирамиды обычно встречается у высоко развитых стран. В таких странах обычно достаточно высокий уровень здравоохранения, как и уровень образования граждан. Вследствии относительно низкой смертности и рождаемости, население имеет высокую ожидаемую продолжительность жизни. Все эти факторы, наряду с множестом других, приводят к старению населения (повышают средний возраст населения).
Источник: Данные этой секции основаны на последних публикациях Департамента Статистики ООН в области демографической и социальной статистики .
Коэффициент демографической нагрузки
Коэффициент демографической нагрузки показывает нагрузку на общество и экономику со стороны населения, не относящегося к трудоспособному населению (зависимая часть населения).
Под населением, не относящимся к трудоспособному населению понимают суммарное население младше 15 лет и население старше 64 лет.
Возраст населения трудоспособного возраста (производительная часть населения), соответственно, между 15 и 65 годами.
Коэффициент демографической нагрузки напрямую отражает финансовые разходы на социальную политику в государстве. Например, при увеличении данного коэффициента, должны быть увеличены расходы на постройку образовательных учреждений, социальную защиту, здравоохранение, выплаты пенсий и т.д.
Общий коэффициент нагрузки
Общий коэффициент демографической нагрузки рассчитывается как отношение зависимой части населения к трудоспособной или производительной части населения.
Для Кубы Коэффициент общей демографической нагрузки равен 40.7 %.
Значение в 40.7 % — относительно низкое. Оно показывает, что численность трудоспособного населения более чем в два раза превышает численность населения нетрудоспособного возраста. Такое отношение создаёт относительно низкую социальную нагрузку для общества.
Коэффициент потенциального замещения
Коэффициент потенциального замещения (коэффициент детской нагрузки) рассчитывается как отношение численности населения ниже трудоспособного возраста к численности трудоспособного населения.
Коэффициент потенциального замещения для Кубы равен 24.3 %.
Коэффициент пенсионной нагрузки
Коэффициент пенсионной нагрузки рассчитывается как отношение численности населения выше трудоспособного возраста к численности трудоспособного населения.
Коэффициент пенсионной нагрузки в на Кубе составляет 16.4 %.
Источник: Данные этой секции основаны на последних публикациях Департамента Статистики ООН в области демографической и социальной статистики .
Ожидаемая продолжительность жизни
Ожидаемая продолжительность жизни это один из наиболее важных демографических показателей.
Он показывает среднее количество лет предстоящей жизни человека.
То есть количество лет, которое теоретически может прожить человек, при условии, что текущие показатели рождаемости и смертности будут оставаться неизменными на протяжении всей жизни человека.
Как правило, под «ожидаемой продолжительностью жизни» понимают ожидаемую продолжительность жизни при рождении, то есть в возрасте 0 лет.
Средняя ожидаемая продолжительность жизни при рождении (для обоих полов) на Кубе составляет 77.7 лет (года).
Это выше средней ожидаемой продолжительности жизни в мире, которая находится на уровне около 71 года
(по данным отдела народонаселения Департамента ООН по экономическим и социальным вопросам).
Средняя ожидаемая продолжительность жизни мужчин при рождении — 75.5 лет (года).
Средняя ожидаемая продолжительность жизни женщин при рождении — 80.1 лет (года).
Грамотность населения
По нашим подсчётам на Кубе около 9 372 274 человека старше 15 лет могут читать и писать на каком- либо языке. Это составляет 99.71% от общего числа взрослого населения. Под взрослым населением в данном случае подразумеваются все люди старше 15 лет. Соответственно, около 27 052 человека все ещё остаются безграмотными.
Уровень грамотности среди мужского взрослого населения составляет 99.65% (4 627 295 человек).
16 066 человек — безграмотны.
Уровень грамотности среди женского взрослого населения составляет 99.77% (4 744 979 человек).
10 986 человек — безграмотны.
Уровень грамотности среди молодёжи 99.87% и 99.91% для мужчин и женщин соответственно. Общий уровень грамотности среди молодёжи составляет 99.89%. Понятие молодёжи в данном случае покрывает население в возрасте от 15 до 24 лет включительно.
Источник: Данные для раздела «Грамотность населения Кубы» основаны на последних данных, опубликованных Институтом Статистики ЮНЕСКО (данные были взяты 13 марта 2016) .
История населения Кубы (1951 — 2022)
Данные показаны на 1 января соответствующего года.
История населения Кубы
| Год | Население | Прирост населения |
|---|---|---|
| 1951 | 5 985 599 | N/A % |
| 1952 | 6 114 828 | 2.16 % |
| 1953 | 6 241 785 | 2.08 % |
| 1954 | 6 364 294 | 1. 96 % 96 % |
| 1955 | 6 482 141 | 1.85 % |
| 1956 | 6 596 076 | 1.76 % |
| 1957 | 6 708 773 | 1.71 % |
| 1958 | 6 823 115 | 1.70 % |
| 1959 | 6 943 390 | 1.76 % |
| 1960 | 7 073 507 | 1.87 % |
| 1961 | 7 216 837 | 2.03 % |
| 1962 | 7 373 035 | 2.16 % |
| 1963 | 7 539 115 | 2.25 % |
| 1964 | 7 708 743 | 2.25 % |
| 1965 | 7 876 392 | 2.17 % |
| 1966 | 8 037 476 | 2.05 % |
| 1967 | 8 191 550 | 1.92 % |
| 1968 | 8 340 363 | 1.82 % |
| 1969 | 8 488 078 | 1.77 % |
| 1970 | 8 637 584 | 1.76 % |
| 1971 | 8 790 950 | 1.78 % |
| 1972 | 8 947 147 | 1.78 % |
| 1973 | 9 102 709 | 1. 74 % 74 % |
| 1974 | 9 250 460 | 1.62 % |
| 1975 | 9 384 208 | 1.45 % |
| 1976 | 9 500 608 | 1.24 % |
| 1977 | 9 600 542 | 1.05 % |
| 1978 | 9 685 413 | 0.88 % |
| 1979 | 9 757 722 | 0.75 % |
| 1980 | 9 820 314 | 0.64 % |
| 1981 | 9 874 377 | 0.55 % |
| 1982 | 9 919 773 | 0.46 % |
| 1983 | 9 960 977 | 0.42 % |
| 1984 | 10 006 615 | 0.46 % |
| 1985 | 10 065 053 | 0.58 % |
| 1986 | 10 141 255 | 0.76 % |
| 1987 | 10 235 692 | 0.93 % |
| 1988 | 10 342 385 | 1.04 % |
| 1989 | 10 451 180 | 1.05 % |
| 1990 | 10 550 859 | 0.95 % |
| 1991 | 10 635 575 | 0.80 % |
| 1992 | 10 705 132 | 0. 65 % 65 % |
| 1993 | 10 763 067 | 0.54 % |
| 1994 | 10 814 088 | 0.47 % |
| 1995 | 10 863 558 | 0.46 % |
| 1996 | 10 913 905 | 0.46 % |
| 1997 | 10 964 715 | 0.47 % |
| 1998 | 11 014 419 | 0.45 % |
| 1999 | 11 061 878 | 0.43 % |
| 2000 | 11 105 662 | 0.40 % |
| 2001 | 11 145 707 | 0.36 % |
| 2002 | 11 182 314 | 0.33 % |
| 2003 | 11 214 546 | 0.29 % |
| 2004 | 11 239 835 | 0.23 % |
| 2005 | 11 256 024 | 0.14 % |
| 2006 | 11 261 412 | 0.05 % |
| 2007 | 11 256 137 | -0.05 % |
| 2008 | 11 244 007 | -0.11 % |
| 2009 | 11 231 801 | -0.11 % |
| 2010 | 11 226 268 | -0. 05 % 05 % |
| 2011 | 11 231 297 | 0.04 % |
| 2012 | 11 246 947 | 0.14 % |
| 2013 | 11 270 022 | 0.21 % |
| 2014 | 11 294 915 | 0.22 % |
| 2015 | 11 315 916 | 0.19 % |
| 2016 | 11 329 971 | 0.12 % |
| 2017 | 11 337 199 | 0.06 % |
| 2018 | 11 338 696 | 0.01 % |
| 2019 | 11 335 796 | -0.03 % |
| 2020 | 11 330 031 | -0.05 % |
| 2021 | 11 346 346 | 0.14 % |
| 2022 | 11 362 685 | 0.14 % |
Все данные в этой таблице даны на 1 января соответствующего года.
Прогноз численности населения (2020-2100)
| Год | Население | Прирост населения |
|---|---|---|
| 2020 | 11 495 479 | N/A % |
| 2025 | 11 513 017 | 0.15 % |
| 2030 | 11 496 002 | -0. 15 % 15 % |
| 2035 | 11 410 644 | -0.74 % |
| 2040 | 11 266 071 | -1.27 % |
| 2045 | 11 070 600 | -1.74 % |
| 2050 | 10 823 143 | -2.24 % |
| 2055 | 10 523 827 | -2.77 % |
| 2060 | 10 187 703 | -3.19 % |
| 2065 | 9 836 518 | -3.45 % |
| 2070 | 9 512 436 | -3.29 % |
| 2075 | 9 229 431 | -2.98 % |
| 2080 | 8 984 800 | -2.65 % |
| 2085 | 8 748 563 | -2.63 % |
| 2090 | 8 517 746 | -2.64 % |
| 2095 | 8 309 000 | -2.45 % |
| 2100 | 8 119 501 | -2.28 % |
Данные даны на 1 июля соответствующего года (средний вариант прогноза).
Источник : Департамент по экономическим и социальным вопросам ООН: Отдел народонаселения
Число 64, 0x000040, шестьдесят четыре
Энциклопедия чисел
Свойства натурального числа 64, 0x000040, 0x40:
Системы счисления Основные свойства Степени, корни
Тригонометрия Хэши, криптография Языки программирования
Дата и время Цвет по числу Интернет
Другие свойства
Рейтинг 8. 4 из 10,
оценок: 5.
4 из 10,
оценок: 5.
Системы счисления, перевод в систему счисления
Десятичное число 64
- 64 в шестнадцатеричной системе счисления
- 40
- 64 в двоичной системе счисления
- 1000000
- 64 в восьмеричной системе счисления
- 100
Шестнадцатеричное число 40
- 40 в десятичной системе
- 64
- 40 в двоичной системе
- 1000000
- 40 в восьмеричной системе
- 100
Двоичное число 1000000
- 1000000 в десятичной системе
- 64
- 1000000 в шестнадцатеричной системе
- 40
- 1000000 в восьмеричной системе
- 100
Восьмеричное число 100
- 100 в десятичной системе
- 64
- 100 в шестнадцатеричной системе
- 40
- 100 в двоичной системе
- 1000000
Основные арифметические и алгебраические свойства
- Число 64 на русском языке, number in Russian, число 64 прописью:
- шестьдесят четыре
- Четность
- Четное число 64
- Разложение на множители, делители числа 64
- 2, 2, 2, 2, 2, 2, 1
- Простое или составное число
- Составное число 64
- Числа делящиеся на целое число 64
- 128, 192, 256, 320, 384, 448, 512, 576
- Число 64 умноженное на число два
- 128
- 64 деленное на число 2
- 32
- Список 8-ми простых чисел перед числом
- 61, 59, 53, 47, 43, 41, 37, 31
- Сумма десятичных цифр
- 10
- Количество цифр
- 2
- Десятичный логарифм 64
- 1.
 8061799739839
8061799739839
- Натуральный логарифм 64
- 4.1588830833597
- Это число Фибоначчи?
- Нет
- Число на 1 больше числа 64,
следующее число - число 65
- Число на 1 больше числа 64,
- Число на 1 меньше числа 64,
предыдущее число - 63
- Число на 1 меньше числа 64,
Степени числа, корни
- 64 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 4096
- 64 во второй степени (в квадрате)
- В третьей степени (в кубе, 64 в степени 3, x³) равно
- 262144
- Корень квадратный из 64
- 8
- Корень кубический из числа 64 =
- 4
Тригонометрические функции, тригонометрия
- Синус, sin 64 градусов, sin 64°
- 0.8987940463
- Косинус, cos 64 градусов, cos 64°
- 0.4383711468
- Тангенс, tg 64 градусов, tg 64°
- 2.0503038416
- Синус, sin 64 радиан
- 0.
 92002603819679
92002603819679
- Косинус, cos 64 радиан
- 0.39185723042955
- Тангенс, tg 64 радиан равно
- 2.3478603091954
- 64 градуса, 64° =
- 1.1170107212764 радиан
- 64 радиан =
- 3666.9298888373 градуса, 3666.9298888373°
Контрольные суммы, хэши, криптография
- MD-5 хэш(64)
- ea5d2f1c4608232e07d3aa3d998e5135
- CRC-32, CRC32(64)
- 3916527423
- SHA-256 hash, SHA256(64)
- a68b412c4282555f15546cf6e1fc42893b7e07f271557ceb021821098dd66c1b
- SHA1, SHA-1(64)
- c66c65175fecc3103b3b587be9b5b230889c8628
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(64)
- df57bb9a97bd8ee619cb1f4052bd83ae339cd6a15c041684add9aeadc44e62a1
- Base64
- NjQ=
Языки программирования
- C++, CPP, C значение 64
- 0x000040, 0x40
- Delphi, Pascal значение числа 64
- $000040
Дата и время
- 64-й день года
- 5 марта
- 64-й день високосного года
- 4 марта
- Конвертация UNIX timestamp 64 в дату и время
- UTC
- в Москве, Россия
- в Лондоне, Великобритания
- в Нью-Йорке, США
Интернет
- Конвертация в IPv4 адрес Интернет
- 0.0.0.64
- 64 в Википедии:
- 64
Другие свойства числа
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/64
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x40
- Номер телефона
- 64
- Телефонный код страны
- +64 Новая Зеландия
Цвет по числу 64, цветовая гамма
- html RGB цвет 64, 16-ричное значение
- #000040 — (0, 0, 64)
- HTML CSS код цвета #000040
- .
 color-mn { color: #000040; }
color-mn { color: #000040; }
.color-bg { background-color: #000040; }
Цвет для данного числа 64
Здесь вы можете изменить составляющую цвета для данного числа 64 или цвета 000040:
55 лет назад на Кубу были доставлены советские баллистические ракеты
Сам Карибский кризис, а точнее его наиболее острая и решающая фаза, продолжался 13 дней, с 22 октября 1962 года, когда в американских политических кругах было почти согласовано нанесение ракетного удара по Кубе, где к тому времени был размещен внушительный советский воинский контингент.
Министерство обороны РФ накануне обнародовало список официальных потерь советских граждан, которые погибли на острове с 1 августа 1962 по 16 августа 1964 года: в этом скорбном реестре 64 имени.
Наши соотечественники погибли при спасении кубинцев во время сильнейшего урагана «Флора», пронесшегося над Кубой осенью 1963 года, в ходе боевой подготовки, от несчастных случаев и болезней. В 1978 году по предложению Фиделя Кастро в окрестностях Гаваны был построен мемориал памяти советских воинов, похороненных на Кубе, который окружен максимальной заботой. Комплекс представляет собой две бетонные стены в форме траурно склоненных знамен обеих стран. Его содержание в образцовом порядке курируется высшим руководством страны. Кстати, советские военные, которые вместе с кубинцами были задействованы в береговой обороне острова осенью 1962 года, были одеты в кубинскую форму. Но в самые напряженные дни, с 22 по 27 октября, достали из своих чемоданчиков тельняшки и бескозырки и приготовились отдать жизнь за далекую карибскую страну.
В 1978 году по предложению Фиделя Кастро в окрестностях Гаваны был построен мемориал памяти советских воинов, похороненных на Кубе, который окружен максимальной заботой. Комплекс представляет собой две бетонные стены в форме траурно склоненных знамен обеих стран. Его содержание в образцовом порядке курируется высшим руководством страны. Кстати, советские военные, которые вместе с кубинцами были задействованы в береговой обороне острова осенью 1962 года, были одеты в кубинскую форму. Но в самые напряженные дни, с 22 по 27 октября, достали из своих чемоданчиков тельняшки и бескозырки и приготовились отдать жизнь за далекую карибскую страну.
Решение принял Хрущев
Итак, осенью 1962 года мир стоял перед настоящей опасностью ядерной войны между двумя сверхдержавами. И реального уничтожения человечества.
В официальных кругах США, среди политиков и в СМИ одно время получил распространение тезис, согласно которому причиной Карибского кризиса явилось якобы размещение Советским Союзом «наступательного оружия» на Кубе, а ответные меры администрации Кеннеди, поставившие мир на грань термоядерной войны, были «вынужденными». Однако эти утверждения далеки от истины. Их опровергает объективный анализ событий, предшествовавших кризису.
Однако эти утверждения далеки от истины. Их опровергает объективный анализ событий, предшествовавших кризису.
Отправка советских баллистических ракет на Кубу из СССР в 1962 году была инициативой Москвы, а конкретно Никиты Хрущева. Никита Сергеевич, потрясавший ботинком на трибуне Генассамблеи ООН, не скрывал своего желания «засунуть ежа в штаны американцам» и ждал удобной возможности. И это забегая вперед, ему это блестяще удалось — советские ракеты убойной силы не только разместились в сотне километров от Америки, но в США целый месяц не знали, что они уже развернуты на Острове свободы!
После провала операции в Заливе Свиней в 1961 году стало ясно, что американцы не оставят Кубу в покое. Об этом говорило все увеличивающееся количество диверсионных актов в отношении Острова свободы. Москва чуть ли не ежедневно получала сводки об американских военных приготовлениях.
В марте 1962 года на совещании в Политбюро ЦК КПСС, по воспоминаниям выдающегося советского дипломата и разведчика Александра Алексеева (Шитова), Хрущев спросил его, как прореагирует Фидель на предложение установить на Кубе наши ракеты.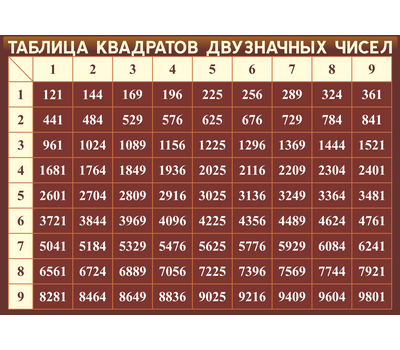 «Мы, сказал Хрущев, должны найти столь эффективное средство устрашения, которое удержало бы американцев от этого рискованного шага, ибо наших выступлений в ООН в защиту Кубы уже явно недостаточно <… > Поскольку американцы уже окружили Советский Союз кольцом своих военных баз и ракетных установок различного назначения, мы должны заплатить им их же монетой, дать им попробовать собственное лекарство, чтобы на себе почувствовали, каково живется под прицелом ядерного оружия. Говоря об этом, Хрущев подчеркнул необходимость проведения этой операции в условиях строгой секретности, чтобы американцы не обнаружили ракет до того, как они будут приведены в полную боевую готовность».
«Мы, сказал Хрущев, должны найти столь эффективное средство устрашения, которое удержало бы американцев от этого рискованного шага, ибо наших выступлений в ООН в защиту Кубы уже явно недостаточно <… > Поскольку американцы уже окружили Советский Союз кольцом своих военных баз и ракетных установок различного назначения, мы должны заплатить им их же монетой, дать им попробовать собственное лекарство, чтобы на себе почувствовали, каково живется под прицелом ядерного оружия. Говоря об этом, Хрущев подчеркнул необходимость проведения этой операции в условиях строгой секретности, чтобы американцы не обнаружили ракет до того, как они будут приведены в полную боевую готовность».
Фидель Кастро не отверг эту идею. Хотя он прекрасно понимал, что размещение ракет повлечет изменение стратегического ядерного баланса в мире между социалистическим лагерем и Соединенными Штатами. Американцы уже разместили боеголовки в Турции, и ответное решение Хрущева разместить ракеты на Кубе было своего рода «ракетным уравниванием шансов». Конкретное решение о размещении советских ракет на Кубе было принято на заседании Политбюро ЦК КПСС 24 мая 1962 года. А 10 июня 1962 года, до июльского приезда Рауля Кастро в Москву, на совещании в Политбюро ЦК КПСС министр обороны СССР маршал Родион Малиновский представил проект операции по переброске ракет на Кубу. Он предполагал размещение на острове двух видов баллистических ракет — Р-12 с радиусом действия около 2 тысяч километров и Р-14 с дальностью в 4 тысячи километров. Оба типа ракет были снабжены ядерными боеголовками мощностью в одну мегатонну.
Конкретное решение о размещении советских ракет на Кубе было принято на заседании Политбюро ЦК КПСС 24 мая 1962 года. А 10 июня 1962 года, до июльского приезда Рауля Кастро в Москву, на совещании в Политбюро ЦК КПСС министр обороны СССР маршал Родион Малиновский представил проект операции по переброске ракет на Кубу. Он предполагал размещение на острове двух видов баллистических ракет — Р-12 с радиусом действия около 2 тысяч километров и Р-14 с дальностью в 4 тысячи километров. Оба типа ракет были снабжены ядерными боеголовками мощностью в одну мегатонну.
Текст соглашения о поставке ракет был передан Фиделю Кастро 13 августа послом СССР на Кубе Александром Алексеевым. Фидель немедленно подписал его и направил с ним в Москву Че Гевару и председателя Объединенных революционных организаций Эмилио Арагонеса, якобы для обсуждения «актуальных экономических вопросов». Никита Хрущев принял кубинскую делегацию 30 августа 1962 года на своей даче в Крыму. Но, приняв соглашение из рук Че, он даже не удосужился подписать его. Таким образом, это историческое соглашение осталось оформленным без подписи одной из сторон.
Таким образом, это историческое соглашение осталось оформленным без подписи одной из сторон.
К тому времени, советские приготовления к отправке на остров людей и техники уже начались и приняли необратимый характер.
О цели миссии не знали капитаны
Операция «Анадырь» по переброске людей и техники через моря и океаны из СССР на Кубу вписана золотыми буквами в анналы мирового военного искусства. Такой ювелирной операции, проведенной под носом у сверхмощного противника с его образцовыми на тот момент системами слежения, мировая история не знает и не знала до этого.
Технику и личный состав доставили в шесть разных портов Советского Союза, на Балтике, Черном и Баренцевом морях, выделив для переброски 85 кораблей, которые в общей сложности совершили 183 рейса. Советские моряки были убеждены, что они отправляются в северные широты. В целях конспирации на суда грузили маскировочные халаты, лыжи, чтобы создать иллюзию «похода на Север» и тем самым исключить любую возможность утечки информации. У капитанов судов имелись соответствующие пакеты, которые нужно было вскрыть в присутствии замполита только после прохождения Гибралтарского пролива. Что говорить о простых моряках, если даже капитаны судов не знали, куда они плывут и что везут в трюмах. Их изумлению не было предела, когда, вскрыв пакет после Гибралтара, они читали: «Держать курс на Кубу и избегать конфликта с кораблями НАТО». Для маскировки военные, которых, естественно, всю поездку нельзя было держать в трюмах, выходили на палубу в штатской одежде.
У капитанов судов имелись соответствующие пакеты, которые нужно было вскрыть в присутствии замполита только после прохождения Гибралтарского пролива. Что говорить о простых моряках, если даже капитаны судов не знали, куда они плывут и что везут в трюмах. Их изумлению не было предела, когда, вскрыв пакет после Гибралтара, они читали: «Держать курс на Кубу и избегать конфликта с кораблями НАТО». Для маскировки военные, которых, естественно, всю поездку нельзя было держать в трюмах, выходили на палубу в штатской одежде.
Общий замысел Москвы состоял в развертывании на Кубе Группы советских войск в составе воинских соединений и частей Ракетных войск, ВВС, ПВО и ВМФ. В итоге на Кубу прибыло более 43 тысяч человек. Основу Группы советских войск составила ракетная дивизия в составе трех полков, оснащенных ракетами средней дальности Р-12, и двух полков, на вооружении которых находились ракеты Р-14 — всего 40 ракетных установок с дальностью действия ракет от 2,5 до 4,5 тысячи километров. Хрущев писал позднее в своих «Воспоминаниях», что «этой силы было достаточно, чтобы разрушить Нью-Йорк, Чикаго и другие промышленные города, а о Вашингтоне и говорить нечего. Маленькая деревня». Вместе с тем перед этой дивизией не ставилась задача нанесения упреждающего ядерного удара по Соединенным Штатам, она должна была служить сдерживающим фактором.
Маленькая деревня». Вместе с тем перед этой дивизией не ставилась задача нанесения упреждающего ядерного удара по Соединенным Штатам, она должна была служить сдерживающим фактором.
Только спустя десятилетия стали известны некоторые, до той поры секретные, детали операции «Анадырь», которые говорят об исключительном героизме советских моряков. Людей на Кубу перевозили в грузовых отсеках, температура в который при входе в тропики доходила до 60 с лишним градусов. Кормили их два раза в сутки в темное время. Пища портилась. Но, несмотря на тяжелейшие условия похода, моряки перенесли длительный морской переход в 18-24 суток. Узнав об этом, президент США Кеннеди заявил: «Если бы у меня были такие солдаты, весь мир был бы под моей пятой».
Первые корабли пришли на Кубу в начале августа 1962 года. Один из участников этой беспримерной операции позже вспоминал: «Бедняги шли из Черного моря в трюме грузового судна, перевозившего до этого сахар с Кубы. Условия, конечно, были антисанитарные: наспех сколоченные многоэтажные нары в трюме, никаких туалетов, под ногами и на зубах — остатки сахарного песка. Из трюма выпускали подышать воздухом по очереди и на очень короткое время. При этом по бортам выставляли наблюдающих: одни следили за морем, другие — за небом. Люки трюмов оставляли открытыми. В случае появления какого-нибудь постороннего объекта «пассажиры» должны были быстро вернуться в трюм. Тщательно замаскированная техника находилась на верхней палубе. Камбуз был рассчитан на приготовление пищи для нескольких десятков человек, составляющих команду судна. Так как людей было значительно больше, то кормили, мягко говоря, неважно. Ни о какой гигиене, конечно, не могло быть и речи. В общем, провалялись в трюме две недели практически без дневного света, без минимальных удобств и нормальной пищи».
Из трюма выпускали подышать воздухом по очереди и на очень короткое время. При этом по бортам выставляли наблюдающих: одни следили за морем, другие — за небом. Люки трюмов оставляли открытыми. В случае появления какого-нибудь постороннего объекта «пассажиры» должны были быстро вернуться в трюм. Тщательно замаскированная техника находилась на верхней палубе. Камбуз был рассчитан на приготовление пищи для нескольких десятков человек, составляющих команду судна. Так как людей было значительно больше, то кормили, мягко говоря, неважно. Ни о какой гигиене, конечно, не могло быть и речи. В общем, провалялись в трюме две недели практически без дневного света, без минимальных удобств и нормальной пищи».
Пощечина для Белого дома
Операция «Анадырь» стала крупнейшим провалом американских спецслужб, аналитики которых все высчитывали, сколько человек могли перевезти на Кубу советские пассажирские суда. И получалась у них какая-то до смешного маленькая цифра. Они не понимали, что на этих теплоходах можно было разместить значительно больше людей, чем положено для обычного рейса. А то, что людей можно перевозить в трюмах сухогрузов, им не могло прийти и в голову.
А то, что людей можно перевозить в трюмах сухогрузов, им не могло прийти и в голову.
В начале августа американские спецслужбы получили от западногерманских коллег информацию о том, что Советы почти в десять раз увеличивают число своих судов в Балтике и Атлантике. А кубинцы, которые проживали в США, узнавали от своих родственников, находившихся на Кубе, о завозе на остров «странных советских грузов». Впрочем, американцы до начала октября просто «пропускали эту информацию мимо ушей».
Скрывать очевидное для Москвы и Гаваны означало бы подогреть еще больший интерес американцев к отправке грузов на Кубу и, главное, к их содержимому. Поэтому 3 сентября 1962 года в совместном советско-кубинском коммюнике о пребывании в Советском Союзе делегации Кубы в составе Че Гевары и Э. Арагонеса отмечалось, что «советское правительство пошло навстречу просьбе кубинского правительства об оказании Кубе помощи вооружением». В коммюнике было сказано, что это вооружение и военная техника предназначены исключительно для целей обороны.
Обнародован список официальных потерь советских граждан с 1 августа 1962 года по 16 августа 1964 года. В скорбном реестре 64 имени
Факт поставки СССР ракет на Кубу был делом абсолютно легальным и разрешенным международным правом. Несмотря на это, американская пресса опубликовала ряд критических статей о «приготовлениях на Кубе». 4 сентября президент США Джон Кеннеди сделал заявление о том, что Соединенные Штаты не потерпят размещения на Кубе стратегических ракет типа «земля-земля» и других видов наступательного оружия. 25 сентября 1962 года Фидель Кастро заявил, что Советский Союз намерен создать на Кубе базу для своего рыболовного флота. Поначалу ЦРУ действительно полагало, что на Кубе идет строительство крупного рыбацкого поселка. Правда, потом в Лэнгли стали подозревать, что под его видом на самом деле Советский Союз создает крупную судоверфь и базу для советских подводных лодок. Наблюдение американской разведки за Кубой было усилено, значительно увеличилось число разведывательных полетов самолетов У-2, которые беспрерывно фотографировали территорию острова. Вскоре американцам стало очевидно, что Советский Союз сооружает на Кубе стартовые площадки для зенитных управляемых ракет (ЗУР). Они были созданы в СССР несколько лет назад в глубоко засекреченном конструкторском бюро Грушина. С их помощью в 1960 году был сбит американский самолет-разведчик У-2, пилотируемый летчиком Пауэрсом.
Вскоре американцам стало очевидно, что Советский Союз сооружает на Кубе стартовые площадки для зенитных управляемых ракет (ЗУР). Они были созданы в СССР несколько лет назад в глубоко засекреченном конструкторском бюро Грушина. С их помощью в 1960 году был сбит американский самолет-разведчик У-2, пилотируемый летчиком Пауэрсом.
Ястребы были за удар по Кубе
2 октября 1962 года Джон Кеннеди отдает приказ Пентагону привести американские вооруженные силы в состояние боевой готовности. Кубинским и советским руководителям стало ясно, что необходимо ускорить строительство объектов на острове.
Тут на руку Гаване и Москве, обеспокоенным скорейшим завершением наземных работ, сыграла плохая погода. Из-за сильной облачности в начале октября полеты У-2, приостановленные к тому времени на шесть недель, начались только 9 октября. Увиденное 10 октября поразило американцев. Данные фоторазведки показали наличие хороших автомобильных дорог там, где еще недавно была пустынная местность, а также огромных тягачей, не вмещавшихся в узкие проселочные дороги на Кубе.
Тогда Джон Кеннеди дал распоряжение активизировать фоторазведку. В этот момент на Кубу обрушился новый тайфун. И новые снимки с самолета-шпиона, барражировавшего на крайне низкой высоте в 130 метров, были сделаны только в ночь на 14 октября 1962 года в районе Сан-Кристобаля в провинции Пинар-дель-Рио. На их обработку ушли сутки. У-2 обнаружил и сфотографировал стартовые позиции советских ракетных войск. Сотни снимков свидетельствовали, что на Кубе уже установлены не просто зенитные ракеты, а ракеты «земля-земля».
16 октября советник президента Макджордж Банди доложил Кеннеди о результатах облета кубинской территории. Увиденное Джоном Кеннеди в корне противоречило обещаниям Хрущева поставлять на Кубу только оборонительное оружие. Обнаруженные самолетом-шпионом ракеты были способны стереть с лица земли несколько крупных американских городов. В тот же день Кеннеди собрал в своем кабинете так называемую рабочую группу по кубинскому вопросу, в которую вошли высокопоставленные сотрудники Госдепартамента, ЦРУ и министерства обороны. Это было историческое совещание, на котором «ястребы» всячески давили на президента США, склоняя его к немедленному удару по Кубе.
Это было историческое совещание, на котором «ястребы» всячески давили на президента США, склоняя его к немедленному удару по Кубе.
Генерал Николай Леонов вспоминал о том, как тогдашний шеф Пентагона Роберт Макнамара сообщил ему на конференции в Москве в 2002 году, что большинство в политической элите США в октябре 1962 года настаивало на ударе по Кубе. Он даже уточнил, что 70 процентов лиц из тогдашней администрации США придерживались подобной точки зрения. К счастью для мировой истории, возобладала точка зрения меньшинства, которой придерживались сам Макнамара и президент Кеннеди. «Надо отдать должное мужеству и смелости Джона Кеннеди, который нашел нелегкую возможность пойти на компромисс наперекор подавляющему большинству из своего окружения и проявил удивительную политическую мудрость», — говорил автору этих строк Николай Леонов.
До кульминации Карибского кризиса, о котором расскажет «РГ», оставались считанные дни…
Цитата
Николай Леонов, генерал-лейтенант госбезопасности в отставке, автор биографий Фиделя и Рауля Кастро:
— ЦРУ откровенно проморгало переброску такого большого количества людей и оружия с одного полушария на другое, причем в непосредственной близости от берегов Соединенных Штатов. Переместить скрытно сорокатысячную армию, огромное количество боевой техники — авиацию, бронетанковые силы и конечно же сами ракеты — такая операция, на мой взгляд, является образцом штабной деятельности. Равно как классическим примером дезинформации противника и маскировки. Операция «Анадырь» была разработана и проведена так, что комар носа не подточит. Уже во время ее проведения приходилось принимать экстренные и оригинальные решения. Например, ракеты, уже при транспортировке на самом острове, попросту не вписывались в рамки узких кубинских сельских дорог. И их приходилось расширять.
Переместить скрытно сорокатысячную армию, огромное количество боевой техники — авиацию, бронетанковые силы и конечно же сами ракеты — такая операция, на мой взгляд, является образцом штабной деятельности. Равно как классическим примером дезинформации противника и маскировки. Операция «Анадырь» была разработана и проведена так, что комар носа не подточит. Уже во время ее проведения приходилось принимать экстренные и оригинальные решения. Например, ракеты, уже при транспортировке на самом острове, попросту не вписывались в рамки узких кубинских сельских дорог. И их приходилось расширять.
*Это расширенная версия текста, опубликованного в номере «РГ»
Кубический корень из 64 — Как найти кубический корень из 64? [Решено]
LearnPracticeDownload
Значение кубического корня из 64 равно 4. Это действительное решение уравнения x 3 = 64. Кубический корень из 64 выражается как ∛64 в радикале и как (64) ⅓ или (64) 0,33 в экспоненциальной форме. Поскольку кубический корень из 64 — целое число, 64 — совершенный куб.
Поскольку кубический корень из 64 — целое число, 64 — совершенный куб.
- Кубический корень из 64: 4
- Кубический корень из 64 в экспоненциальной форме: (64) ⅓
- Кубический корень из 64 в подкоренной форме: ∛64
| 1. | Что такое кубический корень из 64? |
| 2. | Как вычислить кубический корень из 64? |
| 3. | Является ли кубический корень из 64 иррациональным? |
| 4. | Часто задаваемые вопросы о кубическом корне из 64 |
Что такое кубический корень из 64?
Кубический корень из 64 — это число, которое при трехкратном умножении само на себя дает произведение 64. Поскольку 64 можно выразить как 2 × 2 × 2 × 2 × 2 × 2. Следовательно, кубический корень из 64 = ∛ (2 × 2 × 2 × 2 × 2 × 2) = 4,
Как вычислить значение кубического корня из 64?
В этом разделе мы научимся пошагово вычислять кубический корень из 64.
Кубический корень из 64 с помощью простой факторизации
- Шаг 1 : Определите простую факторизацию 64, т.е. 64 = 2 × 2 × 2 × 2 × 2 × 2
- Шаг 2 : Сгруппируйте простые множители числа 64 в группы по три в каждой. 64 = (2 × 2 × 2) × (2 × 2 × 2) = 2 3 × 2 3
- Шаг 3 : Используйте закон экспонент: 64 = 2 3 × 2 3 = 4 3
- Шаг 4 : Извлеките кубический корень из обеих частей уравнения.
Таким образом, кубический корень из 64 по простой факторизации равен (2 × 2 × 2 × 2 × 2 × 2) 1/3 = 4,
Является ли кубический корень из 64 иррациональным?
Нет, потому что ∛64 = ∛(2 × 2 × 2 × 2 × 2 × 2) можно выразить в виде p/q, т.е. 4/1. Следовательно, значение кубического корня из 64 является целым числом (рациональным).
☛ Также проверьте:
- Кубический корень из 288
- Кубический корень из 36
- Кубический корень из 225
- Кубический корень из 361
- Кубический корень из 12
- Кубический корень из 19
- Кубический корень из 40
Кубический корень из 64 решенных примеров
Пример 1: Найдите действительный корень уравнения x 3 − 64 = 0.

Решение:
x 3 − 64 = 0, т. е. x 3 00159 Решение для x дает нам,
.
x = ∛64, x = ∛64 × (-1 + √3i))/2 и x = ∛64 × (-1 — √3i))/2
где я называется мнимой единицей и равен √-1.
Игнорирование мнимых корней,
х = ∛64
Следовательно, действительный корень уравнения x 3 − 64 = 0 равен x = ∛64 = 4,Пример 2: Объем сферического шара равен 64π в 3 . Каков радиус этого шара?
Решение:
Объем сферического шара = 64π в 3
= 4/3 × π × R 3
⇒ Р 3 = 3/4 × 64
⇒ R = ∛(3/4 × 64) = ∛(3/4) × ∛64 = 0, × 4 (∵ ∛(3/4) = 0, и ∛64 = 4)
⇒ R = 3,63424 в 3Пример 3: Каково значение ∛64 ÷ ∛(-64)?
Решение:
Кубический корень из -64 равен минусу кубического корня из 64.

⇒ ∛-64 = -∛64Следовательно,
⇒ ∛64/∛(-64) = ∛64/(-∛64) = -1
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о кубическом корне из 64
Каково значение кубического корня из 64?
Мы можем выразить 64 как 2 × 2 × 2 × 2 × 2 × 2, т. е. ∛64 = ∛(2 × 2 × 2 × 2 × 2 × 2) = 4. Следовательно, значение кубического корня из 64 равно 4.
Как упростить кубический корень из 64/125?
Мы знаем, что кубический корень из 64 равен 4, а кубический корень из 125 равен 5. Следовательно, ∛(64/125) = (∛64)/(∛125) = 4/5 = 0,8.
Является ли 64 идеальным кубом?
Число 64 при разложении на простые множители дает 2 × 2 × 2 × 2 × 2 × 2. Объединение простых делителей в группы по 3 дает 4. Таким образом, кубический корень из 64 = ∛(2 × 2 × 2 × 2 × 2 × 2) = 4 (совершенный куб).
Объединение простых делителей в группы по 3 дает 4. Таким образом, кубический корень из 64 = ∛(2 × 2 × 2 × 2 × 2 × 2) = 4 (совершенный куб).
Если кубический корень из 64 равен 4, найдите значение ∛0,064.
Представим ∛0,064 в форме p/q, т. е. ∛(64/1000) = 4/10 = 0,4. Следовательно, значение ∛0,064 = 0,4.
Почему значение кубического корня из 64 рационально?
Значение кубического корня из 64 можно выразить в виде p/q, т.е. = 4/1, где q ≠ 0. Следовательно, ∛64 рационально.
Каково значение кубического корня из -64?
Мы знаем, что кубический корень из отрицательных чисел отрицателен.
- Запишите -64 как произведение его простых множителей: -64= -(2 × 2 × 2 × 2 × 2 × 2)
- Разделите множители на группы по три в каждой: -64 = -2 3 × 2 3 = -4 3
- Извлеките кубический корень из обеих частей уравнения: 3 √ -64 = 3 √ -4 3 = -4
Следовательно, кубический корень из -64 равен -4.
Найти, является ли кубический корень из 64 минус кубический корень из 8 рациональным числом?
Значение кубического корня из 64 и 8 равно 4 и 2 соответственно, т.е. кубический корень из 8 является рациональным числом.
Что такое куб кубического корня из 64?
Куб кубического корня из 64 — это само число 64, т. е. (∛64) 3 = (64 1/3 ) 3 = 64.0003
Кубический корень из 64 — Калькулятор кубического корня
Калькулятор кубического корня
| Пожалуйста, введите реальное число: |
| Результат кубического корня: Кубический корень из 64 равен 4, потому что 4 × 4 × 4 = 64. |
| Котировки |
Вот ответ на вопросы типа: Кубический корень из 64 или что такое кубический корень из 64?
Что такое кубический корень?
Определение кубического корня
Кубический корень числа а — это число х, такое что х 3 = а, другими словами, число х, кубом которого является а. Например, 4 — это кубический корень из 64, потому что 4 3 = 4•4•4 = 64, -4 — это кубический корень из -64, потому что (-4) 3 = (-4)•(-4) •(-4) = -64.
Например, 4 — это кубический корень из 64, потому что 4 3 = 4•4•4 = 64, -4 — это кубический корень из -64, потому что (-4) 3 = (-4)•(-4) •(-4) = -64.
Perfect Cube Roots Table 1-100
См. Также нашу кубическую корневую таблицу от 1 до 1000.
| x | Корень куба |
|---|---|
| 1 | 1 |
| 1 | 1 |
| 1 | 1 |
| 1 | 1 |
| 1 | 1 |
| 8 | 2 |
| 27 | 3 |
| 64 | 4 |
| 125 | 5 |
| 216 | 6 |
| 343 | 7 |
| 512 | 8 |
| 729 | 9 |
| 1000 | 10 |
| 1331 | 11 |
| 1728 | 12 |
| 2197 | 13 |
| 2744 | 14 |
| 3375 | 15 |
| 4096 | 16 |
| 4913 | 17 |
| 5832 | 18 |
| 6859 | 19 |
| 8000 | 20 |
| 9261 | 21 |
| 10648 | 22 |
| 12167 | 23 |
| 13824 | 24 |
| 15625 | 25 |
| x | Cube Root |
|---|---|
| 17576 | 26 |
| 19683 | 27 |
| 21952 | 28 |
| 24389 | 29 |
| 27000 | 30 |
| 29791 | 31 |
| 32768 | 32 |
| 35937 | 33 |
| 39304 | 34 |
| 42875 | 35 |
| 46656 | 36 |
| 50653 | 37 |
| 54872 | 38 |
| 59319 | 39 |
| 64000 | |
| 6000 | |
| 6000 | |
| 6000 60038 | 77777776666878787878778778787787878778769878 | 777777777777698787878787769878 7987877877777778778787877878.
| 74088 | 42 |
| 79507 | 43 |
| 85184 | 44 |
| 45 | |
| 97336 | 46 |
| 103823 | 47 |
| 110592 | 48 |
| 117649 | 49 |
| 125000 | 50 |
| x | Cube Root |
|---|---|
| 132651 | 51 |
| 140608 | 52 |
| 148877 | 53 |
| 157464 | 54 |
| 166375 | 55 |
| 175616 | 56 |
| 185193 | 57 |
| 195112 | 58 |
| 205379 | 59 |
| 216000 | 60 |
| 226981 | 61 |
| 238328 | 62 |
| 250047 | 63 |
| 262144 | 64 |
| 274625 | 65 |
| 287496 | 66 |
| 300763 | 67 |
| 314432 | 68 |
| 328509 | 69 |
| 343000 | 70 |
| 357911 | 71 |
| 373248 | 72 |
| 389017 | 73 |
| 405224 | 74 |
| 421875 | 75 |
| x | Cube Root |
|---|---|
| 438976 | 76 |
| 456533 | 77 |
| 474552 | 78 |
| 493039 | 79 |
| 512000 | 80 |
| 531441 | 81 |
| 551368 | 82 |
| 571787 | 83 |
| 592704 | 84 |
| 614125 | 85 |
| 636056 | 86 |
| 658503 | 87 |
| 681472 | 88 |
| 704969 | 89 |
| 729000 | 90 |
| 753571 | 91 |
| 778688 | 92 |
| 804357 | 93 |
| 830584 | 94 |
| 857375 | 95 |
| 884736 | 96 |
| 3 | 97 |
| 941192 | 98 |
| 970299 | 99 |
| 1000000 | 100 |
Cube Croot Calculator
Пожалуйста, приведите ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.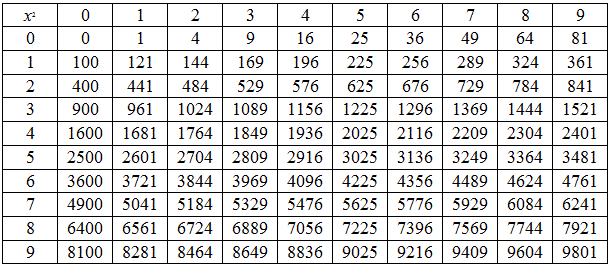
Пример кубических корней.
- кубический корень из 12167
- кубический корень из 27
- кубический корень из 9261
- кубический корень из 5832
- кубический корень из 6859
- кубический корень из 4096
- кубический корень из 12167
- кубический корень из 15625
- кубический корень из 512
Отказ от ответственности
ни этот веб-сайт, ни его авторы не несут ответственности за любые ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Кубический корень из 64 — способы поиска, примеры решений и часто задаваемые вопросы
Символом квадратного корня является √, а кубический корень числа обозначается ∛. Тем не менее, кубический корень числа y — это число, куб которого дает y. Таким образом, мы обозначаем кубический корень из y через ∛y. В качестве примера кубического корня из 64 обозначим его как 64, что дает 4³ = 4 × 4 × 4 = 64. Например:
Например:
(i) Поскольку (4 × 4 × 4) = 64, мы имеем ∛64 = 4, аналогично
(ii) Поскольку (6 × 6 × 6) = 216, мы имеем ∛216 = 6
\[\sqrt[3]{64}\]
Что такое кубирование?
Это может застать вас врасплох, но процесс возведения в куб такой же, как и в квадрате, только число умножается три раза, а не два. Показатель степени или мощность множителя, используемого для кубов, равна 3, что также обозначается верхним индексом³. Например, кубический корень из 64 равен 4 и математически выражается как 4³ = 4 × 4 × 4 = 64 или 7³ = 7 × 7 × 7 = 343.
Введение в кубическую функцию
Кубическая функция утверждает функция один к одному. Вам может быть интересно, как и почему это так. Это связано с тем, что 4 кубирования отрицательных чисел приводят к результату, отличному от результата кубирования его положительной координаты. Кроме того, когда мы умножаем три отрицательных числа вместе, два отрицательных числа сокращаются, а одно остается, поэтому полученный результат также отрицательный. 9³ = 9 × 9 × 9 = 729 = (-9) × (-9) × (-9) = -729. Подобно идеальному квадрату, кубическое число или идеальный куб — это целое число, полученное в результате кубирования другого целого числа. 729 и -729 являются примерами идеальных кубов.
9³ = 9 × 9 × 9 = 729 = (-9) × (-9) × (-9) = -729. Подобно идеальному квадрату, кубическое число или идеальный куб — это целое число, полученное в результате кубирования другого целого числа. 729 и -729 являются примерами идеальных кубов.
Метод факторизации для нахождения кубического корня
Мы можем легко найти кубический корень из заданного числа, используя метод факторизации. Чтобы определить кубический корень из данного числа, выполните следующие действия:
Шаг I. Запишите данное число как произведение простых чисел.
Шаг II. Создайте группу из троек одного и того же простого числа.
Этап III. Определите произведение простых чисел, выбрав по одному из каждой тройки.
Этап IV. Полученное произведение и есть искомый кубический корень из заданного числа.
Помните, что если группировка в триплеты одних и тех же простых множителей не может быть завершена, то мы не можем найти совершенный кубический корень.
(Изображение будет добавлено в ближайшее время)
Как рассчитать коэффициенты простых чисел?
Если вы думаете, что найти множители простых или натуральных чисел сложно, то это не так. Проще говоря, чтобы получить число, которое вы факторизуете, вам просто нужно умножить любое число в наборе целых чисел на другое в том же наборе. Например:
Например, число 3 имеет два делителя 1 и 3. Число 8 само имеет четыре делителя 1, 2, 4 и 8. Разложить числа на множители в наборе натуральных чисел очень просто, поскольку все числа имеют как минимум два множителя (один и само себя). Однако, чтобы найти другие множители, вам придется начать делить число, начиная с 2, и продолжать увеличивать делители, пока не достигнете числа, которое было разделено на 2 в начале.
Помните, что все числа, не имеющие остатков, являются делителями, включая сам делитель. Возьмем пример факторизации с числом 9. Число 9 не делится на 2 без остатка, поэтому мы его пропустим. Обратите внимание на цифры 4 и 5, чтобы вы знали, где остановиться позже. Число 9 делится на 3, поэтому прибавьте 3 к своим множителям. Продолжайте, пока не дойдете до 5 (9/2, округлено). Наконец, у вас есть 1, 3 и 9 в виде списка факторов.
Обратите внимание на цифры 4 и 5, чтобы вы знали, где остановиться позже. Число 9 делится на 3, поэтому прибавьте 3 к своим множителям. Продолжайте, пока не дойдете до 5 (9/2, округлено). Наконец, у вас есть 1, 3 и 9 в виде списка факторов.
Решенные примеры кубического корня
Давайте быстро найдем кубический корень, используя пошаговую процедуру с пояснением
Пример 1: Найдите кубический корень из 216.1030 Шаг I. Выразите данное число как ∛216
Шаг II. Using the method of prime factorization, we have
2 | 216 |
2 | 108 |
2 | 54 |
3 | 27 |
3 | 9 |
3 | 3 |
3 | 1 |
This means: 2 × 2 × 2 × 3 × 3 × 3 = 216
Этап III. Создавая группу из троек одного и того же простого числа, мы имеем
Создавая группу из троек одного и того же простого числа, мы имеем
= [2 × 2 × 2] × [3 × 3 × 3]
Таким образом, ∛216 = [2 × 3] = 6
Пример 2. Вычисление кубический корень числа 9261.
Решение 2:
Следуя той же процедуре факторизации, мы получаем
3 | 9261 | |
3 | 3087 | |
3 | 1029 | |
7 | 343 | |
7 | 49 | |
7 | 7 | |
7 | ||
70003 | ||
70003 | ||
70003 | ||
7 | ||
| 1030 | 1 |
Это означает: 3 × 3 × 3 × 7 × 7 × 7 = 9261
(3 × 3 × 3) 7 0 3 9 7 0 0 7 = 21
Таким образом, ∛9261 = [3 × 7] = 21
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | 9(1/2)||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценить | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
Кубические корни | Brilliant Math & Science Wiki
Содержание
- Определение и обозначения
- Основные расчеты
- Кубические корни отрицательных чисел
- Упрощение кубических корней 93=а.
- Коэффициенты 64: 1, 2, 4, 8, 16, 32 и 64.
- Отрицательные множители 64: -1, -2, -4, -8, -16, -32 и -64.
- Простые множители 64:2.
- Простая факторизация 64: 2 × 2 × 2 × 2 × 2 × 2 = 2 6
- Сумма множителей 64:127.
- 1×64 = 64.
- 2×32 = 64.
- 4×16 = 64.
- 8×8 = 64.
- 16×4 = 64.
- 32×2 = 64.
- .
- Найдите разложение каждого числа на простые множители.
- Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали.
- Сократите простые числа в каждом столбце.
- Умножьте множители, чтобы получить LCM.
 б3=а.
б3=а.Символ кубического корня действует аналогично символу квадратного корня. Его часто называют радикалом , а число или выражение под верхней строкой символа называют радикалом и . Символ кубического корня — это символ группировки , означающий, что все операции в подкоренном члене сгруппированы так, как если бы они были заключены в круглые скобки.
В отличие от квадратного корня результатом кубического корня может быть любое действительное число: положительное, отрицательное или ноль. Кроме того, от квадратного корня отличается доменное ограничение на подкоренное число: подкоренное число кубического корня может быть отрицательным, но при этом достигается реальный результат для кубического корня. 93=12553=125.
Отсюда следует, что 271253=35.\sqrt[3]{\dfrac{27}{125}}=\dfrac{3}{5}.312527=53. □_\квадрат□
В отличие от квадратного корня, кубический корень не имеет доменных ограничений по действительным числам.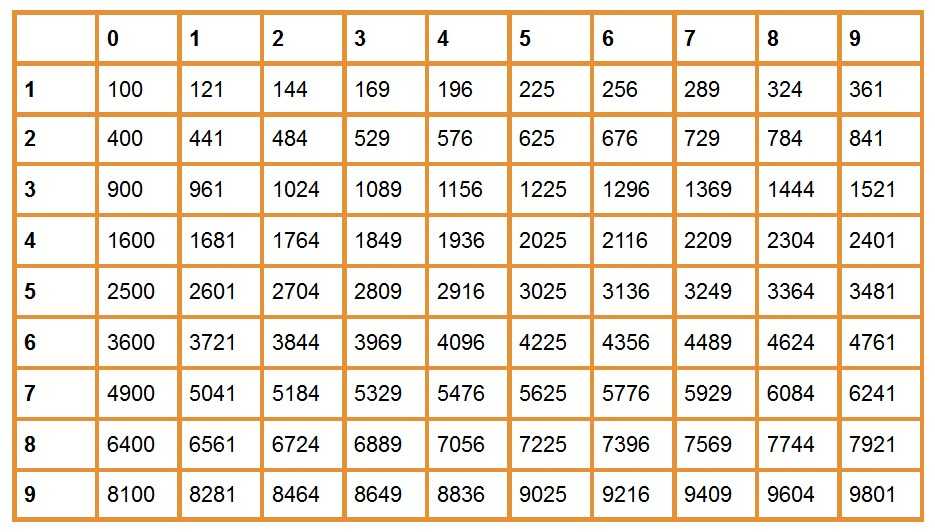 Подкоренной может быть любое действительное число, и результатом кубического корня будет действительное число.
Подкоренной может быть любое действительное число, и результатом кубического корня будет действительное число.
Каково значение −83\sqrt[3]{-8}3−8?
Как и в предыдущих примерах, кубический корень из -8-8-8 является ответом на вопрос: «Какое число при возведении в куб дает -8-8-8?» 93=-8(-2)3=-8, откуда следует, что -83=-2. □\sqrt[3]{-8}=-2.\ _\square3−8=−2. □
Обычно, если операция извлечения кубического корня выполняется над отрицательным числом, результат будет отрицательным.
Пусть ааа будет действительным числом. Тогда
-a3=-a3.\sqrt[3]{-a}=-\sqrt[3]{a}.3-a=-3a.
Процесс упрощения кубических корней несовершенных кубов аналогичен процессу упрощения квадратных корней.
Пусть ааа — целое несовершенное кубическое число.
Упрощенная радикальная форма кубического корня из ааа равна
.bc3.b\sqrt[3]{c}.
b3c.
В этой форме a3=bc3\sqrt[3]{a}=b\sqrt[3]{c}3a=b3c, bbb и ccc — целые числа, а ccc положительна и не имеет полных кубических множителей, отличных от 111. .
Чтобы упростить кубический корень, сначала найдите наибольший совершенный кубический множитель подкоренного числа. Затем примените следующее свойство:
Пусть aaa и bbb — действительные числа. Тогда
ab3=a3×b3.\sqrt[3]{ab}=\sqrt[3]{a}\times \sqrt[3]{b}.3ab=3a×3b.
Упростить 813.\sqrt[3]{81}.381.
Цель состоит в том, чтобы найти наибольший совершенный кубический множитель числа 818181. Поскольку 272727 является этим множителем, мы имеем813=27×33=273×33=333. □\begin{выровнено} \sqrt[3]{81}&=\sqrt[3]{27\times 3} \\ &=\sqrt[3]{27}\times\sqrt[3]{3} \\ &=3\sqrt[3]{3}.\ _\квадрат \end{выровнено}381=327×3=327×33=333. □
Примечание : Когда число помещается слева от символа кубического корня, подразумевается умножение.
Таким образом, «3333\sqrt[3]{3}333» читается как «333, умноженный на кубический корень из 333».
Кубический корень комплексного числа несколько неоднозначен. Недействительные комплексные числа не являются ни положительными, ни отрицательными, поэтому четко не определено, какой кубический корень является главным корнем. Следовательно, когда операция извлечения кубического корня выполняется над комплексным числом, результат интерпретируется как все решения уравнения:
Пусть zzz будет комплексным числом. Тогда существует до трех значений для z3\sqrt[3]{z}3z, и они равны решениям уравнения 9{i3\pi/2} & = & -i. \end{array}i3i3i3i3i=====eiπ/2i1/3(eiπ/2)1/3(ei5π/2)1/3(ei9π/2)1/3 ====ei5π/2eiπ/6ei5π/6ei3π/2====ei9π/223+2i−23+2i−i.
Есть три возможных результата для i3\sqrt[3]{i}3i: 32+i2\dfrac{\sqrt{3}}{2}+\dfrac{i}{2}23+2i, −32+i2-\dfrac{\sqrt{3}}{2}+\dfrac{i}{2}−23+2i и −i-i−i. □_\квадрат□
Процитировать как: Кубические корни. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/cube-root/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/cube-root/
Чему равен кубический корень из 64*? – Reviews Wiki
Значение кубического корня из 64 равно 4 .
Здесь, является ли 64 идеальным квадратом? Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или нулевое) на само себя, полученное произведение называется квадратным числом, или полным квадратом, или просто «квадратом». Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — все квадратные числа.
Какие множители числа 64? Коэффициенты 64
Дополнительно Почему 64 — это совершенный квадрат и куб? 4 x 16 = 64 — это произведение двух квадратов , так что это тоже квадрат. Но вы также можете записать его как 64 = 4 x 4 x 4, сделав его кубом. … 9х 81 = 729, это произведение двух квадратов, так что это тоже квадрат. Вы также можете записать это как 729 = 9 x 9 x 9, сделав его кубом.
Но вы также можете записать его как 64 = 4 x 4 x 4, сделав его кубом. … 9х 81 = 729, это произведение двух квадратов, так что это тоже квадрат. Вы также можете записать это как 729 = 9 x 9 x 9, сделав его кубом.
Чему кратно 64? Число, кратное 64, равно 64, 128, 192, 256, 320, 384, 448, 512, 576 и так далее. Число, кратное 72, равно 72, 144, 216, 288, 360, 432, 504, 576 и так далее.
Что такое LCM 64?
LCM 64 и 96: 192 . Чтобы найти наименьшее общее кратное (НОК) чисел 64 и 96, нам нужно найти числа, кратные 64 и 9.6 (кратные 64 = 64, 128, 192, 256; кратные 96 = 96, 192, 288, 384) и выберите наименьшее кратное, которое точно делится на 64 и 96, т. е. 192.
Что может равняться 64 ? Список пар факторов для 64
Сколько делителей имеет число 64? Показатель степени в простой факторизации равен 6. Когда вы добавляете число 1 с показателем степени 6, мы получаем 7. т. е. 6 + 1 = 7. Следовательно, число 64 имеет 7 баллов .
Когда вы добавляете число 1 с показателем степени 6, мы получаем 7. т. е. 6 + 1 = 7. Следовательно, число 64 имеет 7 баллов .
Является ли 64 числом в квадрате или в кубе?
Квадратное число — это число, умноженное само на себя. Квадратные числа до 100: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100. Кубическое число — это число, умноженное само на себя 3 раза. Кубические числа до 100: 1, 8, 27 и 64.
Также Является ли 64 совершенным квадратом, совершенным кубом и то и другое или ни то, ни другое? И, согласно некоторым другим ответам, 0, 1 и 64 — не единственные идеальных квадратов , которые также являются идеальными кубами; подойдет любое число в шестой степени. Любое число в двенадцатой степени — это совершенный квадрат, совершенный куб и совершенная четвертая степень. Например, 0, 1 и 4096.
Почему 64 — совершенное число?
В математике
Это наименьшее число, имеющее ровно семь делителей. Это наименьшая положительная степень двойки, которая не является смежной ни с простым числом Мерсенна, ни с простым числом Ферма. … 64 также первое целое число (больше 1) , который является и идеальным квадратом, и идеальным кубом.
… 64 также первое целое число (больше 1) , который является и идеальным квадратом, и идеальным кубом.
Что такое таблица 64? Повторное сложение 64 — это таблица умножения 64. Например, 64 + 64 + 64 = 3 × 64 = 192.
…
Таблица 64 до 10.
| 64 × 1 = 64 | 64 x 6 = 384 |
|---|---|
| 64 × 2 = 128 | 64 × 7 = 448 |
| 64 × 3 = 4 192 | 0038|
| 64 × 4 = 256 | 64 × 9 = 576 |
| 64 × 5 = 320 | 64 × 10 = 640 |
в таблице.
Tables 2 to 10
| Table of 2 | Table of 3 | Table of 8 |
|---|---|---|
| 2 6 × = 12 | 3 6 × = 18 | 8 6 × = 48 |
| 2 7 × = 14 | 3 7 × = 21 | 8 7 × = 56 |
| 2 8 × = 16 | 3 8 × = 24 | 8 × 8 = 64 |
| 2 9 × = 18 | 3 9 × = 27 | 8 9 × = 72 |
Чему равен GCF числа 64?
GCF 64 и 100 равен 4 . Чтобы вычислить наибольший общий множитель (НОД) чисел 64 и 100, нам нужно разложить каждое число на множители (множители 64 = 1, 2, 4, 8, 16, 32, 64; множители 100 = 1, 2, 4, 5). , 10, 20, 25, 50, 100) и выбрать наибольший множитель, который точно делит и 64, и 100, т. е. 4,9.0003
Чтобы вычислить наибольший общий множитель (НОД) чисел 64 и 100, нам нужно разложить каждое число на множители (множители 64 = 1, 2, 4, 8, 16, 32, 64; множители 100 = 1, 2, 4, 5). , 10, 20, 25, 50, 100) и выбрать наибольший множитель, который точно делит и 64, и 100, т. е. 4,9.0003
Как найти HCF 64? HCF 64 и 72 с помощью простой факторизации
Простая факторизация 64 и 72 равна (2 × 2 × 2 × 2 × 2 × 2) и (2 × 2 × 2 × 3 × 3) соответственно. Как видно, числа 64 и 72 имеют общие простые делители. Следовательно, HCF чисел 64 и 72 равен 2×2×2 = 8 .
Как вы решаете для LCM? Найдите НОК, используя метод простых множителей
В какой таблице находится число 64?
Tables 2 to 10
| Table of 2 | Table of 3 | Table of 8 |
|---|---|---|
| 2 6 × = 12 | 3 6 × = 18 | 8 6 × = 48 |
| 2 7 × = 14 | 3 7 × = 21 | 8 7 × = 56 |
| 2 8 × = 16 | 3 8 × = 24 | 8 × 8 = 64 |
| 2 9 × = 18 | 3 9 × = 27 | 8 9 × = 72 |
Что такое Факторное дерево 64? Все множители Пара 64
Здесь вы можете увидеть все пары множителей 64. ( 1,64 ) — множители 64, так как 1 × 64 равно 64. (2, 32) — множители 105, поскольку 2 × 32 равно 64. (4, 16) — это коэффициенты 105, так как 4 × 16 равно 64. (8, 8) — это коэффициенты 105, поскольку 8 × 8 равно 64,
( 1,64 ) — множители 64, так как 1 × 64 равно 64. (2, 32) — множители 105, поскольку 2 × 32 равно 64. (4, 16) — это коэффициенты 105, так как 4 × 16 равно 64. (8, 8) — это коэффициенты 105, поскольку 8 × 8 равно 64,
Как найти квадратный корень?
IS 64 — идеальный куб? Так как 64 является совершенным кубом , поэтому легко найти его кубический корень, но для несовершенных кубов мы должны оценить значения. Но иногда становится трудно оценить. Ниже приведена таблица кубов от 1 до 10 чисел, чтобы легко найти кубический корень.
Что такое x2 в математике?
x в квадрате — это запись, которая используется для представления выражения x×xx×x. т.е. х в квадрате равно x, умноженному на .
Рационально ли 64? 64 — это , рациональное число , потому что его можно выразить как частное двух целых чисел: 64 ÷ 1.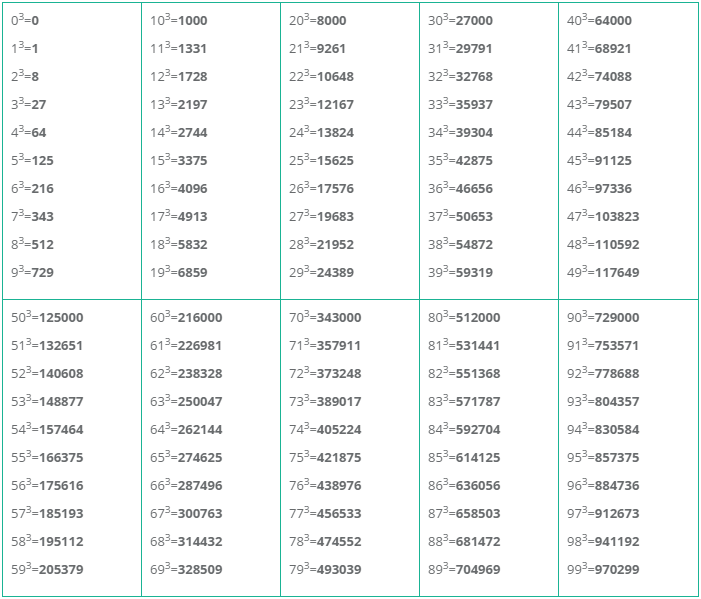

 8061799739839
8061799739839 92002603819679
92002603819679 color-mn { color: #000040; }
color-mn { color: #000040; } 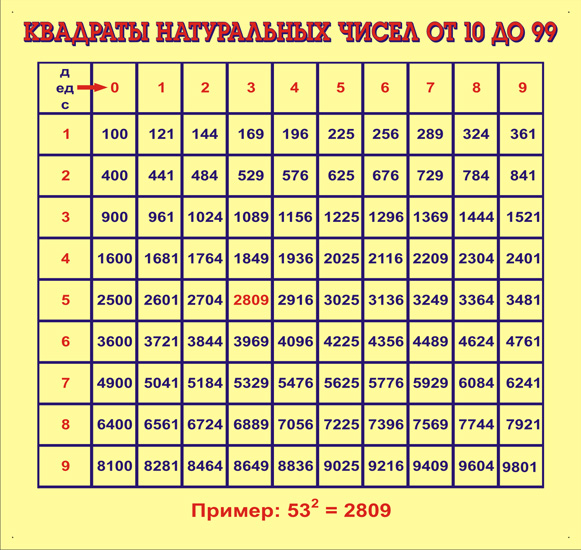

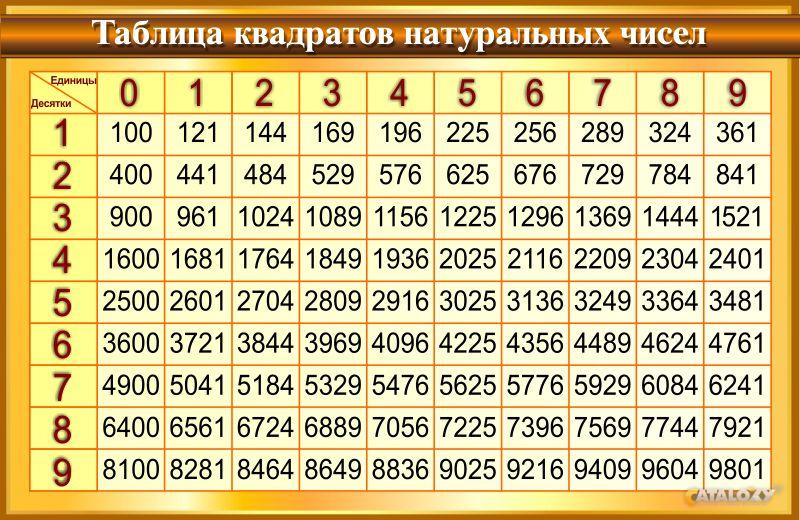 0041
0041 b3c.
b3c. Таким образом, «3333\sqrt[3]{3}333» читается как «333, умноженный на кубический корень из 333».
Таким образом, «3333\sqrt[3]{3}333» читается как «333, умноженный на кубический корень из 333».