Приложение 1 — Примеры решения задач и комментарии
Пример 1. Даны два вектора {3, 1, –5} и {6, –3, 0}. Найти сумму и разность этих векторов
= + и = –.
Решение. Найдем координаты векторов и .
Xc = 3+6= 9; Yc = 1 – 3= – 2; Zc = – 5+0 = – 5;
Xd = 3 – 6 = – 3; Yd = 1 – (–3) = 4; Zd = –5 – 0 = –5.
Ответ: {9, –2, –5}, { –3, 4, –5}.
Пример 2. Даны два вектора {3, 1, –5} и {6, –3, 0}. Найти линейную комбинацию этих векторов = 2 +3 .
Решение. Найдем координаты вектора .
Xc = ; Yc =; Zc = ;
Ответ. {24, –7, –10}.
Пример 3. Даны три вектора {1, 1, –2}, {2, –1, 0} и . Найти тот вектор, модуль которого будет наибольшим.
Решение. найдем модули трех векторов: ;
; .
Ответ. Наибольший модуль у вектора .
Пример 4. Даны два вектора {1, 1, –2} и {2, –1, 0}.
Решение. Найдем координаты векторов и .
Xc = 2 ´ 1 – 2 = 0; Yc = 2 ´ 1 – (–1) = 3; Zc = 2 ´ (–2) – 0 = -4;
Xd = 1 + 2 = 3; Yd = 1 + (–1) = 0; Zd = –2 + 0 = –2.
Итак: {0, 3, –4}, {3, 0, –2}.
Вычислим модули этих векторов и их скалярное произведение:
Теперь можно вычислить косинус угла J между этими векторами:
.
Пример 5. При каком значении векторы – и a + ортогональны? (Координаты векторов и заданы в примере 4.)
Решение. Найдем координаты векторов – и a + :
;
.
Запишем условие ортогональности полученных векторов:
,
Или –a – 2 + 2a – 2 + 4a = 0.
После преобразования получим 5a – 4 = 0 ; откуда .
Пример 6. Вычислить определитель третьего порядка
.
Решение
Способ 1. Разложив определитель по первой строке, получим
Способ 2. Вычислим теперь тот же определитель, используя свойства определителя.
Вычислим теперь тот же определитель, используя свойства определителя.
К элементам второй строки прибавим соответствующие элементы первой, умноженные на
(–2), а к элементам 3-й строки прибавим элементы первой строки, первую строку оставим без изменения (определитель не изменится):
.
Здесь произведены следующие действия: (1) – ко 2-й строке прибавили 3-ю; (2) – общий множитель второй строки вынесли за знак определителя; (3) – к 3-й строке прибавили 2-ю, умноженную на (–5). В результате получили определитель, под главной диагональю которого стоят нули (определитель верхней треугольной матрицы). Такой определитель равен произведению элементов главной диагонали (можно разложить по первому столбцу). Итак, мы вновь получили тот же ответ D = –2.
Этот способ выгодно использовать при вычислении определителей порядка
Пример 7. Решить систему уравнений методом Крамера
.
Решение. Выпишем определитель системы и вектор-столбец правых частей:
.
Вычислим теперь определители D, D1, D2, D3.
.
Поясним проделанные вычисления. Из второй строки определителя мы вычли первую строку, умноженную на 3. В результате получили вторую строку нового определителя. Затем из третьей строчки определителя вычли первую строку, умноженную на 2. В результате получили третью строку нового определителя. Полученный новый определитель разложен по первой строке.
, здесь определитель равен нулю, так как элементы первого столбца пропорциональны соответствующим элементам 3-го столбца.
, так как элементы второго столбца пропорциональны элементам третьего столбца.
.
Так как элементы третьего столбца являются четными числами, то мы вынесли число 2 за знак определителя. Далее из второй строки мы вычли элементы первой строки, умноженные на 3, а из элементов третьей строки вычли элементы первой строки, умноженные на 2. Величина определителя при этих преобразованиях не изменяется. В результате мы получили определитель, у которого в первом столбце стоят два нуля, и этот определитель можно вычислить путем разложения по первому столбцу.
Теперь, по правилу Крамера найдем решение системы:
Полезно сделать проверку, подставив решение в исходную систему. Проделав выкладки, легко убедиться, что решение найдено верно.
Пример 8. При каком значении С равен нулю определитель ?
Решение. Выпишем определитель . По условию задачи
. Отсюда следует, что .
Пример 9. Во сколько раз изменится определитель матрицы третьего порядка, если все его элементы увеличить в два раза?
Решение. Если все элементы матрицы увеличить в два раза, то из каждой строки матрицы можно за знак определителя вынести число 2. Так как таких строк три, то определитель исходной матрицы увеличится в раз.
Пример 10. Вычислить определитель матрицы А = .
Решение. Так как все элементы определителя, кроме элементов главной диагонали, равны нулю, то определитель равен произведению членов, стоящих на главной диагонали. Это следует как из общего правила вычисления определителя, так и из разложения определителя по первой строке (или по первому столбцу).
Ответ: .
Пример 11. Вычислить определитель матрицы А = .
Решение. Так как все элементы определителя, расположенные выше элементов побочной диагонали, равны нулю, то определитель равен произведению членов, стоящих на побочной диагонали, причем этот член будет входить в определитель со знаком минус. Это следует как из общего правила вычисления определителя, так и из разложения определителя по первой строке (или по первому столбцу).
Ответ: .
Пример 12. Вычислить определитель .
Решение. Так как все элементы определителя, расположенные в первой строке, пропорциональны элементам третьей строки, то определитель равен нулю.
Пример 13. Вычислить определитель .
Решение. Поскольку во второй строке определителя имеется только один ненулевой член, имеет смысл разложить определитель по элементам второй строки. В результате получим
.
На последнем шаге мы воспользовались основным тригонометрическим тождеством.
Пример 14. Матрица А равна А = . Написать матрицу, составленную из алгебраических дополнений ( i=1,2; j = 1,2) исходной матрицы.
Решение. Напомним, что алгебраическим дополнением элемента называется число , где – минор элемента , а минором элемента матрицы А называется определитель Mij, полученный из матрицы А путем вычеркивания из матрицы i-ой строки и j-го столбца. В нашем случае для элемента алгебраическим дополнением будет , для элемента алгебраическое дополнение равно , для алгебраическое дополнение равно (знак минус написан потому, что для этого элемента сумма номера строки и столбца – нечетное число), для алгебраическое дополнение .
Ответ: матрица алгебраических дополнений для исходной матрицы имеет вид .
Пример 15. Для матрицы А = написать матрицу, составленную из ее алгебраических дополнений.
Решение. Выпишем алгебраические дополнения для каждого элемента матрицы. В данном случае алгебраическими дополнениями будут определители второго порядка.
; ; .
; ; .
; ; .
Знаки алгебраических дополнений определяются по правилу, описанному в предыдущем примере.
Ответ: матрица алгебраических дополнений имеет вид .
Пример 16. Вычислить определитель 4-го порядка .
Решение. При внимательном рассмотрении элементов определителя можно заметить, что каждый элементы третьей строки равен сумме соответствующих элементов первой и второй сроки. По разобранном в разделе 1.4 свойствам определителя это означает, что рассматриваемый определитель равен нулю.
Пример 17. Определить, при каких значения переменной верно следующее неравенство
<0 ?
Решение. Для решения задачи необходимо выразить определитель как функцию переменной и решить полученное неравенство. В данном случае удобно к первой строке определителя прибавить элементы третьей строки, после чего в первой строке останется только один ненулевой элемент.
Полученное неравенство справедливо при .
Ответ: .
| < Предыдущая |
|---|
Типовые примеры Действия над матрицами
Занятие № 1. Матрицы. Операции над матрицами.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
1. Что называется матрицей.
2. Какие две матрицы называются равными.
3. Какая матрица называется квадратной, диагональной, единичной.
4. Как выполнить операции сложения матриц и умножение матрицы на число.
5. Для каких матриц вводится операция умножения и правило ее выполнения.
6. Какие преобразования над матрицами являются элементарными.
7. Какую матрицу называют канонической.
Задача № 1. Даны матрицы
Найти матрицу D=(1)
Решение.По определению произведения матрица на число получаем:
Далее вычисляем выражение (1):
D=
Задача
№ 2. Найти произведение АВ двух
квадратных матриц:
Найти произведение АВ двух
квадратных матриц:
Решение.Обе матрицы являются квадратными матрицами 2-го порядка. Такие матрицы можно умножить, используя формулу
(2)
Формула (2) имеет следующий смысл: чтобы получить элемент матрицы С = АВ, стоящий на пересечении строки истолбца нужно взять сумму произведений элементов-ой строки матрицы А на соответствующие элементы-го столбца матрицы В.
В соответствии с формулой (2) найдем:
Следовательно, произведение С = АВ будет иметь вид:
Задача № 3.Найти произведение АВ и ВА матриц:
Решение.Согласно формуле (2),элементы матриц АВ и ВА будут иметь вид:
Вывод:Сравнивая матрицы АВ и ВА и пользуясь определением равенства матриц, делаем вывод, что АВВА, т. е. умножение матриц не подчиняется переместительному закону.
Задача
№ 4(устно). Даны матрицыСуществуют ли произведения (в скобках
даны правильные ответы): АВ (да), ВА (нет),
АС (да), СА (нет), АВС (нет), АСВ (да), СВА
(нет).
Задача № 5.Найти произведение АВ и ВА двух матриц вида:
Решение.Приведенные матрицы видаследовательно, существуют произведения АВ и ВА данных матриц, которые будут иметь вид:
Задача № 6. Найти произведение АВ матриц:
Ответ:
Задачи для самостоятельного решения:
Даны матрицы
Найти матрицу D=2А-4В+3С.
2. Найти произведения АВ и ВА квадратных матриц:
Найти произведение матриц:
Найти произведение матриц:
Найти произведение матриц:
Найти произведение матриц:
7. Найти произведение матриц:
8. Найти матрицу: В=6А2+8А, если.
Найти матрицу: В=6А2+8А, если.
9. Дана матрица .Найти все матрицы В, перестановочные с матрицей А.
10. Доказать, что если А — диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с А, тоже диагональная.
Занятие 2. Определители квадратных матриц и их вычисление. Обратная матрица.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Что называется определителем n-го порядка? Правила вычисления приn=1,2,3.
Свойства определителей.
Какая матрица называется невырожденной?
Какая матрица называется единичной?
Какая матрица называется обратной по отношению к данной?
Что является необходимым и достаточным условием для существования обратной матрицы?
Сформулировать правило нахождения обратной матрицы.

Ранг матрицы. Правила нахождения.
Задача № 1. Вычислить определитель:
а ) по правилу треугольника;
б) с помощью разложения по первой строке;
в) преобразованием, используя свойства определителей.
а)
б)
в)
Задача № 2. Найти минор и алгебраическое дополнение элементаa23 определителяи вычислить его разложением по элементам строки или столбца.
Решение.
М23; А23
Задача № 3.Вычислить определитель с помощью разложения по 2 строке:
Ответ:
Задача № 4.Решить уравнение
Решение.
Задача № 5.Вычислить определитель 4-го порядка разложением по элементам строки или столбца:
Ответ: 63.
Решение матриц. Объясняем, как решать матрицы. Решение матричных уравнений: теория и примеры
Занятие № 1. Матрицы. Операции над
матрицами.
Матрицы. Операции над
матрицами.
1. Что называется матрицей.
2. Какие две матрицы называются равными.
3. Какая матрица называется квадратной, диагональной, единичной.
4. Как выполнить операции сложения матриц и умножение матрицы на число.
5. Для каких матриц вводится операция умножения и правило ее выполнения.
6. Какие преобразования над матрицами являются элементарными.
7. Какую матрицу называют канонической.
Задача № 1. Даны матрицы
Найти матрицу D=
(1)
Решение. По определению произведения матрица на число получаем:
D=
Задача № 2 . Найти произведение АВ двух квадратных матриц:
Решение. Обе матрицы являются квадратными матрицами 2-го порядка. Такие матрицы можно умножить, используя формулу
Формула (2) имеет следующий смысл: чтобы
получить элемент матрицы С = АВ, стоящий
на пересечении
строки истолбца нужно взять сумму произведений
элементов-ой
строки матрицы А на соответствующие
элементы-го
столбца матрицы В.
В соответствии с формулой (2) найдем:
Следовательно, произведение С = АВ будет иметь вид:
Задача № 3. Найти произведение АВ и ВА матриц:
Решение. Согласно формуле (2),элементы матриц АВ и ВА будут иметь вид:
Вывод: Сравнивая матрицы АВ и ВА и пользуясь определением равенства матриц, делаем вывод, что АВВА, т. е. умножение матриц не подчиняется переместительному закону.
Задача
№ 4 (устно). Даны матрицы
Существуют ли произведения (в скобках
даны правильные ответы): АВ (да), ВА (нет),
АС (да), СА (нет), АВС (нет), АСВ (да), СВА
(нет).
Задача № 5. Найти произведение АВ и ВА двух матриц вида:
Решение. Приведенные матрицы вида
следовательно, существуют произведения
АВ и ВА данных матриц, которые будут
иметь вид:
Задача № 6 . Найти произведение АВ матриц:
Ответ:
Задачи для самостоятельного решения:
Даны матрицы
Найти матрицу D=2А-4В+3С.
2. Найти произведения АВ и ВА квадратных матриц:
Найти произведение матриц:
Найти произведение матриц:
7. Найти произведение матриц:
8.Найти матрицу: В=6А 2 +8А, если
.
9. Дана матрица
.Найти
все матрицы В, перестановочные с матрицей
А.
10. Доказать, что если А — диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с А, тоже диагональная.
Занятие 2. Определители квадратных матриц и их вычисление. Обратная матрица.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Что называется определителем n-го порядка? Правила вычисления приn=1,2,3.
Свойства определителей.
Какая матрица называется невырожденной?
Какая матрица называется единичной?
Какая матрица называется обратной по отношению к данной?
Что является необходимым и достаточным условием для существования обратной матрицы?
Сформулировать правило нахождения
обратной матрицы.
Ранг матрицы. Правила нахождения.
Типовые примеры Вычисление определителей
Задача
№ 1. Вычислить определитель
:
а) по правилу треугольника;
б) с помощью разложения по первой строке;
в) преобразованием, используя свойства определителей.
в)
Задача
№ 2 . Найти минор и алгебраическое
дополнение элементаa 23
определителя
и вычислить его разложением по элементам
строки или столбца.
Решение.
М 23
;
А 23
Задача № 3. Вычислить определитель с помощью разложения по 2 строке:
Ответ:
Задача
№ 4. Решить уравнение
Задача № 5. Вычислить определитель 4-го порядка разложением по элементам строки или столбца:
Группа компаний «Оргпром» 2 МИССИЯ Мы содействуем развитию общества, помогая бизнесу и людям увидеть и реализовать свой потенциал через проведение корпоративных программ развития производственных систем Ведущий российский провайдер, оказывающий полный спектр услуг по развитию производственных систем на основе концепции «бережливое производство» (Lean Production, Lean Thinking, Toyota Production System, кайдзен)
Что такое политика Брокгауз и Ефрон: Политика (греч. politikó государственные или общественные дела, от pólis государство) — одна из социальных наук, а именно учение о способах достижения государственных целей. Ушаков: – Общий характер, отличительные черты деятельности или поведения (государства, общественной группы, отдельного лица в той или иной области). Держаться разумной политики. Недальновидная п. Твердая п. Нерешительная п. – перен. Хитрость и уловки в отношениях с людьми, хитрый, уклончивый образ действий (разг.). Я твою политику насквозь вижу. Отец протопоп Савелий начал своею политикой еще более уничтожать меня. Лесков. Словарь по экономике и финансам: Политика предприятия — формулировка целей предприятия и выбор средств для их реализации
politikó государственные или общественные дела, от pólis государство) — одна из социальных наук, а именно учение о способах достижения государственных целей. Ушаков: – Общий характер, отличительные черты деятельности или поведения (государства, общественной группы, отдельного лица в той или иной области). Держаться разумной политики. Недальновидная п. Твердая п. Нерешительная п. – перен. Хитрость и уловки в отношениях с людьми, хитрый, уклончивый образ действий (разг.). Я твою политику насквозь вижу. Отец протопоп Савелий начал своею политикой еще более уничтожать меня. Лесков. Словарь по экономике и финансам: Политика предприятия — формулировка целей предприятия и выбор средств для их реализации
«Хосин Канри» — «Развертывание политики», «Управление на основе политики» Типичные проблемы Финансы – Прошло уже полтора месяца! Что откуда? Почему? Клиенты, рынки – Труднодоступная информация Внутренние процессы – Недостаточно знаний по выбору и мониторингу Персонал, инновации – Недостаточно знаний по выбору и мониторингу
Что такое Хосин Канри? Стратегический инструмент исполнения и контроля хода выполнения при управлении изменениями в критичных бизнес процессах. Система развертывания стратегического плана по всей организации. Координирует усилия сотрудников и их деятельность со стратегическими планами.
Система развертывания стратегического плана по всей организации. Координирует усилия сотрудников и их деятельность со стратегическими планами.
Зачем развертывать политику? «Кто не знает, куда направляется, очень удивится, попав не туда» Марк Твен «Вы должны на что-то опираться, иначе вы в любом случае упадете» Следствие законов Ньютона и Мэрфи Компании, работники которых понимают их миссию и цели, имеют на 29% большую производительность, в сравнении с другими фирмами Watson Wyatt Work Study
Развертывание политики позволяет Сфокусироваться на разделяемых целях и приоритетах Согласовать цели и приоритеты среди всех лидеров Вовлечь каждого лидера в достижение целей и следование приоритетам Согласовать роль и ответственность каждого члена команды в достижении разделяемых целей Сделать программу РПС — востребованной и увязанной на всех уровнях с актуальными бизнес-целями («вытягивание» вместо «выталкивания»)
Происхождение «Хосин Канри» Словосочетание «Хосин Канри» состоит из четырех иероглифов: – Хо — направление,курс; – Син — игла, стрелка; «Хосин» — компас, направление стрелки компаса – Кан — контроль, управление; – Ри — логика, причина; «Канри» — менеджмент, развертывание, логика управления «Хосин Канри» — «Развертывание политики», «Управление на основе политики»
Развертывание политики Россия, XVII век Необходимо и младшим начальникам постоянно иметь его в мыслях, чтобы вести войска согласно с ним. Мало того, даже батальонные, эскадронные, ротные командиры должны знать его по той же причине, даже унтер-офицеры и рядовые. Каждый воин должен знать свой маневр. Александр Васильевич Суворов Не довольно, чтобы одни главные начальники извещены были о плане действия.
Мало того, даже батальонные, эскадронные, ротные командиры должны знать его по той же причине, даже унтер-офицеры и рядовые. Каждый воин должен знать свой маневр. Александр Васильевич Суворов Не довольно, чтобы одни главные начальники извещены были о плане действия.
Развертывание политики от А.В. Сувоврова План операционный — в главную армию, в корпус, в колонну! Ясное распределение полков, везде расчет времени Ученье — свет, неученье – тьма За одного битого двух небитых дают Люби солдата, и он будет любить тебя – в этом вся правда Я командую вправо, ты видишь надо влево меня не слушай ты ближний!
Миссия = Предназначение Набор фундаментальных, глубинных причин существования компании\подразделения. Суть, душа. Отражает важность, которую люди придают работе – она определяет их, именно, идеалистические представления. Главная роль миссии – направлять и вдохновлять людей на долгие годы, и даже столетия.
Система ценностей Какими принципами и приоритетами при реализации миссии должны руководствоваться – Менеджмент – Сотрудники Кто заинтересованные стороны (в реализации миссии) – Что они ожидают? – Каков их вклад? ОСНОВА ДЕЛЕГИРОВАНИЯ – Наравне с обучением
Факторы успешности реализации миссии в аспекте баланса интересов 1. Финансы 2. Клиенты 3. Процессы 4. Развитие Качество Точно вовремя Сокращение потерь Качество Точно вовремя Сокращение потерь Безопасность Вовлеченность Развитие персонала Финансы / Рынки Акценты управления Вклад в экосферу
Финансы 2. Клиенты 3. Процессы 4. Развитие Качество Точно вовремя Сокращение потерь Качество Точно вовремя Сокращение потерь Безопасность Вовлеченность Развитие персонала Финансы / Рынки Акценты управления Вклад в экосферу
Ежедневный контроль прогресса в достижении результатов При реализации Хосин Ежедневный вал событий и ежеквартальный прессинг получения финансовых результатов не превалируют над стратегическими планами, Наоборот, эта оперативная работа определяется и направляется самими планами (по достижению стратегических целей). Йодзи Акао ДНМКГ ДНМКГ
Управление тремя потоками создания ценности Поток создания ценности Выход потока Потери в потоке Инструменты управления 1) Поток создания потребительской ценности Качество Доставка Себестоимость Довольный заказчик /потом довольные владельцы, сотрудники, поставщики, общество Работа без добавления потр.цен-ти (мура, 7 типов муда, мури) Инструменты Лин (VSM, Just-In-Time, Jidoka, 5S, TPM, VC, SOP, RCA), SCM, … 2) Поток развития талантов Безопасность Вовлеченность Рост Довольный сотрудник/ потом довольный заказчик и общество Работа с угрозой для здоровья или без обучения OHSAS, лидерство, хосин канри, A3, PDCA, SDCA, 5W2H, … 3) Поток создания эко-социума Дивиденды владельцам Сообщество Экологический статус-кво Гармоничный эко-социум/ Затем довольные владельцы, общество и будущие поколения Работа без определения интересов ЗС и их балансировки Отчетность GRI, Natural Step, регулярные совещания с ЗС, … + все вышеперечисленное
Матрица развертывания целей заместителя Гендиректора Оргпром Зам. Генерального директора Миссия: Поток ДеньНеделя МесяцКвартал Год QКачество Выполнение ГУК в срок Коэффициент качества DСроки Доля подразделений в графике (выполняющих суточные задания) Выполнение производственного плана (товар) Выполнение производственного плана (товар) Выполнения плана квартального Выполнение плана годового CСокращение потерь Доля подразделений без дефектов и простоев Выполнение графика ОТМ Количество исполненныых проектов эффективности (расшитых «узких» мест) Количество комплектов на сотрудника Экономический эффект от реализации предложений, проектов и программ повышения эффективности SОхрана труда и безопасность Количество дней без несчастных случаев Доля подразделений без нарушений ОТ и дисциплины Доля подразделений с улучшением оценки по условиям труда, 5С и безопасности Средняя оценка подразделений по условиям труда, 5С и безопасности Доля аттестованных рабочих мест IВовлеченность персонала Количество поданных предложений Реализация предложений (Кол-во реализованных \ Кол- во поданных за последние 3 месяца, %) Доля подразделений с растущим уровнем подачи И реализации Среднее количество реализованных предложений на сотрудника GРазвитие компетенций Выполнение графика обучения (с учетом количества)Средняя зарплата MИнтересы бизнеса Выполнение текущих графиков реконструкции и перевооружения Выполнение текущих графиков компьютеризации, автоматизации, механизации, роботизации AРазвитие партнеров EСоциальное развитие и экология Выполнение плана социальной работы Матрица Периодической Системы Управления Устойчивым Развитием Перспекктива Поток создания потребительсккой ценности (развитие процессов) Поток создания талантливых сотрудников (развитие людей) Поток устойчивого развития бизнеса
Генерального директора Миссия: Поток ДеньНеделя МесяцКвартал Год QКачество Выполнение ГУК в срок Коэффициент качества DСроки Доля подразделений в графике (выполняющих суточные задания) Выполнение производственного плана (товар) Выполнение производственного плана (товар) Выполнения плана квартального Выполнение плана годового CСокращение потерь Доля подразделений без дефектов и простоев Выполнение графика ОТМ Количество исполненныых проектов эффективности (расшитых «узких» мест) Количество комплектов на сотрудника Экономический эффект от реализации предложений, проектов и программ повышения эффективности SОхрана труда и безопасность Количество дней без несчастных случаев Доля подразделений без нарушений ОТ и дисциплины Доля подразделений с улучшением оценки по условиям труда, 5С и безопасности Средняя оценка подразделений по условиям труда, 5С и безопасности Доля аттестованных рабочих мест IВовлеченность персонала Количество поданных предложений Реализация предложений (Кол-во реализованных \ Кол- во поданных за последние 3 месяца, %) Доля подразделений с растущим уровнем подачи И реализации Среднее количество реализованных предложений на сотрудника GРазвитие компетенций Выполнение графика обучения (с учетом количества)Средняя зарплата MИнтересы бизнеса Выполнение текущих графиков реконструкции и перевооружения Выполнение текущих графиков компьютеризации, автоматизации, механизации, роботизации AРазвитие партнеров EСоциальное развитие и экология Выполнение плана социальной работы Матрица Периодической Системы Управления Устойчивым Развитием Перспекктива Поток создания потребительсккой ценности (развитие процессов) Поток создания талантливых сотрудников (развитие людей) Поток устойчивого развития бизнеса
Матрица развертывания целей начальника цеха Оргпром Начальник цеха 43 Миссия: Поток ДеньНеделя МесяцКвартал Год QКачество Количество дней без дефектов Количество принятых в работу новыхили усовершенствованных техпроцессов Коэффициент качества DСроки Доля выполняющих задание участков комплекты Выполнение плана номенклатурного Выполнение производственного плана Выполнения плана квартального Выполнение плана годового CСокращение потерь Количество реализуемых и процент выполнения Доля расшитых «узких» мест Экономический эффект Количество комплектов на сотрудника SОхрана труда и безопасность Количество дней без несчастных случаев Выполнение графика обходов Доля участков улучшивших свои показатели по безопастности и 5S Средний балл аудита по безопастности и 5S Доля рабочих мест без вредных условий и опасностей IВовлеченность персонала Количество выявленных возможностей Количество поданных предложений Реализация предложений (Кол- во реализованных \ Кол-во поданных за последние 3 месяца, %) Доля лидеров (подающих И реализующих предложения) Среднее количество реализованных предложений на сотрудника GРазвитие компетенций Выполнение графика обучения Количество наставников Доля рабочих мест, укомплектованных сотрудниками с соответствующими компетенциями Средняя зарплата MИнтересы бизнеса Выполнение графика техперевооружения Доля механизированного труда Мощность цеха в комплектах в год AРазвитие партнеров EСоциальное развитие и экология Выполнение плана социальной работы Поток устойчивого развития бизнеса Перспекктива Матрица Периодической Системы Управления Устойчивым Развитием Мы своевременно изготавливаем качественные фитинги для сборочных цехов Поток создания потребительсккой ценности (развитие процессов) Поток создания талантливых сотрудников (развитие людей)
Матрица развертывания целей начальника участка Оргпром Начальник участка цеха 43 Миссия: Поток ДеньНеделя МесяцКвартал Год QКачество Количество дней без дефектов Доля стабилизированных процессов обработки деталей Выход годного с первого раза DСроки Выполнение сменно- суточных заданий (%) Выполнение плана по номенклатуре Выполнение производственного плана CСокращение потерь Коэффициент полной эффективности оборудования (ОЕЕ) Выполнение нормативного времени на переналадку оборудования (общее время переналадки станков/количество переналадок) SОхрана труда и безопасность Количество дней без травм Количество замечаний по ТБ (2 ступень) Оценка состояния рабочий зоны и рабочих мест (5С) IВовлеченность персонала Количество выявленных возможностей Количество поданных предложений Реализация предложений (Кол- во реализованных \ Кол-во поданных за последние 3 месяца, %) GРазвитие компетенций Доля операторов освоивших быструю переналадку Количество переходов в развитии компетенций (матрица компетенций) MИнтересы бизнеса AРазвитие партнеров EСоциальное развитие и экологияколичество невыходов по причине заболеваний Доля рабочих мест, соответствующих требованиям экологии и безопасности Поток устойчивого развития бизнеса Матрица Периодической Системы Управления Устойчивым Развитием Мы своевременно изготавливаем качественные фитинги для сборочных цехов Перспекктива Поток создания потребительсккой ценности (развитие процессов) Поток создания талантливых сотрудников (развитие людей)
Second Level Hoshin Kanri Primary Responsibility Secondary Responsibility RESOURCES ВТОРОЙ УРОВЕНЬ Danaher Business System Office — Hoshin Kanri 1998 Primary Responsibility Secondary Responsibility Resources ВЫСШИЙ УРОВЕНЬ – Хосин канри и показатели успешности (матрица Оргпрома) для достижения целей предприятия Цели, стратегии развития развернуты и доведены до подразделений Определены ключевые исполнители и индикаторы достижения целей Цели Заготовите льное Мех обработка Агрегатная сборка Сборка Испытания Х-матрицы Доска производственного анализа участка Доска показателей цеха Показатели цехов и участков раскрывают содержание деятельности и степень достижения развернутых целей Рекомендуется использовать в системе вознаграждения
Последовательность Хосин 1. Сформулируйте или уточните философию компании – Предназначение (миссию) Ради чего существует наша компания? – Систему Ценностей Что является и будет являться нашими приоритетами? – Принципы управления На основе каких принципов мы будем обеспечивать эти приоритеты? – Видение будущего компании Какой компанией мы хотим стать? 2. Доведите до персонала, партнеров, общества 3. Неустанно следуйте, согласуйте и сверяйте
Сформулируйте или уточните философию компании – Предназначение (миссию) Ради чего существует наша компания? – Систему Ценностей Что является и будет являться нашими приоритетами? – Принципы управления На основе каких принципов мы будем обеспечивать эти приоритеты? – Видение будущего компании Какой компанией мы хотим стать? 2. Доведите до персонала, партнеров, общества 3. Неустанно следуйте, согласуйте и сверяйте
Периодическая система управления устойчивым развитием бизнеса Устойчивое развитие бизнес- системы Формули рование и развертывание основ бизнеса Лидерская визуализа ция Гармониза ция и балансиро вка потоков Лидерская стандарти зация Непрерыв- ное обучение действием и решение проблем Формулиров ание и развертывание прорывного видения 1. Периодическое определение состава заинтересованных сторон (ЗС), определение и согласование их ценностей = интересов ЗС (целевых состояний) 2. Периодическое определение и лидерская визуализация потоков создания этих ценностей, потерь в них 3. Периодическая балансировка и гармонизация потоков создания ценностей через сокращение потерь 4. Периодический диалог ЗС и лидерская стандартизация для «вытягивания» соответствующих ценностей 5. Периодическая последовательность в непрерывном совершенствовании и развертывании прорывного видения
Периодическая балансировка и гармонизация потоков создания ценностей через сокращение потерь 4. Периодический диалог ЗС и лидерская стандартизация для «вытягивания» соответствующих ценностей 5. Периодическая последовательность в непрерывном совершенствовании и развертывании прорывного видения
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m ×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В .
В общем виде матрицу размером m ×n записывают так
.
Числа,
составляющие матрицу, называются элементами
матрицы . Элементы матрицы удобно снабжать двумя индексами a ij : первый указывает номер
строки, а второй – номер столбца. Например, a 23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице число строк равно числу столбцов, то матрица называется квадратной , причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной . В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом .
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,
.
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная
матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю,
называется треугольной матрицей.
.
Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц . Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a ij = b ij . Так если и , то A=B , если a 11 = b 11 , a 12 = b 12 , a 21 = b 21 и a 22 = b 22 .
Транспонирование . Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно
сопоставить такую матрицу B из n строк и m столбцов, у которой каждая
строка является столбцом матрицы A с
тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак,
если , то .
Итак,
если , то .
Эту матрицу B называют транспонированной матрицей A , а переход от A к B транспонированием .
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A , обычно обозначают A T .
Связь между матрицей A и её транспонированной можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры . Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B , стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C , которая определяется по правилу, например,
Примеры. Найти сумму матриц:
Легко проверить,
что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B )+C =A +(B+C ).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .
Для любых чисел a и b и матриц A и B выполняются равенства:
Примеры.
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB , элементы которой составляются следующим образом:
Таким образом,
например, чтобы получить у произведения (т.е. в матрице C ) элемент, стоящий в 1-ой
строке и 3-м столбце c 13 , нужно в 1-ой матрице взять
1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на
соответствующие элементы столбца и полученные произведения сложить. И другие
элементы матрицы-произведения получаются с помощью аналогичного произведения
строк первой матрицы на столбцы второй матрицы.
И другие
элементы матрицы-произведения получаются с помощью аналогичного произведения
строк первой матрицы на столбцы второй матрицы.
В общем случае, если мы умножаем матрицу A = (a ij) размера m ×n на матрицу B = (b ij) размера n ×p , то получим матрицу C размера m ×p , элементы которой вычисляются следующим образом: элемент c ij получается в результате произведения элементов i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным
случаем является умножение матрицы–строки на матрицу–столбец, причём ширина
первой должна быть равна высоте второй, в результате получим матрицу первого
порядка (т. е. один элемент). Действительно,
е. один элемент). Действительно,
.
Примеры.
Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A . Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC .
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A , причём AE=EA=A .
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например , если , то
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов .
Определителем второго порядка , соответствующим данной матрице, называется число, получаемое следующим образом: a 11 a 22 – a 12 a 21 .
Определитель обозначается символом .
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка , соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
.
Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a 11 , a 12 , a 13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
Аналогично можно ввести понятия определителей
четвёртого, пятого и т. д. порядков, понижая их порядок разложением по элементам
1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
д. порядков, понижая их порядок разложением по элементам
1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
Пусть имеется квадратная матрица n-го порядка
Матрица А -1 называется обратной матрицей по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…А n) называется невырожденной , если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
- Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
- Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
- Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
- Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А -1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2
Решить уравнение АХ = В, если
Решение : Так как обратная матрица равняется (см. пример 1)
пример 1)
Матричный метод в экономическом анализе
Наряду с другими в находят применение также матричные методы . Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.
В процессе применения матричных методов анализа можно выделить несколько этапов.
На первом этапе осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2,….,n) , а по вертикальным графам — номера показателей (j = 1,2,….,m) .
На втором этапе по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.
После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .
На третьем этапе все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k . Величина последнего определяется экспертным путем.
На последнем, четвертом этапе найденные величины рейтинговых оценок R j группируются в порядке их увеличения или уменьшения.
Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.
Ответ на этот вопрос компания «Тойота», мировой лидер не только в автомобилестроении, но и в создании эффективных бизнес-систем, нашла для себя в инструменте Хосин Канри еще в 1950-1960-х годах. Это словосочетание можно перевести с японского языка как компас, а в более широком смысле — управление политикой. Практически все крупные мировые компании уже давно переняли этот инструмент и успешно его используют, в том числе в компании «Альстом».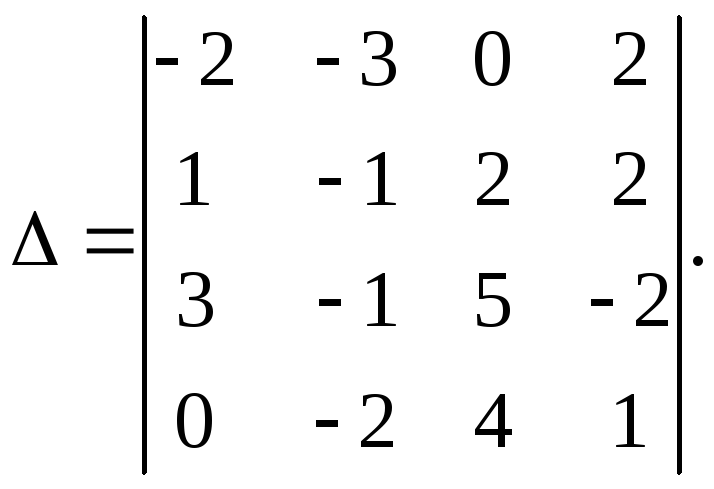 В качестве примера можно привести ОАО «РЖД», которое еще в прошлом году применило методику Хосин Канри на Октябрьской железной дороге.
В качестве примера можно привести ОАО «РЖД», которое еще в прошлом году применило методику Хосин Канри на Октябрьской железной дороге.
Хосин Канри — это структурированный, регулярно повторяющийся процесс, результатом которого является документ, называемый Х-матрица, формулирующий основные направления развития компании. Развертывание стратегии происходит через встроенные друг в друга планы мероприятий (PDCA).
Схематически процесс Хосин Канри применительно для отдельного завода ТМХ может быть представлен на рис. 1.
Х-матрица каждого уровня состоит из четырех основных блоков: глобальные цели, стратегия, тактики и количественные цели. При этом стратегии и глобальные цели нижестоящих уровней неразрывно связаны с тактиками и количественными целями вышестоящих уровней.
Поэтому изменение, произведенное на одном из уровней, быстро транслируется и вызывает перемены на всех остальных. Принцип заполнения Х-матрицы схематически представлен на рис. 3 .
Внедрение Х-матриц на заводах холдинга
В настоящее время в холдинге происходит формирование технической стратегии развития предприятий. В эту работу также вовлечено и высшее руководство «Альстом Транспорт». Для всех заводов актуальными являются следующие стратегии: осуществление прорыва в области качества выпускаемой продукции, развитие персонала, внедрение проектного менеджмента и управление затратами, завершение реструктуризации предприятий.
В эту работу также вовлечено и высшее руководство «Альстом Транспорт». Для всех заводов актуальными являются следующие стратегии: осуществление прорыва в области качества выпускаемой продукции, развитие персонала, внедрение проектного менеджмента и управление затратами, завершение реструктуризации предприятий.
Для обеспечения эффективного внедрения стратегии развития холдинга на предприятиях в феврале — апреле 2014 года группой по производственной системе были проведены двухдневные семинары по практическому обучению руководства заводов методологии работы с Х-матрицами. К сегодняшнему моменту обучен высший менеджмент семи предприятий: БМЗ, НЭВЗ, ТВЗ, КЗ, ЦСМ, ДМЗ, МВМ.
В рамках подготовки к семинару с каждым генеральным директором прорабатывалась Х-матрица уровня завода (уровень L1), которая основывалась в свою очередь на входящих данных из матрицы уровня холдинга. Обозначенные выше стратегии были дополнены тактическими инициативами завода. Так, для ЗАО «УК «БМЗ» были определены 19 тактик уровня завода, среди которых создание двух эталонных линий сборки основных продуктов, создание новой платформы (ТЭМ23), совершенствование системы производственного планирования, пересмотр системы мотивации персонала. Сам проект трансформации завода, реализация которого была начата ранее, получил громкий лозунг «БМЗ — первый в любом составе!».
Сам проект трансформации завода, реализация которого была начата ранее, получил громкий лозунг «БМЗ — первый в любом составе!».
В ходе семинара были построены Х-матрицы основных дирекций предприятия: дирекции по производству, технические дирекции и дирекции по материально-техническому обеспечению и логистике (уровень L2). Затем руководители представили стратегии развития их подразделений начальникам отделов (цехов), которые в свою очередь составили Х-матрицы уровня L3 с тактическими задачами отделов. Далее начальники отделов (цехов) «каскадировали» задачи начальникам бюро, которые составили очень конкретные планы мероприятий для достижения общей стратегии дирекции. Если в Х-матрицах дирекций и отделов горизонт планирования равен одному году, то в случае плана мероприятий для руководителей бюро — три месяца. Завершающим этапом семинара стало формирование стендов с индикаторами для управления деятельностью подразделения на каждом уровне.
Таким образом, была выстроена система управления трансформацией завода, включающая взаимосвязанные планы тактических и операционных задач, а также индикаторов, позволяющих оценить как процессы, так и степень реализации задач.
В настоящий момент заводы дорабатывают Х-матрицы, добиваясь полной взаимосвязанности между матрицами разных уровней. Особое внимание уделено работе с индикаторами процессов, большинство из которых можно найти в будущей единой панели индикаторов завода.
Связь Х-матриц и панели индикаторов
Для принятия обоснованных решений руководителям различных уровней необходимо полагаться на достоверную и своевременную бизнес-информацию. Панели индикаторов хранят данные о результативности и эффективности протекающих в организации бизнес-процессов. Эти данные используются для мониторинга, анализа, управления.
В 2013 году на НЭВЗ была проведена работа по внедрению ключевых показателей эффективности, и в качестве пилотного участка был выбран цех, где происходит сборка электропоездов ЭП20 «Олимп». Опыт оказался успешным, и руководство завода получило перекрестную систему КПЭ, благодаря которой можно быстро и эффективно проанализировать данные.
С начала 2014 года в холдинге ведется активная работа по формированию стандартной панели индикаторов для заводов, которая включит в себя все наиболее важные КПЭ предприятия и будет ежемесячно обновляться. Планируется официально включить в бизнес-план 2015 года помимо показателей результативности еще и показатели эффективности деятельности заводов.
Планируется официально включить в бизнес-план 2015 года помимо показателей результативности еще и показатели эффективности деятельности заводов.
Среди наиболее важных КПЭ , которые будут включены в панель, можно выделить следующие: эффективность производственных рабочих, отношение РСС и вспомогательных рабочих к основным рабочим, оборачиваемость сырья и материалов, оборачиваемость незавершенного производства, выработка нормо-часов в год с 1 м2 производственных площадей .
В 2014 году работа по построению Х-матриц была проведена под руководством группы по производственной системе, в следующем году такая работа должна стать обычной задачей по планированию деятельности предприятия на год.
Следующие шаги по развертыванию стратегии на заводах
Большинство российских предприятий, и заводы Трансмашхолдинга не исключение, имеют очень сложную иерархическую структуру с множеством уровней. Это значит, что каскадирование задач — долгий процесс, при котором важно обеспечить полную открытость и прозрачность направлений развития компании. Поэтому ключевым этапом в развертывании стратегии становится информирование всех сотрудников о предстоящих переменах. Информированность, понимание и вовлеченность — вот цепочка действий коллектива каждого предприятия. И здесь немаловажно участие корпоративных газет, которые должны регулярно транслировать ключевые решения руководства, работы по Х-матрицам, рассказывать о преобразованиях, происходящих на заводах.
Поэтому ключевым этапом в развертывании стратегии становится информирование всех сотрудников о предстоящих переменах. Информированность, понимание и вовлеченность — вот цепочка действий коллектива каждого предприятия. И здесь немаловажно участие корпоративных газет, которые должны регулярно транслировать ключевые решения руководства, работы по Х-матрицам, рассказывать о преобразованиях, происходящих на заводах.
Для успешной реализации стратегии нужна полная поддержка всех уровней, поэтому сейчас заводы работают над поиском запоминающегося названия проекта и его лозунга. Через заводские газеты, в ходе коллективных собраний, а главное — от непосредственных руководителей работники заводов должны не только узнать о планах предприятия, но и понять свою роль в этом процессе.
Александр Альбертович Василенко, генеральный директор ЗАО «УК «БМЗ»:
Для достижения указанных целей руководством предприятия определены тактические задачи, которые необходимо решить в 2014 году.Далее директора по направлениям на основании матрицы стратегии развития завода разработали матрицы по каждой службе и так до уровня отделов. Это позволило довести глобальные цели и тактические задачи ТМХ, определенные руководством, до конкретных исполнителей. Таким образом, все сотрудники стали понимать свою личную роль и вклад в стратегическое развитие предприятия. В настоящее время перед руководителями завода всех уровней стоит задача по ежемесячному анализу исполнения тактических задач и планов мероприятий для оперативного реагирования на возможные отклонения. Такой подход позволил систематизировать деятельность различных подразделений в рамках целей завода, установил целевые состояния процессов.
Дмитрий ДЬЯКОВ, заместитель начальника отдела производства ЗАО «УК «БМЗ»:
Можно предположить, что несколько веков назад Суворов уже занимался выстраиванием производственной системы… в армии. Ведь ему приписывают слова «Каждый солдат должен понимать свой маневр».Это как раз и есть принцип каскадирования. Когда командующий ставит цели, каждый солдат должен не только знать, но и понимать свой маневр. Применительно к нашему производству: оператор не просто пришел и сделал деталь, но и знает, почему сегодня такой уровень заказов, почему требуется оптимизация площадей, рационализация техпроцессов, внедрение системы 5С на рабочих местах и т. д. Это один из методов производственной системы, который позволяет создать команду, способную улавливать и видеть изменения обстановки, уметь их анализировать, вырабатывать на эти изменения комплекс действий и претворять их в жизнь.
Марк-Антуан Жювин, финансовый контролер Трансмашхолдинга, уже имевший опыт работы с данным инструментом, отмечает:
Использование в ТМХ Х-матриц именно сегодня отвечает на вызовы современной экономической среды, которая отличается высокой изменчивостью и непредсказуемостью. Вследствие этого нужно действовать коллективно, не нарушая равновесия всей системы.
Примеры решения матриц методом крамера. Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1. 8)
8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A — 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A — 1 , мы получим решение системы:
14) слева на A — 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).
18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
…………………………………………………………………. . . | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
…………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = — 3 + 2t
x 2 = — 1 — 3t
x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ — определитель матрицы системы ,
Δ i — определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2. 5)
5)
где – определитель основной матрицы , i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя
понятие алгебраического дополнения
можно сформулировать теорему
о разложении определителя n -го
порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.
 5. Основные свойства определителей
5. Основные свойства определителейРазлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство
1 . Определитель
не изменится, если в нем поменять местами
строки и столбцы, т. е. при транспонировании
матрицы :
е. при транспонировании
матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство
4 . Определитель
не изменится, если к элементам одной
строки (столбца), прибавить элементы
другой строки (столбца), умноженной на
какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$.
 Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса. - Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус.
 B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель.
 Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. - При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами
В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.
С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.
Содержание
- Понятие выражения
- Сложение и вычитание
- Умножение на число
- Операция перемножения
- Возведение в степень
- Расчёт определителя
- Обратная матрица
- Нахождение собственных векторов
- Метод Гаусса
- Способ Крамера
Понятие выражения
Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.
От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:
- a — действительная часть числа;
- b — мнимая часть;
- i — мнимая единица (квадратный корень из -1).
На приведенном примере показаны варианты.
Простейшие действия с матрицами могут быть разными. К их числу относятся:
- умножение;
- вычитание;
- умножение на число;
- перемножение между собой;
- транспортирование матриц.
Сложение и вычитание
Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.
В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.
Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.
Умножение на число
Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:
Операция перемножения
Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.
Возведение в степень
Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:
Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:
Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.
2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.
3 этап: в итоге получаем:
Расчёт определителя
В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.
Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:
Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:
Наглядный пример:
Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:
Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.
Обратная матрица
Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:
По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.
Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.
Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:
Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:
Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:
Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.
2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.
При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:
На выходе должна получиться таблица:
3 этап: находят алгебраические дополнения.
4 этап: определяют транспонированную матрицу.
Итогом будет:
Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.
В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.
Нахождение собственных векторов
Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:
Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:
Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.
Метод Гаусса
Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:
- действия, когда в системе переставляются местами два уравнения;
- произведение одного из уравнений в системе на действительное ненулевое число;
- сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.
Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.
Следует переписать эту систему в матричный вид:
А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.
В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.
Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:
Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:
На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 . .m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:
.m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:
Обращают внимание на последние строки.
В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).
Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Способ Крамера
Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:
Её необходимо заменить равноценным матричным уравнением.
Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:
В итоге получают выражения:
Из представленных уравнений выделяют формулы Крамера:
Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:
Он может быть описан следующим алгоритмом:
Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.
Предыдущая
АлгебраЧетность и нечетность функции как определить, примеры решения задач на исследование функции на определение четности и нечетности, условие
Следующая
АлгебраФункция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач
что это такое в математике, операции и действия, как составить, примеры
При решении алгебраических или дифференциальных уравнений студенты сталкиваются с понятием матрицы. Этот термин используется в программировании, электронике, фотоискусстве, но основная область применения — математика. Рассмотрим, что это такое, как применяется и какие операции позволяет осуществить.
Что такое матрицы в математике
Матрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные).
Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n.
Элементы матрицы, т.е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три».
Откуда они взялись и чем полезны
Первые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».
Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».
Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв.) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.
В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы.
Источник: ruspekh.ruСпособ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений.
В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.
Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.
Для решения уравнений таким способом необходимо записать расширенную матрицу системы.
Источник: ruspekh.ruВ отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений.
Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус.
Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г.
В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц.
Обозначения матриц
Помимо самого термина «матрицы», при их решении нужно знать и другие обозначения.
Элементы матрицы — любые математические объекты: числа, переменные, другие матрицы. Элемент обозначается как aab, где a — номер строки расположения элемента, b — номер столбца.
Главная диагональ матрицы — диагональ, пересекающая квадратную матрицу из верхнего левого угла в нижний правый угол (квадратные матрицы имеют одинаковое количество строк и столбцов). Прямоугольные матрицы также могут иметь диагонали: они пересекают элементы с одинаковыми индексами.
Побочная диагональ матрицы — диагональ, пересекающая верхний правый и нижний левый углы. Для прямоугольного вида матриц понятие «побочные диагонали» не используется.
Диагональные элементы — числа и другие математические величины матрицы, расположенные на главной диагонали.
Размер (порядок) матрицы — произведение количества строк на количество столбцов: m×n. Например, если матрица содержит 2 строки и 3 столбца, то ее обозначают матрицей 2×3.
Например, если матрица содержит 2 строки и 3 столбца, то ее обозначают матрицей 2×3.
След матрицы — сумма элементов матрицы, расположенных на главной диагонали. Обозначается как Sp (А) или Tr (A), где A — название матрицы.
Равные матрицы — матрицы, у которых соответствующие элементы равны.
Виды матриц, какие бывают
В математике существует несколько видов матриц в зависимости от их размера.
- Матрица–строка. Имеет размер 1×n, т.е. состоит из одной строки и нескольких столбцов.
\(\begin{vmatrix}54&2&-7&0&4\end{vmatrix}\) - Матрица–столбец. Имеет размер m×1, т.е. состоит из одного столбца и нескольких строк.
\(\begin{vmatrix}3\\-6\\64.5\end{vmatrix}\)
Также различают матрицы по значениям их элементов.
- Нулевая матрица. Все элементы матрицы равны 0.
\(\begin{vmatrix}0&0&0\\0&0&0\end{vmatrix}\) - Квадратная матрица.
 Количество строк и столбцов одинаковое: m=n.
Количество строк и столбцов одинаковое: m=n.
\(\begin{vmatrix}4&5&1\\5&0&0\\-2&2&-8\end{vmatrix}\) - Диагональная матрица — разновидность квадратной матрицы, у которой все элементы равны 0, за исключением диагональных элементов.
\(\begin{vmatrix}3&0&0\\0&-8&0\\0&0&1.5\end{vmatrix}\) - Единичная матрица — разновидность диагональной матрицы. На главной диагонали расположены 1, а все остальные элементы равны 0. Обозначается латинской буквой E.
\(\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}\) - Треугольная матрица. Имеет 2 разновидности: верхняя и нижняя. У верхней треугольной матрицы равны 0 элементы под главной диагональю, а у нижней треугольной матрицы — над главной диагональю.
\(A=\begin{vmatrix}4&1.5&-2\\0&1&7\\0&0&4\end{vmatrix}\)
Треугольная матрица всегда квадратная: m=n. T=\begin{vmatrix}0&-5&-217\\5&0&43\\217&-43&0\end{vmatrix}\)
T=\begin{vmatrix}0&-5&-217\\5&0&43\\217&-43&0\end{vmatrix}\)
Кососимметрическая матрица всегда квадратная.
- Симметрическая матрица. Элементы лежат симметрично по отношению к главной диагонали. Матрица всегда квадратная.
\(A=\begin{vmatrix}1&3&0\\3&2&6\\0&6&5\end{vmatrix}\) - Трапециевидная матрица. Есть ряд условий, при которых матрица становится такого вида. Например, она должна быть квадратной или прямоугольной, при этом количество столбцов обязательно больше числа строк. Также элементы, расположенные над главной диагональю, не равны 0, а элементы под главной диагональю равны 0.
\(A=\begin{vmatrix}1&2&3&4&5&6\\0&-1&0&7&-3&2\\0&0&4&1&-1&-2\end{vmatrix}\)
Применение матриц в математико-экономическом моделировании
С древности и по настоящее время матрицы используются для решения и удобной записи системы линейных алгебраических или дифференциальных уравнений. Но их также применяют в математико-экономическом моделировании для структурирования данных и комфортной работы с ними.
Но их также применяют в математико-экономическом моделировании для структурирования данных и комфортной работы с ними.
Наиболее популярной является матричная модель экономики «затраты–выпуск». Ее внедрил Василий Леонтьев — американский экономист. За развитие этого метода он получил нобелевскую премию: матричная модель упростила решение некоторых экономических проблем. В последствии Леонтьева стали называть «апостолом планирования».
Суть модели «затраты–выпуск» в том, что экономист разделил производственный сектор экономики на отрасли, число которых обозначается n. 1 отрасль — 1 вид продукции. Значит, n количество отраслей выпускает n количество продуктов. Это приводит к появлению межотраслевых связей: одна отрасль заимствует у другой продукт и использует в процессе производства своей продукции. Данная балансовая модель представлена в виде системы линейных уравнений, решаемых с помощью матрицы.
Какие операции можно производить с матрицами
С матрицами можно проводить несколько операций.
- Сложение и вычитание. Это действие можно проводить только с теми матрицами, у которых одинаковый размер. Например, матрица размера 3×2. Ответом будет матрица такого же размера. Чтобы получить ответ нужно вычесть или сложить соответствующие элементы двух матриц. Т.е. при сложении элемент a11 складывается с элементом b11.
- Умножение матрицы на число. Каждый элемент матрицы нужно умножить на число. Получится матрица такого же размера.
- Умножение матриц. Не все матрицы можно умножить между собой. Обязательное свойство: число столбцов первой матрицы должно равняться числу строк второй матрицы. Например, можно умножить матрицу A размером 3×2 и матрицу B размером 2×3. Как осуществляется умножение: чтобы получить элемент a11 новой матрицы, нужно поочередно умножить элементы строки матрицы A на соответствующие элементы столбца матрицы B, а затем суммировать эти произведения.

При умножении матрицы нельзя менять местами.
- Транспонирование матрицы. Смена мест строк и столбцов матрицы. Первая строка матрицы становится первым столбцом. Дальше по аналогии.
Примеры решения задач на матрицы
Пример решения задачи на умножение.
Дано: \( A=\begin{vmatrix}1&-1\\2&0\\3&0\end{vmatrix},\;B=\begin{vmatrix}1&1\\2&0\end{vmatrix}\)
Найти: \(A*B\)
Решение:
Назовем искомую матрицу \(C\). Она будет иметь следующий вид:
\(C=\begin{vmatrix}c_{11}&c_{12}\\c_{21}&c_{22}\\c_{31}&c_{32}\end{vmatrix}\)
Найдем значение каждого элемента:
\(с_{11}=a_{11}*b_{11}+a_{12}*b_{21}=1*1+(-1)*2=-1\)
\(c_{12}=a_{11}*b_{12}+a_{12}*b_{22}=1*1+(-1)*0=1\)
\(c_{21}=a_{21}*b_{11}+a_{22}*b_{21}=2*1+0*2=2\)
\(c_{22}=a_{21}*b_{12}+a_{22}*b_{22}=2*1+0*0=2\)
\(c_{31}=a_{31}*b_{11}+a_{32}*b_{21}=3*1+0*2=3\)
\(c_{32}=a_{31}*b_{12}+a_{32}*b_{22}=3*1+0*0=3\)
Ответ: \(C=\begin{vmatrix}-1&1\\2&2\\3&3\end{vmatrix}\)
Пример решения задачи на умножение матрицы на число 5.
Дано: \(A=\begin{vmatrix}12&-1\\7&0\end{vmatrix}\)
Найти: \(A*5\)
Решение: \(5\ast\begin{vmatrix}12&-1\\7&0\end{vmatrix}=\begin{vmatrix}5\ast12&5\ast(-1)\\5\ast7&5\ast0\end{vmatrix}=\begin{vmatrix}60&-5\\35&0\end{vmatrix}\)
Ответ: \(\begin{vmatrix}60&-5\\35&0\end{vmatrix}\)
Учитесь работать с матрицами и продолжайте осваивать математику, а если задач накопилось слишком много и «горят» сроки, вам поможет сервис Феникс.Хелп. Обращайтесь!
Матрицы и матричная алгебра — Статистические инструкции
Матрицы и матричная алгебра. Матрица представляет собой прямоугольный массив чисел, расположенных в столбцах и строках (очень похоже на электронную таблицу). Матричная алгебра используется в статистике для выражения наборов данных. Например, следующий лист Excel со списком оценок за экзамены: 
Преобразование в матричную алгебру просто включает в себя удаление идентификаторов столбца и строки. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, встречающиеся в матрице, называются элементами матрицы
Матрицы: обозначения
Почему странные обозначения?
Мы используем другое обозначение (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений облегчает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть такой список: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a+3b+5g, чтобы придерживаться условности.
Некоторые из наиболее распространенных терминов, с которыми вы столкнетесь при работе с матрицами:
- Измерение (также называемое порядком): количество строк и столбцов в матрице. Сначала перечисляются строки, затем столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Единичная матрица (I): Диагональная матрица с нулями в качестве элементов, кроме диагональной, которая имеет единицы.
- Скаляр : любое действительное число.
- Функция матрицы: скаляр, умноженный на матрицу, для получения другой матрицы.
Алгебра матриц: сложение и вычитание
Размер матрицы (т. е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерности должны быть точно одинаковыми. Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не к матрице 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одни и те же числа в одно и то же место (например, добавляете все числа в столбец 1, строку 1 и все числа в столбец 2, строку 2).
Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не к матрице 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одни и те же числа в одно и то же место (например, добавляете все числа в столбец 1, строку 1 и все числа в столбец 2, строку 2).
Примечание об обозначениях: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123) для указания местоположения ячейки, например A1 или D2. Для матриц обычно используются такие обозначения, как g ij , что означает i-ю строку и j-й столбец матрицы G.
Вычитание матриц работает точно так же.
Вернуться к началу
Сложение матриц — это просто набор сложений. Для матрицы 2×2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа вместе и запишите сумму в верхнем правом углу.
- Сложите нижние левые числа вместе и напишите сумму внизу слева.

- Сложите нижние правые числа вместе и напишите сумму внизу справа:
Используйте точно такую же процедуру для матрицы 2×3:
Фактически, вы можете использовать эту базовую технику для любого сложения матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк). Другими словами, , если матрицы одинакового размера, их можно добавить. Если они не одного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Описанный выше метод иногда называют «поэлементной суммой», так как вы просто складываете записи вместе и отмечаете результат.
Другой способ подумать об этом…
Подумайте о том, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] может равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
И эта матрица [2 1 6] может равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Сложение матриц для неравных размеров
Если у вас есть неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод. Одним из таких методов является прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q есть матрица размера (m + p) × (n + q):
Например:
Вернуться к началу
Сравнительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новое число. матрица. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результаты четырех умножений дают числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы вместе, процесс немного усложняется. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и вниз по столбцам второй матрицы. После умножения сложите произведения и запишите ответы в виде новой матрицы.
Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и вниз по столбцам второй матрицы. После умножения сложите произведения и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Умножение матриц
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Умножение матриц на двух матрицах возможно только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице. Например, вы можете умножить матрицу 2 х 3 (две строки и три столбца) на матрицу 3 х 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти много хороших инструментов для умножения матриц в Интернете. Мне нравится этот от Matrix Reshish. После вычисления вы можете умножить результат на другую матрицу и еще на одну, что означает, что вы можете перемножать несколько матриц вместе.
Microsoft Excel также может выполнять умножение матриц, используя функции «массива». Инструкции можно найти здесь, на веб-сайте Стэнфорда. Прокрутите вниз до раздела «Матричные операции в Excel».
Вернуться к началу
Беглый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец нулей или два равных столбца или две равные строки, то это сингулярная матрица. Например, все следующие десять матриц являются сингулярными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так легко обнаружить. Поэтому необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет обратного.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) одинаковое количество строк и столбцов. Говоря более формально, можно сказать, что матрица из m столбцов и n строк является квадратной, если m=n. Матрицы, которые не являются квадратными, являются прямоугольными.
Говоря более формально, можно сказать, что матрица из m столбцов и n строк является квадратной, если m=n. Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица — это квадратная матрица, но не все квадратные матрицы являются сингулярными.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это сингулярная матрица.
Обратная матрица — это та же идея, что и обратная величина числа. Если вы умножите матрицу на обратную, вы получите единичную матрицу , матричный эквивалент 1. Единичная матрица в основном состоит из единиц и нулей. Матрица идентичности различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Определитель нуля
Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы. Например, матрица 2×2, формула ad-bc.
Эта простая матрица 2×2 является сингулярной, потому что ее определитель равен нулю:
Вернуться к началу
Единичная матрица представляет собой квадратную матрицу, в которой единицы являются элементами главной диагонали сверху слева направо и нулями в остальных местах. Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
Идея аналогична элементу идентификации. В базовой математике элемент идентичности оставляет число неизменным. Например, кроме того, элемент идентичности равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. д., а при умножении элемент идентичности равен 1, потому что любое число, умноженное на 1, равно этому числу (т. е. 10 * 1 = 10). ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x. По той же логике единичная матрица I получил свое название потому, что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре элемент идентичности различается в зависимости от размера матрицы, с которой вы работаете; в отличие от единственного числа 1 для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n . На главной диагонали всегда будут единицы, а все остальные пробелы будут нулями. На следующем рисунке показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Аддитивная матрица идентичности
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности. Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что все элементы этих матриц — нули. Поэтому их иногда называют нулевая матрица .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Для обзора поиска инверсий посмотрите это короткое видео:
Инверсия матрицы 2×2
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Обратные матрицы — это та же идея, что и обратные. В элементарной алгебре (а может быть, и раньше) вы сталкивались с идеей обратной величины: одно число, умноженное на другое, может равняться 1.
Изображение предоставлено LTU
Если вы умножите одну матрицу на обратную, вы получите матричный эквивалент 1: Идентификационная матрица , которая в основном представляет собой матрицу с единицами и нулями.
Шаг 1: Найдите сопряжение матрицы. Сопряженная матрица может быть найдена путем перестановки одной диагонали и взятия минусов другой:
Чтобы найти сопряженную матрицу 2×2, поменяйте местами диагонали a и d, затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. изображение выше), определитель равен (a*d)-(b*c).
Шаг 3: Умножить 1/детерминант * вспомогательный. .
Проверка ответа
Вы можете проверить свой ответ умножением матриц. Умножьте свою матрицу ответов на исходную матрицу, и вы должны получить единичную матрицу. Здесь же можно воспользоваться онлайн-калькулятором.
Умножьте свою матрицу ответов на исходную матрицу, и вы должны получить единичную матрицу. Здесь же можно воспользоваться онлайн-калькулятором.
Вернуться к началу
Собственное значение (λ) — это специальная скалярная величина, используемая при умножении матриц и имеющая особое значение в нескольких областях физики, включая анализ устойчивости и малые колебания вибрирующих систем. Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственное значение. Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, что и если вы возьмете собственное значение и умножите его. по вектору x .
Собственное значение Пример
В следующем примере 5 является собственным значением A, а (1,2) является собственным вектором:
Давайте рассмотрим это пошагово, чтобы наглядно продемонстрировать, что такое собственное значение. В общем умножении, если вы умножаете матрицу размера n x n на вектор размера n x 1, в результате вы получаете новый вектор размера n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
В общем умножении, если вы умножаете матрицу размера n x n на вектор размера n x 1, в результате вы получаете новый вектор размера n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что, если бы вместо новой матрицы n x 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, умножающий вектор (т. е. тот, который есть и в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением. Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (можно иметь несколько значений для одной и той же матрицы) известно в так называемых собственное разложение . Собственное разложение всегда возможно, если матрица, состоящая из собственных векторов A, квадратная.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ. Единичная матрица для любой матрицы 2×2 имеет вид [1 0; 0 1], поэтому:
Шаг 2: Вычтите из матрицы A ответ из шага 1, используя вычитание матриц:
Шаг 3: Найдите определитель матрицы, которую вы вычислили в шаге 2:
det = (5-λ)(-1-λ) – (3)(3)
Упрощая, получаем:
-5 – 5λ + λ + λ 2 – 9
= λ 2 – 4λ – 14
Шаг 4: Приравняйте уравнение, полученное на шаге 3, к нулю и найдите λ:
0 = λ 2 – 4λ – 14 = 2
Мне нравится использовать мой TI-83 для поиска корней, но Вы также можете использовать алгебру или этот онлайн-калькулятор. Находя корни (нули), получаем x = 2 + 3√2, 2 – 3√2
Ответ : 2 + 3√2 и 2 – 3√2
Математика для больших матриц такая же, но расчеты могут стать очень сложными. Для матриц 3×3 используйте этот калькулятор; для больших матриц попробуйте этот онлайн-калькулятор.
Вернуться к началу
На изображении выше показана увеличенная матрица (A|B) внизу. Дополненные матрицы обычно используются для решения систем линейных уравнений и, собственно, поэтому они и были впервые разработаны. Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (то есть значений справа от знака равенства в наборе уравнений). это называется расширенная матрица , поскольку матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Может быть помещена в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас нет для использования вертикальной черты в расширенной матрице. Обычно можно увидеть матрицы вообще без линий. Панель просто облегчает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Будете ли вы вообще использовать вертикальную полосу, зависит от используемого вами учебника и предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном порядке, чтобы написать систему линейных уравнений с расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Напишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Запишите коэффициенты для второго столбца, а затем «y». Прибавьте, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Запишите коэффициенты для второго столбца, а затем «z». Прибавьте, если это положительное число, вычтите, если оно отрицательное:
Прибавьте, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y – 7
6x + 2y + 9
Шаг 3: Запишите константы в третьем столбце, перед которым ставится знак равенства.
-1x + 7y + 3 = 0
2x + 4y – 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом этапе у вас отрицательный знак, просто сделайте константу отрицательным числом.
Вернуться к началу
Определитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении. Определение на простом английском языке невозможно определить точно; это обычно определяется в математических терминах или с точки зрения того, что это может помочь вам сделать. Определитель матрицы имеет несколько свойств:
- Это действительное число. Это включает в себя отрицательные числа.
- Определители существуют только для квадратных матриц.

- Обратная матрица существует только для матриц с ненулевыми определителями.
Символом определителя матрицы A является |A|, который также является тем же символом, который используется для абсолютного значения, хотя они не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2×2
Формула определителя матрицы 2×2: ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3×3
Определитель матрицы 3×3 находится по следующей формуле:
|A| = a(ei – fh) – b(di – fg) + c(dh – eg)
Это может показаться сложным, но как только вы обозначите элементы a,b,c в верхней строке, d,e, f во второй строке и g,h,i в последней, это становится базовой арифметикой.
Пример :
Найдите определитель следующей матрицы 3×3:
=3(6×2-7×3)—5(2×2-7×4)+4(2×3-6×4)
=-219 что вы умножаете a, b и d на определители меньших 2×2 в матрице 3×3. Этот шаблон продолжается для нахождения определителей матриц более высокого порядка.
Этот шаблон продолжается для нахождения определителей матриц более высокого порядка.
Определитель матрицы 4×4
Чтобы найти определитель матрицы 4×4, сначала нужно найти определители четырех матриц 3×3, которые входят в матрицу 4×4. В виде формулы:
Вернуться к началу
Диагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая идет от верхнего левого угла к нижнему правому.
Элементы самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями по-прежнему можно назвать диагональной матрицей.
Единичная матрица, в которой все 1s расположены по диагонали, также является диагональной матрицей. Любая матрица с одинаковыми элементами на диагонали (т. е. 2, 2, 2 или 9, 9, 9) является скалярным числом, кратным единичной матрице, и также может быть классифицирована как диагональная.
Диагональная матрица имеет не более n чисел, не равных нулю, где n — порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Для описания диагональной матрицы обычно используется обозначение diag(a,b,c) , где abc представляет числа на ведущей диагонали. Для приведенной выше матрицы это обозначение будет diag(3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхнетреугольные матрицы. Матрица нижнего треугольника имеет числа под диагональю; верхнетреугольная матрица имеет числа выше диагонали.
Диагональная матрица является одновременно матрицей с более низкой диагональю и с более низкой диагональю.
Прямоугольные диагональные матрицы
В большинстве случаев диагональная матрица представляет собой квадратную матрицу с порядком (размером) n . Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы — нули. Старшая диагональ берется из самого большого квадрата в неквадратной матрице.
Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы — нули. Старшая диагональ берется из самого большого квадрата в неквадратной матрице.
Вернуться к началу
Матрица транспонирования (или транспонирование матрицы) — это просто перестановка всех строк матрицы в столбцы. Транспонированные матрицы полезны при сложном умножении.
Альтернативный способ описания матрицы транспонирования заключается в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2 столбца 3 будет транспонирован в столбец 2 строки 3. Размерность матрицы также изменится. Например, если бы у вас была матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица является частным случаем транспонированной матрицы; он равен своей транспонированной матрице.
Говоря более формально, A = A T .
Символы для матрицы транспонирования
Обычный символ для матрицы транспонирования A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и .
Свойства транспонированных матриц
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы сталкивались в основах алгебры (таким как ассоциативность и коммутативность). Основные свойства матриц:
- (A T ) T = A: транспонирование транспонированной матрицы является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, на которую можно умножить матрицу).

- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, такое же, как произведение их транспонированных матриц в обратном порядке.
- (A -1 )T = (A T ) -1 : транспонирование и обращение матрицы можно выполнять в любом порядке.
Вернуться к началу
Симметричная матрица — это квадратная матрица, имеющая симметрию вокруг своей ведущей диагонали, начиная с левого верхнего угла и заканчивая правым нижним. Представьте себе складку матрицы по диагонали (не включайте числа на реальной диагонали). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда по ведущей диагонали), как в примере справа, у вас есть симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна своей транспонированной. Транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию. С математической точки зрения, M=M T , где M T — транспонированная матрица.
Максимальное количество чисел
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n(n+1)/2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, может быть максимум 4(4+1)/2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6,9. 0006
0006
Диагональные матрицы
Диагональная матрица является частным случаем симметричной матрицы. Диагональная матрица имеет все нули, кроме главной диагонали.
Что такое кососимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является кососимметричной:
Математически кососимметричная матрица удовлетворяет условию a ij =-a ji . Например, возьмем запись в строке 3, столбце 2, которая равна 4. Ее симметричным аналогом является -4 в строке 2, столбце 3. Это условие также можно записать в терминах транспонированной матрицы: A T =- А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T транспонированная матрица.
Все ведущие диагональные элементы в кососимметричной матрице должны быть равны нулю. Это потому, что a i,i = −a i,i означает i,i =0.
Это потому, что a i,i = −a i,i означает i,i =0.
Другое интересное свойство матрицы этого типа состоит в том, что если у вас есть две кососимметричные матрицы A и B одинакового размера, то вы также получите кососимметричную матрицу, если сложите их вместе:
Сложение двух кососимметричных матриц вместе .
Этот факт поможет вам доказать, что две матрицы кососимметричны. Первый шаг — заметить, что все элементы на главной диагонали равны нулю (что невозможно «доказать» математически!). Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что ij = – a ji .
Косоэрмитова
Косоэрмитова матрица по существу аналогична кососимметричной матрице, за исключением того, что косоэрмитова может содержать комплексные числа. Косоэрмитова матрица, показывающая комплексные числа. Фактически, кососимметричная и косоэрмитова эквивалентны для действительных матриц (матрица, которая почти полностью состоит из действительных чисел).
Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в воображаемой сфере ноль считается мнимым числом.
В начало
Матрица дисперсии-ковариации (также называемая ковариационной матрицей или матрицей дисперсии) представляет собой квадратную матрицу, которая вместе отображает дисперсию и ковариацию двух наборов двумерных данных. Дисперсия является мерой того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины движутся вместе в одном направлении.
Дисперсия отображается в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсия находится на диагоналях ковариационной матрицы, потому что в основном эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках. Например, ковариация для А и В равна -0,21, а ковариация для А и С равна -0,10. Вы можете просмотреть столбец и строку или строку и столбец (т. е. AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, дисперсия-ковариация матрица также является симметричной матрицей.
Например, ковариация для А и В равна -0,21, а ковариация для А и С равна -0,10. Вы можете просмотреть столбец и строку или строку и столбец (т. е. AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, дисперсия-ковариация матрица также является симметричной матрицей.
Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать вариационно-ковариационную матрицу. Обратите внимание, что Excel вычисляет ковариацию для совокупности (знаменатель n), а не для выборки (n-1). Это может привести к несколько неправильным расчетам матрицы дисперсии-ковариации. Чтобы исправить это, вам придется умножить каждую ячейку на n/n-1.
Если вы хотите изготовить вручную:
Шаг 1: Вставьте дисперсии ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A/B в приведенном выше примере появляется в двух местах (AB и B A). На следующей диаграмме показано, где каждая ковариация и дисперсия появятся для каждого варианта.
На следующей диаграмме показано, где каждая ковариация и дисперсия появятся для каждого варианта.
Вернуться к началу
См. также:
Что такое матрица путаницы?
Следующий : Форма рядного эшелона / Сокращенная форма рядного эшелона
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Матрицы и матричная алгебра» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/matrices-and-matrix-алгебра/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
6. Матрицы и линейные уравнения
М. Борн
Мы хотим решить систему одновременных линейных уравнений с использованием матриц:
a 1 x + b 1 y = c 1
а 2 х + б 2 у = с 2
Если мы позволим
`A=((a_1,b_1),(a_2,b_2))`, `\ X=((x),(y))\ ` и `\ C=((c_1),(c_2))`
, затем `AX=C` . (впервые мы увидели это в «Умножении матриц»).
Если мы теперь умножим каждую сторону
АХ = С
слева от
А -1 , у нас есть:
А -1 АХ = А -1 С .
Однако мы знаем, что А -1 А = I , Матрица идентичности. Получаем
Получаем
IX = А -1 С .
Но IX = X , поэтому решение системы уравнения:
Х = А -1 С
См. поле в верхней части Обратной матрицы для получения дополнительных сведений о том, почему это работает.
Примечание: Мы не можем изменить порядок умножения и использовать CA -1 потому что умножение матриц не является коммутативным.
Пример — решение системы с использованием обратной матрицы
Решите систему с помощью матриц.
− х + 5 у = 4
2 х + 5 у = -2
Всегда проверяйте свои решения!
Ответ
Имеем:
`A=((-1,5),(2,5)),` ` \ X=((x),(y))\ ` и `\ C=((4), (-2))`
Чтобы решить систему, нам нужно обратное A , которое мы запишем как A -1 .
Поменять местами ведущую диагональ:
`((5,5),(2,-1))`
Изменить знаки двух других элементов: 9-1C` `=((-0,333,0,333),(0,133,0,067))((4),(-2))` `=((-2),(0,4)) `
Этот ответ означает, что мы нашли решение `x = -2` и `y = 0,4`.
Решение верное?
Проверяем в исходной системе уравнений:
`{:(-x+5y,=4),(2x+5y,=-2):}`
Подставляя `x = -2` и `y = 0,4`, получаем:
`-(-2) + 5×(0,4) = 2 + 2 = 4` [Проверка OK]
`2×(−2) + 5×(0,4)` ` = −4 + 2` ` = −2` [Проверка OK]
Итак, решение исходной системы уравнений
`x = -2,\ \ y = 0,4`.
Мы можем распространить описанный выше метод на системы любого размера. Мы не можем использовать тот же метод для нахождения обратных матриц больше 2×2.
Мы будем используйте систему компьютерной алгебры, чтобы найти инверсию больше, чем 2×2.
Пример — Система 3×3 Уравнения
Решите систему, используя матричные методы.
`{: (x+2y-z=6),(3x+5y-z=2),(-2x-y-2z=4) :}` 9-1С`
`=((5.5,-2.5,-1.5),(-4,2,1),(-3.5,1.5,0.5))((6),(2),(4))`
`=((22),(-16),(-16))`
Чек:
`22 + 2(-16) — (-16) = 6` [Проверка ОК]
`3(22) + 5(-16) — (-16) = 2` [Проверка ОК]
`-2(22) — (16) — 2(-16) = 4` [Проверка ОК]
Итак, решение `x = 22`, `y = -16` и `z = -16`.
Пример — Электронное применение системы 3×3 Уравнения
Найдите электрические токи, показанные решение матричного уравнения (получено по закону Кирхгофа) возникающие из этой схемы: 9-1((0),(24),(0))`
Используя систему компьютерной алгебры для выполнения обратной операции и умножения на постоянную матрицу, мы получаем:
`I_1= -6\ «А»`
`I_2= 4\ «А»`
`I_3= 2\ «А»`
Мы видим, что I 1 является отрицательным, как и ожидалось из принципиальной схемы.
Упражнение 1
Найдены следующие уравнения в конкретной электрической цепи. Найдите токи, используя матрицу методы. 9-1C`
`=((0,294,0,353,0,294),(0,118,-0,059,0,118),(0,588,-0,294,-0,412))((0),(6),(-3))`
`=((1,236),(-0,708),(-0,528))`
Поэтому
`I_A= 1,236\ «А»`,
`I_B= -0,708\ «А»` и
`I_C= -0,528\ «А»`
Упражнение 2
Помните эту проблему раньше? Если мы знаем задействованные одновременные уравнения, мы сможем решить система с использованием обратных матриц на компьютере.
Уравнения цепи с использованием закона Кирхгофа:
−26 = 72 I 1 − 17 I 3 − 35 I 4
34 = 122 I 2 − 35 I 3 − 87 I 7
−4 = 233 I 7 − 87 I 2 − 34 I 3 − 72 I 6
−13 = 149 I 3 − 17 I 1 − 35 I 2 − 28 I 5 − 35 I 6 − 34 I 7
−27 = 105 I 5 − 28 I 3 − 43 I 4 − 34 I 6
24 = 141 I 6 − 35 I 3 − 34 I 5 − 72 I 7
5 = 105 I 4 − 35 I 1 − 43 I 5
Каковы отдельные токи, I 1 до I 7 ?
Пользователи телефонов
ПРИМЕЧАНИЕ: Если вы пользуетесь телефоном, вы можете прокручивать любые широкие матрицы на этой странице вправо или влево, чтобы увидеть выражение целиком.
Ответ
Решение токов в цепи (система 7 × 7)
Мы решаем это с помощью компьютера следующим образом. Просто записываем слева матрицу коэффициентов, находим обратную (возводим матрицу в степень -1) и умножаем результат на постоянную матрицу.
Для этого можно использовать Matlab, Mathcad или аналогичное математическое программное обеспечение. Wolfram|Alpha — бесплатная альтернатива.
`Х=[(72,0,-17,-35,0,0,0), (0,122,-35,0,0,0,-87), (0,-87,-34,0,0,-72,233), (-17,-35,149-3),(-0,22243),(-0,27848),(0,21115),(0,20914)]`
Ответ означает, что токи в этой цепи равны (до 4 знаков после запятой):
`I_1 = -0,4680\ «А»`
`I_2= 0,4293\ «А»`
`I_3= 0,0005\ «А»`
`I_4= -0,2224\ «А»`
`I_5= -0,2785\ «А»`
`I_6= 0,2112 \ «А»`
`I_7= 0,2091 \ «А»`
Упражнение 3
Хотим 10 литров бензина содержащий 2% добавки. У нас есть следующие барабаны:
Бензин без присадки
Бензин с 5% присадкой
Бензин с 6% присадкой
Нам нужно использовать в 4 раза больше чистого
бензин как бензин с 5% присадкой. Сколько нужно каждого?
Сколько нужно каждого?
Всегда проверяйте свои решения!
Ответ
Пусть
x = нет. литров чистого бензина
y = нет. литров 5% бензина
с = нет. литров 6% бензина
Из первого предложения имеем:
`х + у + z = 10`
Второе предложение дает нам:
Мы не получаем присадки из чистого бензина.
Получаем (5% от y ) л присадки из второго барабана.
Получаем (6% от з ) л присадки из третьего барабана.
НУЖНО 2% на 10 л добавки = 0,2 л = 200 мл.
Так
`0,05y + 0,06z = 0,2`
Умножая на 100, мы получаем:
`5y + 6z = 20`
Второе последнее предложение дает нам:
`х = 4у`
Мы можем записать это как:
`х — 4у = 0`
Это дает нам набор одновременных уравнений:
х + у + z = 10
5 у + 6 у = 20
х − 4 у 9-1` `=((0.
96,-0.16,0.04),(0.24,-0.04,-0.24),(-0.2,0.2,0.2))`
Умножение обратной матрицы на C :
`( (0,96,-0,16,0,04),(0,24,-0,04,-0,24),(-0,2,0,2,0,2))((10),(20),(0))` `=((6.4),( 1.6),(2))`
Таким образом, у нас есть 6,4 л чистого бензина, 1,6 л 5%-й присадки и 2 л 6%-й присадки.
Правильно?
`6,4 + 1,6 + 2 = 10` л [Проверка в порядке]
`5% xx 1,6 + 6% xx 2 = 200` мл [Проверка в порядке]
`4 × 1,6 = 6,4` [Проверка в порядке]
Упражнение 4
Эта статическая задача была представлена ранее в Разделе 3: Матрицы.
Из диаграммы получаем следующие уравнения (эти уравнения взяты из теории статики):
Вертикальные силы:
F 1 sin 69,3° − F 2 sin 71,1° − F 3 sin 56,6° + 926 = 0
Горизонтальные силы:
Ф 1 cos 69,3° − F 2 cos 71,1° + F 3 cos 56,6° = 0
Моменты:
7,80 F 1 sin 69,3° − 1,50 F 2 sin 71,1° − 5,20 F 3 sin 56,6° = 0
Используя матрицы, найти силы F 1 , F 2 и F 3 .
Ответ
Запишем первое уравнение так, чтобы постоянный член был в правой части:
Ф 1 sin 69,3° − F 2 sin 71,1° − F 3 sin 56,6° = −926
В матричной форме запишем уравнения в виде:
`((sin 69,3°,-sin 71,1°,-sin 56,6°),(cos 69,3°,-cos 71,1°,cos 56,6°),(7,80 sin 69,3°,-1,50 sin 71,1°,-5,20 sin 56,6°))((F_1),(F_2),(F_3))`
`=((-926),(0),(0))`
Итак, решение для системы:
`((F_1),(F_2),(F_3))=((sin 69,3°,-sin 71,1°,-sin 56,6°),(cos 69,3°,-cos 71,1°, cos 56,6°), (7,80 sin 69-1((-926),(0),(0))`
`=((425,5),(1079,9),(362,2))`
Так
`F_1= 425,5\ «Н»`
`F_2= 1079,9\ «Н»`
`F_3= 362.2\ «N»`
Это очень просто и быстро в научном Notebook, Matlab или любая другая система компьютерной алгебры!
Как перемножать матрицы? С Примерами
Умножение матриц является одной из фундаментальных, но продвинутых концепций матриц.
Вы должны быть осторожны при умножении матриц. Это не так просто, как кажется. Вы должны хорошо знать все основные понятия, такие как, что такое матрица, строки и столбцы в матрице, как представлять матрицу и как умножать матрицы.
Снова в школу: Матрицы — это группы чисел, переменных, символов или выражений в прямоугольной таблице с различным количеством строк и столбцов. Это прямоугольные массивы с различными операциями, такими как сложение, умножение и транспонирование. Элементами матрицы являются числа или элементы, составляющие матрицу. Горизонтальные элементы матриц — это строки, а вертикальные — столбцы.
Количество строк и столбцов можно изобразить с помощью переменных. Например, пусть количество строк в матрице K равно «m», а количество столбцов — «n». Таким образом, мы можем представить матрицу K как [K] м х п . Матрица представлена в квадратных скобках «[]» с произведением ее строк и столбцов в нижнем индексе.
До 1812 года человечеству не было известно умножение матриц.
Филипп Мари Бине, французский математик, изобрел умножение матриц в 1812 году для описания линейных карт с матрицами. Он обнаружил, что умножение матриц является бинарной операцией. Две матрицы перемножаются, образуя одну матрицу.
Далее в этой статье вы узнаете правила и основные принципы умножения матриц.
Что такое умножение матриц?Во введении к этой статье вы прочитали, что умножение матриц — это бинарная операция. Это означает, что всякий раз, когда вы находите произведение двух или более матриц, ответом является единственная матрица, следующая за исходными матрицами. Для перемножения двух матриц проверяется их совместимость. Это означает, что две матрицы должны следовать набору правил для умножения.
Эти параметры совместимости описаны ниже:
- Значение количества столбцов в матрице один должно быть равно значению количества строк в матрице 2.
- Если вышеуказанное условие не выполняется, матрицы нельзя перемножать.
- Если матрицы являются квадратными матрицами одного порядка, их можно умножать друг на друга.
- Квадратную матрицу 2 x 2 нельзя умножить на квадратную матрицу 3 x 3. Ее можно умножить на другую квадратную матрицу 2 x 2.
Давайте рассмотрим пример, чтобы лучше понять это:
Пример 1: Предположим, у нас есть две матрицы, K и L. Порядок матриц задан как m x n и n x o соответственно. Выяснить, можно ли перемножать матрицы?
Решение: Дано
Матрица 1 = [ K ] m x n
Матрица 2 = [ L ] n x o
Мы видим, что количество столбцов в матрицах равно количеству строк K матрица L. Следовательно, две матрицы можно перемножить.
Результирующая матрица: Матрица, полученная путем умножения двух матриц, является результирующей матрицей. Эта матрица может быть представлена как:
- Имя матрицы в квадратных скобках
- Произведение количества строк матрицы 1 на количество столбцов матрицы два в порядке.
Снова обратимся к приведенному выше примеру:
Мы знаем, что K и L совместимы с умножением. Таким образом, результирующая матрица, скажем, D, будет = [D] m x o , где m = количество строк матрицы один и o = количество столбцов матрицы 2.
Пример 2: Матрица [ K ] 2 x 4 умножается на матрицу [ X ] 4 х 2 . Если [ Y ] результирующая матрица, то каков порядок Y.
Решение: Нам дано
Матрица 1 = [ K ] 2 x 4
Матрица 2 = [ X ] 4 x 2
Поскольку количество столбцов матрицы K равно количеству строк матрицы X, K и X можно перемножить. Следовательно,
Матрица Y = [ Y ] 2 x 2
Порядок матрицы Y равен 2 x 2. Y — квадратная матрица.
Ориентация двух матриц также является решающим фактором для определения произведения матриц. Если есть две матрицы, K и L, то чтобы найти произведение K и L, вы должны сначала написать матрицу K, а затем написать матрицу L.
Если вы запишете матрицу L перед матрицей K, вы получите совершенно другую матрицу . Коммутативный закон не применяется при умножении матриц. Это означает, что KL ≠ LK.
Теперь, когда мы разобрались с правилами умножения двух матриц, давайте научимся умножать матрицы.
Как умножать матрицы?Давайте изучим пошаговую процедуру умножения двух матриц. Поначалу это может показаться вам запутанным, но когда вы освоитесь, перемножать матрицы так же просто, как намазать маслом свой тост.
Шаг 1: Проверить совместимость предоставленных матриц. Если они несовместимы, оставьте умножение.
Шаг 2: Возьмите первую строку матрицы 1 и умножьте ее на первый столбец матрицы 2. Затем умножьте первую строку матрицы 1 на 2-й столбец матрицы 2. Теперь умножьте первую строку матрицы 1 на 3-й столбец матрицы 2 и так далее. Полученные из них значения заполнят первую строку матрицы продукта.
Шаг 3: Теперь возьмите вторую строку матрицы 1 и умножьте ее на первый столбец матрицы 2 и выполните те же шаги, что и для 2.
Это заполнит вторую строку матрицы произведения.
Шаг 4: Продолжайте эти шаги, выполняя каждую строку, пока не будет получена матрица произведения.
Под умножением строк и столбцов мы подразумеваем, что элементы, присутствующие в этих строках и столбцах, будут умножены. Не забудьте умножить соответствующие элементы, а затем добавить продукты, чтобы найти элемент матрицы продукта.
Если вы не уверены в шагах, посмотрите на пример пошагового решения ниже:
Пример: Найдите произведение матриц, приведенных ниже:
K = и L =
Решение:
Шаг 1: Матрица K имеет порядок 1 x 4, а матрица L имеет порядок 4 x 2. Поскольку количество столбцов матрицы K соответствует количеству строк матрицы L, поэтому матрицы совместимы для умножения. Полученная матрица имеет порядок 1 x 2.
Шаг 2: Поскольку K имеет только 1 строку, умножьте ее на первый столбец матрицы L следующим образом: (2 x 4) + (4 x 5) + (1 x 4) + (7 x 3) = 51.
Обратите внимание, как 1-й элемент строки умножается на 1-й элемент столбца 1, аналогично 2-му, 3-му и 4-му. Затем они складываются вместе, чтобы получить результирующий матричный элемент.
Шаг 3: Теперь аналогичным образом умножьте 1-ю строку на второй столбец матрицы L. Результат будет (2 x 3) + (4 x 2) + (1 x 9) + (7 x 6) = 65 .
Шаг 4: Разместите результат в матрице продуктов. Предположим, что [ X ] — результирующая матрица; следовательно, X = [51 65].
Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).
Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).
Как умножить матрицу 2 x 2Для умножения матриц 2 x 2 вы должны хорошо знать шаги, описанные в предыдущем разделе. Поскольку мы перемножаем 2 квадратные матрицы одного порядка, нам не нужно проверять совместимость в этом случае.
Помните, что матрица произведения также будет иметь тот же порядок, что и квадратная матрица. Давайте решим пример, чтобы понять, как умножить матрицу 2 x 2.
Пример: Умножить квадратную матрицу на
A = и B =
Шаг 1: Умножая первую строку матрицы A на первый столбец матрицы B. Получаем (2 x 1) + (9 x 3) = 29. Теперь умножаем первую строку матрицы A со вторым столбцом матрицы B. Получаем (2 x -4) + (9 x 7) = -8 + 63 = 55.
Шаг 2: Повторим шаг 1, но изменим строку матрица A. Первый и второй столбцы матрицы B будут умножены на строку 2 матрицы A. Результатом будет
(3 x 1) + (-7 x 3) = 3 – 21 = -18, и (3 x -4) + (-7 х 7) = -12 – 49= -61
Шаг 3: Правильно расположите результаты
.
Следовательно, результирующая матрица C =
Точно так же вы можете решать квадратные матрицы, такие как 3 x 3, 4 x 4 и так далее.
Матричное уравнение – объяснение и примеры
Матричное уравнение похоже на алгебраические уравнения.
У нас есть переменные в алгебраических уравнениях, а в матричных уравнениях мы имеем дело с матрицами, которые действуют как переменная.
Итак, что такое матричные уравнения?
Матричное уравнение — это уравнение, в котором целая матрица представляет собой переменную.
В этом уроке мы увидим матричное уравнение, как писать матричные уравнения и как решать матричные уравнения. Давайте начнем!
Что такое матричное уравнение?
Матричное уравнение — это уравнение, в котором матрица действует как переменная. Мы можем решать простые матричные уравнения, используя такие операции, как сложение матриц, вычитание матриц и скалярное умножение.
Мы также рассмотрим очень простые матричные уравнения, в которых выполняется умножение матриц, и используется идея матрицы , обратной . Примеры: $
$ 2x = 18 $
- Для первого уравнения, чтобы решить $ x $, мы выполняем процесс вычитания .
- Для решения второго уравнения относительно $ x $ мы выполняем процесс сложения .
- Для решения третьего уравнения для $ x $ мы объединяем вычитание и деление .
- В последнем уравнении, чтобы найти $ x $, мы используем деление .
У нас могут быть похожие формы матричных уравнений , в которых мы должны выполнять те же операции, НО над матрицами! Давайте проверим несколько примеров того, как писать матричные уравнения:
$ \begin{bmatrix} {a} & {b} \\ {c} & {d} \end {bmatrix} + X = \begin{bmatrix} {e} & {f} \\ {g} & { h } \end {bmatrix} $
$ \begin{bmatrix} { a } & { b } \\ { c } & { d } \ end {bmatrix} – X = \begin{bmatrix} { e } & {f} \\ {g} & {h} \end {bmatrix} $
$ 3 \times \begin{bmatrix} {a} & {b} \\ {c} & {d} \end {bmatrix } = \begin{bmatrix} { 6 } & { 12 } \\ { – 18 } & { 9 } \ end {bmatrix} $
$ X \begin{bmatrix} { a } & { b } \\ { c } & { d } \ end {bmatrix} = \begin{bmatrix} { e } & { f } \\ { g } & { h } \end {bmatrix} $
Эти $ 4 $ уравнения являются матричными уравнениями.
Нам нужно будет выполнить те же операции, но с матрицами, чтобы найти неизвестную матрицу ! Далее мы рассмотрим, как решать эти типы матричных уравнений.
Как решать матричные уравнения
Как мы упоминали ранее, способ решения матричных уравнений заключается в простом выполнении основных арифметических операций, но с учетом правил сложения матриц, вычитания матриц, скалярного умножения и умножения матриц.
Проверим простую задачу сложения матриц:
$ A – \begin{bmatrix} { 3 } & { – 3 } \\ { 1 } & { 0 } \end {bmatrix} = \begin{bmatrix} { – 10 } & { 2 } \\ { – 1 } & { 1 } \end {bmatrix} $
Обратите внимание, что $ A $ является матрицей.
Подобно уравнениям, чтобы найти матрицу $A$, мы можем сложить первую матрицу со второй матрицей. Процесс показан ниже:
$ A = \begin{bmatrix} { – 10 } & { 2 } \\ { – 1 } & { 1 } \end {bmatrix} + \begin{bmatrix} { 3 } & { – 3 } \\ { 1 } & { 0 } \ end {bmatrix} $
$ A = \begin{bmatrix} { – 10 + 3 } & { 2 + ( – 3 ) } \\ { -1 + 1 } & { 1 + 0 } \ end {bmatrix} $
$ A = \begin{bmatrix} { – 7 } & { – 1 } \\ { 0 } & { 1 } \end {bmatrix} $
Чтобы добавить две матрицы, первое условие должно состоять в том, что порядок обеих матриц должен быть равным! Обе матрицы здесь были $ 2 \times 2 $ матрицами.
Чтобы выполнить сложение матриц, мы добавили каждую соответствующую запись друг к другу. Узнайте больше о добавлении матриц, прочитав эту статью!
Давайте рассмотрим пару примеров!
Пример 1Решение для матрицы $ B $:
$ B + \begin{bmatrix} { 0 } & { – 1 } & 4 \\ { 11 } & { – 2 } & 0 \\ {3} & {6} & { – 2 } \end {bmatrix} = \begin{bmatrix} { 6 } & { 1 } & – 1 \\ { – 1 } & { 4 } & – 1 \\ { – 1 } & { – 2 } & { – 3 } \end {bmatrix} $
РешениеКак и в уравнениях, чтобы найти $ B $, мы должны вычесть первую матрицу из второй матрицы. Обе они являются матрицами $ 3 \times 3 $, и, таким образом, матрица $ B $ также будет матрицей $ 3 \ x 3 $. Процесс показан ниже:
$ B = \begin{bmatrix} { 6 } & { 1 } & – 1 \\ { – 1 } & { 4 } & – 1 \\ { – 1 } & { – 2 } & { – 3 } \ end {bmatrix} – \begin{bmatrix} { 0 } & { – 1 } & 4 \\ { 11 } & { – 2 } & 0 \\ {3} & {6} & { – 2 } \end {bmatrix } $
$ B = \begin{bmatrix} { 6 – 0 } & { 1 + 1 } & { -1 – 4} \\ { -1 – 11 } & { 4 + 2 } & -1 – 0 \ \ {-1 – 3} & {-2 – 6} & {-3 + 2} \end {bmatrix} $
$ B = \begin{bmatrix} {6} & {2} & {-5} \ \ {-12} & {6} & -1 \\ {-4} & {-8} & {-1} \end {bmatrix} $
Чтобы узнать больше о вычитании матриц, посмотрите этот урок!
Пример 2Решите следующее матричное уравнение для значений $ x $ и $ y $: 4 } \end {bmatrix} \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} { 4 } \\ 8 \end {bmatrix} $
Решение
Обработка второй матрицы в качестве переменной мы знаем, что нам придется разделить матрицу с элементами $4$ и $8$ (третья матрица) на матрицу $2\times 2$ (первая матрица).
9{ – 1 } = \frac{1}{ad – bc} \begin{bmatrix} { d } & {-b } \\ {-c } & {a} \end {bmatrix}$.
Найдем обратную матрицы $ \begin{bmatrix} { 2 } & {2 } \\ { 3 } & {4 } \end {bmatrix}$ :
$ = \frac{1} { (2)(4) – (2)(3) } \begin{bmatrix} { 4 } & {-2 } \\ { – 3 } & { 2 } \end {bmatrix} $
$ = \frac {1}{2} \begin{bmatrix} { 4 } & { -2 } \\ { – 3 } & { 2 } \end {bmatrix} $
$ = \begin{bmatrix} { 2 } & { — 1 } \\ { – \frac{3}{2} } & { 1 } \end {bmatrix} $
Теперь мы можем решить наше уравнение:
$ \begin{bmatrix} { 2 } & {2 } \\ { 3 } & {4 } \end {bmatrix} \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} { 4 } \\ 8 \end {bmatrix} $
$ \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} { 2 } & { -1 } \\ { – \frac{3}{2} } & { 1 } \end {bmatrix} \begin{bmatrix} { 4 } \\ 8 \end {bmatrix} $
$ \ begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} {(2)(4) + (-1)(8)} \\ {(-\frac{3}{2} )(4) + (1)(8)}\end {bmatrix} $
$ \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} {8 – 8} \\ {-6 + 8}\end {bmatrix} $
$ \begin{ bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} {0} \\ 2\end {bmatrix} $
Таким образом,
$ x = 0 $ и $ y = 2 $.
Чтобы узнать больше о том, как мы делали это умножение, ознакомьтесь с нашим уроком по умножению матриц.
Практические вопросы
- Решите для $a$, $b$, $c$ и $d$.
$ 3 \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} = \begin{bmatrix} { – 6 } & { 12 } \\ { – 9} & { – 3 } \end {bmatrix} $- Учитывая матрицы:
$ A = \begin{bmatrix} 0 & 1 \\ 2 & 6 \end {bmatrix} $
$ B = \begin{bmatrix} 3 & -1 \\ 2 & 3 \end {bmatrix} $
$ C = \begin{bmatrix} 4 & 3 \\ -2 & 5 \end {bmatrix} $Решить матричное уравнение $ X \cdot A + В = С$.
Ответы
Предыдущий урок | Главная страница | Следующий урок
Это скалярное матричное уравнение умножения .
$ 3 \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} = \begin{bmatrix} { – 6 } & { 12 } \\ { – 9} & { – 3 } \end {bmatrix} $
Нам нужно найти переменные $ a $, $ b $, $ c $ и $ d $. В левой части мы умножаем каждый элемент первой матрицы на скаляр «3».
Сделаем так:
$ \begin{bmatrix} { 3a } & {3 b } \\ { 3c } & {3 d } \end {bmatrix} = \begin{bmatrix} { – 6 } & { 12 } \ \ { – 9 } & { – 3 } \end {bmatrix} $
Теперь у нас есть две матрицы $ 2 \times 2 $, равные друг другу. Это означает, что каждый соответствующий элемент равен друг другу. Приравниваем каждую и находим значения всех $4$ переменных.
$ 3a = – 6 $
$ a = – 2 $
Тогда
$ 3b = 12 $
$ b = 4 $
Далее,
c 90 $ 3c = – 0 9
$ 9002 $ 3c = – 0 9 = – 3 $
Наконец,
$ 3d = – 3 $
$ d = – 1 $
Итак, мы имеем $ a = – 2 $, $ b = 4 $, $ c = – 3 $, и $ д = -1 $. Таким образом, неизвестная матрица может быть записана как:
$ \begin{bmatrix} { -2 } & { 4 } \\ { – 3 } & { – 1 } \end {bmatrix} $
- Лечение $X$ в качестве переменной имеем:
$ X \cdot A +B = C $
$ X \cdot A = C – B $
$ X = \frac{C-B}{A} $Вместо деления умножим обратное число $A$ с матрицей $C-B$.
{-1}$: 9{-1}(C – B) $
$ X = \begin{bmatrix} -3 & \frac{1}{2} \\ 1 & 0 \end {bmatrix} \begin{bmatrix} 1 & 4 \\ -4 & 2 \end {bmatrix} $
$ X = \begin{bmatrix} (-3)(1) + (\frac{1}{2})(-4) & (-3)(4) + (\ frac{1}{2})(2) \\ (1)(1)+(0)(-4) & (1)(4)+(0)(2) \end {bmatrix} $
$ X = \begin{bmatrix} -5 & -11 \\ 1 & 4 \end {bmatrix} $Использование матриц для решения систем уравнений | безграничная алгебра |
Матричные уравнения
Матрицы можно использовать для компактного написания и работы с системами нескольких линейных уравнений.
Цели обучения
Определите, как матрицы могут представлять систему уравнений. ×1n \times 1n×1
матрица) изnnn
переменныхx1,x2,…,xnx_1, x_2,…, x_nx1,x2,…,xn
иbbb
представляет собой вектор-столбец размеромм × 1 м × 1 м × 1
, тогда матричное уравнение:Ax=bAx=bAx=b
.Ключевые термины
- матрица : прямоугольное расположение чисел или термов, имеющее различное применение, такое как преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.
Матрицы можно использовать для компактной записи и работы с системами уравнений. Как мы узнали из предыдущих разделов, матрицами можно манипулировать так же, как и обычным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений. Полезно понять, как организовать матрицы для решения этих систем.
Написание системы уравнений с матрицами
Эту систему можно решить методом исключения или замены, но можно и с помощью матричной операции. Прежде чем мы начнем настраивать матрицы, важно сделать следующее:
- Убедитесь, что все уравнения написаны одинаково, то есть все переменные должны быть в одном порядке.
- Убедитесь, что одна часть уравнения состоит только из переменных и их коэффициентов, а другая часть — только из констант.
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц:
XXX
матрица, представляющая переменные системы, и
BBB
матрица, представляющая константы. Используя умножение матриц, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:
A⋅X=B\displaystyle A\cdot X=BA⋅X=B
Чтобы решить систему линейных уравнений с использованием обратной матрицы, пусть
AAA
матрица коэффициентов, пусть
XXX
матрица переменных, а
BBB
матрица констант.
Учитывая систему:
x+8y=72x−8y=−3\displaystyle \начать{выравнивать} х+8у&=7 \\ 2x-8y&=-3 \end{align}x+8y2x−8y=7=−3
Матрица коэффициентов:
A=[182−8]A=\begin{bmatrix} 1 и 8\\ 2 и -8 \end{bmatrix}A=[128−8]
Переменная матрица:
X=[xy]\displaystyle X=\begin{bmatrix} х\\у \end{bmatrix}X=[xy] 9{-1} \right)(A−1)
существует, эта формула решит систему.
Если матрица коэффициентов необратима, система может быть несовместной и не иметь решения или быть зависимой и иметь бесконечно много решений.
Матрицы и операции со строками
Две матрицы эквивалентны по строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.
Цели обучения
Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы
Ключевые выводы
Ключевые моменты
- Элементарная операция со строками — это любое из следующих действий: переключение строк (перестановка двух строк матрицы), умножение строк (умножение строки матрицы на ненулевую константу) , или сложение строк (добавление к одной строке матрицы некоторого числа, кратного другой строке).
- Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраическим путем из уравнений системы.
Ключевые термины
- пространство строк : Набор всех возможных линейных комбинаций его векторов-строк.
- эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой с помощью последовательности элементарных операций над строками.
Элементарные операции с рядами (ERO)
В линейной алгебре две матрицы эквивалентны по строкам, если одну можно заменить на другую с помощью последовательности элементарных операций со строками. Или два
m×nm \times nm×n
матрицы эквивалентны по строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство строк матрицы представляет собой набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраическим путем из уравнений системы.
Две матрицы одинакового размера эквивалентны по строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что эквивалентно, матрицы имеют одно и то же нулевое пространство. Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Элементарной операцией со строками является любой из следующих трех ходов:
- Переключение строк (своп): поменять местами две строки матрицы.
- Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
- Добавление строки (поворот): добавление к одной строке матрицы числа, кратного другой строке.
Создание эквивалентных матриц с использованием элементарных операций со строками
Поскольку матрица по существу представляет собой коэффициенты и константы линейной системы, операции с тремя строками сохраняют матрицу.
Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных инверсий, чтобы переменная сокращалась. Наконец, добавление строк также совпадает с методом исключения, когда для получения переменной выбирают добавление или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод решения системы уравнений.
Пример 1: Покажите, что эти две матрицы эквивалентны по строкам:
A=(1−10211)B=(301031)\displaystyle A=\begin{pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \end{pmatrix}\quad B=\begin{pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \end{pmatrix }A=(12−1101)B=(300311)
Начните с
AAA
, добавьте вторую строку к первой:
A=(301211)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \end{pmatrix}A=(320111)
Затем умножьте вторую строку на 3, а затем вычтите первую строку из второй:
A=(301332)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \end{pmatrix}A=(330312)
Наконец, вычтите первую строку из второй:
A= (301031)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \end{pmatrix}A=(300311)
Вы можете видеть, что
A=BA=BA=B
, чего мы достигли с помощью серии элементарных операций над строками.
Сокращение строк: решение системы линейных уравнений
При сокращении строк линейная система:
x+3y−2z=53x+5y+6z=72x+4y+3z=8\displaystyle х+3у-2г=5 \\ 3х+5у+6з=7\\ 2x+4y+3z=8x+3y−2z=53x+5y+6z=72x+4y+3z=8
Представляется расширенной матрицей:
A=(13−2535672438)\displaystyle A=\begin{pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \end{pmatrix}A=⎝
⎛132354−263578⎠
⎞
Эта матрица затем модифицируется с помощью элементарных операций со строками до тех пор, пока она не примет форму сокращенного эшелона строк.
Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.
Существует несколько конкретных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана.
Это вычисление можно выполнить вручную (используя три типа ERO) или на калькуляторе с помощью матричной функции ‘rref’ (уменьшенная ступенчатая форма строки).
Окончательная матрица имеет форму сокращенного эшелонированного ряда и представляет систему
.
A=(100−1501080012)\displaystyle A=\begin{pmatrix} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{pmatrix}A=⎝
⎛100010001 −1582⎠
⎞
Упрощение матриц с помощью операций со строками
Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелонирования строк.
Цели обучения
Используйте элементарные операции со строками, чтобы представить матрицу в упрощенной форме
Ключевые выводы
Ключевые моменты
- Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк эшелонированной формы строк такое же, как и исходное.
матрица.
- Существует три типа операций с элементарными строками: поменять местами две строки, умножить строку на ненулевой скаляр и добавить к одной строке скаляр, кратный другому.
- На практике системы обычно не рассматриваются в терминах уравнений, а вместо этого используется расширенная матрица (которая также подходит для компьютерных манипуляций).
Ключевые термины
- расширенная матрица : Матрица, полученная путем сложения столбцов двух данных матриц, обычно с целью выполнения одних и тех же элементарных операций над строками на каждой из данных матриц.
С помощью конечной последовательности элементарных операций над строками, называемой методом исключения Гаусса, любая матрица может быть преобразована в ступенчатую форму строк. Это преобразование необходимо для решения системы линейных уравнений.
Прежде чем перейти к более подробному рассмотрению, следует упомянуть несколько ключевых терминов:
- Расширенная матрица : расширенная матрица — это матрица, полученная путем сложения столбцов двух заданных матриц, обычно с целью выполнения одни и те же элементарные операции над строками на каждой из заданных матриц.
- Форма верхнего треугольника : Квадратная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это либо нижняя треугольная, либо верхняя треугольная. Матрица, имеющая как верхнюю, так и нижнюю треугольную форму, является диагональной матрицей.
- Элементарные операции со строками : Перестановка строк, добавление строк или умножение строк.
Исключение Гаусса
- Напишите расширенную матрицу для линейных уравнений.
- Используйте элементарные операции со строками над расширенной матрицей
[A∣b][A|b][A∣b]
, чтобы преобразоватьAAA
в форму верхнего треугольника. Если на диагонали стоит ноль, меняйте местами строки, пока на его месте не окажется ненулевое значение.- Используйте обратную замену, чтобы найти решение.
Пример 1: Решить систему методом исключения Гаусса:
2x+y−z=8−3x−y+2z=−11−2x+y+2z=−3\displaystyle 2x+y-z=8\\ -3x-y+2z=-11\\ -2x+y+2z=-32x+y-z=8-3x-y+2z=-11-2x+y+2z=-3
Запишите расширенную матрицу:
[21-18-3-12 −11−212−3]\left[\begin{array}{rrr|r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & — 3 \end{array} \right] ⎣
⎡2−3−21−11−1228−11−3⎦
⎤
Используйте элементарные операции над строками, чтобы уменьшить матрицу до уменьшенной форма эшелона ряда:
[10020103001−1]\left[\begin{array}{rrr|r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{array } \right] ⎣
⎡10001000123−1⎦
⎤
Используя элементарные операции со строками для получения сокращенной эшелонированной формы строки (‘rref’ в калькуляторе), решение системы в последнем столбце:
x=2,y=3,z=-1x=2, y=3, z=-1x=2,y=3,z=-1
.
Лицензии и атрибуты
Контент под лицензией CC, опубликованный ранее
- Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Решающие системы с инверсиями. Предоставлено : Openstax. Расположен по адресу : https://openstax.org/books/college-алгебра/pages/7-7-solving-systems-with-inverses. Лицензия : CC BY-SA: Attribution-ShareAlike
- Матричное уравнение. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Система линейных уравнений. Предоставлено : Википедия.
Лицензия : CC BY-SA: Attribution-ShareAlike
- матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Эквивалентность строк. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Матрица (математика). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- система линейных уравнений. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/System_of_linear_equations. Лицензия : CC BY-SA: Attribution-ShareAlike
- эквивалент строки. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Исключение Гаусса. Предоставлено : Википедия.
Лицензия : CC BY-SA: Attribution-ShareAlike
- Форма эшелона строк. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Треугольная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Дуг Дэниелс и Стивен Кокс, Сокращенная форма строки. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Элементарные операции со строками. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Дополненная матрица.
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- дополненная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Матрицы и операции с матрицами | Колледж Алгебра
Результаты обучения
- Определение размеров матрицы.
- Сложите и вычтите две матрицы.
- Умножить матрицу на скаляр, суммировать скаляры, кратные матрицам.
- Перемножить две матрицы вместе.
- Используйте калькулятор для выполнения операций с матрицами.
Две клубные футбольные команды, Wildcats и Mud Cats, надеются получить новую экипировку к предстоящему сезону. В таблице показаны потребности обеих команд.
Дикие кошки Грязевые коты Цели 6 10 Шарики 30 24 Трикотажные изделия 14 20 Две команды соревнуются в футбольном матче.
(кредит: «SD Dirk», Flickr)
Гол стоит 300 долларов; мяч стоит 10 долларов; а майка стоит 30 долларов. Как мы можем найти общую стоимость оборудования, необходимого для каждой команды? В этом разделе мы открываем метод, в котором данные в таблице футбольного оборудования могут отображаться и использоваться для расчета другой информации. После этого мы сможем рассчитать стоимость оборудования.
Сложение и вычитание матриц
Чтобы решить задачу, подобную описанной для футбольных команд, мы можем использовать матрицу , которая представляет собой прямоугольный массив чисел. Строка в матрице — это набор чисел, выровненных по горизонтали. Столбец в матрице представляет собой набор чисел, выровненных по вертикали. Каждое число представляет собой элемент , иногда называемый элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами. Например, ниже показаны три матрицы с именами [latex]A,B,\text{}[/latex] и [latex]C[/latex].
[латекс]A=\left[\begin{array}{cc}1&2\\ 3&4\end{массив}\right],B=\left[\begin{array}{ccc}1&2&7\ \ 0& -5& 6\\ 7& 8& 2\end{массив}\right],C=\left[\begin{массив}{c}-1\\ 0\\ 3\end{массив}\begin{массив} {c}3\\ 2\\ 1\end{массив}\right][/latex]
Описание матриц
Матрица часто упоминается по ее размеру или измерениям: [latex]\text{ }m\text { }\times \text{ }n\text{ }[/latex] с указанием [latex]m[/latex] строк и [latex]n[/latex] столбцов. Элементы матрицы определяются сначала по строке, а затем по столбцу. Например, чтобы найти запись в матрице [latex]A[/latex], идентифицированную как [latex]{a}_{ij},\text{}[/latex], мы ищем запись в строке [latex]i, \text{}[/latex] столбец [latex]j[/latex]. В матрице [latex]A[/latex], показанной ниже, записью в строке 2 столбца 3 является [latex]{a}_{23}[/latex].
[латекс]A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {a}_{21} & {a}_{22}& {a}_{23}\\ {a}_{31}& {a}_{32}& {a}_{33}\end{массив}\right][ /latex]
Квадратная матрица — это матрица с размерами [latex]\text{ }n\text{ }\times \text{ }n,\text{}[/latex], что означает, что она имеет тот же номер строк как столбцов.
Матрица [latex]3\times 3[/latex] выше является примером квадратной матрицы.
Матрица из строк — это матрица, состоящая из одной строки с размерами [latex]1\text{ }\times \text{ }n[/latex].
[латекс]\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{array}\right][/latex ]
Матрица из столбцов — это матрица, состоящая из одного столбца с размерами [latex]m\text{ }\times \text{ }1[/latex].
[латекс]\left[\begin{array}{c}{a}_{11}\\ {a}_{21}\\ {a}_{31}\end{array}\right][ /latex]
Матрица может использоваться для представления системы уравнений. В этих случаях числа представляют собой коэффициенты переменных в системе. Матрицы часто облегчают решение систем уравнений, потому что они не перегружены переменными. Мы исследуем эту идею подробнее в следующем разделе, но сначала мы рассмотрим основные матричные операции .
A Общее примечание: Матрицы
A Матрица представляет собой прямоугольный массив чисел, который обычно обозначается заглавной буквой: [latex]A,B,C,\text{}[/latex] и так далее.
Каждая запись в матрице обозначается как [latex]{a}_{ij}[/latex], так что [latex]i[/latex] представляет строку, а [latex]j[/latex] представляет столбец. Матрицы часто упоминаются по их размерам: [латекс]m\times n[/латекс] указывает [латекс]m[/латекс] строк и [латекс]n[/латекс] столбцов.
Пример: определение размеров данной матрицы и поиск элементов
Данная матрица [latex]A:[/latex]
- Каковы размеры матрицы [latex]A?[/latex]
- Что такое записи в [latex]{a}_{31}[/latex] и [latex]{a}_{22}?[/latex]
[латекс]A=\left[\begin{array}{rrrr}\hfill 2& \hfill & \hfill 1& \hfill 0\\ \hfill 2& \hfill & \hfill 4& \hfill 7\\ \hfill 3& \ hfill & \hfill 1& \hfill -2\end{массив}\right][/latex]
Показать решение
Попробуйте
Сложение и вычитание матриц
Мы используем матрицы для перечисления данных или для представления систем. Поскольку записи являются числами, мы можем выполнять операции над матрицами.
Мы добавляем или вычитаем матрицы, добавляя или вычитая соответствующие элементы.
Для этого записи должны совпадать. Следовательно, сложение и вычитание матриц возможны только тогда, когда матрицы имеют одинаковые размеры . Мы можем добавить или вычесть матрицу [латекс]\текст{ }3\текст{ }\times \text{ }3\текст{ }[/латекс] и другую матрицу [латекс]\текст{ }3\текст{ }\times \text{ }3\text{ }[/latex] матрица, но мы не можем складывать или вычитать матрицу [latex]\text{ }2\text{ }\times \text{ }3\text{ }[/latex] и матрица [latex]\text{ }3\text{ }\times \text{ }3\text{ }[/latex], поскольку некоторым элементам в одной матрице не будет соответствующего элемента в другой матрице.
A Общее примечание: сложение и вычитание матриц
Даны матрицы [латекс]А[/латекс] и [латекс]В[/латекс] одинакового размера, сложение и вычитание [латекс]А[/латекс] и [латекс ]B[/latex] создаст матрицу [latex]C[/latex] или матрицу [latex]D[/latex] того же размера.
[латекс]A+B=C\текст{ такой, что }{a}_{ij}+{b}_{ij}={c}_{ij}[/latex]
[латекс]A-B= D\text{ такое, что }{a}_{ij}-{b}_{ij}={d}_{ij}[/latex]
Сложение матриц коммутативно.
[латекс]А+В=В+А[/латекс]
Это тоже ассоциативно.
[латекс]\влево(А+В\вправо)+С=А+\влево(В+С\вправо)[/латекс]
Пример. Нахождение суммы матриц
Нахождение суммы [латекс]А [/latex] и [latex]B \text{}[/latex] задано
[latex]A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right] \text{ и }B=\left[\begin{array}{cc}e& f\\ g& h\end{array}\right][/latex]
Показать решение
Пример: добавление матрицы
A и Matrix BНайдите сумму [латекс]А[/латекс] и [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}4& 1\\ 3& 2\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 5& 9\\ 0& 7\end{массив}\right][/latex]
Показать решение
Пример: нахождение разности двух матриц
Найдите разность [латекс]А[/латекс] и [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}-2& 3\\ 0& 1\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 8& 1\\ 5& 4\end{массив}\right][/латекс]Показать решение
Пример: нахождение суммы и разности двух матриц 3 x 3
Даны [латекс]А[/латекс] и [латекс]В:[/латекс]
- Найдите сумму.
- Найди разницу.
[латекс]A=\left[\begin{array}{rrr}\hfill 2& \hfill -10& \hfill -2\\ \hfill 14& \hfill 12& \hfill 10\\ \hfill 4& \hfill -2& \ hfill 2\end{массив}\right]\text{ и }B=\left[\begin{array}{rrr}\hfill 6& \hfill 10& \hfill -2\\ \hfill 0& \hfill -12& \hfill — 4\\ \hfill -5& \hfill 2& \hfill -2\end{массив}\right][/latex]
Показать решение
Попробуйте
Добавьте матрицу [латекс]А[/латекс] и матрицу [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{rr}\hfill 2& \hfill 6\\ \hfill 1& \hfill 0\\ \hfill 1& \hfill -3\end{массив}\right]\ text{и}B=\left[\begin{array}{rr}\hfill 3& \hfill -2\\ \hfill 1& \hfill 5\\ \hfill -4& \hfill 3\end{array}\right][ /латекс]
Показать решение
Произведения матриц
Помимо сложения и вычитания целых матриц, во многих ситуациях нам нужно умножить матрицу на константу, называемую скаляром. Напомним, что скаляр — это действительная числовая величина, которая имеет величину, но не направление.
Например, время, температура и расстояние являются скалярными величинами. Процесс скалярного умножения включает умножение каждого элемента матрицы на скаляр. Скалярное число , кратное , — это любой элемент матрицы, полученный в результате скалярного умножения.
Рассмотрим реальный сценарий, в котором университету необходимо добавить к своему инвентарю компьютеры, компьютерные столы и стулья в двух лабораториях кампуса в связи с увеличением числа учащихся. По их оценкам, в обеих лабораториях требуется на 15% больше оборудования. Текущий инвентарь школы отображается в таблице ниже.
Лаборатория А Лаборатория Б Компьютеры 15 27 Компьютерные столы 16 34 Стулья 16 34 Преобразовав данные в матрицу, мы имеем
[латекс]{C}_{2013}=\left[\begin{array}{c}15\\ 16\\ 16\end{array}\ begin{array}{c}27\\ 34\\ 34\end{array}\right][/latex]
Чтобы рассчитать, сколько потребуется компьютерного оборудования, мы умножаем все записи в матрице [latex]C[/latex] на 0,15.
[латекс]\влево(0,15\вправо){C}_{2013}=\влево[\begin{массив}{c}\влево(0,15\вправо)15\\ \влево(0,15\вправо)16\ \\left(0.15\right)16\end{массив}\begin{массив}{c}\left(0.15\right)27\\ \left(0.15\right)34\\ \left(0.15\right)34 \end{массив}\right]=\left[\begin{массив}{c}2.25\\ 2.4\\ 2.4\end{массив}\begin{массив}{c}4.05\\ 5.1\\ 5.1\end{ array}\right][/latex]
Мы должны округлить до следующего целого числа, поэтому количество необходимого нового оборудования равно
[латекс]\влево[\begin{array}{c}3\\ 3\\ 3\end{массив}\begin{array}{c}5\\ 6\\ 6\end{массив}\right ][/latex]
Складывая две матрицы, как показано ниже, мы видим новые суммы запасов.
[латекс]\влево[\begin{массив}{c}15\\ 16\\ 16\конец{массив}\begin{массив}{c}27\\ 34\\ 34\конец{массив}\вправо ]+\left[\begin{array}{c}3\\ 3\\ 3\end{array}\begin{array}{c}5\\ 6\\ 6\end{array}\right]=\ left[\begin{array}{c}18\\ 19\\ 19\end{array}\begin{array}{c}32\\ 40\\ 40\end{array}\right][/latex]
Это означает
[латекс]{C}_{2014}=\left[\begin{array}{c}18\\ 19\\ 19\end{array}\begin{array}{c}32\\ 40\\ 40\end{array}\right][/latex]
Таким образом, в лаборатории А будет 18 компьютеров, 19 компьютерных столов и 19 стульев; В лаборатории B будет 32 компьютера, 40 компьютерных столов и 40 стульев.
A Общее примечание: Скалярное умножение
Скалярное умножение включает в себя нахождение произведения константы по каждому элементу матрицы. Учитывая
[латекс]A=\left[\begin{array}{cccc}{a}_{11}& & & {a}_{12}\\ {a}_{21}& & & {a }_{22}\end{массив}\right][/latex]
скалярное кратное [латекс]cA[/латекс] равно
[латекс]\begin{array}{ll}cA & =c\left[\begin{array}{ccc}{a}_{11}& & {a}_{12}\\ {a}_{21}& & {a}_{22}\end{массив}\right]\hfill \\ & =\left[\begin{массив}{ccc }c{a}_{11}& & c{a}_{12}\\ c{a}_{21}& & c{a}_{22}\end{массив}\right]\hfill \ end{array}[/latex]
Скалярное умножение является дистрибутивным. Для матриц [latex]A,B[/latex] и [latex]C[/latex] со скалярами [latex]a[/latex] и [latex]b[/latex],
[латекс]\begin{array}{l}\\ \begin{array}{c}a\left(A+B\right)=aA+aB\\ \left(a+b\right)A= aA+bA\end{array}\end{array}[/latex]
Пример: умножение матрицы на скаляр
Умножение матрицы [latex]A[/latex] на скаляр 3.
[latex]A =\left[\begin{array}{cc}8& 1\\ 5& 4\end{array}\right][/latex]
Показать решение
Попробуйте
По заданной матрице [латекс]B,\текст{}[/латекс] найдите [латекс]-2В[/латекс], где
[латекс]В=\left[\begin{array}{cc} 4& 1\\ 3& 2\end{массив}\right][/latex]
Показать решение
Пример: нахождение суммы скалярных кратных
Найдите сумму [латекс]3А+2В[/латекс].
[латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill -2& \hfill 0\\ \hfill 0& \hfill -1& \hfill 2\\ \hfill 4& \hfill 3& \hfill -6\end{массив}\right]\text{ и }B=\left[\begin{array}{rrr}\hfill -1& \hfill 2& \hfill 1\\ \hfill 0& \hfill -3& \hfill 2 \\ \hfill 0& \hfill 1& \hfill -4\end{массив}\right][/latex]
Показать решение
Попробуйте
Нахождение произведения двух матриц
Помимо умножения матрицы на скаляр, мы можем умножать две матрицы. Нахождение произведения двух матриц возможно только тогда, когда внутренние размерности совпадают, что означает, что количество столбцов первой матрицы равно количеству строк второй матрицы. Если [latex]A[/latex] является матрицей [latex]\text{ }m\text{ }\times \text{ }r\text{ }[/latex], а [latex]B[/latex] является [latex]\text{ }r\text{ }\times \text{ }n\text{ }[/latex] матрица, то матрица произведения [latex]AB[/latex] является [latex]\text{ } m\text{ }\times \text{ }n\text{ }[/latex] матрица.
Например, продукт [latex]AB[/latex] возможен, потому что количество столбцов в [latex]A[/latex] совпадает с количеством строк в [latex]B[/latex]. Если внутренние размеры не совпадают, товар не определяется.
Мы умножаем записи [latex]A[/latex] на записи [latex]B[/latex] в соответствии с определенным шаблоном, как показано ниже. Процесс умножения матрицы на становится понятнее при решении задачи с вещественными числами.
Чтобы получить элементы в строке [latex]i[/latex] массива [latex]AB,\text{}[/latex], мы умножаем элементы в ряду [latex]i[/latex] массива [latex]A[ /latex] по столбцу [latex]j[/latex] в [latex]B[/latex] и добавить. Например, даны матрицы [латекс]А[/латекс] и [латекс]В,\текст{}[/латекс], где размеры [латекс]А[/латекс] равны [латекс]2\текст{ }\times \text{ }3[/latex] и размеры [latex]B[/latex] равны [latex]3\text{ }\times \text{ }3,\text{}[/latex] произведению [ latex]AB[/latex] будет матрицей [latex]2\text{ }\times \text{ }3[/latex].
[латекс]A=\left[\begin{array}{rrr}\hfill {a}_{11}& \hfill {a}_{12}& \hfill {a}_{13}\\ \ hfill {a}_{21}& \hfill {a}_{22}& \hfill {a}_{23}\end{массив}\right]\text{ и }B=\left[\begin{массив }{rrr}\hfill {b}_{11}& \hfill {b}_{12}& \hfill {b}_{13}\\ \hfill {b}_{21}& \hfill {b} _{22}& \hfill {b}_{23}\\ \hfill {b}_{31}& \hfill {b}_{32}& \hfill {b}_{33}\end{массив} \right][/latex]
Умножьте и сложите следующим образом, чтобы получить первую запись матрицы произведений [latex]AB[/latex].
- Чтобы получить запись в строке 1, столбце 1 [latex]AB,\text{}[/latex] умножьте первую строку в [latex]A[/latex] на первый столбец в [latex]B[ /латекс] и добавить.
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right]\cdot \left [\begin{массив}{c}{b}_{11}\\ {b}_{21}\\ {b}_{31}\end{массив}\right]={a}_{11} \cdot {b}_{11}+{a}_{12}\cdot {b}_{21}+{a}_{13}\cdot {b}_{31}[/latex]
- Чтобы получить запись в строке 1, столбце 2 [latex]AB,\text{}[/latex] умножьте первую строку [latex]A[/latex] на второй столбец в [latex]B[/latex]. ] и добавить.
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right]\cdot \left [\begin{массив}{c}{b}_{12}\\ {b}_{22}\\ {b}_{32}\end{массив}\right]={a}_{11} \cdot {b}_{12}+{a}_{12}\cdot {b}_{22}+{a}_{13}\cdot {b}_{32}[/latex]
- Чтобы получить запись в строке 1, столбце 3 в [latex]AB,\text{}[/latex] умножьте первую строку [latex]A[/latex] на третий столбец в [latex]B[/latex].
] и добавить.
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right]\cdot \left [\begin{массив}{c}{b}_{13}\\ {b}_{23}\\ {b}_{33}\end{массив}\right]={a}_{11} \cdot {b}_{13}+{a}_{12}\cdot {b}_{23}+{a}_{13}\cdot {b}_{33}[/latex]
Таким же образом получаем вторую строку [latex]AB[/latex]. Другими словами, строка 2 таблицы [latex]A[/latex] умножается на столбец 1 таблицы [latex]B[/latex]; 2-я строка [latex]A[/latex] умножается на 2-й столбец [latex]B[/latex]; строка 2 из [latex]A[/latex] умножается на столбец 3 из [latex]B[/latex]. По завершении матрица продукта будет иметь вид
[латекс]AB=\left[\begin{array}{c}\begin{array}{l}{a}_{11}\cdot {b}_{11} +{a}_{12}\cdot {b}_{21}+{a}_{13}\cdot {b}_{31}\\ \end{массив}\\ {a}_{21} \cdot {b}_{11}+{a}_{22}\cdot {b}_{21}+{a}_{23}\cdot {b}_{31}\end{массив}\begin {массив}{c}\begin{массив}{l}{a}_{11}\cdot {b}_{12}+{a}_{12}\cdot {b}_{22}+{a }_{13}\cdot {b}_{32}\\ \end{массив}\\ {a}_{21}\cdot {b}_{12}+{a}_{22}\cdot { b}_{22}+{a}_{23}\cdot {b}_{32}\end{массив}\begin{массив}{c}\begin{массив}{l}{a}_{11 }\cdot {b}_{13}+{a}_{12}\cdot {b}_{23}+{a}_{13}\cdot {b}_{33}\\ \end{массив }\\ {a}_{21}\cdot {b}_{13}+{a}_{22}\cdot {b}_{23}+{a}_{23}\cdot {b}_ {33}\end{массив}\right][/latex]
A Общее примечание: свойства умножения матриц
Для матриц [latex]A,B,\text{}[/latex] и [latex]C[/latex] выполняются следующие свойства.
- Умножение матриц ассоциативно:
[латекс]\влево(AB\вправо)C=A\влево(BC\вправо)[/латекс]
- Умножение матриц распределительное:
[латекс]\begin{массив}{l}\begin{массив}{l}\\ C\left(A+B\right)=CA+CB,\end{массив}\hfill \\ \left(A +B\right)C=AC+BC.\hfill \end{массив}[/latex]
Обратите внимание, что умножение матриц не является коммутативным.
Пример: перемножение двух матриц
Умножьте матрицу [латекс]А[/латекс] и матрицу [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 5& 6\\ 7& 8\end{массив}\right][/latex]
Показать решение
Пример: умножение двух матриц
Даны [латекс]А[/латекс] и [латекс]В:[/латекс]
- Найдите [латекс]AB[/латекс].
- Найти [латекс]БА[/латекс].
[латекс]A=\left[\begin{array}{l}\begin{array}{ccc}-1& 2& 3\end{array}\hfill \\ \begin{array}{ccc}4& 0& 5 \end{массив}\hfill \end{массив}\right]\text{ и }B=\left[\begin{массив}{c}5\\ -4\\ 2\end{массив}\begin{массив }{c}-1\\ 0\\ 3\end{массив}\right][/latex]
Показать решение
Вопросы и ответы
Можно ли определить AB, но не BA?
Да, рассмотрим матрицу A размерностью [латекс]3\умножить на 4[/латекс] и матрицу В размерностью [латекс]4\умножить на 2[/латекс].
Для продукта AB внутренние размеры равны 4, и продукт определен, но для продукта BA внутренние размеры равны 2 и 3, поэтому продукт не определен.
Пример: использование матриц в реальных задачах
Вернемся к проблеме, представленной в начале этого раздела. У нас есть таблица ниже, представляющая потребности в оборудовании двух футбольных команд.
Дикие кошки Грязевые коты Цели 6 10 Шарики 30 24 Трикотажные изделия 14 20 Также указаны цены на оборудование, как показано в таблице ниже.
Цель 300 долларов Шар 10 долларов Джерси $30 Преобразуем данные в матрицы.
Таким образом, матрица потребности в оборудовании записывается как
[латекс]E=\left[\begin{array}{c}6\\ 30\\ 14\end{array}\begin{array}{c}10\\ 24\\ 20\end{array}\ right][/latex]
Матрица стоимости записывается как
[latex]C=\left[\begin{array}{ccc}300& 10& 30\end{array}\right][/latex]
Выполняем умножение матриц для получения стоимости оборудования.
[латекс]\begin{array}{l}\hfill \\ \hfill \\ CE & =\left[\begin{array}{rrr}\hfill 300& \hfill 10& \hfill 30\end{массив}\right ]\cdot \left[\begin{array}{rr}\hfill 6& \hfill 10\\ \hfill 30& \hfill 24\\ \hfill 14& \hfill 20\end{массив}\right]\hfill \\ & = \left[\begin{array}{rr}\hfill 300\left(6\right)+10\left(30\right)+30\left(14\right)& \hfill 300\left(10\right) +10\влево(24\вправо)+30\влево(20\вправо)\конец{массив}\вправо]\hfill \\ & =\влево[\begin{массив}{rr}\hfill 2520& \hfill 3840 \end{массив}\right]\hfill \end{массив}[/latex]Общая стоимость снаряжения для Диких Котов составляет 2520 долларов, а общая стоимость снаряжения для Грязных Котов — 3840 долларов.
Практическое руководство. Вычисление матричной операции с помощью калькулятора
- Сохранение каждой матрицы как матричной переменной
[латекс]\влево[A\вправо],\влево[B\вправо],\влево[C\вправо],..[/латекс]
- Введите операцию в калькулятор, вызывая каждую переменную матрицы по мере необходимости.
- Если операция определена, калькулятор представит матрицу решения; если операция не определена, будет отображаться сообщение об ошибке.
Пример: использование калькулятора для выполнения операций с матрицами \hfill 32\\ \hfill 41& \hfill -7& \hfill -28\\ \hfill 10& \hfill 34& \hfill -2\end{массив}\right],B=\left[\begin{array}{rrr} \hfill 45& \hfill 21& \hfill -37\\ \hfill -24& \hfill 52& \hfill 19\\ \hfill 6& \hfill -48& \hfill -31\end{массив}\right],\text{and}C =\left[\begin{массив}{rrr}\hfill -100& \hfill -89& \hfill -98\\ \hfill 25& \hfill -56& \hfill 74\\ \hfill -67& \hfill 42& \hfill -75\end{массив}\right][/latex].
Показать решение
Основные понятия
- Матрица представляет собой прямоугольный массив чисел. Записи расположены в строках и столбцах.
- Размеры матрицы относятся к количеству строк и количеству столбцов. Матрица [latex]3\times 2[/latex] имеет три строки и два столбца.
- Мы складываем и вычитаем матрицы одинаковой размерности, добавляя и вычитая соответствующие элементы каждой матрицы.
- Скалярное умножение включает умножение каждого элемента матрицы на константу.
- Перед сложением или вычитанием часто требуется скалярное умножение.
- Умножение матриц возможно при одинаковых внутренних размерностях — количество столбцов в первой матрице должно совпадать с количеством строк во второй.
- Произведение двух матриц, [латекс]А[/латекс] и [латекс]В[/латекс], получается путем умножения каждой записи в строке 1 матрицы [латекс]А[/латекс] на каждую запись в столбце 1 матрицы [латекс]В[/латекс]; затем умножьте каждую запись строки 1 [latex]A[/latex] на каждую запись в столбцах 2 [latex]B,\text{}[/latex] и так далее.


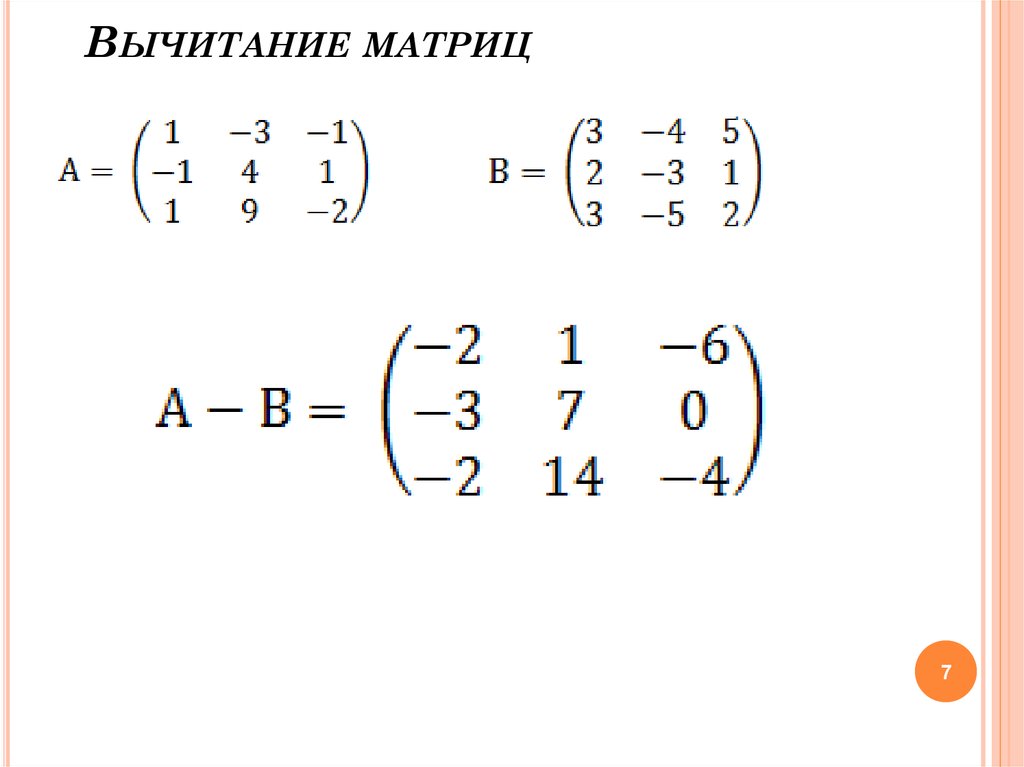
 Далее директора по направлениям на основании матрицы стратегии развития завода разработали матрицы по каждой службе и так до уровня отделов. Это позволило довести глобальные цели и тактические задачи ТМХ, определенные руководством, до конкретных исполнителей. Таким образом, все сотрудники стали понимать свою личную роль и вклад в стратегическое развитие предприятия. В настоящее время перед руководителями завода всех уровней стоит задача по ежемесячному анализу исполнения тактических задач и планов мероприятий для оперативного реагирования на возможные отклонения. Такой подход позволил систематизировать деятельность различных подразделений в рамках целей завода, установил целевые состояния процессов.
Далее директора по направлениям на основании матрицы стратегии развития завода разработали матрицы по каждой службе и так до уровня отделов. Это позволило довести глобальные цели и тактические задачи ТМХ, определенные руководством, до конкретных исполнителей. Таким образом, все сотрудники стали понимать свою личную роль и вклад в стратегическое развитие предприятия. В настоящее время перед руководителями завода всех уровней стоит задача по ежемесячному анализу исполнения тактических задач и планов мероприятий для оперативного реагирования на возможные отклонения. Такой подход позволил систематизировать деятельность различных подразделений в рамках целей завода, установил целевые состояния процессов. Это как раз и есть принцип каскадирования. Когда командующий ставит цели, каждый солдат должен не только знать, но и понимать свой маневр. Применительно к нашему производству: оператор не просто пришел и сделал деталь, но и знает, почему сегодня такой уровень заказов, почему требуется оптимизация площадей, рационализация техпроцессов, внедрение системы 5С на рабочих местах и т. д. Это один из методов производственной системы, который позволяет создать команду, способную улавливать и видеть изменения обстановки, уметь их анализировать, вырабатывать на эти изменения комплекс действий и претворять их в жизнь.
Это как раз и есть принцип каскадирования. Когда командующий ставит цели, каждый солдат должен не только знать, но и понимать свой маневр. Применительно к нашему производству: оператор не просто пришел и сделал деталь, но и знает, почему сегодня такой уровень заказов, почему требуется оптимизация площадей, рационализация техпроцессов, внедрение системы 5С на рабочих местах и т. д. Это один из методов производственной системы, который позволяет создать команду, способную улавливать и видеть изменения обстановки, уметь их анализировать, вырабатывать на эти изменения комплекс действий и претворять их в жизнь.
 Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
 Количество строк и столбцов одинаковое: m=n.
Количество строк и столбцов одинаковое: m=n.
