Вектор как решать: 3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»

Задачи с векторами

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-11-10

    Задачи с векторами на ЕГЭ. Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.

Также загляните в справочник на блоге. Если нужно вспомнить, что такое абсцисса и ордината точки, тогда посмотрите эту статью. Кратко повторим:

Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала:

Формула для определения длины вектора, если известны координаты его начала и конца:

Формула для определения длины вектора, если известны его координаты:

27725. Вектор АВ с началом в точке A(2;4) имеет координаты (6;2). Найдите ординату точки B.

Как уже сказано координаты вектора находятся следующим образом: из соответствующих координат конца вычитаются координаты начала вектора. То есть:

Координаты вектора нам даны, координаты его начала тоже, значит:

Следовательно можем найти координаты точки В:

х₂ – 2 = 6         у₂ – 4 = 2

х₂  = 8             у₂  = 6

Таким образом, ордината точки В равна 6.

Ответ: 6

27726. Вектор АВ с началом в точке A(3;6) имеет координаты (9;3). Найдите сумму координат точки B. 

Задача по процессу решения такая же как и предыдущая, но иначе поставлен вопрос. Вычисления так же находятся в пределах устного счёта. Ещё раз запишем координаты вектора, когда известны координаты его начала и конца:

Координаты вектора и координаты его начала даны, значит:

Можем найти координаты точки В:

х₂ – 3 = 9         у₂ – 6 = 3

х₂  = 12             у₂  = 9

Таким образом, сумма координат точки В равна 21.

Ответ: 21

27727. Вектор АВ с концом в точке B (5;3) имеет координаты (3;1). Найдите абсциссу и ординату точки A, также сумму её координат. 

Нам известны  координаты вектора и координаты его конца, значит:

Можем найти координаты точки А:

5 – х₁  = 3        3 – у₁  = 1

х₁  = 2             у₁  = 2

Таким образом, абсцисса точки А равна двум,  ордината тоже равна двум, а сумма координат равна  2+2 = 4.

Ответ: 4

27731 Найдите квадрат длинны вектора a+b.

В данной задаче необходимо найти координаты вектора, который является суммой указанных векторов, затем найти его длину и возвести её в квадрат. Запишем формулу длины вектора, если известны его координаты:

Или в другой форме:

Найдём координаты вектора, который является суммой данных векторов. Для этого сначала найдём координаты данных векторов. 

Рассмотрим вектор:

Рассмотрим вектор:

*Можно было глядя на эскиз сразу их записать, так как точки их начал совпадают с началом координат.

Теперь найдём координаты вектора являющегося их суммой:

(2 + 8; 6 + 4) = (10;10)

Таким образом, длина  вектора являющегося суммой векторов a и b равна:

Следовательно квадрат длины будет равен 200.

*Имея опыт в решении подобных задач, можно сразу записывать:

Как видите, вычисления можно осуществить устно. Здесь для вас умышленно представлено подробное решение.

Ответ: 200

27733. Найдите квадрат длины вектора a – b.

Задача аналогична предыдущей. Необходимо найти координаты вектора, который является разностью представленных векторов, затем найти его длину и результат возвести в квадрат.

Координаты данных векторов нам уже известны (из предыдущей задачи):

Теперь найдём координаты вектора, который является их разностью: 

(2 – 8; 6 – 4) = (–6;2)

Таким образом, длина  вектора, который является разностью векторов

Следовательно квадрат её длины будет равен 40.

*Можно сразу записывать и вычислять:

Ответ: 40

27723. Найдите сумму координат вектора АВ.

Посмотреть решение

27724.Вектор АВ с началом А(2;4) имеет координаты (6;2) Найдите абсциссу точки В.

Посмотреть решение

27730. Найдите сумму координат вектора а + b.

Посмотреть решение

27732. Найдите сумму координат вектора а–b.

Посмотреть решение

27736. Найдите сумму координат вектора а + b

Посмотреть решение

27739. Найдите квадрат длины вектора а–b.

Посмотреть решение

Вы убедились, что задачи с векторами на ЕГЭ это одни из самых простых заданий. Есть, конечно, задания со скалярным произведением векторов, но о они сложности не представляют, нужно лишь знать формулу скалярного произведения. Такие задачи мы также рассмотрим, не пропустите!

На этом всё. Если что-то непонятно, пишите. Успеха Вам!

С уважением, Александр Крутицких

Уроки сделаны… Мама охрипла… Сын оглох … Соседи выучили всё наизусть, собака пересказала!!!. .

P.S: Делитесь  этой статьёй в сетях.

Категория: Векторы | ЕГЭ-№1

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Применение векторов в решении задач

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Применение
векторов в решении
задач
Цели урока:
1.Повторить понятие
“вектор”, действия над
векторами;
2.Рассмотреть применение
векторов в задачах разного
вида.
Понятие вектора
в физике
в математике

Изучаем векторные величины
( F, v , S )
Изучаем векторы ( a ,b , c )
Чаще есть точка приложения ( на теле
)
Вектор можно отложить от любой точки
плоскости
Правила сложения векторов
Чаще применяем правило
параллелограмма
Правило треугольника и правило
параллелограмма
Длину вектора называем длиной
Длину вектора называем модулем

4. Главное отличие – точка приложения!

Понятия вектора в
физике отличается
от понятия вектора
в математике –
точкой приложения.

5. Разминка Задачи на движение : векторные величины направлены вдоль одной прямой

1
Определите скорость катера относительно
берега.
vпо теч. =6м/с
vсоб =5м/c
vтеч =1м/с
2
Определите скорость катера
относительно берега.
vпр. теч. =4м/с
vсоб =5м/c
vтеч =1м/с

8. Задачи на движение : векторные величины лежат в одной плоскости

3
4
5
6
далее
3
v
Fп
На рисунке показаны силы,
действующие на самолет, и
направление вектора скорости
в некоторый момент времени.
F – сила тяги,
FC
F
Fc– сила лобового
сопротивления,
Fт – сила тяжести,
FT
В каком направлении движется
самолет, если
FT = Fп
F = FC
Fп – подъемная сила.
4
Fп
v
F
На рисунке показаны силы,
действующие на самолет, и
направление вектора
скорости в некоторый момент
времени.
FC
R
F – сила тяги,
Fc– сила лобового
сопротивления,
Fт – сила тяжести,
FT
В каком направлении движется
самолет, если
FT = Fп
F > FC
Fп – подъемная сила.
5
v
На рисунке показаны силы,
действующие на самолет, и
направление вектора скорости
в некоторый момент времени.
Fп
F
FC
R
FT
В каком направлении движется
самолет, если
FT > Fп
F = FC
F – сила тяги,
Fc– сила лобового
сопротивления,
Fт – сила тяжести,
Fп – подъемная сила.
6
v
Fп
На рисунке показаны силы,
действующие на самолет, и
направление вектора скорости
в некоторый момент времени.
R
F – сила тяги,
FC
F
FT
В каком направлении движется
самолет, если
FT < Fп
F = FC
Fc– сила лобового
сопротивления,
Fт – сила тяжести,
Fп – подъемная сила.
Fп
7
555 Н
5Н
162 Н
F
150 Н
12 Н
FC
FT
550 Н
На самолет действует в
вертикальном направлении
сила тяжести 550 Н и
подъемная сила 555 Н, а в
горизонтальном
направлении – сила тяги
162 Н и сила сопротивления
воздуха 150 Н. Найти
модуль и направление
равнодействующей.
Катер, переправляясь через реку,
движется перпендикулярно течению реки
со скоростью 4 м/с в системе отсчета,
связанной с водой. На сколько метров
будет снесен катер течением, если
ширина реки 800 м, а скорость течения 1
м/с?
1 м/с
8
800 м
А
4 м/с В
С
D
?
200 м
E
9
А
4
м/c
С
3
м/c
5
м/c
Груз опускается на парашюте
с высоты 120 м с постоянной
вертикальной скоростью 4
м/с. Ветер, дующий
горизонтально, относит его в
сторону со скоростью 3 м/с.
Какой путь пролетает груз?
В
120 м
150 м
E

16. Применение векторов в литературных произведениях

17. Вектор в сказке!

18. Почему дед не смог вытянуть репку, а мышь смогла? Разве она самая сильная?

10
Почему дед не смог вытянуть репку, а мышь
смогла?
Разве она самая сильная?

19. Вектор в басне!

English     Русский Правила

Как решать задачи кинематики: руководство по векторам

Эта статья является третьей главой в серии о том, как понимать задачи кинематики и подходить к ним. В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.

Что такое вектор?

Есть много способов думать о векторах, но основное определение — это величина (число) и направление. Так что «четыре метра на восток» — это просто вектор в словесной форме. Вы также можете думать о векторе как о стрелке; он указывает определенное расстояние в определенном направлении.

Все это векторы, причем красивые векторы.

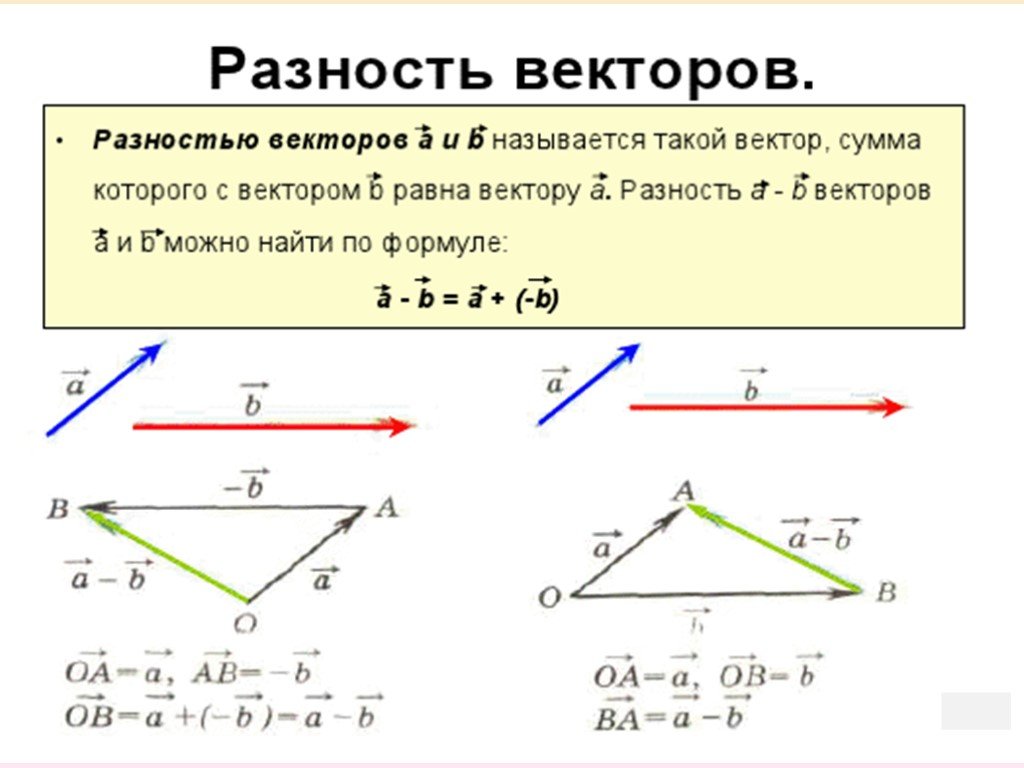
Добавление векторов

Добавление векторов работает не так, как добавление чисел. Мы не можем просто суммировать величины (это распространенная ошибка), потому что это не учитывает направление. В конце концов, если вы пройдете 8 метров на восток, а затем 5 метров на запад, вы не окажетесь в 13 метрах от того места, откуда начали; вам будет всего 3 года (мы видели вариант этой идеи в главе 1, посвященной перемещению)

При сложении векторов вместо суммирования величин мы наклеиваем один на конец другого и смотрим, где они окажутся.

Итак, если я хочу добавить этот вектор к этому вектору

, я могу соединить их вместе, чтобы получить:

Мы называем красный вектор «результирующим». потому что это вектор, который получается от сложения двух векторов вместе

Компоненты вектора

Чтобы прояснить векторы, мы часто записываем их как сумму их «компонентов». Каждый компонент сообщает, как далеко заходят векторы в определенном направлении. Обычно согласованный набор направлений составляет x̂,   ŷ , ẑ . В книгах по физике эти направления иногда называют х , х , k̂ , потому что они глупы (на самом деле это делается для упрощения векторных полей, когда дело доходит до продвинутого уровня).

Почему это работает? Добавление вектора! Поскольку векторы складываются, мы можем думать о каждом векторе как о сумме 2 (в 2D) или 3 (в 3D) векторов, которые движутся только в направлениях x, y или z.

Запись компонентов означает единичный вектор, который представляет собой просто вектор, указывающий в определенном направлении (например, x̂   точек в направлении x) и имеющий длину, равную единице. Умножая этот единичный вектор на число, вы создаете более длинный вектор в том же направлении.

Нахождение компонентов вектора

Допустим, вы получили вектор с определенной величиной и углом от горизонтали (также известный как ось x) и хотите найти компоненты векторов. Это очень распространено в кинематике и за ее пределами, но как вы это делаете? Ответ тот же, что и у любой успешной фолк-рок группы: правильное использование треугольников.

Помните, мы разделили наш вектор на компоненты? Вы могли заметить, что компоненты и исходный вектор образуют прямоугольный треугольник. Это связано с тем, что оси x и y по определению всегда расположены под углом 90° друг к другу. Вы также можете помнить из геометрии, что если у нас есть угол и гипотенуза прямоугольного треугольника, то мы можем найти другие стороны (называемые катетами) с помощью SOH-CAH-TOA.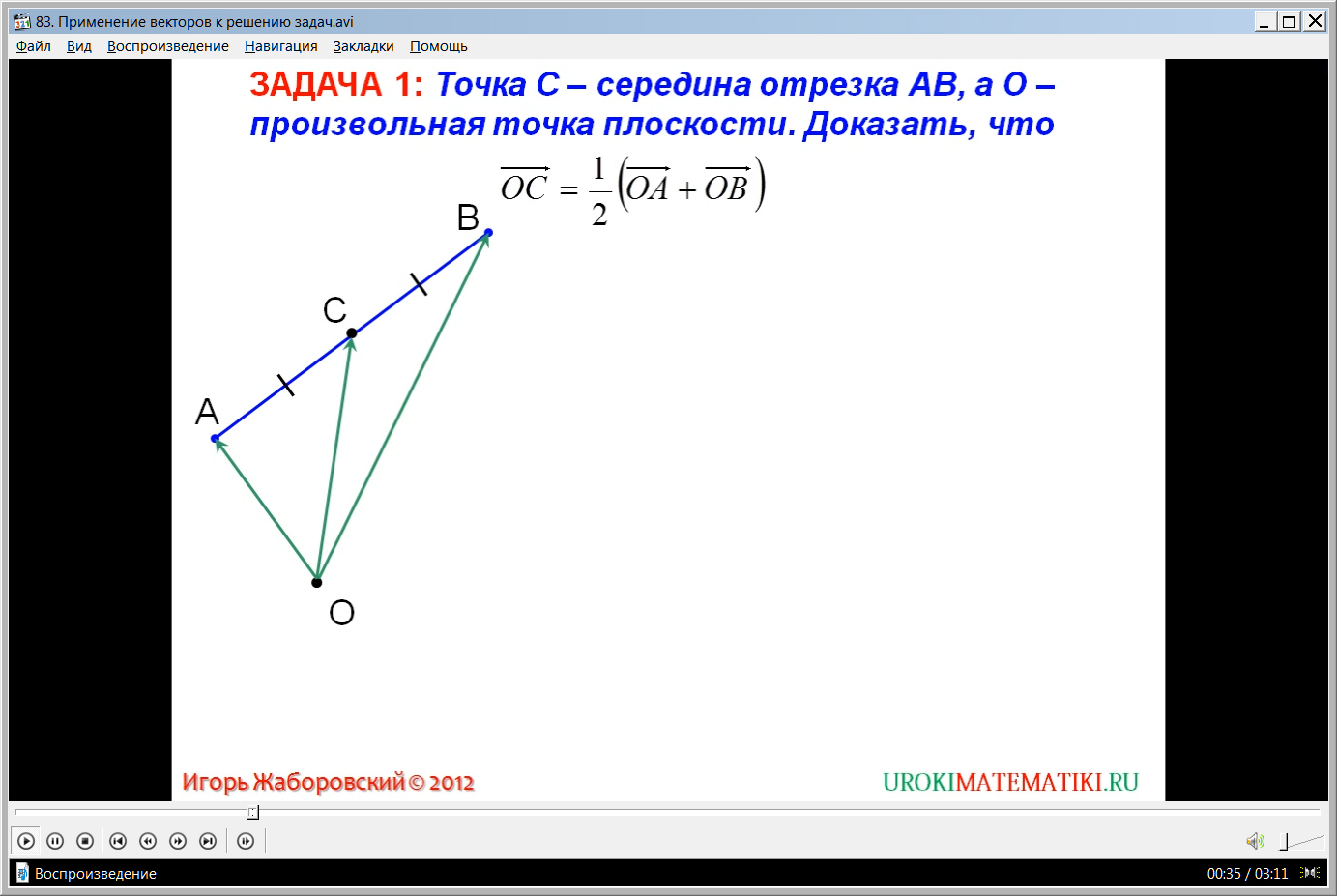

Краткий обзор SOH-CAH-TOA

Вы можете найти более подробные обзоры в Интернете, но основная идея SOH-CAH-TOA заключается в том, что синус угла равен стороне, противоположной углу деленная на гипотенузу (таким образом, S=O/H или SOH). Точно так же косинус равен прилежащей стороне относительно гипотенузы (C=A/H), а тангенс равен противолежащей стороне прилежащей стороны (T=O/A). Используя это, легко доказать, что вертикальный катет, направление y, нашего составного треугольника будет гипотенузой*sin(угол). Или, поскольку гипотенуза — это исходный вектор, векторная величина*sin(угол). Точно так же направление x будет просто векторной величиной * cos (угол).

Пример: Нахождение компонентов вектора

У меня есть вектор величиной 5 метров, который направлен вверх и вправо под углом 37 градусов к оси x. Я хочу знать форму компонента. Давайте проработаем это.

Шаги:

1. Нарисуйте вектор.
   
2. Добавьте треугольные ножки.
   
3. Math

   Y-направление = величина * sin(угол) = 5 метров * sin (37) = 3 метра

   x-направление = величина * cos(угол) = 5 метров * cos (37) = 4 метра
4. Подставьте решения к определению вектора

   Вектор = 3x̂ + 4 х

   Тада, просто как π!

Определение величины и направления с помощью компонентов

Иногда вам могут быть заданы компоненты вектора, и вы хотите найти общую величину и угловое направление этого вектора. И снова на помощь приходят треугольники.

Величину вектора легко вычислить по теореме Пифагора. Из теоремы Пифагора a ² +b ² =c ² , поэтому, когда мы применим это к векторам: — компонент) ² .

Чтобы найти угловое направление вектора, мы можем использовать арктангенс. Поскольку тангенс равен стороне, противоположной прилежащей стороне (T=O/A):

tan(угол вектора)=(y-компонента)/(x-компонента)

Затем используйте функцию invtan на вашем калькуляторе, чтобы найти обратную сторону этого тангенса, которая дает вам угол.

Добавление векторов с компонентами

Самое лучшее в векторных компонентах то, что они упрощают добавление векторов. Пока мы сохраняем компоненты x, y и z разными, мы можем просто добавлять компоненты. Таким образом, если V ₁ = (x ₁ , y ₁ , z ₁ ) и V ₂ = (x ₂ , y _{2 901 80 , з 2 ), то вектор их суммы равен V 1 +V 2 =(x 1 +x 2 , y 1 +y 2 , я 1 + я 2 ). Когда у вас есть этот новый вектор, вы можете использовать предыдущий раздел, чтобы найти величину и угловое направление.}

Заключение

Теперь мы знаем, что такое вектор, как разделить его на компоненты, как сложить эти компоненты и как рекомбинировать его по величине и углу. В нашем следующем блоге мы обсудим, как использовать эти векторы для кинематики в двух измерениях.

Нахождение компонентов вектора

Как упоминалось ранее в этом уроке, любой вектор, направленный под углом к ​​горизонтали (или вертикали), можно рассматривать как состоящий из двух частей (или компонент). То есть любой вектор, направленный в двух измерениях, можно рассматривать как имеющий две компоненты. Например, если цепь тянет вверх под углом ошейник собаки, то возникает сила натяжения, направленная в двух измерениях. Эта сила натяжения имеет две составляющие: направленную вверх и направленную вправо составляющую. В качестве другого примера рассмотрим самолет, который перемещается на северо-запад из международного аэропорта О’Хара (в Чикаго) в пункт назначения в Канаде. Вектор смещения плоскости находится в двух измерениях (северо-запад). Таким образом, этот вектор смещения имеет две составляющие: северную и западную.

В этом разделе мы изучаем два основных метода определения величин компонент вектора, направленного в двух измерениях. Процесс определения величины вектора известен как разрешение вектора . Мы рассмотрим два метода векторного разрешения:

• метод параллелограмма
• тригонометрический метод

 

Параллелограммный метод векторного разрешения

Метод параллелограмма векторного разрешения включает использование точно нарисованной масштабированной векторной диаграммы для определения компонентов вектора. Кратко говоря, этот метод включает в себя рисование вектора в масштабе в указанном направлении, рисование параллелограмма вокруг вектора таким образом, чтобы вектор был диагональю параллелограмма, и определение величины компонентов (сторон параллелограмма) с использованием масштаба. . Если кто-то хочет определить компоненты, направленные вдоль традиционных осей координат x и y, то параллелограмм представляет собой прямоугольник со сторонами, вытянутыми по вертикали и горизонтали. Пошаговая процедура использования метода параллелограмма векторного разрешения:

1. Выберите масштаб и точно нарисуйте вектор для масштабирования в указанном направлении.
2. Нарисуйте параллелограмм вокруг вектора: начиная с конца вектора, нарисуйте вертикальные и горизонтальные линии; затем нарисуйте горизонтальные и вертикальные линии в начале вектора; нарисованные линии встретятся, образуя прямоугольник (частный случай параллелограмма).
3. Нарисуйте компоненты вектора. Компонентами являются сторон параллелограмма. Хвост компонентов начинается в хвосте вектора и тянется по осям до ближайшего угла параллелограмма. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо).
4. Осмысленно пометьте компоненты векторов символами, чтобы указать, какой компонент представляет какую сторону. Компонент сил, направленный на север, может быть обозначен F _север . Компонент скорости, направленный вправо, можно обозначить как v _x ; и т.д.
5. Измерьте длину сторон параллелограмма и с помощью шкалы определите величину компонентов в реальных единицах. Обозначьте величину на схеме.

Пошаговая процедура, описанная выше, проиллюстрирована на диаграмме ниже, чтобы показать, как вектор скорости с величиной 50 м/с и направлением 60 градусов выше горизонтали может быть разделен на две составляющие. На диаграмме показано, что вектор сначала рисуется в масштабе в указанном направлении; вокруг вектора начерчен параллелограмм; компоненты обозначены на схеме; и результат измерения длины компонентов вектора и преобразования в м/с с использованием шкалы. (ПРИМЕЧАНИЕ: поскольку разные компьютерные мониторы имеют разное разрешение, реальная длина вектора на вашем мониторе может быть меньше 5 см.)

 

 

Тригонометрический метод разрешения вектора

Тригонометрический метод разрешения вектора включает использование тригонометрических функций для определения компонентов вектора. Ранее в уроке 1 было описано использование тригонометрических функций для определения направления вектора. Теперь в этой части урока 1 тригонометрические функции будут использоваться для определения компонентов одного вектора. Вспомните из предыдущего обсуждения, что тригонометрические функции связывают отношение длин сторон прямоугольного треугольника с мерой острого угла внутри прямоугольного треугольника. Таким образом, тригонометрические функции можно использовать для определения длины сторон прямоугольного треугольника, если известна мера угла и длина одной стороны.

Метод использования тригонометрических функций для определения компонентов вектора следующий:

1. Построить грубый набросок (масштаб не требуется) вектора в указанном направлении. Обозначьте его величину и угол, который он образует с горизонтом.
2. Нарисуйте прямоугольник вокруг вектора так, чтобы вектор был диагональю прямоугольника. Начиная с хвоста вектора, нарисуйте вертикальные и горизонтальные линии. Затем нарисуйте горизонтальные и вертикальные линии в начале вектора. Нарисованные линии встретятся, образуя прямоугольник.
3. Нарисуйте компоненты вектора. Компонентами являются сторон прямоугольника. Хвост каждой компоненты начинается в хвосте вектора и тянется по осям до ближайшего угла прямоугольника. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо).
4. Осмысленно пометьте компоненты векторов символами, чтобы указать, какой компонент представляет какую сторону. Составляющая силы, направленная на север, может быть обозначена как F 9.0179 север . Направленная вправо составляющая скорости силы может быть обозначена как v _x ; и т.д.
5. Чтобы определить длину стороны, противоположной указанному углу, используйте функцию синуса. Замените модуль вектора на длину гипотенузы. С помощью алгебры решите уравнение для длины стороны, противоположной указанному углу.
6. Повторите предыдущий шаг, используя функцию косинуса, чтобы определить длину стороны, примыкающей к указанному углу.

Описанный выше метод показан ниже для определения компонентов силы, действующей на Фидо.

Поскольку сила натяжения в 60 ньютонов действует на Фидо вверх и вправо под углом 40 градусов, компоненты этой силы можно определить с помощью тригонометрических функций.

 

 

 

Таким образом, вектор, направленный в двух измерениях, имеет две компоненты, то есть влияние в двух отдельных направлениях. Величину влияния в заданном направлении можно определить с помощью методов векторного разрешения. Здесь описаны два метода векторного разрешения — графический метод (метод параллелограмма) и тригонометрический метод.

Больше практики

Используйте виджет Компоненты вектора ниже, чтобы разложить вектор на его компоненты. Просто введите величину и направление вектора. Затем нажмите кнопку Submit

, чтобы просмотреть горизонтальные и вертикальные компоненты.