Векторы a b – .

§8. Векторное произведение векторов

1. Определение. Векторным произведением ab неколлинеарных векторов а и b называется вектор, удовлетворяющий трем условиям:

(ВП1) Вектор ab ортогонален векторам а и b .

(ВП2) | ab | = |а||b|sin(a,b) .

(ВП3) Базис (a,b, ab) векторного пространства V₃ положительно ориентирован.

Векторное произведение коллинеарных векторов по определению полагают равным нулевому вектору. Проверьте, что условия (ВП1) и (ВП2) выполняются и в этом случае.

Замечания. (8.1) Условие (ВП3) показывает, что векторное произведение, как и смешанное, имеет смысл только в ориентированном трехмерном векторном пространстве.

(8.2) Отложим от произвольной точки А векторы АВ = а и AD = b, достроим треугольник ABD до параллелограмма ABCD и заметим, что площадь этого параллелограмма равна |АВ||АD|sinBAD = |а||b|sin(a,b). Таким образом, условие (ВП2) имеет простой геометрический смысл: модуль векторного произведения численно равен площади параллелограмма, построенного на векторах-сомножителях.

(

8.3) Векторное произведение равно 0 тогда и только тогда, когда сомножители коллинеарны. «Тогда» здесь следует прямо из определения, а «только тогда» – из 8.2: ведь если векторы неколлинеарны, то площадь построенного на них параллелограмма отлична от 0.

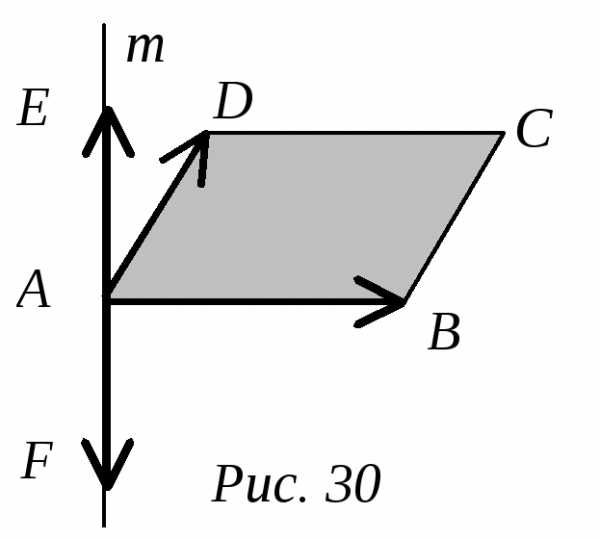
Покажем, как построить векторное произведение двух данных неколлинеарных векторов. Для этого снова построим параллелограмм ABCD, у которого АВ = а и AD = b, и проведем через точку А прямую т перпендикулярно плоскости АВС. На этой прямой от точки А отложим отрезки AE и AF, длиной |а||b|sin

(a,b) (рис.30). В силу условий (ВП1) и (ВП2) вектор ab должен совпадать с AE или AF. Поскольку AE = –AF, базисы (а, b, АЕ) и (а, b, АF) противоположно ориентированы (упражнение 6.6). Поэтому ровно один из этих базисов ориентирован положительно. Входящий в него вектор (AE или AF) и будет единственным, удовлетворяющим все трем условиям (ВП1)-(ВП3). Таким образом у любых двух векторов есть векторное произведение, и притом только одно.

2. Связь скалярного, векторного и смешанного произведений.

(8.4) Теорема. Для любых векторов а, b и с выполняется равенство abc = (ab)c. Подробнее: смешанное произведение трех векторов равно векторному произведению двух первых векторов, скалярно умноженному на третий вектор.

 Если векторы а и b коллинеарны, то abc = 0 в силу компланарности векторов а, b и с, а (a

b)c = 0, поскольку ab = 0. Если векторы а и b неколлинеарны, а вектор с компланарен с ними, то abc = 0 и (ab)c = 0, поскольку вектор ab перпендикулярен плоскости, которой параллельны векторы а, b и с. Таким образом, в этих двух случаях теорема справедлива.

Если векторы а, b и с некомпланарны, разложим вектор с по базису (а, b, ab): с = xa + yb + z(ab). Поскольку ab  а и ab  b, имеем:

(ab)c = (ab)( xa + yb + z(ab)) = x(ab)a + y(ab)b + z(ab)(ab) = z(ab)² (*).

Построим прямой параллелепипед АВСDА₁

В₁C₁D₁, у которого АВ = а, AD = b и АА₁ = ab. Базис (а, b, ab) по определению положительно ориентирован. Поэтому смешанное произведение ab(ab) положительно. Но тогда

ab(ab) = =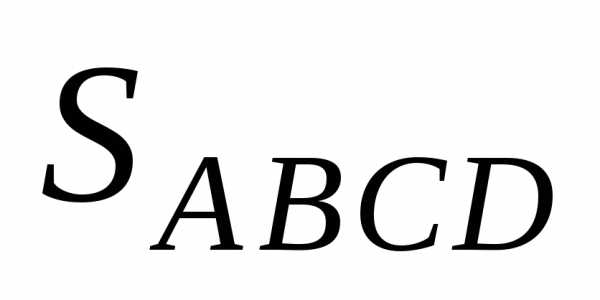|АА₁| = |ab||ab| = |ab|² = (ab)²,

откуда

abc = ab(xa + yb + z(ab)) = хaba + yabb + z ab(ab) = z(ab)² (**),

ибо aba = abb = 0 в силу компланарности сомножителей.

Сравнивая равенства (*) и (**), получаем требуемый результат.



3. Выражение векторного произведения в координатах и его алгебраические свойства.

(8.5) Теорема. Пусть в некотором положительно ориентированном ортонормированном базисе пространства V₃ заданы векторы а(а₁, а₂, а₃) и b(b₁, b₂, b₃). Тогда вектор ab имеет в этом базисе координаты

(, –,).

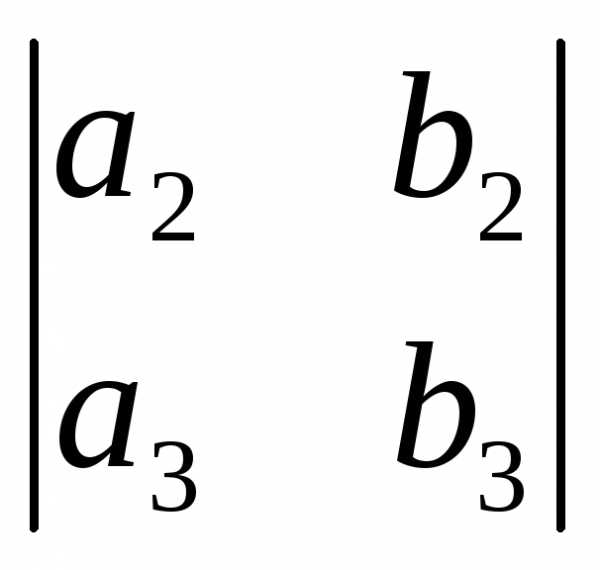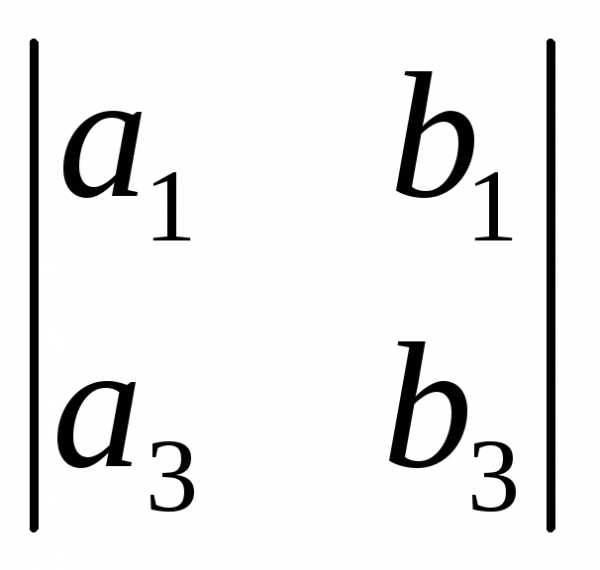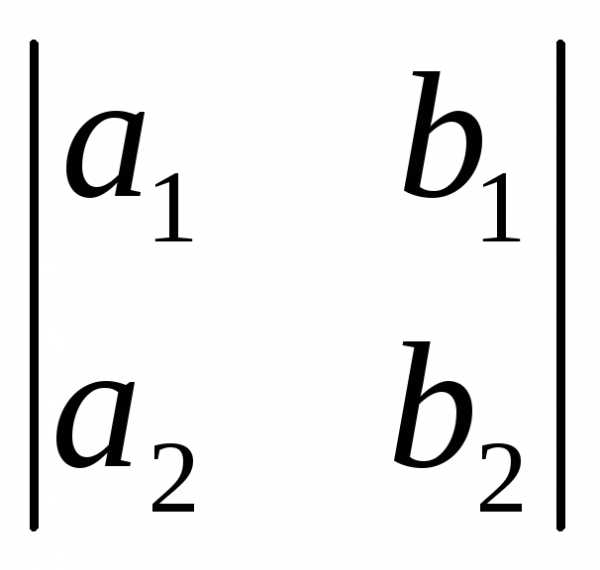 Пусть в данном базисе ab(x,y,z). По формуле 5.14, теореме 8.4 и свойству 7.9 имеем:

х = (ab)i = abi

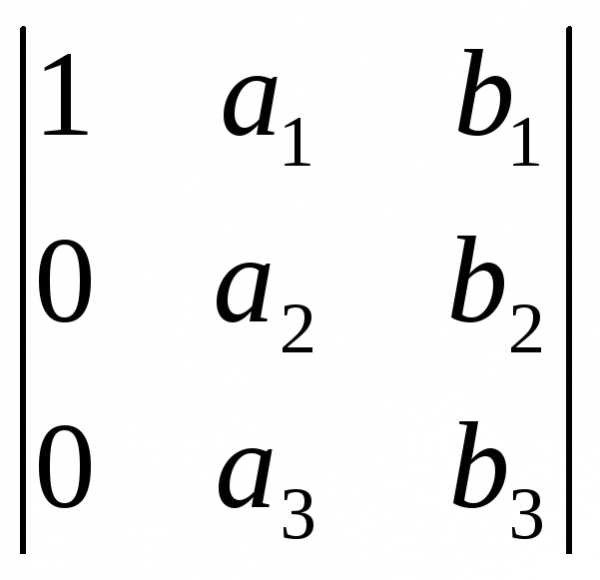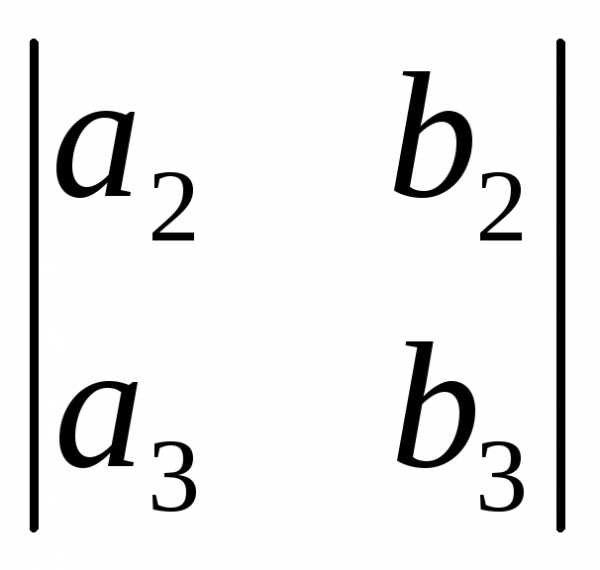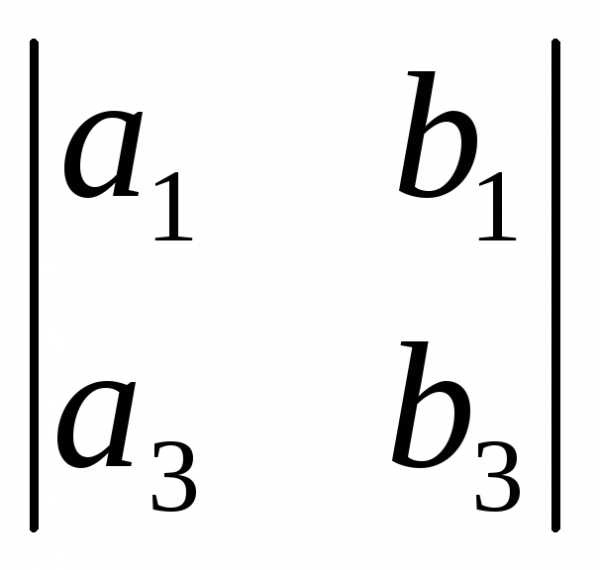= – aib = iab = = 1– 0+ 0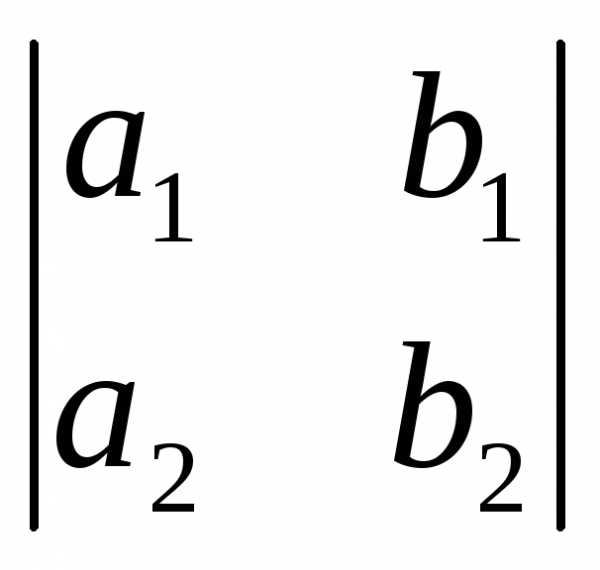=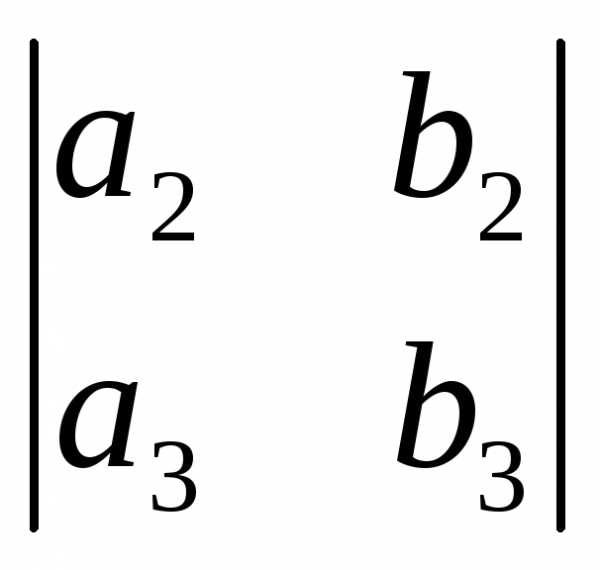. Аналогично (как?)y = jab = –, a z = kab = . 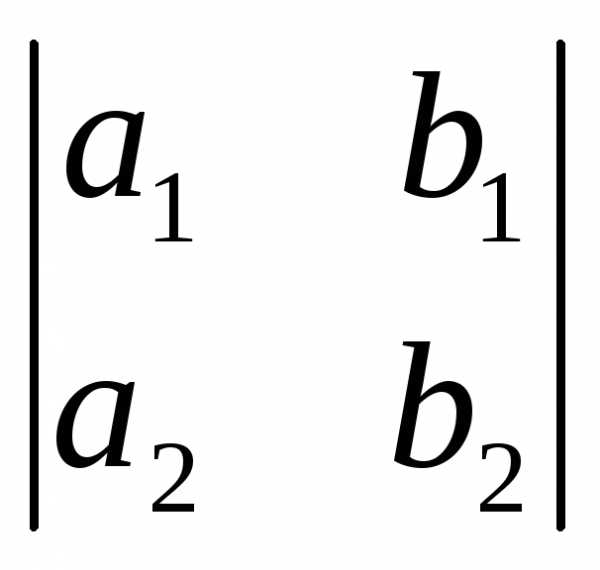

Теперь нетрудно доказать другие алгебраические свойства векторного произведения:

(8.6) ab = – ba (антикоммутативность) .

(8.7) (а₁+а₂)b = a₁b + a₂b и a(b₁+b₂

) = ab₁ + ab₂ (дистрибутивность) .

(8.8) (хa)b = a(xb) = х(ab) (однородность) .

 Проверим, например, антикоммутативность. По теореме 8.5

ab(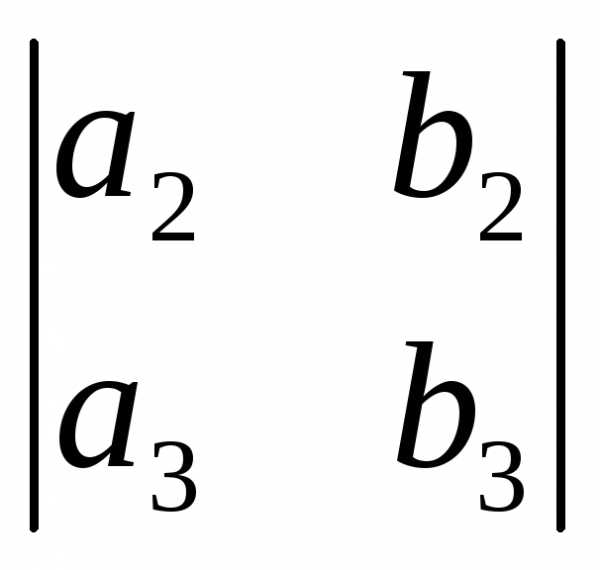, –, 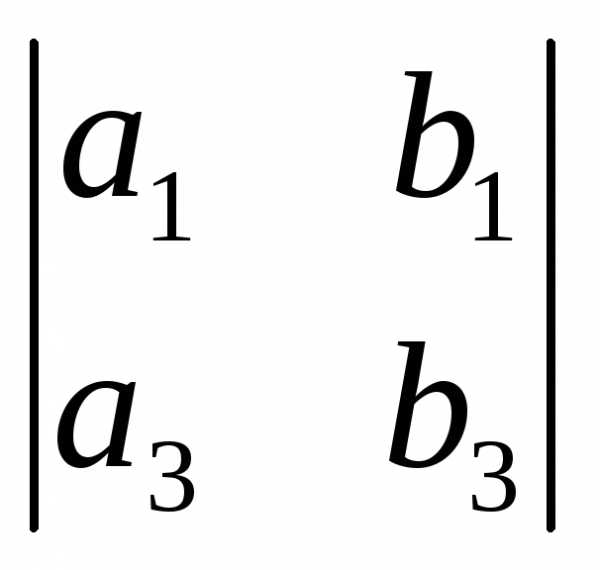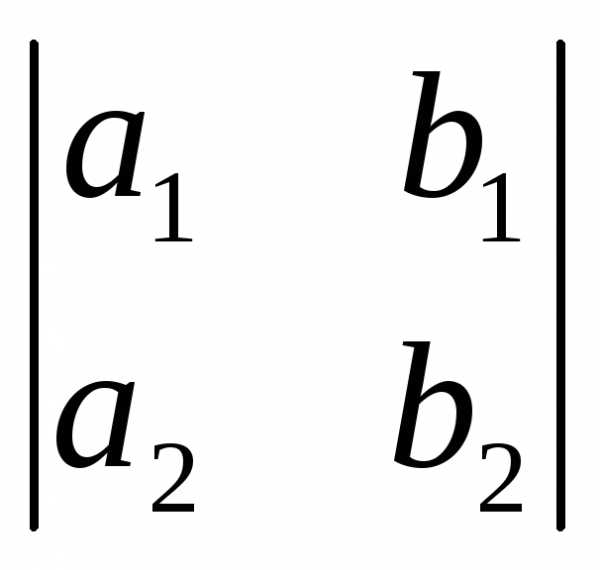) = (a₂b₃–a₃b₂ , a₃b₁–a₁b₃ , a₁b₂–a₂b₁).

По той же

теореме

ba(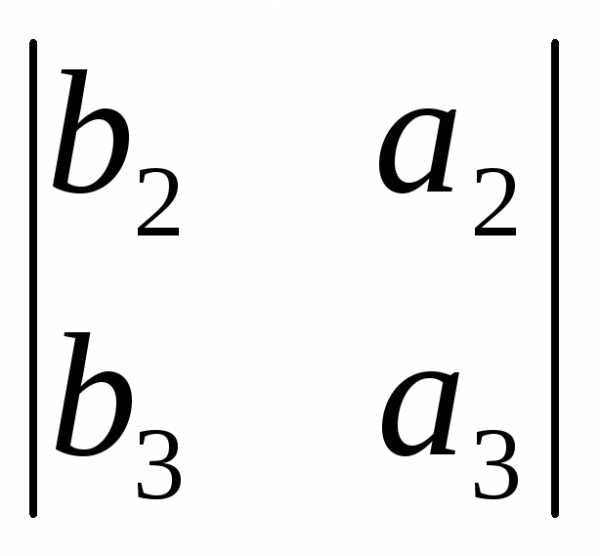, –, 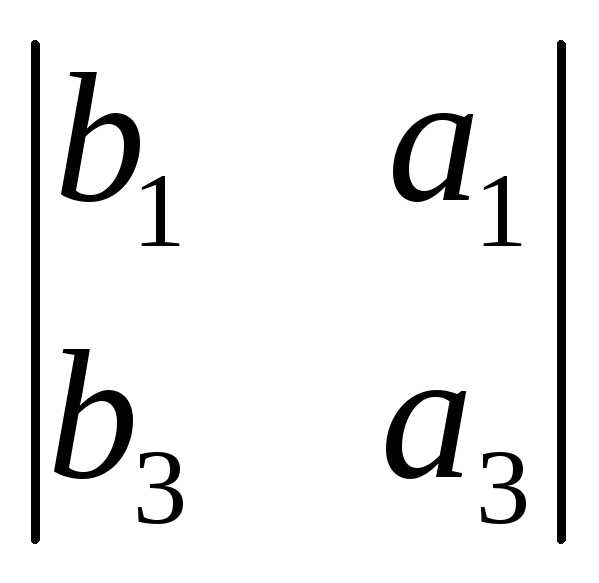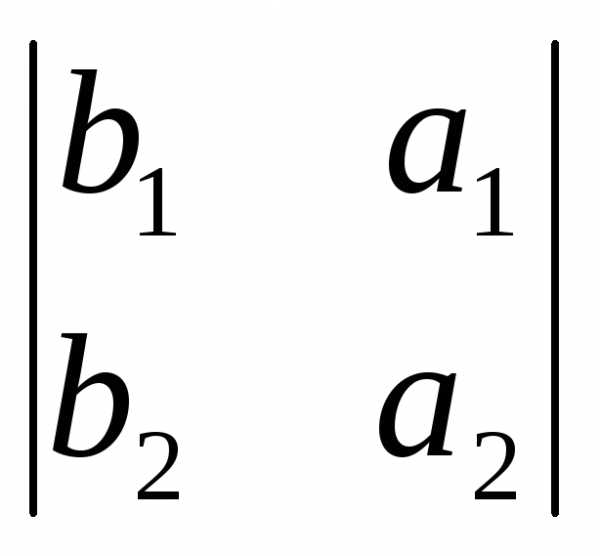) = (a₃b₂ – a₂b₃, a₁b₃ – a₃b₁, a₂b₁ – a₁b₂) = –ab. 

Вычисления, проверяющие свойства 8.7 и 8.8, проведите сами.

4. Площади параллелограмма и треугольника. Возьмем произвольный треугольник АВD и достроим его до параллелограмма ABCD. В силу замечания 8.2 площадь параллелограмма ABCD равна модулю векторного произведения АВAD:

(8.9) 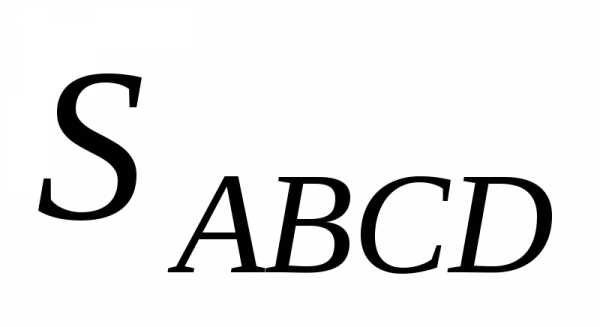= |ABAD|.

Площадь параллелограмма ABCD вдвое больше площади треугольника АВD. Поэтому

(8.10) 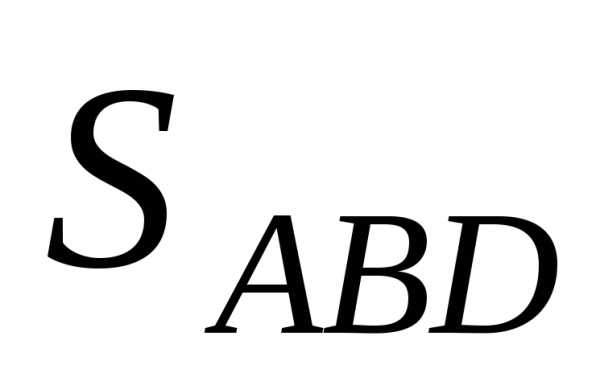=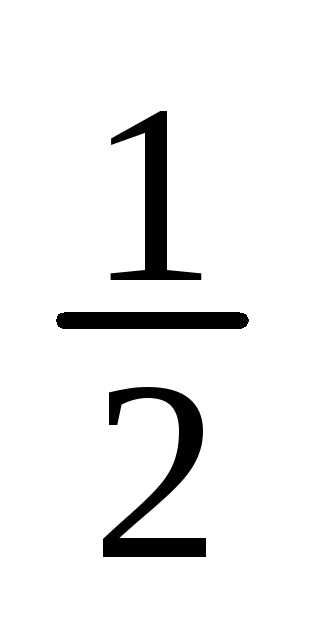|ABAD|.

Полученные формулы в соединении теоремой 8.5 позволяют находить площадь параллелограмма или треугольника по известным координатам векторов его сторон (базис при этом, разумеется, должен быть ортонормированным).

(8.11) Упражнение. Выведите соответствующие координатные формулы.

studfiles.net

Векторы. Использование векторов при разработке компьютерных игр

Внимание! Данный сайт не обновляется. Новая версия: shatalov.su

Дата создания: 2009-04-11 15:25:51
Последний раз редактировалось: 2012-02-08 09:19:45

Долго я не хотел писать данную статью — думал как подавать материал. Ещё и картинки нужно рисовать. Но, видать сегодня удачно сложились звёзды и статье про векторы быть. Хотя, это всего лишь черновой вариант. В будущем данную статью разобью на несколько отдельных — материала достаточно. Также, постепенно статья будет улучшаться: буду вносить в неё изменения — т.к. за один присест не получится раскрыть все аспекты.

Векторы были введены в математику в девятнадцатом века, для описания величин, которые трудно было описывать с помощью скалярных значений.

Векторы интенсивно применяются при разработке компьютерных игр. Применяются они не только традиционно — для описания таких величин как сила или скорость, но и в областях, которые казалось бы никак не связаны с векторами: хранение цвета, создание теней.

Скаляры и векторы

Для начала напомню, что такое скаляр, и чем он отличается от вектора.

Скалярные значения хранят какую-то величину: масса, объём. То есть это сущность, которая характеризуется только одним числом (например, количество чего-либо).

Вектор в отличии от скаляра описывается с помощью двух значений: величина и направление.

Важное отличие векторов от координат: векторы не привязаны к конкретному местоположению! Ещё раз повторюсь, главное в векторе — длина и направление.

Вектор обозначается жирной буквой латинского алфавита. Например: a, b, v.

На первом рисунке можно увидеть как вектор обозначают на плоскости.

Векторы в пространстве

В пространстве векторы можно выражать с помощью координат. Но прежде нужно ввести одно понятие:

Радиус-вектор точки

Возьмём в пространстве какую-нибудь точку M(2,1). Радиус-вектор точки — это вектор начинающийся в начале координат и заканчивающийся в точке.

У нас здесь ни что иное как вектор OM. Координаты начала вектора (0,0), координаты конца (2,1). Обозначима этот вектор как a.

В данном случае вектор можно записать следующим образом a = <2, 1>. Это координатная форма вектора a.

Координаты вектора называются его компонентами относительно осей. Напрмер, 2 — компонета вектора a относительно оси x.

Давайте ещё раз остановимся на том, что такое координаты точки. Координата точки (например x) — это проекция точки на ось, т.е. основание перпендикуляра, опущенного из точки на ось. В нашем примере 2.

Но вернёмся к первому рисунку. У нас здесь две точки A и B. Пусть координатами точек будут (1,1) и (3,3). Вектор v в данном случае можно обозначить так v = <3-1, 3-1>. Вектор лежащий в двух точках трёхмерного пространстве будет выглядеть так:

v = <x₂-x₁, y₂-y₁, z₂-z₁>

Думаю никаких сложностей тут нет.

Умножение вектора на скаляр

Вектор можно умножать на скалярные значения:

kv = <k*v_x, k*v_y> = <k*2, k*1>

Здесь и далее, * — знак умножения.

При этом скалярное значение перемножается с каждой компонентой вектора.

Если k > 1, то вектор увеличится, если k меньше единицы, но больше нуля — вектор уменьшится в длину. Если же k меньше нуля, то вектор поменяет направление.

Единичные векторы

Единичные векторы — это векторы длина которых равна единице. Заметьте, вектор с координатами <1,1,1> не будет равным единице! Нахождение длины вектора описано ниже по тексту.

Существуют так называемые орты — это единичные векторы, которые по направлению совпадают с осями координат. i — орт оси x, j — орт оси y, k — орт оси z.

При этом i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Теперь мы знаем что такое умножение вектора на скаляр и что такое единичные векторы. Теперь мы можем записать v в векторной форме.

v = v_xi + v_yj + v_zk, где v_x, v_y, v_z — соответствующие компоненты вектора

Сложение векторов

Чтобы полностью разобраться в предыдущей формуле необходимо понять, как работает сложение векторов.

Тут всё просто. Возьмём два вектора v1 = <x₁,y₁,z₁> и v₂ = <x₂,y₂,z₂>

v₁ + v₂ = <x₁+x₂, y₁+y₂, z₁+z₂>

Мы всего лишь складываем соответствующие компоненты двух векторов.

Разность вычисляется так же.

Это, что касается математической формы. Для полноты, стоит рассмотреть как будет выглядеть сложение и вычитание векторов графически.

Для того, чтобы сложить два вектора a+b. Нужно совместить начало вектора b и конец вектора a. Затем, между началом вектора a и концом вектора b провести новый вектор. Для наглядности смотрите второй рисунок (буква «а»).

Для вычитания векторов нужно совместить начала двух векторов и провести новый вектор из конца второго вектора к концу первого. На втором рисунке (буква «б») показано как оно выглядит.

Длина и направление вектора

Сначала рассмотрим длину.

Длина — это числовое значение вектора, без учёта направления.

Длина определяется по формуле (для трёхмерного вектора):

корень квадратный из суммы квадратов компонент вектора.

Знакомая формула, не правда ли? В общем-то — это формула длины отрезка

Направление вектора определяется по направляющим косинусам углов образованных между вектором и осями координат. Для нахождения направляющих косинусов используются соответствующие компоненты и длина (картинка будет позже).

Представление векторов в программах

Представлять векторы в программах можно различными способами. Как с помощью обычных переменных, что не эффективно, так и с помощью массивов, классов и структур.

float vector3[3] = {1,2,3}; // массив для хранения вектора

struct vector3 // структура для хранения векторов
{
  float x,y,z;
};

Самые большие возможности при хранении векторов нам предоставляют классы. В классах мы можем описать не только сам вектор (переменные), но и векторные операции (функции).

Скалярное произведение векторов

Существует два типа перемножения векторов: векторное и скалярное.

Отличительная особенность скалярного произведения — в результате всегда будет скалярное значение, т.е. число.

Тут стоит обратить внимание вот на какой момент. Если результат данной операции равен нулю, значит, два вектора перпендикулярны — угол между ними 90 градусов. Если результат больше нуля — угол меньше 90 градусов. Если результат меньше нуля, угол больше 90 градусов.

Данную операцию представляет следующая формула:

a · b = a_x*b_x + a_y*b_y + a_z*b_z

Скалярное произведение — это сумма произведений соответствующих компонент двух векторов. Т.е. Берём x’ы двух векторов, перемножаем их, затем складываем с произведением y’ов и так далее.

Векторное произведение векторов

Результатом векторного произведения двух векторов будет вектор перпендикулярный этим векторам.

a x b = <a_y*b_z — a_z*b_y, a_z*b_x — a_x*b_z, a_x*b_y — a_y*b_x>

Мы пока не будем обсуждать подробно эту формулу. К тому же она довольно трудна для запоминания. Мы ещё вернёмся к этому моменту после знакомства с определителями.

Ну и для общего развития полезно знать, что длина полученного вектора, равна площади параллелограмма построенного на векторах a и b.

Нормализация вектора

Нормализованный вектор — это вектор, длина которого равна единице.

Формула для нахождения нормализованного вектора следующая — все компоненты вектора необходимо разделить на его длину:

v_n = v/|v| = <v_x/|v|, v_y/|v|, v_z/|v|>

Послесловие

Как Вы, наверное, убедились, векторы не сложны для понимания. Мы рассмотрели ряд операций над векторами.

В следующих статьях раздела «математика» мы будем обсуждать матрицы, определители, системы линейных уравнений. Это всё теория.

После этого, мы рассмотрим преобразования матриц. Именно тогда Вы поймёте насколько важна математика в создании компьютерных игр. Данная тема как раз и станет практикой по всем предыдущим темам.

oldshatalov.ghost17.ru

Вопрос 11. Операции над векторами

Для раскрытия первого вопроса достаточно дать определения скалярного, векторного и смешанного произведения векторов, пере­числить их основные свойства (которые в ряде учебных пособий представлены в виде теории), и представить доказательство некоторых свойств. Необходимо знать специфические свойства каждого из произведений. Например, некоторые свойства скалярного произведения векторов совпадают с соответствующими свойствами произведе­ния чисел: а*в= в* а, а*(в+с}=а*в+а*с. Но скалярное произведение обладает и особыми свойствами, которыми не обладает произведение чисел. Вот некоторые из них: а) Скалярное произведение двух векторов есть число, множественное. Объект не той природы, что сомножители, а другой, б) Для чисел, если х-y=о, то это означает, что одно из чисел равно нулю. Аналогичного свойства для векторов нет. в) Ес­ли a¹о, то числовое уравнение ах=b имеет единственное решение (х=b/2).Но уравнение для скалярного произведения в-в a=х=b не имеет смысла (а для векторного произведения вопроса не имеет). Затем целесообразно перечислить приложение скалярного, векторного и смешанного произведения векторов к решению задач. Например, векторное произведение векторов находит свое, применение при нахождении площади треугольника, смешанное произведение — объема тетраэдра и привести примеры задач.

При ответе на этот вопрос от студента требуется знание основных понятий , включая понятия вектора , базиса векторов , линейно за­висимые и линейно независимые векторы , линейной комбинации векторов. Необходимо знать, как выражается различное произведение векторов через координаты вектора.

Теорема 1: Скалярное произведение векторов и , заданные в ортонормированном базисе, выражается формулой:

.

Теорема 2: Если векторы в ортонормированном базисе имеют координаты , то , где = 1, если базис правый, и = -1, если базис левый

Теорема 3: Если векторы и в ортонормированном правом базисе имеют координаты и , то вектор [ ]имеет координаты:

[ ] Докажем это.

Пусть координаты вектора [ ] (x,y,z).

Тогда [ ]=

[ ] =

[ ] =

[ ] =

С учетом предыдущей теоремы и условий ортонормированности базиса( ), получили

X= ; Y= ; Z= что и требовалось доказать.

Основные определения:

Направленный отрезок (упорядоченную пару точек) называют вектором. Обозначают АВили Здесь A – начало вектора, B – конец вектора. Расстояние между началом и кон­цом вектора называют его длиной (или модулем, или абсолютной ве­личиной). Обозначают |АВ | или | |. Если точки А и В совпадают, то вектор называют нулевым и обозначают знаком Его модуль равен нулю.

Векторы называются коллинеарными, если они лежат на па­раллельных прямых (или на одной прямой). Ненулевые коллинеарные векторы либо имеют одно и тоже направление и называются в этом случае сонаправленными, или одинаково направленными, либо имеют противоположные направления и называются противоположно на­правленными. Векторы называются компланарными, если они ле­жат в одной плоскости или параллельных плоскостях. Нулевой вектор коллинеарен любому вектору. Два ненулевых вектора называются равными, если они одинаково направлены и имеют одну и ту же длину. От каждой точки можно отложить единственный вектор, рав­ный данному.

Над векторами можно выполнять следующие операции:

1) Сложение векторов.

Суммой а+b двух векторов a и bназывается вектор, кото­рый идет из начала вектора aв конец вектора b, при условии, что вектор b отложен от конца вектора a. Это построение называется правилом треугольника. Сумма векторов a + b не зависит от вы­бора начала вектора a.

Если векторы а и b приведены к общему началу и на них по­строен параллелограмм, то сумма а + bесть вектор, совпадающий с диагональю этого параллелограмма, идущей из общего начала векто­ров а и b. Это построение называется правилом параллелограмма.

2) Вычитание векторов.

Разностью векторов а и bназываетсятакой вектор x, что b+x=a.Если векторы аиb имеют общее начало, то их разность есть вектор, идущий из конца вектора bв конец вектора a.

Изобразим перечисленные правила на чертеже.

 

3)Умножение вектора на число.

Произведениемненулевого вектора aна действительное число a¹0 называется вектор b,обозначаемыйb= aа,и определенный следующими условиями

1. | b | = | a| |а |

2. Вектор bколлинеарен вектору a.

3. Векторы b и aнаправлены одинаково, если a > 0 и противоположно, если a <0.Если a=или a=0, то полагают aa =.

Система векторов а₁, а₂, …,а_m называется линейно зависимой, если существуют такие действительные числа с₁, с₂, …,с_m, одновре­менно не равные нулю, что имеет место равенство c₁a₁+с₂a₂+..с_ma_m =0. В противном случае эта система векторов называется линейно не­зависимой.

Имеют место следующие теоремы:

Т1. Любые два коллинеарных вектора линейно зависимы и на­оборот, два неколлинеарных вектора линейно независимы.

Т2. Три компланарных вектора линейно зависимы и наоборот, три некомпланарных вектора линейно независимы.

Т3. Каждые четыре вектора в пространстве линейно зависимы.

Базисом на плоскостиявляется любая упорядоченная пара неколлинеарных векторов этой плоскости.Базисом в пространствеявляется любая упорядоченная тройка некомпланарных векторов.

Рассмотрим систему векторов a₁, a₂,….,a_mи зададим m действи­тельных чисел c₁, с₂, …,с_m. Вектор b= c₁a₁+с₂a₂+…+с_ma_mназываетсялинейной комбинацией данных векторов a₁, a₂,…,a_m.

Т4. Пусть на плоскости выбран базис е₁, е_2. Тогда любой вектор аэтой плоскости можно представить, и притом единственным обра­зом, как линейную комбинацию векторов базиса.

Т5. Пусть в пространстве выбран базис е₁, е₂, е₃ .Тогда любой вектор а пространства можно представить, и притом единственным образом, как линейную комбинацию векторов базиса.

Если е_1, е_2, е₃ – базис и вектор а = a₁е₁ +a₂ е₂ + a₃е₃, то числа a_1, a_{2 ,} a₃ называются координатами вектора а в данном базисе. Записыва­ется а(a_1, a_{2 ,}a₃). Равные векторы имеют равные координаты.

Для векторов, заданных своими координатами, имеют место следующие свойства:

1) При умножении вектора а = a₁е₁+a₂ е₂+a₃е₃ на число l его координаты умножаются на это число: l а =(la₁)е₁+(la₂)е₂+(la₃)е_3.

2) При сложении (вычитании) векторов а = a₁е_{1 +} a₂ е₂ +a₃е₃и b = b₁е_{1 +} b₂ е₂ +b₃е₃ складываются (вычитаются) их соответствующие координаты: а±b = (a₁ ± b₁ ) е₁ + (a₂ ± b₂ ) е₂ + (a₃ ± b₃ ) е₃

Углом между двумя ненулевыми векторами а и b, где a=ОА, b=OB называется меньший угол АОВ между этими векторами.

Скалярным произведением двух ненулевых векторов называ­ется число, равное произведению длин векторов-сомножителей на косинус угла между ними. Скалярное произведение обозначается (а,b).

По определению, (а , b) = | a | |b | cos a, где a- угол между век­торамиа и b. Если хотя бы один из векторов нулевой, то их скалярное произведение считают равным нулю.

Свойства скалярного произведения:

1. (а , b) = (b , a) для любых а и b

2. (а, a) = а²=| a |²для любогоa

3. Если a ¹ , b ¹ ,a =p / 2, то (а , b) = 0. Если a ¹ , b ¹ ,(а ,b)=0, то a ^b

4. (lа , b) = (а ,lb) = l (а , b) для любых а и b.

5. (а, b + c) = ( a , b) + ( а , c) для любых а , b,с

Пусть в прямоугольной системе координат в пространстве век­торы а и bзаданы своими координатами: а(X_1, Y_1,Z₁), b(X_2, Y_{2 ,}Z₂). Тогда (а , b) = X₁X₂ + Y₁Y₂ + Z₁Z₂.

Обозначим через a, b, g углы, которые составляет вектор ас осями координат. Косинусы этих углов называются направляющими косинусами вектора а. При этом справедливы следующие соотношения: X = | а| cosa, Y = | а | cosb , Z = | а | cosg, где X, Y, Z – координаты вектора а.

Упорядоченная тройка ненулевых векторов а_1, а_2, а₃ – с общим началом называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден в направле­нии, противоположном направлению движения часовой стрелки. В противном случае тройка называется левой.

Векторным произведением ненулевого вектора а на ненулевой вектор b называется вектор с, определенный следующими условиями:

1) | c| = |a | | b | sin a ( a — угол между векторами а и b)

2) c перпендикулярен к плоскости векторов а и b,если они приведены к общему началу.

3) если с¹, то вектор с направлен так, чтобы тройка векторов а, b, c была правая.

Обозначается a´b или [a, b] .

Свойства векторного произведения:

1. [a, b] = — [b, a] для любых а и b.

2. [ l a, b] = [a,lb] = l [a, b] для любых а и b и любогоl.

3. [a + b , c] = [a, c] + [b, c] для любых а, b, с.

4. a и b коллинеарны тогда и только тогда, когда [a, b] =

Модуль векторного произведения ненулевых и неколлинеарных векторов аиb, приведенных к общему началу,численно равен площади параллелограмма, построенного на этих векторах. Если век­торы а и b в ортонормированном правом базисе имеют координаты а(a₁,a₂,a₃), b(b₁,b₂,b₃), то вектор [a, b] имеет координаты [a, b]( a₂b₃-a₃b₂, a₃b₁— a₁b₃, a₁b₂— a₂b₁).

Смешанным произведением трех векторов a, b, c называется число, которое получается при умножении векторного произведения [a, b] скалярно на вектор с. Оно обозначается ([a, b], c). Смешанное произведение некомпланарных ненулевых векторов a, b, cпо модулю численно равно объему параллелепипеда, построенного на векторах-сомножителях, если они приведены к общему началу. Оно положи­тельно, если тройка векторов a, b, c правая, и отрицательно, если она левая. Верно и обратное утверждение. Три вектора компланарны то­гда и только тогда, когда их смешанное произведение равно нулю.

Свойства смешанного произведения:

1. ( [ a, b], c) = ( a, [b, c]) — для любых а, b,с.

2. Круговая перестановка трех сомножителей смешанного произведения не меняет его значения. Перестановка же двух со­седних сомножителей меняет знак смешанного произведения на противоположный.

Пусть в прямоугольной системе координат векторы a, b, cза­даны своими координатами: а(X_1, Y_1,Z₁), b(X_2, Y_{2 ,}Z₂), с(X_3, Y_3,Z₃). Тогда

 

 



infopedia.su

Векторное пространство ВЕКТОРЫ множество векторов a b

Векторное пространство ВЕКТОРЫ (множество векторов) { a, b, c, d, … } 1. Операция сложения векторов (коммутативная): a+b = b+a = c 2. Вспомогательная операция умножения вектора на число: a = a = d Правило: результат обеих операций — вектор, принадлежащий тому же множеству, что и исходные векторы

Условия ассоциативности (a + b) = a + b ( + ) a = a + а Линейные комбинации a + b + c +… = d СИНТЕЗ a + b + c +… d АНАЛИЗ d a + b + c +…

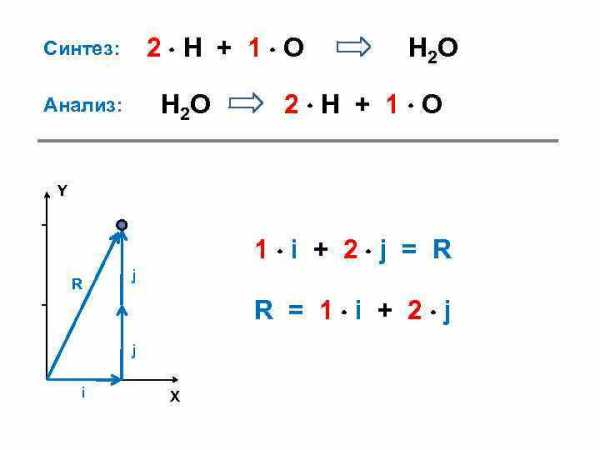2 Н + 1 О Синтез: Н 2 О Анализ: Н 2 О 2 Н + 1 О Y 1 i + 2 j = R R j R = 1 i + 2 j j i X

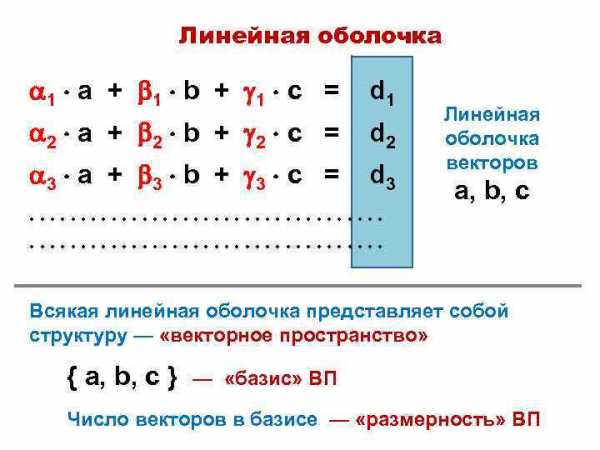Линейная оболочка 1 a + 1 b + 1 c = d 1 2 a + 2 b + 2 c = d 2 3 a + 3 b + 3 c = d 3 Линейная оболочка векторов a, b, c • • • • • • • • • • • • • • • • • • Всякая линейная оболочка представляет собой структуру — «векторное пространство» { a, b, c } — «базис» ВП Число векторов в базисе — «размерность» ВП

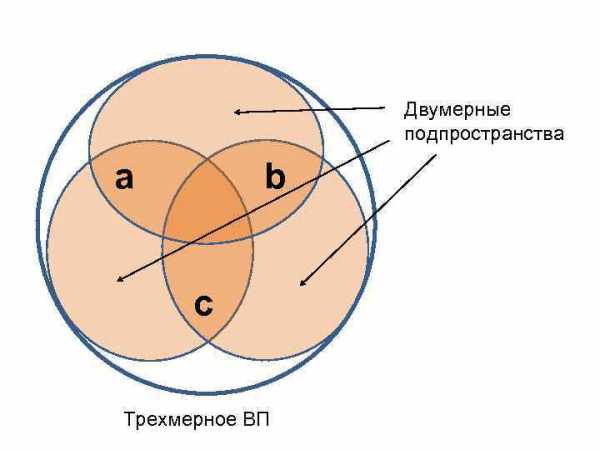Двумерные подпространства a b c Трехмерное ВП

В любом ЛП существует не один базис, а бесконечно много эквивалентных между собой базисов (несмотря на то, что в такие наборы входят различные векторы, их линейные оболочки в точности совпадают и составляют одно и то же ЛП). Число векторов в любом базисном наборе одинаково Все ЛП одинаковой размерности изоморфны другу, т. е. для каждой размерности существует только одно ЛП (если абстрагироваться от физического смысла векторов)

Координатное представление векторов ВП — базис { е 1, е 2, …, еn } X = x 1 e 1 + x 2 e 2 + … + xn e n Y = y 1 e 1 + y 2 e 2 + … + yn e n Z = z 1 e 1 + z 2 e 2 + … + zn en • • • • • • • • • • X = ( x 1, x 2, … , x n ) Y = ( y 1, y 2, … , y n ) Z = ( z 1, z 2, … , zn ) Координатные представления векторов X, Y, Z относительно базиса { е 1, е 2, …, еn }

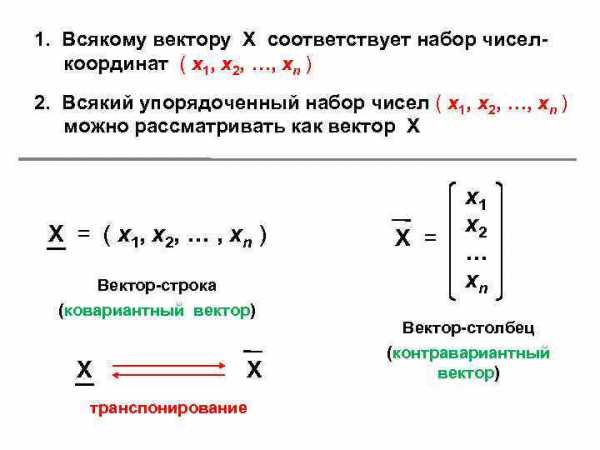1. Всякому вектору Х соответствует набор чиселкоординат ( х1, х2, …, хn ) 2. Всякий упорядоченный набор чисел ( х1, х2, …, хn ) можно рассматривать как вектор Х X = ( x 1, x 2, … , x n ) Вектор-строка (ковариантный вектор) Х Х транспонирование X = x 1 x 2 … xn Вектор-столбец (контравариантный вектор)

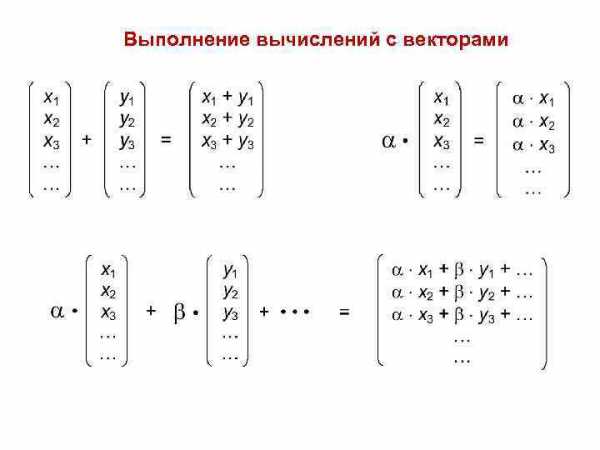Выполнение вычислений с векторами

Домашнее задание Задача 2. 1. Даны три вектора: R 1 = ( 5 , – 3 , – 5 , 0 ) R 2 = ( 3 , 2 , 0 , – 4 , – 1 ) R 3 = ( – 1 , 2, 3, 4 , – 5 ) Вычислить координаты вектора S, являющегося линейной комбинацией заданных векторов: S = R 1 + R 2 + R 3

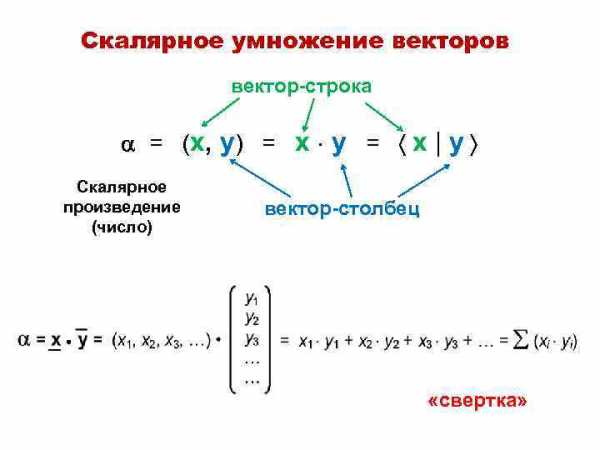Скалярное умножение векторов вектор-строка = (x, y) = x y = x | y Скалярное произведение (число) вектор-столбец «свертка»

Скалярный квадрат Х Х = (xi xi) = (xi)2 = |X| 2 | X | — модуль (норма) вектора Х Нормировка векторов X = ( x 1, x 2, … , xn ) |X| ≠ 1 Обычный (ненормированный) вектор ~ X = x 1 x 2 |X| Нормированный вектор • • • xn |X| ~ |X| = 1

Луч — совокупность векторов, различающихся только длиной (модулем, нормой). {k X} где k — любое число, а X — нормированный вектор Домашнее задание Задача 2. 2. Нормировать вектор S, полученный при решении задачи 2. 1. 1) вычислить модуль вектора S, ~ 2) вычислить координаты нормированного вектора S.

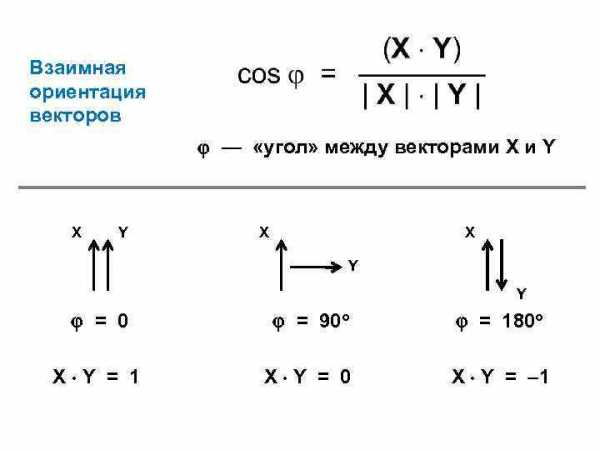Взаимная ориентация векторов — «угол» между векторами X и Y X X Y Y = 0 = 90 o = 180 o X Y = 1 X Y = 0 X Y = – 1

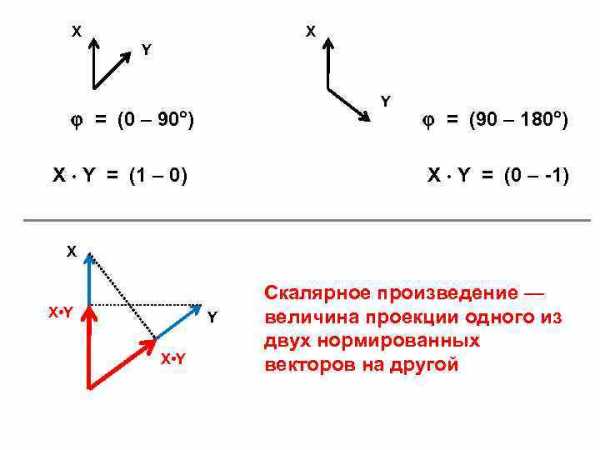X X Y Y = (0 – 90 ) X Y = (1 – 0) = (90 – 180 ) X Y = (0 – -1) X X • Y Y X • Y Скалярное произведение — величина проекции одного из двух нормированных векторов на другой

Домашнее задание Задача 2. 3. Вычислить (в градусах) величины углов между вектором S (см. задачу 2. 2. ) и исходными векторами (см. задачу 2. 1. ): (S, R 1) = ? (S, R 2) = ? (S, R 3) = ?

Дополнение 1. Комплексные векторы Z = ( z 1, z 2, … , zn ) Комплексные числа Z | = ( z 1, z 2, … , zn ) бра-вектор Z| = |Z + Z (z 1)* (z 2)* … (zn)* |Z = Z| Эрмитово-сопряженные векторы = |Z кет-вектор +

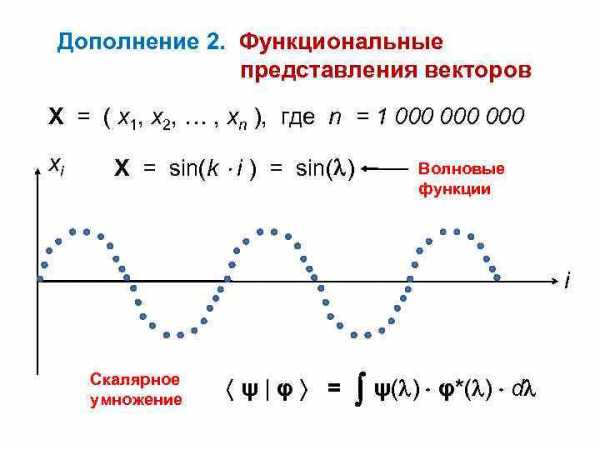Дополнение 2. Функциональные представления векторов X = ( x 1, x 2, … , xn ), где n = 1 000 000 xi X = sin(k i ) = sin( ) Волновые функции i Скалярное умножение ψ|φ = ψ( ) φ*( ) d

present5.com