Навигация по странице:
Определение вектораОпределение. Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
Обозначение вектораВектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a. Длина вектораОпределение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB. Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|. Нулевой векторОпределение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают. Нулевой вектор обычно обозначается как 0. Длина нулевого вектора равна нулю. Коллинеарные вектораОпределение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
Сонаправленные вектораОпределение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
Противоположно направленные вектораОпределение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис.
Компланарные вектораОпределение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные. Равные вектораОпределение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины: a = b, если a↑↑b и |a| = |b|. Единичный векторОпределение. Единичным вектором или ортом — называется вектор, длина которого равна единице. Вектора
Вектор: определение и основные понятия
Определение координат вектора заданного координатами его начальной и конечной точки
Модуль вектора. Онлайн калькуляторы с векторами Онлайн упражнения с векторами на плоскости Онлайн упражнения с векторами в пространстве Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
Что такое вектор: определение, обозначение, виды
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое вектор: определение, обозначение, виды
В данной публикации мы рассмотрим, что такое вектор, как он обозначается, а также какие виды бывают.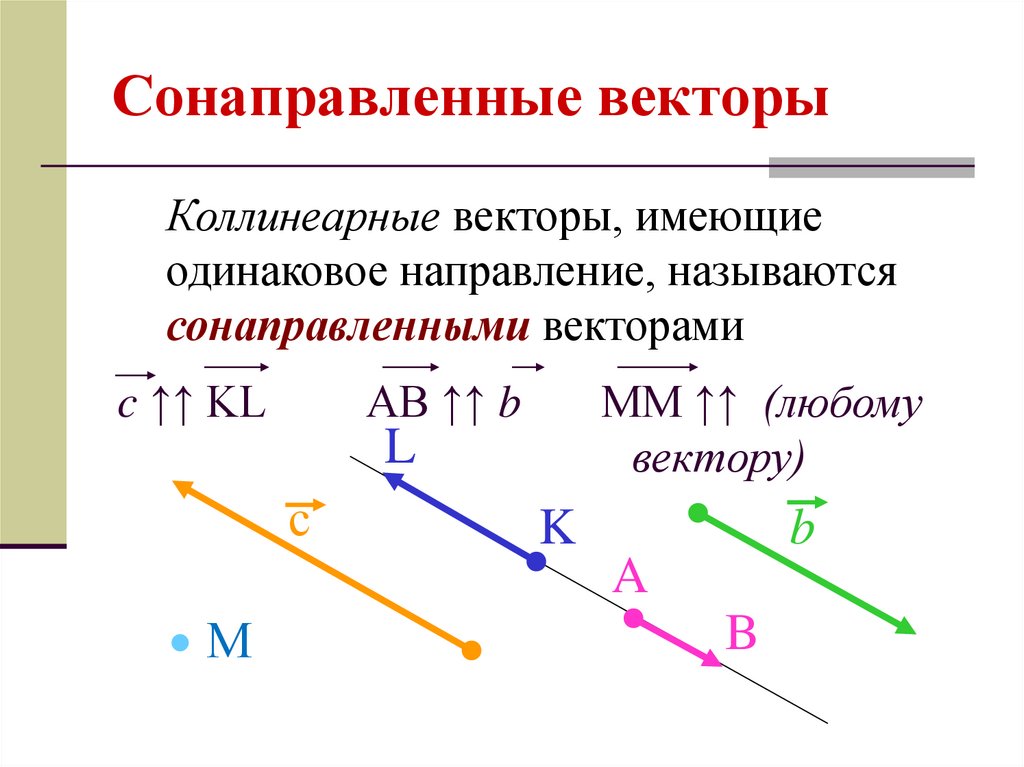 Теоретическую информацию сопроводим рисунками для лучшего восприятия.
Теоретическую информацию сопроводим рисунками для лучшего восприятия.
- Определение вектора
- Виды векторов
Определение вектора
Вектор – это направленный отрезок. Другими словами, это отрезок определенной длины, который направлен в конкретную сторону.
У вектора есть начало и конец. На рисунке ниже – это точки A и B, соответственно. Направление вектора показывается соответствующей стрелкой.
Обозначается вектор путем записи его точек (начало, потом – конец) с вертикальной черточкой сверху, т.е. в нашем случае – AB.
Альтернативный вариант обозначения – малеьнкая латинская буква, например, a.
Примечание: нахождение длины вектора (|AB| или |a|) мы подробно рассмотрели в отдельной публикации.
Виды векторов
1. Нулевой – начало и конец вектора совпадают. Обычно обозначается как 0. Длина нулевого вектора равняется нулю.
Обычно обозначается как 0. Длина нулевого вектора равняется нулю.
2. Единичный – вектор, длина которого равна единице. Также называется ортом.
3. Коллинеарные – векторы лежат на одной и той же или на параллельных прямых.
4. Сонаправленные – коллинеарные векторы, направления которых совпадает. Например, на рисунке ниже a и b являются сонаправленными.
Обозначение: a ↑↑ b.
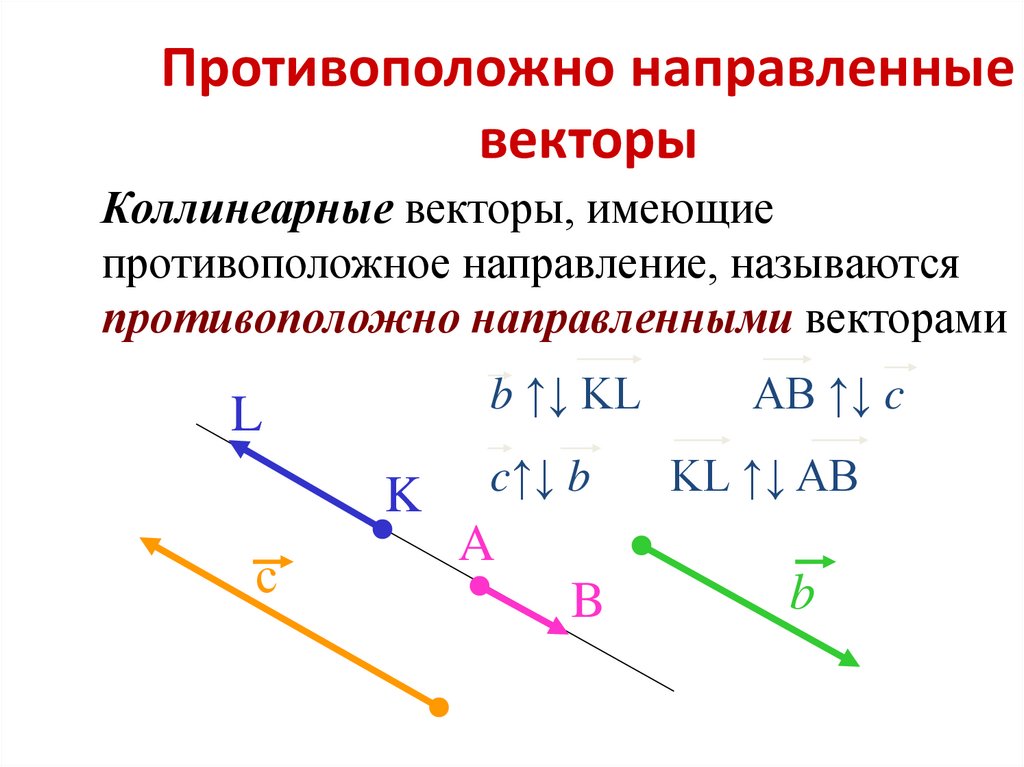
5. Противоположно направленные – коллинеарные векторы, направления которых противоположны.
Обозначение: a ↑↓ b.
6. Компланарные – векторы, параллельные одной плоскости или лежащие на одной плоскости.
Примечание: любые два вектора компланарны, так как всегда найдется плоскость, параллельная им обоим.
7. Равные – векторы, имеющие одинаковую длину и направление, а также лежащие на одной или параллельных прямых.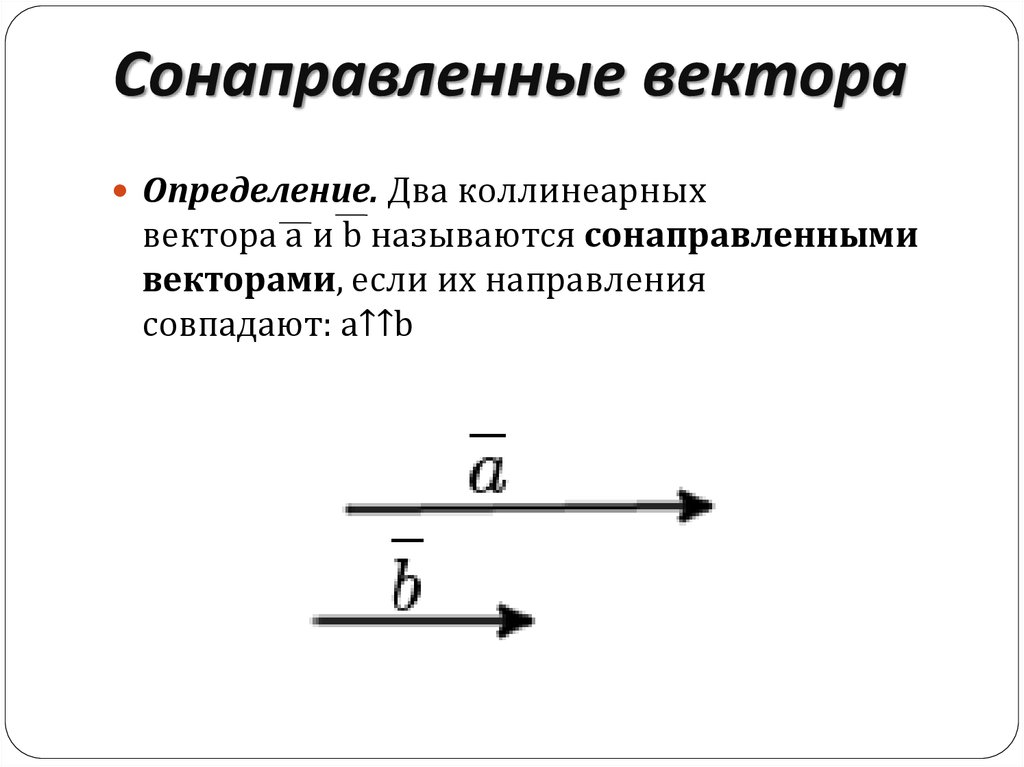
Примечание: для вектора AB в произвольной точке C пространства удастся построить только один единственный вектор (например, CD) той же длины.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Счет, математика и статистика — Набор академических навыков
Обозначение i,j (Механика)
Главное меню ContentsToggle 1 Векторное обозначение 2 Обозначение $i,j$ 3 Рабочий пример: представление векторов 4 Рабочий пример: задачи с векторами
Векторная нотация
Индексная нотация для векторного исчисления включает базисные векторы $\underline{e}_x$ и $\underline{e}_y$ для двух измерений.
Однако в следующих примерах в механике мы будем использовать нотацию $i,j$.
Обозначение $i,j$
Вектор может быть описан с использованием обозначения $\mathbf{i, j}$.
Единичный вектор — это вектор длины 1, в декартовых координатах орты вдоль оси обозначаются $\mathbf{i}$ и $\mathbf{j}$ соответственно.
Любой двумерный вектор можно записать в виде $a\mathbf{i} + b\mathbf{j}$.
Рабочий пример: Представление векторов
Нарисуйте диаграмму
Нарисуйте диаграмму для представления вектора $5\mathbf{i} — 2\mathbf{j}$.
Решение
Возьмем 5 единиц в направлении единичного вектора $\mathbf{i}$ и 2 единицы в направлении единичного вектора $-\mathbf{j}$.
Пример работы: задачи с векторами
задачи
Учитывая, что $\mathbf{x} = 8\mathbf{i} + 4\mathbf{j}$ и $\mathbf{y} = 12\mathbf{i} — 3\mathbf{j}$, найти $\mathbf{x}+\mathbf{y}$, $\mathbf{y}-\mathbf{x}$, $3\mathbf{x}+\frac{1} {2}\mathbf{y}$, величина $\mathbf{x}$ и угол между $\mathbf{y}$ и положительной осью $x$.
Решение
Мы можем добавить векторы, рассматривая члены $\mathbf{i}$ и $\mathbf{j}$ по отдельности. \begin{align} \mathbf{x} + \mathbf{y} & = \left(8\mathbf{i} + 4\mathbf{j}\right) + \left(12\mathbf{i} — 3\ mathbf{j}\right), \\ & =\left(8 \mathbf{i} + 12 \mathbf{i}\right) + \left(4 \mathbf{j} — 3\mathbf{j}\right ),\\ & = 20\mathbf{i} + \mathbf{j}. \end{align} Мы можем сделать то же самое при вычитании векторов. \begin{align} \mathbf{y} — \mathbf{x} & = \left(12\mathbf{i} — 3\mathbf{j}\right) — \left(8\mathbf{i} + 4\ mathbf{j}\right), \\ & = \left(12\mathbf{i} — 8\mathbf{i}\right) + \left(- 3\mathbf{j} — 4\mathbf{j}\ справа), \\ & = 4\mathbf{i} — 7 \mathbf{j}. \end{align} У нас также есть это \begin{align} 3\mathbf{x} + \frac{1}{2} \mathbf{y} & = 3 \left(8\mathbf{i} + 4\mathbf {j}\right) + \frac{1}{2} \left(12\mathbf{i} — 3\mathbf{j}\right), \\ & = \left(24\mathbf{i} + 12 \mathbf{j}\right) + \left(6\mathbf{i} — \frac{3}{2}\mathbf{j}\right), \\ & = \left( 24\mathbf{i} + 6\mathbf{i}\right) + \left(12\mathbf{j} — \frac{3}{2} \mathbf{j}\right), \\ & = 30 \mathbf{i} + \frac {21}{2}\mathbf{j}. 2}, \\ & = \sqrt{80}, \\ & = 4\sqrt{5}, \ \ & = 8,9{\circ} \text{ (3 sf).} \end{align}
2}, \\ & = \sqrt{80}, \\ & = 4\sqrt{5}, \ \ & = 8,9{\circ} \text{ (3 sf).} \end{align}
Векторная запись — GCSE Maths
Введение
Что такое векторная запись?
Как использовать векторную запись
Рабочий лист векторных обозначений
Распространенные заблуждения
Практические вопросы по векторным обозначениям
Векторные обозначения GCSE вопросы
Контрольный список обучения
Следующие уроки
Вы знали?
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое векторная запись?
Как использовать векторную запись
Рабочий лист векторных обозначений
Распространенные заблуждения
Вопросы по практике векторной записи
Векторные обозначения GCSE вопросы
Контрольный список обучения
Следующие уроки
Вы знали?
Все еще застряли?
Здесь мы узнаем о векторных обозначениях, в том числе о том, что такое векторы и как мы используем обозначения в математике, чтобы писать о них.
Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое векторная запись?
Запись векторов — это то, как мы записываем векторы в математике.
Вектор – это величина, которая имеет как величину, так и направление. Его можно использовать для демонстрации движения.
Мы можем записывать векторы несколькими способами:
- Используя стрелку ,
- Использование жирным шрифтом
- Подчеркнутый .
\overrightarrow{AB} =\textbf{a}=\underline{a}
На этой диаграмме показан вектор, представляющий движение из точки A в точку B.
- Параллельные векторы с одинаковым направлением и одинаковой длиной являются одинаковыми (эквивалентными) :
Все они представляют один и тот же вектор \textbf{a} .
- Параллельные векторы одинаковой длины с противоположными направлениями называются отрицательными векторами:
Вектор, представляющий движение из точки B в точку A, будет направлен в противоположном направлении, но будет иметь ту же длину.
\overrightarrow{BA}=-\textbf{a}=-\underline{a}
- Вектор можно умножить на скаляр , чтобы изменить его длину:
Длина также называется величиной вектора
Например.
- Векторы также можно суммировать вместе:
На этой схеме показано, как добраться из точки А в точку С, пройдя через точку В.
Вектор \textbf{a} добавлен к вектору \textbf{b} .
\begin{align} \overrightarrow{AC}&=\overrightarrow{AB}+\overrightarrow{BC}\\\\ &= \\textbf{a} \ +\ \textbf{b}\\\\ \text{ или от руки как}\\\\ &=\ \underline{a} \ +\ \underline{b} \end{align}
Добавление отрицательного вектора становится вычитанием.
\begin{выровнено} &\textbf{a} \ + \ — \ \textbf{b}=\textbf{a} \ — \ \textbf{b}\\\\ &\text{или написано от руки}\\\ \ &\underline{a} \ + \ — \ \underline{b} = \underline{a} \ — \ \underline{b} \end{align}
Что такое векторная запись?
Как использовать векторную запись
Чтобы использовать векторную запись:
- Проверьте начальную и конечную точки.
- Выберите маршрут.
- Напишите вектор.
- Упростите ответ.
Как использовать векторную запись
Рабочий лист векторов (включает векторную запись)
Получите бесплатный векторный лист с более чем 20 векторными вопросами и ответами. Включает рассуждения и прикладные вопросы.СКОРО
ИксРабочий лист векторов (включает векторные обозначения)
Получите бесплатный рабочий лист векторных обозначений, содержащий более 20 вопросов и ответов по векторам. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКОРО
Примеры векторной записи
Пример 1: использование векторной записи
Запишите вектор \overrightarrow{AO} в терминах \textbf{a} и \textbf{b}
- Проверьте начальную и конечную точки.
\overrightarrow{АО}
Вектор начинается в точке А и заканчивается в точке О.
2 Определите маршрут.
Начните с начальной точки и пройдите вдоль сторон фигуры до конечной точки.
Однако двигаться можно только по линиям с векторами.
Здесь мы движемся в направлении, противоположном вектору \textbf{a} .
3 Запишите вектор.
Напишите маршрут из пункта А в пункт О.
\overrightarrow{AO}=-\textbf{a}=-\underline{a}
Пример 2: использование векторной записи
Запишите вектор \overrightarrow{AC} через \textbf{a} и \textbf{b}
Проверьте начальную и конечную точки.
\overrightarrow{AC}
Вектор начинается в точке A и заканчивается в точке C.
Определите маршрут.
Начните с начальной точки и пройдите вдоль сторон фигуры до конечной точки.
Однако двигаться можно только по линиям с векторами.
Напишите вектор.
Напишите маршрут из пункта А в пункт С.
\begin{aligned}
\overrightarrow{AC}&=\overrightarrow{AB}+\overrightarrow{BC}\\\\
&=\ \textbf{a} \ +\ \textbf{b}\\\\
\text{или написанный от руки}\\\\
&=\ \underline{a} \ +\ \underline{b}
\end{выровнено}
Пример 3: использование векторной записи
Запишите вектор \overrightarrow{BA} в терминах \textbf{a} и \textbf{b}
Проверьте начальную и конечную точки.
\overrightarrow{БА}
Вектор начинается в точке B и заканчивается в точке A.
Определите маршрут.
Начните с начальной точки и пройдите вдоль сторон фигуры до конечной точки.
Однако двигаться можно только по линиям, имеющим вектора. Мы не можем перейти напрямую из точки B в точку A, потому что нет вектора. Нам нужно пройти через точку C. Так как нам нужно идти назад по вектору \textbf{b} , нам нужен отрицательный вектор.
Запишите вектор.
Напишите маршрут из пункта B в пункт A.
\begin{aligned} \overrightarrow{BA}&=\overrightarrow{BO}+\overrightarrow{OA}\\\\ &=\ -\textbf{ b} \ +\ \textbf{a}\\ \text{или написанный от руки}\\\\ &=\ -\underline{b} \ +\ \underline{a} \end{align}
Альтернативно, окончательный ответ можно записать так:
\overrightarrow{BA}=\textbf{a}-\textbf{b}=\underline{a}-\underline{b}
Пример 4: оставить ответ в своем простейшая форма
Запишите вектор \overrightarrow{BC} через \textbf{a} и \textbf{b}
Проверьте начальную и конечную точки.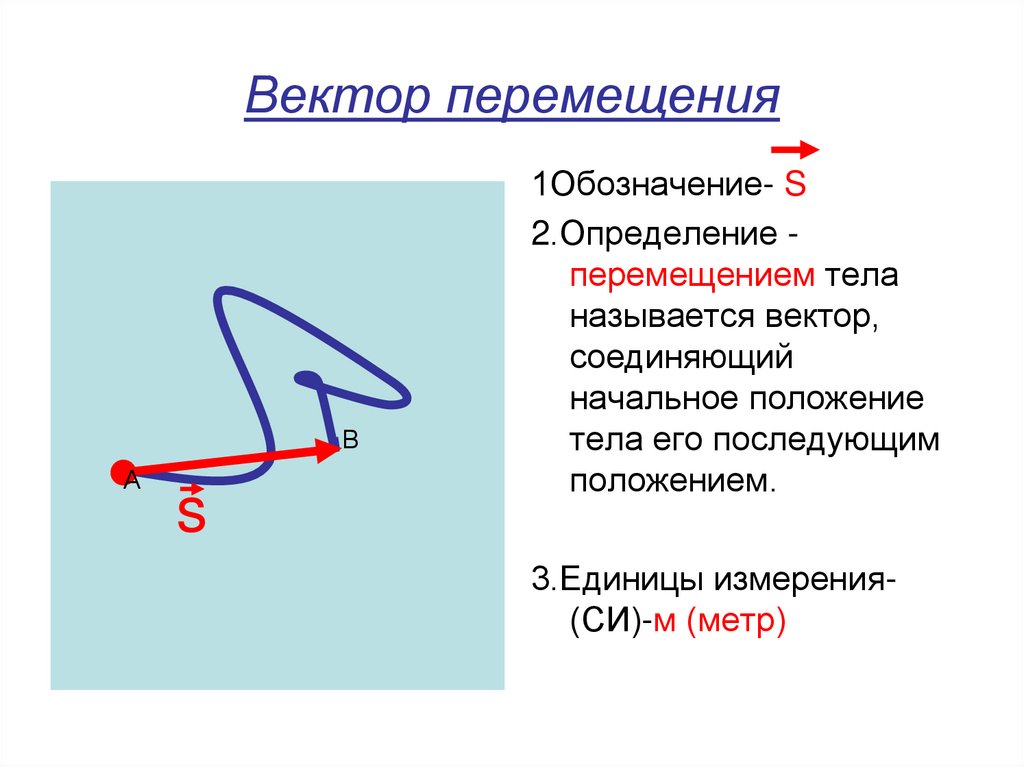
\overrightarrow{BC}
Вектор начинается в точке B и заканчивается в точке C.
Определите маршрут.
Начните с начальной точки и пройдите вдоль сторон фигуры до конечной точки.
Однако двигаться можно только по линиям, имеющим вектора. Мы не можем пойти напрямую из точки B в точку C. Нам нужно пройти через точку O и точку A. Поскольку нам нужно идти назад по вектору \textbf{b} , нам нужен отрицательный вектор.
Запишите вектор.
Напишите маршрут из точки B в точку C.
\begin{aligned}
\overrightarrow{BC}&=\overrightarrow{BO}+\overrightarrow{OA}+\overrightarrow{AC}\\\\
&=\ -\textbf{b} \ +\ \textbf{a} \ + 2\textbf{b}\\\\
\text{или написанный от руки}\\\\
&=\ -\underline{b} \ +\ \underline{a} \ + \ 2\underline{b}
\end{выровнено}
Упростите свой ответ.
Для простоты соберем одинаковые члены.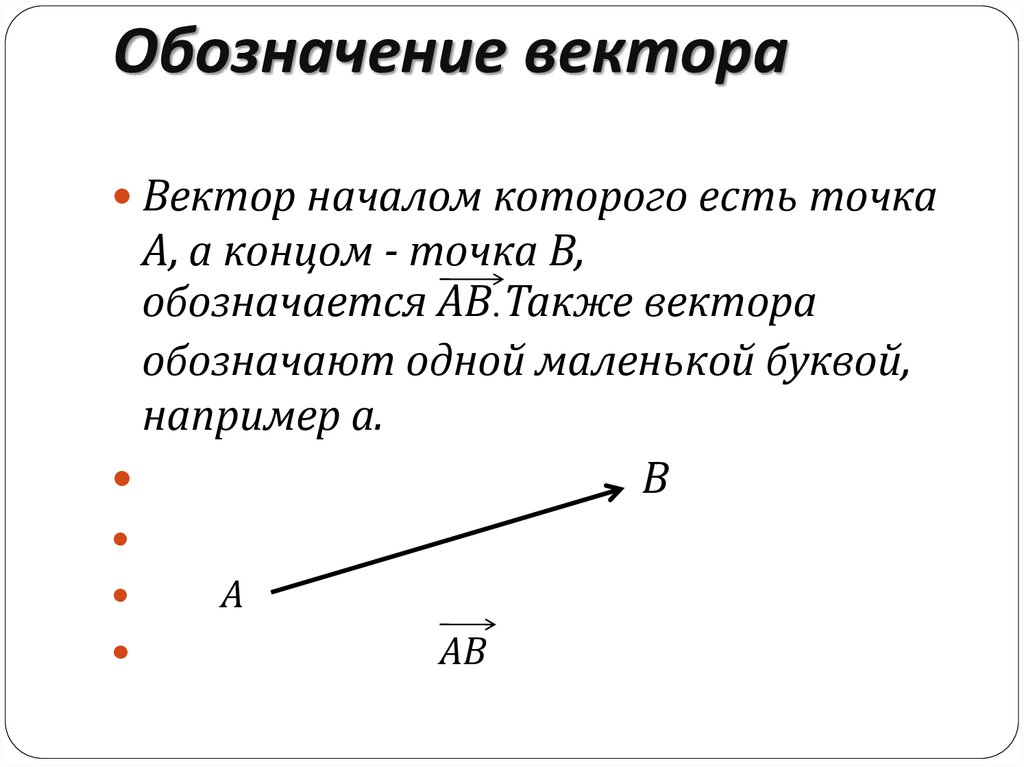 Таким образом, окончательный ответ:
Таким образом, окончательный ответ:
\overrightarrow{BC}=\textbf{a}+\textbf{b}=\underline{a}+\underline{b}
Пример 5: оставить ответ в его простейшей форме
Запишите вектор \overrightarrow{CA} через \textbf{a} и \textbf{b}
Проверьте начальную и конечную точки.
\overrightarrow{CA}
Вектор начинается в точке C и заканчивается в точке A.
Определите маршрут.
Начните с начальной точки и пройдите вдоль сторон фигуры до конечной точки.
Однако двигаться можно только по линиям с векторами. Мы не можем пойти напрямую из точки C в точку A. Нам нужно пройти через точку B и точку O. Поскольку мы иногда идем в противоположном направлении, нам понадобятся отрицательные векторы.
Напишите вектор.
Напишите маршрут из точки C в точку A.
\begin{aligned}
\overrightarrow{CA}&=\overrightarrow{CB}+\overrightarrow{BO}+\overrightarrow{OA}\\\\
&=\ -5\textbf{a} \ -\ 2\textbf{b} \ +\ 4\textbf{a}\\\\
\text{или написанный от руки}\\\\
&=\ -5\подчеркивание{а} \ -\ 2\подчеркивание{b} \ + \ 4\подчеркивание{а}
\end{выровнено}
Упростите ответ.
Для простоты соберем одинаковые члены. Итак, окончательный ответ:
\overrightarrow{CA}=-\textbf{a}-2\textbf{b}=-\underline{a}-2\underline{b}
Пример 6: оставить ответ в его простейшей форме
Вот шестиугольник.
Сторона OA параллельна стороне BE
Сторона OB параллельна стороне CD
Сторона AC параллельна стороне ED
Запишите вектор \overrightarrow{OE} через \textbf{a}, \; \textbf{b} и \textbf{c}
Проверьте начальную и конечную точки.
\overrightarrow{ОЕ}
Вектор начинается в точке O и заканчивается в точке E.
Определите маршрут.
Начните с начальной точки и пройдите вдоль сторон фигуры до конечной точки.
Однако двигаться можно только по линиям, имеющим вектора. Но мы можем использовать эту информацию, чтобы добавить на диаграмму больше векторов.
Запишите вектор.
Напишите маршрут из точки О в точку Е.
\begin{aligned}
\overrightarrow{OE}&=\overrightarrow{OA}+\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DE}\\\\
&=\ \ \\textbf{a} \ +\ \textbf{c} \ +\ \textbf{b} \ -\ \textbf{c}\\\\
\text{или написанный от руки}\\\\
&=\ \ \\underline{a} \ +\ \underline{c} \ + \ \underline{b} \ — \ \underline{c}
\end{выровнено}
Упростите свой ответ.
Для упрощения собираем одинаковые термины. Итак, окончательный ответ:
\overrightarrow{OE}=\textbf{b}+\textbf{a}=\underline{b}+\underline{a}
В качестве альтернативы мы могли бы уйти из точки O в точку B, а затем в точку E.
Это будет
\begin{aligned} \overrightarrow{OE}&=\overrightarrow{OB}+\overrightarrow{BE}\\\\ &=\ \textbf {b} \ +\ \textbf{a}\\\\ \text{или написанный от руки}\\\\ &=\ \underline{b} \ +\ \underline{a} \end{aligned}
Что идентично нашему предыдущему ответу.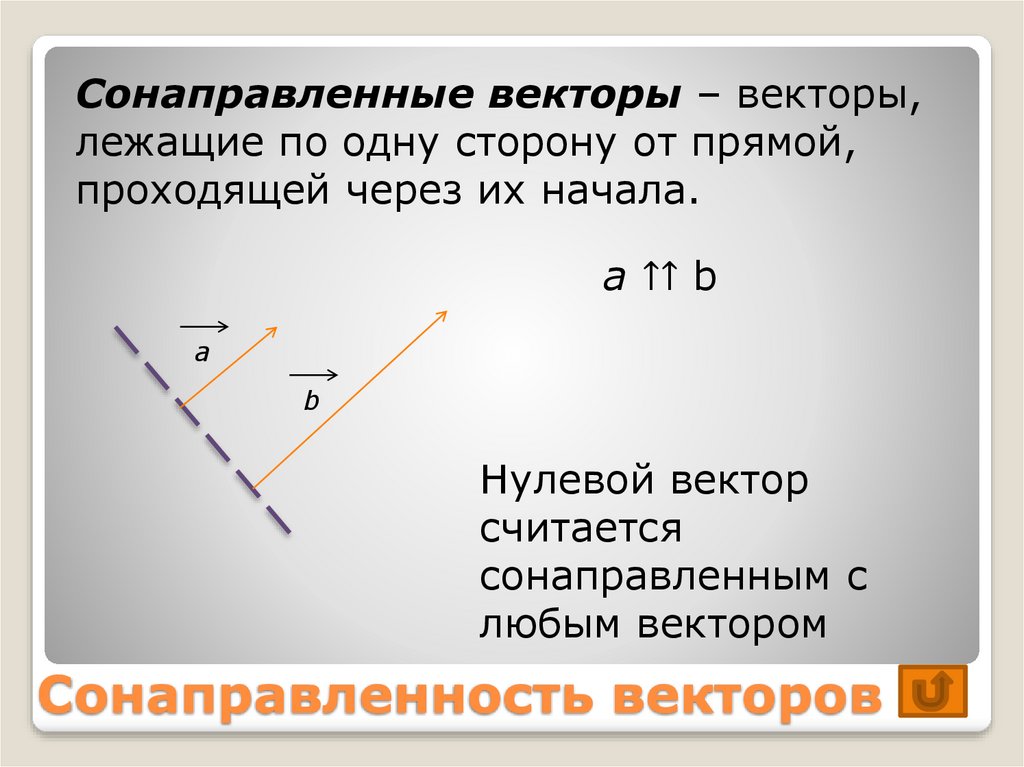
Распространенные заблуждения
- Окончательные ответы могут включать только один вектор
Вас могут попросить написать вектор в терминах вектора \textbf{a} и вектора \textbf{b} , но окончательный ответ может включать только один из векторов.
- Векторы могут содержать дроби или десятичные дроби
Вот схема вектора \textbf{c} . Вектор в том же направлении, но половина его длины будет \frac{1}{2}\textbf{c} или 0,5\textbf{a} .
Практические вопросы по векторным обозначениям нужно идти в направлении, противоположном вектору \textbf{b} , поэтому нам нужен отрицательный вектор \textbf{b} .
\overrightarrow{BO}=-\textbf{b}=-\underline{b}
\textbf{a}-3\textbf{b}
\textbf{a}+\textbf{b}
\textbf{a}+3\textbf{b}
\textbf{a}-\textbf{b}
Нам нужно пройти из точки O в точку B через точку A.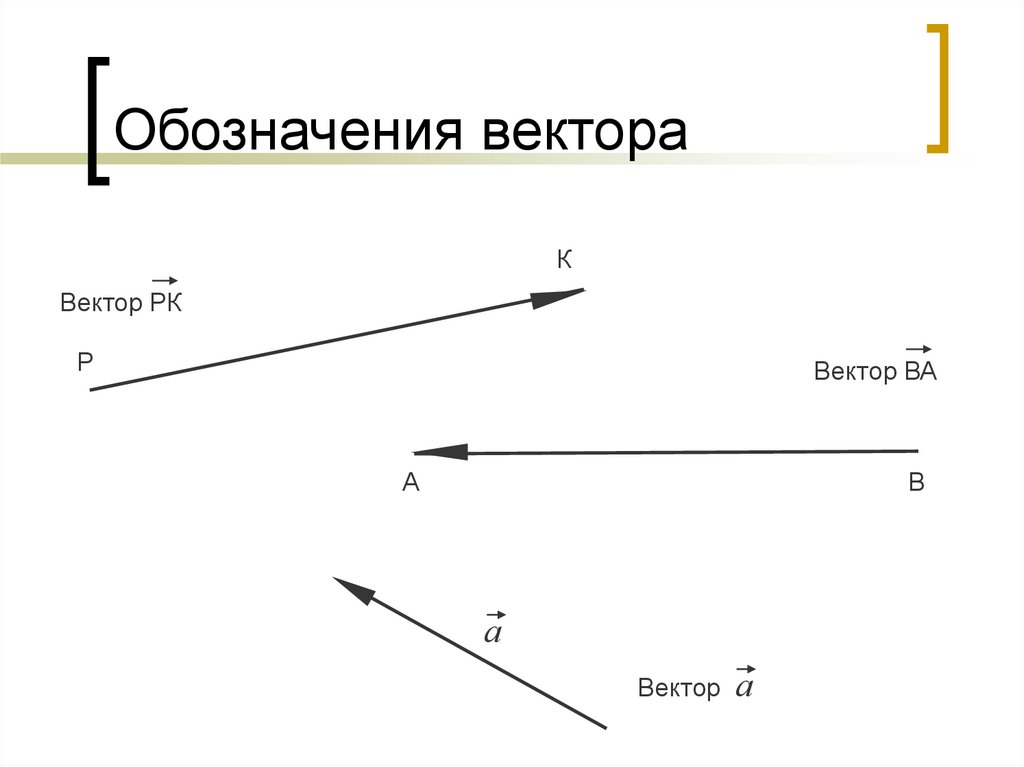
\begin{align} \overrightarrow{OB}&=\overrightarrow{OA}+\overrightarrow{AB}\\\\ &=\ \\textbf{a} \ +\ 3\textbf{b}\\\\ \text{или написанный от руки}\\\\ &=\ \ \underline{a} \ +\ 3\underline{b} \end{выровнено}
\textbf{b}-\textbf{a}
2\textbf{b}+\textbf{a}
\textbf{a}+\textbf{b} 5
004 \textbf{a}-\textbf{b}
Нам нужно пройти из точки A в точку B через точку O. Нам нужно пойти в направлении, противоположном вектору \textbf{a} , поэтому нам нужен отрицательный вектор \textbf{а} .
\begin{align} \overrightarrow{AB}&=\overrightarrow{AO}+\overrightarrow{OB}\\\\ &= -\textbf{a} \ +\ \textbf{b}\\\\ &= \ \ \textbf{b} \ – \ \textbf{a}\\\\ \text{или написанный от руки}\\\\ &=\ \ \underline{b} \ -\ \underline{a} \end{выровнено}
7\textbf{b}-\textbf{a}
-\textbf{b}-\textbf{a}
\textbf{a}+7\textbf{b}
\textbf{ a}-\textbf{b}
Нам нужно пройти из точки B в точку C через точку A и точку D.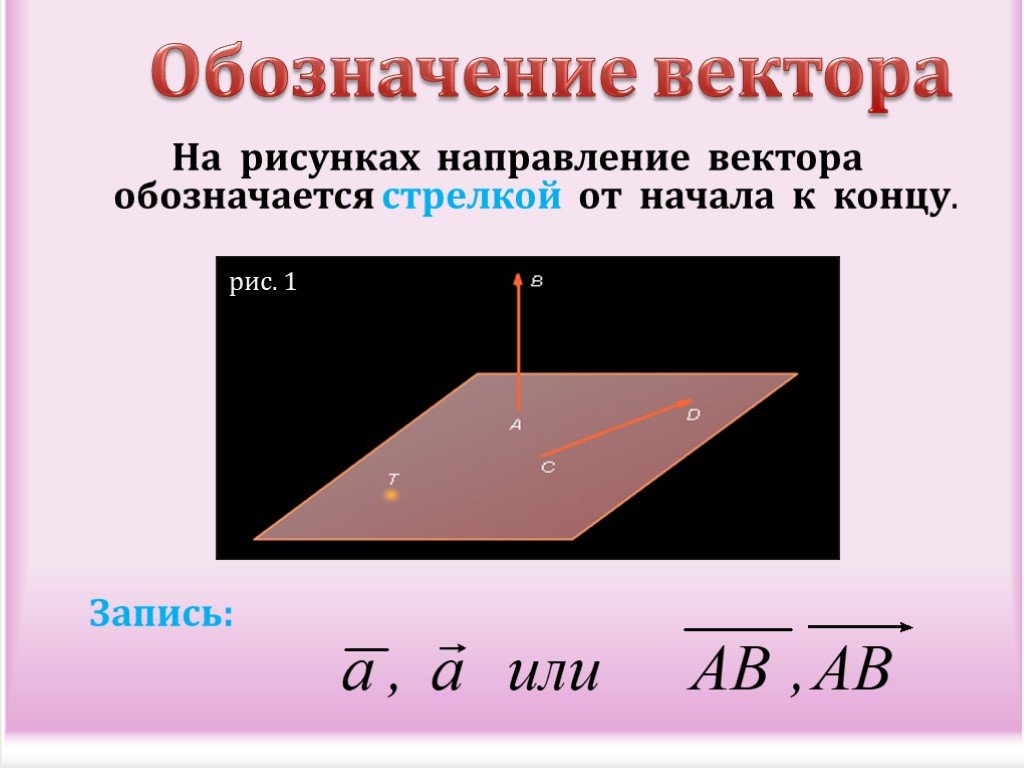 Нам нужно идти в направлении, противоположном вектору 4\textbf{b} , поэтому нам нужен отрицательный вектор .
Нам нужно идти в направлении, противоположном вектору 4\textbf{b} , поэтому нам нужен отрицательный вектор .
Нам нужно двигаться в направлении, противоположном вектору \textbf{a} , поэтому нам нужен еще один отрицательный вектор. Когда мы разработали маршрут, нам нужно упростить ответ.
\begin{align} \overrightarrow{BC}&=\overrightarrow{BA} \ +\ \overrightarrow{AD} \ + \ \overrightarrow{DC}\\\\ &= -4\textbf{b} \ -\ \textbf{a} \ + \ 3\textbf{b}\\\\ &= \ \ -\textbf{b} \ + \ \textbf{a}\\\\ \text{или написанный от руки}\\\\ &=\ \ -\underline{b} \ -\ \underline{a} \end{выровнено}
2\textbf{a}+3\textbf{b}
12\textbf{a}+3\textbf{b}
-2\textbf{a}+3\textbf{b}
12\textbf{a}-3\textbf{b}
Нам нужно пройти из точки B в точку A через точки C и D. Нам нужно идти в направлении, противоположном вектору 7\textbf{a} , поэтому нам нужен отрицательный вектор.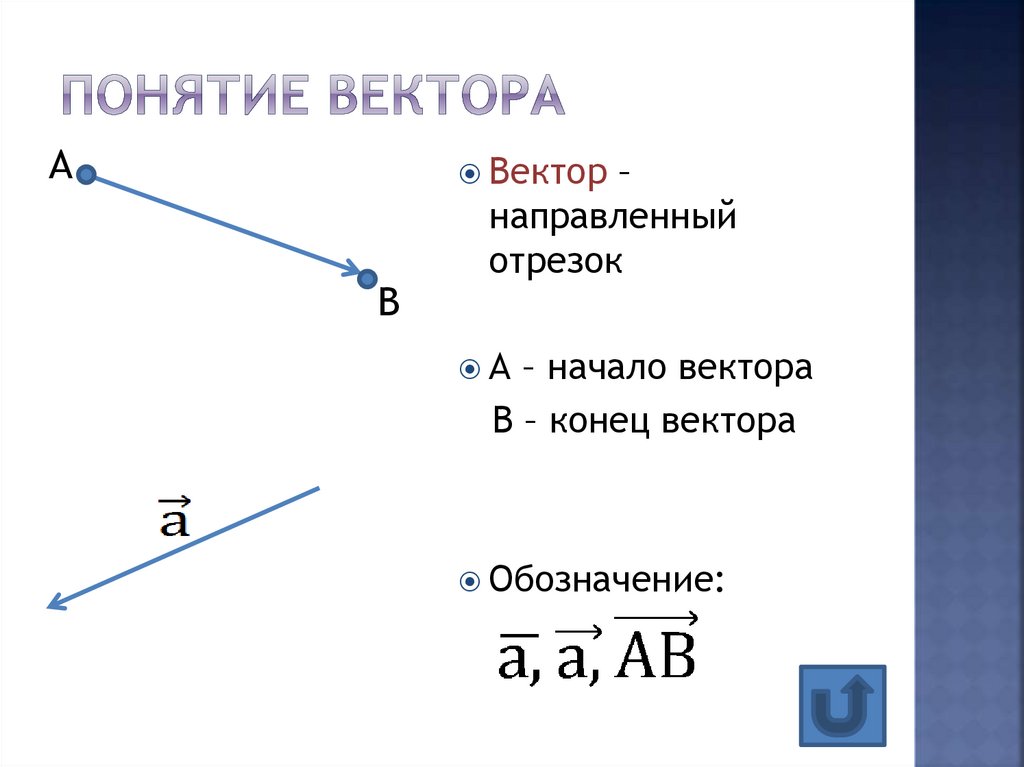 Когда мы разработали маршрут, нам нужно упростить ответ.
Когда мы разработали маршрут, нам нужно упростить ответ.
\begin{align} \overrightarrow{BA}&=\overrightarrow{BC} \ + \ \overrightarrow{CD} \ + \ \overrightarrow{DA}\\\\ &= -7\textbf{a} \ +\ 3\textbf{b} \ + \ 5\textbf{a}\\\\ &= \ \ -2\textbf{a} \ + \ 3\textbf{b}\\\\ \text{или написанный от руки}\\\\ &=\ \ -2\подчеркивание{а} \ + \ 3\подчеркивание{б} \end{выровнено}
\textbf{b}-\textbf{c}
\textbf{a}+\textbf{b}+\textbf{c}
2\textbf{a}+\textbf{c} b}+\textbf{c}
\textbf{b}+\textbf{c}
Нам нужно перейти из точки O в точку D. Используйте факты о параллельных сторонах, чтобы добавить больше векторов.
\begin{выровнено} \overrightarrow{OD}&=\overrightarrow{OE} + \overrightarrow{ED}\\\\ &=\ \textbf{c} \ + \ \textbf{b}\\\\ &= \\textbf{b} \ + \\textbf{c}\\\\ \text{или написанный от руки}\\\\ &=\ \underline{b} \ + \ \underline{c} \end{выровнено}
Векторная запись GCSE вопросы
1. OABC является трапецией
OABC является трапецией
AB параллелен OC .
(a) Найти через \textbf{b} вектор \overrightarrow{BA}
(b) Найти через \textbf{a} и \textbf{ b} , вектор \overrightarrow{CA}
(2 балла)
Показать ответ
(а)
\overrightarrow{BA}=-5\textbf{b}=-5\underline{b}
(1)
(б)
\overrightarrow{CA}=\textbf{a} \ – \ 3\textbf{b}=\underline{a} \ – \ 3\underline{b}
(1)
2. ABCD — параллелограмм.
Диагонали параллелограмма пересекаются в точке O .
\begin{выровнено} \overrightarrow{ОА}=\textbf{а}\\ \overrightarrow{OB}=\textbf{b} \end{выровнено}
(a) Найти в терминах \textbf{a} вектор \overrightarrow{AO}
(b) Найти в терминах \textbf{a} вектор \ overrightarrow{CA}
(c) Найдите через \textbf{a} и \textbf{b} вектор \overrightarrow{BA}
(3 балла)
Показать ответ
(а)
\overrightarrow{AO}=-\textbf{a} =-\underline{a}
(1)
(б)
\overrightarrow{CA}=2\textbf{a} =2\underline{a}
(1)
(в)
\overrightarrow{BA}=\textbf{a} \ – \ \textbf{b} =\underline{a} \ – \ \underline{b}
(1)
3. ABCD — трапеция.
ABCD — трапеция.
AB параллелен DC .
(a) Найдите в терминах \textbf{a} вектор \overrightarrow{AO}
(b) Найдите в терминах \textbf{a} и \textbf{b} вектор vector \overrightarrow{DB}
(c) Найдите в терминах \textbf{a} и \textbf{b} вектор \overrightarrow{CB}
(4 отметки)
Показать ответ
(а)
\overrightarrow{AD}=-5\textbf{a} =-5\underline{a}
(1)
(б)
\overrightarrow{DB}=5\textbf{a} \ + \ 9\textbf{b} =5\underline{a} \ + \ 9\underline{b}
(1)
(в)
\overrightarrow{CB}=-7\textbf{b} \ + \ 5\textbf{a} \ + \ 9\textbf{b} =-7\underline{b} \ + \ 5\underline{a} \ + \ 9\подчеркивание{б}
Для правильного маршрута
(1)
\overrightarrow{CB}=5\textbf{a} \ + \ 2\textbf{b} = 5\underline{a} \ + \ 2\underline{b}
Для правильного упрощенного ответа
(1)
Учебный контрольный список
Теперь вы научились:
- Использовать векторную запись для записи вектора
- Использовать векторную запись для решения геометрической задачи ты знаешь?
Векторы очень полезны, и их можно расширить за пределы математики GCSE.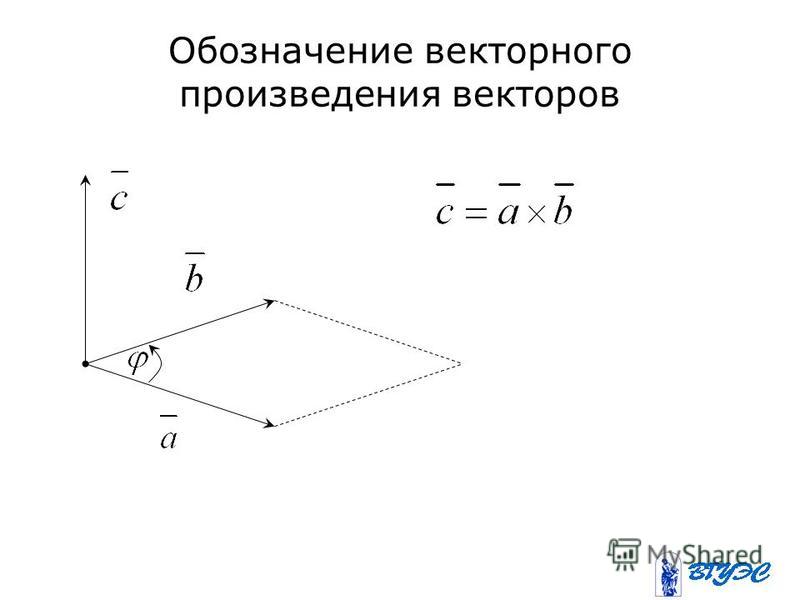


 4).
4).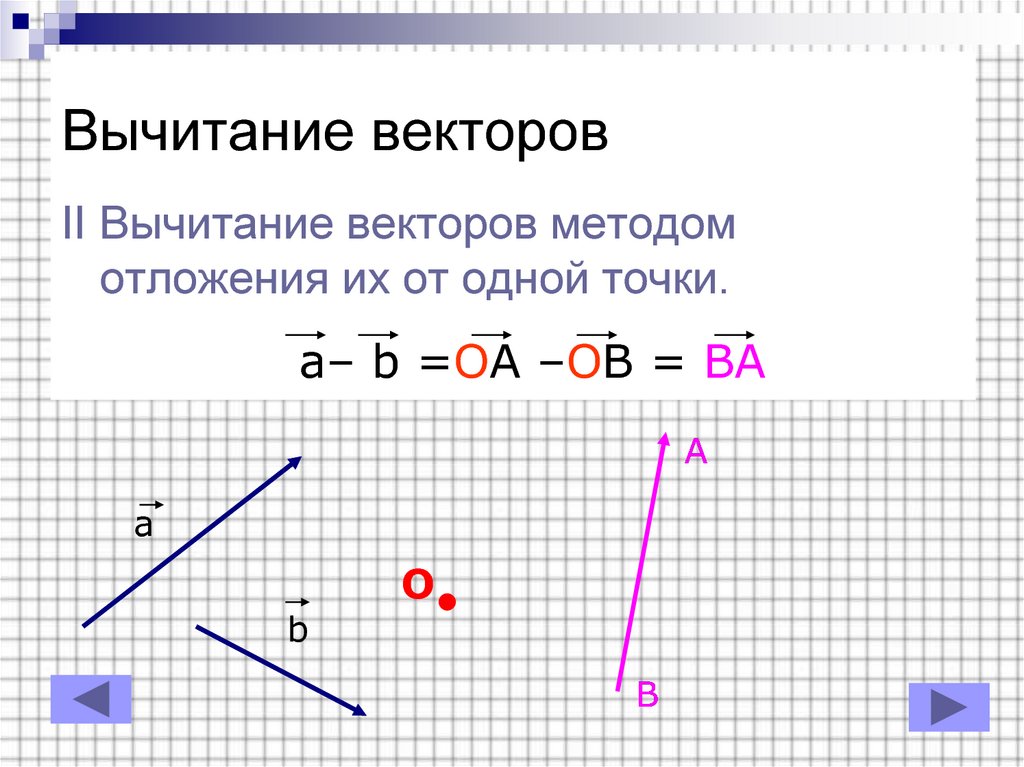 Длина вектора
Направляющие косинусы вектора
Равенство векторов
Ортогональность векторов
Коллинеарность векторов
Компланарность векторов
Угол между векторами
Проекция вектора
Сложение и вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Линейно зависимые и линейно независимые вектора
Разложение вектора по базису
Длина вектора
Направляющие косинусы вектора
Равенство векторов
Ортогональность векторов
Коллинеарность векторов
Компланарность векторов
Угол между векторами
Проекция вектора
Сложение и вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Линейно зависимые и линейно независимые вектора
Разложение вектора по базису