Вероятности сложных событий
Сложным событиемназывается наблюдаемое событие, выраженное через другие наблюдаемые в том же опыте события с помощью допустимых алгебраических операций.
Записав равенство (4) в виде
, (8)
получаем так называемую формулу умножения вероятностей. Если оба события и обладают ненулевой вероятностью, то формула умножения может быть записана двояким образом:
. (9)
Формула (9) позволяет находить вероятности совместного наступления событий и в тех случаях, когда условная вероятность известна из дополнительных опытов или определена методом вспомогательного эксперимента.
Из (9) по индукции нетрудно получается формула умножения для произвольного числа событий:
. (10)
Для вероятности наступления хотя бы одного из двух событий и справедлива следующая формула сложения вероятностей:
. (11)
Если события независимы в совокупности, то вероятность наступления хотя бы одного из них проще вычисляется не по формуле сложения, а с помощью формулы умножения:
. (12)
Пример. В продукции предприятия брак составляет 5% от общего объема выпускаемых изделий. Для контроля качества случайно отобрано 20 изделий. Найти вероятность того, что среди них будет хотя бы одно бракованное.
◄ Обозначим через события ={ — ое по счету отобранное изделие бракованное}, 1, 2, …, 20. По условию вероятность того, что изделие в продукции предприятия является бракованным, равна . Очевидно, что нас интересует событие . В условиях стабильного технологического процесса производства можно считать, что события независимы в совокупности. Учитывая, что , по формуле (12) получаем ►
Похожие статьи:
poznayka.org
4.4.2. Основные правила вычисления вероятностей сложных событий
Ниже приведены основные правила, позволяющие определить вероятность появления сложного события на основании известных вероятностей составляющих его более простых событий.
1. Вероятность достоверного события равна единице:
. (4.2)
2. Вероятность объединения (суммы) несовместных событий равна сумме их вероятностей:
(4.3)
Эти два равенства являются аксиомами теории вероятностей, т. е. принимаются в качестве исходных, но требующих доказательства свойств вероятностей. На их основе строится вся теория вероятностей.
Все остальные, приведенные ниже без доказательств формулы могут быть выведены из принятых аксиом.
3. Вероятность невозможного события равна нулю:
. (4.4)
4. Вероятность события, противоположного событию А, равна
(4.5)
Формула (4.5) оказывается полезной на практике в тех случаях, когда вычисление вероятности непосредственно события А затруднительно, в то время как вероятность противоположного события находится просто (см. ниже п.9).
5. Теорема сложения вероятностей. Вероятность объединения произвольных событий равна сумме их вероятностей за вычетом вероятности произведения событий:
. (4.6)
Для несовместных событий и формула (4.6) переходит в (4.3).
6. Условная вероятность. Если требуется найти вероятность события В при условии, что произошло некоторое другое событие А, то такую ситуацию характеризуют с помощью условной вероятности. Условная вероятность равна отношению вероятности произведения событийА и В к вероятности события А:
(4.7)
В тех случаях, когда события А и В несовместны, и соответственно.
7. Определение условной вероятности в виде (4.7) дает возможность записать следующую формулу для вычисления вероятности произведения событий
(4.8)
8. Поскольку вероятность события А (или В) для независимых событий по определению не изменяется при появлении другого события, то условная вероятность совпадает с вероятностью событияА, а условная вероятность — сР(В). Вероятности Р(А) и Р(В) в отличие от условных вероятностей называются безусловными.
, , (4.9)
Теорема умножения вероятностей для независимых событий записывается следующим образом:
, (4.10)
т. е. вероятность произведения независимых событий равна произведению их вероятностей.
9. Вычислим вероятность появления хотя бы одного события в n испытаниях
А – появление в n испытаниях хотя бы один раз интересующего нас события.
– интересующее нас событие не появлилось в n испытаниях ни разу.
А1 – интересующее нас событие появлилось в первом испытании.
А2 – интересующее нас событие появлилось во втором испытании.
….
Аn – интересующее нас событие появлилось в n-ом испытании.
(4.11)
10. Формула полной вероятности.
Если событие А может произойти только при появлении одного из несовместных событий Н1, Н2, …, Нn, то
. (4.12)
Пример 4.3
В урне 5 белых, 20 красных и 10 черных шаров, не отличающихся по размеру. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым или черным?
Решение. Пусть событие А – появление белого или черного шара. Разобьем это событие на более простые. Пусть В1 – появление белого шара, а В2 – черного. Тогда, А=В1+В2по определению суммы событий. Следовательно Р(А)=Р(В1+В2). Так как В1 и В2 – несовместные события, то по теореме о вероятности суммы несовместных событий (формула 4.3)Р(В1+В2) = Р(В1)+Р(В2 ).
Вычислим вероятности событий В1 и В2. В этом примере имеется 35 равновозможных (шары не отличаются по размеру) исходов опыта, событию В1 (появлению белого шара) благоприятствуют 5 из них, поэтому . Аналогично,. Следовательно,.
Пример 4.4
Ведутся поиски двух преступников. Каждый из них независимо от другого может быть обнаружен в течение суток с вероятностью 0,5. Какова вероятность того, что в течение суток будет обнаружен хотя бы один преступник?
Решение. Пусть событие А – “обнаружен хотя бы один преступник”. Разобьем это событие на более простые. Пусть В1 – обнаружен первый преступник, а В2 – обнаружен второй преступник. Тогда, А=В1+В2 по определению суммы событий. Следовательно
Р(В1+В2) = Р(В1)+Р(В2)-Р(В1 В2) = 0,5+0,5 – 0,25=0,75.
Можно решать и через обратное событие: .
Пример 4.5 а)
Преступник имеет 3 ключа. В темноте он открывает дверь выбирая ключ случайным образом. На открытие каждой из дверей он тратит 5 сек. Найти вероятность того, что он откроет все двери за 15 сек.
Решение. Пусть событие А – “открыты все двери”. Разобьем это событие на более простые. Пусть В – “открыта 1-я“, С – “ открыта 2-я“, а D – “ открыта 3-я“. Тогда, А=ВСD по определению произведения событий. Следовательно Р(А)=Р(ВСD). По теореме о вероятности произведения независимых событий (формула 4.10) Р(ВСD) = Р(В)Р(C) Р(D).
Вычислим вероятности событий В, Cи D. В этом примере имеется 3 равновозможных (каждый ключ выбираем из 3-х) исходов опыта. Каждому из событий В, Cи Dблагоприятствует 1 из них, поэтому ..
Пример 4.5 б)
Изменим задачу: считаем, что преступник – забывчивый человек. Пусть преступник открыв дверь, оставляет ключ в ней. Какова тогда вероятность, что он откроет все двери за 15 сек?
Решение. Событие А – “открыты все двери”. Опять, А=ВСD по определению произведения событий. Следовательно Р(А)=Р(ВСD). Но, теперь события В, Cи D – зависимы. По теореме о вероятности произведения зависимых событий Р(ВСD) = Р(В)Р(C|B) Р(D|BC).
Пример 4.6
Ведутся поиски двух преступников. Каждый из них независимо от другого может быть обнаружен в течение суток с вероятностью 0,5. После поимки одно из них, в связи с увеличением количества сотрудников, занятых в поисках, вероятность найти второго возрастает до 0,7. Какова вероятность того, что в течение суток будет обнаружены оба преступника.
Решение. Пусть событие А – “обнаружены два преступника”. Разобьем это событие на более простые. Пусть В1 – обнаружен первый преступник, а В2 – обнаружен второй преступник, после того, как пойман первый. Тогда, А=В1В2 по определению произведения событий. Следовательно Р(А)=Р(В1В2). Так как В1 и В2 – зависимые события, то по теореме о вероятности произведения зависимых событий (формула 4.8) Р(В1В2) = Р(В1)Р(В2/В1) = 0,5 0,7=0,35.
Пример 4.7
Найти вероятность того, что при подбрасывании монеты 10 раз герб выпадет хотя бы 1 раз.
Решение. Пусть событие А – “герб выпадет хотя бы 1 раз”. Рассмотрим обратное событие: – “герб не выпадетни разу”. Очевидно, что обратное событие легче чем исходное разбить на более простые. Пусть А1 – герб не выпал при первом броске, А2 – герб не выпал при втором броске, … А10 – герб не выпал при 10-м броске. Все события А1…А10 независимы, следовательно, (формула 4.11)
.
Пример 4.8
В проведении операции по освобождению заложников участвуют 2 группы снайперов: 10 человек с винтовкой ОП21 и 20 человек с АКМ47. Вероятность поражения из ОП21 – 0,85, а АКМ47 – 0,65. Найти вероятность того, что при одном выстреле произвольного снайпера преступник будет поражен.
Решение. Пусть событие А – “преступник поражен”. Разобьем это событие на более простые. Преступник может быть поражен либо из ОП21, либо из АКМ47. Вероятность того, что произвольный снайпер вооружен ОП21 (событие Н1) равна 10/30. Вероятность того, что произвольный снайпер вооружен АКМ47 (событие Н2) равна 20/30.
Вероятность того, что преступник поражен равна (формула 4.12)
.
В подобных задачах полезно изобразить дерево всех возможных исходов (с указанием вероятностей каждого исхода):
.
studfiles.net
4. Вычисление вероятностей сложных событий. Теоремы сложения и умножения вероятностей. Условная вероятность
Теорема 1. (Сложения вероятностей)
Вероятность суммы двух совместных
событий  и
и  равна сумме вероятностей этих событий
без вероятности их совместного
наступления
равна сумме вероятностей этих событий
без вероятности их совместного
наступления
.
Вероятность суммы несовместных событий рвана сумме их вероятностей, т.е.
.
Эта
теорема обобщается на случай произвольного
числа попарно несовместных событий: 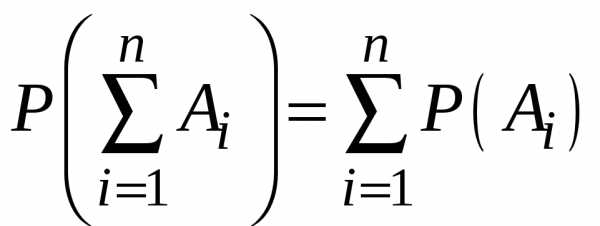 .
.
События  и
и  называются независимыми, если вероятность
называются независимыми, если вероятность  не зависит
от того, произошло событие
не зависит
от того, произошло событие  или нет.
или нет.
Событие  называется зависимым от события
называется зависимым от события  , если
вероятность события
, если
вероятность события  зависит от того, произошло или не
произошло событие
зависит от того, произошло или не
произошло событие  .
.
Вероятность
события  , вычисленная
при условии, что
, вычисленная
при условии, что  имело место, называется условной
вероятностью
имело место, называется условной
вероятностью  .
.
Теорема 2. (Умножения вероятностей)
Вероятность
произведения двух зависимых событий  и
и  равна произведению вероятности одного
их этих событий на условную вероятность
другого, при условии, что первое наступило:
равна произведению вероятности одного
их этих событий на условную вероятность
другого, при условии, что первое наступило:
.
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:
.
Обобщенная теорема умножения:
.
Вероятность произведения событий, независимых в совокупности, равна произведению вероятностей этих событий:
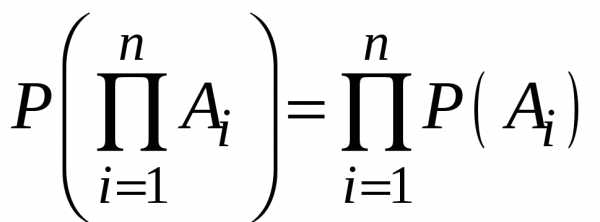
Пример 1.
Три стрелка независимо друг от друга стреляют по цели Вероятность попадания в цель для первого стрелка − 0,75; для второго − 0,3; для третьего − 0,9. Найти вероятность того, что все три стрелка попадут в цель.
Решение.
Пусть
событие  – первый
стрелок попал в цель; событие
– первый
стрелок попал в цель; событие  – второй стрелок попал в цель; событие
– второй стрелок попал в цель; событие  – третий стрелок попал в цель;
– третий стрелок попал в цель;
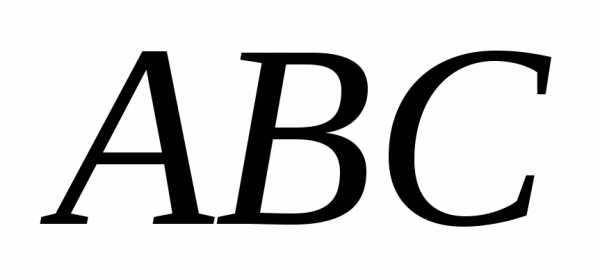 – все три стрелка попадут в цель.
– все три стрелка попадут в цель.
.
Пример 2.
Идет бомбардировка трех складов боеприпасов. Сбрасывают одну бомбу. Вероятность попадания в первый склад равна 0,01; во второй равна 0,008; в третий − 0,025. При попадании в любой их них взрываются все. Найти вероятность того, что склады будут взорваны.
Решение.
Событие  – взрыв
складов;
– взрыв
складов;  – попадание
в первый склад;
– попадание
в первый склад;  – попадание
во второй склад;
– попадание
во второй склад;  – попадание
и третий склад.
– попадание
и третий склад.
, так как несовместны, то:
.
Пример 3.
Имеется три ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение.
Вероятность
того, что из первого ящика вынута
стандартная деталь (событие  )
равна
)
равна 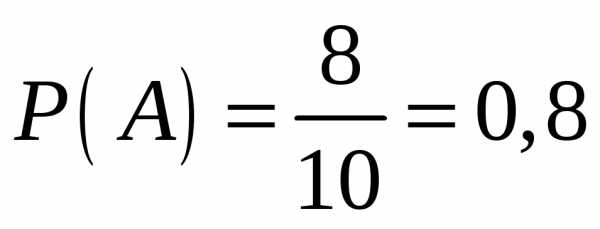 .
.
Вероятность
того, что из второго ящика вынута
стандартная деталь (событие  )
равна
)
равна 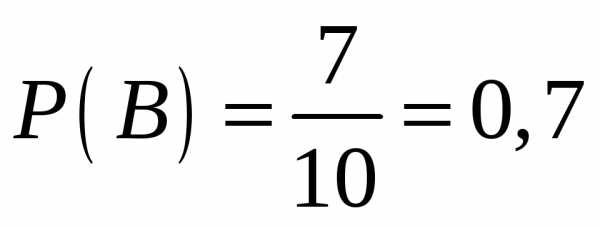 .
.
Вероятность
того, что из третьего ящика вынута
стандартная деталь (событие  )
равна
)
равна 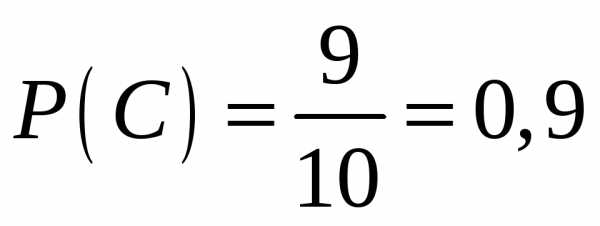 .
.
Так
как события  ,
,  и независимы, то искомая вероятность
события
и независимы, то искомая вероятность
события 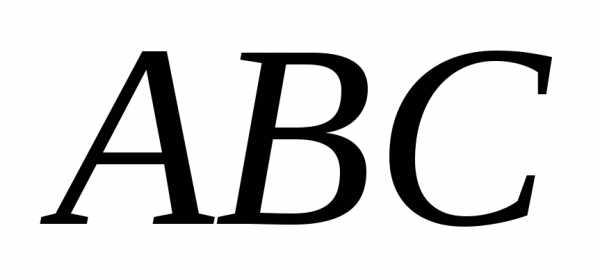 (по теореме умножения) равна
(по теореме умножения) равна
.
Пример 4.
Вероятности
появления каждого из трех независимых
событий  ,
,  ,
,  соответственно равны
соответственно равны 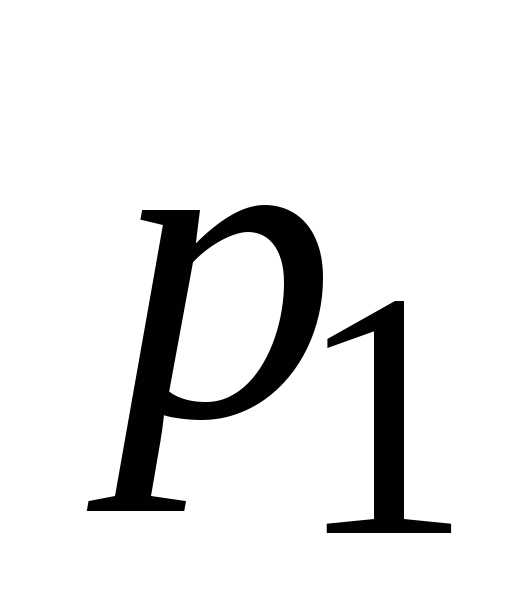 ,
, 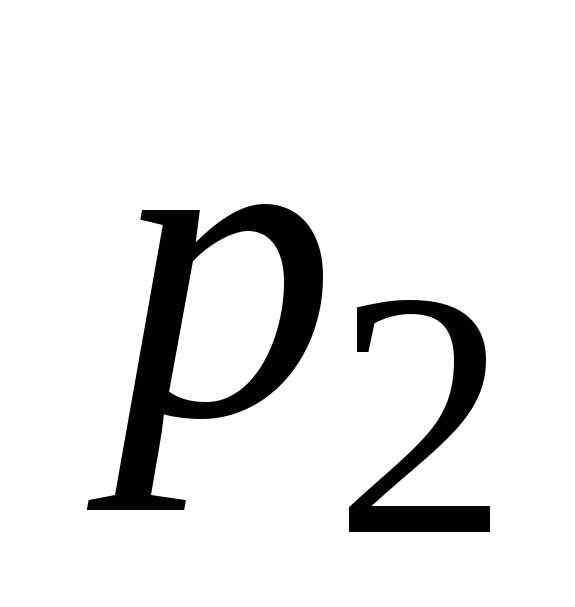 ,
,  Найти вероятность появления только
одного из этих событий.
Найти вероятность появления только
одного из этих событий.
Решение.
Заметим,
что, например, появление только первого
события  ,
равносильно появлению события
,
равносильно появлению события 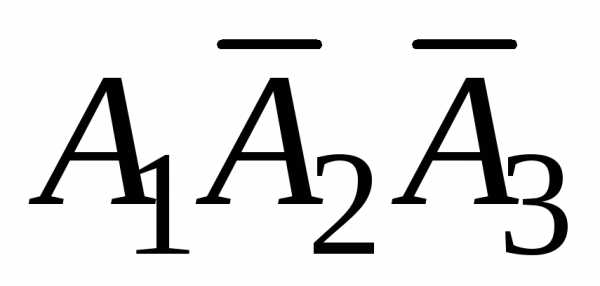 (появилось первое и не появились второе
и третье события).
(появилось первое и не появились второе
и третье события).
Обозначим:  – появление
только события
– появление
только события  ,
т.е.
;
,
т.е.
;
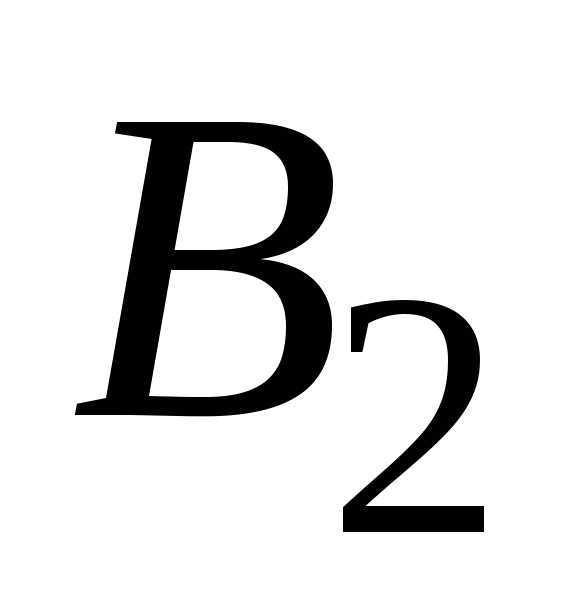 – появление
только события
– появление
только события  ,
т.е.
;
,
т.е.
;
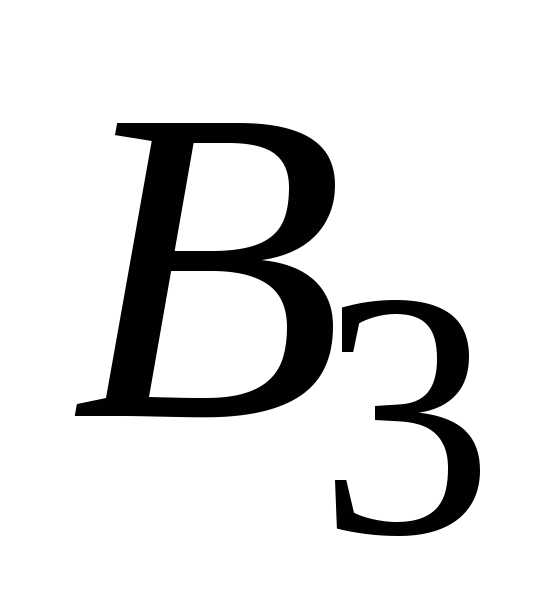 – появление
только события
– появление
только события  ,
т.е.
.
,
т.е.
.
Таким
образом, чтобы найти вероятность
появления только одного из событий  ,
,  ,
,  ,
воспользуемся теоремой сложения
несовместных событий:
.
,
воспользуемся теоремой сложения
несовместных событий:
.
Определим вероятности каждого из событий .
События  ,
,  ,
,  – независимы, поэтому
– независимы, поэтому
,,,
и тогда
.
Пример 5.
Вероятность
попадания в цель при стрельбе из трех орудий
соответственно равны 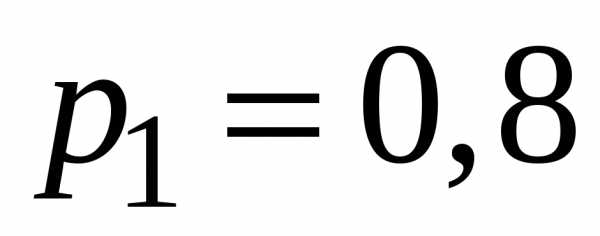 ,
, 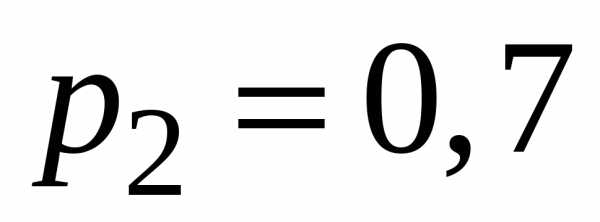 ,
, 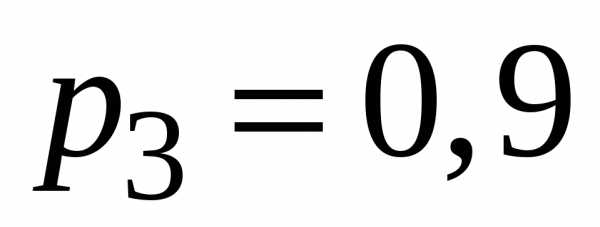 .
Найти вероятность хотя бы одного
попадания (событие
.
Найти вероятность хотя бы одного
попадания (событие  )
при одном залпе из всех орудий.
)
при одном залпе из всех орудий.
Решение.
Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий.
Рассмотрим события;
 – попадание
первым орудием;
– попадание
первым орудием;
 – попадание
вторым орудием;
– попадание
вторым орудием;
 – попадание
третьим орудием.
– попадание
третьим орудием.
; 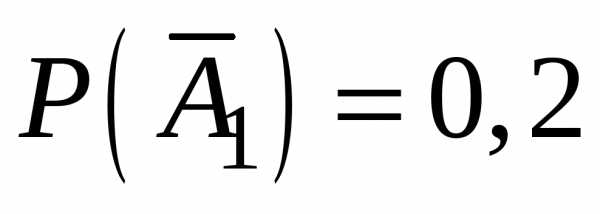 ;
;
;
; 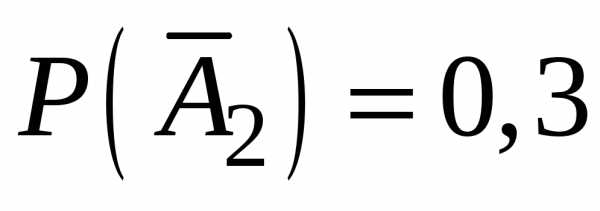 ;
;
;
; 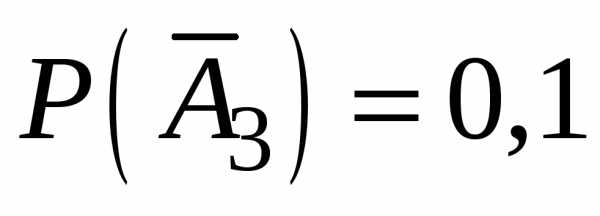 ;
;
.
Пусть
событие  – хотя бы
одно попадание, а
– хотя бы
одно попадание, а  –
ни одрого попадания, тогда
.
–
ни одрого попадания, тогда
.
Событие , тогда .
и .
Пример 6.
Из
урны, содержащей 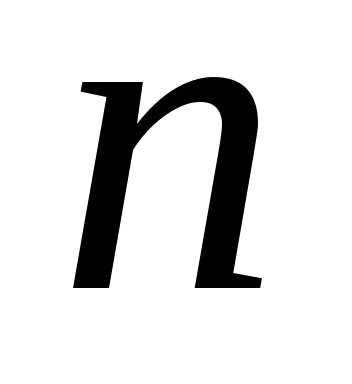 белых и
белых и 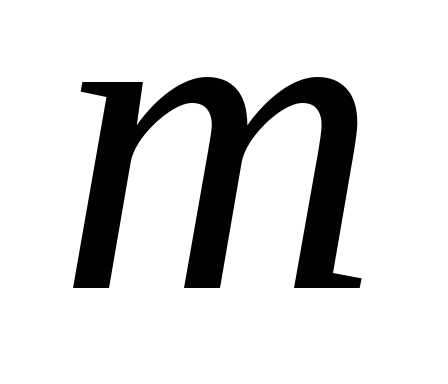 черных шаров,
вынимают два шара. Какова вероятность
того, что они будут разных цветов?
черных шаров,
вынимают два шара. Какова вероятность
того, что они будут разных цветов?
Решение.
Представим
событие  ,
состоящее в том, что вынуты шары разных
цветов, в виде
, где событие
,
состоящее в том, что вынуты шары разных
цветов, в виде
, где событие  состоит в том, что первый
шар −белый,
а второй − черный, событие
состоит в том, что первый
шар −белый,
а второй − черный, событие  состоит в том, что первый шар − черный,
а второй − белый. Так как события
состоит в том, что первый шар − черный,
а второй − белый. Так как события  и
и  несовместны,
то
.
несовместны,
то
.
Тогда .
Аналогично , .
Ответ: 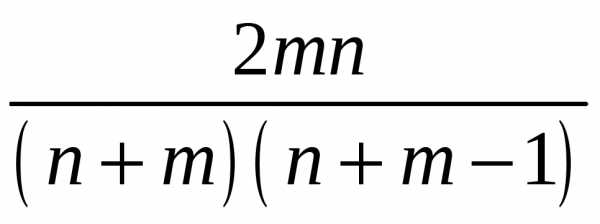 .
.
Пример 7.
Бросаются
две монеты. Рассматриваются события:  – выпадение герба на первой монете,
– выпадение герба на первой монете,  – выпадение герба на второй монете.
Найти вероятность события .
– выпадение герба на второй монете.
Найти вероятность события .
Решение.
Так
как  и
и  – несовместны, то
– несовместны, то
,
или через противоположное событие .
Пример 8.
Система 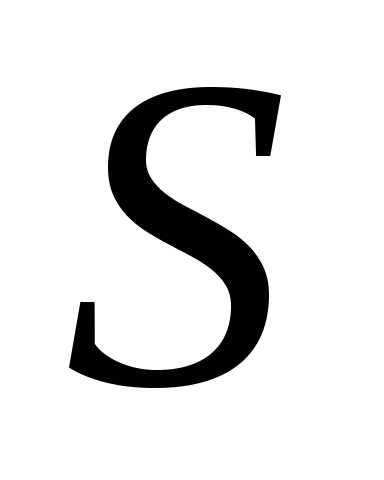 состоит из двух дублирующих блоков
состоит из двух дублирующих блоков 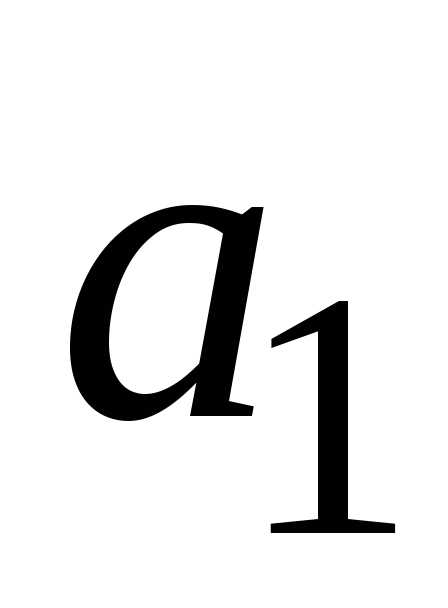 ,
,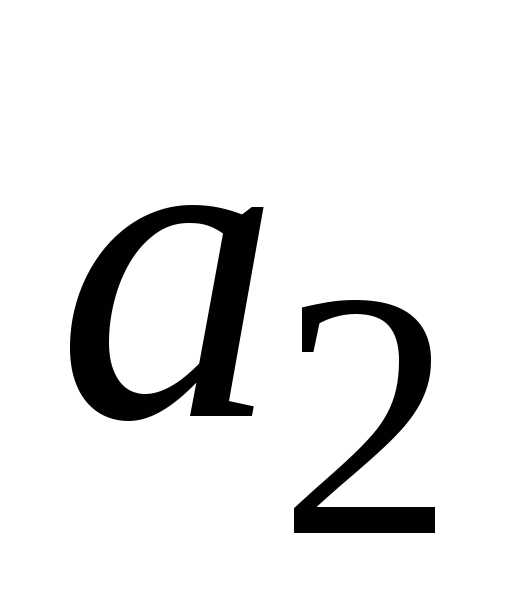 и управляющего устройства – блока
и управляющего устройства – блока 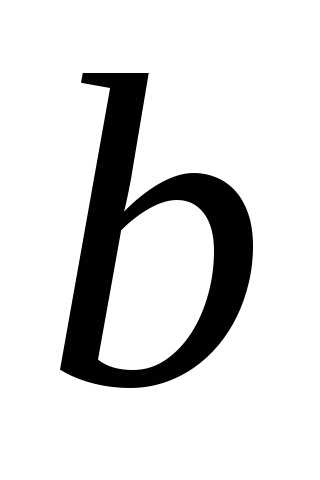 . В случае
исправности блока
. В случае
исправности блока 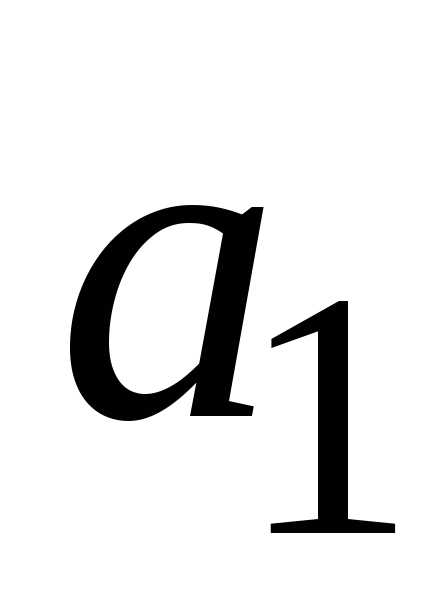 работает
блок
работает
блок 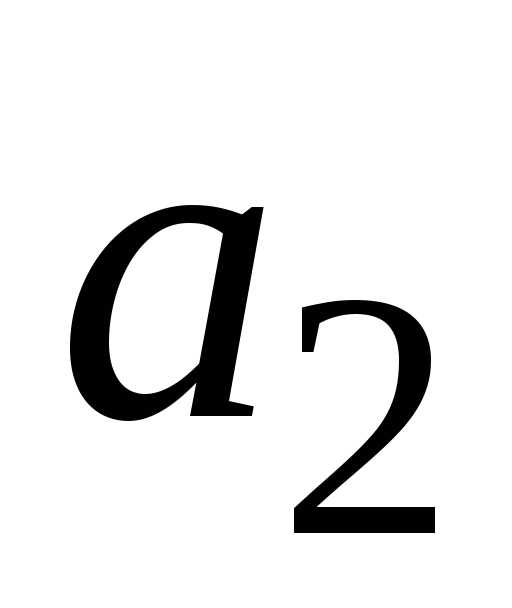 ;
если блок
;
если блок 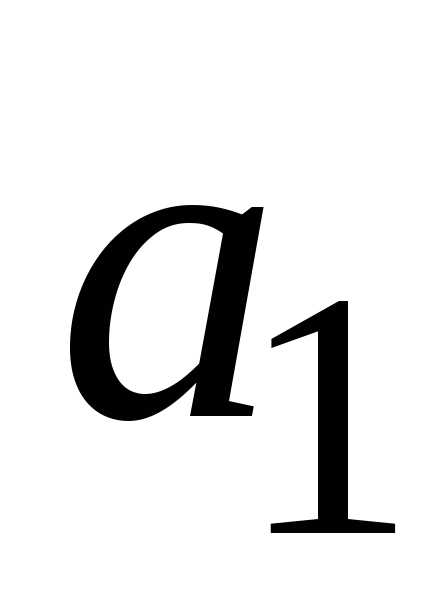 выходит из строя, управляющее устройство
выходит из строя, управляющее устройство 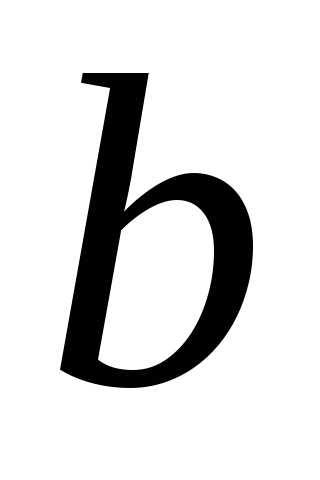 включает
блок
включает
блок 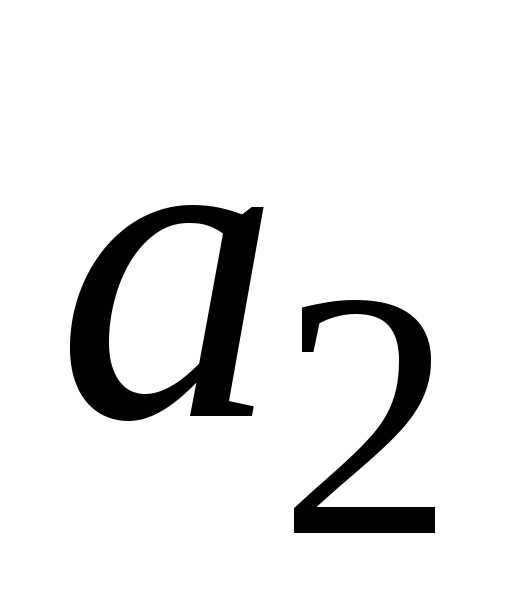 .
Если блок
.
Если блок 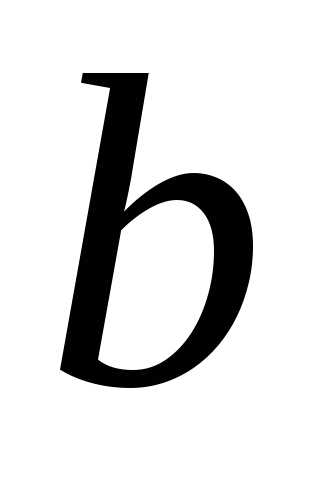 не исправен, то он не включает блок
не исправен, то он не включает блок 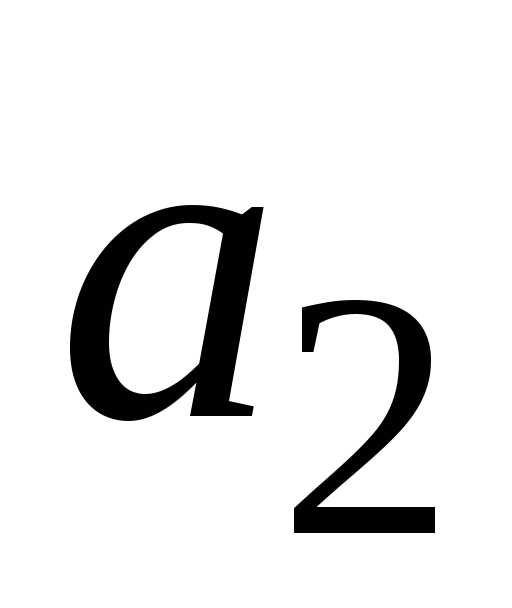 . Известны
вероятности блоков
, . Найти
надежность системы, если блоки независимые.
. Известны
вероятности блоков
, . Найти
надежность системы, если блоки независимые.
Решение.
Обозначим – события, состоящие в том, что блоки 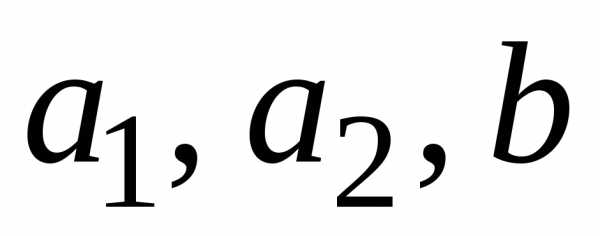 и система
и система 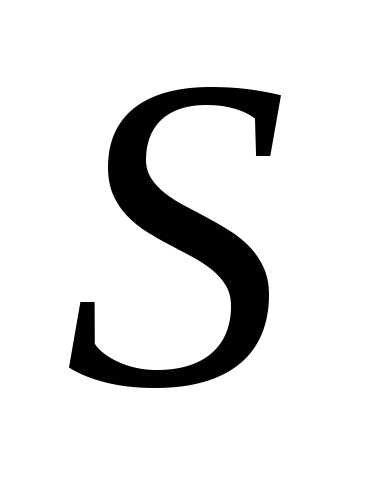 соответственно
исправны.
соответственно
исправны.
1
решение. Система 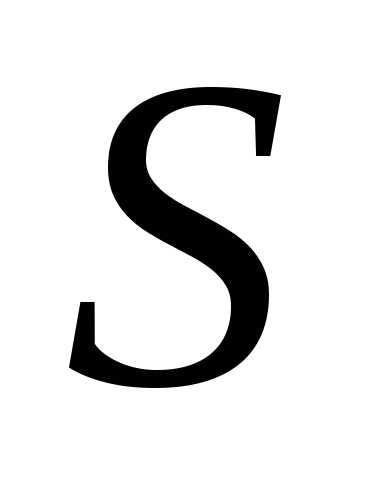 будет
исправна, если исправен или блок
будет
исправна, если исправен или блок 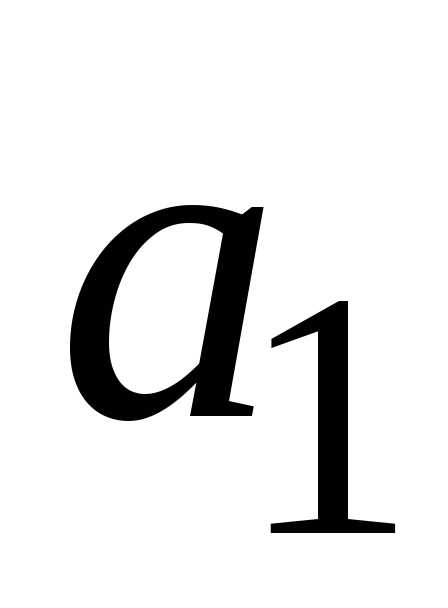 или оба блока
или оба блока 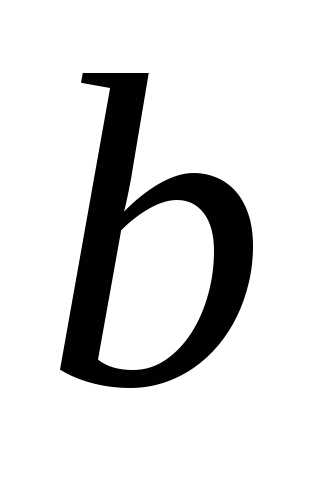 и
и 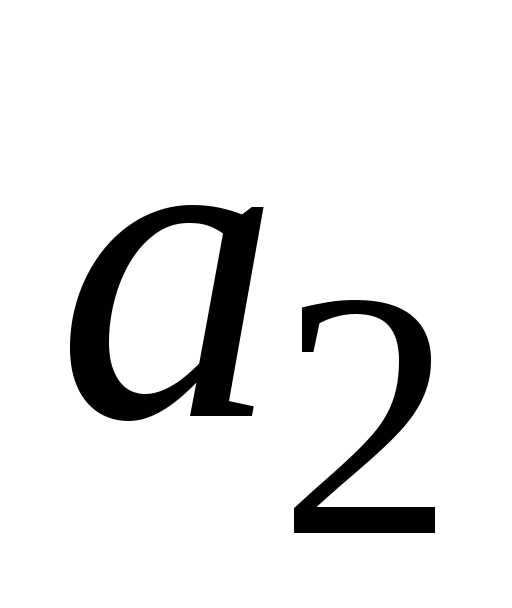 ,
или все три блока.
,
или все три блока.
Тогда , ,
.
2
решение. Воспользуемся понятием противоположного
события. Система неисправна, если
неисправен блок 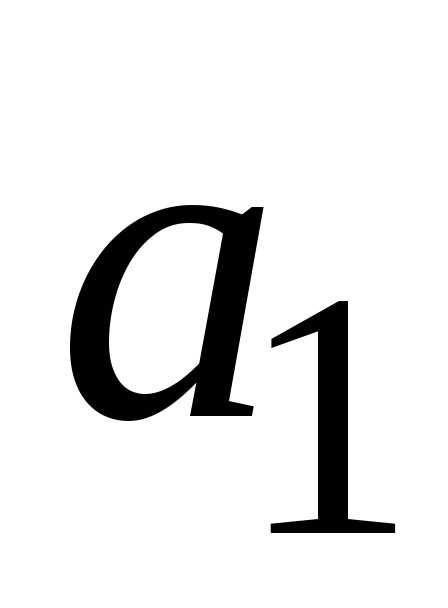 и
хотя бы один из блоков
и
хотя бы один из блоков 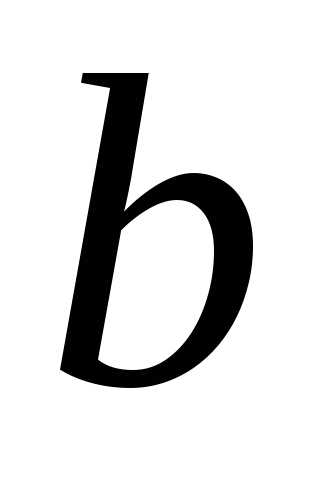 или
или 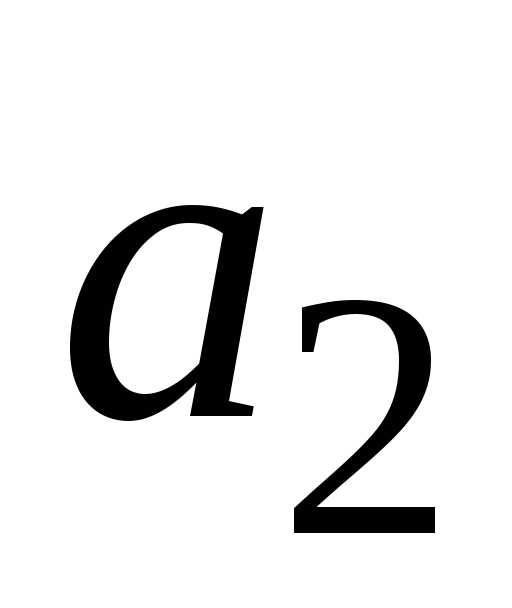 ,
т.е.
,
т.е.
,
; ; ;
;
.
Пример 9.
Среди 12 аппаратов четыре первого тина и восемь второго. Случайным образом из них выбирают три аппарата последовательно (без возвращения). Найти вероятность того, что при первом и третьем будут выбраны, аппараты второго типа, а вторым – аппарат первого типа.
Решение.
Пусть  – выбран первый аппарат,
– выбран первый аппарат,  – выбран второй аппарат,
– выбран второй аппарат,  – выбран третий аппарат.
– выбран третий аппарат.
По
классической формуле 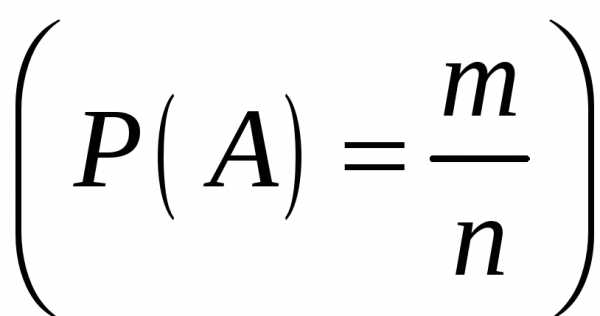 определим
определим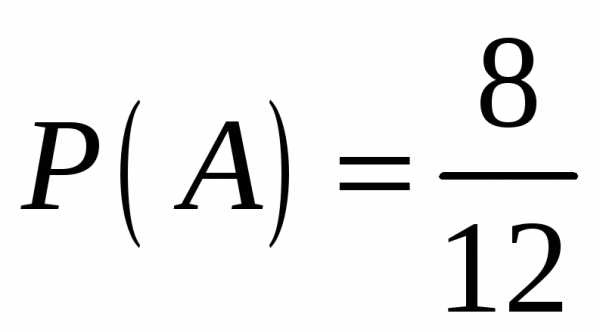 , т. е. первый
аппарат второго типа;
, т. е. первый
аппарат второго типа; 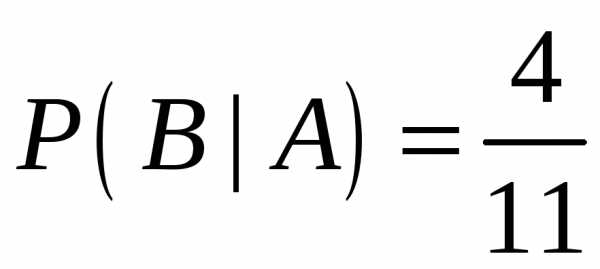 ,
т.е. второй аппарат первого типа, а всего
аппаратов осталось 11;
,
т.е. второй аппарат первого типа, а всего
аппаратов осталось 11; 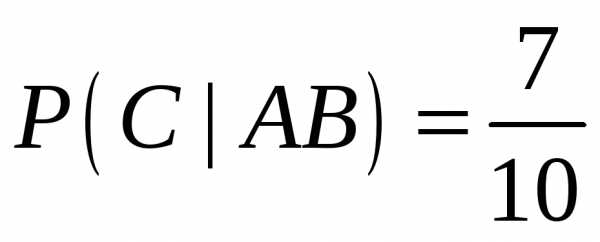 ,
т. к. третий аппарат второго типа, а их
осталось 7, и всего аппаратов 10.
,
т. к. третий аппарат второго типа, а их
осталось 7, и всего аппаратов 10.
.
studfiles.net
4.Классическое определение вероятности. Основные формулы комбинаторики.
События является исходами одного и того же испытания каждое из которых может наступить с одной и той же вероятностью и не является более объективным по отношению к другим наз-ся равно возможными.
Вероятность события— число, которое является исходом испытания с равно возможными исходами равна отношению числа благоприятных исходов к общему числу равно возможных исходов.
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1
Свойство 2. Вероятность невозможного события равна нулю.
В этом случае m=0, следовательно, P(A)=m/n=0/n=0
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно,
0<P(A)<1
Итак, вероятность любого события удовлетворяет двойному неравенству
0P(A)1
Основные формулы комбинаторики
Сочетание (из n по m) называется соединение из n элементов и отличающим друг от друга составом элементов.
Числу сочетания равно числу способов выбора m элементов из n.
Если в сочетание элементы могут повторяться, то их называют сочетание с повторением
Размещение из называется соединение состоящих из m элементов и отличающихся друг от друга либо составом элементов либо порядком их следования.
Если в размещения элемента могут повторятся, то их называют размещением с повторением
Перестановка называется соединение состоящих из n элементов и отличающихся друг от друга порядком следования элементов.
5.Геометрическое определение вероятности. Достоинства и ограничения
Вероятность события, эксперимент по произведению которого можно разложить на бесконечное число равновозможных, равна отношению меры области благоприятствующей наступлению этого события мере всей области.
m(G)-благоприятствующая (благоприятная) область
m(S)-вся область
В качестве меры области может выступать длина отрезка, площадь плоской фигуры и объем тела.
Необходимые условия применения геометрического определения вероятности:
1.области S и G должны быть замкнутыми, д.б. измеримыми.
2.случайно выбранная точка в области S окажется в одной из заштрихованной подобласти S1 и S2
s1 и s2- часть множества S
Пример: задача о встрече (студенты условились встретиться в опр.месте….Какова вероятность того, что студенты встретятся)
Достоинство: может преодолеть недостаток классического определения вероятности в предположении конечного числа возможных исходов испытания.
6.Простые и сложные события. Сумма событий. Теорема сложения вероятностей
Теория сложных событий позволяет по вероятностям простых событий определять вероятности сложных. Она базируется на теоремах сложения и умножения вероятностей.
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.
Если A и B — совместные события, то суммой 2ух событий A и B называется событие С, состоящее в наступлении либо события A, либо события B, либо обоих событий вместе. Если A и B — несовместные события, то их сумма означает наступление или события A, или соб. B.
Теорема сложения вероятностей.
Вероятность суммы 2х событий равна сумме вероятностей этих событий без вероятности их совместного наступления.
Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:
P(A+B+….+K)=P(A)+P(B)+….+P(K)
Следствие 1. Сумма вероятностей событий, образующих полную группу равна единице.
, где А1,А2..An-полная группа событий⇒
Следствие 2. Сумма вероятностей противоположных событий равна единице.
studfiles.net
Лекция 2 Определение вероятностей сложных событий
От простых событий к сложному
Вычисление вероятностей сложных событий сводится к применению формул сложения и умножения вероятностей, если вероятности всех составляющих простых событий известны. В объектно-ориентированной среде вероятность события, выраженного через суммы и произведения простых событий, вычисляется автоматически методами классов Accid или Accident.Рис. 2.1. Кривые вероятностей пробития
Проблемы связаны с оценками вероятностей простых событий, таких как попадание поражающего элемента (ПЭ) в уязвимый агрегат (УА) и поражение УА при попадании в него. Вероятность прямого попадания снаряда определяется характеристиками рассеивания, вероятность попадания осколка в УА – плотностью осколочного поля, зависящей от условий встречи снаряда с целью. Действие УА попавшим осколком (пробивное, зажигательное, инициирующее) зависит от массы осколка q и скорости соударения v, а также от случайных факторов (места попадания, угла встречи, ракурса и т.д.). Поэтому от определяющих параметров q и v зависит не сам факт поражения, а вероятность этого события, которую в диапазоне скоростей соударения оценивают как статистическую (рис. 2.1). Чтобы получить эти зависимости, нужно произвести большой объем испытаний для различных комбинаций определяющих параметров. Разумное применение вероятностных законов позволяет минимизировать необходимый объем опытных данных и извлечь из них максимум информации. Так, определив критерии поражения УА одним попавшим осколком, вероятность поражения при попадании в УА случайного числа осколков вычисляют в рамках вероятностной модели пуассоновского поля (редких и независимых) событий.Применение той или иной вероятностной модели сложных событий должно быть согласовано с условиями реального опыта. Модели, предполагающие независимость простых событий, сильно упрощают вычисления, но могут привести к ошибочным выводам. Если события поражения отдельного УА каждым попавшим в него осколком еще можно считать независимыми, то каждое попадание снаряда в трудноуязвимую цель повышает вероятность поражения в следующих попаданиях из-за накопления ущерба. В таких случаях статистическая вероятность поражения цели одним попавшим снарядом r1 не вполне характеризует уязвимость цели. Приходится в статистических испытаниях определять закон поражения – условную вероятность поражения цели при m попаданиях G(m) = P(A/m), m = 1, 2, … с учетом накопления ущерба: G(m) > 1– (1 – r1)m. Чтобы применить формулу полной вероятности (1.17) к событию поражения одиночной цели в n выстрелах, нужны также вероятности гипотез Am, n (m попаданий в n выстрелах). В некоторых случаях вероятности pm,n = P(Am, n) можно определить по вероятности попадания в одном выстреле p1, используя закономерности повторяющихся в одинаковых условиях независимых опытов, но реальная стрельба (очередью, залпом) не вполне соответствует такой вероятностной модели. Тем не менее, модель независимых испытаний в неизменных условиях дает фундаментальные соотношения, необходимые для разумного применения статистических методов при определении вероятностей простых событий.
studfiles.net
7.Простые и сложные события. Произведение событий. Условная вероятность события. Теорема умножения вероятностей.
Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.
Условная вероятность события B — это полученная вероятность события B, найденная при условии, что событие A произошло. Обозначается (B) или P(B/A)
Теорема умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.
Док-во: пусть n-число равновозможных исходов эксперимента по воспр-ию соб.А и В. Из них m исходов способств.А(m~A), k~B, l~AB. ; ; .
Рассм.усл.вер.соб.А при В наступившим: ⇒
⇒ условная вер.соб.В при А наступившем
Теорема умножения для несовм.событий
Вероятность произведения независимых событий равна произведению вероятностей этих событий
A и B-независимые.
8. Формула Бернулли. Формула Пуассона. Сфера их применения.
Формула Бернулли
Т-ма: Если вероятность p наступления события A в каждом испытании постоянна, то вероятность P k,n того, что событие А наступит k раз в n независимых испытаниях равна:
где q = 1-p
В формуле Бернулли используется число сочетаний. Для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const Распределение вероятностей в схеме Бернулли — биномиальное.
Применяется при решении задач на нахождение вероятности возможного числа появления бракованных деталей; в задаче с условием найти количество подбросов игральной кости, при заданном наивероятнейшем выпадении
Формула Пуассона
Применяется в случае, когда мы хотим вычислить вероятность Pm,n появления события A при большом числе испытаний n, например P300,500. Например, найти вероятность того, что из 1825 студентов 1ое сентября будет днем рождением одновременно четырех студентов. По формуле Бернулли вычисление технически сложно.
Для больших n есть так называемые асимптотические формулы. Наиболее простой из них является теорема Пуассона.
Т-ма: Если вероятность p наступления события А в каждом испытании стремится к нулю при неограниченном увеличении числа n испытаний, причем произведение np стремится к постоянному числу λ, то вероятность Pm,n того, что событие A появится m раз в n независимых испытаниях, удовлетворяет предельному равенству
Приближенная формула Пуассона:
9.Локальная и интегральная теоремы Муавра-Лапласа.
Локальная Теорема.
Если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1,то вероятность P(m,n) того, что событие А произойдет m раз в n независимых испытаниях при n достаточно больших, приближенно равна ; g=1-р
Гауссовая
кривая 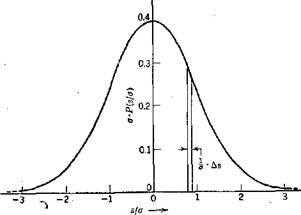
f(-x)=f(x)-свойство четной функции
Существует таблица значений функций f(x)для x[0;5] при x >=5 f(x)
Интегральная теорема.
Если вероятность P наступления события A в отдельных испытаниях постоянна и отлично от 0 и 1, то вероятность того, что число m наступления события A в n Независимых испытаниях заключено в пределах от A до B включительно при достаточно большом числе испытаний n приблизительно равна
Следствие. Если вероятность P наступления события А в отдельных испытаниях постоянна и отлична от 0 до 1, то при достаточно большом числе n независимых испытаний вероятность того что,
а) число m наступления события А отличается от произведения np не более чем на величину E>0 приближенна равна p(
б)Частота события А в n независимых испытаниях заключена в пределах от α До β включительно приближенна равна P(α
z1=; z2=
В) частота отличаются от вероятности (p) его наступления в отдельном испытании на величину ∆≥0 по абсолютной величине приближенно равна )
studfiles.net
Тема 14 Основные теоремы и формулы теории вероятностей
Лекция 3.14.1 «Условные вероятности. Вероятности сложных событий»
Учебные вопросы:
1. Условные вероятности. Независимость событий. Формулы умножения и сложения вероятностей
2. Формула полной вероятности
3. Формула Байеса
Условные вероятности. Независимость событий. Формулы умножения и сложения вероятностей
Условные вероятности.
Аксиоматически определенную выше вероятность можно назвать безусловной вероятностью, подчеркивая этим, что она не зависит ни от каких дополнительных условий, кроме фиксированного комплекса условий , которым характеризуется опыт.
Пусть в опыте, соответствующему некоторому комплексу условий, могут произойти случайные события и . Допустим также, что стало известно, что осуществилось событие . Эта новая информация равносильна дополнительному условию, накладываемому на опыт и адекватному осуществлению события . В изменившемся комплексе условий опыта изменится и вероятностное распределение на его поле событий.
Пусть . Условная вероятность наступления события при условии, что событие произошло в результате данного опыта, определяется следующей аксиомой:
. (4)
Условную вероятность для краткости называют «вероятность события при условии ». При условная вероятность не определена.
Пример. При бросании правильной игральной кости стало известно, что выпало четное число очков. Какова вероятность того, что выпала: а) двойка; б) пятерка?
◄ Исходное множество элементарных исходов для данного опыта , где {число выпавших очков равно }, содержит исходов. Три из них благоприятствуют событию ={выпало четное число очков}, один исход благоприятствует событию , где ={выпала двойка}. Число исходов, благоприятствующих событию , где ={выпала пятерка}, равно нулю. По формуле (4) получаем: , . ►
На практике для вычисления условной вероятности часто применяется метод вспомогательного эксперимента, при котором формулируется новый опыт, соответствующий комплексу условий . В этом новом комплексе условий получают соответствующее ему множество элементарных исходов . Безусловная вероятность осуществления события в этом новом опыте и принимается за условную вероятность . Этот метод обычно применяется в тех случаях, когда вероятностное пространство для вспомогательного опыта строится проще, чем для исходного.
Пример. В условиях предыдущего примера новым множеством исходов будет . Один из этих исходов благоприятствует событию ={выпала двойка}, событию же ={выпала пятерка} – ни один. По формуле классической вероятности получаем , .
Независимость событий
Понятие условной вероятности позволяет в свою очередь ввести в математической модели понятие независимости. Будем считать, что событие не зависит от события , если выполняется равенство
. (5)
Если , то из равенств (74) и (5) следует, что , т. е. независимость является взаимным свойством: если не зависит от события , то и не зависит от события . Более удобным определением независимости по сравнению с (5) является следующее.
События и называются независимыми, если
. (6)
События называются взаимно независимыми (или независимыми в совокупности, или просто независимыми), если для любого набора из событий ( =2, 3, …, ) выполняется равенство
, . (7)
Если (7) выполняется только при =2, то события называютпопарнонезависимыми. Отметим, что из попарной независимости не следует независимость в совокупности.
Формулы (6) и (7) позволяют выделять независимые события в тех случаях, когда построена формализованная вероятностная модель случайного опыта и вероятности всех рассматриваемых событий определены. Однако далеко не всегда события, независимые в таком теоретико-вероятностном смысле, являются независимыми и в реальности. На практике в любых сомнительных случаях обычно стараются принять меры для объективной проверки гипотезы о независимости событий, основываясь на теоретико-вероятностной независимости, введенной равенствами (6) и (7), с причинной независимостью реальных событий. Решение подобных задач, основанное на применении методов проверки статистических гипотез, рассматривается в математической статистике.
Пример. В группе 25 студентов. Из них 10 человек курят, 13 носят очки, а 8 и курят и носят очки. Наудачу выбирается один студент. События: ={выбранный студент курит}, ={выбранный студент носит очки}. Установить, зависимы или нет события и .
◄ Так как , т. е. условие (6) независимости не выполняется, делаем вывод, что события и зависимы.
Необходимо отметить, что полученный вывод справедлив лишь для данного частного эксперимента, и следует остерегаться распространять его на всех студентов вообще. Хотя гипотеза о зависимости между курением и состоянием зрения кажется разумной, для ее подтверждения необходимо было бы провести статистическое обследование всех студентов на определенной территории, которое включало бы проверку зрения у каждого и регистрацию длительности и интенсивности курения для тех, кто курит. Полученные статистические данные позволили бы на основе определенного критерия подтвердить либо отвергнуть наличие статистической зависимости между курением и состоянием зрения в той группе населения, которую составляют студенты. ►
Вероятности сложных событий
Сложным событиемназывается наблюдаемое событие, выраженное через другие наблюдаемые в том же опыте события с помощью допустимых алгебраических операций.
Записав равенство (4) в виде
, (8)
получаем так называемую формулу умножения вероятностей. Если оба события и обладают ненулевой вероятностью, то формула умножения может быть записана двояким образом:
. (9)
Формула (9) позволяет находить вероятности совместного наступления событий и в тех случаях, когда условная вероятность известна из дополнительных опытов или определена методом вспомогательного эксперимента.
Из (9) по индукции нетрудно получается формула умножения для произвольного числа событий:
. (10)
Для вероятности наступления хотя бы одного из двух событий и справедлива следующая формула сложения вероятностей:
. (11)
Если события независимы в совокупности, то вероятность наступления хотя бы одного из них проще вычисляется не по формуле сложения, а с помощью формулы умножения:
. (12)
Пример. В продукции предприятия брак составляет 5% от общего объема выпускаемых изделий. Для контроля качества случайно отобрано 20 изделий. Найти вероятность того, что среди них будет хотя бы одно бракованное.
◄ Обозначим через события ={ — ое по счету отобранное изделие бракованное}, 1, 2, …, 20. По условию вероятность того, что изделие в продукции предприятия является бракованным, равна . Очевидно, что нас интересует событие . В условиях стабильного технологического процесса производства можно считать, что события независимы в совокупности. Учитывая, что , по формуле (12) получаем ►
Формула полной вероятности
Пусть – наблюдаемые события для данного опыта, причем система множеств { } образует разбиение множества элементарных исходов этого опыта, т. е. выполняются следующие условия: , при любых , 1, 2, …, . Для любого наблюдаемого в опыте события имеет место следующая формула (формула полной вероятности):
. (13)
События принято называтьгипотезами по отношению к событию . Безусловные вероятности , для которых должно выполняться равенство , трактуются как априорные(доопытные) вероятности гипотез. Для вычисления вероятности интересующего нас события по формуле (13) важно удачно подобрать набор гипотез. Если зависимость события от гипотез неясна и условные вероятности не могут быть просто вычислены, то такое разбиение не принесет практической пользы при решении задачи.
Пример. Партия изделий, среди которых 5% дефектных, поступила на проверку. Схема проверки такова, что с вероятностью 0,95 обнаруживается дефект (если он есть) и существует ненулевая вероятность 0,03 того, что годное изделие будет признано дефектным. Найти вероятность того, что случайно выбранное из партии изделие будет признано дефектным.
◄ Нас интересует событие ={случайно выбранное изделие признано дефектным}. С этим событием тесно связаны две гипотезы: ={поступившее на проверку изделие дефектно}, ={поступившее на проверку изделие годно}. Безусловные априорные вероятности этих гипотез равны , . Условные вероятности заданы в условии задачи: , . По формуле полной вероятности получаем . ►
Формула полной вероятности
Пусть { } – разбиение множества элементарных исходов для данного опыта, интерпретируемое как совокупность гипотез по отношению к интересующему нас событию . Пусть опыт проведен, и стало известно, что событие осуществилось, Какова апостериорная(послеопытная) вероятность наступления гипотезы при условии, что событие имело место? Ответ дается формулой Байеса:
, (14)
которая является следствием формулы полной вероятности (13).
Формулу Байеса иногда называют формулой гипотез. Она позволяет «переоценить» вероятность каждой из гипотез после поступления новой информации относительно наступления тех или иных наблюдаемых событий. Формула Байеса может служить также для принятия решений в тех случаях, когда гипотезы непосредственно не наблюдаемы, хотя априорные вероятности и соответствующие условные вероятности , =1, 2, …, известны из дополнительных опытов.
Пример. В условиях предыдущего примера случайно выбранное из партии изделие было признано дефектным. Какова вероятность того, что на самом деле изделие годно?
◄ В обозначениях предыдущего примера требуется найти (апостериорную условную вероятность гипотезы ). По формуле Байеса имеем . Таким образом, апостериорная условная вероятность того, что изделие на самом деле годное, если известно, что оно было признано дефектным, существенно меньше априорной вероятности гипотезы , что явилось следствием поступившей информации. ►
Пример. Из урны, содержащей 4 белых и 9 черных шаров, один шар неизвестного цвета был утерян. Какова вероятность того, что шар, извлеченный из урны после утери, окажется белым? Какова вероятность того, что утерян черный шар, если после утери извлечен белый шар?
◄ Нас интересует событие ={шар, извлеченный из оставшихся шаров, белый}. Выберем следующие гипотезы: ={утерян белый шар}, ={утерян черный шар}. В силу формулы классической вероятности , , , . По формуле полной . Отметим, что вероятность извлечения белого шара из урны до утери также равна . Для нахождения апостериорной условной вероятности гипотезы используем формулу Байеса: .►
Лекция 3.14.2 «Последовательность испытаний»
Учебные вопросы:
1. Последовательность испытаний
2. Последовательность независимых испытаний. Схема Бернулли
3. Предельные теоремы в схеме Бернулли
infopedia.su
