Вид треугольника по сторонам: Виды треугольников по углам и сторонам

Какие треугольники бывают по сторонам?

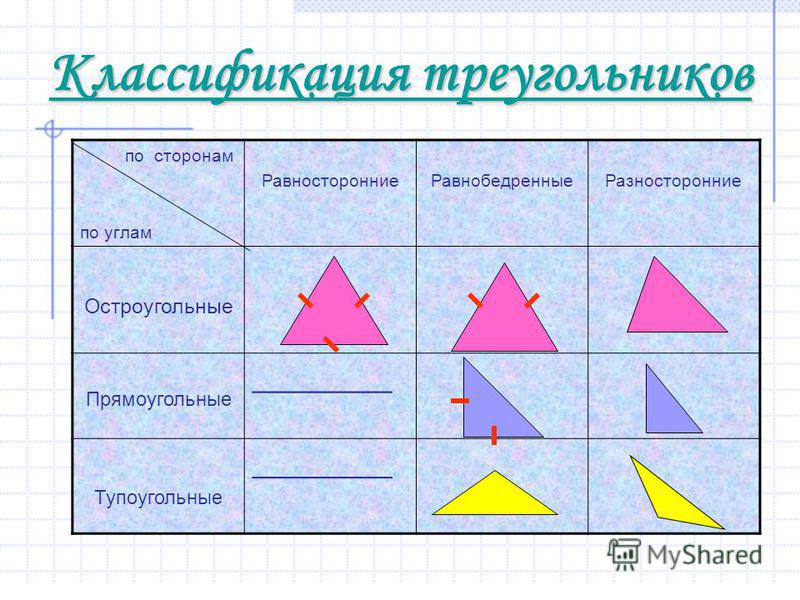
Какие треугольники бывают по сторонам?

По сторонам различают 3 вида треугольников: разносторонние, равнобедренные и равносторонние.

Как называется треугольник?

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. Треугольник называется равнобедренным, если у него две стороны равны.

Как определить какой вид треугольника?

Если выполняется теорема Пифагора: с²=a²+b² , где с — наибольшая сторона, а и b две других, – треугольник прямоугольный. Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² треугольник остроугольный.

Как определить тип треугольника по углам?

те, у которых есть прямой угол, – прямоугольные, те, у которых есть тупой угол, – тупоугольные. Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира. Обычно вид треугольника можно определить на глаз.

Какие углы в Остроугольном треугольнике?

В остроугольном треугольнике каждый угол меньше 90 градусов. Общая сумма углов здесь также равняется 180 градусов. Нельзя забывать о характерных линиях треугольника.

Какие бывают углы в треугольнике?

), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой. ), то треугольник называется тупоугольным, Остальные два угла, очевидно, острые (треугольников с двумя тупыми или прямыми углами быть не может).

Что называется равнобедренным треугольником?

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. По определению, каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно.

Как выглядит равнобедренный треугольник?

Равнобедренный треугольник − это треугольник с двумя равными сторонами. Две равные стороны называются боковыми, третья сторона называется основанием. Ниже на рисунке боковые стороны обозначены буквой b, основание − буквой a. Под a и b понимаются также длины этих сторон.

Как узнать что треугольник равнобедренный?

Признаки равнобедренного треугольника

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.

Как найти равнобедренный треугольник?

Признаки равнобедренного треугольника

1. Если в некотором треугольнике два угла равны, то он – равнобедренный;
2. Если в некотором треугольнике совпадают: а) высота и биссектриса или б) высота и медиана или в) медиана и биссектриса, проведённые к одной стороне, то такой треугольник – равнобедренный.

Что такое равнобедренный треугольник и его свойства?

Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. Свойство: Если треугольник является равнобедренным треугольником, то углы при его основании равны.

Как доказать что треугольник равнобедренный 7 класс?

Треугольник называется равнобедренным, если две его стороны равны.

1. AB = BC. ∆ABC – равнобедренный. …
2. AB = BC = AC. ∆ABC – равносторонний. …
3. Дано: ΔABC – равнобедренный. …
4. Доказательство: ∆ABF = ∆ACF (т. …
5. Доказательство: ∆ABF = ∆ACF т. …
6. Дано: ∆ ABС: …
7. Решение: ∠1 и ∠АСВ – смежные →∠1 + ∠АСВ = 180, значит: ∠АСВ = 180 – 120 = 60.

Когда треугольник является равнобедренным?

Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми сторонами. Третья сторона называется основанием. … Углы при основании равнобедренного треугольника равны.

Какие бывают треугольники 7 класс?

Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. В любом треугольнике: Против большей стороны лежит больший угол. Против равных сторон лежат равные углы.

Что такое треугольник в геометрии 7 класс?

Определение: Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. … Точки А, В, С называются вершинами треугольника, а отрезки АВ, АС, ВС называются его сторонами. Логично, что треугольник имеет три угла: ∠А, ∠В, ∠С, или ∠ВАС, ∠АВС, ∠ВСА.

Можно ли считать равносторонний треугольник равнобедренным?

Нет, нельзя. Равнобедренный треугольник — треугольник, у которого 2 стороны равны. Соответственно, третья сторона не равна остальным двум. Равносторонний треугольник — тот, у которого все 3 стороны равны, что не скажешь о равнобедренном.

Как называется треугольник в котором два угла равны?

Если в треугольнике два угла равны, то этот треугольник — равнобедренный. Доказать: ∆ ABC — равнобедренный.

Когда два угла равны?

Если в треугольнике два угла равны, то он равнобедренный. Если ∠А=∠ С, то АВ = ВС.

Как называют и обозначают треугольник?

Треугольник называется по обозначениям его вершин. Вершины обозначаются заглавными латинскими буквами. … Периметр треугольника — это сумма длин всех его сторон.

Как найти сторону треугольника зная два угла и одну сторону?

Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов. Если известны одна сторона и два прилежащих угла, то с помощью теоремы синусов можно вычислить остальные две стороны треугольника.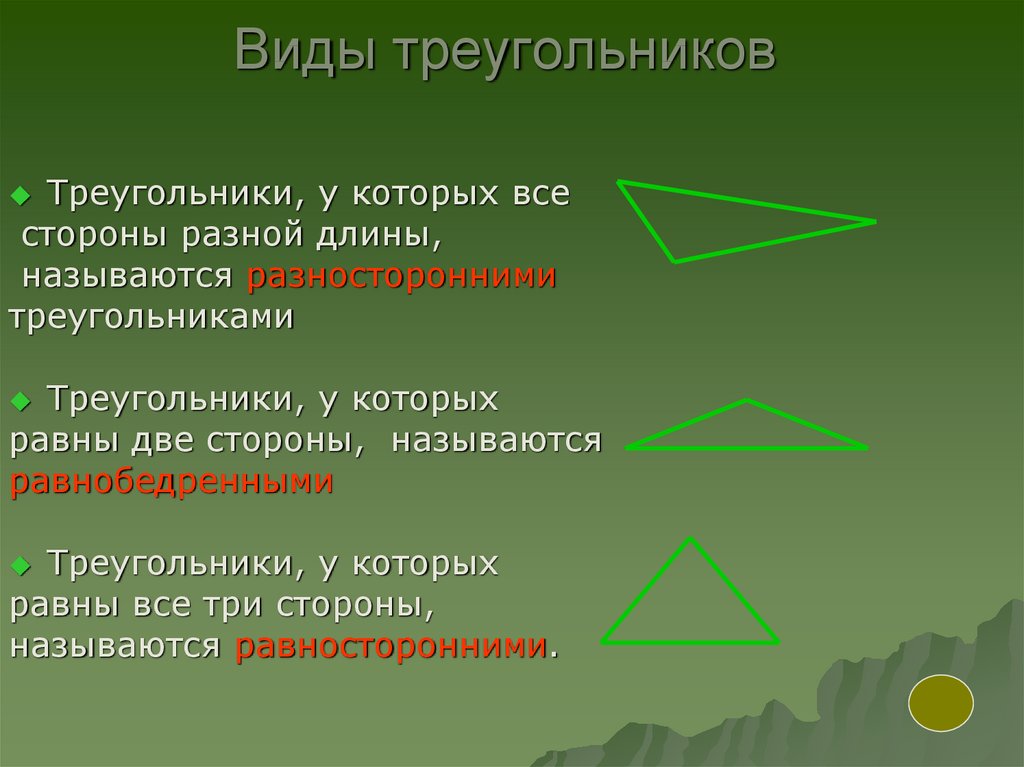

Как найти сторону треугольника зная угол и гипотенузу?

Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.

Как найти 2 угла в треугольнике?

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

Виды треугольников: прямоугольный тупоугольный, остроугольный

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Урок математики 3 класс

ТЕМА. Виды треугольников:
прямоугольный тупоугольный,
остроугольный
scul32.ucoz.ru

2. Цель урока

• Закрепить знания о видах треугольников;
• Развивать умения различать треугольники в
зависимости от их углов;
• Развивать вычислительные навыки,
математические знания;
• Развивать память, логическое мышление
scul32.ucoz.ru

3. Запишем в тетрадь

29 апреля
Классная работа
1. Минутка каллиграфии
-Запишите ответы таблицы умножения числа
на 8. Уменьшите каждый ответ в 2 раза .
Ответы запишите.
scul32.ucoz.ru
• 2. Устный счёт. Математический диктант
• Дежурным надо расставить 12 горшков с цветами на 4 окна поровну.
Сколько горшков с цветами должно быть на каждом окне?
• 2. У продавца осталось 18 стаканов компота и 9 стаканов сока. Во сколько
раз меньше осталось стаканов сока, чем стаканов компота?
• 3. На пляже загорало 9 детей, а взрослых в 6 раз больше. Сколько взрослых
загорало на пляже?
• 4.На соревнованиях команда спортсменов выиграла 18 золотых медалей и 6
бронзовых. На сколько больше выиграла команда золотых медалей, чем
бронзовых?
• 5.К цирку подъехало 10 машин с пассажирами, по 7 человек в каждой.
Сколько всего человек приехало на этих машинах?
• 6. Сколько пятёрок в числе 40?
• 7. Сколько недель в 49 днях?
• 8. В одном куске 36 метров шёлка, в другом 44 метра. Всю материю продали
10 покупателям поровну. Сколько метров шёлка купил каждый?
scul32.ucoz.ru
3. Актуализация знаний
• Геометрия — это раздел математики, изучающий
геометрические фигуры и их свойства.
Треугольник — геометрическая фигура, образованная тремя
отрезками, которые соединяют три точки, не лежащие на
одной прямой. Указанные три точки
называются вершинами треугольника, а отрезки —
сторонами треугольника.
• Давайте вспомним, что вы уже знаете о видах треугольников.
• По длине сторон различают: разносторонние,
равнобедренные и равносторонние треугольники.
scul32.ucoz.ru
scul32.ucoz.ru

7. 4. Объяснение нового материала

• Углы бывают:
• Острые – меньше
прямого
• Прямые – угол 90
градусов
• Тупые – больше
прямого
scul32.ucoz.ru
Оказывается, по величине углов все треугольники тоже
можно разделить на 3 вида:
• те, у которых все углы острые – остроугольные,
• те, у которых есть прямой угол – прямоугольные,
• те, у которых есть тупой угол – тупоугольные.
scul32.ucoz.ru

9. Посмотрите видео урок по ссылке

• https://www.youtube.com/watch?time_continue=1&v=ES0xc_Gx3eg&feat
ure=emb_logo
scul32.ucoz.ru
5. Закрепление изученного материала
• Обычно вид треугольника можно определить на глаз.
• Попробуйте определить виды треугольников по величине
углов без измерений.
Прямоугольные №….
Остроугольные№….
Тупоугольные №…..
scul32.ucoz.ru
Делаем вывод:
По величине углов различают 3 вида
треугольников:
Остроугольные, прямоугольные и тупоугольные
Определить вид треугольника можно тремя
способами:
• с помощью измерений, на глаз и по
условным обозначениям.
scul32.ucoz.ru

12. Теперь ты можешь различать виды треугольников по сторонам и по углам

scul32.ucoz.ru

13. Работа с учебником

• 1)с.85 №1. Начертите треугольники
• 2) с.85 №2. Решить и сравнить задачи(без кр. записи)
1) 1кусок – 24м ткани
2 кусок — ?, на 8 м меньше, из него сшили,
расходуя по 4м
Платьев -?
ПОДСКАЗКА: 2 действия
2) 1кусок – 24м ткани
2 кусок — ?, на 8 м меньше
ПОДСКАЗКА: 3 действия
scul32.ucoz.ru
?, сшили,
расходуя по 4м -?
платьев вышло

14. 6.Итог урока

Закончите предложения:
• Остроугольный треугольник — это
треугольник, у которого ………………………….
• Прямоугольный треугольник — это
треугольник, у которого ……………………..
• Тупоугольный треугольник —
треугольник, все стороны которого
………………………..
• 7. Д/з. С.85, №4
scul32.ucoz.ru

English     Русский Правила

Назовите реальный объект, который имеет вид сверху в виде треугольника, а вид сбоку и спереди — прямоугольники.

значок-вопрос Спросите репетитора

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«Назовите реальный объект, который имеет вид сверху в виде треугольника, а вид сбоку и спереди — прямоугольники». eNotes Editorial , 22 января 2015 г., https://www.enotes.com/homework-help/name-a-real-word-object-that-has-a-top-view-of-a-473839. По состоянию на 3 декабря 2022 г.

Ответы экспертов

Обратите внимание, что треугольник — это многоугольник с тремя сторонами. В то время как прямоугольник — это многоугольник с 4 сторонами и 4 углами, равными 90 градусам. Одним из примеров, который имеет вид сверху на треугольник, а также вид сбоку и спереди, каждый из которых представляет собой прямоугольник, является коробка…

См.

Этот ответ сейчас

Запустите 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Обратите внимание, что треугольник — это многоугольник с тремя сторонами. В то время как прямоугольник — это многоугольник с 4 сторонами и 4 углами, равными 90 градусам. Одним из примеров, который имеет вид сверху на треугольник, а также вид сбоку и спереди, каждый из которых представляет собой прямоугольники, является коробка шоколадных конфет.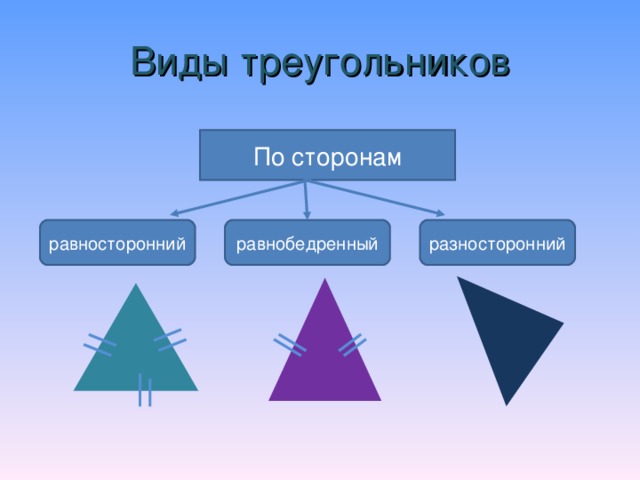 Вы можете обратиться к изображению ниже.

Вам может прийти в голову, что крыша является одним из примеров, однако будьте осторожны с этим, потому что вид сверху на крышу не является треугольником. Вы можете обратиться к изображению, которое я включил ниже.

Изображения:

Это изображение было помечено как неприемлемое Нажмите, чтобы снять отметку

Изображение (1 из 1)

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 ответов воспитателя

математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.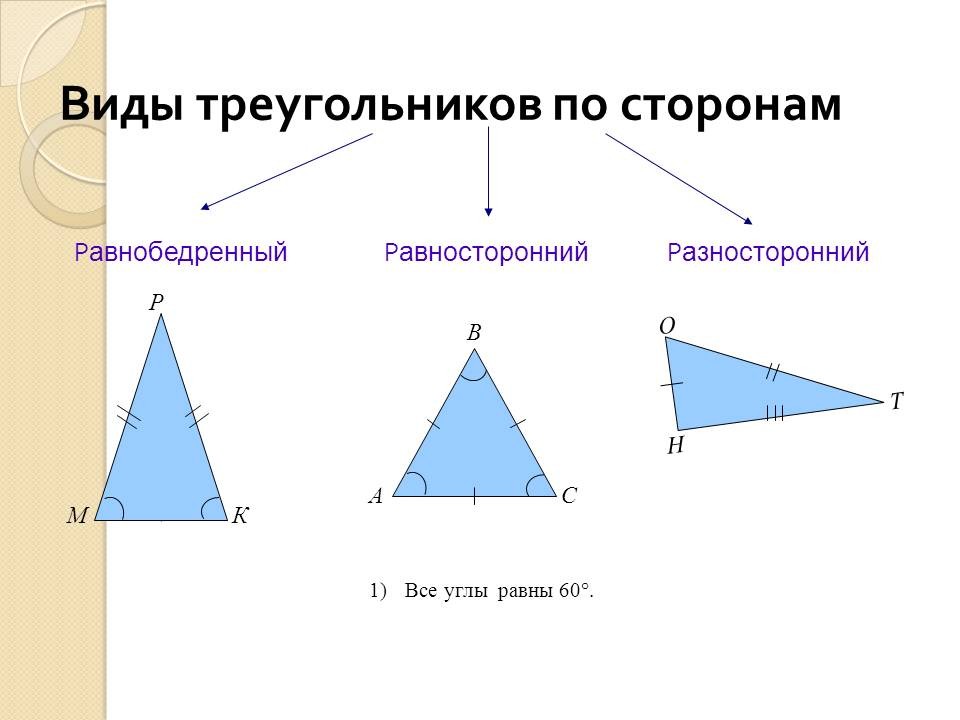

Как определить, является ли это уравнение линейной или нелинейной функцией?

84 Ответы воспитателя

Математика

Последний ответ опубликован 14 ноября 2011 г. в 5:49:28.

Решите для b2:A= 1/2h (b1+b2)

1 Ответ учителя

Математика

Последний ответ опубликован 3 октября 2011 г. в 14:12:01.

Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0  [(4-й корень из)(16+h)-2]/h    a=? ф=?

1 Ответ учителя

Математика

Последний ответ опубликован 17 августа 2010 г. в 8:49:11.

Учитывая f(x) и g(x), найдите (туман)(X) и (gof)(x) f(x) = 2x   g(x) = x+3

8 ответов воспитателя

Как построить (начертить) треугольник по трем сторонам (SSS)

На этой странице показано, как построить треугольник по длине всех трех сторон с помощью циркуля и линейки или линейки.

Он работает по первому копирование одного из сегментов линии, чтобы сформировать одну сторону треугольника. Затем он находит третий вершина откуда два дуги пересекаются на заданном расстоянии от каждого его конца.

Возможно несколько треугольников

Можно нарисовать более одного треугольника с тремя сторонами заданной длины. Например, на рисунке ниже по основанию АВ можно нарисовать четыре треугольника, соответствующих требованиям. Все четыре правильны в том смысле, что они удовлетворяют требованиям и являются конгруэнтны друг другу.

Примечание: эта конструкция не всегда возможна

См. рисунок справа. Если сумма двух сторон меньше третьей, треугольник невозможен.

Печатные пошаговые инструкции

Вышеупомянутая анимация доступна как распечатанная пошаговая инструкция, которую можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.

Доказательство

Изображение ниже является окончательным рисунком выше с добавленными красными элементами.

	Аргумент	Причина
1	Отрезок LM конгруэнтен отрезку AB.	Нарисовано с одинаковой шириной компаса. См. Копирование сегмента линии
2	Третья вершина N треугольника должна лежать где-то на дуге P.	Все точки на дуге P находятся на расстоянии AC от L, поскольку дуга была нарисована с шириной компаса, установленной на AC.
3	Третья вершина N треугольника должна лежать где-то на дуге Q.	Все точки на дуге Q находятся на расстоянии BC от M, поскольку дуга была нарисована с шириной компаса, установленной на BC.
4	Третья вершина N должна лежать там, где пересекаются две дуги	Единственная точка, которая удовлетворяет 2 и 3.
5	Треугольник LMN удовлетворяет указанным трем длинам сторон. LM конгруэнтно AB, LN конгруэнтно AC, MN конгруэнтно BC,

— Q.E.D

Попробуйте сами

Нажмите здесь, чтобы распечатать рабочий лист, содержащий две задачи на построение треугольника, где вам даны длины трех сторон. Когда вы попадете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Распечатанный результат не защищен авторским правом.

Другие страницы по конструкциям на этом сайте

• Список рабочих листов по конструкциям для печати

Линии

• Введение в конструкции
• Скопируйте сегмент линии
• Сумма n отрезков
• Разница двух отрезков
• Биссектриса отрезка
• Перпендикуляр в точке на прямой
• Перпендикуляр от прямой через точку
• Перпендикулярно от конечной точки луча
• Разделить отрезок на n равных частей
• Параллельная линия через точку (угловая копия)
• Параллельная линия через точку (ромб)
• Параллельная линия через точку (перемещение)

Углы

• Разделение угла пополам
• Скопируйте угол
• Построение угла 30°
• Построение угла 45°
• Построение угла 60°
• Построить угол 90° (прямой угол)
• Сумма n углов
• Разность двух углов
• Дополнительный уголок
• Дополнительный уголок
• Построение углов 75° 105° 120° 135° 150° и более

Треугольники

• Копия треугольника
• Равнобедренный треугольник с основанием и стороной
• Равнобедренный треугольник с данными основанием и высотой
• Равнобедренный треугольник с катетом и углом при вершине
• Равносторонний треугольник
• Треугольник 30-60-90 по гипотенузе
• Треугольник по трем сторонам (sss)
• Треугольник по одной стороне и прилежащим углам (asa)
• Треугольник с двумя углами и не включенной стороной (aas)
• Треугольник по двум сторонам и углу между ними (sas)
• Медианы треугольника
• Средняя часть треугольника
• Высота треугольника
• Высота треугольника (вне корпуса)

Прямоугольные треугольники

• Прямоугольный треугольник с одним катетом и гипотенузой (HL)
• Прямоугольный треугольник с учетом обеих сторон (LL)
• Прямоугольный треугольник по гипотенузе и одному углу (HA)
• Прямоугольный треугольник по одному катету и одному углу (LA)

Центры треугольников

• Центры треугольников
• Центр окружности треугольника
• Ортоцентр треугольника
• Центр тяжести треугольника

Окружности, дуги и эллипсы

• Нахождение центра окружности
• За круг дается 3 очка
• Касательная в точке окружности
• Касательные через внешнюю точку
• Касательные к двум окружностям (внешние)
• Касательные к двум окружностям (внутренние)
• Вписанная окружность треугольника
• Точки фокусировки данного эллипса
• Окружность треугольника

Многоугольники

• Квадрат с одной стороной
• Квадрат, вписанный в круг
• Шестиугольник с одной стороной
• Шестиугольник, вписанный в данную окружность
• Пятиугольник вписан в заданный круг

Неевклидовы конструкции

• Построение эллипса с помощью нити и булавок
• Найдите центр круга с любым прямоугольным объектом

(C) 2011 Copyright Math Open Reference.