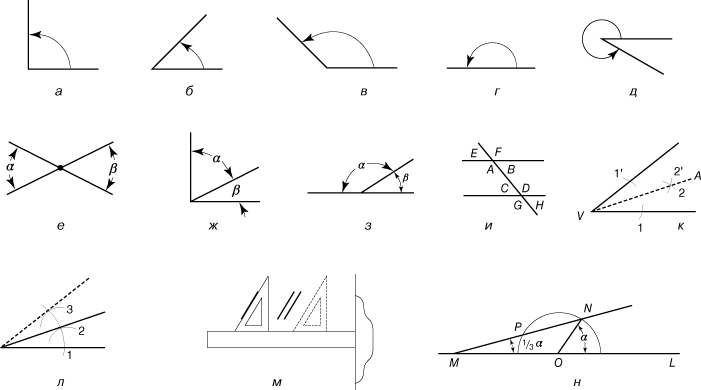
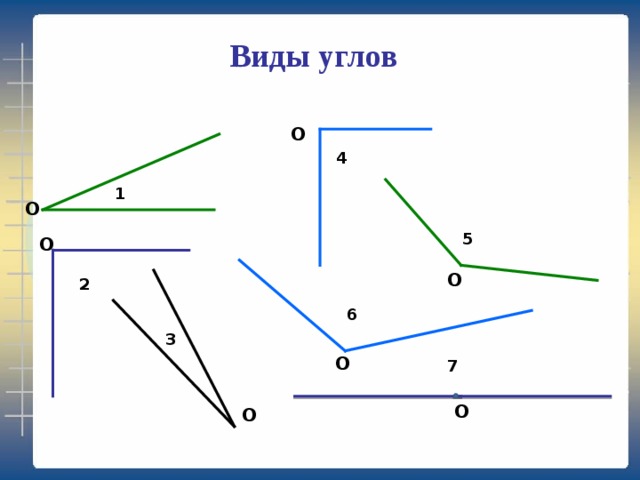
Виды углов. Измерение углов
Давайте представим себе такую историю.
– Ну и как же мне здесь разобраться? – бормотал Саша.
– Саша, что случилось? – спросил Паша.
– Мама, прежде чем уйти на работу, сказала, что купила один очень важный предмет, который мне пригодится на уроках математики.
– Здорово! – обрадовался за друга Паша. – И что это за предмет такой важный?
– Вот в этом и проблемка – загрустил Саша. – Мама спрятала этот предмет, но, чтобы я его нашёл, она подготовила инструкцию, где написано, что мне нужно сделать.
– Так давай я тебе помогу! – предложил Паша. – Показывай свою инструкцию!
– Смотри! – обрадовался Саша.
– В первом пункте написано, что я должен сделать 10 шагов прямо.
– Ну и что тут сложного? – удивился Паша.
– Ничего! – ответил Саша. – Шаги то я сделал,
а вот в следующих пунктах сказано, что я должен повернуть вправо на величину,
равную прямому углу, а затем сделать ещё 5 шагов.
– Да… проблемка! – задумался Паша. – Давай спросим у Электроши. Он точно сможет нам помочь!
– Ребята, прежде чем я вам расскажу об измерении углов, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь поговорим об измерении углов, – предложил Электроша. – Но для начала давайте вспомним, что вообще называют углом.
– Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки – сказал Саша.
– Молодец! – похвалил Сашу Электроша. – Вы уже знаете, как измеряют отрезки. Скажите, что значит измерить отрезок?
– Измерить отрезок – означает
подсчитать, сколько единичных отрезков в нём помещается – сказал Паша.
– Правильно! – подтвердил Электроша. – Тогда, как вы думаете, что значит измерить угол?
– Ну, наверное, – начал Паша, – измерить угол – означает подсчитать, сколько единичных углов в нём помещается.
– Верно! – сказал Электроша. – Однако для измерения углов у нас пока ещё нет такого единичного угла. Но мы можем сами его создать. И сейчас я вам покажу, как это сделать.
– Давайте нарисуем круг и разделим его на 360 равных частей. Угол, образованный двумя соседними лучами, выбирают за единицу измерения. И такой уголок принято называть градусом. Кстати, градус происходит от латинского слова и переводится как «шаг», «ступенька».
– Правильно! – сказал Электроша. Запомните! Градус – это общепринятая единица, которой пользуются для измерения углов. Для обозначения градусов в тексте используют вот такой знак: о.
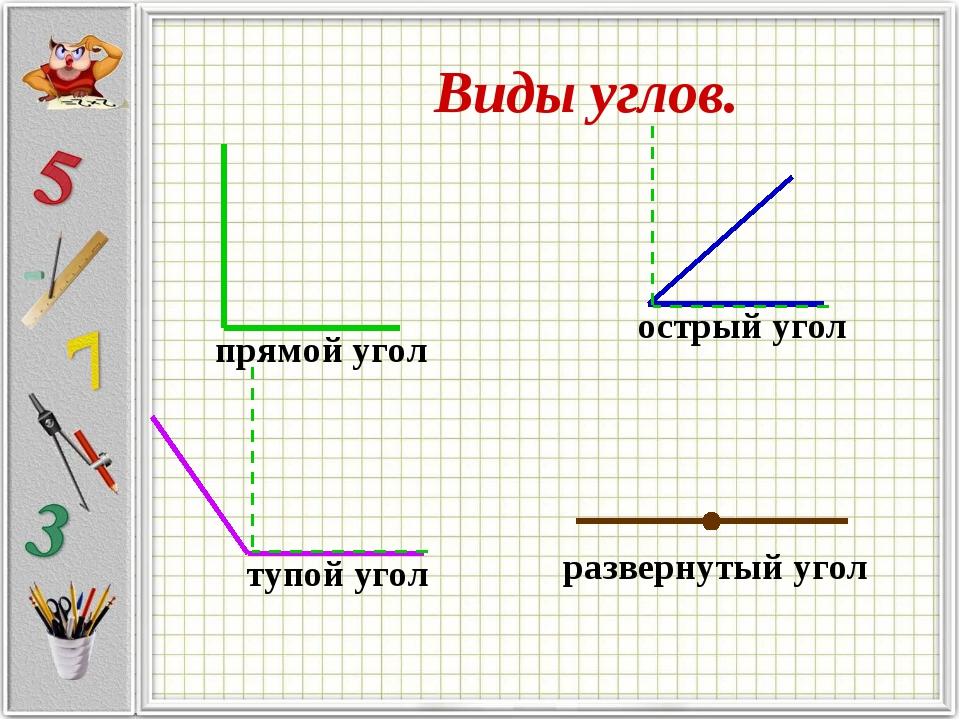
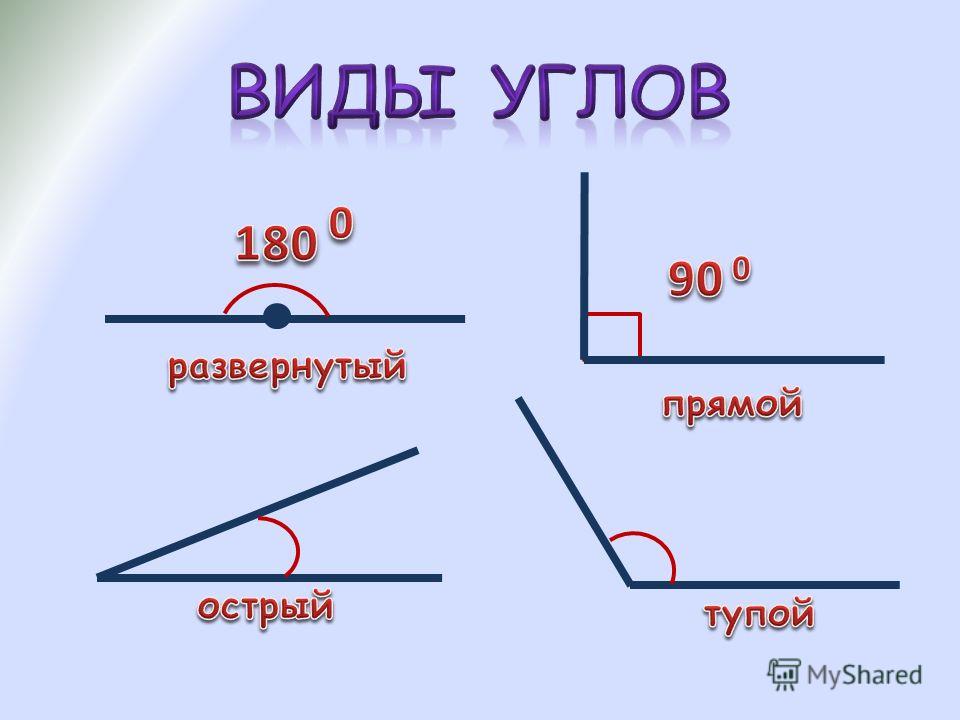
Так как мы с вами делили круг на 360 равных частей, то угол, равный плоскости круга, составляет 360 градусов, и называется такой угол полным углом.
– Электроша, а если полный угол разделить пополам, мы получим половинный угол? – поинтересовался Паша.
– Если плоскость круга разделить на 2 равные части, то плоскость одного полукруга составит угол в 180 градусов.
Запомните! Угол, равный полуплоскости круга, составляет 180 градусов и называется развёрнутым углом. Обратите внимание, стороны развёрнутого угла образуют прямую.
– А если бы мы разделили круг на 4 части? – спросил Саша.
– Если плоскость круга разделить на 4 равные
части, то плоскость одной части составит угол в 90 градусов.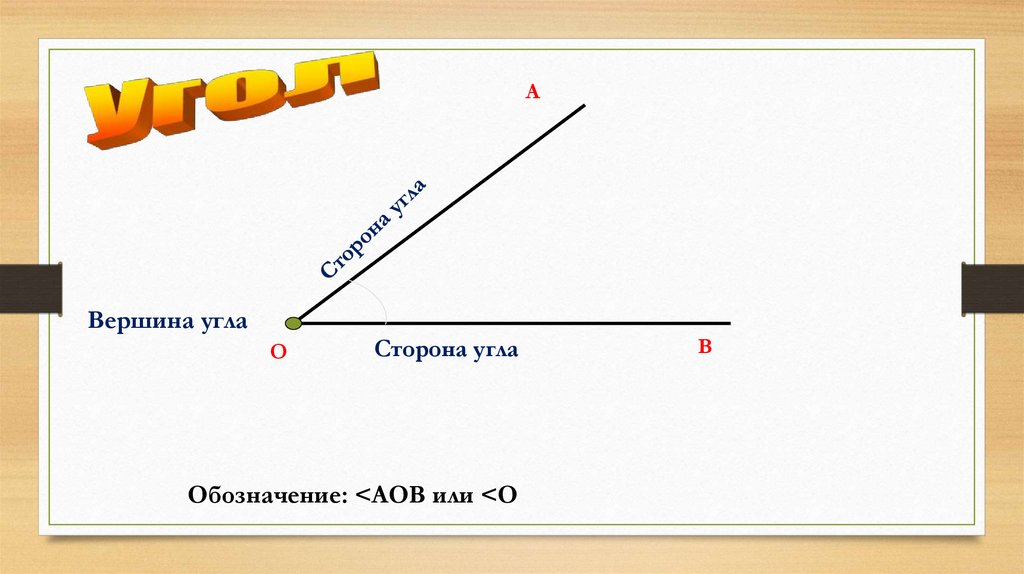
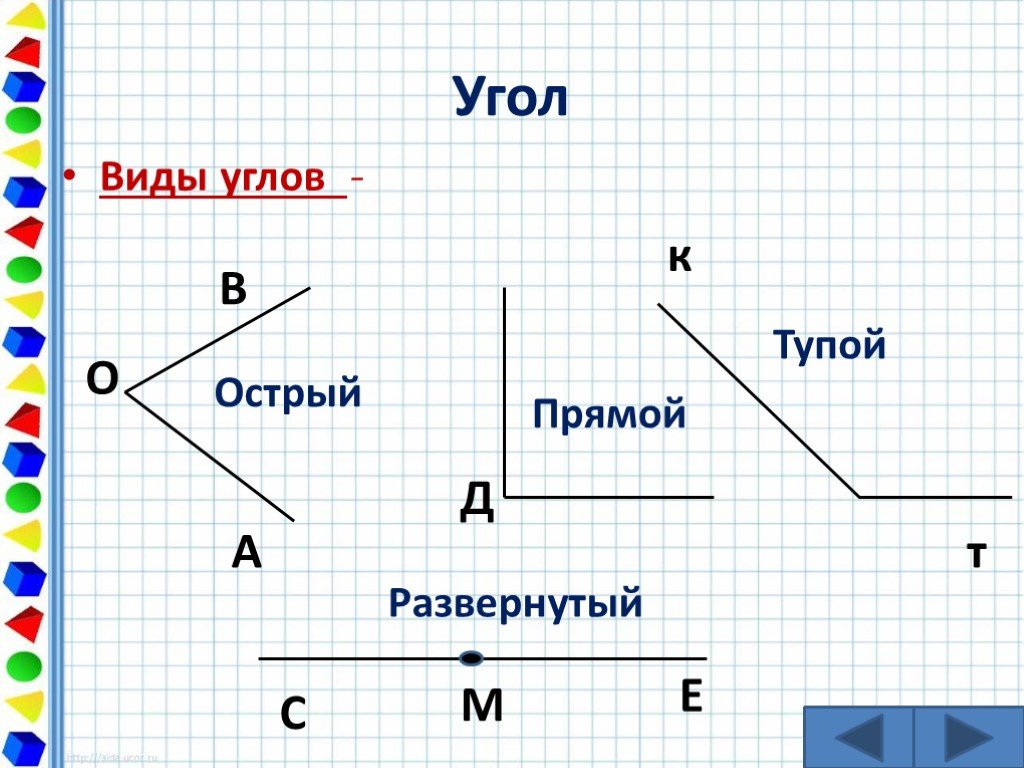
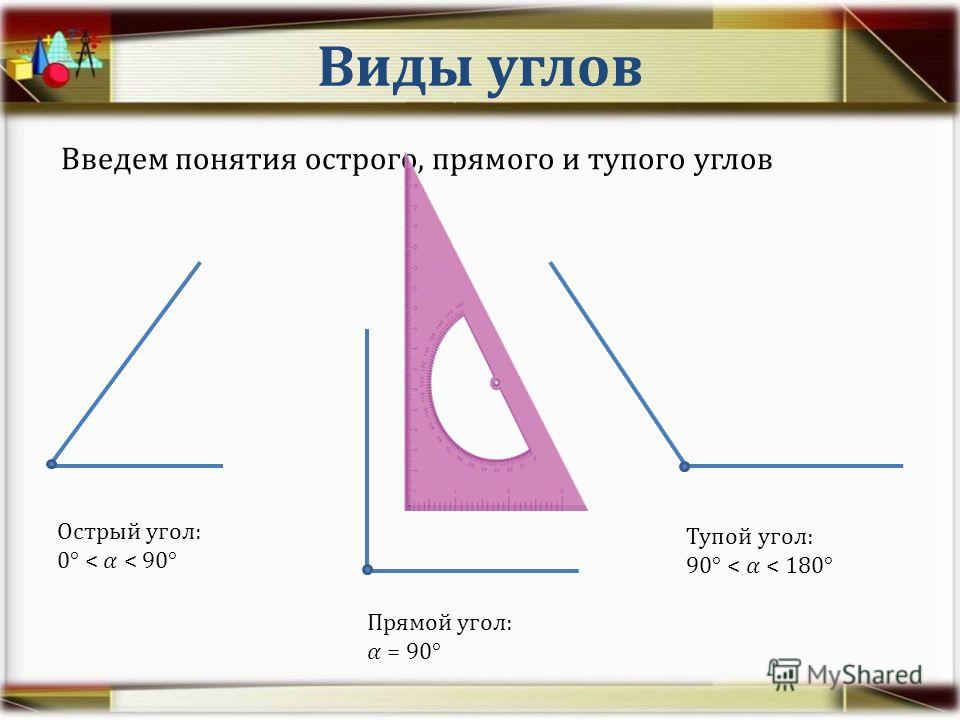
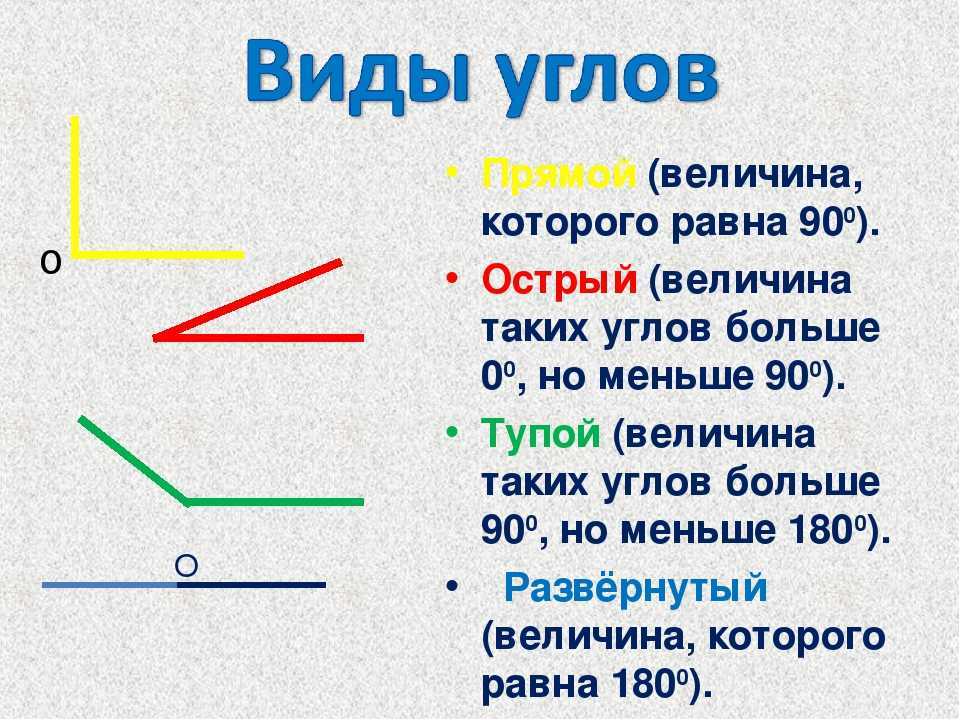
Запомните! Угол, равный четвёртой части круга, составляет девяноста градусов и называется прямым углом. Прямой угол обозначают вот таким значком: .
Существуют и другие виды углов.
Так, например, угол, градусная мера которого меньше 90 градусов, называют острым.
Угол, градусная мера которого больше 90 градусов, но меньше 180 градусов, называют тупым.
– Электроша, спасибо! Теперь я понял, что значит повернуть вправо на величину, равную прямому углу. Сейчас я быстренько найду предмет, который спрятала мама.
– Смотрите, какую необычную линейку купила мне мама! – воскликнул Саша. – Разве такая линейка пригодится на уроках математики?
– Саша, конечно, пригодится! – успокоил
мальчика Электроша. – Такую линейку используют для
измерения углов, а также для построения угла нужной величины. А называется эта
линейка «транспортир».
– Вообще, этот инструмент может иметь разный внешний вид, но у любого транспортира есть шкала, которая расположена на полуокружности.
Давайте поближе рассмотрим Сашин транспортир.
Посмотрите, внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части – полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов. Каждое деление шкалы транспортира равно 1 градусу. Центр шкалы отмечен штрихом или отверстием.
– Электроша, а как измерять углы транспортиром? – уточнили ребята.
– Это совсем несложно, – сказал Электроша. – Давайте рассмотрим алгоритм измерения углов на примере.
Итак, найдём величину угла АОВ. Для начала
совместим вершину угла с центром транспортира. Затем расположим транспортир
так, чтобы одна из сторон угла прошла по линейке.
У нас это сторона ОВ. А
теперь найдём штрих на шкале, через который проходит вторая сторона угла. Этот
штрих и укажет градусную меру (величину) нашего угла. Посмотрите, в нашем
случае градусная мера угла АОВ равна 60 градусам. Записывают это так: .
– Электроша, ты говорил, что с помощью транспортира можно строить углы, – решил уточнить Саша. – Научишь нас?
– Конечно! – обрадовался Электроша. – Давайте рассмотрим алгоритм построения углов на конкретном примере.
– Итак, давайте построим угол АВС, равный 120
градусам. Для начала отметим произвольную точку и обозначим её буквой В. Затем
начертим луч с началом в точке В и на нём отметим точку А. Получим луч ВА.
Теперь приложим к этому лучу транспортир так, чтобы его центр совпал с точкой В,
а сам луч ВА прошёл через начало отсчёта на шкале. Затем на этой же шкале
найдём штрих, который соответствует 120 градусам. За штрихом отметим точку и
обозначим её буквой С.
Осталось провести луч ВС. Вот так мы с вами построили
угол АВС, равный 120 градусам.
– Как видите, всё очень легко! Нужно просто один раз попробовать и всё обязательно получится!
– А теперь скажите, какие углы мы называем равными? – спросил у ребят Электроша.
– Два угла называют равными, если они совпадают при наложении, – ответили мальчишки.
– Молодцы! – похвалил ребят Электроша. – Так как равные углы полностью совмещаются при наложении, то можем сделать вывод, что равные углы имеют равные градусные меры. А значит, из двух неравных углов большим будем считать тот, градусная мера которого больше, и, соответственно, меньшим тот, градусная мера которого меньше.
– Посмотрите, я нарисовал 3 разных угла, – продолжил Электроша. – Что вы можете сказать об их величинах?
– Даже не измеряя транспортиром, видно, что
угол MNP
больше угла QST, –
начал Паша. – Ещё можно сказать, что угол EFG меньше угла MNP.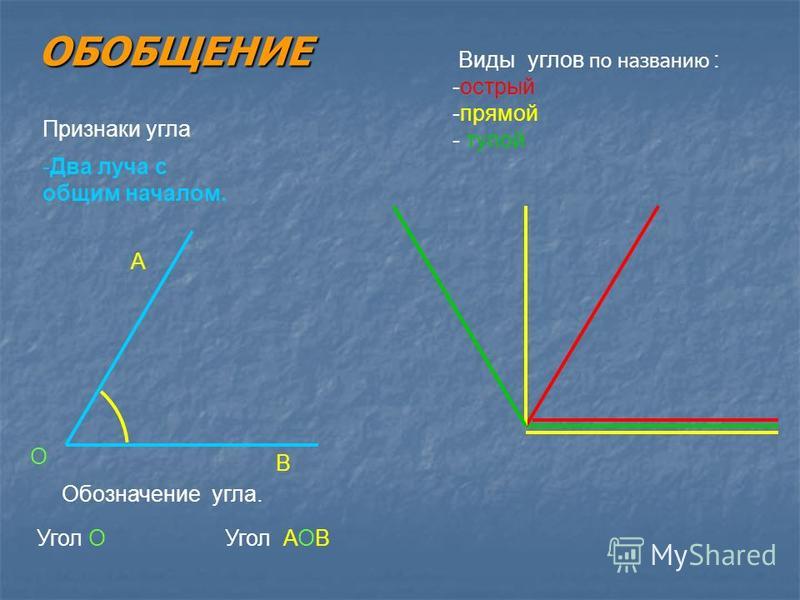
– А если измерить эти углы, – продолжил Саша, то увидим, что угол QST равен углу EFG.
– Ещё вам следует знать свойство величины угла.
Запомните! Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC. Записывают это свойство так: .
– Вот, например, градусная мера угла ABD равна 30 градусам, а градусная мера угла DBC равна 20 градусам. Тогда чему будет равна градусная мера угла ABC?
– По свойству величины угла, – начал Паша, – мы должны сложить величины углов ABD и DBC. Тогда величина угла ABC равна 50 градусам.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.
Итак, угол ABC разделён лучом BD на два угла ABD и DBC так, что градусная мера угла ABD равна 29 градусам, а градусная мера угла DBC равна 61 градусу. Постройте угол ABC и определите его вид.
Решение: для начала нам нужно выяснить
градусную меру угла ABC.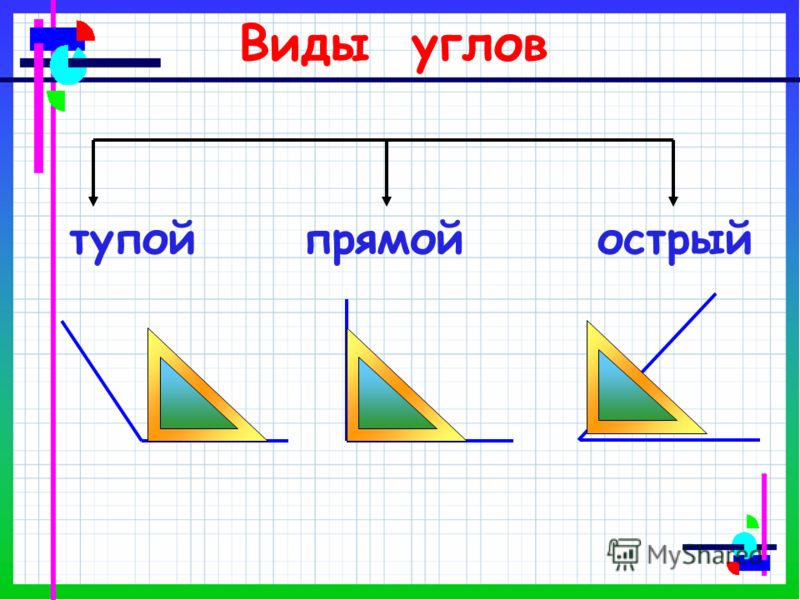
Применяя свойство величины угла, получаем, что угол ABC равен 90 градусов. Теперь построим этот угол.
И осталось определить его вид. Мы знаем, что угол, который составляет 90 градусов,
называется прямым углом. Значит, наш угол ABC – прямой.
МБОУ Школа № 112 г.о. Самара 2 класс Математика Тема урока: «Угол. Виды углов». УМК «Школа России» | ||
Тема урока: Угол. Виды углов. Тип урока: Изучение нового материала. Цели деятельности учителя: Дать представление о прямом угле; учить отличать прямой угол от острого и тупого при помощи модели прямого угла Используемые элементы технологий: личностно-ориентированной направленности, технология деятельностного обучения. | ||
Планируемые образовательные результаты | ||
Предметные: | Метапредметные(критерии сформированности/оценки компонентов УУД): | Личностные: |
знают: что такое угол, виды углов; геометрические фигуры; умеют: определять вид угла при помощи модели прямого угла. | познавательные: определяют последовательность промежуточных целей с учетом конечного результата; строят логическую цепочку рассуждений; умеют пользоваться учебником; регулятивные: оценивают свои достижения на уроке; коммуникативные: слушают собеседника и ведут диалог; умеют вступать в речевое общение. | принимают и осваивают социальную роль обучающегося; стремятся развивать мотивы учебной деятельности, навыки сотрудничества со сверстниками и со взрослыми, умение доказывать свою точку зрения, проявляют самостоятельность |
Этап урока | Деятельность учителя | Деятельность учащихся |
Организационный момент (Эмоциональный настрой) | Итак, друзья, внимание, Ведь прозвенел звонок! Садитесь поудобнее — Начнём скорей урок. | Запись числа. Классной работы |
Актуализация знаний | Мы сегодня будем в роли исследователей. Кто такие исследователи? Начнем наше исследование с геометрических фигур. Поработаем в паре. — Перед вами лежат карточки. (Приложение 1) Разделите фигуры на группы. Как называются группы? Какая фигура лишняя? Почему? — Почему эти фигуры назвали многоугольники? | Учащиеся делят на группы фигуры. ( замкн, незамкн; многоугол, линии) |
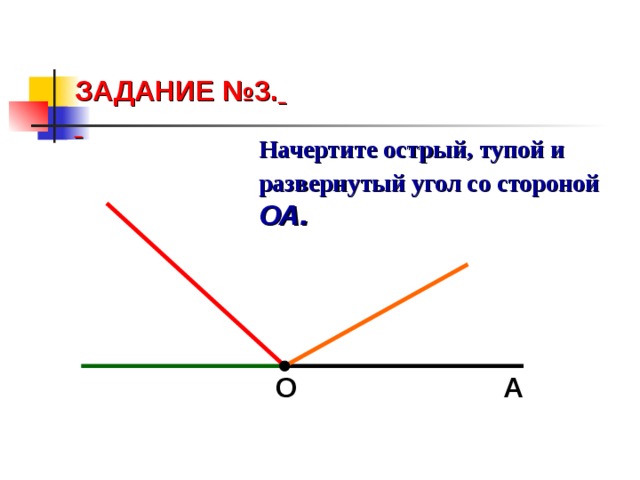
Открытие нового знания. Постановка цели (проблемная ситуация). | Прочитайте тему урока. «Угол. Виды углов» Какие учебные задачи поставим? Что проводят исследователи? В результате работы у них получается какой-то продукт (материалы работы). — А кто знает, что такое угол? Построим угол в тетради. Что нам понадобится? Выполняем работу самостоятельно. У вас получилась фигура. Как построили угол? Давайте сделаем вывод, что такое угол. Открываем учебник на стр 8. Прочитаем. Наши выводы совпали с выводами авторов учебника? Какое открытие сделали? Что имеет угол? Покажите стороны угла, вершину. Что такое угол? У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла) Где можно найти угол? Рассмотрите кабинет. Человеку каких профессий нужны знания о углах? Как вы думаете, мы всё узнали про угол? | Читают тему на доске — Они проводят наблюдения, ставят эксперименты. — Угол Предположения учащихся. Готовят линейку и карандаш и строят произвольный угол. Читают вывод в учебнике. Строителю, инженеру |
Практическая работа. Построение модели прямого угла. | Давайте продолжим наше исследование -У каждого на парте лежит лист цветной бумаги. Согните его пополам, ещё раз пополам. Проведите пальчиком по линиям сгиба. Что у вас получилось? Покажите пальчиком вершину угла, а теперь стороны угла. Какой угол у вас получился? У вас получилась модель прямого угла. Разверните. — Сколько углов получилось? — На пересечении линий сгиба поставьте точку. Как она называется? (вершина угла) Обведите стороны прямого угла. Заштрихуйте цветным карандашом его внутреннюю часть. А у нас в классе есть прямые углы? Рассмотрите парту. Какой угол? Проверьте. Как будете проверять? Мы можем проверить угол парты путем наложения модели прямого угла на угол парты. | Выполняют по образцу, совместно с учителем. Показывают вершину и сторону. (Четыре). Штрихуют внутреннюю часть. |
Первичное закрепление. | Что мы узнали? Что ещё надо узнать? Мы получили модель прямого угла при помощи листа бумаги. А как начертить прямой угол? Какие инструменты вам понадобятся? Какой инструмент нужно взять? Строим. Как обозначить угол? Прочитайте, как называется ваш угол -Почему выбрали эту линейку? Объясните (угольник). -Для чего еще можно использовать угольник? -Для измерения длины и для построения прямых углов. Задание: Используя модель прямого угла, найди на рисунке прямые углы и выпиши их номера. (Приложение 2) | Учащиеся самостоятельно строят прямой угол Находят прямые углы. |
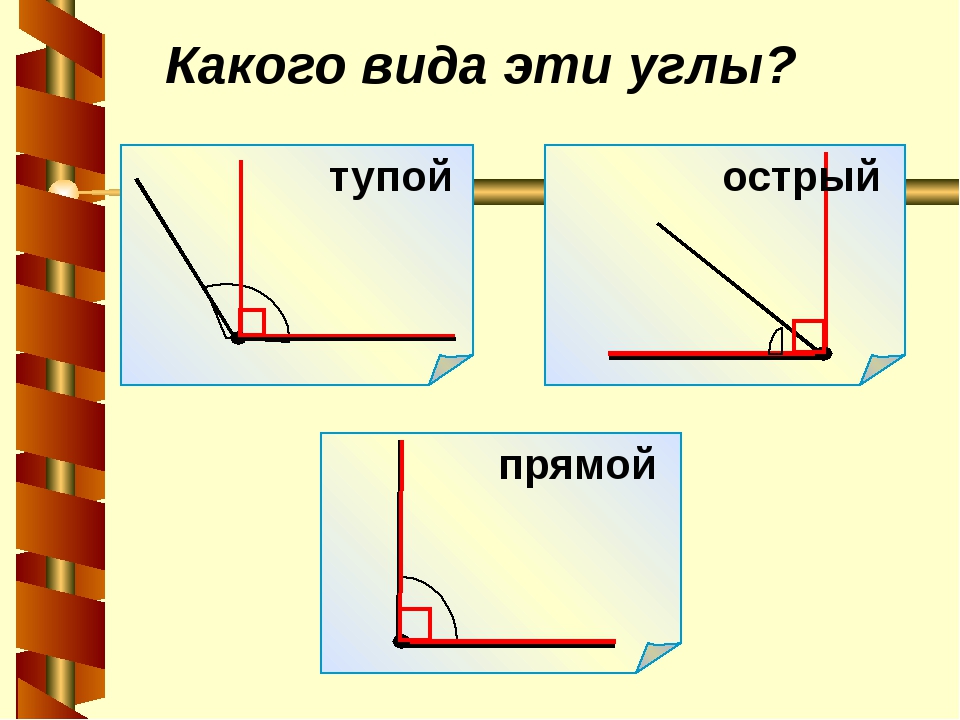
Построение модели острого и тупого углов. | — На рисунке видно, что бывают и другие углы — не прямые. Можно ли сравнивать углы по величине? Каждый из углов имеет своё название. — Я хочу вам показать один угол. Видите, он такой острый, что его вершиной даже можно слегка уколоться. А теперь посмотрите, угол развернулся, раскрылся. Его вершиной уже вряд ли можно уколоться. Теперь угол стал тупым. С помощью модели прямого угла узнайте, будут ли прямыми остальные углы угольника. Видим, что угол угольника меньше прямого угла, значит он какой? — Проверим третий угол. Наложим модель прямого угла на угол угольника и сравним. Значит, он как называется? (острый) Острый угол – это угол, который меньше прямого. Тупой угол – это угол, который больше прямого. — Определим виды углов, используя прямой угол чертежного угольника. Если стороны угла и прямого угла угольника совпали, то это какой угол? (прямой) Если угол меньше, чем прямой угол угольника, то это…? (острый угол) Если угол больше, чем прямой угол угольника, то это тупой угол. Какие же виды углов бывают? (повесить табличку) (Приложение 3) | С помощью модели прямого угла находят острые и тупые углы. Делают выводы о видах углов. |
Этап самостоятельной работы с самопроверкой по эталону. Закрепление на практике. | Все исследования всегда подкрепляются практикой. 1 задание. Моделирование углов. С помощью пластилина и зубочисток постройте прямой, острый и тупой угол. 2 задание. (Приложение 4) Из конверта достаньте часы. Определи угол, который образует часовая и – минутная стрелки. Покажите часы, на которых 3 часа дня. Какой угол они образуют? — 17 часов. Какой угол они образуют? — 2 часа. Какой угол они образуют? | С помощью пластилина и зубочисток строят прямой, острый и тупой углы. По часам определяют время и угол С помощью модели ищут углы и записывают их количество на карточке. |
Рефлексия | Какие учебные задачи мы ставили? Нам удалось их решить? Какой продукт получили? Что же такое угол? Что есть у угла? Какие виды углов вы знаете? | |
Домашнее задание | Вам необходимо раскрасить внутреннюю область углов: углы прямые в синий цвет, острые — в зелёный цвет, тупые углы в жёлтый цвет. И записать количество на карточке. (Приложение 5) | |
Какой продукт должны получить мы?
Разные повороты, разные техники: оптимизируйте каждый поворот
В зависимости от конкретного поворота трассы ваше торможение, гоночная траектория и весь метод могут меняться. Как гонщики, мы пытаемся извлечь из времени круга каждую десятую долю секунды, поэтому важно понимать эти различия.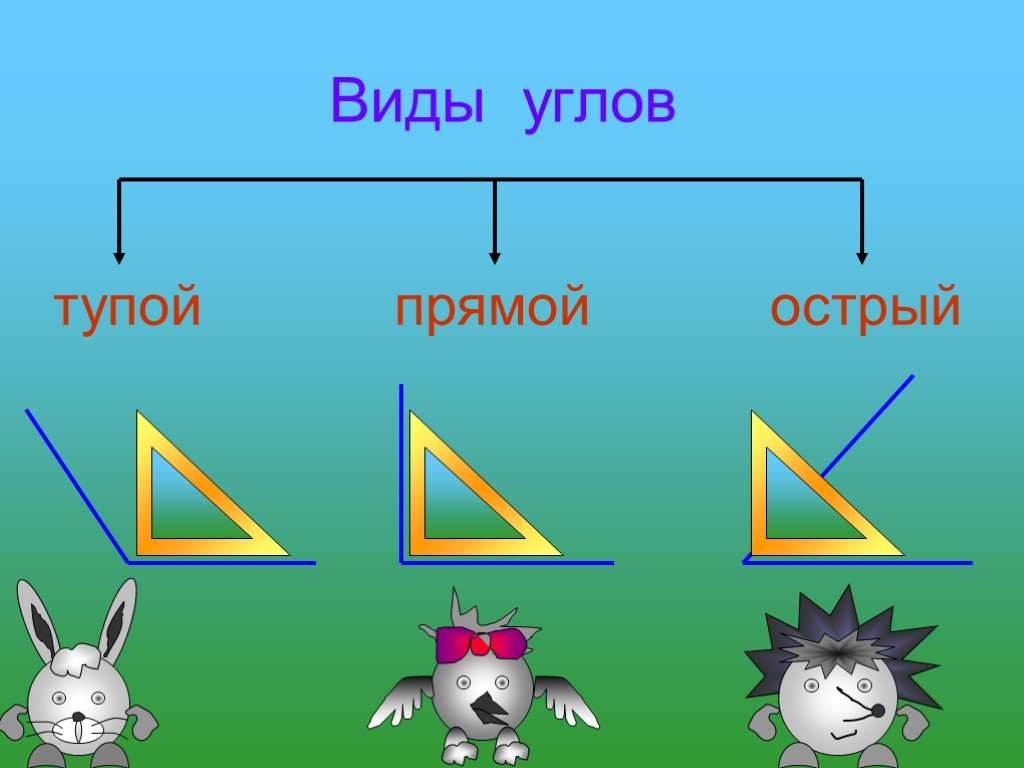
Добро пожаловать в урок №11 из нашей серии «Университет водителей». Сегодня мы собираемся изучить, как мы должны изменить нашу технику для различных типов углов.
Три типа поворотов
Конечно, на любой гоночной трассе не бывает двух одинаковых поворотов, но мы можем разделить повороты на три основных типа, основываясь больше на том, что следует за ними, а не на самом повороте.
Мы можем использовать эти три категории — при условии, что водитель быстр и последователен на входе в поворот, — потому что прямая, следующая за поворотом, важнее для времени прохождения круга, чем сам поворот.
Следовательно, мы можем разделить каждый угол на бытие:
- Перед длинной прямой
- Перед короткой прямой
- Непосредственно перед другим поворотом (или последовательностью поворотов)
С каждым из этих различных типов поворотов мы получаем наибольшую пользу, если используем разную технику вождения.
Во-первых, вы можете спросить, как мы определяем короткий или длинный стрит? Очевидно, что это немного сложно, но для целей этого урока я скажу, что длинная прямая — это участок, на котором вы можете подумать об обгоне, а в дни трека — прямые, на которых организаторы разрешают обгон.
Повороты перед длинной прямой
Автомобиль быстрее всего движется по прямой.
Это не значит, что мы должны вести свои машины только по прямой линии и в прямом направлении, но с поворотами, которые предшествуют длинной прямой, мы должны стараться максимально открывать выходы из поворотов, чтобы сократить время прохождения круга.
Выходите из этих поворотов, имея на выходе всего одну милю в час, и вы продолжите использовать это преимущество на протяжении всей следующей прямой. В совокупности это приводит к значительной экономии времени.
На приведенной ниже диаграмме показан пример медленного поворота с длинным прямым движением.
В этом типе поворота выгодно затормозить немного раньше, достаточно поздно входить в поворот, поздно выходить из поворота и открывать выход из поворота, чтобы можно было быстро выйти на полный газ.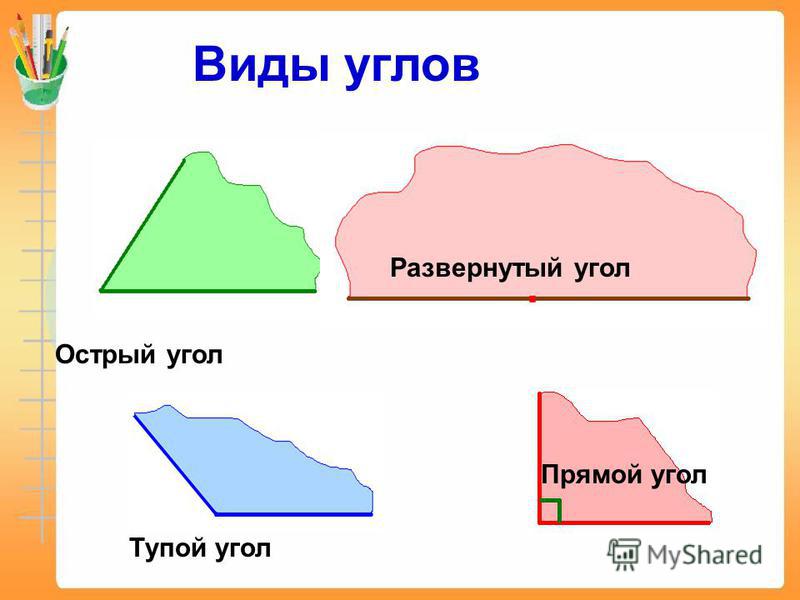
Вот краткое изложение того, что вам нужно сделать:
- Затормозить относительно рано, так как минимальная скорость будет в начале поворота
- Повернуть довольно поздно, «выравнивая» вход
- Апекс поздно, обычно около ⅔ – ¾ поворота – это открывает выход, позволяет быстрее выровнять машину, а затем раньше дать полный разгон
- Используйте всю трассу на выезде, открывая угол поворота руля
- Продолжайте использовать преимущество в скорости на протяжении всей следующей прямой, что приведет к более быстрому времени прохождения круга
Поворот перед короткой прямой
Диаграмма ниже показан пример того, что я имею в виду под короткой прямой – это просто связующая прямая между двумя поворотами без времени на длительный период ускорения или обгона.
В этом типе поворота возможность выиграть время есть только на входе в поворот, а также на выходе из второго поворота в зависимости от длины следующей прямой. Для простоты мы пока проигнорируем второй угол.
Поскольку прямая после первого поворота такая короткая, приоритетом является не выход – скоро нам снова придется нажимать на тормоза для второго поворота, и поэтому любая дополнительная скорость выхода, которую мы несем, не так уж важна. важный.
Поскольку нам не нужно сосредотачиваться на скорости на выходе, вы должны попытаться максимально увеличить скорость до первого апекса. Идея состоит в том, чтобы держать газ как можно дольше и поворачивать к апексу немного раньше, чем мы могли бы подумать.
Как видно из приведенной ниже диаграммы, большая часть токарной обработки выполняется на вершине и после нее. Мы немного едем поперек трассы в зоне торможения, что позволяет водителю сильнее тормозить даже после поворота.
После прохождения апекса необходимо расположить машину так, чтобы максимально увеличить выход из второго поворота.
В нашем примере есть длинная прямая, поэтому мы должны изменить нашу технику, чтобы открыть выход из второго поворота и как можно скорее дать полный газ.
Вот краткое изложение того, что вам нужно сделать:
- Затормозить как можно позже, чтобы выиграть время на прямой
- Повернуть немного раньше, чем обычно, и подвести машину к апексу. Это отрезает несколько метров пути, и вы можете сделать платформу автомобиля более плоской
- Вы должны были набрать большую скорость в апексе, теперь продолжайте замедлять машину и расположите ее так, чтобы максимально увеличить выход из второго поворота
Последовательность поворотов
Последовательность поворотов, пожалуй, самое веселое в гонке отслеживать. Вспомните Maggots, Becketts, Chapel в Сильверстоуне или повороты 6, 7 и 8 на COTA. однако вызывают определенные трудности у водителей. Вот почему эти типы изгибов так полезны, когда вы делаете их правильно.
Когда один угол следует за другим, ваша линия выхода из одного является линией входа в следующий. Итак, как нам принять решение о том, что важнее и какую гоночную трассу выбрать?
Как всегда, поворот, предшествующий следующей длинной прямой, является самым важным — любая дополнительная скорость на выходе здесь переносится на прямую и способствует более быстрому кругу.
Думая о гоночной трассе, нам нужно работать в обратном направлении от последнего поворота в последовательности перед прямой.
Думайте о последнем повороте в серии так же, как о любом повороте перед длинной прямой. Стремитесь к позднему апексу и как можно раньше нажмите на педаль акселератора на выходе, чтобы максимально ускориться на следующей прямой.
На карте трассы ниже видно, что мы максимально раскрыли последний поворот в последовательности. Все повороты, предшествующие этому, являются чем-то вроде компромисса, но идея состоит в том, чтобы сохранить высокий импульс и занять хорошую позицию для последнего поворота.
Когда вы держите машину на грани сцепления (дополнительную информацию см. в руководстве здесь), ваша траектория не будет идеально одинаковой на каждом круге.
Я говорю не об огромных ошибках, а скорее о небольших изменениях в гоночной траектории, поскольку машина естественным образом движется немного теснее или шире, чем предполагалось.
В последовательности поворотов важно быть динамичным. Если вы бежите немного шире на выходе из одного поворота, вы выиграете немного времени, но поставите под угрозу вход в следующий.
Всеми этими изменениями можно управлять, и они не будут стоить вам никакого времени, но вы не должны слишком далеко отклоняться от идеальной гоночной траектории — хороший обзор на протяжении всей последовательности поворотов имеет решающее значение для того, чтобы сделать все правильно.
Вкратце
При движении по трассе я обнаружил, что если моя линия прохождения поворота кажется правильной, значит, она быстрая. Это приходит с опытом и временем, но используйте информацию в этом руководстве, чтобы подтвердить свое внутреннее чувство об оптимизации гоночных трасс для разных поворотов.
Если вы не уверены в некоторых сложных линиях или хотите провести дополнительное исследование, прежде чем отправиться дальше, обязательно ознакомьтесь с нашими подробными руководствами по схемам, где мы объясним идеальные линии вокруг различных схем.
Как всегда, спасибо за внимание, до новых встреч, Скотт.
Тип уголков — GammaStone
МОНОЛИТНЫЙ 90°
1) Несущая стена
2) Кронштейн
3) Анкер
4) Стойка
. Винт
6) Изоляция
7) Изоляция. Крепление
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Рейка GammaStone *
12) Зажим GammaStone *
13) Крепежный винт
14) Регулировка. Винт
15) Угол конструкции в нержавеющей стали
* В черном анодированном алюминиевом
Монолитный> 90 °
1) Структурная стена
2) Шпонка
3). Анкер
4) Mullion
2). Винт
6) Изоляция
7) Изоляция. Фиксация
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Направляющая GammaStone *
12) Зажим GammaStone *
13) Крепежный винт
14) Отрегулируйте. Винт
15) Угол конструкции в нержавеющей стали
* В черном анодированном алюминиевом
Монолитик
<90 °1) Структурная стенка
2) Кроншена
3).
Приземление 4) Mullion
2). Винт
6) Изоляция
7) Изоляция. Крепление
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Рейка GammaStone *
12) Зажим GammaStone *
13) Крепежный винт
14) Отрегулируйте. Винт
15) Несущий уголок из нержавеющей стали
* из черного анодированного алюминия
QUIRK MITRE
1) Несущая стена
2) Кронштейн
3) Анкер 1) Self 9012 Винт
6) Изоляция
7) Изоляция. Крепление
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Рейка GammaStone *
12) Зажим GammaStone *
13) Фиксирующий винт
14) Отрегулируйте. Винт
15) Несущий уголок из нержавеющей стали
* из черного анодированного алюминия
MITER
1) Несущая стена
2) Кронштейн
3) Анкер 9.12121 4) Винт
6) Изоляция
7) Изоляция. Крепление
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Направляющая GammaStone *
12) Зажим GammaStone *
13) Крепежный винт
14) Отрегулировать.
Винт 15) Несущий уголок из нержавеющей стали
* из черного анодированного алюминия
УГЛОВОЙ СВЕТИЛЬНИК
1) Несущая стена
2) Кронштейн
5)
Анкер
Винт
6) Изоляция
7) Изоляция. Крепление
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Рейка GammaStone *
12) Зажим GammaStone *
13) Крепежный винт
14) Регулировка. Винт
15) Конструкционный уголок из нержавеющей стали
* из черного анодированного алюминия
QUIRK ASSEMBLED
1) Несущая стена
2) Кронштейн
3) Анкер
4) Стойка
5) Саморез. Винт
6) Изоляция
7) Изоляция. Крепление
8) Вентиляция
9) Панель GammaStone AIR
10) Заклепка
11) Рейка GammaStone *
12) Зажим GammaStone *
13) Крепежный винт
14) Регулировка. Винт
15) Конструкционный уголок из нержавеющей стали
* из черного анодированного алюминия
СТЫКОВОЕ СОЕДИНЕНИЕ
1) Несущая стена
2) Кронштейн
3) Анкер
4) Стойка
5) Самосверл.
