Дифференциальные уравнения: виды, методы решения
Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения.
В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1-го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2-го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y’=dxdy, если y является функцией аргумента x.
Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y’=f(x)
Начнем с примеров таких уравнений.
Пример 1y’=0, y’=x+ex-1, y’=2xx2-73
Оптимальным для решения дифференциальных уравнений f(x)·y’=g(x) является метод деления обеих частей на f(x).
Решение относительно производной позволяет нам прийти к уравнению вида y’=g(x)f(x). Оно является эквивалентом исходного уравнения при f(x) ≠ 0.
Приведем примеры подобных дифференциальных уравнений:
ex·y’=2x+1, (x+2)·y’=1
Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х, при которых функции f(x) и g(x)одновременно обращаются в 0. В качестве дополнительного решения в уравнениях f(x)·y’=g(x) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х.
Пример 3Наличие дополнительных решений возможно для дифференциальных уравнений x·y’=sin x, (x2-x)·y’=ln(2×2-1)
Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1-го порядка».
Дифференциальные уравнения с разделяющимися переменными вида f1(y)·g1(x)dy=f2(y)·g2(x)dx или f1(y)·g1(x)·y’=f2(y)·g2(x)
Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f(y)dy=g(x)dx.
Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у, разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.
Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫f(y)dy=∫f(x)dx
Пример 4К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:
y23dy=sin xdx, eydy=(x+sin 2x)dx
Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f2(y) ⋅ g1(x). Так мы придем к уравнению f1(y)f2(y)dy=g2(x)g1(x)dx. Преобразование можно будет считать эквивалентным в том случае, если одновременно f2(y) ≠ 0 и g1(x) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.
Пример 5В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: dydx=y·(x2+ex), (y2+arccos y)·sin x·y’=cos xy.
К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = ax+by. Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y’=f(ax+by), a,b∈R.
Пример 6Подставив z = 2x+3y в уравнение y’=1e2x+3y получаем dzdx=3+2ezez.
Заменив z=xy или z=yx в выражениях y’=fxy или y’=fyx, мы переходим к уравнениям с разделяющимися переменными.
Пример 7Если произвести замену z=yx в исходном уравнении y’=yx·lnyx+1, получаем x·dzdx=z·ln z.
В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.
Пример 8Предположим, что в условии задачи нам дано уравнение y’=y2-x22xy. Нам необходимо привести его к виду y’=fxy или y’=fyx. Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x2 или y2.
Нам дано уравнение y’=fa1x+b1y+c1a2x+b2y+c2, a1, b1, c1, a2, b2, c2 ∈R.
Для того, чтобы привести исходное уравнение к виду y’=fxy или y’=fyx, нам необходимо ввести новые переменные u=x-x1v=y-y1, где (x1;y1) является решением системы уравнений a1x+b1y+c1=0a2x+b2y+c2=0
Введение новых переменных u=x-1v=y-2 в исходное уравнение y’=5x-y-33x+2y-7 позволяет нам получить уравнение вида dvdu=5u-v3u+2v.
Теперь выполним деление числителя и знаменателя правой части уравнения на u. Также примем, что z=uv. Получаем дифференциальное уравнение с разделяющимися переменными u·dzdu=5-4z-2z23+2z.
Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».
Линейные неоднородные дифференциальные уравнения первого порядка y’+P(x)·y=Q(x)
Приведем примеры таких уравнений.
Пример 10К числу линейных неоднородных дифференциальных уравнений 1-го порядка относятся:
y’-2xy1+x2=1+x2;y’-xy=-(1+x)e-x
Для решения уравнений этого вида применяется метод вариации произвольной постоянной.
Также мы можем представить искомую функцию у в виде произведения y(x) = u(x)v(x). Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».
Дифференциальное уравнение Бернулли y’+P(x)y=Q(x)ya
Приведем примеры подобных уравнений.
Пример 11К числу дифференциальных уравнений Бернулли можно отнести:
y’+xy=(1+x)e-xy23;y’+yx2+1=arctgxx2+1·y2
Для решения уравнений этого вида можно применить метод подстановки z=y1-a, которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1-го порядка. Также применим метод представления функции у в качестве y(x) = u(x)v(x).
Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.
Уравнения в полных дифференциалах P(x,y)dx+Q(x,y)dy=0
Если для любых значений x и y выполняется ∂P(x,y)∂y=∂Q(x,y)∂x, то этого условия необходимо и достаточно, чтобы выражение P(x, y)dx+Q(x, y)dy представляло собой полный дифференциал некоторой функции U(x, y)=0, то есть, dU(x, y)=P(x, y)dx+Q(x, y)dy.
Выражение, расположенное в левой части записи уравнения (x2-y2)dx-2xydy=0 представляет собой полный дифференциал функции x33-xy2+C=0
Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».
Дифференциальные уравнения второго порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y»+py’+qy=0, p,q∈R
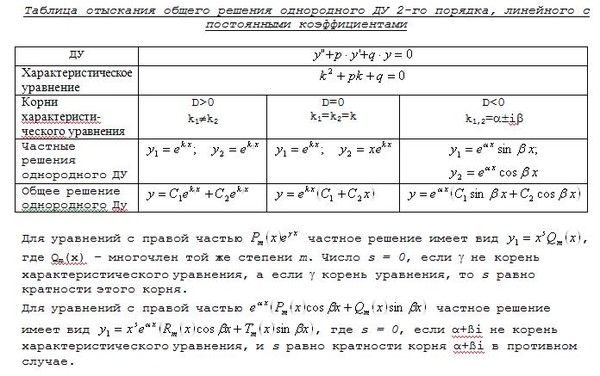
Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k2+pk+q=0. Здесь возможны три варианта в зависимости от различных p и q:
- действительные и различающиеся корни характеристического уравнения k1≠k2, k1, k2∈R;
- действительные и совпадающие k1=k2=k, k∈R;
- комплексно сопряженные k1=α+i·β, k2=α-i·β.
Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:
- y=C1ek1x+C2ek2x;
- y=C1ekx+C2xekx;
- y=ea·x·(C1cos βx+C2sin βx).
Предположим, что у нас есть линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами y»+3y’=0. Найдем корни характеристического уравнения k2+3k=0. Это действительные и различные k1 =-3 и k2=0. Это значит, что общее решение исходного уравнения будет иметь вид:
y=C1ek1x+C2ek2x⇔y=C1e-3x+C2e0x⇔y=C1e-3x+C2
Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами».
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y»+py’+qy=f(x), p,q∈R
Основным способом решение уравнений данного вида является нахождение суммы общего решения y0, которое соответствует линейному однородному дифференциальному уравнению y»+py’+qy=0, и частного решения y~ исходного уравнения.
Способ нахождения y0 мы рассмотрели в предыдущем пункте. Найти частное решение y~ мы можем методом неопределенных коэффициентов при определенном виде функции f(x), которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.
Пример 14К числу линейных неоднородных дифференциальных уравнений 2-го порядка с постоянными коэффициентами относятся:
y»-2y’=(x2+1)ex;y»+36y=24sin(6x)-12cos(6x)+36e6x
Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2-го порядка с постоянными коэффициентами».
Линейные однородные дифференциальные уравнения (ЛОДУ) y»+p(x)·y’+q(x)·y=0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y»+p(x)·y’+q(x)·y=f(x)
Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.
На некотором отрезке [a; b] общее решение линейного однородного дифференциального уравнения y»+p(x)·y’+q(x)·y=0 представлено линейной комбинацией двух линейно независимых частных решений y1 и y2 этого уравнения, то есть, y=C1y1+C2y2.
Частные решения мы можем выбрать из систем независимых функций:
1) 1, x, x2, …, xn2) ek1x, ek2x, …, eknx3) ek1x, x·ek1x, …, xn1·ek1x,ek2x, x·ek2x, …, xn2·ek2x,…ekpx, x·ekpx, …, xnp·ekpx4) 1, chx, shx
Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.
Пример 15Возьмем для примера линейное однородное дифференциальное уравнение xy»-xy’+y=0.
Общее решение линейного неоднородного дифференциального уравнения y»+p(x)·y’+q(x)·y=f(x) мы можем найти в виде суммы y=y0+y~, где y0 — общее решение соответствующего ЛОДУ, а y~ частное решение исходного дифференциального уравнения. Найти y0 можно описанным выше способом. Определить y~ нам поможет метод вариации произвольных постоянных.
Пример 16Возьмем для примера линейное неоднородное дифференциальное уравнение xy»-xy’+y=x2+1.
Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».
Дифференциальные уравнения высших порядков
Дифференциальные уравнения, допускающие понижение порядка
Мы можем провести замену y(k)=p(x) для того, чтобы понизить порядок исходного дифференциального уравнения F(x, y(k), y(k+1), .
.., y(n))=0, которое не содержит искомой функции и ее производных до k-1 порядка.
В этом случае y(k+1)=p'(x), y(k+2)=p»(x), …, y(n)=p(n-k)(x), и исходное дифференциальное уравнение сведется к F1(x, p, p’, …, p(n-k))=0. После нахождения его решения p(x) останется вернуться к замене y(k)=p(x) и определить неизвестную функцию y.
Пример 17Дифференциальное уравнение y»’xln(x)=y» после замены y»=p(x) станет уравнением с разделяющимися переменными y»=p(x), и его порядок с третьего понизится до первого.
В уравнении, которое не содержит аргумента х и имеет вид F(y, y’, y», …, y(n))=0, порядок может быть заменен на единицу следующим образом: необходимо провести замену dydx=p(y), где p(y(x)) будет сложной функцией. Применив правило дифференцирования, получаем:
d2ydx2=dpdydydx=dpdyp(y)d3ydx3=ddpdyp(y)dx=d2pdy2dydxp(y)+dpdydpdydydx==d2pdy2p2(y)+dpdy2p(y)
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.
Рассмотрим решение уравнения 4y3y»=y4-1. Путем замены dydx=p(y) приведем исходное выражение к уравнению с разделяющимися переменными 4y3pdpdy=y4-1.
Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0 и y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x)
Решение уравнений данного вида предполагает выполнение следующих простых шагов:
- находим корни характеристического уравнения kn+fn-1·kn-1+…+f1·k+f0=0;
- записываем общее решение ЛОДУ y0 в стандартной форме, а общее решение ЛНДУ представляем суммой y=y0+y~, где y~ — частное решение неоднородного дифференциального уравнения.
Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y~ целесообразно использовать метод вариации произвольных постоянных.
Линейному неоднородному ДУ с постоянными коэффициентами y(4)+y(3)-5y»+y’-6y=xcosx+sinx соответствует линейное однородное ДУ y(4)+y(3)-5y»+y’-6y=0.
Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков y(n)+fn-1(x)·y(n-1)+…+f1(x)·y’+f0(x)·y=0 и y(n)+fn-1(x)·y(n-1)+…+f1(x)·y’+f0(x)·y=f(x)
Найти решение ЛНДУ высших порядков можно благодаря сумме y=y0+y~, где y0 — общее решение соответствующего ЛОДУ, а y~ — частное решение неоднородного дифференциального уравнения.
y0 представляет собой линейную комбинацию линейно независимых функций y1, y2, …, yn, каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y(n)+fn-1(x)·y(n-1)+…+f1(x)·y’+f0(x)·y=0 в тождество. Частные решения y1, y2, …, yn обычно подбираются из известных систем линейно независимых функций.
Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y=y0+y~=∑Cj·yj+y~j=1n
Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».
Системы дифференциальных уравнений вида dxdt=a1x+b1y+c1dydt=a2x+b2y+c2
Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.
Дифференциальные уравнения: виды, методы решения
Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1-го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2-го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y’=dxdy, если y является функцией аргумента x.
Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y’=f(x)
Начнем с примеров таких уравнений.
Пример 1y’=0, y’=x+ex-1, y’=2xx2-73
Оптимальным для решения дифференциальных уравнений f(x)·y’=g(x) является метод деления обеих частей на f(x). Решение относительно производной позволяет нам прийти к уравнению вида y’=g(x)f(x). Оно является эквивалентом исходного уравнения при f(x) ≠ 0.
Пример 2Приведем примеры подобных дифференциальных уравнений:
ex·y’=2x+1, (x+2)·y’=1
Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х, при которых функции f(x) и g(x)одновременно обращаются в 0.
В качестве дополнительного решения в уравнениях f(x)·y’=g(x) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х.
Наличие дополнительных решений возможно для дифференциальных уравнений x·y’=sin x, (x2-x)·y’=ln(2×2-1)
Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1-го порядка».
Дифференциальные уравнения с разделяющимися переменными вида f1(y)·g1(x)dy=f2(y)·g2(x)dx или f1(y)·g1(x)·y’=f2(y)·g2(x)
Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f(y)dy=g(x)dx. Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у, разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.
Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫f(y)dy=∫f(x)dx
Пример 4К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:
y23dy=sin xdx, eydy=(x+sin 2x)dx
Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f2(y) ⋅ g1(x).
Так мы придем к уравнению f1(y)f2(y)dy=g2(x)g1(x)dx. Преобразование можно будет считать эквивалентным в том случае, если одновременно f2(y) ≠ 0 и g1(x) ≠ 0. Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.
В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: dydx=y·(x2+ex), (y2+arccos y)·sin x·y’=cos xy.
К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = ax+by. Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y’=f(ax+by), a,b∈R.
Пример 6Подставив z = 2x+3y в уравнение y’=1e2x+3y получаем dzdx=3+2ezez.
Заменив z=xy или z=yx в выражениях y’=fxy или y’=fyx, мы переходим к уравнениям с разделяющимися переменными.
Пример 7Если произвести замену z=yx в исходном уравнении y’=yx·lnyx+1, получаем x·dzdx=z·ln z.
В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.
Пример 8Предположим, что в условии задачи нам дано уравнение y’=y2-x22xy. Нам необходимо привести его к виду y’=fxy или y’=fyx. Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x2 или y2.
Пример 9Нам дано уравнение y’=fa1x+b1y+c1a2x+b2y+c2, a1, b1, c1, a2, b2, c2 ∈R.
Для того, чтобы привести исходное уравнение к виду y’=fxy или y’=fyx, нам необходимо ввести новые переменные u=x-x1v=y-y1, где (x1;y1) является решением системы уравнений a1x+b1y+c1=0a2x+b2y+c2=0
Введение новых переменных u=x-1v=y-2 в исходное уравнение y’=5x-y-33x+2y-7 позволяет нам получить уравнение вида dvdu=5u-v3u+2v.
Теперь выполним деление числителя и знаменателя правой части уравнения на u. Также примем, что z=uv. Получаем дифференциальное уравнение с разделяющимися переменными u·dzdu=5-4z-2z23+2z.
Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».
Линейные неоднородные дифференциальные уравнения первого порядка y’+P(x)·y=Q(x)
Приведем примеры таких уравнений.
Пример 10К числу линейных неоднородных дифференциальных уравнений 1-го порядка относятся:
y’-2xy1+x2=1+x2;y’-xy=-(1+x)e-x
Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y(x) = u(x)v(x). Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».
Дифференциальное уравнение Бернулли y’+P(x)y=Q(x)ya
Приведем примеры подобных уравнений.
Пример 11К числу дифференциальных уравнений Бернулли можно отнести:
y’+xy=(1+x)e-xy23;y’+yx2+1=arctgxx2+1·y2
Для решения уравнений этого вида можно применить метод подстановки z=y1-a, которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1-го порядка. Также применим метод представления функции у в качестве y(x) = u(x)v(x).
Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.
Уравнения в полных дифференциалах P(x,y)dx+Q(x,y)dy=0
Если для любых значений x и y выполняется ∂P(x,y)∂y=∂Q(x,y)∂x, то этого условия необходимо и достаточно, чтобы выражение P(x, y)dx+Q(x, y)dy представляло собой полный дифференциал некоторой функции U(x, y)=0, то есть, dU(x, y)=P(x, y)dx+Q(x, y)dy. Таким образом, задача сводится к восстановлению функции U(x, y)=0 по ее полному дифференциалу.
Пример 12Выражение, расположенное в левой части записи уравнения (x2-y2)dx-2xydy=0 представляет собой полный дифференциал функции x33-xy2+C=0
Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».
Дифференциальные уравнения второго порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y»+py’+qy=0, p,q∈R
Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто.
Нам необходимо найти корни характеристического уравнения k2+pk+q=0. Здесь возможны три варианта в зависимости от различных p и q:
- действительные и различающиеся корни характеристического уравнения k1≠k2, k1, k2∈R;
- действительные и совпадающие k1=k2=k, k∈R;
- комплексно сопряженные k1=α+i·β, k2=α-i·β.
Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:
- y=C1ek1x+C2ek2x;
- y=C1ekx+C2xekx;
- y=ea·x·(C1cos βx+C2sin βx).
Предположим, что у нас есть линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами y»+3y’=0. Найдем корни характеристического уравнения k2+3k=0. Это действительные и различные k1 =-3 и k2=0. Это значит, что общее решение исходного уравнения будет иметь вид:
y=C1ek1x+C2ek2x⇔y=C1e-3x+C2e0x⇔y=C1e-3x+C2
Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами».
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y»+py’+qy=f(x), p,q∈R
Основным способом решение уравнений данного вида является нахождение суммы общего решения y0, которое соответствует линейному однородному дифференциальному уравнению y»+py’+qy=0, и частного решения y~ исходного уравнения. Получаем: y=y0+y~.
Способ нахождения y0 мы рассмотрели в предыдущем пункте. Найти частное решение y~ мы можем методом неопределенных коэффициентов при определенном виде функции f(x), которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.
Пример 14К числу линейных неоднородных дифференциальных уравнений 2-го порядка с постоянными коэффициентами относятся:
y»-2y’=(x2+1)ex;y»+36y=24sin(6x)-12cos(6x)+36e6x
Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2-го порядка с постоянными коэффициентами».
Линейные однородные дифференциальные уравнения (ЛОДУ) y»+p(x)·y’+q(x)·y=0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y»+p(x)·y’+q(x)·y=f(x)
Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.
На некотором отрезке [a; b] общее решение линейного однородного дифференциального уравнения y»+p(x)·y’+q(x)·y=0 представлено линейной комбинацией двух линейно независимых частных решений y1 и y2 этого уравнения, то есть, y=C1y1+C2y2.
Частные решения мы можем выбрать из систем независимых функций:
1) 1, x, x2, …, xn2) ek1x, ek2x, …, eknx3) ek1x, x·ek1x, …, xn1·ek1x,ek2x, x·ek2x, …, xn2·ek2x,…ekpx, x·ekpx, …, xnp·ekpx4) 1, chx, shx
Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.
Пример 15Возьмем для примера линейное однородное дифференциальное уравнение xy»-xy’+y=0.
Общее решение линейного неоднородного дифференциального уравнения y»+p(x)·y’+q(x)·y=f(x) мы можем найти в виде суммы y=y0+y~, где y0 — общее решение соответствующего ЛОДУ, а y~ частное решение исходного дифференциального уравнения. Найти y0 можно описанным выше способом. Определить y~ нам поможет метод вариации произвольных постоянных.
Возьмем для примера линейное неоднородное дифференциальное уравнение xy»-xy’+y=x2+1.
Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».
Дифференциальные уравнения высших порядков
Дифференциальные уравнения, допускающие понижение порядка
Мы можем провести замену y(k)=p(x) для того, чтобы понизить порядок исходного дифференциального уравнения F(x, y(k), y(k+1), …, y(n))=0, которое не содержит искомой функции и ее производных до k-1 порядка.
В этом случае y(k+1)=p'(x), y(k+2)=p»(x), …, y(n)=p(n-k)(x), и исходное дифференциальное уравнение сведется к F1(x, p, p’, …, p(n-k))=0. После нахождения его решения p(x) останется вернуться к замене y(k)=p(x) и определить неизвестную функцию y.
Пример 17Дифференциальное уравнение y»’xln(x)=y» после замены y»=p(x) станет уравнением с разделяющимися переменными y»=p(x), и его порядок с третьего понизится до первого.
В уравнении, которое не содержит аргумента х и имеет вид F(y, y’, y», .
.., y(n))=0, порядок может быть заменен на единицу следующим образом: необходимо провести замену dydx=p(y), где p(y(x)) будет сложной функцией. Применив правило дифференцирования, получаем:
d2ydx2=dpdydydx=dpdyp(y)d3ydx3=ddpdyp(y)dx=d2pdy2dydxp(y)+dpdydpdydydx==d2pdy2p2(y)+dpdy2p(y)
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.
Рассмотрим решение уравнения 4y3y»=y4-1. Путем замены dydx=p(y) приведем исходное выражение к уравнению с разделяющимися переменными 4y3pdpdy=y4-1.
Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0 и y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x)
Решение уравнений данного вида предполагает выполнение следующих простых шагов:
- находим корни характеристического уравнения kn+fn-1·kn-1+. ..+f1·k+f0=0;
- записываем общее решение ЛОДУ y0 в стандартной форме, а общее решение ЛНДУ представляем суммой y=y0+y~, где y~ — частное решение неоднородного дифференциального уравнения.
..+f1·k+f0=0;Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y~ целесообразно использовать метод вариации произвольных постоянных.
Пример 19Линейному неоднородному ДУ с постоянными коэффициентами y(4)+y(3)-5y»+y’-6y=xcosx+sinx соответствует линейное однородное ДУ y(4)+y(3)-5y»+y’-6y=0.
Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков y(n)+fn-1(x)·y(n-1)+…+f1(x)·y’+f0(x)·y=0 и y(n)+fn-1(x)·y(n-1)+…+f1(x)·y’+f0(x)·y=f(x)
Найти решение ЛНДУ высших порядков можно благодаря сумме y=y0+y~, где y0 — общее решение соответствующего ЛОДУ, а y~ — частное решение неоднородного дифференциального уравнения.
y0 представляет собой линейную комбинацию линейно независимых функций y1, y2, …, yn, каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y(n)+fn-1(x)·y(n-1)+…+f1(x)·y’+f0(x)·y=0 в тождество. Частные решения y1, y2, …, yn обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y=y0+y~=∑Cj·yj+y~j=1n
Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».
Системы дифференциальных уравнений вида dxdt=a1x+b1y+c1dydt=a2x+b2y+c2
Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.
ОДУ: Классификация дифференциальных уравнений
Существует множество типов дифференциальных уравнений, и мы классифицируем их по разным категориям в зависимости от их свойств.
2} + c \frac{dx}{dt} + kx = f(t) . & &
\text{(Механические колебания)}
\end{выровнено}
\end{уравнение*} 92} . & &
\text{(Волновое уравнение в 2-х измерениях)}
\end{выровнено}
\end{уравнение*}
Если несколько уравнений работают вместе, мы имеем так называемую систему дифференциальных уравнений . Например,
\begin{уравнение*} у’ = х, \qquad х’ = у \end{уравнение*}
— это простая система обыкновенных дифференциальных уравнений. Уравнения Максвелла для электромагнетизма,
\begin{уравнение*} \begin{выровнено} & \nabla \cdot \vec{D} = \rho, & & \nabla \cdot \vec{B} = 0 , \\ & \nabla \times \vec{E} = — \frac{\partial \vec{B}}{\partial t}, & & \nabla \times \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t} , \end{выровнено} \end{уравнение*}
представляют собой систему дифференциальных уравнений в частных производных. Оператор дивергенции \(\nabla \cdot\) и оператор ротора \(\nabla \times\) могут быть записаны в частных производных функций, участвующих в \(x\text{,}\) \(y\ text{,}\) и \(z\) переменные.
Следующим битом информации является порядок уравнения (или системы). Порядок — это просто порядок наибольшей производной, которая появляется. Если самая высокая производная, которая появляется, является первой производной, уравнение имеет первый порядок. Если наибольшая производная, которая появляется, является второй производной, то уравнение имеет второй порядок. Например, приведенный выше закон охлаждения Ньютона является уравнением первого порядка, а уравнение механических колебаний — уравнением второго порядка. Уравнение поперечных колебаний балки 92} = 0, \end{уравнение*}
— дифференциальное уравнение в частных производных четвертого порядка. Это четвертый порядок, так как по крайней мере одна производная является четвертой производной. Неважно, что производная по \(t\) имеет только второй порядок.
В первой главе мы приступим к рассмотрению обыкновенных дифференциальных уравнений первого порядка, то есть уравнений вида \(\frac{dy}{dx} = f(x,y)\text{.
}\) В общем, С уравнениями более низкого порядка легче работать, и они имеют более простое поведение, поэтому мы начинаем с них.
Мы также различаем, как зависимые переменные появляются в уравнении (или системе). В частности, мы говорим, что уравнение является линейным , если зависимая переменная (или переменные) и их производные появляются линейно, то есть только как первые степени, они не перемножаются между собой и никакие другие функции зависимых переменных не появляются. Другими словами, уравнение представляет собой сумму членов, где каждый член представляет собой некоторую функцию независимых переменных или некоторую функцию независимых переменных, умноженную на зависимую переменную или ее производную. В противном случае уравнение называется 92 года «=» \frac{1}{x}\label{classification_eqlinex}\tag{4} \end{уравнение}
по-прежнему является линейным уравнением, поскольку \(y\) и его производные появляются только линейно.
Все приведенные выше уравнения и системы являются линейными.
2} ,
\end{уравнение*} 92\метка{classification_eqnonlinode}\тег{5}
\end{уравнение}
является нелинейным дифференциальным уравнением первого порядка, поскольку существует вторая степень зависимой переменной \(x\text{.}\)
Линейное уравнение может далее называться однородным , если все члены зависят от зависимой переменной. То есть, если ни один член не является функцией только независимых переменных. В противном случае уравнение называется неоднородным или неоднородным . Например, уравнение экспоненциального роста, волновое уравнение или уравнение переноса выше являются однородными. Приведенное выше уравнение механических колебаний неоднородно, пока \(f(t)\) не является нулевой функцией. Точно так же, если температура окружающей среды \(A\) отлична от нуля, закон охлаждения Ньютона неоднороден. Однородное линейное ОДУ можно представить в виде 9{n-1}} + \cdots + a_{1}(x) \frac{dy}{dx} + а_{0}(х) у = 0 . \end{уравнение*}
Сравните с (3) и обратите внимание на отсутствие функции \(b(x)\text{.
}\)
Если коэффициенты линейного уравнения на самом деле являются постоянными функциями, то говорят, что уравнение имеет постоянных коэффициентов . Коэффициенты — это функции, умножающие зависимую переменную (переменные) или одну из ее производных, а не функцию \ (b (x) \), стоящую отдельно. Неоднородное ОДУ с постоянным коэффициентом представляет собой уравнение вида 9{n-1}} + \cdots + a_{1} \frac{dy}{dx} + а_{0} у = б(х), \end{уравнение*}
, где \(a_0, a_1, \ldots, a_n\) все константы, но \(b\) может зависеть от независимой переменной \(x\text{.}\) Приведенное выше уравнение механических колебаний представляет собой неоднородный постоянный коэффициент ОДУ второго порядка. Та же номенклатура применяется к УЧП, поэтому уравнение переноса, уравнение теплопроводности и волновое уравнение являются примерами линейных УЧП с постоянным коэффициентом.
Наконец, уравнение (или система) называется автономное , если уравнение не зависит от независимой переменной.
Для автономных обыкновенных дифференциальных уравнений независимая переменная рассматривается как время. Автономное уравнение означает уравнение, которое не меняется со временем. Например, закон охлаждения Ньютона автономен, как и уравнение (5). С другой стороны, механические колебания или (4) не автономны.
Подраздел 0.3.1 Упражнения
Упражнение 0.3.1.
Классифицируйте следующие уравнения. Являются ли они ODE или PDE? Это уравнение или система? Каков порядок? Является ли он линейным или нелинейным, и если он линейный, то является ли он однородным, с постоянным коэффициентом? Если это ОДУ, то является ли оно автономным? 94} = 0\)
Ответ.
а) ОДУ, уравнение второго порядка, линейное, неоднородное, с непостоянным коэффициентом, неавтономное.
b) УЧП, уравнение первого порядка, линейное, неоднородное, с постоянным коэффициентом.
в) ОДУ, система, второго порядка, линейная, однородная, с постоянным коэффициентом, автономная.
Примечание: независимая переменная здесь отсутствует.
d) УЧП, уравнение второго порядка, нелинейное.
д) ОДУ, уравнение второго порядка, нелинейное, неавтономное.
f) ОДУ, уравнение, четвертого порядка, линейное, однородное, с постоянным коэффициентом, автономное.
Упражнение 0.3.2.
Если \(\vec{u} = (u_1,u_2,u_3)\) — вектор, то мы имеем дивергенцию \(\nabla \cdot \vec{u} = \frac{\partial u_1}{\partial x} + \ гидроразрыва {\ парциальное и_2} {\ парциальное у} + \frac{\partial u_3}{\partial z}\) и curl \(\nabla \times \vec{u} = \Большой( \frac{\partial u_3}{\partial y} — \frac{\partial u_2}{\partial z} , ~ \frac{\partial u_1}{\partial z} — \frac{\partial u_3}{\partial x} , ~ \frac{\partial u_2}{\partial x} — \frac{\partial u_1}{\partial y} \Bigr)\text{.}\) Обратите внимание, что ротор вектора по-прежнему является вектором. Запишите уравнения Максвелла в терминах частных производных и классифицируйте систему.
Ответ.
\begin{уравнение*} \begin{выровнено} \frac{\partial D_1}{\partial x}+\frac{\partial D_2}{\partial y}+\frac{\partial D_3}{\partial z}=\rho, &\quad \frac{\partial B_1}{\partial x}+\frac{\partial B_2}{\partial y}+\frac{\partial B_3}{\partial z}=0 \\ \frac{\partial E_3}{\partial y}-\frac{\partial E_2}{\partial z}=-\frac{\partial B_1}{\partial t}, &\quad \frac{\partial H_3}{\partial y}-\frac{\partial H_2}{\partial z}=\frac{\partial D_1}{\partial t}+J_1 \\ \frac{\partial E_1}{\partial z}-\frac{\partial E_3}{\partial x}=-\frac{\partial B_2}{\partial t}, &\quad \frac{\partial H_1}{\partial z}-\frac{\partial H_3}{\partial x}=\frac{\partial D_2}{\partial t}+J_2 \\ \frac{\partial E_2}{\partial x}-\frac{\partial E_1}{\partial y}=-\frac{\partial B_3}{\partial t}, &\quad \frac{\partial H_2}{\partial x}-\frac{\partial H_1}{\partial y}=\frac{\partial D_3}{\partial t}+J_3 \end{выровнено} \end{уравнение*}
УЧП, система, первого порядка, линейная, неоднородная, с постоянным коэффициентом, автономная.
Упражнение 0.3.3.
Предположим, что \(F\) является линейной функцией, то есть \(F(x,y) = ax+by\) для констант \(a\) и \(b\text{.}\). Что такое классификация уравнений вида \(F(y’,y) = 0\text{.}\)
Ответ.
ОДУ, линейное, однородное, с постоянным коэффициентом, автономное.
Упражнение 0.3.4.
Запишите явный пример линейной неавтономной неоднородной системы третьего порядка с непостоянными коэффициентами из двух ОДУ, в которой каждая производная, которая могла бы появиться, появляется. 92\)
Ответ.
а) УЧП, уравнение второго порядка, линейное, неоднородное, с постоянным коэффициентом.
б) ОДУ, уравнение первого порядка, линейное, неоднородное, с непостоянным коэффициентом, не автономное.
в) ОДУ, уравнение, седьмого порядка, линейное, однородное, с постоянным коэффициентом, автономное.
г) ОДУ, уравнение второго порядка, линейное, неоднородное, с постоянным коэффициентом, автономное.
д) ОДУ, системное, второго порядка, нелинейное.
f) УЧП, уравнение второго порядка, нелинейное. 9{k+2}\) линейный. Подсказка: есть два ответа.
Ответ.
\(k=0\) или \(k=1\)
Методы решения дифференциальных уравнений — определение, решения
- Автор P_C
- Последнее изменение 25-01-2023
Методы решения дифференциального уравнения: Дифференциальное уравнение – это уравнение, содержащее одну или несколько функций со своими производными. В основном оно используется в физике, технике, биологии и т. д. Основная цель дифференциального уравнения — изучение решений, удовлетворяющих уравнениям. Решением дифференциального уравнения является связь между включенными переменными, которая удовлетворяет данному дифференциальному уравнению.
Существует два типа решений дифференциальных уравнений, а именно общее решение и частное решение. Общие и частные решения дифференциальных уравнений используют некоторые шаги интегрирования для решения уравнений.
В этой статье давайте узнаем больше о методах решения дифференциального уравнения, таких как метод разделения переменных, однородное дифференциальное уравнение и линейное дифференциальное уравнение с помощью формулы неопределенного интегрирования.
Решение дифференциального уравнения представляет собой выражение зависимой переменной через независимую переменную, которая удовлетворяет заданному дифференциальному уравнению, поэтому решение можно разделить на два типа;
- Общее решение
- Частное решение
Решение, состоящее из такого же количества произвольных констант, называется общим решением.
Частное решение Решение получается путем присвоения частных значений произвольным константам в общем решении дифференциального уравнения, и тогда полученное решение является частным решением. Результат исключения одной произвольной константы приводит к дифференциальному уравнению первого порядка, а исключение двух произвольных констант приводит к дифференциальному уравнению второго порядка.
Существует несколько методов решения дифференциального уравнения первой степени;
- Решение методом контроля
- Метод разделимых переменных
- Однородные уравнения
- Линейные уравнения первого порядка
Если дифференциальное уравнение имеет вид \(f\left( {{f_1}\left( {x,y} \right)} \right)d\left( {{f_1}\left( {x,y} \ right)} \right) + \varphi \left( {{f_2}\left( {x,y} \right)} \right)d\left( {{f_2}\left( {x,y} \right) } \right) + \cdots \ldots = 0,\) то каждое слагаемое можно интегрировать отдельно. Итак, решение дифференциального уравнения можно получить, используя метод контроля. Есть несколько результатов, которые помогут нам найти решение дифференциального уравнения 9.2}}}\)
Метод разделения переменных Дифференциальное уравнение первой степени первого порядка имеет вид
\(\frac{{dy}}{{dx}} = f\ left( {x,y} \right)….
\left( i \right)\)
Если \(f\left( {x,y} \right)\) выражается как произведение \(f\left ( x \right)g\left( y \right),\) где \(f\left( x \right)\) является функцией \(x\) и \(g\left( y \right)\ ) является функцией \(y;\), то дифференциальное уравнение называется переменно-сепарабельным типом. Тогда мы можем написать \(\left( i \right)\) как
\(\frac{{dy}}{{dx}} = f\left( x \right)g\left( y \right)\)
Мы можем выполнить три простых шага, чтобы найти решение, используя метод разделения переменных .
Шаг 1: Переместите все члены \(y\), включая \(dy\), в одну часть уравнения, а все члены \(x\), включая \(dx\), в другую часть уравнения.
Шаг 2: Проинтегрируйте одну часть по \(y\) и другую часть по \(x,\) и добавьте постоянную интегрирования.
Шаг 3: Упростите окончательный результат до простейшей формы. 9n}f\left( {x,y} \right),\) при ненулевой константе \(t.\) Итак, общий вид однородного дифференциального уравнения имеет вид \(f\left( {x ,y} \right)dy + g\left( {x,y} \right)dx = 0.
2}}}\)
Этапы решения однородных дифференциальных уравнений
Чтобы решить однородное дифференциальное уравнение, мы выполняем следующие шаги.
Случай 1:
Если дифференциальное уравнение вида \(\frac{{dy}}{{dx}} = F\left( {x,y} \right) = g\left( {\frac{ y}{x}} \right).\)
Шаг 1: Подставим \(y = vx\) в данное дифференциальное уравнение.
Шаг 2: Дифференцируем по \(x,\), тогда \(\frac{{dy}}{{dx}} = v + x\frac{{dv}}{{dx}}.\) Теперь подставим значения \(y\) и \(\frac{{dy}}{{dx}}\) в данное дифференциальное уравнение, тогда получим \(v + x\frac{{dv}}{{ dx}} = g\влево( v \вправо)\)
\( \Rightarrow x\frac{{dv}}{{dx}} = g\left( v \right) – v\)
Шаг 3: Разделение переменных, затем \(\frac{{dv} }{{g\left( v \right) – v}} = \frac{{dx}}{x}.\)
Шаг 4: Примените интегрирование с обеих сторон, затем \(\int {\frac{ {dv}}{{g\left( v \right) – v}}} dv = \int {\frac{{dx}}{x}} + C.
\)
Шаг 5: После интегрирования подставить значение \(v\) из шага \(1.\)
Случай 2:
Если дифференциальное уравнение вида \(\frac{{dx}}{{dy}} = F\left( {x,y} \right) = g\left( {\frac{x}{y}} \right).\) Однородные дифференциальные уравнения такого типа можно решить, положив \(x = vy,\) после этого , выполните те же пять шагов, что и для случая \(1.\)
Линейное дифференциальное уравнение включает в себя переменную, производную от этой переменной и несколько других функций. Стандартное уравнение линейного дифференциального уравнения имеет вид \(\frac{{dy}}{{dx}} + Py = Q,\), где \(P\) и \(Q\) — функции \(x.\ ) Точно так же \(\frac{{dx}}{{dy}} + {P_1}x = {Q_1}\) также является стандартным уравнением линейного дифференциального уравнения. Здесь \({P_1}\) и \({Q_1}\) являются функциями \(y\)
Общее решение линейного дифференциального уравнения 9{\int {P\,dy} }}.
{\int {\sec xdx}} }\) 9{\ пер \ влево | {\sec x + \tan x} \right|}}\) \(\следовательно, I.F = \left| {\sec x + \tan x} \right|\)
Q.3. Покажите, что следующее дифференциальное уравнение \(\left( {x + y} \right)\frac{{dy}}{{dx}} = \left( {x + 2y} \right)\) является однородным дифференциальное уравнение.
Ответ: Дано: \(\left( {x + y} \right)\frac {{dy}}{{dx}} = \left( {x + 2y} \right)\)
Чтобы доказать, что приведенное выше дифференциальное уравнение является однородным дифференциальным уравнением, подставьте \(x = tx,\) и \(y = tx\) 92}}}{2} = \ln \left( {kx} \right)\)
\( \Rightarrow v = \pm \sqrt {\left( {2\ln \left( {kx} \right)} \right)} \)
\( \Rightarrow \ frac{y}{x} = \pm \sqrt {\left( {2\ln \left( {kx} \right)} \right)} \) [восстановить \(v = \frac{y}{x}\)]
\(\следовательно y = \pm x\sqrt {\left({2\ln \left({kx} \right)} \right)} , \), что является требуемым общим решением.
Решением дифференциального уравнения является отношение между включенными переменными, которое удовлетворяет данному дифференциальному уравнению. Существует два типа решений дифференциальных уравнений, таких как общее решение и частное решение. Эти решения дифференциальных уравнений используют некоторые шаги интегрирования для решения уравнений. Позже объясняются типы дифференциальных уравнений, за которыми следуют методы дифференциального уравнения, такие как метод разделимых переменных, однородный метод и линейное дифференциальное уравнение, а также некоторые решенные примеры.
Часто задаваемые вопросы (FAQ) Q.1. Какой метод используется для решения дифференциальных уравнений?
Ответ: Для решения данных дифференциальных уравнений можно использовать следующие методы:
1. Метод проверки
2. Сепарабельная переменная
3. Однородное дифференциальное уравнение
4.
n}f\left( {x,y} \right),\) для ненулевой константы, \(\mu .\) Таким образом, общая форма однородного дифференциального уравнения имеет вид \(f\left ( {x,y} \right)dy + g\left( {x,y} \right)dx = 0.\)
Q.4. Что такое метод разделимых переменных дифференциальных уравнений?
Ответ: Если дифференциальное уравнение имеет вид \(f\left( x \right)dx = g\left( y \right)dy,\), где \(f\left( x \right)\) и \(g\left( y \right)\) являются функциями только \(x\) и \(y\). Тогда говорят, что переменные в дифференциальном уравнении сепарабельны. Таким образом, интегрируя обе части уравнения, получаем его общее решение.
Q.5. Что такое обыкновенное дифференциальное уравнение? Дайте пример.
Ответ: Обыкновенное дифференциальное уравнение — это уравнение, которое содержит только одну независимую переменную и одну или несколько ее производных по переменной. Следовательно, обыкновенное дифференциальное уравнение представляется как отношение, имеющее одну независимую переменную \(x,\) вещественную зависимую переменную \(y,\) с некоторыми своими производными \(y’,y”…\) по \ (x.