Виды дробей все: Виды дробей

Виды дробей

Навигация по странице:

В математике часто применяются следующие виды дробей:
• Обыкновенная дробь
  • Правильная дробь
  • Неправильная дробь
• Смешанная дробь (смешаное число)
• Десятичная дробь

Обыкновенная дробь

Определение.

Обыкновенная дробь или простая дробь — запись рационального числа в виде отношения двух чисел

mn

. Делимое m называется числителем дроби, а делитель n — знаменателем дроби.

Правильная дробь

Определение.

Правильной дробью называется дробь, у которой числитель меньше знаменателя.

7	,	5	— правильные дроби.
9		6

Неправильная дробь

Определение.

Неправильной дробью называется дробь, у которой числитель больше или равен знаменателю.

9	,	3	— неправильные дроби.
7		3

Смешанная дробь (смешаное число)

Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.

Определение.

Смешанной дробью называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

3	2	= 3 +	2	=	21	+	2	=	23
	7		7		7		7		7

Десятичная дробь

Определение.

Десятичная дробь дробь со знаменателем 10ⁿ, где n — натуральное число.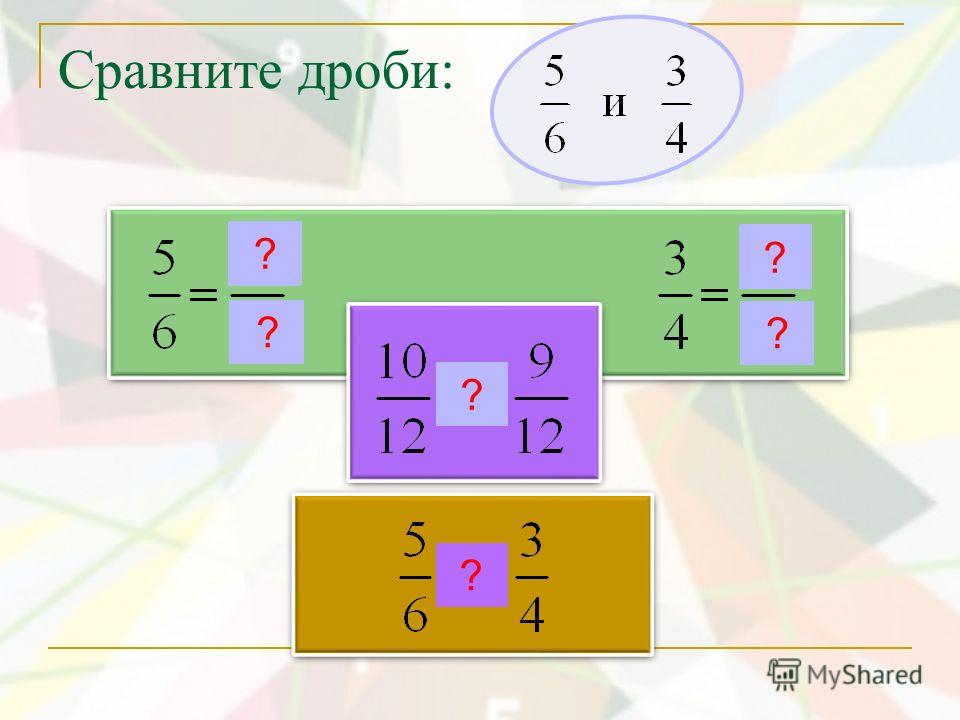

Десятичная дробь имеет следующую форму записи: сначала целая часть, затем разделитель целой и дробной части точка или запятая и затем дробная часть, количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.

3.2609	= 3 +	2	+	6	+	0	+	9	= 3 +	2609
		10		100		1000		10000		10000

Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь

Онлайн калькуляторы дробей

Онлайн упражнения с дробями

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

это что такое? Виды дробей :: SYL.

ru

Изучая царицу всех наук – математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия.

Ее величество дробь: это что такое

Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются​ в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.

Верхнее, или первое из этих чисел – это числитель (показывает, сколько взято долей от числа), а нижнее, или второе – знаменатель (демонстрирует, на столько частей разделена единица).

Дробная черта фактически выполняет функции знака деления. К примеру, 7:9=7/9

Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее.

Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков.

Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.

Виды дробей: обыкновенные и десятичные

Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.

Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.

Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями – отсюда произошло и ее название.

Число, предшествующее запятой, – это целая часть, а все находящееся после — дробная. Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.

Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак «-«, данная дробь отрицательная, если «+» — то положительная.

Подвиды обыкновенных дробей

Есть такие виды дробей простых.

• Правильные. У них значение числителя всегда меньше, чем у знаменателя. Например: 7/8. Это правильная дробь, поскольку числитель 7 меньше, чем знаменатель 8.
• Неправильные. В таких дробях либо числитель и знаменатель равны между собою (8/8), либо значение нижнего числа меньше, нежели верхнего (9/8).
• Смешанная. Так называется правильная дробь, записанная вместе с целым числом: 8 ½. Она понимается как сумма этого числа и дроби. Кстати, довольно просто можно сделать так, чтобы на ее месте появилась неправильная дробь. Для этого 8 нужно записать как 16/2+1/2=17/2.
• Составные. Как понятно из названия, они состоят из нескольких дробных черт: ½ / ¾.
• Сократимые/несократимые. К ним может относиться как правильная, так и неправильная дробь. Все зависит от того, можно ли разделить числитель и знаменатель на одно и то же число. К примеру, 6/9 является сократимой дробью, ведь оба ее составляющих можно поделить на 3 и получится 2/3. А вот 7/9 относится к несократимым, поскольку 7 и 9 – простые числа, которые не имеют общего делителя и не могут быть сокращены.

Подвиды десятичной дроби

В отличие от простой, десятичная дробь делится всего на 2 вида.

• Конечная — получила такое название из-за того, что после запятой у нее ограниченное (конечное) число цифр: 19,25.
• Бесконечная дробь – это число с нескончаемым количеством цифр после запятой. К примеру, при делении 10 на 3 результатом будет бесконечная дробь 3,333…

Сложение дробей

Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда.

Итак, чтобы сложить между собою дроби, прежде всего, нужно сделать так, чтобы у обоих слагаемых были одинаковые знаменатели. Для этого предстоит найти наименьшее число, которое способно поделиться без остатка на знаменатели слагаемых чисел.

Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число.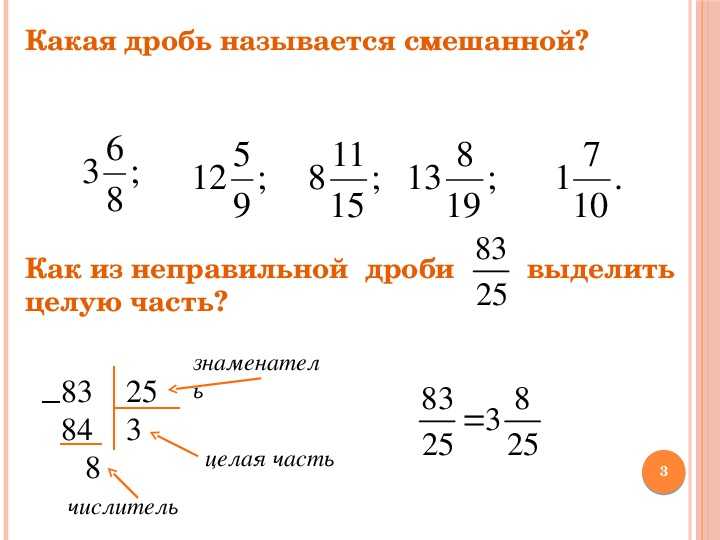 Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 – 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь – это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.

В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными.

Если в примере присутствует десятичная дробь и обычная, необходимо, чтобы обе стали простыми, потом привести их к одному знаменателю и сложить. К примеру 3,1+1/2. Число 3,1 можно записать как смешанную дробь 3 и 1/10 или как неправильную — 31/10. Общим знаменателем для слагаемых будет 10, поэтому нужно умножить поочередно числитель и знаменатель 1/2 на 5, получается 5/10. Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат — неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной — 3,5.

Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.

Вычитание дробей

Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь.

Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат – 3/10.

Умножение дробей

Деление и умножение дробей – значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель.

Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь – это сократимая величина.

Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере – 5/18.

Как делить дроби

Деление дробей — тоже несложное действие, фактически оно все равно сводится к их умножению. Чтобы разделить одну дробь на другую, нужно вторую перевернуть и умножить на первую.

Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 – получается 7/19.

В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.

Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½ : 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную – 2 целых и 5/6.

Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.

Типы дробей — Правильная дробь, Неправильная дробь, Смешанная дробь

Определение дробей

Дроби выражаются в математике как числовое значение, определяющее часть целого или группы объектов. Дробь — это компонент или сектор заданного количества, взятый из целого, который может быть числом, заданным значением или элементом.

Дробь представляет собой часть целого или группы объектов. В дроби числитель (верхнее число) и знаменатель (нижнее число) разделены горизонтальной чертой, известной как дробная черта. Знаменатель представляет собой количество равных частей, на которые делится целое, или общее количество объектов в группе. В числителе берется количество частей целого или количество предметов из группы.

Давайте лучше разберем дроби на примере. Плитка шоколада разделена на четыре равные части. Каждая часть целого столбца представляет собой $\frac{1}{4}$ , что означает 1 из 4 равных частей. Дробь ¼ читается как «1 на 4».

Родственные игры

Типы дробей

Дроби различаются по числителям и знаменателям. Дроби подразделяются на следующие типы:

1. Единицы Дроби : Дроби с числителем 1 называются единичными дробями.

2. Правильные дроби : Дроби, у которых числитель меньше знаменателя, называются правильными дробями. Правильная дробь меньше 1 

3. Неправильные дроби : Дроби, в которых числитель больше или равен знаменателю, называются неправильными дробями. Неправильная дробь больше 1.

4. Смешанные фракции : Смешанные дроби состоят из целого числа и правильной дроби. Поскольку смешанные дроби представляют собой комбинации целых чисел и дроби, смешанные дроби всегда больше 1.

5. Подобные дроби:

Дроби с одинаковыми знаменателями называются однородными.

6. В отличие от дробей : 

Дроби с разными знаменателями называются неодинаковыми.

7. Эквивалентные дроби : Дроби, представляющие одно и то же значение после упрощения, называются эквивалентными дробями. Чтобы получить эквивалентные дроби, мы можем умножить или разделить и числитель, и знаменатель данной дроби на одно и то же число.

Связанные рабочие листы

Решенные примеры  

1. Джон тренирует команду бейсбольной лиги. В команде 10 игроков. Четверо из них бьют левшами. Какая часть игроков правши?

Решение:

Количество игроков-правшей = 10 − 4 = 6

6 из 10 игроков правши, поэтому шесть десятых или $\frac{6}{10}$ игроков правы -ручной.

2. Укажите истинное или ложное значение.

$\frac{4}{9}$ — неправильная дробь

Решение:

Неверно. Дробь $\frac{4}{9}$ имеет числитель 4 и знаменатель 9. Так как числитель меньше знаменателя, $\frac{4}{9}$ равен

правильная дробь . Дробь, числитель которой больше или равен знаменателю, является неправильной дробью.

3. Найдите значение для x .

$\frac{7}{9}$ = $\frac{x}{36}$

Решение:

$\frac{7}{9}$ и  $\frac{x}{36 }$ — эквивалентные дроби.

Итак, $\frac{x}{36}$ = $\frac{7}{9}$ = $\frac{7 ✕ 4}{9 ✕ 4}$ = $\frac{28}{36} $

Следовательно, x должно быть 28.

4. Какова простейшая форма $\frac{30}{45}$?

Решение:

Наибольший общий делитель 30 и 45 равен 15. Разделив числитель и знаменатель на 15, мы получим

$\frac{30}{45}$ = $\frac{30 \div 15 }{45 \div15}$ = $\frac{2}{3}$

Поскольку числа 2 и 3 не имеют общего множителя, $\frac{2}{3}$ имеет простейшую форму.

Практические задачи

1

Какая из следующих дробей эквивалентна $\frac{2}{5}$?

$\frac{2}{10}$

$\frac{6}{10}$

$\frac{4}{10}$

$\frac{5}{10}$

Правильный ответ: $\frac{4}{10}$
$\frac{2}{5} = \frac{2 \times2}{5 \times2} = \frac{4}{10}$

2

Какой из следующих имеет 11 в числителе?

$\frac{11}{17}$

11$\frac{1}{7}$

$\frac{14}{11}$

$\frac{1}{11}$

Правильный ответ: $\frac{11}{17}$
$\frac{11}{17}$ имеет числитель 11 и знаменатель 17

3

Заполните пропуск.

$\frac{1}{4}$, $\frac{2}{8}$, $\frac{3}{12}$, $\frac{4}{16}$ составляют _______

доли единицы

подобная дробь

неправильная дробь

эквивалентная дробь

Правильный ответ: эквивалентная дробь
$\frac{1}{4}$ = $\frac{2}{8}$ = $\frac{3}{ 12}$ = $\frac{4}{16}$

4

Что из перечисленного ниже является долей единиц?

1$\frac{2}{5}$

$\frac{9}{1}$

$\frac{1}{8}$

$\frac{4}{2}$

Правильный ответ: $\frac{1}{8}$
Числитель дроби равен 1.

Часто задаваемые вопросы

Где дроби используются в реальной жизни?

В следующих рецептах, баллы за тест или экзамен, фракции жидкости в безалкогольных коктейлях.

Какие дроби имеют разные знаменатели?

Дроби с разными знаменателями называются неодинаковыми. Например, 7/9, 2/5, 3/6 — разные дроби и у них разные знаменатели.

У дробей число в числителе больше, чем в знаменателе?

Да, есть. Дробь, у которой числитель больше или равен знаменателю, называется неправильной дробью.

Почему предпочтительно упрощать дроби до наименьшей возможной формы?

Упрощенная, наименьшая или сокращенная форма дроби упрощает расчет.

Заключение

Можно узнать намного больше о фракциях, исследуя новые миры и подружившись с волшебными существами. Посетите SplashLearn, чтобы сделать учебу для ваших детей или студентов веселой и простой!

Типы дробей: определение и примеры

• Автор Притам G
• Последнее изменение 24-01-2023

Типы дробей: Фрагмент большей величины, где большей величиной может быть любое число, конкретное значение или элемент. Правильные/неправильные дроби, смешанные дроби, эквивалентные дроби и похожие/непохожие дроби — это шесть типов дробей в математике. Числитель и знаменатель — это две части дроби.
Каждое количество, с которым мы сталкиваемся ежедневно, не может быть точным целым числом. В результате нам придется иметь дело с дробями, частями целого и частями целого. Фракции — это термины, используемые для описания частей целого объекта. Когда пиццу делят на четыре части, каждая часть составляет 1/4 части. Прочтите всю статью, чтобы лучше понять типы дробей, включая примеры правильных дробей, примеры эквивалентных дробей и примеры подобных дробей.

Термин «доля» представляет числовую часть целого объекта. Мы можем понять дроби на примере. Предположим, у нас есть большой торт, и мы разрезаем его на 8 равных частей. Тогда каждая порция ломтика составляет только 1/8 часть от общего количества торта. Здесь 1/8 — это дробь.

Верхняя часть дроби называется числителем, а нижняя — знаменателем. В этом примере 1 — числитель, а 8 — знаменатель. В повседневной жизни мы не всегда имеем дело с целыми объектами. Иногда нам приходится иметь дело с частями или частями целых объектов. Для их количественной оценки нам нужны дроби.

Части дроби

Посмотрите на изображение ниже:

1. 1. Числитель: Верхняя половина дроби, представляющая количество имеющихся у вас частей.
      В приведенном выше примере 5 является числителем.

 

1. 1. Знаменатель: Нижняя половина дроби, представляющая число, на которое делится весь объект. В приведенном выше примере 8 является знаменателем.

 

Как показано на изображении выше, вся дробь читается как «5 на 8». Точно так же ¼ читается как «1 на 4», а ¾ читается как «3 на 4».

Пример дроби

Теперь, когда мы знаем, что такое дробь и какие части дроби, давайте посмотрим, сколько существует типов дробей. По числителям и знаменателям дроби делятся на следующие виды:

1. Правильные дроби

Определение правильной дроби : Когда Числитель<знаменатель , т.е. когда числитель дроби меньше знаменателя, дробь называется правильной дробью. Посмотрите на пример правильной дроби ниже.

2. Неправильные дроби

Определение неправильной дроби: Когда Числитель > Знаменатель , т. е. когда числитель больше знаменателя, дробь называется неправильной дробью.

Обратите внимание, что любое натуральное число можно представить в виде неправильной дроби, так как знаменатель всегда равен 1. Кроме того, все неправильные дроби либо равны, либо больше 1.

3. Смешанные дроби

Смешанные дроби Определение: A дробь, состоящая из натурального числа и дроби, называется смешанной дробью.

Смешанную дробь можно преобразовать в неправильную и наоборот. Смешанная дробь всегда больше 1.

4. Подобные дроби

Подобно дроби Определение : Дроби с одинаковыми знаменателями похожи на дроби. Например, дроби 2/7, 3/7, 5/7 и 6/7 имеют одинаковый знаменатель — 7. Следовательно, они похожи на дроби.

Упрощение подобных дробей легко. Например, если вы хотите сложить указанные выше четыре дроби, все, что вам нужно сделать, это сложить числители. Знаменатель останется прежним. Взгляните на пример подобной дроби ниже.

Итак, (2/7) + (3/7) + (5/7) + (6/7) = (2 + 3 + 5 + 6)/7 = 16/7.

5. В отличие от дробей

В отличие от дробей Определение : Дроби с разными знаменателями не похожи на дроби. Например, дроби 2/3 и 1/4 имеют разные знаменатели. Таким образом, они не похожи на дроби.

Упрощение с использованием разнородных дробей не так просто, как с однотипными дробями.

Сложение непохожих дробей

Например, чтобы сложить две вышеупомянутые непохожие дроби, сначала мы должны преобразовать их в одинаковые дроби. Задействованные шаги:

• Рассчитайте НОК двух знаменателей 3 и 4.
• МОК 3 и 4 = 12. Этот НОК будет знаменателем обеих дробей.
• Вычислите эквивалентное значение первой дроби (2/3). Для этого разделите НОК, рассчитанный на предыдущем шаге (12), на знаменатель первой дроби (3). Итак, 12 ÷ 3 = 4. Теперь умножьте 4 на числитель (2), что даст 8. Таким образом, первая дробь станет 8/12.
• Аналогичным образом рассчитайте эквивалентное значение второй дроби (1/4). Для этого разделите НОК, рассчитанный на первом шаге (12), на знаменатель второй дроби (4). Итак, 12 ÷ 4 = 3. Теперь умножьте 3 на числитель (1), что даст 3. Следовательно, вторая дробь станет 3/12. Теперь обе дроби имеют один и тот же числитель, то есть 12,9.0020
• Теперь сложите две одинаковые дроби, как показано в предыдущем разделе. Итак, (8/12) + (3/12) = (8 + 3)/12 = 11/12. Итак, (2/3) + (1/4) = 11/12.

6. Эквивалентные дроби

Эквивалентные дроби Определение: Дроби, которые дают одно и то же значение, называются эквивалентными дробями при упрощении. Взгляните на пример эквивалентной дроби -1/2 и 50/100 равны 0,5. Следовательно, это равнозначные дроби.

7. Доли единиц

Дробь, числитель которой равен единице, а знаменатель — целое положительное число, называется единичной дробью. Примеры единичных дробей: 1/2. 1.5, 2/8 и т. д.

Часто задаваемые вопросы о типах дробей

Q. 1: Какие существуют типы дробей?

Ответ: В основном существует 3 типа дробей: правильная дробь (например, 2/5), неправильная дробь (например, 7/3) и смешанная дробь (например, 3¾). Кроме этих, существуют и другие виды дробей, такие как однородные дроби, неравные дроби, эквивалентные дроби, единичные дроби и т. д.

Q.2: Что является примером дроби?

Ответ: Примером дроби является 3/8. Мы говорим, что 3 делится поровну на 8 частей. Здесь 3 — числитель, а 8 — знаменатель.

Q.3: В чем разница между одинаковыми и разными дробями?

Ответ: Дроби с одинаковыми знаменателями подобны дробям, тогда как дроби с разными знаменателями не похожи на дроби. Например, 3/8 и 5/8 похожи на дроби, а 1/6 и 2/5 — на разные дроби.

Q.

No related posts.