1.8. Отображения и их виды
Например, это может быть закрепление машин за шоферами и распределение шоферов по машинам в таксопарке. Обратное соответствие обратного со-
ответствия даст прямое соответствие (q-1)-1 = q.
X | x1 |
| x2 x3 | X | x1 x1 | x2 |
|
|
| q | q-1 |
|
|
Y | y1 | y2 | y3 | Y | y1 y2 | y3 |
| а |
|
| Рис. 1.9 | б |
|
|
|
|
|
|
|
Соответствие называется взаимно однозначным, если каждому элементу множества X соответствует (поставлен в пару с ним) единственный элемент множества Y и обратно.
Отображение является частным случаем соответствия. Соответствие, характеризующее правило, по которому каждому элементу множества X сопоставляется один или несколько элементов множестваY, называется отображением и записывается как Г: X ® Y , где множество Г определяет закон отображения. Пусть X = {х1, х2, х3}; Y = {у1, у2, у3, у4, у5, у6}. Каждому элементу xi Îx отображение Г ставит в соответствие некоторое подмножество Г Í Y , называемое образом элемента х: Гx1 = {y1, y2}, Гx1 = {y3}, Г x1 = {y4 , y5 , y6}.
На рис. 1.10 показано геометрическое представление этого отображения.
Определяют три вида отображений: сюръективное, инъективное и биективное.
Отображение называется сюръективным (или отображением «на»), если образы точек множества X заполняют все множество Y, причем различные точки множества X могут иметь один и тот же образ.
x1 | y1 | |
| y2 | |
x |
| y3 |
2 | y4 | |
x3 | ||
| y | y5 |
|
| 6 |
Рис. 1.10
1.10
Отображение называется инъективным (или отображением «в»), если элементы множества X отображаются не на все множествоY, а в его какую-то часть. При этом каждому элементу x Î X соответствует один элемент y ÎY и обратно, прообразом у является один элемент х.
Геометрическое представление сюръективного и инъективного отображений приведено на рис. 1.11, а и б соответственно.
11
а | б |
| Рис. 1.11 |
Биективное отображение является одновременно инъективным и сюръективным, т. е. является взаимно однозначным.
Важным случаем отображения является отображение элементов внутри одного множества. При этом отображение Г: Х→Х будет определяться парой (X, Г), где Г Í Х ´ Х или Г Í Х 2 . С помощью отображений могут быть даны определения таким понятиям, как функция, функционал, оператор, которые широко используются при математическом описании систем. Если отображение Г: X→Y рассматривается как соответствие между множествамиX и Y, то множество f ={(x, y)Î X ´Y : y = f (x)} называется функцией. Таким образом, f является множеством, элементами которого являются пары (х, у), участвующие
Если отображение Г: X→Y рассматривается как соответствие между множествамиX и Y, то множество f ={(x, y)Î X ´Y : y = f (x)} называется функцией. Таким образом, f является множеством, элементами которого являются пары (х, у), участвующие
в соответствии, и f(x) является обозначением для y ÎY , соответствующего данному x Î X [1].
Функционал устанавливает зависимость между множеством чисел, с одной стороны, и некоторым множеством функций с другой. Примером функцио-
b
нала может служить определенный интеграл вида I ( f ) = ò f (x)dx.
a
Оператор устанавливает соответствие между двумя множествами функций. Если обозначить через р оператор дифференцирования, то связь между производной f ¢(x) и функцией f (x) может быть записана в виде операторного соотношения f ¢(x) = p[ f (x)].
1.9. Отношения и их свойства
Для обозначения некоторых видов отображений, заданных на одном и том же множестве, используется понятие «отношение» [1]. Пусть отображение (Х, Г) является отношением.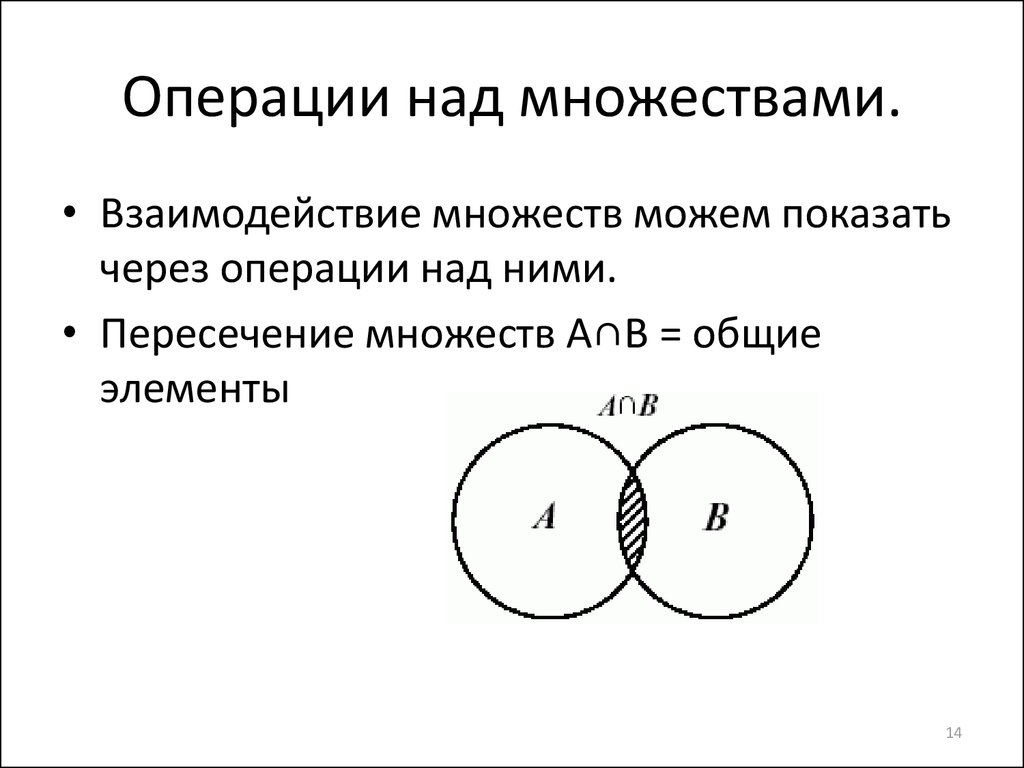 Если элемент x1 находится в отношении R к элементу x2, то это записывается как x1Rx2 или (x1x2 ) Î R , где R – символ отноше-
Если элемент x1 находится в отношении R к элементу x2, то это записывается как x1Rx2 или (x1x2 ) Î R , где R – символ отноше-
ния. Примером отношений могут служить такие понятия, как «меньше, чем», «делится на», «включено в», «больше чем» и т. д.
Отношение между двумя элементами называетсябинарным, | или двух- | |
местным, между тремя-тернарным, или | трехместным, между n элементами | |
n–нарным, или n–местным. Различают | шесть основных свойств | отношений: |
12 |
|
|
рефлексивность, антирефлексивность, симметричность, антисимметричность, тождественность, транзитивность.
Отношение R называется рефлексным на множестве X, если для любого x Î X справедливо xRx или (xx) Î R на множестве X. Например, «равенство», «самообслуживание».
Отношение R называется антирефлексивным, если для любого x Î X не выполняется xRx, т. е. (xx) Ï R . Например, «строгое неравенство», «быть старше», т. е. отношения, которые могут выполняться только для несовпадающих объектов.
Отношение R называется симметричным на множестве X, если для любых x Î X справедливо соотношение: если x1Rx2, тo x2Rx1 или если (x1x2 ) Î R , то
(x2 x1 ) Î R . Например, «расстояние между двумя точками», «быть братом».
Отношение R называется антисимметричным на множестве X, если для любых x Î X справедливо соотношение: если x1Rx2 истинно, то x2Rx1 ложно, или если (x1x2 ) Î R , то (x1x2 ) Ï R . Например, «строгое включение», «быть отцом».
Отношение R называется тождественным на множестве X, если для любых x Î X из одновременной истинностиx1Rx2 и x2Rx1 следует, что х1 = х2. Например, «получают повышенную стипендию» и «сдали сессию на хорошо и отлично» на множестве студентов факультета.
Отношение R называется транзитивным на множестве X, если для любых x Î X справедливо соотношение: если x1Rx2 и x2Rx3, то x1Rx3.
Например, «параллельность», «больше чем». Для каждого отношения R можно определить обратное R-1, считая, что x2 R-1×1 в том и только в том случае, когда x1Rx2.
1.10.Виды отношений
Взависимости от того, какими свойствами обладает отношения, они делятся на три вида; отношение эквивалентности, отношение порядка и отношение доминирования.
Отношение R на множестве X называется отношением эквивалентности, если оно обладает свойствами рефлексивности (xRx для «x Î X ), симмет-
ричности ( x1Rx2 ® x2 Rx1 для всех x1, x2 Î X ), транзитивности (x1Rx2 и x2 Rx3 ® x1Rx3 для всех x1, x2 , x3 Î X ). Элементы множества можно рассматривать как эквивалентные, если любой из этих элементов может быть заменен другим. Для обозначения эквивалентности служит символ º или ~, т. е. x1 º x2
или x1 ~ x2. Примерами отношения эквивалентности являются отношения равенства векторов, фигур, геометрическое отношение подобия, отношение параллельности.
Другим видом отношений является отношение порядка, которое характеризуется определенным порядком расположения элементов множества.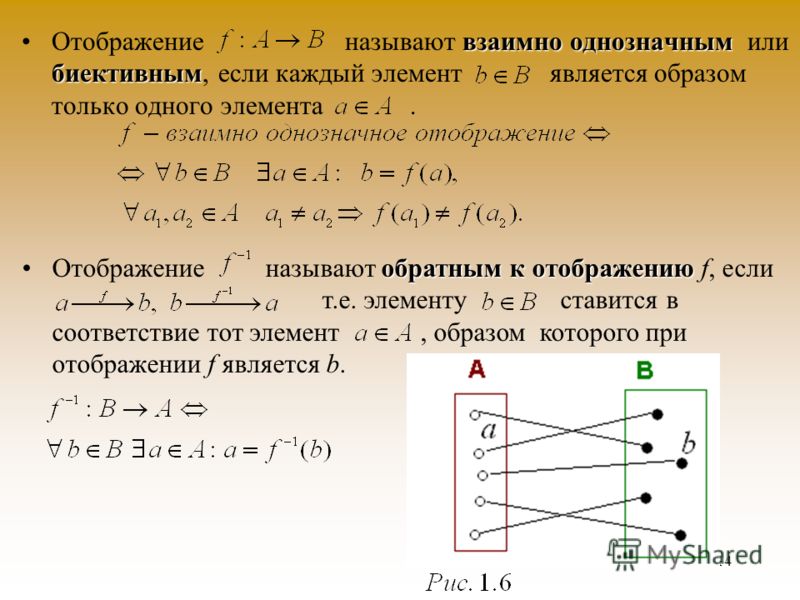 Разли-
Разли-
13
чают отношения нестрогого порядка (квазипорядка) на множестве X и отношения строгого порядка.
Отношение квазипорядка обозначается символом £ , частным случаем является символ Í . Это отношение, которое обладает свойствами рефлексивности (х ≤ х), транзитивности (если x1 £ x2 и x2 £ x3 , то x1 £ x3 ) и тождествен-
ности (если x1 £ x2 и x2 £ x1 , то x1 = x2 ).
Отношение строгого прядка обозначается символом <, частным случаем его являются символы ®, Ì . Это отношение, обладающее свойствами транзитивности (если x1 < x2 и x2 < x3 , то x1 < x3 ) и антисимметричности (если x1 < x2 , то x2 < x1 ). Это отношение характерно для различного рода иерархий с
подчинением одного объекта другому.
При рассмотрении множеств людей, или группы людей, возникает отношение, которое называется отношением доминирования(доминировать ~ это значит преобладать). Обозначается оно символом >>.
Отношением доминирования на множестве х называется отношение, которое обладает свойствами антирефлексивности( x >> x ложно) и антисимметричности (если x1 >> x2 , то x2 >> x1 , ложно). Эти свойства означают, что ника-
Эти свойства означают, что ника-
кой индивидуум не может доминировать самого себя и в каждой паре только один элемент доминирует другого. Например, победившая команда или спортсмен; лицо, пользующееся авторитетом.
1.11. Нечёткие множества. Способы задания. Понятие лингвистической переменной
Теория нечётких множеств ведёт своё начало с1965 года. Основоположником теории нечётких множеств «Fuzzy Sets» является американский учёный Лотфи Заде, который ввёл понятие о нечётких множествах, как обобщение обычных (чётких) множеств. Прилагательное «fuzzy» переводится на русский язык как нечёткий, размытый.
Введение нечётких множеств – это попытка описать математически некоторую нечёткую информацию для создания математической модели. В нечётких множествах объекты, обладающие общим свойством, могут обладать им в различной степени. Поэтому высказывание типа («элемент принадлежит данному множеству») теряет смысл. Необходимо указать «насколько сильно» или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.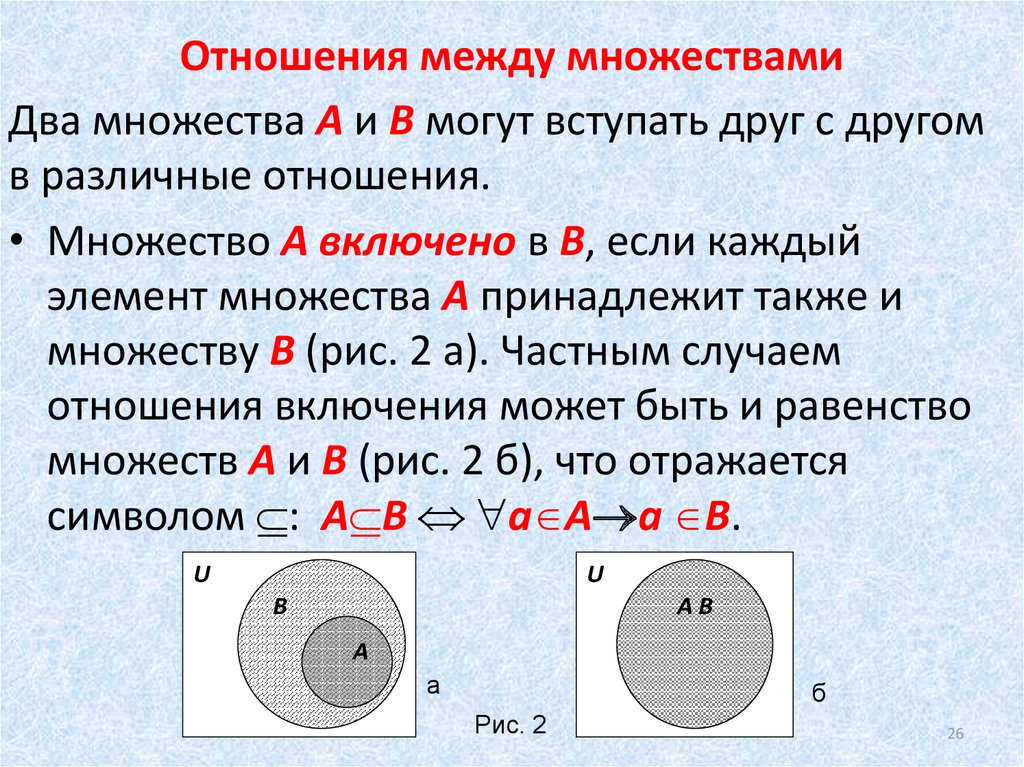
Нечёткое или фази-множество (ФМ) характеризуется двумя показателями:
1)фактом принадлежности объектов к множеству;
2)степенью принадлежности объектов к данному множеству.
Для представления элемента x нечёткого множества A% используется функция принадлежности , которая равна 1, если этот элемент принадлежит к
14
множеству A | или равна0, если элемент не принадлежит множествуA . |
% | % |
В общем случае | . Значения функции принадлежности являются ра- |
циональными числами из интервала[0,1]. Конкретное значение функции при-
надлежности называется коэффициентом или степенью принадлежности.
Эта степень может быть определена явным образом в виде функциональной за-
висимости, либо дискретно для | конечной последовательности значений . |
|
Нечётким множеством | называется совокупность пар ( | ), где |
– степень принадлежности элемента к нечёткому множеству A . |
| |
| % |
|
Так, например, нечёткое множество целых чисел, определённое понятием «около 10», можно задать следующим образом
Другой способ задания этого же множества– задание его функции при-
надлежности зависимостью . График функции представлен
на рис. 1.12.
m
Рис. 1.12
Наибольшей популярностью пользуются функции принадлежности гауссовского типа, а также треугольной и трапецеидальной формы. Гауссовская функция принадлежности переменной с центром в и вариацией для множества описывается выражением
15
и приведена на рис 1.13.
m % ( x) |
|
|
|
|
|
|
|
| C = 1 |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
0,8 |
|
|
|
|
|
|
|
|
|
|
|
| s = 1 |
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
0,4 |
|
|
|
|
|
|
|
|
|
|
|
| s= 0,5 |
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
| s = 0,05 |
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | |||||||||
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
| Рис. |
|
|
|
|
|
|
|
|
| |
Параметр | характеризует форму функции. | Чем меньше , тем больше | ||||||||||||||||||
крутизна функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
C = const = 1 – центр нечёткого множества, при его изменении функция | ||||||||||||||||||||
смещается по горизонтальной оси. |
|
|
|
|
|
|
|
|
|
|
| |||||||||
Сходство |
| с | функцией | распределения | только |
| внешнее. | |||||||||||||
форму (не обязательно симметричную) должен специалист в соответствующей
области. В общем случае | может быть кусочно-непрерывной. | |||
Треугольная симметричная функция m % (x) | ||||
принадлежности описывается выражением | A | |||
| ||||
|
|
|
|
|
и приведена на рис 1.14. |
|
|
|
|
|
|
|
|
| |
Обобщением | треугольной |
| функции |
|
|
| ||||
принадлежности | является трапециедальная |
|
| Рис. | ||||||
функция, которая описывается зависимостью |
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16
Вид | соответствующей | функции |
|
|
|
| |||
показан | на | рис. | принято, |
| m % (x) |
|
|
| |
|
|
| , где S обо- |
| A |
|
|
| |
|
| , |
|
|
|
|
| ||
значает угол наклона. |
|
|
|
|
|
| |||
Выбор значения t = 0 преобразует |
|
|
|
|
| ||||
трапециедальную функцию в треуголь- |
|
|
|
|
| ||||
ную. |
|
|
|
|
| ||||
стемам | объектами | нечётких | множеств |
| Рис. 1.15 |
|
| ||
являются значения некоторых физиче- |
|
|
| ||||||
|
|
|
| ||||||
ских переменных, например, значения |
|
|
|
|
| ||||
температуры, скорости перемещения, электрического напряжения, тока и т. д. | |||||||||
Физическую переменную можно описать словесно(лингвистически), вы- | |||||||||
делив некоторую качественную оценку в лингвистической форме. | |||||||||
обычная переменная может принимать различные значения, лингвистическая | |||||||||
переменная, например, « температура», | может принимать различные значе- | ||||||||
ния такие как: |
|
|
|
|
|
|
| ||
— отрицательная малая ОМ, |
|
|
|
|
| ||||
— нулевая |
|
|
|
|
|
|
| ||
— положительная средняя PS, |
|
|
|
|
| ||||
— положительная высокая PW и т. |
|
|
|
| |||||
Лингвистические переменные называются термами. |
|
| |||||||
Терм-множеством называется множество всех значений лингвистиче- | |||||||||
ской переменной. |
|
|
|
|
|
|
| ||
Лингвистические переменные (термы) количественно оцениваются не | |||||||||
числами, а числовыми множествами, перекрывающими друг друга. Физиче- | |||||||||
ская переменная на заданном интервале X её изменения от | до | ха- | |||||||
рактеризуется рядом фаззи-множеств |
| с функциями принадлеж- | |||||||
ности |
|
| . | места распо- | |||||
ложения центра | и границ интервала | возлагается на эксперта в соответ- | |||||||
ствующей области. |
|
|
|
|
|
|
| ||
На рис. 1.16 переменная температура помещения представлена термами | |||||||||
— положительная низкая PN для |
|
|
|
|
| ||||
— положительная средняя PS для |
|
|
|
|
| ||||
— положительная высокая PW для |
|
|
|
| |||||
На участках перекрытия термов нарушается однозначность принадлеж- | |||||||||
ности значений переменной | только | одному терму. | Ширина участков | пере- | |||||
крытия может быть различной, в пределе и нулевой, однако там, где для одного | |||||||||
терма |
| , для соседних |
|
| . |
|
|
| |
Значение | означает | бесспорную | принадлежность | значения | |||||
к соответствующему терму. |
|
|
|
|
| ||||
17
Отображения и их виды. Обратное отображение. Мощность множества. Счетные множества
Математика \ Математический анализ
Страницы работы
4 страницы (Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
220400
Математический анализ
Толстиков А. В.
В.
Курс 1. Семестр 1. Лекция 2. Отображения.
План
1. Отображения. 2. Виды отображений. 3. Обратное отображение. 4. Мощность множества. Счетные множества.
Литература: Ермаков В.И. с. 276-280. Ильин В.А., с.183-195. Шнейдер В.Е. 285-296. Кремер Н.Ш. 251-266.
1. Отображения.
Определение 1.1. Бинарным отношением f между множествами X и Y называется любое подмножество множества X´Y.
Определение 1.2. Бинарное отношение f между множествами X и Y называется отображением множества X в множество Y, если для любого элемента xÎX существует один и только один элемент yÎY такой, что (x, y)Îf .
Отображение f множества X в Y называется также функцией, определенной
на множестве X со значениями в множестве Y.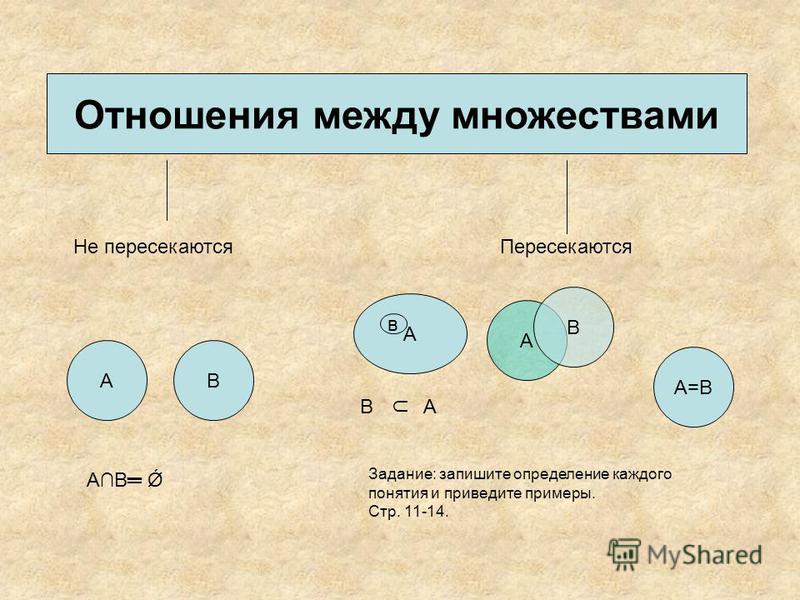
Символически отображение f множества X в Y записывается в виде: f: X ® Y. То, что (x, y)Îf, записывается также в виде y = f(x) или f: x a y.
При этом
область определения D(f)
бинарного отношения f совпадает с X и называется областью определения отображения
или функции f, область значений E(f) называется множеством
значений отображения или функции f. Если
(x, y)Îf, то элемент
y называется образом элемента x при отображении f и обозначается символом y
= f(x), а
элемент x — прообразом
элемента y. Также при этом говорят, что элемент x есть аргумент или более точно, значение
аргумента, а f(x) — значение
функции в точке x. Множество X называется также областью
отправления, Y — областью прибытия отображения
f.
Множество X называется также областью
отправления, Y — областью прибытия отображения
f.
Иногда отображением f множества X в Y называется правило, которое каждому элементу xÎX ставит в соответствие единственный элемент yÎY , обозначаемый f(x).
Отображения задаются теми же способами, что и бинарные отношения. На рис. 1.10 и 1.7 представлены отображения, заданные стрелками и графически.
Стрелочное изображение отображения f: X ® Y имеет следующие особенности:
1) из каждой «точки» множества X выходит только одна стрелка;
2) две стрелки не могут иметь общее начало.
Если X, YÍ R, то функция называется числовой функцией.
Отметим, что множество G точек плоскости xOy является графиком
некоторой числовой функции тогда и только тогда, когда каждая прямая параллельная
оси Oy пересекает
G не более чем в одной точке.
Определение 1.3. Образом множества A Í X при отображении f: X ®Y называется множество f (A) = {f(x)| xÎ A }.
Например, на рис. 1.11 f ({2, 4}) = {b}.
Отметим, что f (X) = E(f).
Определение 1.4. Прообразом или полным прообразом множества BÍ X при отображении f: X ®Y называется множество f -1(A) = {xÎ X | f(x)ÎB }.
Например, на рис. 2.2 f -1({b}) = {2, 4, 5}.
Определение 1.5. Два отображения f1: X1 ® Y1, f2: X2 ® Y2называются равными, обозначается f1 = f2, если
1) X1= X2,
2)
для любого xÎ X1имеем f1(x)= f2(x).
Определение 1.6. Композицией двух отображений f: X®Y, g: Y®W называется отображение : X®W определяемое для любого xÎ X формулой:
Если f и g числовые функции, то называют также сложной функцией.
Приведенная на рис. 1.9 треугольная диаграмма наглядно иллюстрирует то, что при выполнении отображения сначала выполняется отображение f , а затем - отображение g.
Например, если f и g отображения R в R, определенные формулами f: xa x2, g: xa x+1, то : x a x2+1, : x a (x+1)2.
Теорема 1.1. Операция композиции обладает свойством
ассоциативности, т.е. для любых
трех отображений f: X®Y, g: Y®W , h: W®Z.
Доказательство. Так как для любого элемента xÎ X имеем
то по определению 1.4 утверждение теоремы справедливо.
Определение 1.7. Отображение eX: X®X называется единичным или тождественным отображением, если eX(x) =x для любого xÎ X.
Теорема 1.2. Для любого отображения f: X®Y .
Доказательство. ТУ 1.2.
Определение 1.8. Отображение f: X1®Y называется сужением или ограничением отображения g: X2®Y на X1, если
1) X1Í X2,
2)
для любого xÎ X1имеем f(x)= g(x).
В этом случае пишут f= g½A, а также говорят, что g продолжениеили расширение отображения f.
2. Виды отображений. Обратное отображение.
Определение 2.1. Отображение f множества X в Y называется отображением множества X на Y, или сюръективным, или сюръекцией, если для любого yÎ Y найдется такой элемент xÎ X, что f(x) =y.
Таким образом, f: X®Y сюръекция тогда и только тогда, когда E(f) = Y.
Например, отображение f: R®[0, +¥), f: xax2, является сюръекцией, см. также рис. 1.5, 1.11 . Отметим, что отображения на рис 2.2, 1.7 не являются таковыми.
Определение
2. 2. Отображение f множества X в Y называется взаимно
однозначным отображением множества X в
Y , или инъективным, или
инъекцией, или вложением, если для любых
x1, x2
Î X
из x1 ¹ x2 следует, что f(x1) ¹ f(x2).
2. Отображение f множества X в Y называется взаимно
однозначным отображением множества X в
Y , или инъективным, или
инъекцией, или вложением, если для любых
x1, x2
Î X
из x1 ¹ x2 следует, что f(x1) ¹ f(x2).
Например, отображение f:R\{0}®R, f: xa1/x, является инъекцией
Похожие материалы
Информация о работе
Скачать файл
Теория множеств — Функции. Описание поведения с помощью биектив… | Хесус Наджера
Первоначально опубликовано на https://www.setzeus.com/ Сегодня мы собираемся расширить функций в мире теории множеств. Как и в предыдущих введенных концепциях, номенклатура стандартных функций в наборах немного отличается от других областей математики и поэтому требует пересмотра. Есть довольно много терминов, которые нужно ввести, так что давайте сразу к делу! Эта первая таблица функциональных терминов ниже отражает идею домена, диапазона и выходных данных для стандартной функции:
Как и в предыдущих введенных концепциях, номенклатура стандартных функций в наборах немного отличается от других областей математики и поэтому требует пересмотра. Есть довольно много терминов, которые нужно ввести, так что давайте сразу к делу! Эта первая таблица функциональных терминов ниже отражает идею домена, диапазона и выходных данных для стандартной функции:
Функция в мире теории множеств — это просто отображение некоторых (или всех) элементов из множества A в некоторые (или все) элементы из множества B. В В приведенном выше примере набор всех возможных элементов в A известен как домен ; , в то время как элементы в A, которые действуют как входы, имеют специальное имя аргументы . Справа набор всех возможных выходов (также известный как «диапазон» в других ветвях) упоминается как кодовый домен ; в то время как набор фактических выходных элементов в B, сопоставленных с A, известен как изображение .
Пока ничего сложного, только новый способ определения параметров функций с. Далее мы рассмотрим, как описать поведение этих функций отображения с помощью общих типов функций.
В теории множеств для классификации отображений множеств обычно используются три термина: инъективы , сюръективы и биективы. У этих терминов, к сожалению, есть несколько разных названий, которые усугубляют путаницу — поэтому мы сначала рассмотрим каждое определение, а затем рассмотрим несколько наглядных примеров. Все три термина описывают способ отображения аргументов и изображений:
- Функция является инъективной ( также известной как «один-к-одному» ), если каждый элемент кодового домена отображается на не более единиц. элемент домена.
- Функция является сюръективной ( a . k.a «на» ), если каждый элемент кодового домена сопоставляется по крайней мере с одним элементом домена.
 (То есть изображение и кодовый домен функции равны.)
(То есть изображение и кодовый домен функции равны.) - Функция является биективной ( также известной как «один-к-одному и на», «однозначное соответствие» ), если каждый элемент домена сопоставляется с ровно одним элементом домена.
Пресловутая вишенка на вершине сложной номенклатуры здесь распространяется на возможные коннотации слов «инъективный», «сюръективный» и «биективный». Пока привык к описывают функцию (отображение), прежний оттенок правильный; однако также правильно идентифицировать функций (отображение) исключительно по этим характеристикам. Таким образом, функция с инъективным поведением называется -инъекцией , функция с сюръективным поведением называется -сюръекцией , и, наконец, функция с биективным поведением называется -биекцией .
Перечитайте пункты выше. Биекция — это просто функция, которая заполняет оба предыдущие требования — то есть функция и и инъективная, и сюръективная. Инъективная функция не обязательно должна быть сюръективной, а сюръективная функция не обязательно должна быть инъективной. Переходя к наглядному примеру, эти три классификации приводят к функциям множества, следующим четырем возможным комбинациям инъективных и сюръективных признаков, кратко изложенных ниже:
Инъективная функция не обязательно должна быть сюръективной, а сюръективная функция не обязательно должна быть инъективной. Переходя к наглядному примеру, эти три классификации приводят к функциям множества, следующим четырем возможным комбинациям инъективных и сюръективных признаков, кратко изложенных ниже:
И вот! Теперь у нас есть элементарное представление об общих типах отображений, наблюдаемых в мире множеств. Однако это ни в коем случае не конец пути, так как мы оставили этот обзор до введения на высоком уровне — напротив, это самое начало.
Основы теории множеств являются ключом к пониманию высших разделов математики. Чтобы продолжить наше восхождение во многих областях, мы затем рассмотрим одну из абсолютно самых новаторских теорий во всей истории математики, используя наши знания в области теории множеств: теорию множеств Цермело-Френкеля.
первоначально опубликовано на
https://www. setzeus.com/
setzeus.com/
Mapping — Encyclopedia of Mathematics
$
\def\P{\mathcal P} % набор мощности
\def\iff{\Leftrightarrow}
$
Отображение , или сокращенно карта , является одним из многих синонимов, используемых для функции. В частности, термин отображение (ping) используется в общих контекстах, таких как теория множеств, но его использование не ограничивается этими случаями.
- 1 Концепция отображения в теории множеств
- 2 Состав
- 3 Индуцированные отображения
- 4 Каталожные номера
Концепция отображения в теории множеств
В теории множеств отображения представляют собой специальные бинарные отношения.
Отображение $f$ из множества $A$ в множество $B$ (упорядоченная) тройка $ f = (A,B,G_f) $, где $ G_f \subset A \times B $ такой, что
- (a) если $(x,y)$ и $(x,y’)\in G_f$, то $y=y’$, и
- (б) проекция $ \pi_1 (G_f) = \{ x \mid (x,y) \in G_f \} = A $.

Условие (a) выражает, что $f$ является однозначным . а также
условие (b), что он определен на $А$.
$A$ — это домен , $B$ — это кодовый домен , а $G_f$ — это граф отображения.
Следовательно, в этом параметре сопоставления равны тогда и только тогда, когда
все три соответствующих компонента (домен, кодовый домен и граф) равны.
Отображение обычно обозначается как $ f : A \to B $ и $ a \mapsto f(a) $
где $ f(a) := b \iff (a,b) \in G_f $ есть значение $f$ в $a$.
Если два отображения $f_1 = (A_1,B_1,G_1)$ и $f_2 = (A_2,B_2,G_2)$ удовлетворяют
- $ A_1 \subset A_2 $, $ B_1 \subset B_2 $ и $ G_1 \subset G_2 $
тогда $f_2$ называется расширением $f_1$, а $f_1$ ограничением $f_2$. При этом $f_1$ часто обозначается как $f_2\vert A_1$ и, очевидно, $f_1(a) = f_2(a)$ выполняется для всех $a\in A_1$.
Примечание:
Иногда для представления функции используется только граф $G_f$. В этом случае два отображения равны, если они имеют один и тот же граф,
и можно разрешить графы, которые являются не множествами, а классами.
В этом случае два отображения равны, если они имеют один и тот же граф,
и можно разрешить графы, которые являются не множествами, а классами.
В то время как область определения функции может быть получена как проекция $ \pi_1 (G_f) $ первой компоненты,
проекция $ \pi_2 (G_f) $ второго компонента не создает кодовый домен, а только образ домена.
Таким образом, понятие сюръективности неприменимо.
Состав
Два отображения могут быть составлены , если домен одного отображения является подмножеством домена другого отображения:
Для $f=(A,B,G_f)$ и $g=(C,D,G_g)$ с $B\подмножеством C$ композиция $ g \circ f $ — это отображение $ (A,D,G) $ с
- $ G := \{ (a,g(f(a)) \mid a \in A \} = \{ (a,c) \mid (\существует b \in B) ( (a, б) \in G_f \land (b,c) \in G_g ) \} $.
Замечания:
(a) Условие $ B \subset C $ можно смягчить до $ f(A) \subset C $.
(b) Если используются только графы, то граф композиции определяется (как указано выше) формулой
- $ G_{g \circ f} := \{ (a,c) \mid (\exists b ) ( (a,b) \in G_f \land (b,c) \in G_g ) \} $ 9{-1}(Т)$,
но нужно знать, что эти общие обозначения могут быть неоднозначными в определенных ситуациях.



 1.13
1.13 Определить
Определить 1.14
1.14 1.15. Здесь
1.15. Здесь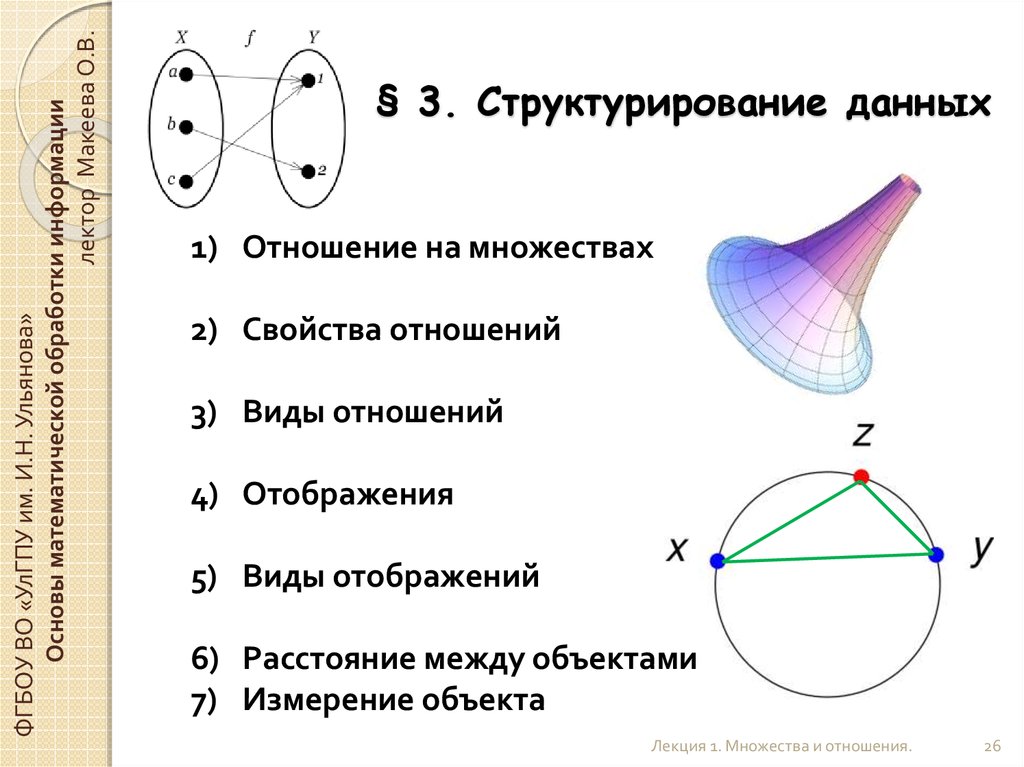 Применительно к техническим си-
Применительно к техническим си- Так же как
Так же как п.
п.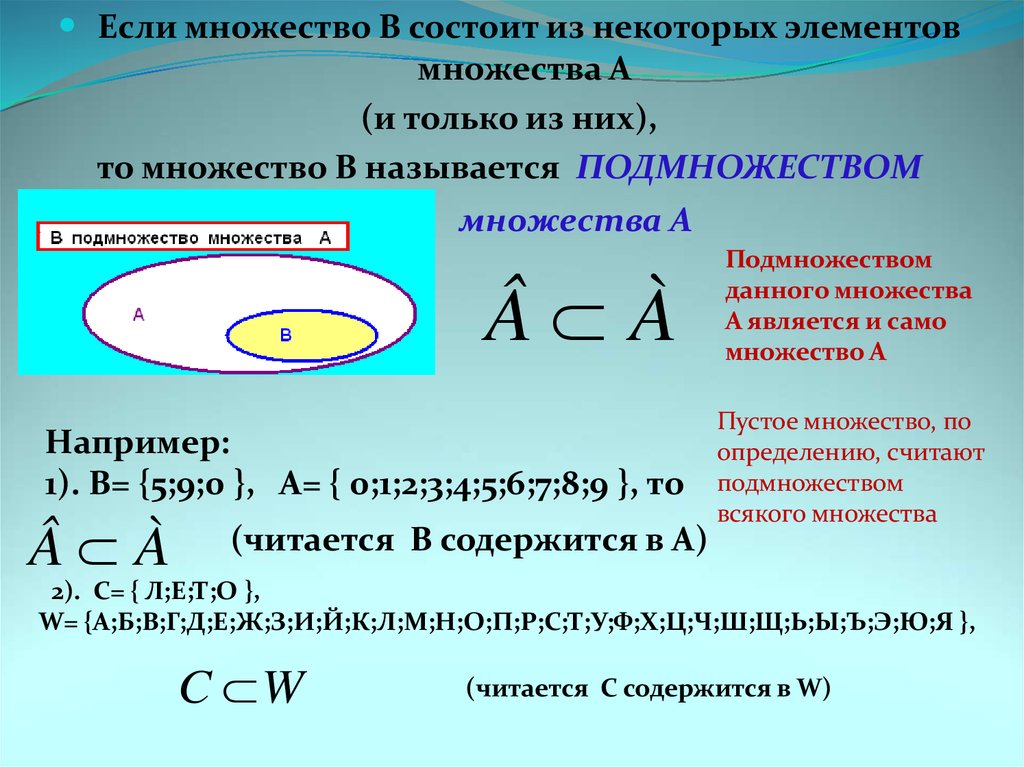 По существу определение формы,
По существу определение формы,
 (То есть изображение и кодовый домен функции равны.)
(То есть изображение и кодовый домен функции равны.)
