Типы векторов, их характеристика, требования предъявляемые к ним
- Главная страница 🏠
- 📚 Библиотека
- 👉 Генетика 👈
- Трансгенные эукариотические организмы
- Типы векторов, их характеристика, требования предъявляемые к ним
Нужна помощь в написании работы?
Узнать стоимость
Вектор – небольшая автономно реплицирующиеся молекула ДНК,
обеспечивающая функционирование встроенного в нее гена
Требования к векторам:
- автономная репликация в клетке;
- стабильное наследование клеткой-
- хозяином;
- достаточная емкость;
- наличие «удобных» сайтов рестрикции;
- наличие селективных маркеров.

Виды векторов:
Фаговые векторы Первыми были разработаны векторы на основе фага λ E. coli. ДНК фага λ составляет примерно 50 т.п.н. Значительная часть (20т.п.н.) несущественна для размножения фага и может быть заменена на чужеродную ДНК. В фаге можно клонировать фрагмент ДНК до 20т.п.н.
Космиды – векторы, объединяющие в себе свойства плазмиды и фага. Созданы искусственно. Могут амплифицироваться в бактерии как плазмиды и упаковываться в фаговые головки. Могут включать вставку чужеродной ДНК до 40т.п.н.
Фазмиды — являются гибридами между фагом и плазмидой После встройки чужеродной ДНК могут в одних условиях развиваться как фаги, в
других – как плазмиды Емкость как у фаговых векторов
Челночные векторы – способны к репликации в разных клетках-хозяевах растений и животных прокариот и эукариот Одни и те же гены получают возможность реплицироваться и экспрессироваться в разных организмах
Основной вектор для клонирования генов животных – геном вируса SV40
Основные векторы для клонирования растений – геномы вирусов растений и
плазмида pTi агробактерий
Поможем написать любую работу на аналогичную тему
Реферат
Типы векторов, их характеристика, требования предъявляемые к ним
От 250 руб
Контрольная работа
Типы векторов, их характеристика, требования предъявляемые к ним
От 250 руб
Курсовая работа
Типы векторов, их характеристика, требования предъявляемые к ним
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Меню
Предмет и задачи курса, связь с другими дисциплинами
Состояние, проблемы, перспективы, практическое значение генной инженерии
Определение важнейших понятий и терминов:трансгеноз, трансгенные, генетически модифицированные организмы (ГМО), генно-инженерная деятельность, вектор
Характеристика рестриктаз как ферментов, применяемых в генной инженерии
Номенклатура рестриктаз
Полимеразы и обратные транскриптазы
Характеристика лигаз как ферментов, применяемых в генной инженерии
Ферменты, обеспечивающие изменение структуры концов фрагментов ДНК
Сшивка по одноименным липким концам (рестриктазно лигазный метод)
Добавить в избранное (необходима авторизация)
Какие виды векторов и матриц есть в Sparl MLlib: примеры с кодом
В Spark MLlib есть разные типы векторов и матриц.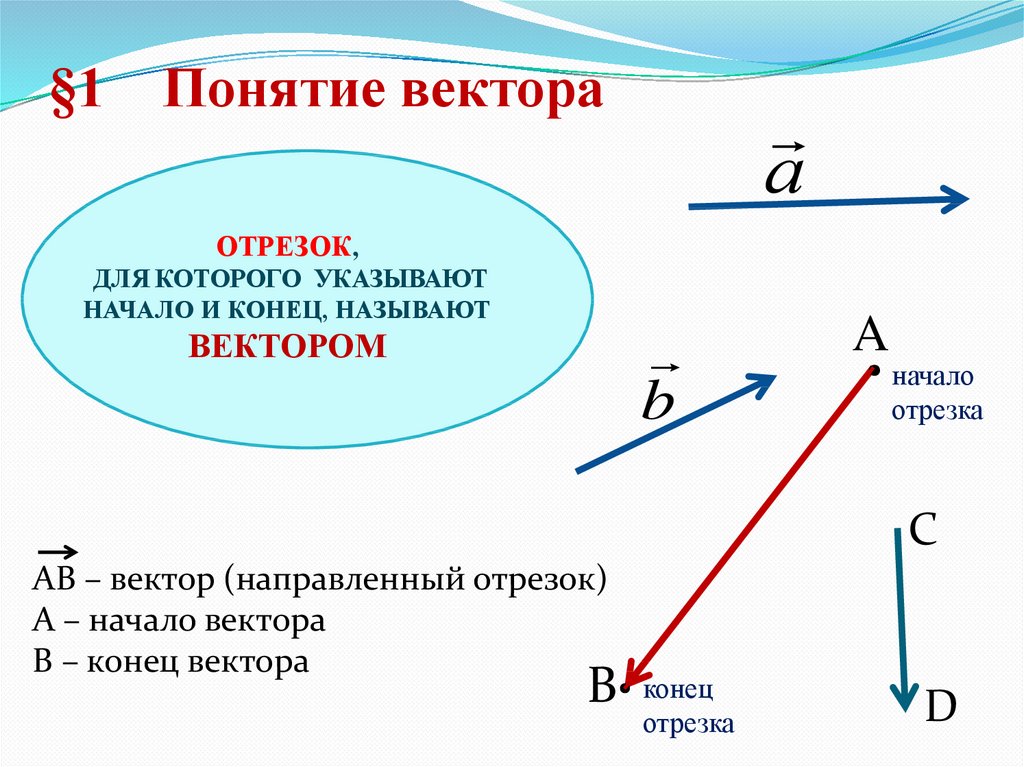 MLlib поддерживает локальные векторы и матрицы, хранящиеся на одной машине, а также распределенные матрицы, поддерживаемые одним или несколькими RDD. Сегодня познакомимся с локальными векторами и матрицами. Читайте в этой статье: как создаются плотные (dense) и разреженные (sparse) векторы, зачем нужны маркированные векторы и как представляются матрицы Spark MLlib с примерами кода на Scala и Python.
MLlib поддерживает локальные векторы и матрицы, хранящиеся на одной машине, а также распределенные матрицы, поддерживаемые одним или несколькими RDD. Сегодня познакомимся с локальными векторами и матрицами. Читайте в этой статье: как создаются плотные (dense) и разреженные (sparse) векторы, зачем нужны маркированные векторы и как представляются матрицы Spark MLlib с примерами кода на Scala и Python.
Локальные векторы: плотные и разреженные
Локальный вектор имеет целочисленные (int) или действительные (double) значения, хранящиеся на одной машине. Spark MLlib поддерживает два типа локальных векторов: плотные и разрезженные
. Плотные векторы представляются обычными массивами, где каждый элемент значимый. Разреженные векторы представляются двумя параллельными массивами, где первый массив – это индексы ненулевых значений, а второй массив – сами ненулевые значения. Например, вектор(1.0, 0.0, 3.0) может быть представлен в виде:- полного вектора
[1., 0, 0.0, 3.0]
0, 0.0, 3.0] - разреженного вектора
(3, [0, 2], [1.0, 3.0]), где 3 – это размер вектора (нулевое значение не записывается).
Оба вида векторов наследуются от класса Vector и имеют соответственно реализации DenseVector и SparseVector [1]. Рекомендуется использовать класс Vectors, реализующий фабричный метод, и вызывать через него методы dense или sparse. В Scala полный и разреженный векторы Spark MLlib выглядят следующим образом:
import org.apache.spark.mllib.linalg.{Vector, Vectors}
// Представляем массив (1.0, 0.0, 3.0)
// в виде полного вектора:
val dv: Vector = Vectors.dense(1.0, 0.0, 3.0)
// в виде разреженного вектора:
val sv1: Vector = Vectors.sparse(3, Array(0, 2), Array(1.0, 3.0))В Python полный и разреженный векторы Spark MLlib создаются аналогичным образом. Причем, полным вектором может выступать стандартные списки Python или массивы NumPy.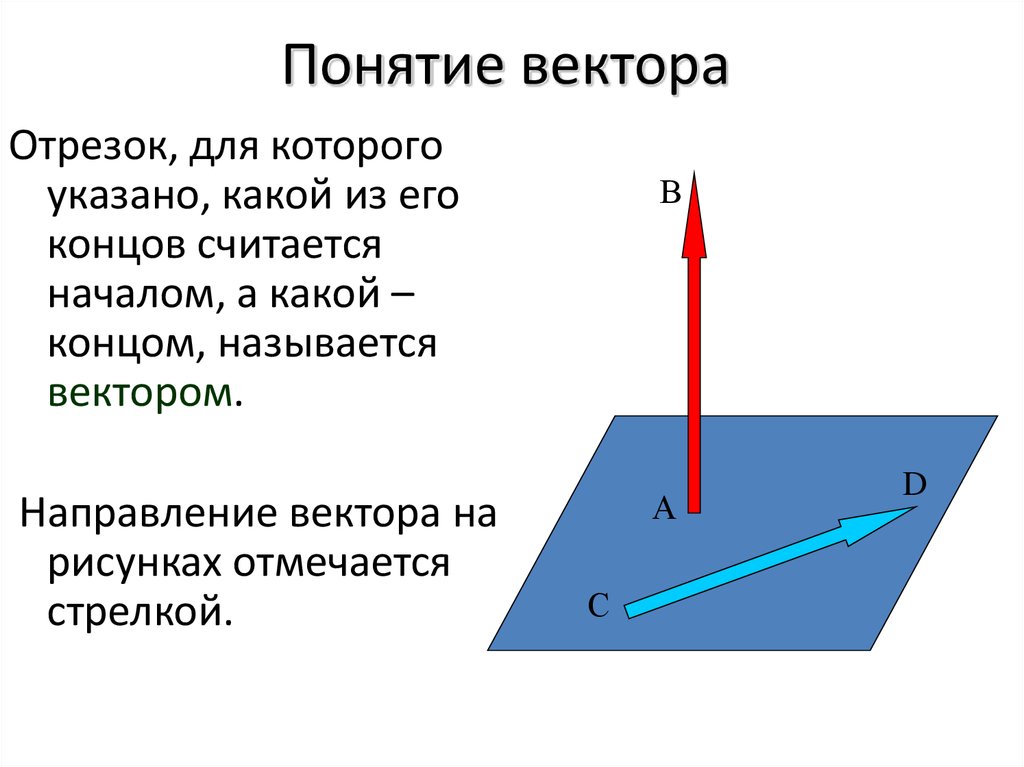 Лучше отдавать предпочтение массивам NumPy, чем стандартным спискам, поскольку первые работают быстрее. В качестве разреженных: массивы
Лучше отдавать предпочтение массивам NumPy, чем стандартным спискам, поскольку первые работают быстрее. В качестве разреженных: массивы csc_matrix от Scipy или SparseVector от MLlib.
Код на Python для создания полных и разреженных векторов выглядит так:
from pyspark.mllib.linalg import Vectors
import numpy as np
import scipy.sparse as sps
# Полные векторы
dv1 = Vectors.dense([1.0, 0.0, 3.0])
dv2 = np.array([1.0, 0.0, 3.0])
# Разреженные:
sv1 = Vectors.sparse(3, [0, 2], [1.0, 3.0])
sv2 = sps.csc_matrix((np.array([1.0, 3.0]),
np.array([0, 2]),
np.array([0, 2])),
shape=(3, 1))Маркированный вектор (Labeled point) в Spark MLlib
Маркированный вектор – это локальный полный или разреженный вектор, который ассоциирован с меткой. В Spark MLlib такие вектора необходимы в качестве данных для алгоритмов машинного обучения (machine learning). Метки имеют тип double, поэтому данные могут быть применяется как для задач регрессии, так и классификации. Для создания маркированного вектора используется класс LabeledPoint
Метки имеют тип double, поэтому данные могут быть применяется как для задач регрессии, так и классификации. Для создания маркированного вектора используется класс LabeledPoint
На Scala маркированные векторы Spark MLlib инициализируются следующим образом:
import org.apache.spark.mllib.linalg.Vectors import org.apache.spark.mllib.regression.LabeledPoint val pos = LabeledPoint(1.0, Vectors.dense(1.0, 0.0, 3.0)) val neg = LabeledPoint(0.0, Vectors.sparse(3, Array(0, 2), Array(1.0, 3.0)))
Код на Python для создания маркированных векторов Spark MLlib:
from pyspark.mllib.linalg import SparseVector from pyspark.mllib.regression import LabeledPoint pos = LabeledPoint(1.0, [1.0, 0.0, 3.0]) neg = LabeledPoint(0.0, SparseVector(3, [0, 2], [1.0, 3.0]))
Локальная матрица (Local matrix) в Spark MLlib
Локальная матрица – это двумерный вектор с действительными значениями, хранящимися на одной машине. Матрицу можно воспринимать как таблицу: обращение к значениям осуществляется через индексы строки и столбца. Локальная матрица может выражаться через плотный вектор, который записывается в порядке перечисления столбцов, или через разреженный вектор со значениями, которые хранятся в формате CSC (Compressed Sparse Column) и записываются также в порядке перечисления столбцов.
Матрицу можно воспринимать как таблицу: обращение к значениям осуществляется через индексы строки и столбца. Локальная матрица может выражаться через плотный вектор, который записывается в порядке перечисления столбцов, или через разреженный вектор со значениями, которые хранятся в формате CSC (Compressed Sparse Column) и записываются также в порядке перечисления столбцов.
Локальная матрица реализуется через классы DenseMatrix и SparseMatrix. Для их создания рекомендуется использовать фабричный метод класса Matrices.
Код на Scala для создания матрицы с плотными и разреженными векторами Spark MLlib выглядит следующим образом:
import org.apache.spark.mllib.linalg.{Matrix, Matrices}
// Матрица:
// [(1.0, 0.0),
(0.0, 4.0),
(0.0, 6.0)]
// в плотных векторах выражается так:
val dm: Matrix = Matrices.dense(3, 2, Array(1.0, 0.0, 0.0, 0.0, 4.0, 6.0))
// в разреженных векторах так:
val sm: Matrix = Matrices.
sparse(3, 2, Array(0, 1, 3), Array(0, 1, 2), Array(1, 4, 6))Обратите внимание, что в плотном векторе сначала перечисляются значения столбцов. Такой порядок называется column-major order [2]. В разреженном векторе первый массив – это кумулятивная составляющая от индексов столбцов, второй – индексы строк, третий – значения. Разреженная матрица записывается по правилам CSC.
Пример кода на Python по созданию матриц с плотными и разреженными векторами выглядит так:
from pyspark.mllib.linalg import Matrices dm2 = Matrices.dense(3, 2, [1, 0, 0, 0, 4, 6]) sm2 = Matrices.sparse(3, 2, [0, 1, 3], [0, 1, 2], [1, 4, 6])
В следующей статье рассмотрим распределенные матрицы. А о том, как применять векторы и матрицы для решения задач Machine Learning с реальными примерами Data Science, вы узнаете на специализированном курсе по машинному обучению «Машинное обучение в Apache Spark» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.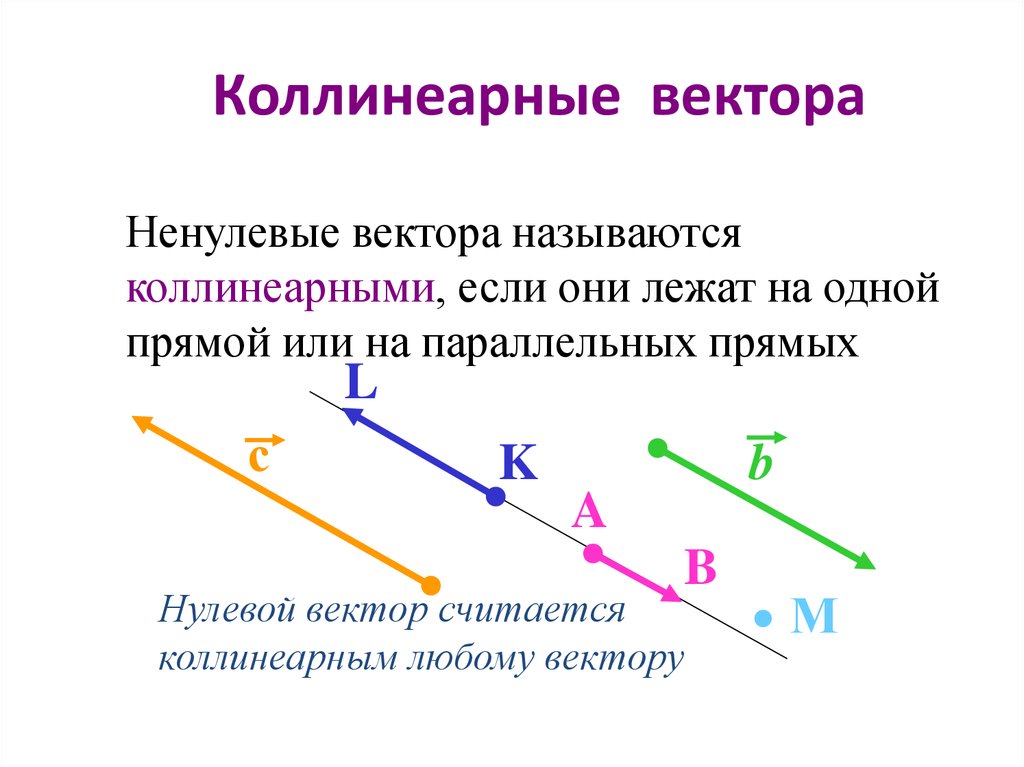
Записаться на курс
Смотреть раcписание
Источники
- docs/latest/api/python/reference/api/pyspark.mllib.linalg.Vectors.html
- en.wikipedia.org/wiki/Row-_and_column-major_order
Типы векторов — Введение, Решенные примеры и часто задаваемые вопросы по математике
Напомним, что в математике физическая величина, имеющая как величину, так и направление, называется вектором. Вектор – это геометрическая единица, имеющая величину и направление. В линии длина линии — это величина, а стрелка — это ее направление. Начальная точка — его хвост, а конечная точка — его голова. Повышение и понижение температуры — лучшие примеры вектора, у него есть и величина, и направление.
Представление векторов
Векторы обычно представляются жирной строчной буквой, такой как a, или стрелкой над буквой. Векторы также могут быть определены их начальными и конечными точками, которые могут указываться стрелкой над ними. Начальная точка вектора также называется хвостом, а конечная или конечная точка — головой. Векторы описывают, как объект перемещается из одного места в другое.
Начальная точка вектора также называется хвостом, а конечная или конечная точка — головой. Векторы описывают, как объект перемещается из одного места в другое.
Операции с векторами
Некоторые базовые векторные операции можно выполнять геометрически без использования системы координат. Сложение, вычитание и умножение на скаляр являются векторными операциями. Кроме того, скалярное произведение и перекрестное произведение — это два метода умножения двух векторов. Они объясняются следующим образом:
Добавление векторов
Вычитание векторов
Скалярная мультипликация
Скалярные тройные продукты Vectors
- Умнозируемый тройной продукт Vectors .
Нулевой вектор
Unit Vector
Position Vector
Co-initial Vector
Like and Unlike Vectors
Coplanar Vector
Collinear Vector
Equal Vector
Вектор смещения
Отрицательный вектор
Нулевой вектор или нулевой вектор
Единичный вектор
Положение в пути
Соначальные векторы
Подобные и отличные векторы
Копланарные векторы
Коллинеарные векторы
Равные векторы
Вектор смещения
Отрицательное значение вектора направление, теперь, если задан любой вектор с той же величиной, но противоположным направлением, то этот вектор называется отрицательным по отношению к этому вектору. Рассмотрим два вектора a и b, имеющих одинаковую величину, но противоположные по направлению, тогда эти векторы можно записать как
a = – b
Решено Примеры:
Пример 1:
Определите векторы
Решение:
векторы, потому что они имеют одинаковую величину и одинаковое направление
Векторы b, c и d имеют одну и ту же начальную точку, поэтому они являются векторами с одинаковым началом.

Пример 2:
Возьмем точки P (1, 0, 0), Q (0, 1, 0) и R (0, 0, 1) на оси x, оси y и оси z- оси соответственно. Определите векторы.
Решение:
OP =1; ОК =1; 0R =1.
Поэтому векторы OP, OQ и OR называются единичными векторами.
Quiz time
Identify the vectors
Solution:
Like vectors
opposite vectors
Unlike vectors
Equal vectors
Types of Vectors | Подробное руководство по 10 основным типам векторов
Вектор определяется как величина, которая имеет как величину, так и направление. Векторы представлены прямой заостренной линией, в которой длина представляет собой вектор, а величина и ориентация представляет собой направление вектора.
 Вектор используется в математике, и существует несколько типов векторов, включая нулевой вектор, единичный вектор, ко-начальный вектор, коллинеарный вектор, равный вектор, отрицательный вектор и многие другие. Векторы используются для представления физических объектов, поскольку они имеют как величину, так и направление.
Вектор используется в математике, и существует несколько типов векторов, включая нулевой вектор, единичный вектор, ко-начальный вектор, коллинеарный вектор, равный вектор, отрицательный вектор и многие другие. Векторы используются для представления физических объектов, поскольку они имеют как величину, так и направление.10 основных типов векторов
Существуют различные типы векторов. Некоторые из них описаны ниже:
1. Ко-начальные векторы
Ко-начальные векторы — это тип векторов, в которых два или более отдельных вектора имеют одинаковые начальные точки. В этом типе вектора все векторы исходят из одной и той же позиции. Исходная точка одинакова для векторов и называется ко-начальными векторами. Например, если у нас есть два AB → и AC → тогда эти векторы называются ко-начальными векторами, так как они оба имеют одинаковую начальную точку, то есть A.
На приведенной выше диаграмме представлены ко-начальные векторы.

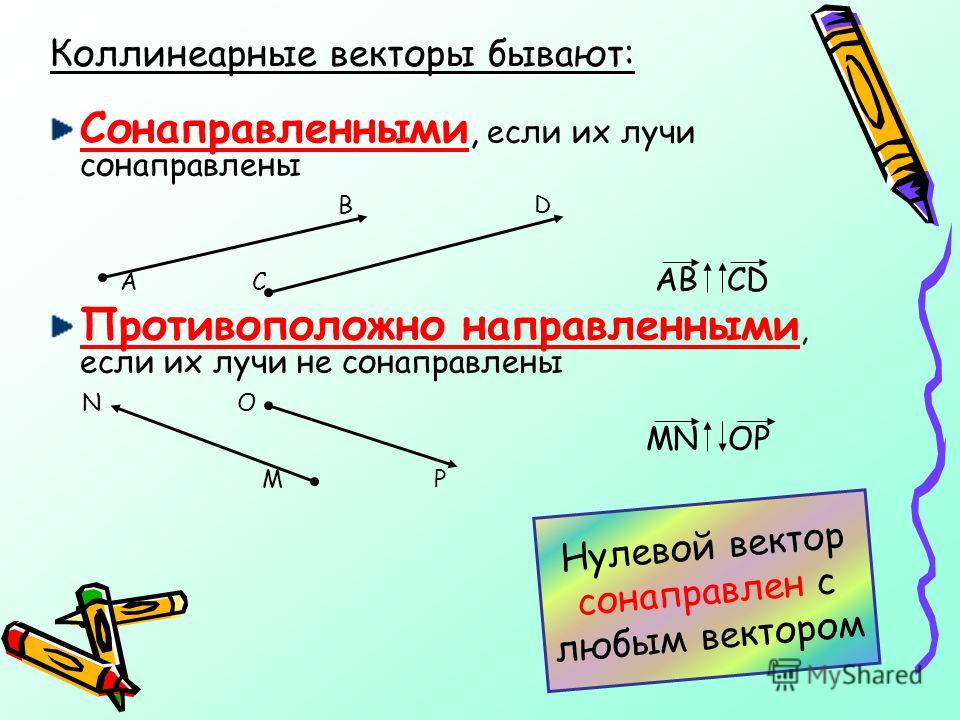
2. Коллинеарные векторы
Коллинеарный — это другой тип вектора, в котором два или более вектора параллельны друг другу, независимо от величины или направления. Параллельность в природе означает, что они никогда не пересекаются друг с другом. Направление обоих векторов по своей природе одинаково. Например, если вектор a находится в направлении x, а b также в том же направлении, то они известны как коллинеарные векторы. Координаты обоих векторов имеют одинаковый характер. Другое свойство коллинеарного вектора состоит в том, что векторное произведение обоих коллинеарных векторов всегда равно нулю. Другое название коллинеарных векторов — параллельные векторы.
На приведенной выше диаграмме два вектора показаны один красным цветом, а другой синим. Оба вектора известны как коллинеарные векторы.
3. Нулевой вектор
Нулевой вектор — это другой тип вектора, в котором модуль вектора равен нулю, а начальная точка вектора совпадает с конечной точкой.
 Например, если вектор AB->, если координаты A и координаты B совпадают, то вектор известен как нулевой вектор. Направление нулевого вектора неопределенно, и величина всегда равна нулю. Нулевой вектор не указывает ни в каком направлении и также имеет все компоненты, равные нулю.
Например, если вектор AB->, если координаты A и координаты B совпадают, то вектор известен как нулевой вектор. Направление нулевого вектора неопределенно, и величина всегда равна нулю. Нулевой вектор не указывает ни в каком направлении и также имеет все компоненты, равные нулю.На приведенной выше диаграмме нулевой вектор показан выше.
4. Единичный вектор
Единичный вектор — это тип вектора, величина которого равна единице длины, равной единице. Все вектора, имеющие модуль, равный единице, известны как единичные векторы. Предположим, что есть вектор x->, который имеет величину x, тогда единичный вектор показан как x̂ , который имеет то же направление вектора x и величину один.
Формула единичного вектора:
Два вектора не считаются равными, если они имеют одинаковую величину, пока они оба не имеют одинаковое направление.
5. Вектор положения
Вектор положения — это еще один тип вектора, в котором исходная точка принимается за 0, а в пространстве есть одна произвольная точка с именем A.
 Тогда вектор OA-> известен как вектор положения, имеющий начало отсчета 0. Вектор положения в основном используется для обозначения местоположения или положения точки в трехмерной декартовой системе измерений. И позиция определяется из любого опорного источника.
Тогда вектор OA-> известен как вектор положения, имеющий начало отсчета 0. Вектор положения в основном используется для обозначения местоположения или положения точки в трехмерной декартовой системе измерений. И позиция определяется из любого опорного источника.6. Копланарные векторы
Копланарные векторы — это тип векторов, в которых три или более трех векторов лежат в одной плоскости или могут лежать в параллельной плоскости, тогда такие векторы называются копланарными векторами. Всегда существует возможность найти любые два случайных вектора, лежащих в одной плоскости и называемых компланарными векторами. Другое свойство копланарных векторов состоит в том, что скалярное тройное произведение трех векторов всегда равно нулю. Компланарные векторы всегда являются линейно зависимыми векторами.
На приведенной выше диаграмме представлены копланарные векторы.
7. Похожие и разные векторы
Подобные векторы — это типы векторов, имеющих одинаковое направление и называемые подобными векторами.
 Векторы, которые имеют противоположное направление независимо друг от друга, известны как непохожие векторы.
Векторы, которые имеют противоположное направление независимо друг от друга, известны как непохожие векторы.8. Равные векторы
Равные векторы — это тип вектора, в котором два вектора или более двух векторов, имеющих одинаковую величину и направление, называются равными векторами.
На приведенной выше диаграмме векторы AB-> и вектор PQ-> являются равными векторами, поскольку они оба имеют одинаковую величину и одинаковое направление.
9. Векторы смещения
Вектор смещения — это тип вектора, когда один вектор смещен от своего положения, тогда этот вектор известен как вектор смещения. Например, если есть какой-либо объект, который находится в точке А в момент времени =0 и через некоторое время находится в точке В в момент времени =t. Смещение можно рассчитать как векторное расстояние между начальной точкой объекта и конечной точкой.
На приведенной выше диаграмме смещение рассчитывается как длина линии AB, выделенной красным цветом.

 обсуждение различных типов векторов. Обычно в математике часто используются 10 различных типов векторов. 10 типов векторов:
обсуждение различных типов векторов. Обычно в математике часто используются 10 различных типов векторов. 10 типов векторов:Давайте обсудим их подробно
Вектор называется нулевым, если величина вектора равна нулю, а начальная и конечная точки совпадают. Например, PQ — это отрезок, координаты точки P такие же, как у точки Q. Нулевой вектор обозначается 0. Нулевой вектор не имеет определенного направления.
Например, PQ — это отрезок, координаты точки P такие же, как у точки Q. Нулевой вектор обозначается 0. Нулевой вектор не имеет определенного направления.
Вектор называется единичным, если длина вектора равна 1 единице. Предположим, что если x является вектором, имеющим величину x, то единичный вектор обозначается через x̂ в направлении вектора, и его величина равна 1. Но двухединичные векторы не могут быть равными, поскольку они могут иметь разные направления.
Точка X, взятая на плоскости, называется вектором положения. Он просто обозначает положение. Пусть OX — точка на плоскости относительно своего начала. Предположим, что O взято за начало отсчета, а X — произвольная точка на плоскости, тогда вектор называется вектором положения точки.
Вектор называется коначальным, если два или более векторов имеют одну и ту же начальную точку, например, векторы AB и AC называются совместно начальными векторами, поскольку они имеют та же отправная точка A.
Векторы, имеющие одинаковые направления, называются подобными, тогда как векторы, имеющие противоположные направления, называются непохожими.
Три или более вектора, лежащие в одной плоскости, известны как копланарные векторы
известны как коллинеарные векторы, также известные как параллельные векторы.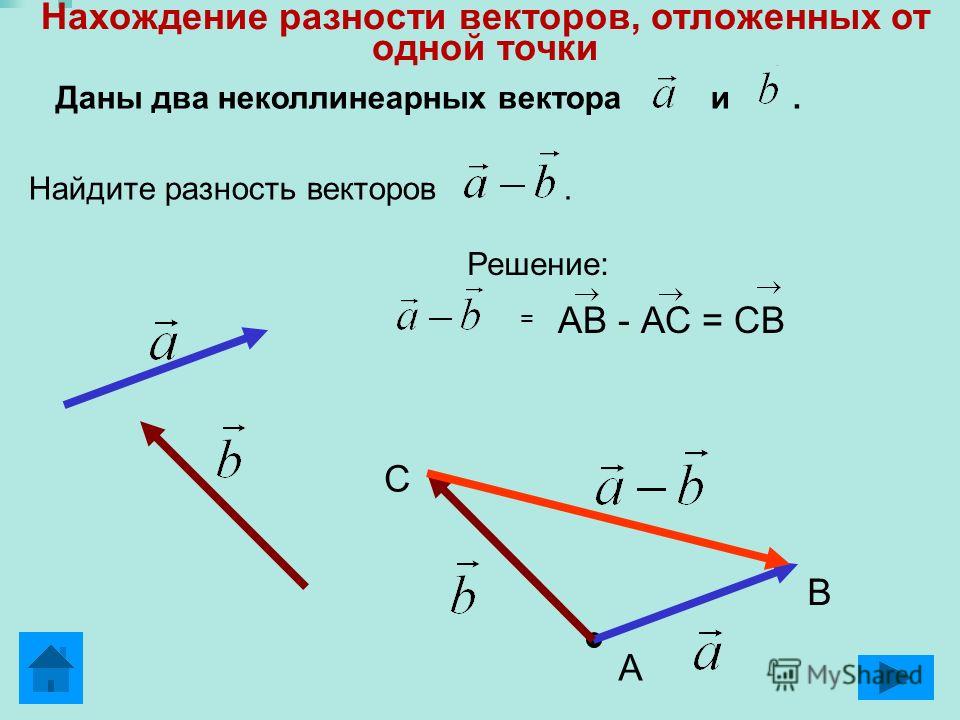
Два вектора называются равными, если они имеют одинаковое направление и модуль, даже если они имеют разные начальные точки.
Вектор AB представляет собой вектор смещения, если точка смещена из положения A в положение B.


 0, 0.0, 3.0]
0, 0.0, 3.0]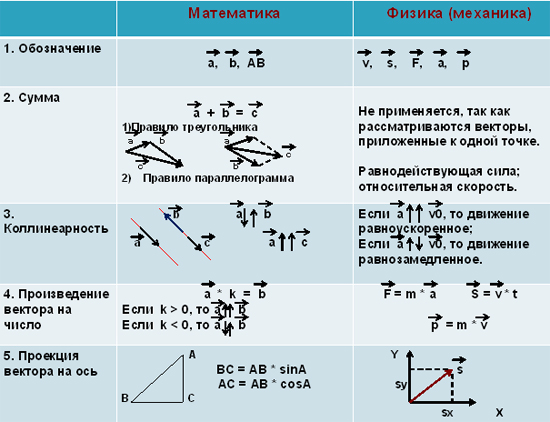

 Вектор используется в математике, и существует несколько типов векторов, включая нулевой вектор, единичный вектор, ко-начальный вектор, коллинеарный вектор, равный вектор, отрицательный вектор и многие другие. Векторы используются для представления физических объектов, поскольку они имеют как величину, так и направление.
Вектор используется в математике, и существует несколько типов векторов, включая нулевой вектор, единичный вектор, ко-начальный вектор, коллинеарный вектор, равный вектор, отрицательный вектор и многие другие. Векторы используются для представления физических объектов, поскольку они имеют как величину, так и направление.
 Например, если вектор AB->, если координаты A и координаты B совпадают, то вектор известен как нулевой вектор. Направление нулевого вектора неопределенно, и величина всегда равна нулю. Нулевой вектор не указывает ни в каком направлении и также имеет все компоненты, равные нулю.
Например, если вектор AB->, если координаты A и координаты B совпадают, то вектор известен как нулевой вектор. Направление нулевого вектора неопределенно, и величина всегда равна нулю. Нулевой вектор не указывает ни в каком направлении и также имеет все компоненты, равные нулю. Тогда вектор OA-> известен как вектор положения, имеющий начало отсчета 0. Вектор положения в основном используется для обозначения местоположения или положения точки в трехмерной декартовой системе измерений. И позиция определяется из любого опорного источника.
Тогда вектор OA-> известен как вектор положения, имеющий начало отсчета 0. Вектор положения в основном используется для обозначения местоположения или положения точки в трехмерной декартовой системе измерений. И позиция определяется из любого опорного источника.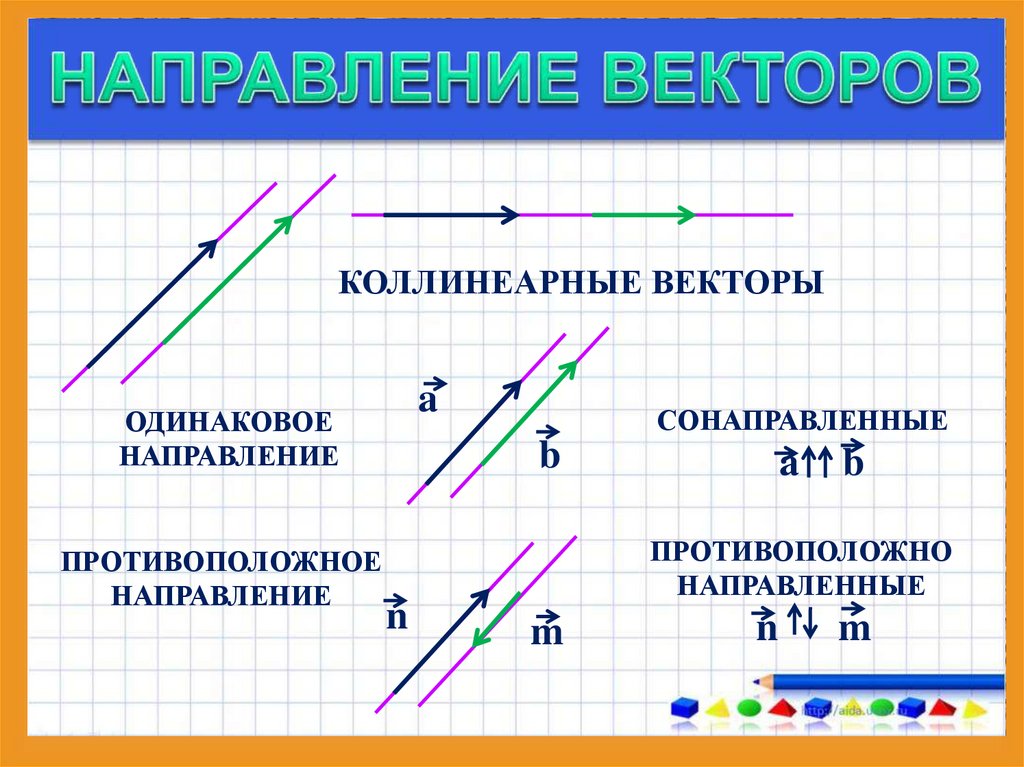 Векторы, которые имеют противоположное направление независимо друг от друга, известны как непохожие векторы.
Векторы, которые имеют противоположное направление независимо друг от друга, известны как непохожие векторы.