Теорема о накрест лежащих углах / Параллельные прямые / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема о накрест лежащих углах
Теорема
| Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. |
Дано: , АВ — секущая, 1 и 2 — накрест лежащие (Рис.1).
Доказать: 1 =2.
Доказательство:
Предположим,что углы 1 и 2 не равны друг другу. Отложим от луча АВ угол РАВ, равный углу 
2).
По построению накрест лежащие углы РАВ и 2 равны, значит АР (по признаку параллельности двух прямых). То есть мы получили, что через точку А проходят две прямые и АР, параллельные прямой . Но это противоречит аксиоме параллельных прямых. Значит наше предположение неверно и 1 = 2. Что и требовалось доказать.
Следствие
| Если прямая перпендикулярна к одной из двух параллельных прямых , то она перпендикулярна и к другой. |
Дано: , (Рис.3).
Доказать: .
Доказательство:
Прямая пересекает прямую , при этом , значит пересекает и прямую (смотри следствие 20 из аксиомы параллельных прямых).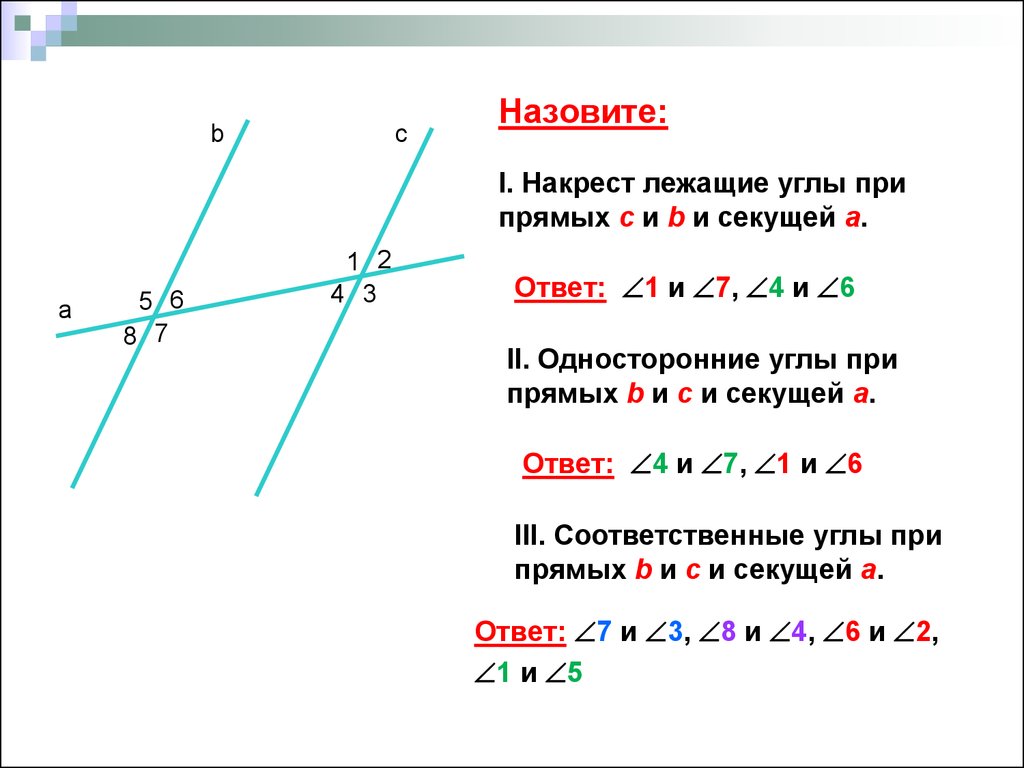
При пересечении параллельных прямых и секущей образуются равные накрест лежащие углы: 1 =2 (по теореме о накрест лежащих углах). По условию , т.е. 1 = 900, значит и 2 = 900 , т.е. . Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 201, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 220, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 245, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 374, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 375, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 428, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 625, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 891, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Теорема о равенстве накрест лежащих углов
Урок 17.
Геометрия 7 классТак как на данном уроке будем рассматривать теорему, которая является обратной признаку параллельности прямых по равенству накрест лежащих углов, то сначала и выясняем, что же называют теоремой, обратной данной. Затем мы приводим формулировку и доказательство теоремы, а после решаем задачи.
Конспект урока «Теорема о равенстве накрест лежащих углов»
В формулировке любой теоремы можно выделить две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – это то, что надо доказать.
Например, рассмотрим один из признаков параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Здесь условие утверждения: если при пересечении двух прямых секущей накрест лежащие углы равны. А заключение: прямые параллельны.
Теоремой, обратной
данной, называется такая теорема, в которой условием является заключение
данной теоремы, а заключением — условие данной теоремы.
Теорема:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Доказательство:
Пусть прямые а и b параллельны и пересечены секущей CD. Доказать, что накрест лежащие углы 1 и 2 равны.
Предположим, что углы 1 и 2 не равны. Тогда от луча CD отложим ∠ЕCD=∠2 так, чтобы ∠ЕCD и ∠2 были накрест лежащими углами при пересечении прямых СЕ и b секущей CD.
По построению эти накрест лежащие углы равны, а поэтому прямая CE параллельна прямой b. Получили, что через точку С проходят две прямые (а и CЕ) параллельные прямой b. А это противоречит аксиоме параллельности прямых. Следовательно, предположение неверно и угол ∠1=∠2. Что и требовалось доказать.
Пример.
Прямая АВ параллельна прямой CD, АD — биссектриса угла BAC, а ∠ADC=50 градусов. Чему равна градусная мера ∠CAD?
Так
как прямые АВ и CD параллельны и AD — секущая при этих параллельных прямых, то
накрест лежащие углы ADC и BAD равны. Значит, ∠BAD=50
градусов.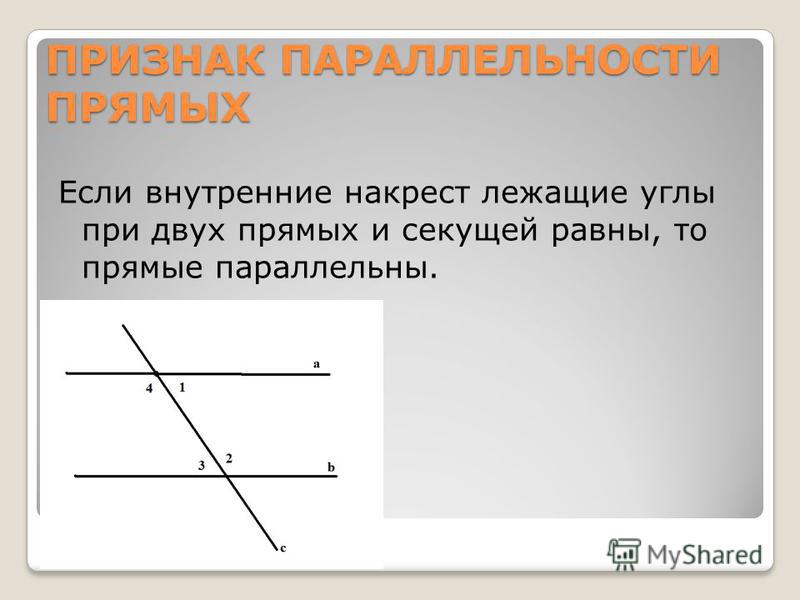
Так как AD — биссектриса ∠BAC, то ∠CAD=∠BAD. Следовательно, градусная мера ∠CAD=50 градусов.
Пример.
Прямые АВ и CD параллельны. Отрезок АВ=СD. Доказать, что прямая АС параллельна прямой BD.
Рассмотрим треугольник ABD и треугольник ACD.
АВ=CD по условию задачи, AD — общая. А углы BAD и ADC равны как накрест лежащие углы при параллельных прямых АВ и CD и секущей АD. Следовательно, треугольники ABD и ACD равны по первому признаку равенства треугольников. А значит, у них соответственные стороны и углы равны.
То есть ∠CAD=∠BDA. А эти углы являются накрест лежащими при прямых AC и BD и секущей AD. Это означает, что прямые AC и BD параллельны. Что и требовалось доказать.
Пример.
На рисунке ∠CBD=∠ADB. Доказать, что ∠ВСА=∠CAD.
Углы CBD и ADB — накрест лежащие углы при прямых AD и BC и секущей BD. А так как эти углы равны, то прямые AD и BC параллельны.
∠ВСА
и ∠CAD
являются накрест лежащими при параллельных прямых AD и BC и секущей АС, а
следовательно, они равны.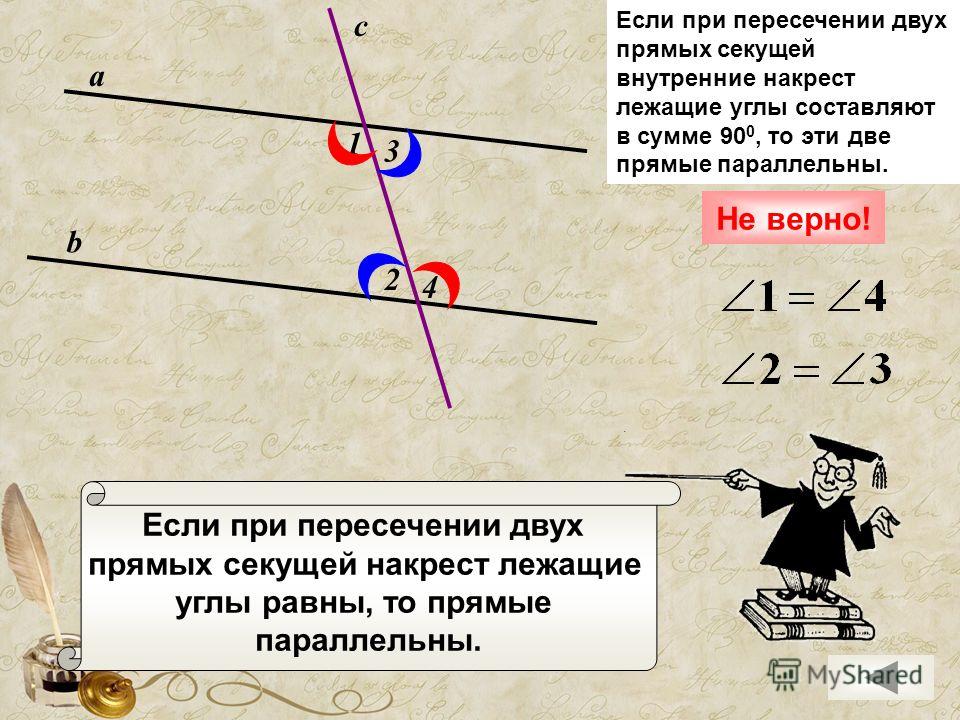
Что и требовалось доказать.
Отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.
Например, если углы вертикальные, то они равны. А вот если углы равны, то это ещё не означает, что они вертикальные.
Предыдущий урок 16 Аксиома параллельных прямых
Следующий урок 18 Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 7 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Внутренние углы с одной стороной — определение, теорема, примеры
Внутренние углы с одной стороной — это два угла, которые находятся внутри (между) двух прямых и, в частности, на одной стороне поперечной.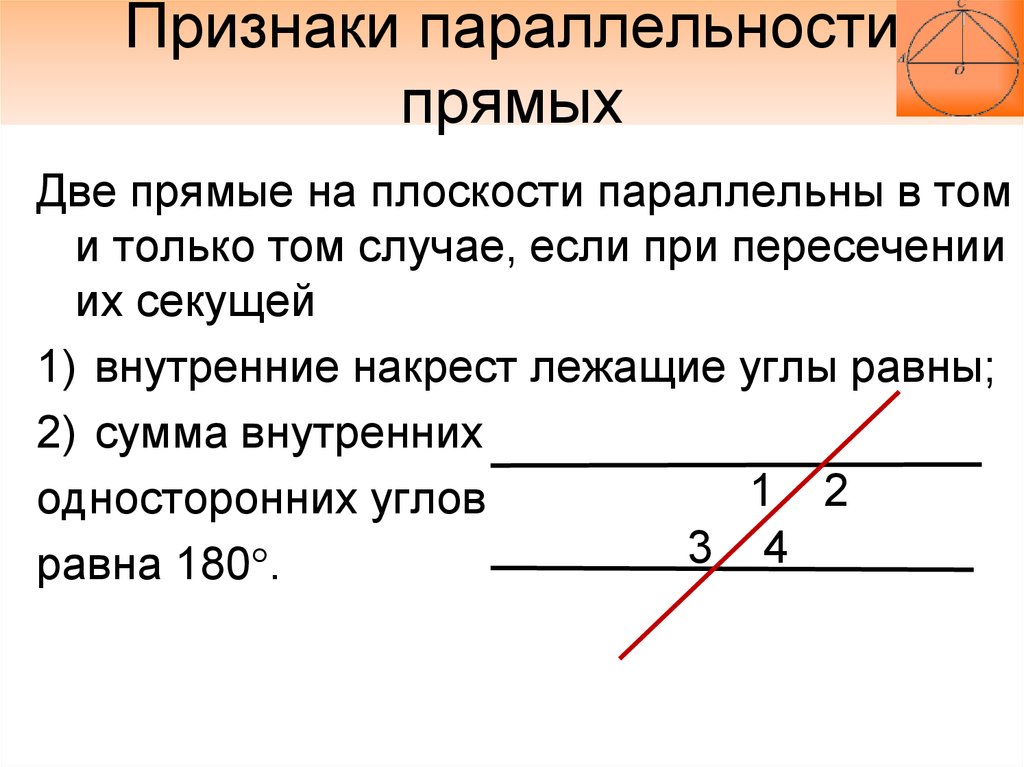
Внутренние углы одной стороны в сумме составляют 180 градусов. При пересечении двух параллельных прямых поперечной они образовали 4 внутренних угла. Два несмежных внутренних угла, лежащих по одну сторону от секущей, являются дополнительными.
| 1. | Что такое внутренние углы с одной стороны? |
| 2. | Теорема об односторонних внутренних углах. |
| 3. | Теорема об обратном преобразовании внутренних углов одной стороны|
| 4. | Часто задаваемые вопросы об односторонних внутренних углах |
Что такое внутренние углы с одной стороны?
При пересечении двух параллельных прямых секущей образуется 8 углов. Односторонние внутренние углы — это пара несмежных внутренних углов, лежащих по одну сторону от секущей.
Таким образом, внутренние углы одинаковых сторон:
- не имеют общих вершин или имеют разные вершины
- лежать между двумя линиями
- и формируется на той же стороне поперечной
«Внутренние углы одной стороны» также известны как «совместные внутренние углы».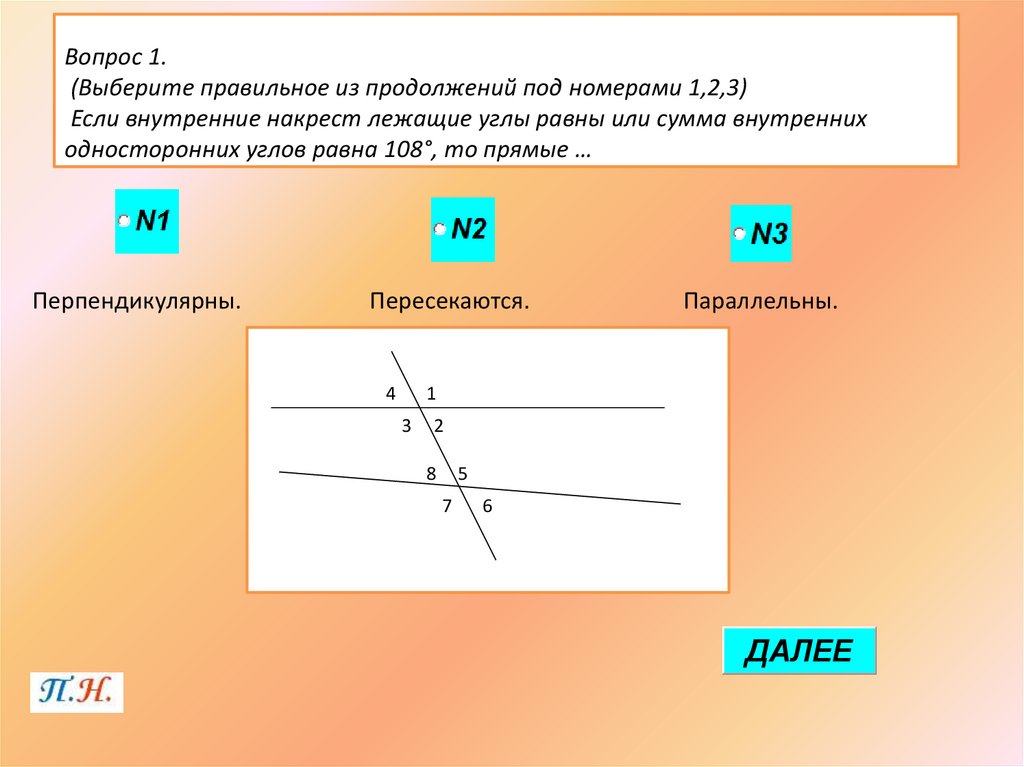
Сформированные таким образом 8 углов классифицируются по различным типам углов, перечисленных ниже:
- Альтернативные внутренние углы
- Соответствующие углы
- Альтернативные внешние углы
- Внутренние углы с одной стороны или совмещенные внутренние углы
На данном рисунке линия AB || CD и прямая l является секущей.
Из «Внутренних углов одной стороны — определение» пары внутренних углов одной стороны на рисунке выше:
- 4 и 5
- 3 и 6
Внутренние углы одной стороны Теорема
Рассмотрим приведенный выше рисунок. На приведенном выше рисунке прямые AB и CD параллельны, а L — поперечной. Мы только что прочитали, что пары внутренних углов с одной и той же стороной на приведенном выше рисунке равны:
- ∠4 и ∠5
- ∠3 и ∠6
Отношение между внутренними углами одной и той же стороны определяется теоремой о внутреннем угле одной и той же стороны.
Теорема для «теоремы об одном и том же внутреннем угле» утверждает: Если секущая пересекает две параллельные прямые, каждая пара односторонних внутренних углов является дополнительной (их сумма равна 180°).
Внутренние углы одной стороны Доказательство теоремы
Еще раз обратимся к приведенному выше рисунку:
∠4 = ∠8 и ∠3 = ∠7 [соответствующие углы равны].
∠5 + ∠8 = 180° и ∠6 + ∠7 = 180° [линейная пара углов].
Из двух предыдущих уравнений
∠4 + ∠5 = 180°
Аналогично, ∠3 + ∠6 = 180°
Отсюда доказано, что каждая пара односторонних внутренних углов является дополнительной.
Обращение внутренних углов одной стороны Теорема
Теорема, обратная теореме об одностороннем внутреннем угле, утверждает, что если секущая пересекает две прямые так, что пара односторонних внутренних углов является дополнительной, то эти две прямые параллельны.
Обратное преобразование внутренних углов одной стороны Доказательство теоремы
Учитывая тот же рисунок выше,
Предположим, что
∠4 + ∠5 = 180° ⇒ (1)
Поскольку ∠5 и ∠8 образуют линейную пару,
∠5 + ∠8 = 180° ⇒ (2)
Из (1) и (2),
∠4 = ∠8
Таким образом, пара соответствующих углов равна, что может произойти только в том случае, если две прямые параллельны.
Таким образом, доказана обратная теорема о внутреннем угле той же стороны.
Важные примечания
Ниже приведены важные моменты, относящиеся к внутренним углам одной стороны.
- Односторонние внутренние углы несмежны и образованы на одной стороне поперечной.
- Две прямые параллельны тогда и только тогда, когда внутренние углы с одинаковыми сторонами являются дополнительными.
☛ Статьи по теме
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о внутренних углах с одной и той же стороной и связанных с ними темах.
- Сегмент линии
- Линии и углы. Основные термины
- Формула параллельных линий
- Дополнительные уголки
- Пересекающиеся и непересекающиеся линии
- Параллельные линии
Часто задаваемые вопросы об односторонних внутренних углах
Почему внутренние углы с одной и той же стороной равны?
Внутренние углы с одинаковыми сторонами НЕ равны.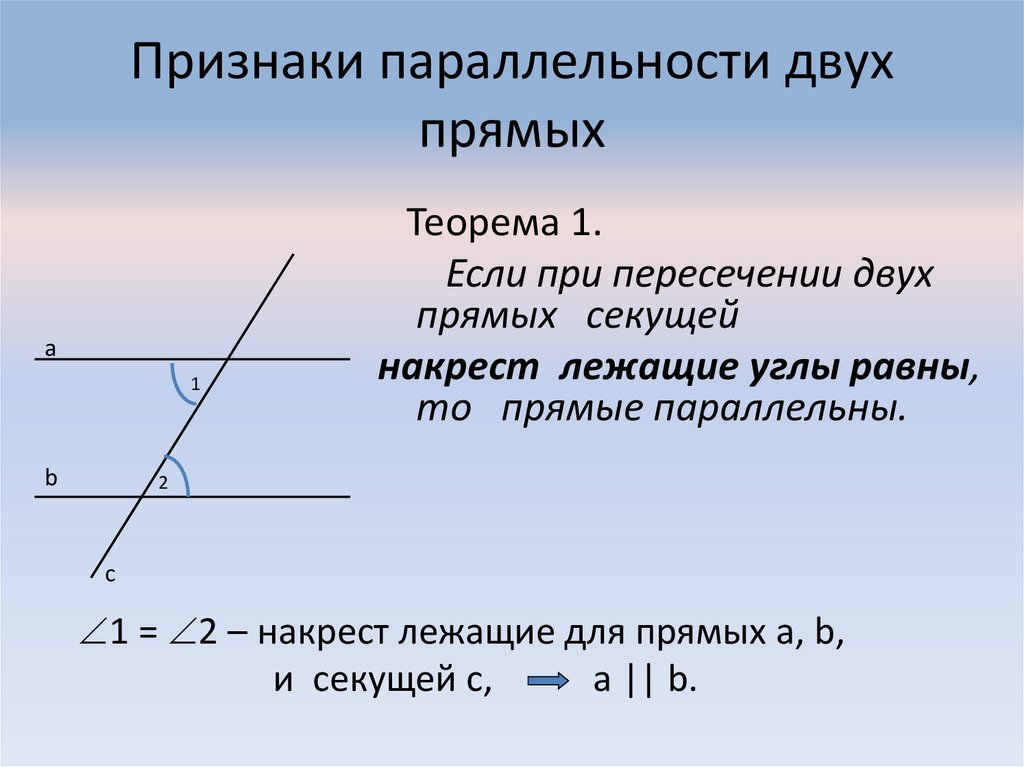
Они являются дополнительными. Такие же боковые внутренние углы образуются при пересечении двух параллельных прямых секущей. Внутренние углы с одинаковыми сторонами могут быть равны только тогда, когда каждый угол равен 90 градусов, потому что тогда сумма внутренних углов одной и той же стороны равна 180 градусам.
Смежны ли внутренние углы одной стороны?
Внутренние углы с одинаковыми сторонами всегда несмежны, потому что углы образованы на двух разных прямых, параллельных друг другу.
Чему равна сумма двух одинаковых боковых внутренних углов на поперечной?
При пересечении двух параллельных прямых секущей они образуют односторонние внутренние углы, сумма которых равна 180 градусам. Так как сумма внутренних углов одной и той же стороны равна 180 градусов, то углы являются дополнительными.
Чему равно обратное значение внутренних углов одной стороны?
Обратное значение внутреннего угла с одной и той же стороной утверждает, что если две прямые пересекаются секущей, а внутренние углы с одной и той же стороны являются дополнительными, или мы можем сказать, что сумма внутренних углов с одной и той же стороны равна 180 градусам, то прямые равны говорят параллельны.
Каково другое название внутренних углов одной стороны?
Внутренние углы с одной и той же стороной также известны как последовательные внутренние углы, поскольку углы находятся на одной стороне поперечной, но внутри двух параллельных линий.
В чем разница между одинаковыми боковыми внутренними углами и одинаковыми боковыми внешними углами?
При пересечении двух параллельных прямых поперечной линией образовалось 8 углов. Внутренние углы с одинаковыми сторонами — это углы внутри параллельных прямых по одну сторону от секущей, а внешние углы с одинаковыми сторонами — это углы вне параллельных прямых по ту же сторону от секущей.
В чем разница между внутренними углами одной стороны и соответствующими углами?
Разница между внутренними углами одной стороны и соответствующими углами состоит в том, что соответствующие углы равны, тогда как в случае внутренних углов одной стороны сумма внутренних углов одной стороны равна 180 градусам, только если поперечная линия пересекает две параллельные линии.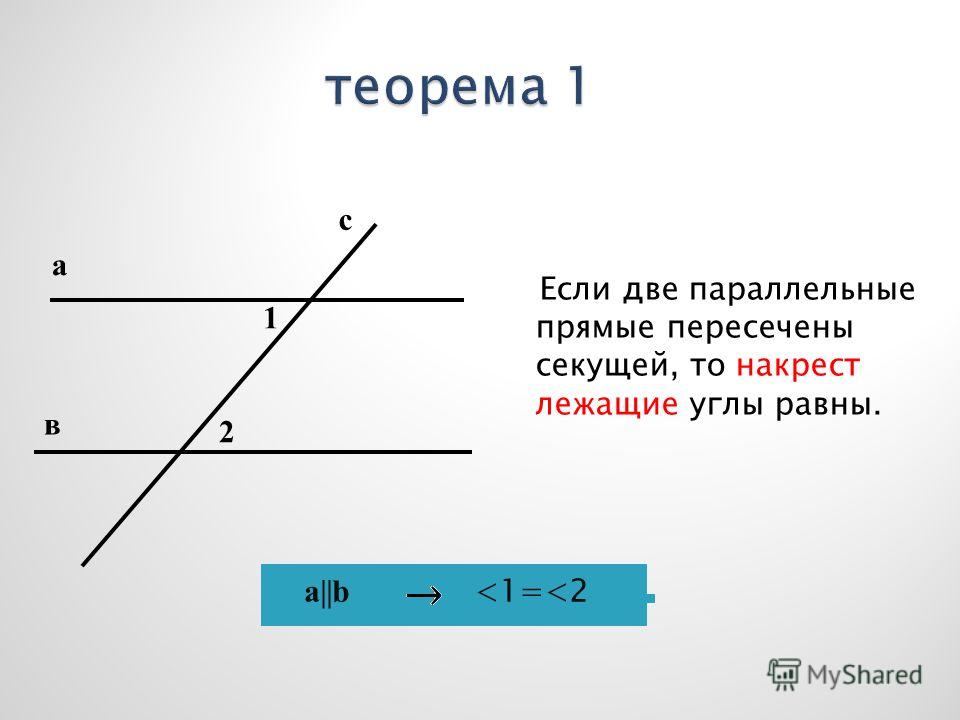
Альтернативные внутренние углы – определение, теоремы, примеры
Альтернативные внутренние углы – это углы, образованные на противоположных сторонах секущей. Другими словами, при пересечении двух параллельных прямых секущей образуется восемь углов. Среди них углы, которые лежат на внутренней стороне параллельных прямых, но на противоположных сторонах поперечной, известны как альтернативные внутренние углы.
| 1. | Что такое альтернативные внутренние углы? |
| 2. | Обращение теоремы о чередующихся внутренних углах |
| 3. | Как найти альтернативные внутренние углы? |
| 4. | Часто задаваемые вопросы по альтернативным внутренним углам |
Что такое альтернативные внутренние углы?
При пересечении двух параллельных прямых секущей пара углов, образованных на внутренней стороне параллельных прямых, но на противоположных сторонах секущей, называется параллельными внутренними углами.
Эти углы всегда равны. Это можно понять и по-другому. Альтернативные внутренние углы могут доказать, параллельны ли данные прямые или нет. Если эти углы равны, то данные прямые, пересекаемые секущей, называются параллельными.
На следующем рисунке показаны альтернативные внутренние углы. Здесь AB и CD — две параллельные прямые, пересекаемые секущей.
По теореме о чередующихся внутренних углах пары чередующихся внутренних углов на рисунке выше:
- ∠4 и ∠6
- ∠3 и ∠5
Давайте кратко обсудим, что такое альтернативные внешние углы и чем они отличаются от альтернативных внутренних углов.
Альтернативные внешние углы
Альтернативные внешние углы — это углы, которые имеют разные вершины, лежат на противоположных сторонах секущей и являются внешними по отношению к прямым. При пересечении секущей двух параллельных прямых образующиеся параллельные внешние углы всегда равны. На том же рисунке ∠1 и ∠7 и ∠2 и ∠8 представляют собой пары чередующихся внешних углов.
Обращение теоремы о чередующихся внутренних углах
Согласно обратной теореме о чередующихся внутренних углах, если секущая пересекает две прямые так, что внутренние углы равны, то эти две прямые называются параллельными.
Поясним это с помощью следующего рисунка, который показывает: ∠1 = ∠5 (соответствующие углы), ∠3 = ∠5 (вертикально противоположные углы). Таким образом, ∠1 = ∠3. Аналогично можно доказать, что ∠2 = ∠4. Это доказывает, что, поскольку внутренние углы у двух заданных прямых равны, эти прямые параллельны друг другу.
Как найти альтернативные внутренние углы?
Согласно теореме о параллельных внутренних углах параллельные внутренние углы двух параллельных прямых равны. Мы используем этот факт, чтобы найти альтернативные внутренние углы. Давайте разберемся в этом на примере.
Пример : На следующем рисунке показана карта, на которой дорога с названием Шестая авеню проходит перпендикулярно улицам 1 st и 2 nd Street, которые параллельны друг другу.
Другая дорога под названием Мейпл-авеню образует угол 40° с 2 -я улица . Сможете ли вы найти величину угла x?
Решение:
Следуя теореме о чередующихся внутренних углах, если две улицы параллельны, а Мэйпл-авеню считается поперечной, то x и 40° являются альтернативными внутренними углами. Следовательно, оба угла равны. Следовательно, х = 40°.
Важные примечания
- Каждая пара чередующихся внутренних углов равна.
- Каждая пара внутренних углов является дополнительной.
- Каждая пара соответствующих углов равна.
- Каждая пара альтернативных внешних углов равна.
Задающий вопрос
На следующем рисунке \(\mathrm{AB}\|\mathrm{CD}\| \mathrm{EF}\)
Найдите значение x.
☛Темы, связанные с альтернативными внутренними углами
Ознакомьтесь с перечисленными ниже интересными статьями, чтобы узнать больше об альтернативных внутренних углах и связанных темах.
- Вертикальные углы
- Альтернативные углы
- Внутренние углы с одной стороны
- Калькулятор внутренних углов многоугольника
Часто задаваемые вопросы об альтернативных внутренних углах
Что такое альтернативные внутренние углы в геометрии?
В геометрии для определения альтернативных внутренних углов нам необходимо проверить следующие перечисленные характеристики:
- Альтернативные внутренние углы равны по размеру.
- Они лежат по разные стороны поперечной.
- Они лежат между внутренней частью двух линий.
- Другими словами, углы, которые лежат на внутренней стороне параллельных прямых, но на противоположных сторонах поперечной.
Как решить альтернативные внутренние углы?
Согласно теореме о внутренних углах, если две параллельные прямые пересечены секущей, то внутренние углы равны по величине. Используя эту теорему, мы можем найти меру альтернативного внутреннего угла, если мы знаем меру соответствующего альтернативного внутреннего угла.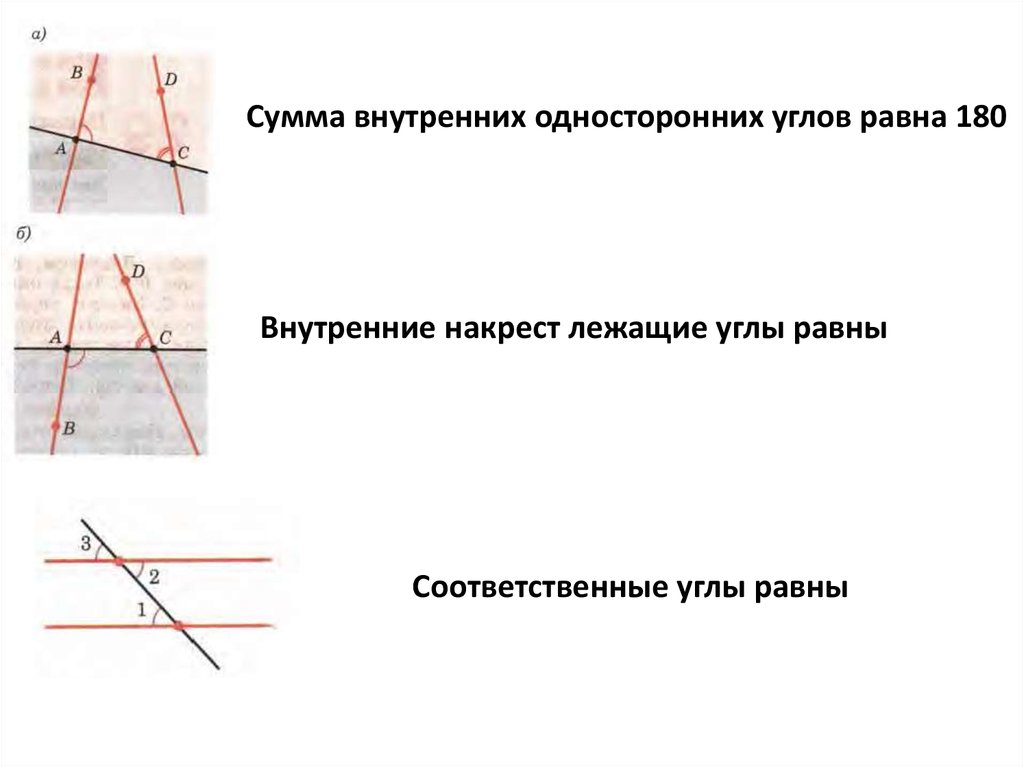
Что является обратной теоремой о чередующихся внутренних углах?
Согласно теореме, обратной теореме о чередующихся внутренних углах, если секущая пересекает две прямые так, что внутренние углы равны, то эти две прямые называются параллельными.
В чем разница между альтернативными внутренними и внешними углами?
Альтернативные внутренние углы — это углы, имеющие разные вершины, лежащие на противоположных сторонах секущей и находящиеся между внутренней частью двух прямых. В то время как противоположные внешние углы — это те углы, которые имеют разные вершины, они лежат на противоположных сторонах секущей, но они лежат на внешней стороне двух прямых.
В чем разница между соответствующими и альтернативными углами?
Соответствующие углы — это два угла, лежащие по одну сторону от секущей, в которой один внутренний, а другой внешний. Боковые углы — это два угла, лежащие по разные стороны от секущей.
Как решить альтернативные внутренние углы?
Согласно теореме о внутренних углах, если две параллельные прямые пересечены секущей, то внутренние углы равны по величине.