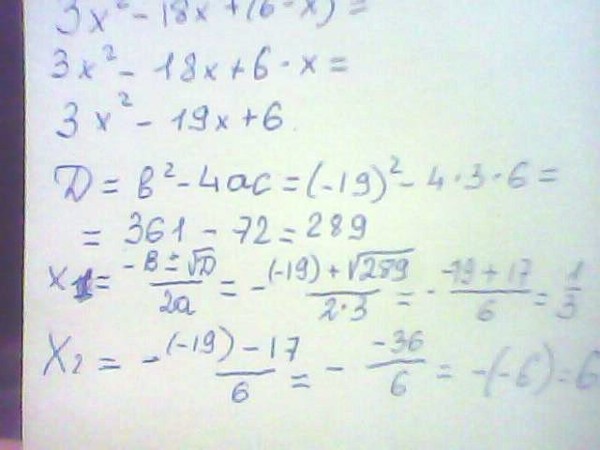Во второй степени х: решите уравнение: 1)x во второй степени-9= 02)y во второй степени-4= 0 3)121-x во второй степени=…

Решение систем уравнений второй степени и решение задач с помощью таких систем 9 класс онлайн-подготовка на Ростелеком

Тема 8.

Решение систем уравнений второй степени и решение задач с помощью таких систем.

Какие основные способы решения систем уравнений вы знаете? (методы сложения, подстановки, графический)

Каким способом можно решить систему, одно из уравнений которой – уравнение второй степени?

Такие системы всегда можно решить способом подстановки. Для этого поступают следующим образом:

1. Выражают из уравнения первой степени одну переменную через другую;
2. Подставляют полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;
3. Решают получившееся уравнение с одной переменной;
4. Находят соответствующие значения второй переменной.

Рассмотрим пример:

Решим систему уравнений:

x2+y=14,y-x=8;

Выразим из первого уравнения переменную y и подставим во второе:

y=14-x2,14-x2-x=8;

Решим второе уравнение, относительно х:

x² + x — 6 = 0, корни которого равны (– 3) и 2.

Вернемся к системе:

x1=-3,y1=14—32;

x1=-3,y1=14—32;

x1=-3,y1=5;

x2=2,y2=10;

Рассмотрим еще один пример, решим систему

x2-y2=17,x-y=2;

Эту систему так же можно решить методом подстановки, выразив переменную x, но можно упростить первое уравнение.

Заметим, что левую часть первого уравнения можно разложить на множители по формуле разности квадратов, получим:

x-yx+y=17,x-y=2;

Из второго уравнения разность x — y = 2.

2x+y=17,x-y=2;

2x+y=17,x-y=2;

Разделим обе части первого уравнения на 2, получим:

x+y=8,5,x-y=2;

А эту систему давай решим методом сложения, сложим два уравнения, а затем из первого уравнения вычтем второе, получим:

2x=10,5,2y=6,5;

x=5,25,y=3,25.

А теперь решим несколько задач с помощью систем: уравнений второй системы:

Сумма двух чисел равна 12, а их произведение равно 35. Найдите эти числа.

Пусть число x – первое число, а y – второе число. Тогда получим:

x+y=12,x∙y=35;

Выразим из первого уравнения переменную х и подставим во второе, получим:

x=12-y,x∙y=35;

x=12-y,12-yy=35;

Решим уравнение:

12y — y² — 35 = 0

y² — 12y + 35 = 0

Получим корни 5 и 7.

Возвращаемся к нашей системе:

y1=55x=35

y2=7,7x=35;

y1=5×1=7

y2=7×2=5

Ответ: (7;5) и (5;7)

Рассмотрим еще одну задачу:

Площадь прямоугольного треугольника равен 24 см², а его гипотенуза равна 10 см. Каковы катеты треугольника?

Пусть a – длина одного катета, а b – длина второго катета.

Вспомним формулу площади прямоугольного треугольника и теорему Пифагора:

Итак, площадь равна половине произведения катетов.

А квадрат гипотенузы равен сумме квадратов катетов:

12ab=24a2+b2=100

Решим эту систему, первое уравнение домножим на 2, получим:

ab=48a2+b2=100

Выразим переменную а из первого уравнения и подставим во второе, получим:

a=48b48b2+b2=100

Решим второе уравнение системы:

2304b2+b2-100=0,

b4-100b2+2304=0, решим это биквадратное уравнение:

Пусть b² = t, тогда получим:

t² — 100t + 2304 = 0, отсюда

t₁ = 64, t₂ = 36

Возвращаемся к нашей замене, получим:

b1,2=±8,b3,4=±6, так как b – это длина катета, то она не может быть отрицательной, следовательно, b равно 6 или 8, тогда второй катет равен 8 или 6 соответственно.

Математика

Литература

Алгебра

Русский язык

Геометрия

Английский язык

Физика

Биология

Другие предметы

История

Обществознание

Окружающий мир

География

Українська мова

Українська література

Қазақ тiлi

Беларуская мова

Информатика

Экономика

Музыка

Французский язык

Немецкий язык

МХК

ОБЖ

Психология

— почему квадратный корень из x равен x в половине степени

Задавать вопрос

спросил

Изменено 4 года, 11 месяцев назад

Просмотрено 94k раз

$\begingroup$ 9(2x+b)

Второе выражение должно быть справа от первого выражения, немного меньше и выше его.

Звучит достаточно просто, но я не могу понять правильно.

Любая помощь — это стиль и макет, спасибо.

• html
• css

HTML довольно ограничен, когда дело доходит до математических выражений. В принципе, спецификации HTML предполагают использование элемента sup для надстрочных индексов, поэтому пример выражения будет равен 9.0003

 (a + b + √c)2x + b
 

 (a< /i> + b + √c)2x + b
 

 .sup {
  положение: родственник;
  низ: 1экс;
  размер шрифта: 80%;
}
 

 ax