Решение
Вычисление матрицы $D$ начнем с нахождения результата произведения $AB$. Матрицы $A$ и $B$ можно перемножать, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. Обозначим $F=AB$. При этом матрица $F$ будет иметь три столбца и три строки, т.е. будет квадратной (если этот вывод кажется неочевидным, посмотрите описание умножения матриц в первой части этой темы). Найдем матрицу $F$, вычислив все её элементы:
$$
F=A\cdot B=\left(\begin{array} {cccc}
1 & 0 & -1 & 2 \\
3 & -2 & 5 & 0 \\
-1 & 4 & -3 & 6
\end{array} \right)\cdot \left(\begin{array} {ccc}
-9 & 1 & 0 \\
2 & -1 & 4 \\
0 & -2 & 3 \\
1 & 5 & 0
\end{array} \right)\\
\begin{aligned}
& f_{11}=1\cdot (-9)+0\cdot 2+(-1)\cdot 0+2\cdot 1=-7; \\
& f_{12}=1\cdot 1+0\cdot (-1)+(-1)\cdot (-2)+2\cdot 5=13; \\
& f_{13}=1\cdot 0+0\cdot 4+(-1)\cdot 3+2\cdot 0=-3;\\ \\
& f_{21}=3\cdot (-9)+(-2)\cdot 2+5\cdot 0+0\cdot 1=-31;\\
& f_{22}=3\cdot 1+(-2)\cdot (-1)+5\cdot (-2)+0\cdot 5=-5;\\
& f_{23}=3\cdot 0+(-2)\cdot 4+5\cdot 3+0\cdot 0=7;\\ \\
& f_{31}=-1\cdot (-9)+4\cdot 2+(-3)\cdot 0+6\cdot 1=23; \\
& f_{32}=-1\cdot 1+4\cdot (-1)+(-3)\cdot (-2)+6\cdot 5=31;\\
& f_{33}=-1\cdot 0+4\cdot 4+(-3)\cdot 3+6\cdot 0=7.
Умножим матрицы в правой части равенства на соответствующие числа (т.е. на 2, 3 и 7):
$$ 2\cdot \left(\begin{array} {ccc} -7 & 13 & -3 \\ -31 & -5 & 7 \\ 23 & 31 & 7 \end{array} \right)-3\cdot \left(\begin{array} {ccc} -5 & 10 & 3 \\ -20 & 12 & -15 \\ 13 & 9 & 8 \end{array} \right)+7\cdot \left(\begin{array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)=\\= \left(\begin{array} {ccc} -14 & 26 & -6 \\ -62 & -10 & 14 \\ 46 & 62 & 14 \end{array} \right)-\left(\begin{array} {ccc} -15 & 30 & 9 \\ -60 & 36 & -45 \\ 39 & 27 & 24 \end{array} \right)+\left(\begin{array} {ccc} 7 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 7 \end{array} \right) $$
Выполним последние действия: вычитание и сложение:
$$
\left(\begin{array} {ccc}
-14 & 26 & -6 \\
-62 & -10 & 14 \\
46 & 62 & 14
\end{array} \right)-\left(\begin{array} {ccc}
-15 & 30 & 9 \\
-60 & 36 & -45 \\
39 & 27 & 24
\end{array} \right)+\left(\begin{array} {ccc}
7 & 0 & 0 \\
0 & 7 & 0 \\
0 & 0 & 7
\end{array} \right)=\\
=\left(\begin{array} {ccc}
-14-(-15)+7 & 26-30+0 & -6-9+0 \\
-62-(-60)+0 & -10-36+7 & 14-(-45)+0 \\
46-39+0 & 62-27+0 & 14-24+7
\end{array} \right)=
\left(\begin{array} {ccc}
8 & -4 & -15 \\
-2 & -39 & 59 \\
7 & 35 & -3
\end{array} \right).

Ответ: $f(A)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right)$.
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
2.4. Возведение матрицы в целую положительную степень
Операция возведения квадратной матрицы в степень определяется в виде:
.
По определению полагают . Легко показать, что .
Замечание 1.3. Возведение в степень матрицы может привести к нулевой матрице.
Замечание 1.4. Операция возведения в степень определена только для квадратных матриц.
Пример выполнения задания:
Найдите значение матричного многочлена
.
Решение:
Ответ: .
Для самостоятельного решения:
а) Найдите матрицу .
1. ; 2. ; 3. .
б) Найдите значение матричного многочлена .
1. ; 2. ;
3. . 4. .
2.5. Транспонирование матрицы
Транспонирование – это замена строк столбцами. Например, пусть дана матрица А размерностью :
.
Если в матрице А поменять местами строки и столбцы, то получится матрица, транспонированная к данной, обозначаемая :
.
1. Двойное транспонирование возвращает исходную матрицу: .
2. Транспонирование суммы матриц эквивалентно сумме транспонирования слагаемых: .
3. Транспонирование
произведения двух матриц эквивалентно
произведению транспонированных матриц,
взятых в обратном порядке: .
4. Произведение матрицы на свою транспонированную или всегда имеет результатом симметричную квадратную матрицу.
5. Если матрица А – квадратная, то значение ее определителя не зависит от транспонирования: .
Примеры выполнения заданий:
Задача 1. Транспонируйте матрицу .
Решение:
Записывая первую и вторую строки матрицы А как первый и, соответственно, второй столбец матрицы , получим матрицу .Ответ: .
Задача 2. Транспонируйте матрицу .
Решение:
Так как у матрицы А две строки и три столбца, то у матрицы будет три строки и два столбца: .
Ответ: .
Для самостоятельного решения:
а) Найдите матрицу
1. ; 2. ;
3. ; 4.
;
; 4.
;
5. .
б) Найдите произведение матриц и .
1. ; 2. ;
3. ; 4. .
2.6. Вычисление обратной матрицы
Определение. Матрица называется обратной для квадратной матрицы
Матрица А имеет обратную тогда и только тогда, когда её определитель не равен нулю.
Определение. Матрица называется невырожденной, если ее определитель не равен нулю.
Квадратная матрица А, определитель которой не равен нулю, имеет единственную обратную матрицу
, где матрицы А. алгебраическое дополнение к элементу матрицы А.
Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)
1. Найти определитель
матрицы А. Если определитель отличен
от нуля, то матрица имеет обратную
матрицу.
2. Поменять местами столбцы матрицы (транспонировать матрицу) А.
3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы А его алгебраическим дополнением: , – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i-ой строки и j-го столбца.
4. Вычисляем обратную матрицу .
5. Проверить правильность вычисления обратной матрицы по формуле: .
Примеры выполнения заданий:
Задача 1. Найти матрицу, обратную к матрице А, если дана матрица .
Решение: Применим алгоритм нахождения обратной матрицы.
1. Найти определитель матрицы А. Если определитель отличен от нуля, то матрица имеет обратную матрицу.
Матрица имеет
обратную матрицу, так как .
2. Найдем матрицу , транспонированную к матрице А: .
3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы
.
4. Вычисляем обратную матрицу .
5. Проверим правильность вычисления обратной матрицы по формуле:
.
Ответ:
Задача 2. Найдите матрицу, обратную к данной матрице .
1. Найдем .
2. Найдем матрицу :___________________________.
3. Найдем алгебраические
дополнения элементов матрицы
:___________________
.
4. Вычисляем обратную матрицу :
_____________________________________________________________________________
.
5. Проверим правильность вычисления обратной матрицы по формуле:
______________________________________________________________________________.
Ответ: .
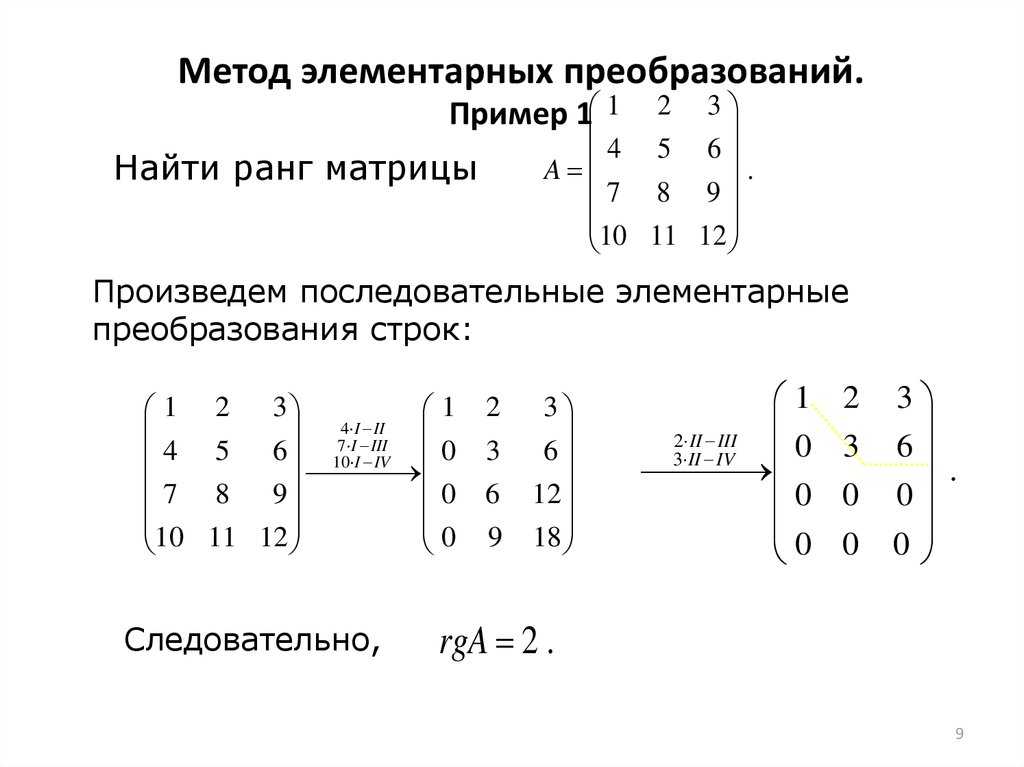
Элементарными преобразованиями строк (столбцов) матрицы называются:
а) умножение i-ой строки (столбца) матрицы на число ;
б) прибавление к i-ой строке (столбцу) j-ой строки (столбца), умноженной на ;
в) перестановка i-ой и j-ой строк (столбцов) матрицы.
Numpy. Матричные вычисления — Документация compute 0.1
Numeric Python (NumPy)- это несколько модулей для вычислений с многомерными массивами, необходимых для многих
численных приложений. Массив — это набор однородных элементов, доступных по индексам. Массивы модуля Numeric
могут быть многомерными, то есть иметь более одной размерности. Количество размерностей и длина массива по
каждой оси называются формой массива (shape). Размещение массива в памяти проводится в соответствии с опциями
и может быть выполнено как в языке С (по последнему индексу), как в языке Fortran (по первому индексу) или
беспорядочно.
Массивы модуля Numeric
могут быть многомерными, то есть иметь более одной размерности. Количество размерностей и длина массива по
каждой оси называются формой массива (shape). Размещение массива в памяти проводится в соответствии с опциями
и может быть выполнено как в языке С (по последнему индексу), как в языке Fortran (по первому индексу) или
беспорядочно.
Особо подчеркнем отличие массива от набора данных (списка или кортежа). Величины, входящие в массив имеют одинаковый тип и их количество жестко задается при инициализации. Элементы массива не являются объектами, это переменные в обычном понимании этого слова. Массивы позволяют экономить память и увеличивать скорость работы с большим количеством однотипных данных.
Как представлены массивы в Python? В Python массивы – это объекты, содержащие буфер данных и информацию о форме,
размерности, типе данных и т.д. Как и у любого объекта, у массива можно менять атрибуты напрямую: array.shape=(2,3) или через вызов функции np. reshape(array,(2,3)). Такая же ситуация и с методами
(функциями для массивов), заданными в этом классе, многие из них могут вызываться как методы array.resize(2,4) или как самостоятельные функции
reshape(array,(2,3)). Такая же ситуация и с методами
(функциями для массивов), заданными в этом классе, многие из них могут вызываться как методы array.resize(2,4) или как самостоятельные функции NumPy: np.resize(array,(2,4)).
Некоторые функции являются только методами: array.flat, array.flatten, array.T.
Для правильного использования таких функций, необходимо обращаться к их описанию.
Типы данных
В качестве элементов массива можно использовать множество типов, которые перечислены в таблице.
Типы Int, UnsignedInteger, Float и Complex соответствуют наибольшим принятым на данной платформе значениям.
| Тип | Описание | Тип | Описание |
|---|---|---|---|
| Логический | Числа с плавающей точкой | ||
| bool_ | Python bool | half | |
| bool8 | 8 бит | single | C float |
| Целый | double | C double | |
| byte | C char | float_ | Python float |
| short | C short | longfloat | C long float |
| intc | C int | float16 | 16 бит |
| int_ | Python int | float32 | 32 бит |
| longlong | C long long | float64 | 64 бит |
| intp | такой ,что может описывать указатели | float96 | 96 бит,??? |
| int8 | 8 бит | float128 | 128 бит ??? |
| int16 | 16 бит | Комплексные | |
| int32 | 32 бит | csingle | |
| int64 | 64 бит | complex_ | Python complex |
| Целый без знака (натуральное) | clongfloat | ||
| ubyte | C unsigned char | complex64 | два 32- битовых |
| ushort | C unsigned short | complex128 | два 64- битовых |
| uintc | C unsigned int | complex192 | два 96- битовых ??? |
| uint | Python int | complex256 | два 128-битовых |
| ulonglong | C long long | Строки | |
| uintp | такой, что может описывать указатели | str_ | Python str |
| uint8 | 8 бит | unicode_ | Python unicode |
| uint16 | 16 бит | void | |
| uint32 | 32 бит | Объекты Python | |
| uint64 | 64 бит | object_ |
|
Операции для работы с массивами
В NumPy реализовано много операций для работы с массивами:
- создание, модификация массива (изменение формы, транспонирование, поэлементные операции),
- выбор элементов,
- операции с массивами (различные типы умножения), сравнение массивов
- решение задач линейной алгебры (системы линейных уравнений, собственые вектора.
 собственные значения)
собственные значения) - создание наборов случайных данных
- быстрое преобразование Фурье
Создание массивов
В NumPy можно выделить три вида массивов:
- произвольные многомерные массивы (array)
- матрицы (matrix) – двухмерные квадратные массивы, для которых дополнительно определены операции возведения в степень и перемножения. Для работы с матрицами можно вместо “numpy” подключать “numpy.matrix”, в котором реализованы те же самые операции, только массивы – результаты операций будут приводится к типу “matrix”.
- сетки (grid) – массивы, в которых записаны значения координат точек сети (обычно ортогональной). Сетки позволяют удобно вычислять значение функций многих переменных.
Создание массивов из имеющихся данных
Для создания массивов существует множество функций. Самая распространенная из них array().
>>> np.array([[1, 2], [3, 4]])
array([[1, 2],
[3, 4]])
| Команда | Описание |
|---|---|
| array(object[, dtype, copy, order, subok, ndmin]) | Создать массив |
| asarray(a[, dtype, order]) | Преобразовать в массив |
| ascontiguousarray(a[, dtype]) | Размещает в памяти непрерывный массив(порядок данных как в Cи) |
| asmatrix(data[, dtype]) | Представить данные как матрицу |
| copy(a) | Возвращает копию объекта |
| frombuffer(buffer[, dtype, count, offset]) | Использует буфер, как одномерный массив |
| fromfile(file[, dtype, count, sep]) | Создает массив из данных файла |
| fromfunction(function, shape, **kwargs) | Создает и заполняет массив значениями функции от индексов элемента |
| fromiter(iterable, dtype[, count]) | Создает одномерный массив из итератора |
| fromstring(string[, dtype, count, sep]) | Создает одномерный массив из строки |
| loadtxt(fname[, dtype, comments, delimiter, …]) | Создает массив из данных текстового файла |
- a — объект или массив
- object — любой объект с упорядоченными данными
- dtype — тип данных (если не указан определяется по данным объекта)
- copy — да/нет, создать копию данных
- order — {‘C’, ‘F’, ‘A’}– порядок размещения элементов в памяти (Си, Фортран, любой)
- ndmin — минимальное число измерений (добавляет пустые массивы по недостающим измерениям)
- buffer — объект буфера
- count — число данных для чтения
- offset — отступ от начала
- file — объект файла
- sep — шаг чтения файла
- string — строка
- function — функция.
 Вызывается function(i,j,k,**kwargs), где i,j,k – индексы ячейки массива
Вызывается function(i,j,k,**kwargs), где i,j,k – индексы ячейки массива - shape — форма массива
- **kwargs — словарь параметров для функции
- fname – имя файла
- comments – символ коментария
- delimiter – разделитель данных
Создание сеток
| Команда | Описание | Пример |
|---|---|---|
| arange([start,] stop [, step,][, dtype]) | Похоже на “range()” | >>> np.arange(3.0) array([ 0., 1., 2.]) |
| linspace(start, stop [, num, endpoint, retstep]) | Равномерный набор точек | >>> np.linspace(2.0, 3.0, num=5) array([ 2., 2.25, 2.5, 2.75, 3.]) |
| logspace(start, stop [, num, endpoint, base]) | Логарифмический набор точек | >>> np.logspace(2.0, 3.0, num=4, base=2.0) array([ 4., 5.03968, 6. |
| meshgrid(x, y) | два вектора, описывающих точки ортогональной сетки. | >>> X, Y = np.meshgrid([1,2,3], [4,5,7])
>>> X
array([[1, 2, 3],
[1, 2, 3],
[1, 2, 3]])
>>> Y
array([[4, 4, 4],
[5, 5, 5],
[7, 7, 7]])
|
| mgrid | полный набор данных, описывающий многомерную равномерную ортогональную сетку (X,Y) или (X,Y,Z). Аргументы по каждому измерению: (start : stop : step). Если step – мнимое (5j) – то задается количество интервалов разбиения | >>> np.mgrid[0:5:3j,0:5:3j]
array([[[0., 0., 0.],
[2.5, 2.5, 2.5],
[5., 5., 5.]],
[[0., 2.5, 5.],
[0., 2.5, 5.],
[0., 2.5, 5.]]])
|
| ogrid | сокращенный набор данных, описывающий многомерную равномерную ортогональную сетку (X,Y) или (X,Y,Z). Аргументы по каждому измерению: (start : stop : step). Если step – мнимое (5j) – то задается количество интервалов разбиения | >>> ogrid[0:5,0:5]
[array([[0],
[1],
[2],
[3],
[4]]), array([[0, 1, 2, 3, 4]])]
|
- start – начало
- stop – окончание (для «arrange» по умолчанию НЕ включается, для остальных функций — включается)
- step – шаг
- num – число точек в выходном наборе
- endpoint – да/нет, включать крайнюю точку в набор данных
- retstep – да/нет, добавить в данные величину интервала
- x, y – одномерные массивы разбиения для осей.

- base – основание логарифма
Создание массивов определенного вида
| Команда | Описание | Пример |
|---|---|---|
| empty(shape[, dtype, order]), empty_like(a [, dtype, order, subok]) | выделяет место без инициализации (случайные числа) | >>> np.empty([2, 2], dtype=int)
array([[-1073741821, -1067949133],
[ 496041986, 19249760]])
|
| eye(N[, M, k, dtype]) | двухмерный диагональный со сдвигом | >>> np.eye(3, k=1)
array([[ 0., 1., 0.],
[ 0., 0., 1.],
[ 0., 0., 0.]])
|
| identity(N[, dtype]) | единичная матрица (квадратная) | >>> np.identity(3)
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
|
| ones(shape[, dtype, order]) ones_like(a[, out]) | все единицы | |
| zeros(shape[, dtype, order]) zeros_like(a[, dtype, order, subok]) | все нули | |
| tri(N[, M, k, dtype]) | нижняя треугольная (из единиц) | >>> np. |
| tril(a[, k]) | вырезание нижней треугольной | >>> np.tril([[1,2,3],[4,5,6],[7,8,9], [10,11,12]], -1)
array([[ 0, 0, 0],
[ 4, 0, 0],
[ 7, 8, 0],
[10, 11, 12]])
|
| triu(a[, k]) | вырезание верхней треугольной | >>> np.triu([[1,2,3],[4,5,6],[7,8,9], [10,11,12]], -1)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 0, 8, 9],
[ 0, 0, 12]])
|
| diag(a[, k]) | вырезает диагональ или создает двумерную диагональную матрицу | |
| diagflat(a[, k]) | двумерная диагональная матрица со всеми элементами из a. | |
| vander(x[, N]) | создает определительВан Дер Монда | >>> x = np.array([1, 2, 3, 5])
>>> N = 3
>>> np.vander(x, N)
array([[ 1, 1, 1],
[ 4, 2, 1],
[ 9, 3, 1],
[25, 5, 1]])
|
| mat(data[, dtype]) | преобразует данные в матрицу | |
| bmat(obj[, ldict, gdict]) | создает матрицу из строки, последовательности или массива |
- shape – форма массива
- dtype – тип данных
- order – порядок размещения данных(Си, Фортран)
- a – объект типа массива
- N – число строк
- M – число столбцов
- k – задает диагональ (к=0 – главная, к>0 – смещение вверх, к<0 – смещение вниз)
- x – одномерный массив или список
Трансформации массива без изменения элементов
| Команда | Описание |
|---|---|
| resize(a, new_shape) | возвращает новый массив заданной формы (если элементов не хватает, то заполняется циклически) |
| reshape(a, newshape[, order]) | новая форма для данных (полный размер обязан совпадать) |
| ravel(a[, order]) | возвращает новый одномерный массив |
ndarray. flat flat | итератор по массиву (вызывается как метод) |
| ndarray.flatten([order]) | копия массива без формы (вызывается как метод) |
| rollaxis(a, axis[, start]) | сдвигает выбранную ось до нужного положения |
| swapaxes(a, axis1, axis2) | меняет две оси в массиве |
| ndarray.T | То же что и транспонирование. (если размерность=1, то не изменяется) |
| transpose(a[, axes]) | транспонирует массив (переставляет измерения) |
| fliplr(a) | симметрично отображает массив относительно вертикальной оси (право-лево) |
| flipud(a) | симметрично отображает массив относительно горизонтальной оси (верх-низ) |
| roll(a, shift[, axis]) | циклический сдвиг элементов вдоль выбранного направления |
| rot90(a[, k]) | поворот массива против часовой стрелке на 90 градусов |
| tile(A, repeats) | создает матрицу повторением заданной определенное количество |
| repeat(a, repeats[, axis]) | повторяет элементы массива |
- a
- newshape
- order
- start
- axis1, axis2
- shift
- k
- repeats
Слияние и разделение массивов
| Команда | Описание |
|---|---|
| column_stack(tup) | собирает одномерные массивы -столбцы в двухмерный |
| concatenate(tup[, axis]) | соединяет последовательность массивов вместе |
| dstack(tup) | собирает массивы «по глубине» (по третьей оси). |
| hstack(tup) | собирает массивы «по горизонтали» (по столбцам). |
| vstack(tup) | собирает массивы «по вертикали» (по строкам). |
| array_split(a, indices_or_sections[, axis]) | разделяет массив по порциям |
| dsplit(a, indices_or_sections) | разделяет массив «по глубине» (по третьей оси) |
| hsplit(a, indices_or_sections) | разделяет массив «по горизонтали» (по столбцам). |
| split(a, indices_or_sections[, axis]) | разделяет массив на части равной длины |
| vsplit(a, indices_or_sections) | разделяет массив «по вертикали» (по строкам). |
- tup – кортеж массивов
- axis – ось
- a – массив
- indices_or_sections – размер порции при разделении
Функции, определенные для массивов
Алгебраические функции
| Функця | Описание |
|---|---|
| isreal(x) | проверка на действительность (по элементам) |
| iscomplex(x) | проверка на комплексность (по элементам) |
| isfinite(x[, out]) | приверка элементов на числовое значение (не бесконечность и не «не число»). |
| isinf(x[, out]) | проверка на бесконечность (по элементам) |
| isnan(x[, out]) | проверка аргумента на «не число» (NaN), результат – логический массив |
| signbit(x[, out]) | истина, если установлен бит знака (меньше нуля) |
| copysign(x1, x2[, out]) | меняет знак x1 на знак x2 (по элементам |
| nextafter(x1, x2[, out]) | следующее в направлении x2 число, представимое в виде с плавающей точкой (по элементам) |
| modf(x[, out1, out2]) | дробная и целая часть числа |
| ldexp(x1, x2[, out]) | вычисляет y = x1 * 2**x2. |
| frexp(x[, out1, out2]) | разделение числа на нормированную часть и степень |
| absolute(x[, out]) | Calculate the absolute value element-wise. |
| rint(x[, out]) | округление элементов массива |
| trunc(x[, out]) | отбрасывание дробной части (по элементам) |
| floor(x[, out]) | целая часть |
| ceil(x[, out]) | минимальное целое большее числа |
| sign(x[, out]) | знаки элементов |
| conj(x[, out]) | комплексное сопряжение (по элементам). |
| exp(x[, out]) | экспонента (по элементам) |
| exp2(x[, out]) | 2**элемент (по элементам) |
| log(x[, out]) | натуральный логарифм (по элементам) |
| log2(x[, out]) | двоичный логарифм (по элементам) |
| log10(x[, out]) | десятичный логарифм (по элементам) |
| expm1(x[, out]) | exp(x) — 1 (по элементам) |
| log1p(x[, out]) | Return the natural logarithm of one plus the input array, element-wise. |
| sqrt(x[, out]) | квадратный корень (для положительных) (по элементам) |
| square(x[, out]) | квадрат (по элементам) |
| reciprocal(x[, out]) | обратная величина (по элементам) |
- x – массив
- out – место для результата
Тригонометрические функции
Все тригонометрические функции работают с радианами.
| Функция | Обратная функция | Описание |
|---|---|---|
| sin(x[, out]) | arcsin(x[, out]) | синус (по элементам) |
| cos(x[, out]) | arccos(x[, out]) | косинус (по элементам) |
| tan(x[, out]) | arctan(x[, out]) | тангенс (по элементам) |
| arctan2(x1, x2[, out]) | арктангенс x1/x2 с правильным выбором четверти (по элементам) | |
| hypot(x1, x2[, out]) | гипотенуза по двум катетам (по элементам) | |
| sinh(x[, out]) | arcsinh(x[, out]) | гиперболический синус (по элементам) |
| cosh(x[, out]) | arccosh(x[, out]) | гиперболический косинус (по элементам) |
| tanh(x[, out]) | arctanh(x[, out]) | гиперболический тангенс (по элементам) |
| deg2rad(x[, out]) | rad2deg(x[, out]) | преобразование градусов в радианы (по элементам) |
- x, x1, x2 – массивы
- out – место для результата
Функции двух аргументов (бинарные функции)
Для правильной работы с логическими бинарными функциям (AND, OR) необходимо явно их записывать через функции
модуля «NumPy», а не полагаться на встроенные функции питона.
| Функция | Описание |
|---|---|
| add(x1, x2[, out]) | сумма (по элементам) |
| subtract(x1, x2[, out]) | разность (по элементам) |
| multiply(x1, x2[, out]) | произведение (по элементам) |
| divide(x1, x2[, out]) | деление (по элементам) |
| logaddexp(x1, x2[, out]) | логарифм суммы экспонент (по элементам) |
| logaddexp2(x1, x2[, out]) | логарифм по основанию 2 от суммы экспонент (по элементам) |
| true_divide(x1, x2[, out]) | истинное деление (с преобразованием типов) |
| floor_divide(x1, x2[, out]) | деление без преобразования типов (целочисленное) |
| negative(x[, out]) | обратные элементы (по элементам) |
| power(x1, x2[, out]) | элементы первого массива в степени элементов из второго массива (по элементам) |
| remainder(x1, x2[, out]), mod(x1, x2[, out]), fmod(x1, x2[, out]) | остаток от деления (по элементам). |
| greater(x1, x2[, out]) | истина, если (x1 > x2) (по элементам). |
| greater_equal(x1, x2[, out]) | истина, если (x1 > =x2) (по элементам). |
| less(x1, x2[, out]) | истина, если (x1 < x2) (по элементам). |
| less_equal(x1, x2[, out]) | истина, если (x1 =< x2) (по элементам). |
| not_equal(x1, x2[, out]) | истина, если (x1 != x2) (по элементам). |
| equal(x1, x2[, out]) | истина, если (x1 == x2) (по элементам). |
| logical_and(x1, x2[, out]) | истина, если (x1 AND x2) (по элементам). |
| logical_or(x1, x2[, out]) | истина, если (x1 OR x2) (по элементам). |
| logical_xor(x1, x2[, out]) | истина, если (x1 XOR x2) (по элементам). |
| logical_not(x[, out]) | истина, если (NOT x1) (по элементам). |
| maximum(x1, x2[, out]) | максимум из элементов двух массивов(по элементам). |
- x1, x2 – массивы
- out – место для результата
Бинарные функции поддерживают дополнительные методы, позволяющие накапливать значения результата различными способами.
- accumulate() Аккумулирование результата.
- outer() Внешнее «произведение».
- reduce() Сокращение.
- reduceat() Сокращение в заданных точках.
Методы accumulate(), reduce() и reduceat() принимают необязательный аргумент — номер размерности, используемой для соответствующего действия. По умолчанию применяется нулевая размерность.
Другие функций для массивов
| Функция | Описание |
|---|---|
| apply_along_axis(func1d, axis, a, *args) | Применить функцию к одномерному срезу вдоль оси |
| apply_over_axes(func, a, axes) | применить функцию последовательно вдоль осей. |
| vectorize(pyfunc[, otypes, doc]) | обобщить функцию на массивы |
| frompyfunc(func, nin, nout) | берет произвольную функцию Python и возвращает функцию Numpy |
| piecewise(a, condlist, funclist, *args, **kw) | применение кусочно-определенной функции к массиву |
- func1d – функция для вектора
- func – скалярная функция
- axis – индекс оси
- arr – массив
- *args, **kw – дополнительные аргументы
- nin – число входных параметров
- nout – число выходных параметров
- condlist — список условий
- funclist – список функций (для каждого условия)
Сортировка, поиск, подсчет
| Команда | Описание |
|---|---|
| sort(a[, axis, kind, order]) | отсортированная копия массива |
| lexsort(keys[, axis]) | Perform an indirect sort using a sequence of keys. |
| argsort(a[, axis, kind, order]) | аргументы, которые упорядочивают массив |
| array.sort([axis, kind, order]) | сортирует массив на месте (метод массива) |
| msort(a) | копия массива отсортированная по первой оси |
| sort_complex(a) | сортировка комплексного массива по действительной части, потом по мнимой |
| argmax(a[, axis]) | индексы максимальных значений вдоль оси |
| nanargmax(a[, axis]) | индексы максимальных значений вдоль оси (игнорируются NaN). |
| argmin(a[, axis]) | индексы минимальных значений вдоль оси |
| nanargmin(a[, axis]) | индексы минимальных значений вдоль оси (игнорируются NaN). |
| argwhere(a) | массив индексов ненулевых элементов. данные сгруппированы по элементам([x1,y1,..],[x2,y2,..]….) |
| nonzero(a) | массивы индексов ненулевых элементов. сгруппированы по размерностям (индексы X, индексы Y, т. д.) д.) |
| flatnonzero(a) | индексы ненулевых элементов в плоской версии массива |
| where(condition, [x, y]) | возвращает массив составленный из элементов x (если выполнено условие) и y (в противном случае). Если задано только condition, то выдает его «не нули». |
| searchsorted(a, v[, side]) | индексы мест, в которые нужно вставить элементы вектора для сохранения упорядоченности массива |
| extract(condition, a) | возвращает элементы (одномерный массив), по маске (condition) |
| count_nonzero(a) | число ненулевых элементов в массиве |
- a – массив
- axis – индекс оси для сортировки (по умолчанию «–1» — последняя ось)
- kind – {‘quicksort’, ‘mergesort’, ‘heapsort’} тип сортировки
- order – индексы элементов, определяющие порядок сортировки
- keys – (k,N) массив из k элементов размера (N). k “колонок” будут отсортированы. Последний элемент – первичный ключ для сортировки.

- condition – матрица условий (маска)
- x, y – массивы для выбора элементов
- v – вектор
- side – {‘left’, ‘right’} позиция для вставки элемента (слева или справа от найденного индекса)
Дискретное преобразование Фурье (numpy.fft)
| Прямое преобразование | Обратное преобразование | Описание |
|---|---|---|
| fft(a[, s, axis]) | ifft(a[, s, axis]) | одномерное дискретное преобразование Фурье |
| fft2(a[, s, axes]) | ifft2(a[, s, axes]) | двумерное дискретное преобразование Фурье |
| fftn(a[, s, axes]) | ifftn(a[, s, axes]) | многомерное дискретное преобразование Фурье |
| rfft(a[, s, axis]) | irfft(a[, s, axis]) | одномерное дискретное преобразование Фурье (действительные числа) |
| rfft2(a[, s, axes]) | irfft2(a[, s, axes]) | двумерное дискретное преобразование Фурье (действительные числа) |
| rfftn(a[, s, axes]) | irfftn(a[, s, axes]) | многомерное дискретное преобразование Фурье (действительные числа) |
| hfft(a[, s, axis]) | ihfft(a[, s, axis]) | преобразование Фурье сигнала с Эрмитовым спектром |
| fftfreq(n[, d]) | частоты дискретного преобразования Фурье | |
| fftshift(a[, axes]) | ifftshift(a[, axes]) | преобразование Фурье со сдвигом нулевой компоненты в центр спектра |
- a — массив
- s – число элементов вдоль каждого направления преобразования (если больше размерности, то дополняются нулями)
- axes – последовательность осей для преобразования
- n – ширина окна
- d – шаг по частоте при выводе
Линейная алгебра (numpy.
 linalg)
linalg)Модуль numpy.linalg содержит алгоритмы линейной алгебры, в частности нахождение определителя матрицы, решений системы линейных уравнений, обращение матрицы, нахождение собственных чисел и собственных векторов матрицы, разложение матрицы на множители: Холецкого, сингулярное, метод наименьших квадратов и т.д.
| Команда | Описание |
|---|---|
| dot(a, b[, out]) | скалярное произведение массивов |
| vdot(a, b) | векторное произведение векторов |
| inner(a, b) | внутреннее произведение массивов |
| outer(a, b) | внешнее произведение векторов |
| tensordot(a, b[, axes]) | тензорное скалярное произведение вдоль оси (размерность больше 1) |
| einsum(subscripts, *operands[, out, dtype, …]) | суммирование Эйншнейна Evaluates the Einstein summation convention on the operands. |
| linalg.matrix_power(M, n) | возведение квадратной матрицы в степень n |
| kron(a, b) | произведение Кронекера двух массивов |
| linalg.norm(a[, ord]) | норма матрицы или вектора. |
| linalg.cond(a[, ord]) | число обусловленности матрицы. |
| linalg.det(a) | определитель |
| linalg.slogdet(a) | знак и натуральный логарифм определителя |
| trace(a[, offset, axis1, axis2, dtype, out]) | сумма элементов по диагонали. |
| linalg.cholesky(a) | разложение Холецкого |
| linalg.qr(a[, mode]) | разложение QR |
| linalg.svd(a[, full_matrices, compute_uv]) | сингулярное разложение |
| linalg.solve(a, b) | решение линейного матричного уравнения или системы скалярных уравнений. |
| linalg.tensorsolve(a, b[, axes]) | решение тензорного уравнения a x = b для x. |
| linalg.lstsq(a, b[, rcond]) | решение матричного уравнения методом наименьших квадратов |
| linalg.inv(a) | обратная матрица (для умножения) |
| linalg.pinv(a[, rcond]) | псевдо-обратная матрица (Мура-Пенроуза) |
| linalg.tensorinv(a[, ind]) | «обратный» к многомерному массиву |
| linalg.eig(a) | собственные значения и правые собственные вектора квадратной |
| linalg.eigh(a[, UPLO]) | собственные значения и собственные вектора эрмитовой или симметричной матрицы |
| linalg.eigvals(a) | собственные значения произвольной матрицы |
| linalg.eigvalsh(a[, UPLO]) | собственные значения эрмитовой или действительной симметричной матрицы |
- a, b — матрицы
- out — место для результата
- ord – определяет способ вычисления нормы
- axes – массив осей для суммирования
- axis – индекс оси
- subscripts – индексы для суммирования
- *operands – список массивов
- dtype – тип результата
- offset – положение диагонали
- mode — {‘full’, ‘r’, ‘economic’} – выбор алгоритма разложения
- full_matrices – составлять полные матрицы
- compute_uv – выводить все матрицы
- rcond – граница для отбрасывания маленьких собственных значений
- ind – число индексов для вычисления обратной
- UPLO — {‘L’, ‘U’} выбирает часть матрицы для работы
Случайные величины (numpy.
 random)
random)В модуле numpy.random собраны функции для генерации массивов случайных чисел различных распределений и свойств. Их можно применять для математического моделирования. Функция random() создает массивы из псевдослучайных чисел, равномерно распределенных в интервале (0, 1). Функция RandomArray.randint() для получения массива равномерно распределенных чисел из заданного интервала и заданной формы. Можно получать и случайные перестановки с помощью RandomArray.permutation(). Доступны и другие распределения для получения массива нормально распределенных величин с заданным средним и стандартным отклонением:
Следующая таблица приводит основные функции модуля.
seed([seed])- перезапуск генератора случайных чисел
| Команда | Описание |
|---|---|
| rand(d0, d1, …, dn) | набор случайных чисел заданной формы |
| randn([d1, …, dn]) | набор (или наборы) случайных чисел со стандартным нормальным распределением |
| randint(low[, high, size]) | случайные целые числа от low (включая) до high (не включая). {-x/2}\) {-x/2}\) |
| mtrand.dirichlet(alpha[, size]) | числа с распределением Дирихле (alpha – массив параметров). |
| exponential([scale, size]) | числа с экспоненциальным распределением \(f(x,\frac{1}{\beta})=\frac{1}{\beta}exp(-\frac{x}{\beta})\) |
| f(dfnum, dfden[, size]) | числа с F распределением (dfnum – число степеней свободы числителя > 0; dfden –число степеней свободы знаменателя >0.) |
| gamma(shape[, scale, size]) | числа с Гамма — распределением |
| geometric(p[, size]) | числа с геометрическим распределением |
| gumbel([loc, scale, size]) | числа с распределением Гумбеля |
| hypergeometric(ngood, nbad, nsample[, size]) | числа с гипергеометрическим распределением (n = ngood, m = nbad, and N = number of samples) |
| laplace([loc, scale, size]) | числа с распределением Лапласа |
| logistic([loc, scale, size]) | числа с логистическим распределением |
| lognormal([mean, sigma, size]) | числа с логарифмическим нормальным распределением |
| logseries(p[, size]) | числа с распределением логарифмического ряда |
| multinomial(n, pvals[, size]) | числа с мультиномиальным распределением |
| multivariate_normal(mean, cov[, size]) | числа с мульти нормальным распределением (mean – одномерный массив средних значений;
cov – двухмерный симметричный, полож. определенный массив (N, N) ковариаций определенный массив (N, N) ковариаций |
| negative_binomial(n, p[, size]) | числа с отрицательным биномиальным распределением |
| noncentral_chisquare(df, nonc[, size]) | числа с нецентральным распределением хи-квадрат |
| noncentral_f(dfnum, dfden, nonc[, size]) | числа с нецентральным F распределением (dfnum — целое > 1; dfden – целое > 1; nonc : действительное >= 0) |
| normal([loc, scale, size]) | числа с нормальным распределением |
| pareto(a[, size]) | числа с распределением Паретто |
| poisson([lam, size]) | числа с распределением Пуассона |
| power(a[, size]) | числа со степенным распределением [0, 1] |
| rayleigh([scale, size]) | числа с распределением Релея |
| standard_cauchy([size]) | числа со стандартным распределением Коши |
| standard_exponential([size]) | числа со стандартным экспоненциальным распределением |
| standard_gamma(shape[, size]) | числа с гамма- распределением |
| standard_normal([size]) | числа со стандартным нормальным распределением (среднее=0, сигма=1). |
| standard_t(df[, size]) | числа со стандартным распределением Стьюдента с df степенями свободы |
| triangular(left, mode, right[, size]) | числа из треугольного распределения |
| uniform([low, high, size]) | числа с равномерным распределением |
| vonmises(mu, kappa[, size]) | числа с распределением Майсеса (I- модифицированная функция Бесселя) |
| wald(mean, scale[, size]) | числа с распределением Вальда |
| weibull(a[, size]) | числа с распределением Вайбулла |
| zipf(a[, size]) | числа с распределением Зипфа (зетта функция Римана) |
- size — число элементов по каждому измерению
Статистика
| Команда | Описание |
|---|---|
| amin(a[, axis, out]) | минимум в массиве или минимумы вдоль одной из осей |
| amax(a[, axis, out]) | максимум в массиве или максимумы вдоль одной из осей |
| nanmax(a[, axis]) | максимум в массиве или максимумы вдоль одной из осей (игнорируются NaN). |
| nanmin(a[, axis]) | минимум в массиве или минимумы вдоль одной из осей (игнорируются NaN). |
| ptp(a[, axis, out]) | диапазон значений (максимум — минимум) вдоль оси |
| average(a[, axis, weights, returned]) | взвешенное среднее вдоль оси |
| mean(a[, axis, dtype, out]) | арифметическое среднее вдоль оси |
| median(a[, axis, out, overwrite_input]) | вычисление медианы вдоль оси |
| std(a[, axis, dtype, out, ddof]) | стандартное отклонение вдоль оси |
| corrcoef(x[, y, rowvar, bias, ddof]) | коэффициенты корреляции |
| correlate(a, v[, mode, old_behavior]) | кросс-корреляция двух одномерных последовательностей |
| cov(m[, y, rowvar, bias, ddof]) | ковариационная матрица для данных |
| histogram(a[, bins, range, normed, weights, …]) | гистограмма из набора данных |
| histogram2d(x, y[, bins, range, normed, weights]) | двумерная гистограмма для двух наборов данных |
| histogramdd(sample[, bins, range, normed, …]) | многомерная гистограмма для данных |
| bincount(x[, weights, minlength]) | число появление значения в массиве неотрицательных значений |
| digitize(x, bins) | возвращает индексы интервалов к которым принадлежат элементы массива |
- a – массив
- axis – индекс оси
- out – место для результата
- weights- веса
- returned – дополнительно выдать сумму весов
- dtype – тип данных для накопления суммы
- overwrite_input – использовать входящий массив для промежуточных вычислений
- ddof- дельта степеней свободы (см.
 описание)
описание) - x,y – данные (строки – переменные, колонки — наблюдения)
- rowvar – если не 0, то строка переменные, колонки – наблюдения (если 0, то наоборот)
- bias – определеяет нормировку, совместно с ddof
- mode — {‘valid’, ‘same’, ‘full’} – объем выводимых данных
- old_behavior – совместимость со старой версией (без комплексного сопряжения)
- bins – разбиение по интервалам
- range – массив границ по x и по y
- normed – нормированное
- minlength – минимальное число интервалов при выводе
Полиномы (numpy.polynomial)
Модуль полиномов обеспечивает стандартные функции работы с полиномами разного вида. В нем реализованы полиномы
Чебышева, Лежандра, Эрмита, Лагерра. Для полиномов определены стандартные арифметические функции ‘+’, ‘-‘, ‘*’, ‘//’,
деление по модулю, деление с остатком, возведение в степень и вычисление значения полинома. Важно задавать область
определения, т.к. часто свойства полинома (например при интерполяции) сохраняются только на определенном интервале. В зависимости от класса полинома, сохраняются коэффициенты разложения по полиномам определенного типа, что позволяет
получать разложение функций в ряд по полиномам разного типа.
В зависимости от класса полинома, сохраняются коэффициенты разложения по полиномам определенного типа, что позволяет
получать разложение функций в ряд по полиномам разного типа.
| Типы полиномов | Описание |
|---|---|
| Polynomial(coef[, domain, window]) | разложение по степеням «x» |
| Chebyshev(coef[, domain, window]) | разложение по полиномам Чебышева |
| Legendre(coef[, domain, window]) | разложение по полиномам Лежандра |
| Hermite(coef[, domain, window]) | разложение по полиномам Эрмита |
| HermiteE(coef[, domain, window]) | разложение по полиномам Эрмита_Е |
| Laguerre(coef[, domain, window]) | разложение по полиномам Лагерра |
- coef – массив коэффициентов в порядке увеличения
- domain – область определения проецируется на окно
- window – окно.
 Сдвигается и масштабируется до размера области определения
Сдвигается и масштабируется до размера области определения
Некоторые функции (например интерполяция данных) возвращают объект типа полином. У этого объекта есть набор методов, позволяющих извлекать и преобразовывать данные.
| Методы полиномов | Описание |
|---|---|
| __call__(z) | полином можно вызвать как функцию |
| convert([domain, kind, window]) | конвертирует в полином другого типа, с другим окном и т.д |
| copy() | возвращает копию |
| cutdeg(deg) | обрезает полином до нужной степени |
| degree() | возвращает степень полинома |
| deriv([m]) | вычисляет производную порядка m |
| fit(x, y, deg[, domain, rcond, full, w, window]) | формирует полиномиальную интерполяцию степени deg для данных (x,y) по методу наименьших квадратов |
| fromroots(roots[, domain, window]) | формирует полином по заданным корням |
| has_samecoef(p) | проверка на равенство коэффициентов. |
| has_samedomain(p) | проверка на равенство области определения |
| has_samewindow(p) | проверка на равенство окна |
| integ([m, k, lbnd]) | интегрирование |
| linspace([n, domain]) | возвращает x,y — значения на равномерной сетке по области определения |
| mapparms() | возвращает коэффициенты масштабирования |
| roots() | список корней |
| trim([tol]) | создает полином с коэффициентами большими tol |
| truncate(size) | ограничивает ряд по количеству коеффициентов |
- p – полином
- x, y – набор данных для аппроксимации
- deg – степень полинома
- domain – область определения
- rcond – относительное число обусловленности элементы матрицы интерполяции с собственными значениями меньшими данного будут отброшены.
- full – выдавать дополнительную информацию о качестве полинома
- w – веса точек
- window – окно
- roots – набор корней
- m – порядок производной (интеграла)
- k – константы интегрирования
- lbnd – нижняя граница интервала интегрирования
- n – число точек разбиения
- size – число ненулевых коэффициентов
(определение, свойства и видео) // Tutors.
 com
comСодержание
Матричная математика применяется в анализе, программировании и инженерии. Математическая матрица представляет собой массив элементов в строках и столбцах.
- Видео
- Определение матрицы
- Что такое квадратная матрица?
- Свойства матрицы
- Вход или элемент
- Таблица размеров и наполнения
- Примеры сложения
Определение матрицы
Матрица представляет собой массив чисел, символов или выражений в строках (поперек) и столбцах (вверх и вниз). Единственное число, матрица , используется при работе с одной матрицей, например:
2-8015-13
Когда у вас есть более одной матрицы, у вас есть матриц . Количество строк и столбцов всегда указывается в одном и том же порядке, поэтому приведенная выше матрица представляет собой матрицу 2 × 3, то есть две строки и три столбца.
Что такое квадратная матрица?
Квадратная матрица — это особый вид матрицы, в которой количество строк в поперечнике равно количеству столбцов вверх и вниз. Вот квадратная матрица:
1115-73-20-5134
Как бы вы определили эту матрицу?
Вы сказали 3 × 3, поскольку в нем три строки и три столбца?
Свойства матрицы
Запись или элемент
В приведенной выше квадратной матрице верхняя строка содержит три числа: 11, 15 и -7. это три записей или элементов . Сама матрица может быть отмечена любой буквой, но каждый элемент в этой матрице будет использовать одну и ту же букву.
Мы назовем нашу квадратную матрицу A, поэтому все позиции всех элементов или записей записываются как a, а затем нижние индексы: ar, c, где первая буква r относится к строкам, а вторая буква c относится к столбцам.
a(строка), (столбец)
В нашей квадратной матрице 11 находится в a1, 1, самой первой позиции для любой записи, а -7 находится в позиции a1, 3.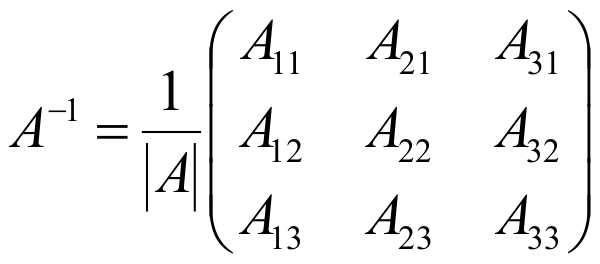 Индекс 1 помещает его в первую строку; индекс 3 делает его третьей записью или элементом.
Индекс 1 помещает его в первую строку; индекс 3 делает его третьей записью или элементом.
Каковы правильные обозначения для -2 во второй строке и 13 в третьей строке?
Надеемся, вы сказали a2, 2 вместо -2 и a3, 2 вместо 13!
Матрица размеров и заполнения
Наименьшая квадратная матрица будет 2 × 2; теоретически не существует ограничений на квадратную матрицу самого большого размера, но для практического использования все, что больше 10 × 10, становится трудным для математических манипуляций.
Квадратная матрица может быть заполнена элементами или элементами, которые являются целыми числами, дробями, алгебраическими выражениями или даже символами. Поскольку одна запись может представлять собой что-то вроде x2 + y3 = z, квадратная матрица, состоящая всего из четырех строк и четырех столбцов, может оказаться сложной задачей.
Матрица идентичности
В компьютерном программировании многие матрицы заполнены только нулями и единицами, что является двоичным языком вычислений. Когда квадратная матрица имеет только 0 в каждой записи, за исключением диагонали из 1, матрица является единичной матрицей . Это пригодится при умножении матриц, к которому мы вернемся ниже.
Когда квадратная матрица имеет только 0 в каждой записи, за исключением диагонали из 1, матрица является единичной матрицей . Это пригодится при умножении матриц, к которому мы вернемся ниже.
Единичная матрица (все нули и диагональ единиц) получила свое название, потому что это матрица, умноженная на другую матрицу, которая дает ответ, идентичный другой матрице; это возвращает матрицу, с которой вы начали, просто 1 × 5 возвращает вам 5, или 2018 × 1 дает вам ответ 2018.
Добавление квадратной матрицы
Вы можете складывать элементы в две матрицы, но только , если обе матрицы имеют одинаковый размер. Вы не можете сложить нашу первую матрицу 2 × 3 с нашей квадратной матрицей 3 × 3, потому что у них разное количество строк.
Даже если они обе являются квадратными матрицами, вы не можете добавить их, если одна, скажем, 2 × 2, а другая 5 × 5.
Чтобы добавить две квадратные матрицы одинакового размера, вам нужно отслеживать каждую позицию записи, поэтому вы добавляете похожие записи между двумя матрицами. Таким образом, вы добавляете a2, 2 + b2, 2; вы добавляете a3, 2 + b3, 2 и т. д. Вам нужно работать осторожно, чтобы не потерять свое положение при перемещении по матрице.
Таким образом, вы добавляете a2, 2 + b2, 2; вы добавляете a3, 2 + b3, 2 и т. д. Вам нужно работать осторожно, чтобы не потерять свое положение при перемещении по матрице.
Пример сложения квадратной матрицы
Вот две маленькие матрицы:
4657 + 612913
Возьмем каждую запись и ее позицию: c1, 1 – это 4, а d1, 1 – это 6. Вы добавляете 4 + 6. В матрице решений на позиции 1, 1 будет отображаться 10.
Каковы правильные суммы для остальной части матрицы?
4657 + 612913 = 10181420
Это работает, даже если записи содержат отрицательные числа. Вы просто «добавляете» выражения, в том числе отрицательные. Ваша матрица ответов может содержать записи, которые являются положительными или отрицательными целыми числами.
-5711-8 + 40-215
Для e1, 1 значения равны -5 + 4 = -1, поэтому матрица решений имеет -1 в позиции входа E+F1, 1. Можете ли вы подставить остальные четыре ценности?
-5711-8 + 40-215 = -1797
Вычитание работает таким же образом. Каждая позиция записи в матрице решения представляет собой разность двух одинаковых записей по позиции.
Каждая позиция записи в матрице решения представляет собой разность двух одинаковых записей по позиции.
Умножение квадратных матриц
Квадратные матрицы можно перемножать. Матрицы умножаются либо на целые числа (скалярное умножение), либо на другие матрицы. Простой способ запомнить, что вы делаете, — подумать, что количество строк первой матрицы должно быть равно количеству столбцов второй матрицы. Для квадратных матриц эта головная боль уже решена.
Чтобы умножить две квадратные матрицы, вы берете каждую запись в первой строке первой матрицы и умножаете ее на соответствующую запись в первом столбце второй матрицы. Если у вас есть все эти продукты, добавьте их вместе!
Вот две очень маленькие матрицы:
10524 × 6839
Чтобы получить матрицу решения для первого элемента, i1, 1, мы перемножаем элементы из первой и второй матриц с позициями 1, 1 (10 x 6), затем умножаем g1,2 на h3,1 (5 х 3). Сложите эти два продукта вместе:
i1, 1 = (10 × 6) + (5 × 3) = 75
Повторите эти шаги для остальных трех записей. В нашей матрице решений i1, 2 будет произведением g1, 1 × g1, 2, добавленным к произведению g1, 2 × h3, 2:
В нашей матрице решений i1, 2 будет произведением g1, 1 × g1, 2, добавленным к произведению g1, 2 × h3, 2:
i1, 2 = (10 × 8) + (5 × 9) = 125
Сможете ли вы самостоятельно определить два других?
Вы получили:
i2, 1 = 24
i2, 2 = 52
Порядок матриц имеет значение при умножении; умножение матрицы G × H дает вам другой ответ, чем H × G!
Если вы нам не верите, попробуйте сами! У вас должно получиться следующее:
6839 × 10524 = 76624851
Итог урока
Изучив этот урок и попробовав матричную математику, вы сможете вспомнить и объяснить, что такое матрица, определить строки, столбцы и элементы матриц, различать уникальные свойства квадратной матрицы и описывать, что такое единичная матрица. Вы также можете выполнять операции сложения, вычитания и умножения с использованием матриц.
Next Lesson:
Математическая индукция
Квадратная матрица — определение, примеры, операции
Квадратная матрица является важным форматом матрицы и имеет идеальное квадратное число элементов. В нем одинаковое количество строк и столбцов, поэтому его порядок имеет вид n × n. Все матричные операции транспонирования, определителя, сопряжения, инверсии и математические операции над матрицами применимы и к квадратной матрице.
В нем одинаковое количество строк и столбцов, поэтому его порядок имеет вид n × n. Все матричные операции транспонирования, определителя, сопряжения, инверсии и математические операции над матрицами применимы и к квадратной матрице.
Квадратная матрица имеет особое применение при решении квадратных уравнений с двумя переменными. Здесь мы изучим различные свойства квадратной матрицы и попытаемся понять, как выполнять математические операции над этими матрицами.
| 1. | Что такое квадратная матрица? |
| 2. | Транспонирование квадратной матрицы |
| 3. | Определитель квадратной матрицы |
| 4. | Обратная квадратная матрица |
| 5. | Операции с матрицами |
| 6. | Важные термины, относящиеся к квадратной матрице |
| 7. | Примеры на квадратной матрице |
8. | Практические вопросы |
| 9. | Часто задаваемые вопросы о квадратной матрице |
Что такое квадратная матрица?
Квадратная матрица — это матрица с равным количеством строк и столбцов. Его порядок имеет вид n x n. Кроме того, произведение этих строк и столбцов дает количество элементов в квадратной матрице. Следовательно, количество элементов в нем всегда является совершенным квадратным числом. Типичная квадратная матрица выглядит следующим образом.
\(A_{n,n} = \begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{ 2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\)
Вот несколько примеров квадратных матриц .
- \(\left(\begin{массив}{ll}
-1&2\\
3 и 4
\end{array}\right)\) — квадратная матрица порядка 2×2 (или просто порядка 2).
Он имеет 2×2 = 4 элемента. - \(\left(\begin{массив}{ccc}
3&-6&2\
2 и 3 и 6 \
6 и 2 и -3
\end{array}\right)\) — квадратная матрица порядка 3×3 (или просто порядка 3).
Он имеет 3×3 = 9 элементов.
Транспонирование квадратной матрицы
Матрица, полученная преобразованием строк в столбцы и столбцов в строки, называется транспонированием данной матрицы. Как правило, порядок матрицы изменяется при преобразовании ее в транспонированную. Для матрицы порядка m × n транспонирование матрицы имеет порядок n × m. Здесь для квадратной матрицы транспонированная матрица имеет тот же порядок, что и данная матрица.
A = \(\begin{pmatrix}a & b & c\\d&e&f\\g&h&i\end{pmatrix}\) A T = \(\begin{pmatrix}a & d & g\\b&e&h\\c&f&i \end{pmatrix}\)
Попробуем понять два важных термина, связанных с транспонированием матрицы. Квадратная матрица, транспонирование которой равно данной матрице, называется симметричной матрицей. Квадратная матрица, транспонирование которой равно отрицательному значению данной матрицы, называется кососимметричной матрицей.
Симметричная матрица: A T = A
Кососимметричная матрица: A T = -A
Определитель квадратной матрицы
Определитель квадратной матрицы представляет собой одно числовое значение или суммарное значение, представляющее весь набор элементов матрицы. Определитель матрицы порядка 2 × 2 можно легко вычислить по формуле. Определитель матрицы порядка 2 × 2 равен разности произведения диагональных элементов матрицы. Это можно наблюдать в приведенной ниже работе.
Определитель матрицы порядка 2 × 2 можно легко вычислить по формуле. Определитель матрицы порядка 2 × 2 равен разности произведения диагональных элементов матрицы. Это можно наблюдать в приведенной ниже работе.
A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\)
|A| = ad — bc
Кроме того, давайте проверим несколько матриц, которые были названы на основе значений их определителей. Матрица, определитель которой равен нулю, называется сингулярной матрицей (|A| = 0). Для сингулярной матрицы обратной матрицы не существует. А матрица, значение определителя которой не равно нулю, называется невырожденной матрицей (|A| ≠ 0).
Обратная квадратная матрица
Обратная квадратная матрица используется для деления одной матрицы на другую матрицу. Чтобы найти обратную матрицу, нужно сначала найти определитель матрицы. Затем вычисляется сопряжение квадратной матрицы. Наконец, обратное получается путем деления присоединенной матрицы на определитель квадратной матрицы.
A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) A -1 = \(\dfrac{1}{|A|}.Adj A\) = \ (\frac{1}{ad — bc}\begin{pmatrix}d &-b\\\\-c&a\end{pmatrix}\)
Попробуем рассмотреть важный термин, относящийся к обратной матрице. Квадратная матрица называется ортогональной матрицей, если ее выворот равен обратному.
Ортогональная матрица: A T = A -1
Матричные операции над квадратной матрицей
Математические операции сложения, вычитания и умножения также можно выполнять над двумя квадратными матрицами. Для сложения или вычитания соответствующие элементы добавляются для получения результирующей матрицы. Сложение матриц следует коммутативному свойству (A + B = B + A).
A + B = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) + \(\begin{pmatrix}1 &2\\\\3&4\end{pmatrix }\) = \(\begin{pmatrix}a \pm1 &b \pm2\\\\c \pm3&d \pm4\end{pmatrix}\)
Умножение матричного скаляра очень просто. Для умножения квадратной матрицы на константу каждый элемент матрицы умножается на константу.
Для умножения квадратной матрицы на константу каждый элемент матрицы умножается на константу.
kA = k\(\begin{pmatrix}a &b \\\\c &d \end{pmatrix}\) = \(\begin{pmatrix}ka &kb \\\\kc &kd \end{pmatrix}\)
Умножение двух квадратных матриц включает в себя последовательность шагов. Рассмотрим две квадратные матрицы порядка 2 × 2. Здесь мы рассматриваем элементы строки в первой матрице и элементы столбца во второй матрице. Следующие расчеты показывают последовательность вычислений, связанных с процессом умножения матриц.
Важные термины, относящиеся к квадратной матрице
Давайте проверим несколько важных терминов, относящихся к квадратной матрице, которые помогут нам глубже понять концепцию квадратной матрицы.
- Порядок матрицы: это произведение строк и столбцов в матрице. Квадратная матрица имеет равное количество строк и столбцов и имеет порядок n × n.
- След матрицы: равен сумме диагональных элементов квадратной матрицы.

- Идентификационная матрица: это квадратная матрица с единицами в качестве диагональных элементов, а все остальные элементы — нули.
- Скалярная матрица: Квадратная матрица, имеющая то же число, что и все ее диагональные элементы, а все остальные элементы равны нулю.
- Симметричная матрица: Матрица, транспонирование которой равно данной матрице, называется симметричной матрицей.
- Кососимметричная матрица: Матрица, транспонирование которой равно отрицательному значению той же матрицы, называется кососимметричной матрицей.
- Ортогональная матрица: Матрица называется ортогональной, если обратная матрица равна транспонированной матрице.
☛ Связанные темы:
- Калькулятор сложения матриц
- Умножение матриц
- Матричная формула
Часто задаваемые вопросы о квадратной матрице
Что такое определение квадратной матрицы?
Квадратная матрица — это матрица, в которой количество строк равно количеству столбцов. Например, матрицы порядка 2×2, 3×3, 4×4 и т. д. являются квадратными матрицами. Матрицы порядка 2×3, 3×2, 4×5 и т. д. НЕ являются квадратными матрицами (это прямоугольные матрицы).
Например, матрицы порядка 2×2, 3×3, 4×4 и т. д. являются квадратными матрицами. Матрицы порядка 2×3, 3×2, 4×5 и т. д. НЕ являются квадратными матрицами (это прямоугольные матрицы).
Как найти обратную квадратную матрицу?
Обратная квадратная матрица получается после нахождения определителя и сопряженной матрицы данной матрицы. Для матрицы A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) ее определитель равен |A| = ad — bc и Adj A =\( \begin{pmatrix}d &-b\\\\-c&a\end{pmatrix}\). Комбинируя эти два понятия, матрица, обратная A -1 = \(\dfrac{1}{|A|}.Adj A\) = \(\frac{1}{ad — bc}\begin{ pmatrix}d &-b\\\\-c&a\end{pmatrix}\). Обратная матрица возможна только для невырожденных матриц. Несингулярная матрица — это матрица, определитель которой не равен нулю |A| ≠ 0,
Как определить, обратима ли квадратная матрица?
Квадратная матрица обратима, только если определитель матрицы не равен нулю |A| ≠ 0. Для матрицы A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) ее определитель равен |A| = объявление — до н. э. Для матриц, имеющих |A| = 0, обратного ему не существует.
э. Для матриц, имеющих |A| = 0, обратного ему не существует.
Как умножать квадратные матрицы?
Две квадратные матрицы можно перемножить, если обе матрицы одного порядка. Рассматриваются строки первой матрицы и рассматриваются столбцы второй матрицы для умножения.
Как найти определитель квадратной матрицы?
Определитель квадратной матрицы порядка 2 × 2 равен разности произведения элементов первой диагонали и второй диагонали. Для матрицы A = \(\begin{pmatrix}a &b\\ \\c&d\end{pmatrix}\). его определитель равен |A| = объявление — до н.э.
Что такое Матрица магического квадрата?
Матрица магического квадрата — это квадратная матрица с нечетным числом строк и столбцов (n), так что сумма элементов в каждой строке, столбце или диагонали равна. Эта сумма элементов равна n(n 2 + 1)/2.
Каков порядок квадратной матрицы?
Квадратная матрица имеет порядок n × n и имеет одинаковое количество строк и столбцов. Количество элементов в квадратной матрице можно вычислить по ее порядку и оно равно квадратному числу n 2 .
Что такое транспонирование квадратной матрицы?
Транспонирование квадратной матрицы получается путем записи элементов строки данной матрицы в виде элементов столбца. Для матрицы A = \(\begin{pmatrix}a & b & c\\c&e&f\\g&h&i\end{pmatrix}\) ее транспонирование равно A T = \(\begin{pmatrix}a & d & g\\b&e&h\\c&f&i\end{pmatrix}\). Элементы первой строки данной матрицы были записаны в первый столбец, а элементы второй строки матрицы были записаны во второй столбец, чтобы получить транспонированную матрицу.
Что такое невырожденная квадратная матрица?
Несингулярная матрица имеет ненулевое значение определителя (|A| ≠ 0. Для матрицы A =\(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) Условие для того, чтобы это была невырожденная матрица, таково: ad — bc ≠ 0. Обратная заданная квадратная матрица существует только в том случае, если это невырожденная матрица.0005
Сложная матрица без квадратного корня
Алгебра
Обратимые матрицы
Комплексная матрица \(T\) подобна матрице \[
J=\begin{bmatrix}
J_1 & & \\
& \ddots &\\
& & J_p
\end{ bmatrix}\], где каждый блок \(J_i\) представляет собой квадратную матрицу вида \[
J_i=\begin{bmatrix}
\lambda_i & 1 & &\\
& \lambda_i & \ddots &\\
& & \ddots & 1\\
& & & \lambda_i
\end{bmatrix}\] \(J\) называется нормальной формой Жордана матрицы \(T\). Если \(T\) предполагается обратимым, \(\lambda_i\) отличны от нуля, а \(J\) имеет квадратный корень. Для доказательства докажем, что блок Жордана \[
J(\lambda)=\begin{bmatrix}
\lambda & 1 & &\\
& \lambda & \ddots &\\
& & \ddots & 1 \\
& & & \lambda
\end{bmatrix}\] с \(\lambda \neq 0\) имеет квадратный корень. Запись \(J(\lambda)=\lambda(I+N)\), где \(N=\frac{J(0)}{\lambda}\) и \(I\) единичная матрица, это достаточно, чтобы доказать, что \(I+N\) имеет квадратный корень \(K\) для любой нильпотентной матрицы \(N\), поскольку тогда \(cK\) является квадратным корнем из \(J(\lambda)\) для \(c\) квадратный корень из \(\lambda\).

 собственные значения)
собственные значения) Вызывается function(i,j,k,**kwargs), где i,j,k – индексы ячейки массива
Вызывается function(i,j,k,**kwargs), где i,j,k – индексы ячейки массива 34960, 8.])
34960, 8.])
 tri(3, 5, 2, dtype=int)
array([[1, 1, 1, 0, 0],
[1, 1, 1, 1, 0],
[1, 1, 1, 1, 1]])
tri(3, 5, 2, dtype=int)
array([[1, 1, 1, 0, 0],
[1, 1, 1, 1, 0],
[1, 1, 1, 1, 1]])

 описание)
описание) Сдвигается и масштабируется до размера области определения
Сдвигается и масштабируется до размера области определения