Все формулы площади треугольников: Все формулы площади треугольника — найти онлайн

Как найти площадь если известны три стороны. Площадь треугольника

Школьная программа предусматривает обучение детей геометрии с раннего возраста. Одно из самых базовых знаний этой области — это нахождение площади различных фигур. В этой статье мы постараемся привести все возможные способы получения этой величины, от простейших до самых сложных.

Основа

Первая формула, которую изучают дети в школе, предусматривает нахождение площади треугольника через длину его высоты и основания. Высота — это отрезок, проведённый из вершины треугольника под прямым углом к противолежащей стороне, которая будет являться основанием. Как найти площадь треугольника по этим величинам?

Если V — высота, а O — основание, тогда площадь S=V*O:2.

Другой вариант получения искомой величины требует от нас знания длин двух сторон, а также величины угла между ними. Если у нас L и M — длины сторон, а Q — угол между ними, тогда вы можете получить площадь по формуле S=(L*M*sin(Q))/2.

Формула Герона

Кроме всех прочих ответов на вопрос о том, как вычислить площадь треугольника, есть формула, позволяющая получить необходимое нам значение, зная исключительно длины сторон. То есть, если нам известны длины всех сторон, то нам нет необходимости проводить высоту и вычислять её длину. Мы можем воспользоваться, так называемой формулой Герона.

Если M, N, L — это длины сторон, тогда мы можем найти площадь треугольника, следующим образом. P=(M+N+L)/2, тогда необходимая нам величина S 2 =P*(P-M)*(P-L)*(P-N). В итоге, нам останется только вычислить корень.

Для прямоугольного треугольника формула Герона немного упрощается. Если M, L -это катеты, тогда S=(P-M)*(P-L).

Окружности

Другой способ, с помощью которого можно найти площадь треугольника, предусматривает использование вписанных и описанных окружностей. Чтобы получить необходимую нам величину с помощью вписанной окружности, нам потребуется узнать её радиус. Обозначим его «r». Тогда формула, по которой мы будем проводить вычисления, примет следующий вид: S=r*P, где P — это половина от суммы длин всех сторон.

В прямоугольном треугольнике эта формула немного преобразуется. Конечно, вы можете использовать и указанную выше, однако лучше взять для вычислений другое выражение.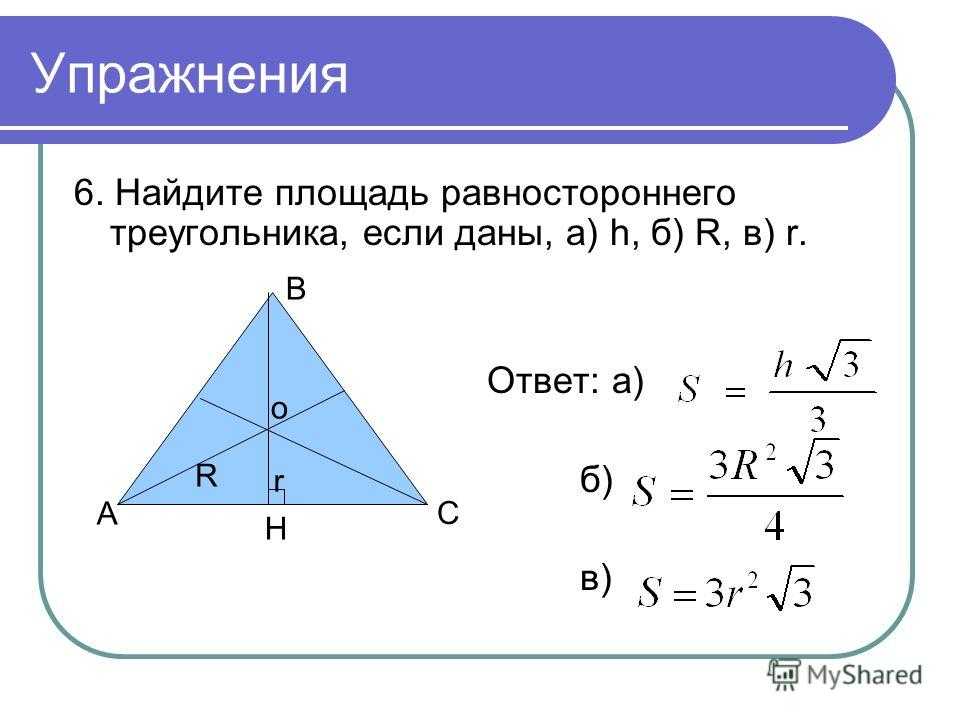 S=E*W, где E и W — это длины отрезков, на которые делится гипотенуза, точкой касания окружности.

Говоря об описанной окружности, найти площадь треугольника, также не составит труда. Введя обозначение R, как радиус описанной окружности, можно получить следующую формулу, необходимую для вычисления искомой величины: S= (M*N*L):(4*R). Где три первые величины — это стороны треугольника.

Говоря о равностороннем треугольнике, за счет ряда простейших математических преобразований можно получить немого изменённые формулы:

S=(3 1/2 *M 2)/4;

S=(3*3 1/2 *R 2)/4;

S=3*3 1/2 *r 2 .

Во всяком случае, любая формула, позволяющая найти площадь треугольника, может быть изменена в соответствии с данными поставленной задачи. Так что все написанные выражения не являются абсолютами. При решении задач поразмышляйте, чтобы найти наиболее подходящий способ решения.

Координаты

При изучении координатных осей задачи, стоящие перед учениками, усложняются. Однако не настолько, чтобы впадать в панику. Для того чтобы найти площадь треугольника по координатам вершин, вы можете воспользоваться всё той же, но немного изменённой формулой Герона. Для координат она приобретает следующий вид:

S=((x 2 -x 1) 2 *(y 2 -y 1) 2 *(z 2 -z 1) 2) 1/2 .

Впрочем, никто не запрещает, используя координаты, вычислить длины сторон треугольника и затем, по формулам, которые были написаны выше, посчитать площадь. Для преобразования координат в длину пользуйтесь следующей формулой:

l=((x 2 -x 1) 2 +(y 2 -y 1) 2) 1/2 .

Примечания

В статье использовались стандартные обозначения величин, которые применяются в условиях большинства задач. При этом степень «1/2» означает, что вам необходимо извлечь корень из всего выражения под скобками.

При выборе формулы будьте внимательнее. Некоторые из них теряют свою актуальность в зависимости от начальных условий. Например, формула описанной окружности. Она способна высчитать вам результат в любом случае, однако может быть такая ситуация, когда треугольника с заданными параметрами может вообще не существовать.

Если вы сидите дома и делаете домашнее задание, тогда можете воспользоваться онлайн-калькулятором. Многие сайты предоставляют возможность вычисления различных величин по заданным параметрам, причем не суть важно, каким именно. Вы просто можете вписать начальные данные в поля, и компьютер (сайт) посчитает за вас результат. Таким образом, вы сможете избежать ошибок, допущенных по невнимательности.

Надеемся наша статья ответила все ваши вопросы касательно вычисления площади самых разных треугольников, и вам не придётся искать допонительную информацию в другом месте. Удачи с учебой!

Чтобы определить площадь треугольника, можно пользоваться разными формулами. Из всех способов самый легкий и часто применяемый — это умножение высоты на длину основания с последующим делением полученного результата на два. Однако данный метод далеко не единственный. Ниже вы сможете прочесть, как найти площадь треугольника, используя разные формулы.

Отдельно мы рассмотрим способы вычисления площади специфических видов треугольника — прямоугольного, равнобедренного и равностороннего.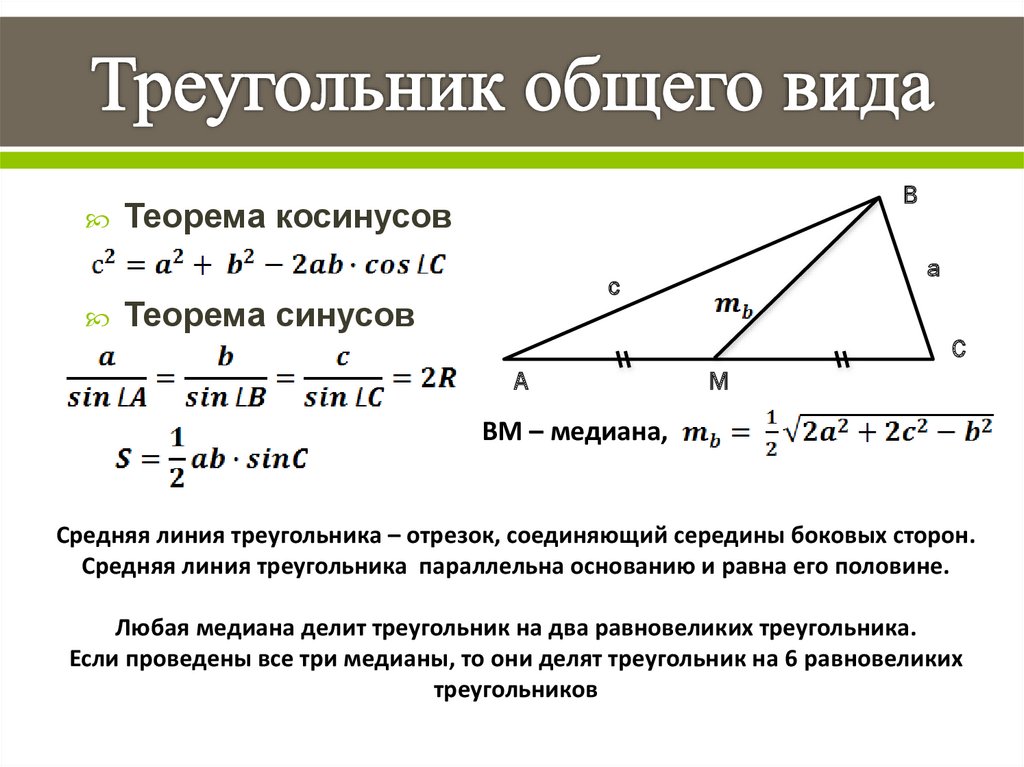 Каждую формулу мы сопровождаем коротким пояснением, которое поможет вам понять ее суть.

Универсальные способы нахождения площади треугольника

В приведенных ниже формулах используются специальные обозначения. Мы расшифруем каждое из них:

• a, b, c – длины трех сторон рассматриваемой нами фигуры;
• r – радиус окружности, которая может быть вписана в наш треугольник;
• R – радиус той окружности, которая может быть описана вокруг него;
• α — величина угла, образованного сторонами b и с;
• β — величина угла между a и c;
• γ — величина угла, образованного сторонами а и b;
• h – высота нашего треугольника, опущенная из угла α на сторону а;
• p – половина суммы сторон a, b и с.

Логически понятно, почему можно находить площадь треугольника этим способом. Треугольник легко достраивается до параллелограмма, в котором одна сторона треугольника будет выполнять роль диагонали. Площадь параллелограмма находится умножением длины одной из его сторон на значение высоты, проведенной к ней.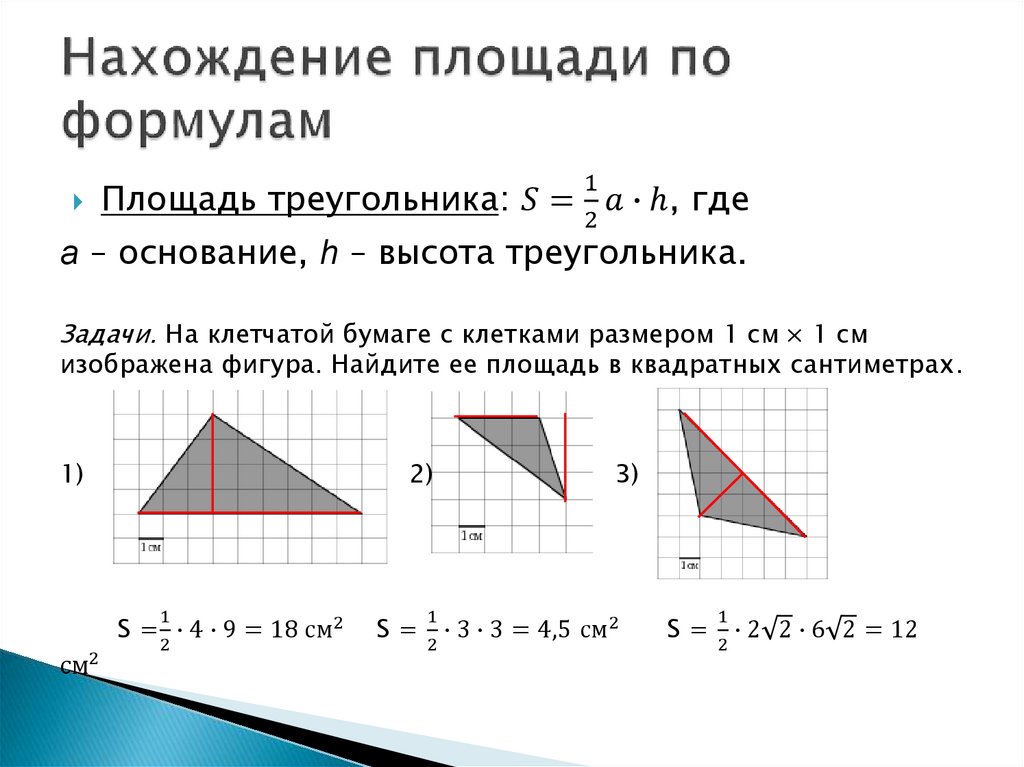

Диагональ разделяет этот условный параллелограмм на 2 одинаковых треугольника. Следовательно, совершенно очевидно, что площадь нашего исходного треугольника должна равняться половине площади этого вспомогательного параллелограмма.

S=½ a · b·sin γ

Согласно этой формуле, площадь треугольника находится умножением длин двух его сторон, то есть а и b, на синус образованного ими угла. Эта формула логически выводится из предыдущей. Если опустить высоту из угла β на сторону b, то, согласно свойствам прямоугольного треугольника, при умножении длины стороны a на синус угла γ получаем высоту треугольника, то есть h.

Площадь рассматриваемой фигуры находим путем умножения половины радиуса окружности, которую в него можно вписать, на его периметр. Иными словами, находим произведение полупериметра на радиус упомянутой окружности.

S= a · b · с/4R

Согласно данной формуле, необходимую нам величину можно найти путем деления произведения сторон фигуры на 4 радиуса окружности, вокруг нее описанной.

Эти формулы универсальны, так как дают возможность определить площадь любого треугольника (разностороннего, равнобедренного, равностороннего, прямоугольного). Можно это сделать и при помощи более сложных вычислений, на которых мы подробно останавливаться не станем.

Площади треугольников со специфическими свойствами

Как найти площадь прямоугольного треугольника? Особенностью этой фигуры является то, что две ее стороны одновременно являются ее высотами. Если а и b являются катетами, а с становится гипотенузой, то площадь находим так:

Как найти площадь равнобедренного треугольника? В нем две стороны с длиной а и одна сторона с длиной b. Следовательно, его площадь определить можно путем деления на 2 произведения квадрата стороны а на синус угла γ.

Как найти площадь равностороннего треугольника? В нем длина всех сторон равняется а, а величина всех углов — α. Его высота равна половине произведения длины стороны а на корень квадратный из 3. Чтобы найти площадь правильного треугольника, нужно квадрат стороны а умножить на корень квадратный из 3 и разделить на 4.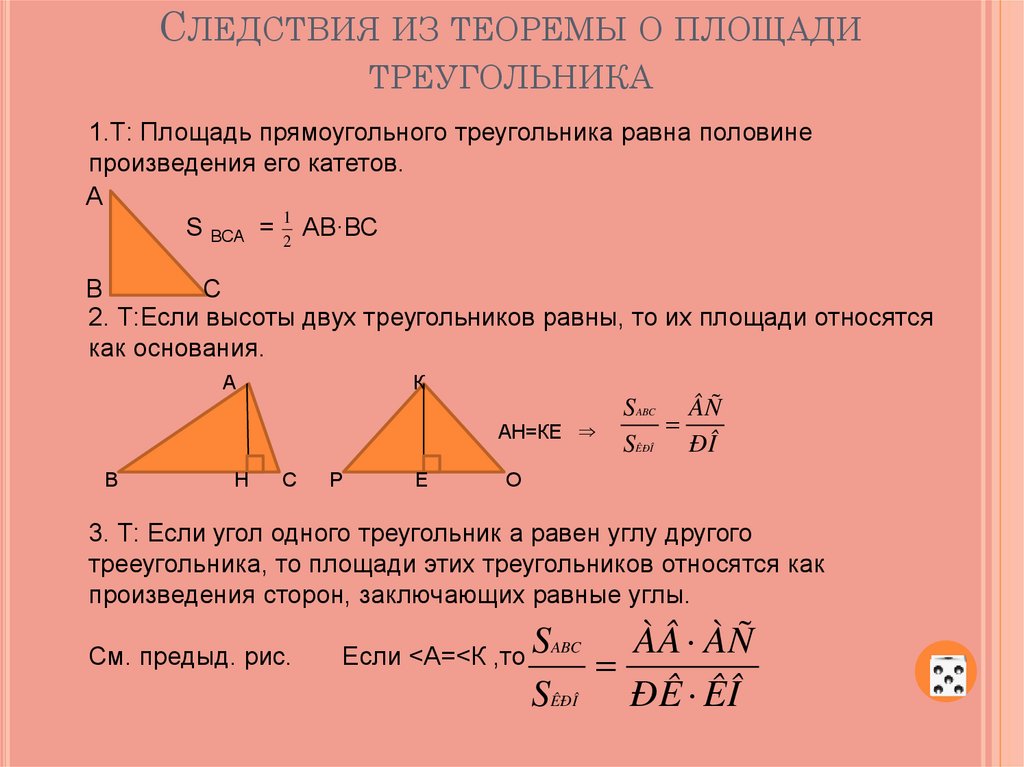

Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.

Примечание . Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:

• «Формулы площади равностороннего треугольника»

Формулы площади треугольника

Пояснения к формулам :
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
h — высота треугольника, опущенная на сторону
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a треугольника
β — угол, противолежащий стороне b треугольника
γ — угол, противолежащий стороне c треугольника
h a , h b , h c — высота треугольника, опущенная на сторону a , b , c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.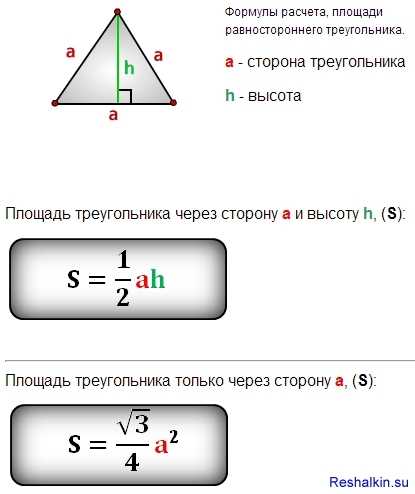

• Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
• Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
• Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
• Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
• Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
• Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
• Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
• Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула 8)
• Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
• Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
• Формула 11 позволяет вычислить площадь треугольника по координатам его вершин , которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

Примечание . Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение . Иногда для простых подкоренных выражений может использоваться символ √

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника .

Решение .

Для решения этой задачи используем формулу номер два из теоретической части урока.

Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
S = 15 √3 / 2

Ответ : 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Задача. Найти площадь равностороннего треугольника

Найти площадь равностороннего треугольника со стороной 3см.

Решение .

Площадь треугольника можно найти по формуле Герона:

S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))

Поскольку a = b = c формула площади равностороннего треугольника примет вид:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

Ответ : 9 √3 / 4.

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение .

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c))
(см. вторую строку на рисунке внизу)

Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — на третьей строке рисунка
S 2 = 1/4 sqrt(256 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

Треугольник — хорошо знакомая всем фигура. И это, несмотря на богатое разнообразие его форм. Прямоугольный, равносторонний, остроугольный, равнобедренный, тупоугольный. Каждый из них чем-то отличается. Но для любого требуется узнавать площадь треугольника.

Общие для всех треугольников формулы, в которых используются длины сторон или высот

Обозначения, принятые в них: стороны — а, в, с; высоты на соответствующие стороны н а, н в, н с.

1. Площадь треугольника вычисляется, как произведение ½, стороны и высоты, опущенной на нее. S = ½ * а * н а. Аналогично следует записать формулы для двух остальных сторон.

2. Формула Герона, в которой фигурирует полупериметр (его принято обозначать маленькой буквой р, в отличии от полного периметра).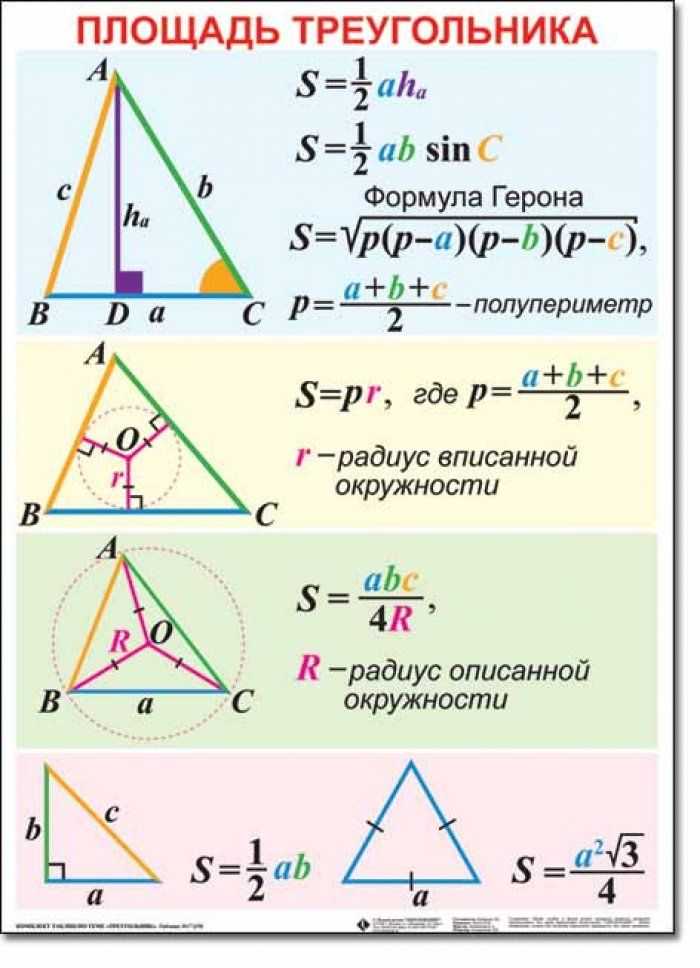 Полупериметр необходимо сосчитать так: сложить все стороны и разделить их на 2. Формула полупериметра: р = (а+в+с) / 2. Тогда равенство для площади фигуры выглядит так: S = √ (р * (р — а) * (р — в) * (р — с)).

3. Если не хочется использовать полупериметр, то пригодится такая формула, в которой присутствуют только длины сторон: S = ¼ * √ ((а + в + с) * (в + с — а) * (а + с — в) * (а + в — с)). Она несколько длиннее предыдущей, но выручит, если забылось, как находить полупериметр.

Общие формулы, в которых фигурируют углы треугольника

Обозначения, которые требуются для прочтения формул: α, β, γ — углы. Они лежат напротив сторон а, в, с, соответственно.

1. По ней половина произведения двух сторон и синуса угла между ними равна площади треугольника. То есть: S = ½ а * в * sin γ. Подобным образом следует записать формулы для двух других случаев.

2. Площадь треугольника можно вычислить по одной стороне и трем известным углам. S = (а 2 * sin β * sin γ) / (2 sin α).

3. Существует еще формула с одной известной стороной и двумя прилежащими к ней углами. Она выглядит таким образом: S = с 2 / (2 (ctg α + ctg β)).

Две последние формулы являются не самыми простыми. Запомнить их довольно сложно.

Общие формулы для ситуации, когда известны радиусы вписанных или описанных окружностей

Дополнительные обозначения: r, R — радиусы. Первый используется для радиуса вписанной окружности. Второй — для описанной.

1. Первая формула, по которой вычисляется площадь треугольника, связана с полупериметром. S = р * r. По-другому ее можно записать так: S = ½ r * (а + в + с).

2. Во втором случае потребуется перемножить все стороны треугольника и разделить их на учетверенный радиус описанной окружности. В буквенном выражении это выглядит так: S = (а * в * с) / (4R).

3. Третья ситуация позволяет обойтись без знания сторон, но потребуются значения всех трех углов. S = 2 R 2 * sin α * sin β * sin γ.

Частный случай: прямоугольный треугольник

Это самая простая ситуация, поскольку требуется знание только длины обоих катетов.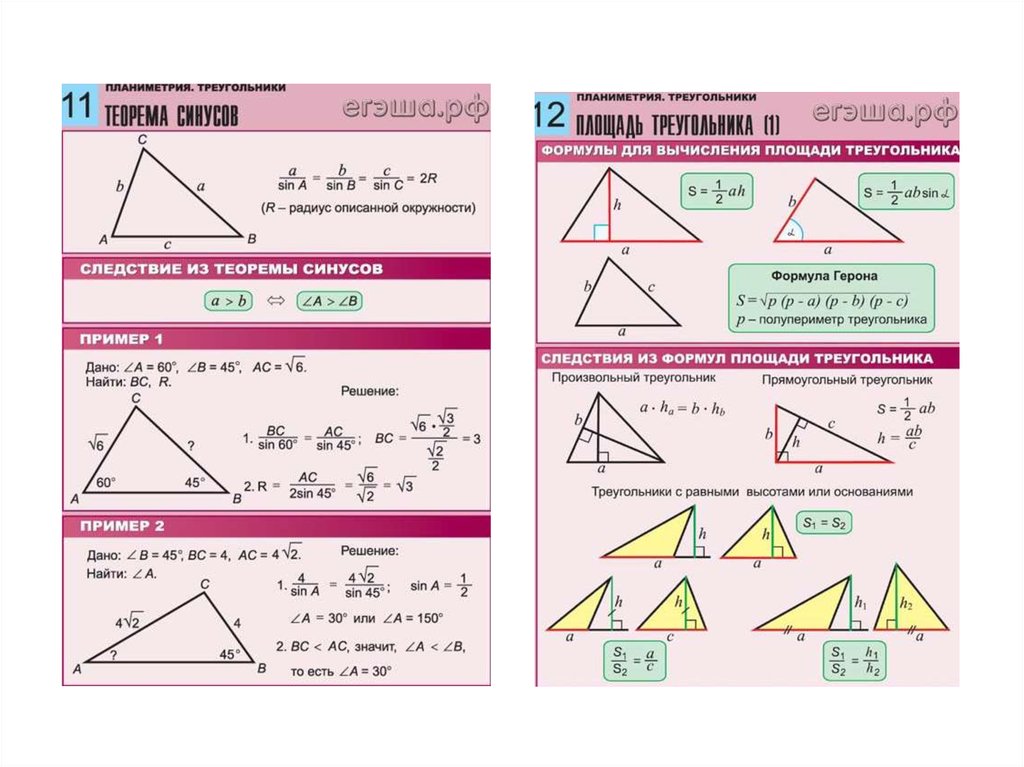 Они обозначаются латинскими буквами а и в. Площадь прямоугольного треугольника равна половине площади достроенного к нему прямоугольника.

Математически это выглядит так: S = ½ а * в. Она запоминается проще всего. Потому что выглядит, как формула для площади прямоугольника, только появляется еще дробь, обозначающая половину.

Частный случай: равнобедренный треугольник

Поскольку у него две стороны равные, то некоторые формулы для его площади выглядят несколько упрощенными. Например, формула Герона, по которой вычисляется площадь равнобедренного треугольника, принимает следующий вид:

S = ½ в √((a + ½ в)*(a — ½ в)).

Если ее преобразовать, то она станет короче. В таком случае формула Герона для равнобедренного треугольника записывается так:

S = ¼ в √(4 * a 2 — b 2).

Несколько проще, чем для произвольного треугольника, выглядит формула площади, если известны боковые стороны и угол между ними. S = ½ a 2 * sin β.

Частный случай: равносторонний треугольник

Обычно в задачах про него известна сторона или ее можно как-либо узнать. Тогда формула, по которой находится площадь такого треугольника, выглядит следующим образом:

S = (а 2 √3) / 4.

Задачи на нахождение площади, если треугольник изображен на клетчатой бумаге

Самой простой является ситуация, когда прямоугольный треугольник начерчен так, что его катеты совпадают с линиями бумаги. Тогда требуется просто посчитать число клеточек, укладывающихся в катеты. Потом перемножить их и разделить на два.

Когда треугольник остроугольный или тупоугольный, его нужно дорисовать до прямоугольника. Тогда в получившейся фигуре будет 3 треугольника. Один — тот что дан в задаче. А два других — вспомогательные и прямоугольные. Определить площади двух последних нужно по описанному выше способу. Потом сосчитать площадь прямоугольника и вычесть из него те, что вычислены для вспомогательных. Площадь треугольника определена.

Гораздо сложнее оказывается ситуация, в которой ни одна из сторон треугольника не совпадает с линиями бумаги. Тогда его нужно вписать в прямоугольник так, чтобы вершины исходной фигуры лежали на его сторонах. В этом случае вспомогательных прямоугольных треугольников будет три.

Пример задачи на формулу Герона

Условие. У некоторого треугольника известны стороны. Они равны 3, 5 и 6 см. Необходимо узнать его площадь.

Теперь можно вычислять площадь треугольника по указанной выше формуле. Под квадратным корнем оказывается произведение четырех чисел: 7, 4, 2 и 1. То есть площадь равна √(4 * 14) = 2 √(14).

Если не требуется большая точность, то можно извлечь квадратный корень из 14. Он равен 3,74. Тогда площадь будет равна 7,48.

Ответ. S = 2 √14 см 2 или 7,48 см 2 .

Пример задачи с прямоугольным треугольником

Условие. Один катет прямоугольного треугольника больше, чем второй на 31 см. Требуется узнать их длины, если площадь треугольника равна 180 см 2 .
Решение. Придется решить систему из двух уравнений. Первое связано с площадью. Второе — с отношением катетов, которое дано в задаче.
180 = ½ а * в;

а = в + 31.
Сначала значение «а» нужно подставить в первое уравнение.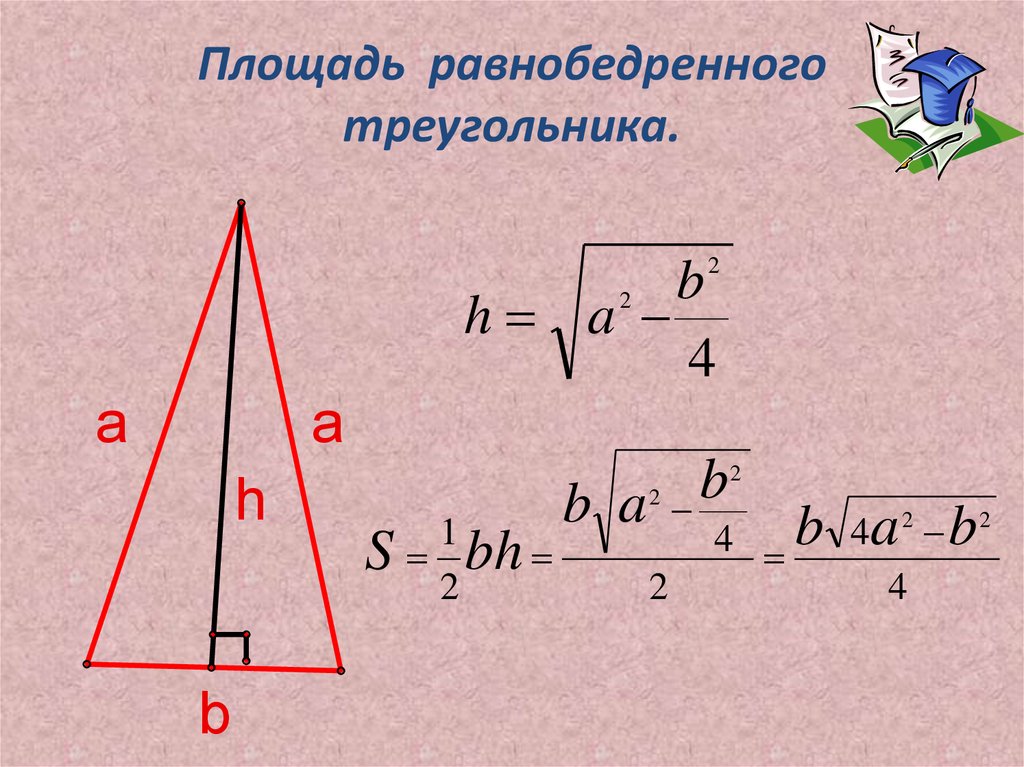 Получится: 180 = ½ (в + 31) * в. В нем только одна неизвестная величина, поэтому его легко решить. После раскрытия скобок получается квадратное уравнение: в 2 + 31 в — 360 = 0. Оно дает два значения для «в»: 9 и — 40. второе число не подходит в качестве ответа, так как длина стороны треугольника не может быть отрицательной величиной.

Осталось вычислить второй катет: прибавить к полученному числу 31. Получается 40. Это искомые в задаче величины.

Ответ. Катеты треугольника равны 9 и 40 см.

Задача на нахождение стороны через площадь, сторону и угол треугольника

Условие. Площадь некоторого треугольника 60 см 2 . Необходимо вычислить одну из его сторон, если вторая сторона равна 15 см, а угол между ними равен 30º.

Решение. Исходя из принятых обозначений, искомая сторона «а», известная «в», заданный угол “γ”. Тогда формула площади можно переписать так:

60 = ½ а * 15 * sin 30º. Здесь синус 30 градусов равен 0,5.

После преобразований «а» оказывается равным 60 / (0,5 * 0,5 * 15). То есть 16.

Ответ. Искомая сторона равна 16 см.

Задача о квадрате, вписанном в прямоугольный треугольник

Условие. Вершина квадрата со стороной 24 см совпадает с прямым углом треугольника. Две другие лежат на катетах. Третья принадлежит гипотенузе. Длина одного из катетов равна 42 см. Чему равна площадь прямоугольного треугольника?

Решение. Рассмотрим два прямоугольных треугольника. Первый — заданный в задаче. Второй — опирается на известный катет исходного треугольника. Они подобны, так как имеют общий угол и образованы параллельными прямыми.

Тогда отношения их катетов равны. Катеты меньшего треугольника равны 24 см (сторона квадрата) и 18 см (заданный катет 42 см вычесть сторону квадрата 24 см). Соответствующие катеты большого треугольника — 42 см и х см. Именно этот «х» нужен для того, чтобы вычислить площадь треугольника.

18/42 = 24/х, то есть х = 24 * 42 / 18 = 56 (см).

Тогда площадь равна произведению 56 и 42, разделенному на два, то есть 1176 см 2 .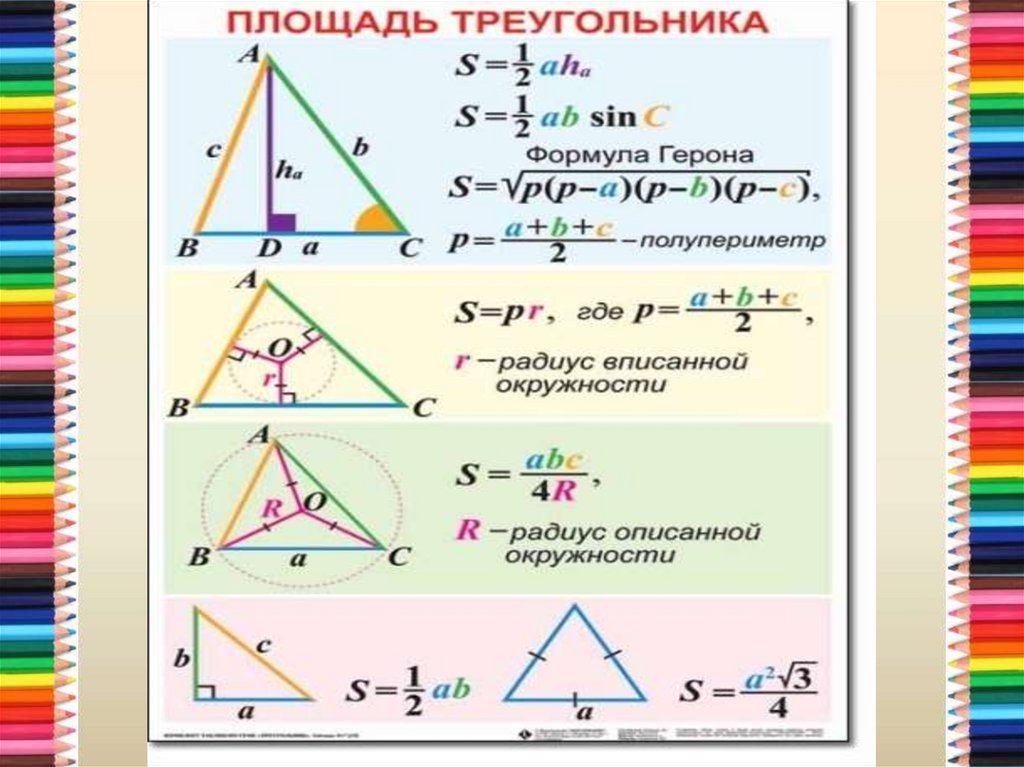

Ответ. Искомая площадь равна 1176 см 2 .

Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.

Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже

На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c – стороны треугольника,
R – радиус описанной окружности,
r – радиус вписанной окружности,
h[b],h[a],h[c] – высоты, проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma – углы возле вершин.

Основные формулы площади треугольника

1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так

Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами

2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью

То с первой формулы площади следуют однотипные вторые

Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).

3. Для углов треугольника справедливо соотношение

Зависимость позволяет применять в вычислениях следующие формулы площади треугольника

Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.

4. Если известна сторона и два прилегающих угла то площадь находится по формуле

5. Формула площади через сторону и котангенс прилегающих углов следующая

Перестановкой индексов можете получить зависимости для других сторон.

6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.

7. Формула Герона применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника

А затем определяют площадь по формуле

или

Ее довольно часто используют в коде программ калькуляторов.

8. Если известны все высоты треугольника то площадь определяют по формуле

Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».

9. Следующие формулы используют известны радиусы вписанных и описанных окружностей.

В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле

10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле

11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.

Ну и напоследок — частные случаи:
Площадь прямоугольного треугольника с катетами a и b равна половине их произведения

Формула площади равностороннего (правильного) треугольника =

= одной четвертой произведения квадрату стороны на корень из тройки.

8 класс. Геометрия. Площадь. Площадь треугольника и трапеции. — Площадь треугольника.

Комментарии преподавателя

Формула для площади треугольника и следствия из неё

На данном уроке мы докажем формулу для площади треугольника и решим несколько задач на её применение.

Будем называть сторону  – основанием, тогда  – высота, опущенная к этой стороне (см. Рис. 1).

Рис. 1. Высота и основание

Теорема о свойстве медианы треугольника

Площадь треугольника равна половине произведения его основания на высоту.

В формульном виде: .

Доказательство:

Рис. 2. Иллюстрация к теореме

Достроим треугольник до параллелограмма  – см. Рис. 2.

 (по трём сторонам:  – общая, ,  – как противоположные стороны параллелограмма).

Из равенства треугольников следует равенство их площадей: . Получаем: . Воспользовавшись формулой для площади параллелограмма: .

Доказано.

Сформулируем несколько следствий из данной теоремы.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов (см. Рис. 3).

Рис. 3. Иллюстрация к следствию 1

.

Следствие 2

Если высоты двух треугольников равны, то их площади относятся как основания (см. Рис. 4).

Рис. 4. Иллюстрация к следствию 2

.

Теорема 2

Медиана треугольника разбивает его на два равновеликих треугольника (см. Рис. 5).

Доказательство:

Рис. 5. Иллюстрация к теореме

Пусть  – треугольник,  – медиана,  – высота. Для треугольников  –  также является высотой. Запишем формулу для площади каждого из этих треугольников: , . Так как  ( – медиана), то: . Значит, эти треугольники являются равновеликими.

Доказано.

Формула для площади ромба

Теорема 3

Площадь ромба равна половине произведения его диагоналей (см. Рис. 6).

В виде формулы: .

Доказательство:

Рис. 6. Иллюстрация к теореме

 (по 3 сторонам:  – общая,  – свойства ромба). Из равенства треугольников следует равенство их площадей. Значит: . Но формулу для площади треугольника мы уже знаем:  (т. к. , поэтому  – высота треугольника ). Получаем следующее равенство:  ( – свойство диагоналей ромба).

Доказано.

Свойство треугольников с равными углами

Теорема 4

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

В виде формулы: .

Доказательство:

Рис. 7. Иллюстрация к теореме

Совместим треугольники так, чтобы вершина  совпала с вершиной , сторона  лежала на прямой , а сторона  лежала на прямой .

Рис. 8. Иллюстрация к теореме

Рассмотрим отношение площадей треугольников  и . Эти треугольники имеют общую высоту, проведённую из вершины , поэтому, по следствию 2 из теоремы 1, их площади относятся как основания, то есть: .

Из аналогичных соображений: . Перемножив эти два равенства, получим: .

Доказано.

Задачи на площадь треугольника и следствия из неё

Теперь решим несколько задач, используя доказанные формулы и свойства.

Задача 1

Площадь прямоугольного треугольника равна . Найдите катеты этого треугольника, если известно, что один из них составляет  другого.

Решение

Пусть один из катетов равен , а второй – . Тогда площадь треугольника можно вычислить по формуле: . Но, по условию: . Подставив это выражение, получаем: . Откуда: .

Ответ: .

Задача 2

В треугольнике  точка  лежит на стороне , точка  лежит на стороне . Кроме того: , , . Чему равна площадь треугольника  (Рис. 9)?

Решение:

Рис. 9. Иллюстрация к задаче

Воспользуемся теоремой 4 для треугольников  и  ( – общий угол этих треугольников). Из этой теоремы следует, что: . Значит: .

Ответ: .

На этом уроке мы рассмотрели понятия площадей треугольника и ромба, вывели из них некоторые следствия.  На следующем уроке мы научимся вычислять площадь трапеции.

ИСТОЧНИК

http://x-uni. com/geometriya/8-klass/video/ploschad-treugolnika

http://www.youtube.com/watch?v=2e7Qf6iEPPs

http://www.youtube.com/watch?v=mCI3Yj4t1O8

http://v.5klass.net/zip/7b9fd7f7274ef33da70777cf1fd1d25d.zip

http://fs01.metod-kopilka.ru/files/2015/01/11/Ploschad_treugolnika_8_klassna_18_noyabrya_pptx_1421009203.pptx

http://5klass.net/datas/geometrija/Ploschad-treugolnika-8-klass/0004-004-Ploschad-treugolnika.jpg

http://www.klassnye-chasy.ru/userfiles/ploshchad-treugolnika1.jpg

http://fs00.infourok.ru/images/doc/309/308291/img18.jpg

Что такое Формула площади треугольника с примерами

Столкнулись с трудностями при определении площади треугольника? Что ж, мы собираемся упростить для всех наших читателей вычисление площади треугольника с нашей формулой площади треугольника . Математика — это весело, но это самый практичный предмет для определения различных размеров площадей.

• Формула интегрирования
• Формула тригонометрии
• Тригонометрические соотношения
• Тригонометрические функции с формулами
• Что такое тригонометрические производные
• Высота и расстояние
• Тригонометрическая формула, включающая сумму разностей идентичностей продуктов
• Триггерные идентификаторы
• Теорема Пифагора
• Формула дифференциации
• Основные идентификаторы триггеров

Область — это, по сути, пространство, состоящее из любого заданного объекта. Этот объект может быть квадратом, многоугольником, треугольником и т. д. Мы ограничим нашу статью только обсуждением площади треугольника. Мы дадим правильное объяснение площади треугольника вместе с соответствующей формулой в нашей статье.

Формула площади треугольника

Ну, как должно быть известно большинству из нас, треугольник — это площадь поверхности, которая содержит три стороны. Другими словами, площадь треугольника состоит из трех сторон, в отличие от квадрата. Итак, нам в основном нужно принять во внимание все эти три стороны, чтобы узнать площадь треугольника.

Одна общая черта всех типов треугольников заключается в том, что стороны многоугольника треугольника всегда остаются половиной базовой временной высоты. Соответственно, мы должны вычислить базовую высоту времени, чтобы узнать точную площадь трехстороннего многоугольника. Мы можем обозначить это уравнение как площадь = 1/2 × b × h, чтобы вычислить высоту базового времени.

С помощью вышеупомянутой формулы мы можем легко вычислить базовую временную высоту треугольника. Хорошо, что вы можете применить эту формулу ко всем типам рассматриваемых треугольников. Обратите внимание, что во всех типах треугольников основание и высота всегда остаются равными друг другу.

Формула площади треугольника

После того, как вы выяснили основание и высоту треугольника, вычисление площади треугольника остается простым вычислением. Здесь мы приводим точную формулу площади треугольника для наших ученых читателей.

Формула расчета площади треугольника = A = ½ (b × h)

Пожалуйста, помните, что результирующий ответ площади треугольника всегда будет в квадратных единицах. Это потому, что площадь треугольника всегда имеет стандартные единицы обозначения в общей и математической областях.

Итак, как видите, проще вычислить площадь треугольника со значениями основания и высоты. Вышеупомянутая тактика и формула работают для расчета всех типов площадей треугольников.

Так что не стесняйтесь использовать эту формулу для личного и академического использования. Ученые могут поделиться этой формулой с другими, чтобы помочь им вычислить площадь треугольника.

The Formula for the Area of ​​Equilateral Triangles

The Formula for the Area of ​​Equilateral Triangles

Jana Russick

June 01, 2021

Online Tutoring

,

Algebra

,

Mathematics

Изображение предоставлено: Десмос

Прежде чем мы начнем, давайте рассмотрим, что такое равносторонний треугольник — треугольник с тремя равными длинами сторон и тремя равными внутренними углами по 60° каждый. Теперь давайте проясним одну вещь: площадь равностороннего треугольника равна , а не периметру равностороннего треугольника. Это общая площадь поверхности треугольника.

Как вы знаете, существует множество различных типов треугольников: прямоугольные, разносторонние и равнобедренные. Опять же, в равностороннем треугольнике длины сторон равностороннего треугольника равны.

Чтобы определить площадь равностороннего треугольника, необходимо знать длины его сторон. Итак, прежде чем погрузиться в формулу площади равностороннего треугольника, давайте посмотрим, как найти длины сторон.

Как найти длины сторон равностороннего треугольника

Зная высоту треугольника, можно определить длины сторон. Как только вы нашли длину стороны, вы можете определить площадь равностороннего треугольника.

Когда вы делите равносторонний треугольник на два прямоугольных треугольника, вы видите высоту равностороннего треугольника. Это делается путем разрезания равностороннего треугольника пополам от вершины вершины до середины одной стороны, чтобы образовать биссектрису угла.

Изображение предоставлено Desmos

Серединный перпендикуляр, прямая линия, образующая два угла по 90°, представляет собой высоту равностороннего треугольника, отмеченную высотой h . Создав эту биссектрису, мы разделили этот равносторонний треугольник на два прямоугольных треугольника. Чтобы найти высоту, можно воспользоваться теоремой Пифагора:

Так как все стороны равностороннего треугольника одинаковы, то сторона А=стороне С. А так как основание прямоугольного треугольника равно половине длины стороны равностороннего треугольника , сторона А=сторона С/2. Теперь давайте подставим высоту, основание и длину стороны C для гипотенузы, чтобы выделить значение h:

Если вы знаете только высоту биссектрисы равностороннего треугольника, вы можете использовать эту формулу для определения длины каждой равносторонней стороны:

![площадь равностороннего треугольника: формула для определения длины

Давайте применим это Формула треугольника, в котором ч = 9, чтобы найти длины сторон:

Теперь, когда мы знаем, как использовать высоту равностороннего треугольника, чтобы определить недостающую длину стороны, давайте научимся находить площадь.

No related posts.