№№ п/п | Понятия, | Содержание, формула |
1 | Множество | Множество $A-$ совокупность каких-либо объектов $a$, называемых элементами множества: $a\in A$ |
2 | Дополнение $\overline A $ | $\overline A $ содержит все элементы, не принадлежащие $A$ |
3 | Равенство | Два множества $A$ и $B$ равны между собой, если они состоят из одних и тех же элементов |
4 | Объединение { сумма } множеств $C=A+B$ | Множество $C$ состоит из всех элементов, принадлежащих или множеству $A$, или множеству $B$ или и $A$ и $B$ одновременно |
5 | Пересечение | Множество $C$ состоит из элементов, принадлежащих одновременно и множеству $A$ и множеству $B$ |
6 | Разность двух | $C$ состоит из элементов множества $A$, которые не являются элементами множества $B$ |
7 | Эквивалентные | Два множества называются эквивалентными, если между ними установлено взаимно-однозначное соответствие. |
12 | Стохастический эксперимент | Это опыт { испытание } , результат которого заранее не определен |
13 | Достоверное | Результат, который обязательно наступает при осуществлении данного комплекса условий { опыта, эксперимента } называется достоверным событием |
14 | Случайное | Это событие, которое может произойти, а может и не произойти в данном испытании |
15 | Невозможное | Это событие, которое не может произойти при данном комплексе условий |
16 | Относительная частота события $A$ | Отношение $\nu (A)=\frac { m } { n } $ числа экспериментов $m$, завершившихся событием $A$, к общему числу $n$ проведенных экспериментов |
17 | Статистическое определение | Если при неограниченном увеличении числа экспериментов относительная частота события $\nu (A)$ стремится к некоторому фиксированному числу, то событие $A$ стохастически устойчиво и это число $p(A)$ называют вероятностью события $A$ |
18 | Определение | $P(A)=\frac { m } { n } $, где $m$ – число исходов стохастического эксперимента, благоприятствующих наступлению события $A$, $n$ – общее число всех равновозможных исходов |
19 | Вероятность | $P(A+B)=P(A)+P(B)-P(AB)$ |
20 | Вероятность | $P(AB)=P(A)\cdot P(B/A)=P(B)\cdot P(A\vert B)$, где $P(B\vert A)$ – условная вероятность события $B$ при условии, что событие $A$ с ненулевой вероятностью произошло |
21 | Независимые | Это такие события, для которых $P(B\vert A)=P(B)$ и $P(A\vert B)=P(A)$. |
27 | Понятие | Случайной величиной называют переменную величину, которая принимает числовые значения в зависимости от исходов испытания случайным образом. |
28 | Понятие | ДСВ $X$ – случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, то есть численные значения которой образуют конечное или счетное множество. |
29 | Закон | Соответствие между значениями $x_1, x_2, \cdots $ дискретной случайной величины и их вероятностями $p_1, p_2, \cdots $ называется законом распределения и может быть задан таблично или аналитически { то есть с помощью формул } . |
30 | Понятие | НСВ $X$ – случайная величина, которая может принимать любые значения из некоторого промежутка, то есть множество значений непрерывной случайной величины несчетно. |
31 | Функция | Функцией распределения случайной величины $X$ называется функция действительного переменного $x$, определяемая равенством $F(x)=P(X\lt x)$, где $P(X\lt x)$ — вероятность того, что случайная величина $X$ принимает значение, меньше $x$ Функция распределения $F(x)$ для ДСВ $X$, которая может принимать значения $x_1 ,x_2 ,…x_n $ c соответствующими вероятностями $p_1 ,p_2 ,…,p_n$ имеет вид $F(x)=\sum\limits_ { x_k \lt x } { P(X\lt x_k ) } $, где символ $x_k \lt x$ означает, что суммируются вероятности $p_k $ тех значений, которые меньше $x$. Функция является разрывной. Случайная величина $X$ называется непрерывной, если ее функция распределения $F(x)$ является непрерывно дифференцируемой. Вероятность того, что СВХ примет значение из промежутка $\left[ { \alpha ;\beta }\right)$, равна разности значений ее функции распределения на концах этого полуинтервала: $P(\alpha \leqslant X\lt \beta )=F(\beta )-F(\alpha )$ Свойства функции распределения 1. $0\leqslant F(x)\leqslant 1$ 2. Если $x_1 \lt x_2 $, то $F(x_1 )\leqslant F(x_2 )$, то есть функция распределения является неубывающей.
|
31 | Функция | 3. Функция $F(x)$ в точке $x_0 $ непрерывна слева, то есть $\mathop { \lim } \limits_ { x\to x_0 -0 } F(x)=F(x_0 )$; $F(x_0 -0)=F(x_0 )$ 4. Если все возможные значения СВХ принадлежат интервалу $(a;b)$, то $F(x)=0$ при $x\leqslant a$, $F(x)=1$ при $x\geqslant b$ 5. Если все возможные значения СВХ принадлежат бесконечному интервалу $\left( { -\infty ;+\infty }\right)$, то $\mathop { \lim } \limits_ { x\to -\infty } F(x)=0;\mathop { \lim } \limits_ { x\to +\infty } F(x)=1;$ Если $X$ – непрерывная случайная величина, то вероятность того, что она примет одно заданное определенное значение, равна нулю: $P(X=\alpha )=0$ Отсюда следует, что для непрерывной случайной величины выполняются равенства: $P(\alpha \lt X\lt \beta )=P(\alpha \leqslant X\leqslant \beta )=P(\alpha \leqslant X\lt \beta )=$ $=P(\alpha \lt X\leqslant \beta )=F(\beta )-F(\alpha )$ |
32 | Плотность Для нормального распределения $Э_x =0$. Кривые, более островершинные по сравнению с нормальной кривой Гаусса, имеют $Э_x \gt 0$. |
n$
2 } { 2 } } } dt$; $\Phi (-x)=-\Phi (x)$ { таблица 4 }
\infty { p_k =1 } $
4 } -3.$Теория вероятности. Основные формулы — презентация онлайн
Похожие презентации:
Основные теоремы и формулы теории вероятности
Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика
Основные понятия теории вероятностей
Основные теоремы теории вероятностей
Основные понятия теории вероятностей
Теория вероятностей и математическая статистика
Основные понятия теории вероятности. Случайные события
Статистическая радиофизика. Модели случайных процессов. (Тема 4)
Основные теоремы теории вероятностей
Теория вероятности
Понятие
Формула
PA =
Вероятность, мера вероятности
n( A)
n
Объединение событий
AÈB={x|xÎAÚxÎB}
Пересечение событий
AÇB={x|xÎAÙxÎB}
Противоположное событие
Ā={xÏA}
Разность, или дополнение события
A\B={xÎA|xÏB}
Включение
AÍBÛ»aÎA:aÎB
Равенство
A=BÛ(AÍB)Ù(BÍA)
Строгое включение
AÌBÛ(AÍB)Ù(A¹B)
Несовместимость
Относительная частота события
n( A)* *
n( A)*
n( A)
P =
; PA Þ PA ; * Þ
*
n
n
n
n®¥
*
A
n®¥
Правило умножения несовместных
событий
n*m
Перестановка n элементов
P = n!
Размещение m элементов n способами
Anm =
n!
= n(n — 1)(n — 2)(n — 3).
..(n — m + 1)(n — m)!
n!
m!(n — m)!
Сочетание m элементов n способами
Cnm =
Условная вероятность события B при
условии, что событие A уже имело место
P( A | B) =
«…есть k объектов, из которых l
обладают интересующим нас признаком;
вероятность
того,
что
среди
m
выбранных объектов данным признаком
будет обладать n объектов, равна…»
PA =
P( A Ç B )
P( B )
n( A)
; n = Ckm ; n( A) = Cln ´ Ckm—l n
n
n
Формула полной вероятности
P( B) = å P( Ai ) P( B | Ai ) = P( A1 ) P( B | A1 ) + P( A2 ) P( B | A2 ) + ..
i =1
Теорема Байеса
P( Bk | A) =
P( Bk ) P( A | Bk )
n
å P( B ) P( A | B )
i =1
i
i
Вероятность k исходов в n
повторяющихся событиях
P( A) = Cnk ´ p k ´ (1 — p ) n-k
Вероятность возникновения исхода
в событии с порядковым номером l
P(t = l ) = p ´ q l -1 = p ´ (1 — p )l -1
Математическая статистика
Понятие
Формула
Размах
R = max(x1;x2;…;xn)-min(x1;x2;…;xn)
X =
Среднее арифметическое
( X + X 2 + X 3 + .
.. + X n )1 n
Xi = 1
å
n i =1
n
1 n
D=
( X i — X )2
å
n — 1 i =1
Дисперсия
s =
Стандартное отклонение
Коэффициент линейной корреляции
1 n
( X i — X )2
å
n — 1 i =1
å (x — x ) × ( y — y )
å (x — x ) × å ( y — y )
i
i
2
2
i
;
df = n — 2
i
( )
n × (n — 1) ;
6 × å D2
Коэффициент ранговой корреляции
r =1-
Коэффициент частной корреляции
rxy — z =
df = n
2
rxy — rxz × ryz
(1 — r )× (1 — r )
2
xz
2
yz
n1 × n2 × (n1 + n2 — 2 ) × ( x — y )
2
2
x
x
+
y
y
× (n1 + n2 )
(
)
(
)
å i
å i
2
t-критерий Стьюдента (в общем случае)
t=
(
t=
t-критерий Стьюдента для независимых групп
)
x-y
(n1 — 1) × s 12 + (n2 — 1) × s 22 × n1 + n2
n1 + n2 — 2
n1 × n2
df = n1 + n2 — 2
t-критерий Стьюдента для зависимых групп
Одновыборочный t-критерий Стьюдента
F-критерий Фишера
t=
å (x — y )
i
i
n × σ ( xi — y i )
t= n×
;
df = n — 1
x-A
σ ; df = n — 1
max( D1; D2 )
F=
min( D1; D2 ) ;
df1 = nmax – 1; df2 = nmin — 1
;
English Русский Правила
Формулы вероятности – Список основных формул вероятности с примерами
Вы, должно быть, слышали термин «вероятность», используемый для предсказания прогноза погоды в новостных телевизионных сводках на следующие несколько дней для некоторых частей страны.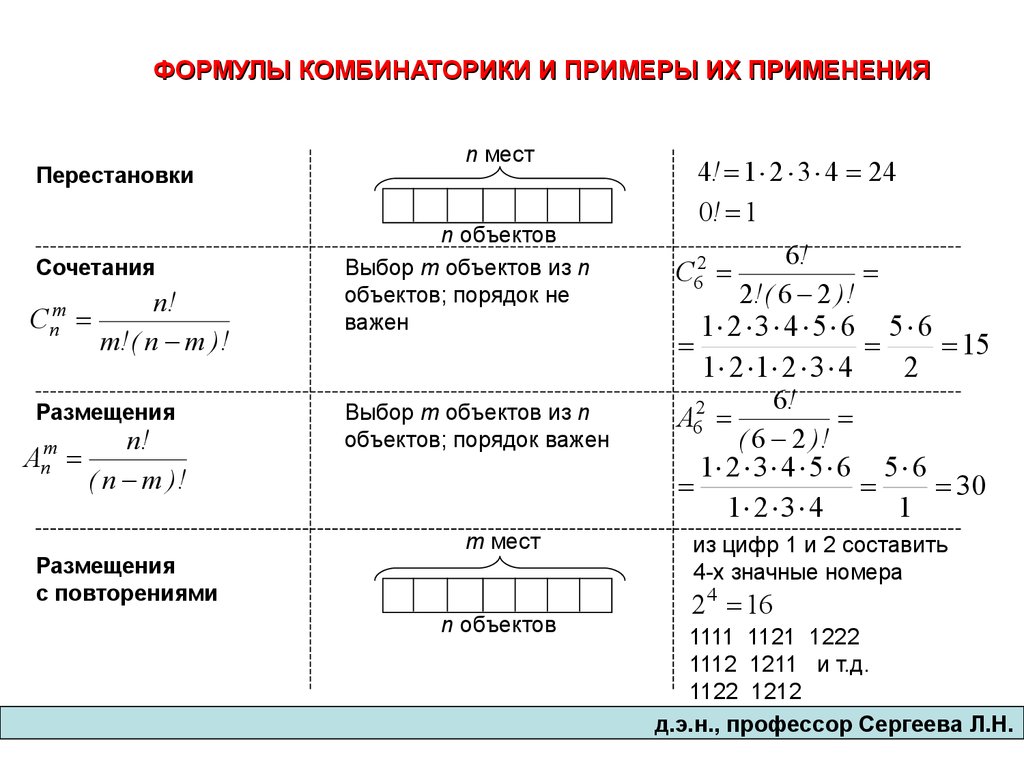
Для расчета вероятности различных типов ситуаций используется формула вероятности и связанные с ней основные понятия. Вероятность — это способ измерения неопределенности, насколько вероятно, что событие произошло или должно произойти.
Вероятность — это раздел математики, связанный с числовым описанием того, насколько вероятны шансы того, что событие произойдет, или насколько вероятно, что конкретное суждение истинно. Для любого события вероятность лежит в диапазоне от 0 до 1. 0 указывает на невозможность события, а 1 указывает на уверенность в том, что событие обязательно произойдет.
Обозначение вероятности
Например: допустим, что происходят два события, а именно А и В. Таким образом, для вероятности того, что событие А может произойти, мы будем писать Р(А), а для вероятности того, что событие В может случиться, мы можем написать P(B).
Термины, относящиеся к формуле вероятности
Есть несколько важных терминов, связанных со всеми формулами вероятности
Результат: результат события после экспериментов с стороной
Событие: Комбинация всех возможных исходов эксперимента, таких как выпадение орла или решки на подброшенной монете, получение четного или нечетного числа на кости и т.
д.
д.Формулы вероятности с примерами
Чтобы рассчитать вероятность события, мы используем эту формулу вероятности, напоминая, что вероятность — это вероятность того, что событие произойдет. Эта формула поможет вам получить вероятность любого конкретного события.
Эта формула представляет собой количество благоприятных исходов к общему числу всех возможных исходов, которые мы уже определили в Пространстве образцов.
Вероятность События = (Количество благоприятных исходов) / (Общее количество возможных исходов)
P(A) = n(E) / n(S)
P(A) < 1
Здесь P(A) означает нахождение вероятности события A, n(E) означает количество благоприятных исходы события, а n(S) означает множество всех возможных исходов события.
Если вероятность наступления события равна P(A), то вероятность того, что событие не произойдет, равна
P(A’) = 1- P(A)
Пример 01: Вероятность получения нечетного числа при броске кости на один раз.
Решение: Пример пространства = {1, 2, 3, 4, 5, 6}
n(S) = 6
Благоприятные исходы = {1, 3, 5}
n(E) = 3
Используя формулу вероятности,
P(A) = n(E) / n(S )
P(получение нечетного числа) = 3 / 6 = ½ = 0,5
Важный список формул вероятности
Вам просто нужно иметь события, для которых вы ищете вероятность, и формулы сделают ваш работать легче. В приведенных ниже формулах мы берем 2 события, а именно A и B. Формулы основаны только на этих событиях.
Событие (A OR B)
P (A U B) = P (A) + P (B) – P (A ∩ B)
Событие (A и B)
Событие (A NOT B)
Событие (B NOT A)
Событие (НЕ A)
P(A.B’) = P(A) — P(A.B)
P(A+B) = P(AB ‘) + P(A’B) + P(A.B)
(А ∩ В) = Р (А) . P (B)
P(A NOT B) = A – B
Вероятность возникновения события P(A)
Некоторые формулы, важные для вероятности, основанные на них, следующие: (A’B) = P(B) — P(A.B)
Пример 01: Два игральных кубика подбрасываются одновременно. Рассчитайте вероятность того, что сумма чисел на двух игральных костях равна 6,9.0003
Решение:
Пространство выборки = (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1), (2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3, 4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)( 5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3) ),(6,4),(6,5),(6,6)(1,1),(1,2),(1,3),(1,4),(1,5),( 1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2) ,(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4 ,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1), (6,2),(6,3),(6,4),(6,5),(6,6){(1, 1), (1, 2), (1,3), (1 ,4), (1,5), (1, 6)} {(2, 1), (2, 2), (2,3), (2,4), (2,5), (2, 6)} {(3, 1), (3, 2), (3,3), (3,4), (3,5), (3, 6)} {(4, 1), (4, 2), (4,3), (4,4), (4,5), (4, 6)} {(5, 1), (5,2), (5,3), (5,4 ), (5,5), (5, 6)} {(6, 1), (6, 2), (6,3), (6,4), (6,5), (6, 6) } n(S) = 36
Благоприятные исходы = {(1, 5), (2, 4), (3, 3), (4, 2) и (5, 1)}
n(E) = 5
Использование, P( A) = n(E) / n(S)
P(Получение суммы чисел на двух игральных костях 6) = 5/ 36
Принц
Формула вероятности: Вероятность наступления события определяется вероятностью.
В этой статье учащиеся могут найти шаги по расчету формул вероятности. Некоторыми из обсуждаемых формул вероятности являются диапазон вероятностей, формула условной вероятности, формула теоремы Байеса и так далее. Студенты могут получить четкое представление о концепции, и это поможет им успешно сдать экзамены. Чтобы узнать больше о формулах вероятности, продолжайте читать статью.
Учащиеся, которые ищут формулу теоремы Байеса, формулу условной вероятности, формулу теоремы Байеса, формулу условной вероятности и формулу распределения Пуассона, могут проверить подробности ниже.
Неопределенность/определенность возникновения события измеряется вероятностью. Хотя теория вероятности началась с азартных игр, сейчас она широко используется в областях физических наук, коммерции, биологических наук, медицинских наук, прогнозирования погоды и т. д. Вероятность для 10-го класса — важная глава для учащихся, в ней объясняются все основные понятия.
Чтобы найти вероятность возникновения одного события, во-первых, мы должны знать общее количество возможных исходов. Например, когда мы подбрасываем монету, выпадает либо орел, либо решка, т.е. возможны только два возможных исхода (H, T). Если мы хотим, чтобы выпал орел, наш благоприятный исход равен H. Итак, мы обозначаем вероятность выпадения орла при подбрасывании монеты как:
= 1/2
Как рассчитать вероятность?
Формула вероятности дает возможность события, которое должно произойти. Он равен отношению числа благоприятных исходов к общему числу исходов. Мы привели формулы вероятности с примерами.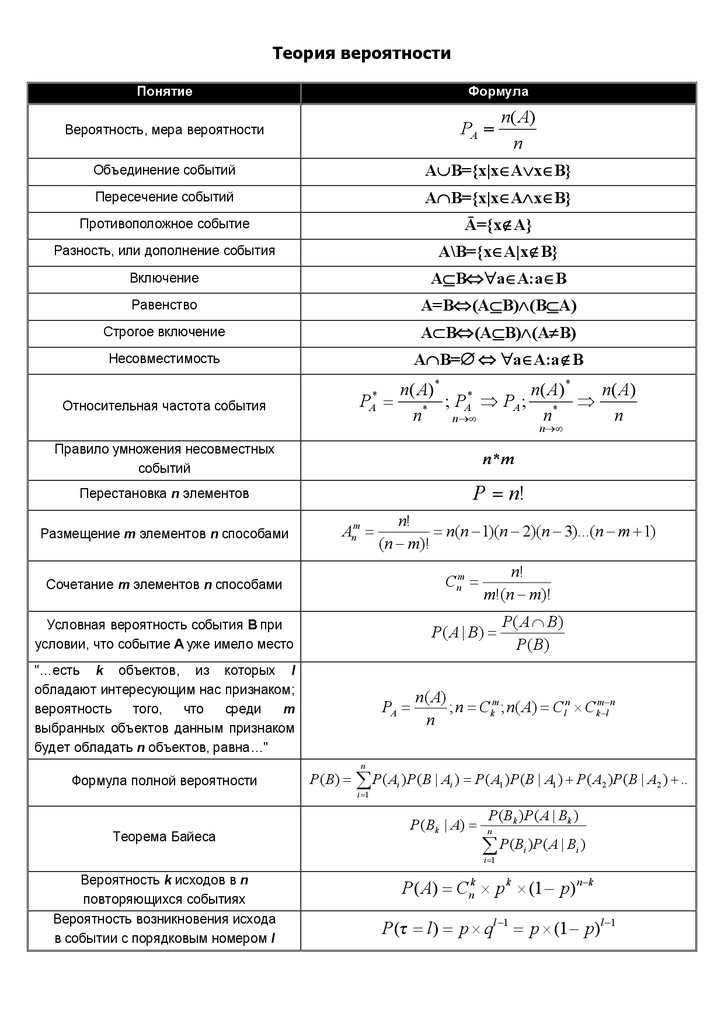
| Вероятность события P(E) = количество благоприятных исходов/общее число исходов |
или
P(A) — вероятность события «A»
n(A) — количество благоприятных исходов
n(S) — общее количество событий в пространстве выборки
результат и «желаемый результат» в контексте вероятности. Иногда студенты путают эти два термина. В некоторых требованиях проигрыш в определенном тесте или появление нежелательного результата может быть благоприятным событием для проведения экспериментов.
Основные формулы вероятности: формула условной вероятности, формула теоремы Байеса
Здесь мы приводим некоторые математические формулы вероятностей, которые будут очень полезны для учащихся: c ) + P(A) = 1
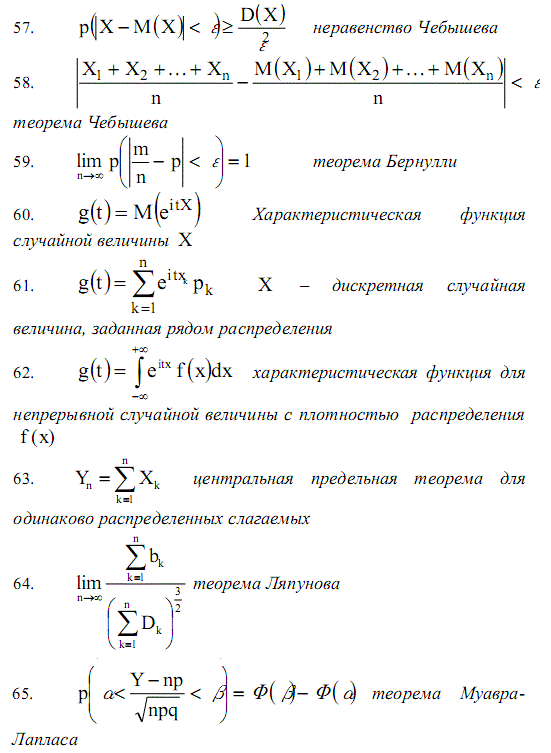События A и B независимы тогда и только тогда, когда 244 x ) = P ( X ≤ x )Помимо этих формул вероятности в классе 10, есть еще несколько важных уравнений вероятности:
Функция массы вероятности
Функция массы вероятности (PMF) (или функция частоты) дискретной случайной величины X присваивает вероятности возможным значениям случайной величины.
Кроме того, если A является подмножеством возможных значений X, то вероятность того, что X примет значение в A , определяется по формуле:0152 , обозначаемый буквой f, непрерывной случайной величины X удовлетворяет следующему: Это обозначается следующей формулой:
Здесь
cov x, y = ковариация между переменными a и y
3
52 i = данные значение хy i = значение данных y
x̄ = 9015 3 x 9000 = среднее значение у
N = Количество значений данных
Скачать – Формулы вероятности PDF
Другие важные статьи по математике:
Решенные примеры по формулам вероятности класс 12
Здесь мы предоставили несколько примеров вероятностного решения.
Вопрос 1: Монету подбрасывают 3 раза. Какова вероятность того, что выпадет хотя бы одна голова?
Решение: Пример пространства = [HHH, HHT, HTH, THH, TTH, THT, HTT, TTT]
Общее количество способов = 2 × 2 × 2 = 8.
Благоприятные случаи = 7 [Необходимо не менее 1 Голова]
P (A) = количество благоприятных исходов/общее количество исходов
= 7/8
Вопрос 2: Из колоды в 52 карты вытягиваются две карты. Найдите вероятность того, что оба бубны или оба короли.
Решение: Всего № путей = 52 C 2
Случай I: Оба бубны = 13 C 2
Случай II: 2 907 2 90 7 2 4 9 2 королей = 4 90 5 2
P (оба ромбовидные или оба короля) = ( 13 C 2 + 4 C 2 ) / 52 C 2 = 14/221
Решение: Выборочное пространство (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Пусть «E» — событие получения нечетного числа, E = { 2, 4, 6}
n(E) = 3
Итак, Вероятность выпадения нечетного числа:
P(E) = (Количество благоприятных исходов)/(Общее количество исходов)
= n(E) /n(S)
= 3/6
= 1/2
Вопрос 4. Какова вероятность выпадения суммы 22 или более при бросании четырех игральных костей?
Решение: Общее количество путей = 6 4
= 1296
(i) Количество способов получить сумму 22 равно 6,6,6,4 = 4! / 3!
= 4 и 6,6,5,5 = 4! / 2!2!
= 6.
(ii) Количество способов получить сумму 23 равно 6,6,6,5 = 4! / 3! = 4
(iii) Количество способов получить сумму 24 равно 6,6,6,6 = 1.
Изб. Количество случаев = 4 + 6 + 4 + 1 = 15 способов.
P (получив сумму 22 или более) = 15/1296
= 5/432
Вопрос 5: Найдите вероятность того, что в високосном году 52 воскресенья.
Решение: В високосном году может быть 52 воскресенья или 53 воскресенья.
В високосном году 366 дней, из которых 52 полных недели и 2 оставшихся дня.
Теперь эти два дня могут быть (сб, вс), (вс, пн), (пн, вт), (вт, ср), (ср, чт), (чт, пт), (пт, сб).
Таким образом, всего 7 случаев, из которых (Сб, Вс) (Вс, Пн) два благоприятных случая.
Итак, P (53 воскресенья) = 2/7
Теперь P(52 воскресенья) + P(53 воскресенья) = 1
Итак, P (52 воскресенья) = 1 – P(53 воскресенья) = 1 – (2/ 7) = (5/7)
Также проверьте:
Практические вопросы по всем формулам вероятности
Здесь мы предоставили вам несколько практических вопросов по формулам вероятности для класса 7:
Если вынутый шар красный, найти вероятность того, что он вынут из третьего мешка.
Если наугад взять из пачки ручку, заменить ее и повторить процесс еще 2 раза, какова вероятность того, что вытащите 2 синие ручки и 1 черную ручку?Часто задаваемые вопросы
Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с формулами статистической вероятности:
Q1: Где я могу скачать формулы вероятности для aptitude?
Ответ: Вы можете скачать формулы вероятности для способностей в формате PDF с Embibe. Мы предоставили все основные формулы вместе с уравнениями вероятности на этой странице.
Q2: Какая платформа лучше всего подходит для начинающих, чтобы изучить основы вероятности?
Ответ: Embibe — одна из лучших образовательных технологий, предлагающая обучающие программы для учащихся от начального до следующего уровня.
Студенты также могут получить доступ к списку всех формул вероятности на Embibe и попробовать некоторые пробные тесты, чтобы подготовиться к экзаменам.
Q3: Как проще всего понять вероятность?
Ответ: Самый простой способ понять вероятность — сначала взглянуть на решенные вопросы и примеры вероятности. После этого учащиеся должны начать с основ вероятности. На Embibe доступно множество пробных тестов на вероятность того, что учащиеся могут попытаться развеять свои сомнения относительно вероятности.
Q4: Что такое формула вероятности?
Ответ: Вероятность события равна количеству благоприятных исходов, деленному на общее число возможных исходов. Это базовое определение вероятности предполагает, что все исходы имеют одинаковую вероятность.
Q5: Какие существуют 3 типа вероятности?
Ответ: Существует 3 типа вероятности:
(i) Теоретическая вероятность.