Основные формулы по тригонометрии — Математика — Теория, тесты, формулы и задачи
- Главная —
- Формулы и прочее —
- Математика: Тригонометрия
Знание формул по тригонометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по тригонометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении тригонометрических задач. На этой странице сайта представлены основные формулы по школьной тригонометрии.
Изучать основные формулы по школьной тригонометрии онлайн:
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше.
 В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Некоторые рекомендации к выполнению тригонометрических преобразований
- Основные тригонометрические формулы
- Дополнительные тригонометрические формулы
- Тригонометрические формулы приведения
- Тригонометрическая окружность
- Тригонометрические уравнения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению.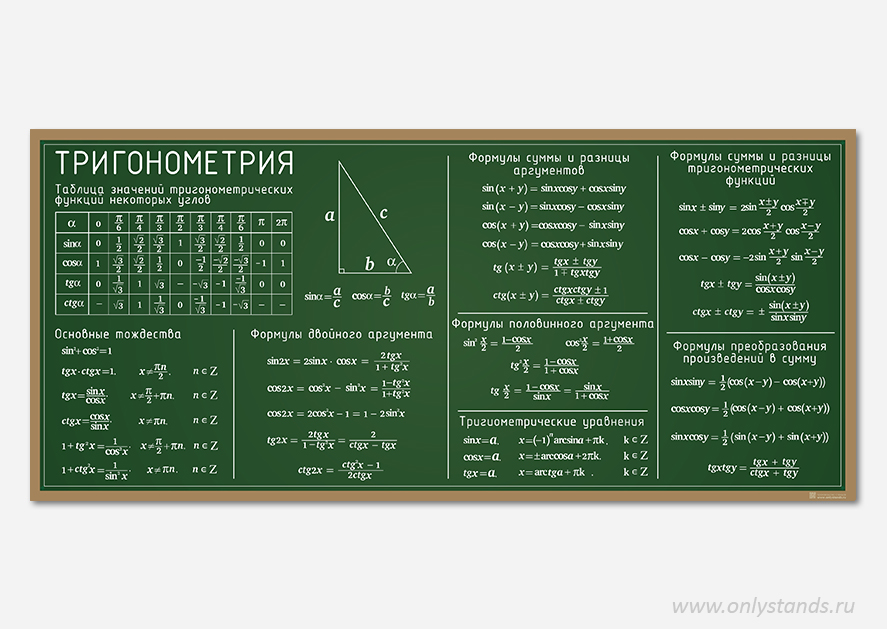 ..
..
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению…
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени.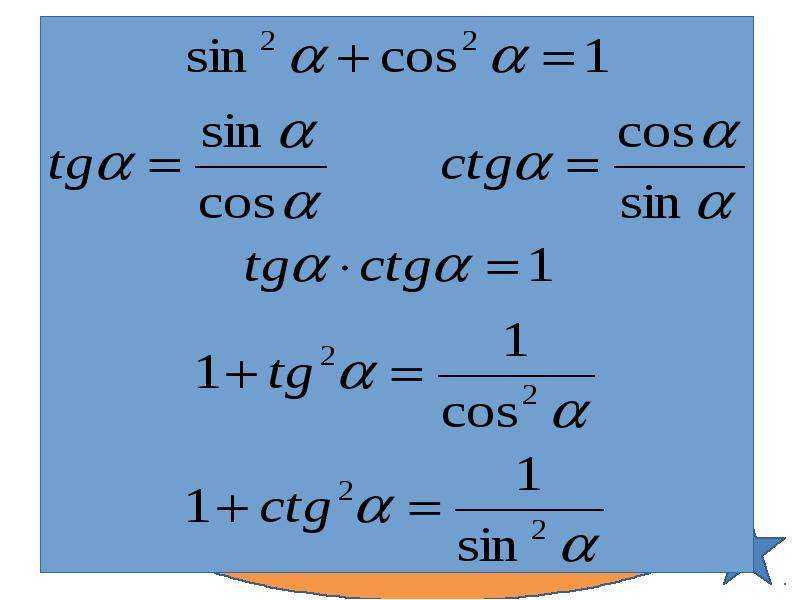 Формула понижения степени для синуса:
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
К оглавлению…
Функцию косинус называют
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.
 е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.

- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней).
 Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Тригонометрические формулы и тождества — полный список
Последнее обновление Teachoo 30 марта 2023 г. В формулах тригонометрии мы узнаем
В формулах тригонометрии мы узнаем
Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Знак греха, потому что, загар в разных квадрантах
радианы
Отрицательные углы (четно-нечетные тождества)
Значение sin, cos, tan повторяется после 2π
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
- Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Закон синуса
Закон косинуса
Что такое обратные тригонометрические функции?
Область и диапазон функций обратной тригонометрии
Обратные тригонометрические формулы
- Подстановки обратной тригонометрии
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Чтобы узнать знак греха, потому что, загар в разных квадрантах,
мы помним
А дд → С
Представление в виде таблицы
Квадрант я | Квадрант II | Квадрант III | Квадрант IV | |
грех | + | + | – | – |
потому что | + | – | – | – |
загар | + | – | + | – |
радианы
Радианная мера = π/180 × градусная мера
Также,
1 градус = 60 минут
то есть 1° = 60’
1 минута = 60 секунд
то есть 1’ = 60’’
Отрицательные углы (четно-нечетные тождества)
грех (–х) = – грех х
соз (–х) = соз х
тангенс (–x) = – тангенс х
сек (–x) = сек х
cosec (–x) = – cosec x
детская кроватка (–x) = – детская кроватка x
Значение sin, cos, tan повторяется после 2π
грех (2π + х) = грех х
потому что (2π + х) = потому что х
загар (2π + х) = загар х
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
sin (π/2 – x) = cos x | потому что (π / 2 — х) = грех х |
грех (π/2 + х) = потому что х | cos (π/2 + x) = – sin x |
sin (3π/2 – x) = – cos x | cos (3π/2 – x) = – sin x |
sin (3π/2 + x) = – cos x | потому что (3π/2 + х) = грех х |
грех (π — х) = грех х | cos (π – x) = – cos x |
грех (π + х) = – грех х | cos (π + x) = – cos x |
грех (2π – х) = – грех х | потому что (2π — х) = потому что х |
грех (2π + х) = грех х | потому что (2π + х) = потому что х |
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Продукт для суммирования тождеств
2 cosx cosy = cos (x + y) + cos(x — y)
-2 sinx siny = cos (x + y) — cos(x — y)
2 sinx cosy = sin (x + y) + sin(x — y)
2 cosx siny = sin (x + y) — sin(x — y)
Закон синуса
Здесь
- A, B, C — вершины Δ ABC
- a — сторона, противоположная A, т.
 е. BC
е. BC - b — сторона, противоположная B, т.е. AC
- c — сторона, противоположная C, т.е. AB
Закон косинуса
Так же, как закон синуса, у нас есть закон косинуса
Что такое обратные тригонометрические функции
Если грех θ = х
Затем положить грех на правую сторону
θ = грех -1 Икс
грех -1 х = θ
Таким образом, обратным греху является угол.
Точно так же обратная ко всем функциям тригонометрии угол.
Примечание : Здесь угол измеряется в радианах, а не в градусах.
Итак, у нас есть
грех -1 Икс
потому что -1 Икс
загар -1 Икс
cosec -1 Икс
сек -1 Икс
загар -1 Икс
Область определения и область значений обратных тригонометрических функций
Домен | Диапазон | |
грех -1 | [–1, 1] | [-π/2,π/2] |
потому что -1 | [–1, 1] | [0,π] |
загар -1 | р | (-π/2,π/2) |
cosec -1 | р – (–1, 1) | [π/2,π/2] — {0} |
сек -1 | р – (–1, 1) | [0,π]-{π/2} |
детская кроватка -1 | р | (0, π) |
Формулы обратной тригонометрии
Некоторые формулы обратной тригонометрии:
грех –1 (–x) = – грех -1 Икс
потому что –1 (–x) = π – грех -1 Икс
загар –1 (–x) = – загар -1 Икс
cosec –1 (–x) = – cosec -1 Икс
сек –1 (–x) = – сек -1 Икс
детская кроватка –1 (–x) = π – детская кроватка -1 Икс
Замена обратной тригонометрии
Тригонометрические формулы и тождества — полный список
Последнее обновление Teachoo 30 марта 2023 г.
В формулах тригонометрии мы узнаем
Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Знак греха, потому что, загар в разных квадрантах
радианы
Отрицательные углы (четно-нечетные тождества)
Значение sin, cos, tan повторяется после 2π
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Закон синуса
Закон косинуса
Что такое обратные тригонометрические функции?
Область и диапазон функций обратной тригонометрии
Обратные тригонометрические формулы
- Подстановки обратной тригонометрии
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Чтобы узнать знак греха, потому что, загар в разных квадрантах,
мы помним
А дд → С угар → Т о → С кофе
Представление в виде таблицы
Квадрант я | Квадрант II | Квадрант III | Квадрант IV | |
грех | + | + | – | – |
потому что | + | – | – | – |
загар | + | – | + | – |
радианы
Радианная мера = π/180 × градусная мера
Также,
1 градус = 60 минут
то есть 1° = 60’
1 минута = 60 секунд
то есть 1’ = 60’’
Отрицательные углы (четно-нечетные тождества)
грех (–х) = – грех х
соз (–х) = соз х
тангенс (–x) = – тангенс х
сек (–x) = сек х
cosec (–x) = – cosec x
детская кроватка (–x) = – детская кроватка x
Значение sin, cos, tan повторяется после 2π
грех (2π + х) = грех х
потому что (2π + х) = потому что х
загар (2π + х) = загар х
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
sin (π/2 – x) = cos x | потому что (π / 2 — х) = грех х |
грех (π/2 + х) = потому что х | cos (π/2 + x) = – sin x |
sin (3π/2 – x) = – cos x | cos (3π/2 – x) = – sin x |
sin (3π/2 + x) = – cos x | потому что (3π/2 + х) = грех х |
грех (π — х) = грех х | cos (π – x) = – cos x |
грех (π + х) = – грех х | cos (π + x) = – cos x |
грех (2π – х) = – грех х | потому что (2π — х) = потому что х |
грех (2π + х) = грех х | потому что (2π + х) = потому что х |
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Продукт для суммирования тождеств
2 cosx cosy = cos (x + y) + cos(x — y)
-2 sinx siny = cos (x + y) — cos(x — y)
2 sinx cosy = sin (x + y) + sin(x — y)
2 cosx siny = sin (x + y) — sin(x — y)
Закон синуса
Здесь
- A, B, C — вершины Δ ABC
- a — сторона, противоположная A, т.


 В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.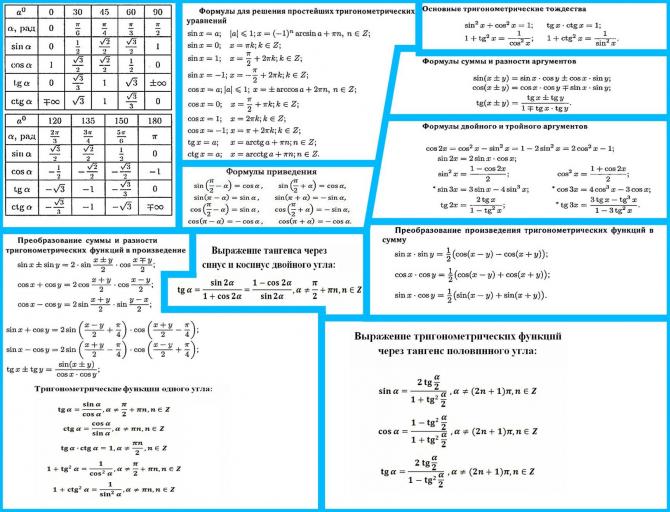
 Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.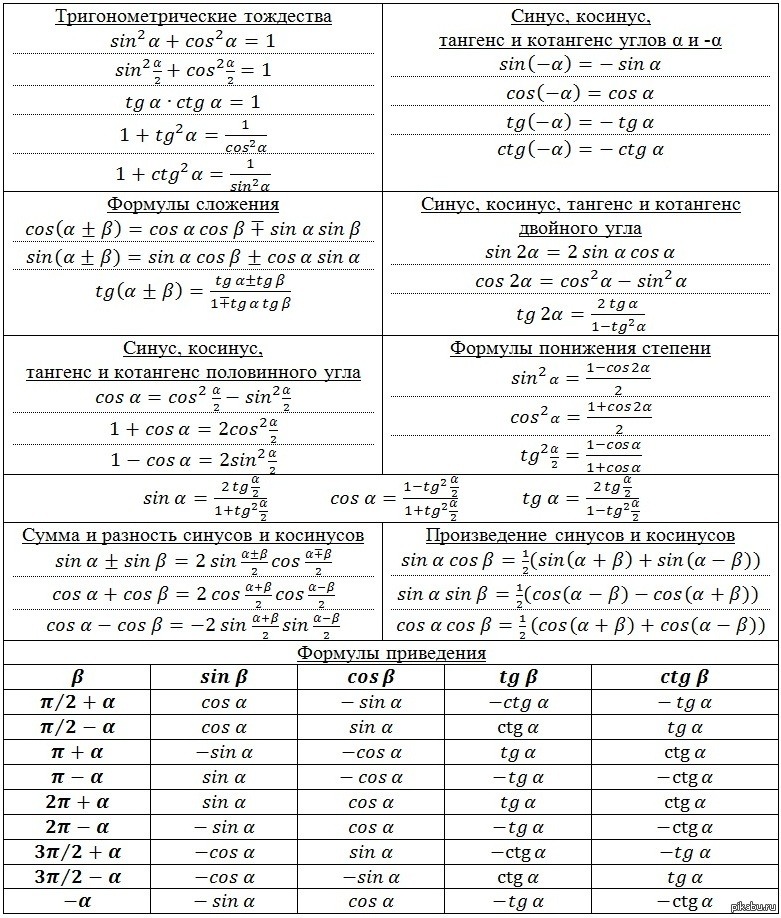 е. BC
е. BC