Теория вероятностей
Теория вероятностей
ОглавлениеГлава 1. ВведениеПРЕДИСЛОВИЕ 1.  Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5.  4. Плотность распределения5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8.  Системы случайных величин8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений.  Общая запись нормального закона для системы произвольного числа случайных величинГлава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин.  Композиция законов распределения12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14.  3. Доверительный интервал. Доверительная вероятность14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15.  7.2. Производная от случайной функции15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17.  17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19.  3. Поток событий. Простейший поток и его свойства19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 8. Значения распределение Пуассона |
Распределения для присвоения произвольных значений—ArcGIS Pro
Ниже приведены доступные распределения для различных инструментов, которые создают произвольные значения.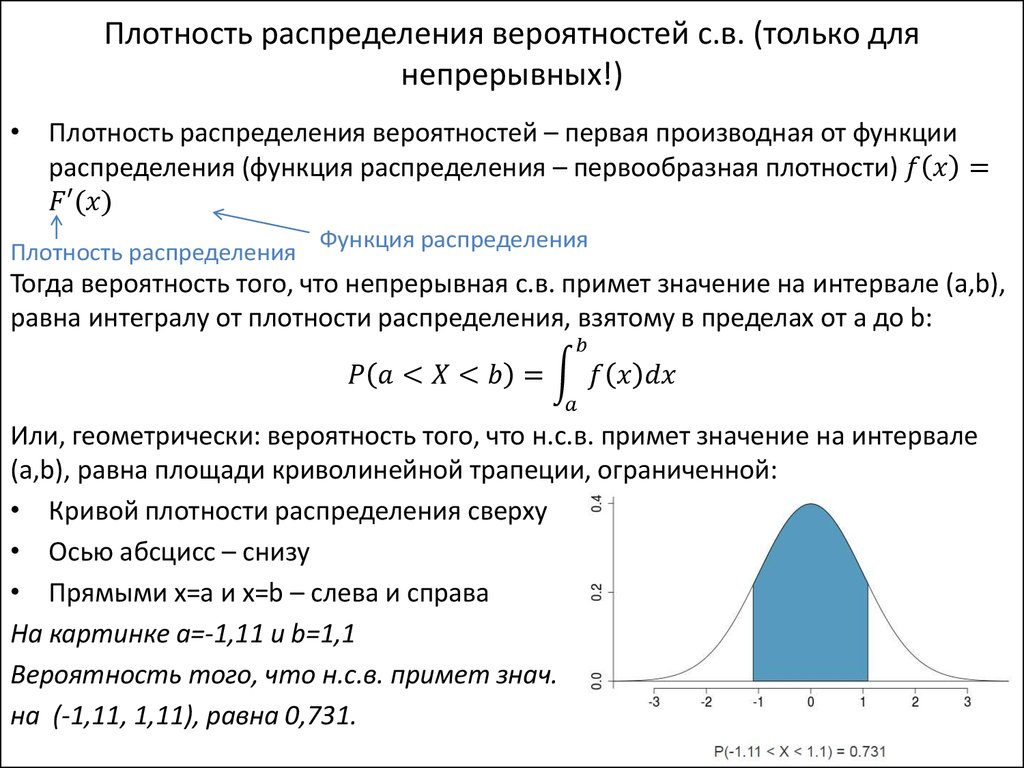
Распределения преобразуют произвольные значения 0 — 1, созданные из заданного потока (определены либо глобально в среде анализа, либо локально в инструменте), в заданное распределение. См. Синтаксис распределения для произвольных значений для синтаксиса и параметров для каждого распределения.
Равномерное распределение
Равномерное распределение — это непрерывное распределение вероятностей, где все значения в установленном диапазоне имеют одинаковую вероятность. Целочисленное распределение — это дискретная версия равномерного распределения (см. ниже). Равномерное распределение может использоваться при моделировании концентрации газа в модели имитации или времени между авариями на перекрестках, а также для размещения точек в инструменте Создать произвольные точки (Create Random Points).
Равномерное распределение часто используется для моделирования произвольных событий, если каждый потенциальный результат или явление имеет одинаковую вероятность возникновения.
Равномерное распределениеФормула для равномерного распределения:
Формула равномерного распределения, где
a — это минимальное значение для интервала с равными возможностями.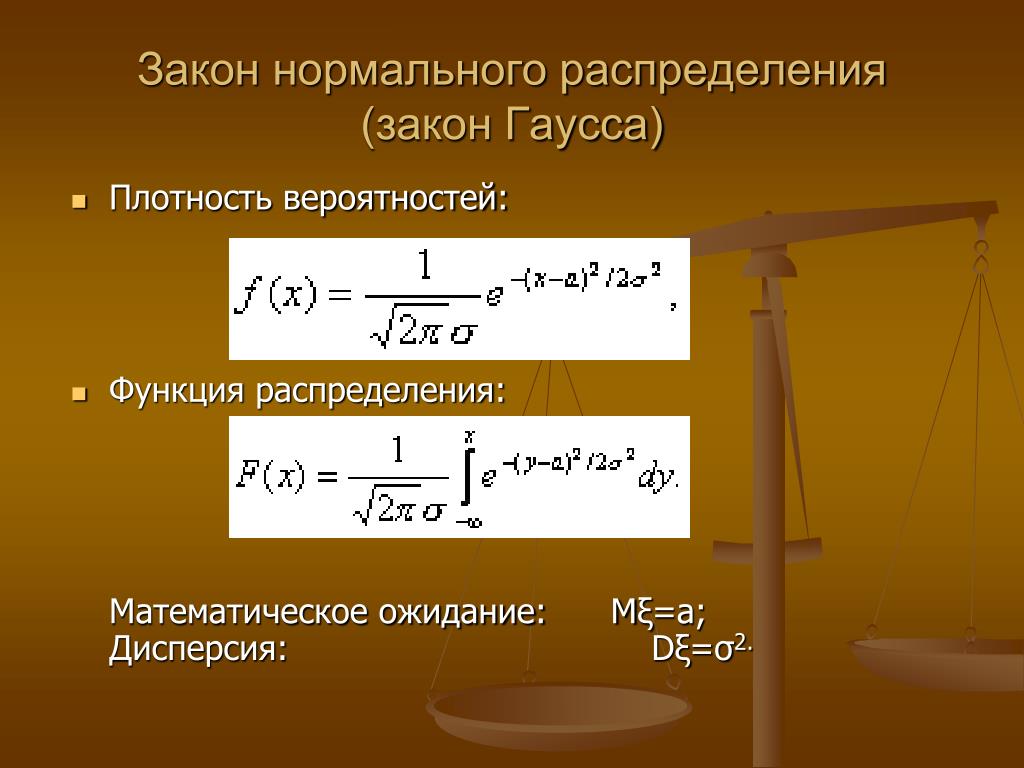
b — это минимальное значение для интервала с равными возможностями.
x — это точки наблюдения.
Выбранные произвольные значения — от минимального до максимального (оба эксклюзивные). Минимум должен быть меньше максимума. Если не заданы минимум и максимум, производятся равномерные переменные от 0,0 до 1,0.
Целочисленное распределение
Целочисленное распределение — это вероятность распределения, в котором все дискретные значения в заданном интервале имеют одинаковую вероятность. Целочисленное распределение — это дискретная версия равномерного распределения (см. выше). Целочисленное распределение может использоваться для моделирования вероятности каждого числа, возникающего, когда вы делаете выбор (каждое число имеет одну шестую вероятности возникновения), моделирующего произвольные события в имитационной модели или выбирающего местоположения выборки для биологического исследования.
Целочисленное распределение часто используется для моделирования произвольных событий, если каждый возможный результат или явление имеет одинаковую вероятность возникновения.
Формула для целочисленного распределения:
Формула целочисленного распределения, где
a — это минимальное значение для интервала с равными возможностями.
b — это минимальное значение для интервала с равными возможностями.
x — это точки наблюдения.
Выбранные произвольные значения — от минимального до максимального (оба эксклюзивные). Минимум должен быть меньше максимума. Если не заданы минимум и максимум, создаются произвольные значения от 1 до 100.
Нормальное распределение
Нормальное распределение моделирует непрерывные произвольные переменные, которые обычно возникают. Нормальное распределение широко используется и применяется во многих приложениях. Оно строится на теореме центрального предела, которая основана на том принципе, что сумма произвольных переменных нормально распределена, если есть большое количество наблюдений. Например, количество раз, которое лицевая сторона монеты появляется при подбрасывании, приблизится к норме, если монету подбросить много раз.
Примеры нормальных распределения по росту людей в стране, значений рельефа в штате и результатов математического теста для 12-летних учеников.
Формула для нормального распределения:
Формула нормального распределения, где
— это среднее значение.
— это стандартное отклонение (положительное число).
Нормальное распределение симметрично относительно среднего значения, режима и медианы, которые равны ?.
Часто биномиальное и пуассоново распределения моделируют будущие дискретные, независимые, произвольные, истинные или ложные события (например, число раз heads возникает при выборе), используя относительно небольшое количество наблюдений, в то время, как нормальное распределение моделирует непрерывные переменные (например, рост, вес и количество), используя большое число наблюдений. Биномиальное и пуассоново распределения основаны на вероятности, в то время как нормальное распределение — это число наблюдений, встречающих величину.
Экспоненциальное распределение
Экспоненциальное распределение — это распределение непрерывных вероятностей.
Как правило, используется для моделирования времени между событиями, которые происходят на постоянной средней скоростью, или распределение может использоваться для моделирования возникновения событий на расстоянии в единицу. Время до следующего дорожно-транспортного происшествия на перекрестке, время между двумя падающими звездами, видными на небе, и расстояние между выбоинами на улице — все это примеры, в которых должно использоваться экспоненциальное распределение. В каждом из этих примеров, вместе с возрастанием времени или расстояния, экспоненциально больше вероятности для изменения состояния или для возникновения события. Появления событий не зависят друг от друга.
Формула для экспоненциального распределения:
Формула экспоненциального распределения, где
e — это натуральный логарифм.
x — это возможное число возникновений события (положительные целые значения).
Экспоненциальное распределение моделирует процессы Пуассона, где явление находится в исходное состояние.
Экспоненциальное распределение — это непрерывная версия геометрического распределения. Если процесс перехода из состояния A в состояние B может быть разбит на несколько независимых задач, было бы лучше моделировать их с распределением гамма. Распределение контрастности моделирует суму нескольких независимых, экспоненциально распределенных переменных. Может быть виден как особые случаи экспоненциального распределения.
Пуассоново распределение
Пуассоново распределение — это дискретное распределение вероятности. Пуассоново распределение моделирует вероятность количества событий, возникающих в течение определенного шага во времени, дающего известное среднее значение. События не зависят от последнего возникновения. На оси x есть дискретные значения для событий 0, 1, 2, 3, 4 и т.д. (часто представляющие количество появлений события), и на оси y — вероятность возникновения явления, которое много раз дает известное среднее значение. Событиями может быть количество несчастных случаев на перекрестках, число врожденных пороков развития, или количество лосей на квадратный километр.
Пуассоново распределение моделирует редкие появления. Распределение иногда называют законом малых чисел, т.к. событие не происходит часто, но есть много возможностей для того, чтобы оно произошло.
Формула показана ниже:
Формула пуассонова распределения, где
e — это натуральный логарифм.
k — это возможное число возникновений для события (положительные целые значения).
k! — это факториал k.
(или среднее) — это положительное число, представляющее расширенное число возникновений в указанном интервале. Если событие возникает каждые 10 минут в час (60 минут), лямбда будет равняться 6.
Пуассоново распределение сходно с биномиальным распределением; однако, пуассоново распределение моделирует возникновение редкого события, не располагая информацией об общем количестве возможных появлений. Пуассоново распределение подсчитывает количество дорожно-транспортных происшествий на перекрестках, в то время, как биномиальное моделирует количество дорожно-транспортных происшествий относительно количества машин, проезжающих перекресток.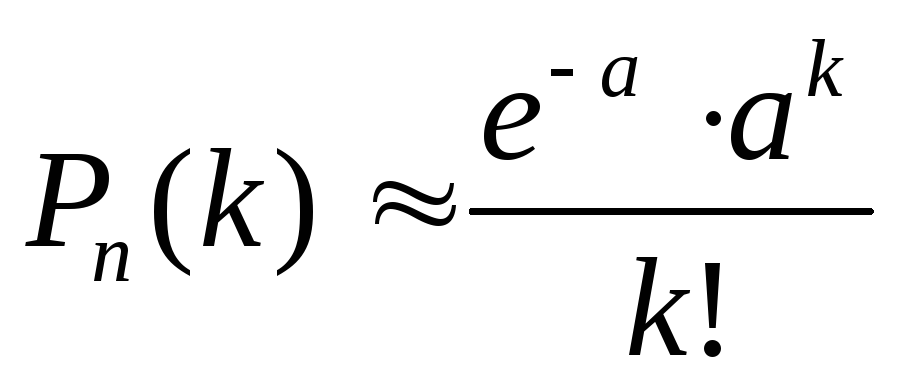
Гамма-распределение
Гамма-распределение — это непрерывное распределение возможности. Распределение контрастности моделирует суму нескольких независимых, экспоненциально распределенных переменных. Может быть виден как особые случаи экспоненциального распределения.
Гамма-распределениеФормула для гамма-распределения:
Формула гамма-распределения 1Другой способ параметризации распределения гамма показан на рисунке:
Формула гамма-распределения 2Для альфа равного 1, распределение гамма равняется экспоненциальному распределению. Если альфа — целое число, гамма-распределение становится распределением Эрланга. Для целых альфа и бета, равных 2, гамма-распределение станет распределением хи в квадрате с 2 степенями альфа свободы.
Полученные переменные больше или равны 0. Альфа и бета должны быть больше 0.
Биномиальное распределение
Биномиальное распределение моделирует число появлений события при наблюдении последовательности потенциальных производителей события.
Например, биномиальное распределение отражает количество людей в клиническом исследовании, умерших от болезни сердца, число людей, которые вышли на втором этаже в переполненном лифте, или количество животных в популяции, которые являются носителями определенных генетических черт.
Биномиальное распределение описывает случаи, а не величины. Оно может моделировать, сколько участников закончили гонку, а не насколько быстрыми были участники.
Формула для биномиального распределения выглядит следующим образом:
Формула биномиального распределения, где
n — число наблюдений.
p — вероятность появления.
x — количество успехов в диапазоне от 0 до n.
Общим примером использования биномиального распределения является определение вероятности количества раз, heads возникает при выборе 10 раз (n = 10). Это может быть 0 heads из 10, 1 из 10 и т.д.; таким образом, x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. А p — это вероятность для каждого x.
Все процессы являются независимыми, и каждый процесс имеет исход успеха или неудачи.
Биномиальное распределение приближается к распределению Пуассона для больших n и малых p. В этом случае легче использовать распределение Пуассона.
Биномиальное распределение выдает произвольную переменную для числа успехов из n процессов, где вероятность успеха в каждом процессе равна p (например, вероятность heads turning up равна p).
Геометрическое распределение
Геометрическое распределение — это дискретное распределение вероятности. Оно моделирует два основных вида явлений: (1) вероятность количества раз, необходимых для достижения успеха (например, сколько раз необходимо бросить кости, чтобы выпало число 6), или (2) вероятность числа отказов до достижения успеха (например, количество походов по следу, прежде чем вы увидите оленя). Вероятность того, что вы не увидите оленей в первом походе в процессе равняется (1 — p). Для второго похода вероятность не видеть оленя: (1 — p) (1 — p). Чем больше походов, тем вероятность не увидеть оленей экспоненциально убывает, и в конце концов олень должен быть выслежен.
События не зависят друг от друга.
Формула для геометрического распределения выглядит следующим образом:
Формула геометрического распределения, где
p — вероятность успеха.
n — число процессов.
Геометрическое распределение — это дискретная версия экспоненциального распределения (см. выше). Геометрическое распределение является частным случаем отрицательного биномиального распределения или распределения Паскаля, где r в распределении Паскаля равняется 1 (см. ниже).
Отрицательное биномиальное распределение
Отрицательное биномиальное распределение — это дискретное распределение вероятности. Отрицательное биномиальное распределение основано на уравнениях Бернулли. Уравнения Бернулли моделируют события, в которых уравнения имеют один из двух результатов (успех и неудача), имеют шансы на успех, p (где p одинаково для каждого уравнения), не зависят друг от друга. Подбрасывание монетки — это процесс Бернулли. Например, отрицательное биномиальное распределение может моделировать, сколько попыток будет, пока не появятся пять заголовков в строке.
Таким образом, отрицательное биномиальное распределение моделирует число отказов до успеха. Если r целочисленное, отрицательное биномиальное распределение станет частным случаем распределения Паскаля.
Формула для отрицательного биномиального распределения выглядит следующим образом:
Формула отрицательного биномиального распределения, где
r — количество неудач.
p — вероятность успеха.
k — количество удавшихся попыток в диапазоне от 0 до n.
Если отрицательное биномиальное распределение представляет собой подбрасывание монеты, выдается произвольное значение раз, которое оно занимает для появления заголовков.
Отзыв по этому разделу?
Формула распределения Пуассона — GeeksforGeeks
Вероятность является одной из основ математики. Распределение Пуассона — это дискретное распределение вероятностей, выражающее вероятность того, что заданное число событий произойдет за фиксированный интервал времени.
Это помогает предсказать вероятность определенных событий, когда вы знаете, как часто это событие происходило. Формула распределения Пуассона проста, и с помощью этой формулы вопросы решаются очень легко.
Распределение Пуассона
Распределение Пуассона — это распределение вероятностей, которое используется для отображения того, сколько раз событие происходит за определенный период. Это дискретное распределение вероятностей количества событий, происходящих в данный период времени, с учетом среднего количества раз, когда событие происходит за этот период времени. Это распределение, связанное с вероятностями событий, которые крайне редки, но имеют большое количество независимых возможностей возникновения. Зачем нужно распределение Пуассона? В распределении у нас есть значение n и p (что требуется для распределения) означает независимые возможности и вероятность событий. но если n велико или стремится к ∞, а p так мало или стремится к 0. Тогда очень сложно узнать распределение вероятностей каким-либо другим методом или с помощью биномиального распределения.
{n-x} P(x) = \frac{n!}{(n-x)! х!} стр. x q n-x ; мы знаем p + q = 1 Итак, P(x) = P(x) = \frac{n!}{(n-x)! x!} p x (1- p) n-x P(x) =\frac{ n(n-1)(n-2) ———(n-x+1) (н-х)! p x (1- p) n-x }{(n-x)! x!} …………..(1) полагаем np = λ , Итак. p = \frac{λ}{n}теперь уравнение (1) становится P(x) =\frac{ n(n-1)(n-2) ———(n-x+1 )}{x!} (\frac{λ}{n}) x (1-\frac{λ}{n}) n-x P(x) = \frac{\frac{λ x } {x!}(\frac{n}{n}(\frac{n-1}{n}+ ——-+(\frac{n-x+1}{n})(1- \frac{λ}{n}) n }{1-(\frac{λ}{n})x} Поскольку n⇢∞, (1-\frac{r}{n}) здесь, r ∈ Natural no. 1so, lim n⇢ ∞ \frac{λ x }{x!}(1-\frac{λ}{n}) n Укажите это свойство пределов, lim x⇢ ±∞ (1+ \frac{1}{x}) x = так. мы можем сказать, что P(x) = (отсюда получено)
График распределения Пуассона
График распределения Пуассона
Свойства распределения Пуассона
- Распределение Пуассона имеет только один параметр «λ»
- λ = np
- Среднее значение = λ , дисперсия = λ , стандартное отклонение = √λ.
- Асимметрия = 1/λ
- Эксцесс = 3 + 1/λ
- Распределение Пуассона имеет положительную асимметрию и лептокуртик.
Примеры задач
Вопрос 1: Если 4% всех изделий, произведенных на заводе, имеют дефекты. Найти вероятность того, что в выборке из 50 изделий менее 2 бракованных изделий.
Решение:
Здесь имеем n = 50, p = (4/100) = 0,04, q = (1-p) = 0,96, λ = 2
Используя распределение Пуассона,
P(X = 0) = = 1/e 2 = 0,13534
P(X = 1) = = 2/e 2 = 0,27068
Следовательно, вероятность того, что в выборке из 50 изделий окажется менее 2 дефектных изделий по:
P( X > 2 ) = P( X = 0 ) + P( X = 1 ) = 0,13534 + 0,27068 = 0,40602
Вопрос 2: Если вероятность плохой реакции на лекарство равна 0,002, определить вероятность того, что из 1000 человек более 3 будут страдать от плохой реакции на лекарство.
Решение:
Здесь мы имеем n = 1000, p = 0,002, λ = np = 2
X = количество людей, страдающих плохой реакцией
P(X >
) = 1 – {P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)}P(X = 0) = = 1/e 2
P(X = 1) = = 2/e 2
P(X = 2) = = 2/e 2
P(X = 3) = = 4/3e 2
3 P (Х > 3) = 1 – [19/3e
2 ] = 1 – 0,85712 = 0,1428
Вопрос 3: Если 1% всех винтов, произведенных на заводе, являются бракованными. Найти вероятность того, что из выборки из 100 винтов окажется менее 3 дефектных.
Решение:
Здесь имеем n = 100, p = 0,01, λ = np = 1
X = количество дефектных винтов (X = 0) + P(X = 1) + P(X = 2)
P(X = 0) = = 1/e
P(X = 1) = =1/e
P(X = 2) = =1/2e
P(X < 3) = 1/e + 1/e +1/2e
= 2,5 /e = 0,919698
Вопрос 4: Если в отрасли есть вероятность, что 5% сотрудников пострадают от короны.
Какова вероятность того, что в группе из 20 сотрудников более 3 сотрудников пострадают от короны?
Решение:
Здесь мы имеем n = 20, p = 0,05, λ = np = 1
X = количество сотрудников, которые будут страдать от короны
Использование распределения Пуассона
P(X > 3) = 1-[P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)]
P(X = 0) = = 1/e
P(X = 1) = = 1/e
P(X = 2) = =1/2e
P(X = 3) = =1/6e
P (X > 3) = 1 – [1/e + 1/e + 1/2e + 1/6e]
= 1 – [ 8/3e] = 0,018988
Вопрос 5: Производитель знает, что лампа он делает состоит из 2% луковиц как бракованные. Если он изготовит 200 лампочек, то какова вероятность того, что бракованными будут менее 4 лампочек.
Решение:
Здесь имеем n = 200, p = 0,02, λ = np = 4 P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
P(X = 0) = = 1/e 4
P(X = 1 ) = = 4/e 4
P(X = 2) = = 8/e 4
P(X = 3) = = 32/3e 4
P(X < 4)= 1/е 4 + 4/е 4 + 8/e 4 + 32/3e 4 = 71/3e 4
= 0,43347
день 0,001.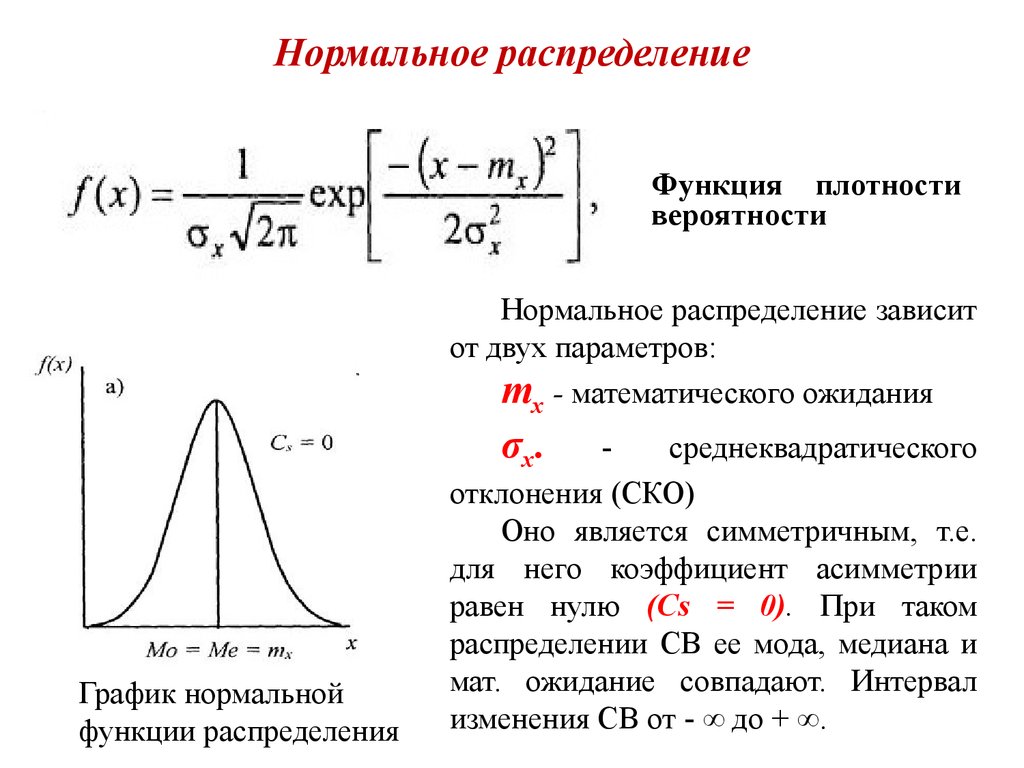
Если в штате 800 человек, подсчитайте вероятность того, что количество отсутствующих в любой день равно 4. X = количество сотрудников, отсутствующих в любой день
Использование распределения Пуассона
P(X = 4) =
= 0,00767 Формула, пример, определение, среднее значение и дисперсия Удары Фау-1 и Фау-2 и распределение Пуассона Смотреть все СМИ Просмотреть весь связанный контент → Распределение Пуассона , в статистике, функция распределения, используемая для характеристики событий с очень низкой вероятностью возникновения в течение определенного времени или пространства. Французский математик Симеон-Дени Пуассон разработал свою функцию в 1830 году, чтобы описать, сколько раз игрок выиграет редко выигрываемую азартную игру за большое количество попыток. Викторина «Британника» Числа и математика Распределение Пуассона в настоящее время признано само по себе жизненно важным распределением. Например, в 1946 г. английский статистик Р. Д. Кларк опубликовал «Применение распределения Пуассона», в котором раскрыл свой анализ распределения попаданий летающих бомб (ракет Фау-1 и Фау-2) в Лондон во время Второй мировой войны. Кларк начал с того, что разделил территорию на тысячи крошечных участков одинакового размера. Внутри каждого из них вряд ли будет хотя бы одно попадание, не говоря уже о большем. Более того, если предположить, что ракеты падали случайным образом, вероятность попадания в любой участок была бы постоянной для всех участков. Таким образом, общее количество попаданий будет очень похоже на количество выигрышей в большом количестве повторений азартной игры с очень малой вероятностью выигрыша. Такого рода рассуждения привели Кларка к формальному выводу распределения Пуассона в качестве модели.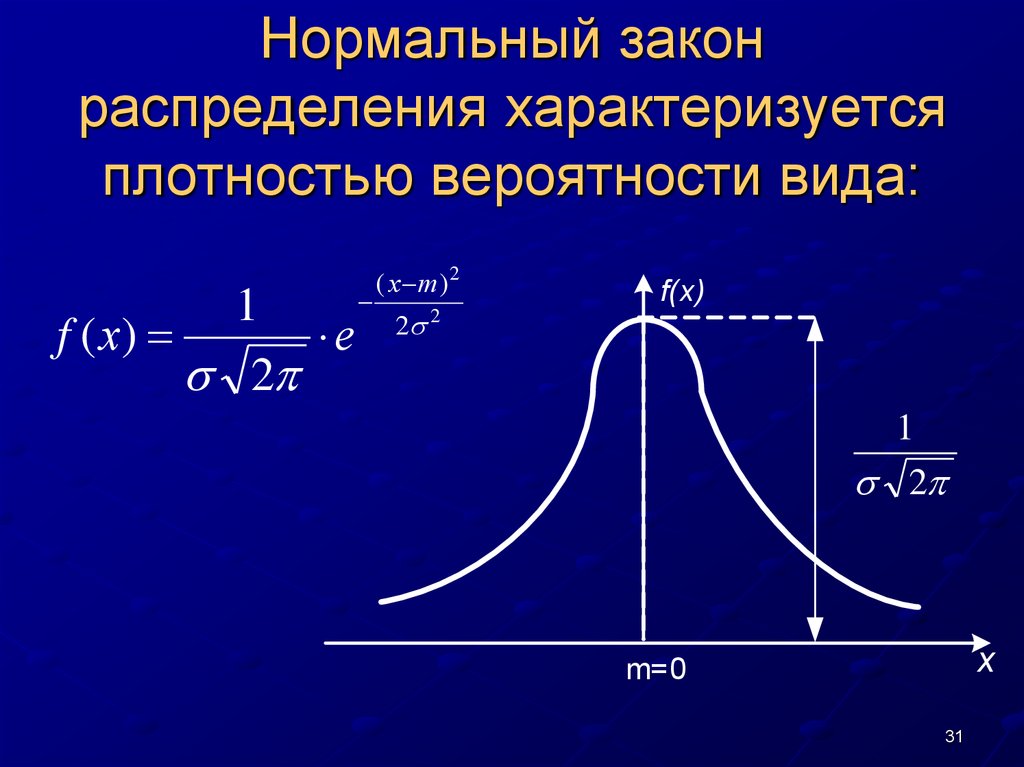
Сдача p представляют вероятность выигрыша при любой заданной попытке, среднее или среднее количество побед (λ) в n попытках будет λ = n p . Используя биномиальное распределение швейцарского математика Якоба Бернулли, Пуассон показал, что вероятность получения k выигрыша приблизительно равна λ k / e −λ k !, где e — показательная функция. к ! = к ( к — 1)( к — 2)⋯2∙1. Примечателен тот факт, что λ равно как среднему, так и дисперсии (мера разброса данных от среднего) для распределения Пуассона.
. Некоторые районы поражались чаще, чем другие. Британские военные хотели знать, нацеливались ли немцы на эти районы (попадания свидетельствовали о высокой технической точности) или их распределение было случайным. Если бы ракеты на самом деле были нацелены только случайным образом (в пределах более общей области), британцы могли бы просто рассредоточить важные объекты, чтобы уменьшить вероятность их поражения.