Все площади параллелограмма формулы: Площадь параллелограмма — найти онлайн и формула

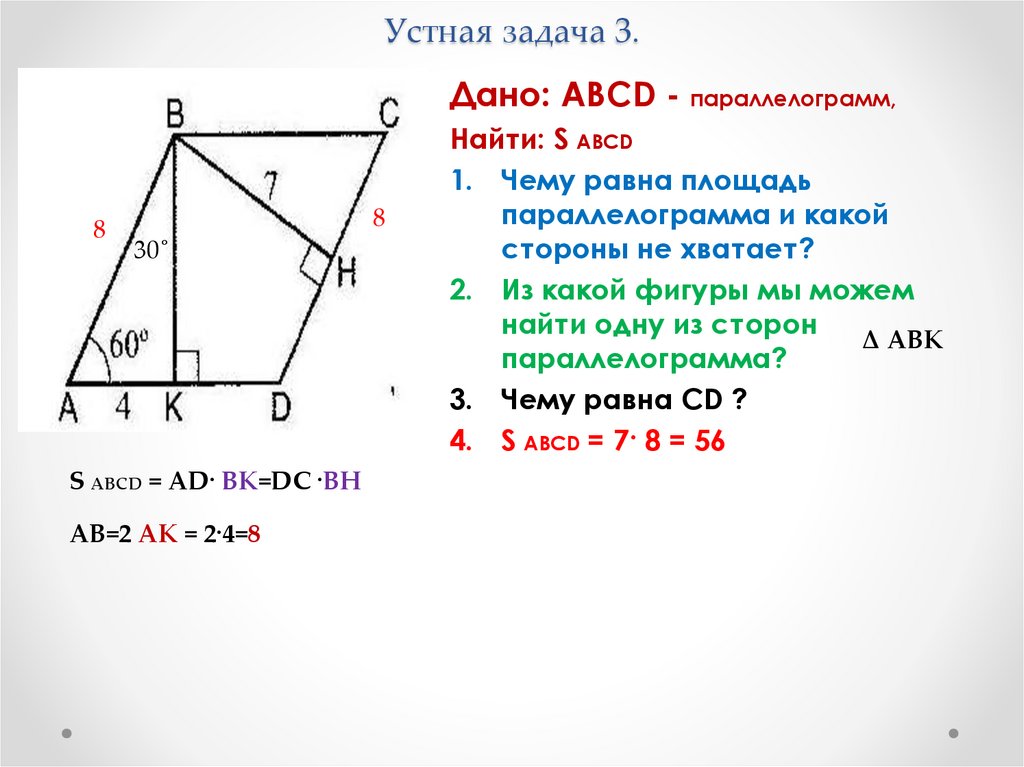
Площадь параллелограмма

• Альфашкола
• Статьи
• Площадь параллелограмма

Теория вопроса

 

Необходимость нахождения площади параллелограммов и их частных случаев – прямоугольников, возникла очень давно. С древних времен человеку необходимо было находить площади земельных участков для сельскохозяйственных нужд и градостроительства.

 

Существует несколько формул нахождения площади параллелограмма. Каждая из них подходит для решения соответствующего круга задач.

 

Вот основные формулы:

1. Площадь параллелограмма через одну из его сторон и высоту, проведенную к этой стороне:

 

2. Площадь параллелограмма через две его стороны и синус угла между ними:

3. Площадь параллелограмма через его диагонали и угол между ними:

 

Давайте разберем задачу, иллюстрирующую применение одной из этих формул:

 

Задача

Даны параллелограмм АВСD и прямоугольник EFKM, которые имеют одинаковую длину соответствующих сторон (см. рисунок ниже). Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

 

 

Решение

 

На первый взгляд, это очень сложная задача, так как мы не знаем ни одного конкретного параметра ни одной из этих геометрических фигур. Давайте попробуем разобраться.

 

По условию задачи, стороны FE = АВ, КМ = СD, ЕМ = АD, FК = ВС.

 

Площадь параллелограмма в данном случае удобно найти через две стороны и синус угла между ними (2-я формула). Площадь прямоугольника в классическом прочтении равна произведению длины на ширину. Но так как прямоугольник – это частный случай параллелограмма, то его площадь также можно представить через две стороны и синус угла между ними. Только в этом случае угол будет равен 90 градусов, а синус 90 градусов равен «1». Поэтому значительно проще при нахождении площади прямоугольников обходится без синусов.

 

Так как по условию задачи соответствующие стороны прямоугольника и параллелограмма равны, мы можем их обозначить одной буквой:

 

FE = АВ = Х

ЕМ = АD = У

 

Острый угол, например, ВАD обозначим одной буквой А.

Тогда площадь параллелограмма равна:

 

Sпар = ХУsinA

 

а площадь прямоугольника равна:

 

Sпрям = ХУ

 

Также по условию площадь прямоугольника вдвое больше площади параллелограмма:

 

Sпрям = 2 Sпар

 

Следовательно, мы можем записать следующее уравнение:

 

ХУ = 2 ХУ sinA

 

Сокращаем обе части этого уравнения на «Х У», получаем:

 

1 = 2 sinA

 

Откуда:

 

sinA = 0,5

 

По таблице синусов находим, что если sinA = 0,5, то угол А = 30 градусов

 

Ответ: 30 

 

Как видите, иногда, зная только один сравнительный параметр, связывающий две геометрические фигуры, мы можем вычислить некоторые параметры одной из фигур, опираясь только на знание формул для нахождения площади этих фигур. 

 

Автор — Андрей Найденов

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Райхан Талгатовна Иманбаева

Репетитор по математике

Стаж (лет)

Образование:

Санкт-Петербургский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Сабина Витальевна Рабцевич

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Илья Игоревич Трацевский

Репетитор по математике

Стаж (лет)

Образование:

Могилевский государственный университет им.

А.А. Кулешова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по геометрии
• Подготовка к ЕГЭ по математике (профильный уровень)
• Репетитор по русскому языку для подготовки к ЕГЭ
• Репетитор по русскому языку для подготовки к ОГЭ
• Подготовка к олимпиадам по английскому языку
• ВПР по математике
• ВПР по физике
• Репетитор по биологии для подготовки к ЕГЭ
• Репетитор по информатике для подготовки к ОГЭ
• Scratch

Похожие статьи

• Математические факты о Великой Пирамиде Хуфу в Египте
• Математические факты о Парфеноне в Греции
• Как разделить число в отношении
• Степенные ряды
• Преобразование алгебраических выражений
• Ребенок отпрашивается в гости с ночевкой: о чем нужно знать?
• Один дома: чем заняться без родителей и как избежать проблем
• 3 навыка, которые нужны детям для успеха в 21 веке

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Площадь параллелограмма — сколько их?

Добавлено: 17 ноября 2021 в 18:46

Содержание

Геометрия — один из наиболее сложных разделов школьного курса математики. Причина такой сложности состоит в том, что для решения геометрических задач часто требуются нестандартные подходы и пространственное мышление.

При это очень мало стандартных алгоритмов, к которым привыкли школьники. Приходится думать с опорой на теоретический багаж, причем довольно простые формулы часто не приходят ученику в голову там, где должны автоматически всплывать подсказки. Одной из таких формул является выражение для определения площади параллелограмма, о которой и пойдет речь в этой статье.

 

Площадь геометрических фигур издавна интересовала людей, как прикладной объект. Уже древние египтяне были довольно хороши в соответствующих подсчетах, потому что их вынуждала окружающая действительность. Землемеры и сборщики налогов интересовались площадями не для решения школьных задач и не для получения высокого балла на ЕГЭ. Их интерес был более приземленным:

• землемеры стремились усовершенствовать методы разметки сложных участков земли под сельскохозяйственные и строительные нужды;
• сборщики податей хотели знать, сколько должен «налогоплательщик».

Площадь параллелограмма

 

Эти простые вопросы приблизили человечество к современной науке и те сложные понятия, которыми оперируют математики, до сих пор базируются на простых формулах. В этом ряду площадь параллелограмма занимает особенное место, потому что это универсальная геометрическая фигура, частными случаями которой являются:

• прямоугольник;
• квадрат;
• ромб.

Даже треугольник — просто половина параллелограмма, что делает операции с этой фигурой важной частью базовых знаний. Давайте вспомним ее основные свойства:

• противоположные стороны параллельны;
• противолежащие углы попарно равны;
• сумма прилежащих углов равна 180°;
• диагонали и средние линии пересекаются в одной точке, которая делит их пополам.

Площадь параллелограмма

С параллелограммом связано несколько интересных формул и площадь — в их числе. Этот параметр можно найти несколькими способами, которые мы подробно изучим ниже с примерами.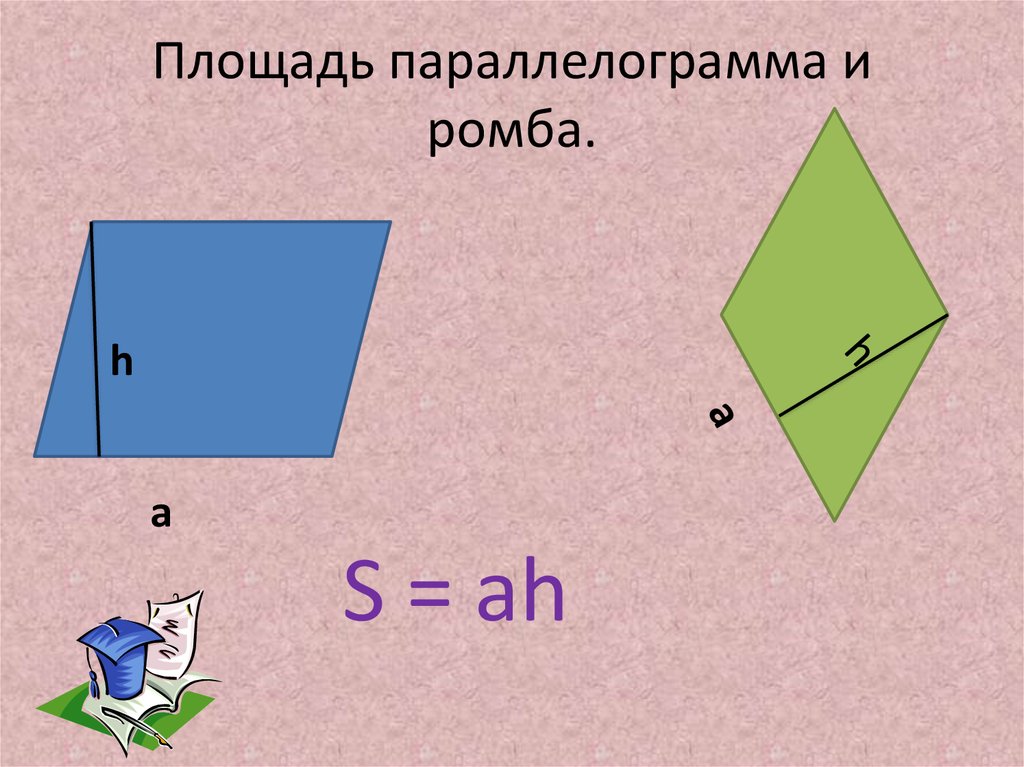

Площадь параллелограмма по стороне и высоте

У нас есть параллелограмм АВСD, из вершины которого на противоположную сторону опущена высота ВН, пересекающая АD под прямым углом. Площадь фигуры АВСD равна произведению стороны АD на ВН.

S _АВСD = АD x ВН.

Площадь параллелограмма

Пример 1. Дан параллелограмм АВСD, площадь которого равна 50 см², а сторона СD — 5 см. Найти высоту ВЕ, опущенную на сторону СD из вершины В.

Решение

Запишем выражение для нахождения площади:

S _АВСD = СD x ВЕ.

Выразим из нее ВЕ и подставим значения из условия:

ВЕ = S _АВСD / СD = 50 / 5 = 10 см.

Ответ: ВЕ = 10 см.

Площадь параллелограмма

Площадь параллелограмма по сторонам и углу между ними

Формулировка: площадь параллелограмма равна произведению двух сторон параллелограмма на синус угла между ними.

S _АВСD = AB x AD х sin ∠BAD = AB x AD х sin ∠ABC.

Пример 2. Найти сторону ромба, если один из его углов равен 30 градусов, а площадь — 50 см².

Решение

Поскольку ромб — это частный случай параллелограмма, воспользуемся соответствующей формулой:

S _АВСD = AB x AD х sin ∠BAD.

В этом уравнении нам известна площадь и угол. Поскольку стороны ромба равны, то преобразуем выражение следующим образом:

AB x AD = S _АВСD / sin ∠BAD,

AB² = S _АВСD / sin ∠BAD.

Подставим значения из условия:

AB² = 50 / sin 30°.

Значение синуса посчитаем на калькуляторе, выберем из таблицы Брадиса (для тех, кто помнит этого прекрасного человека) или из представленной в этой статье таблицы. В итоге выражение преобразуется следующим образом:

AB² = 50 / 0,5 = 100.

Выразим из этого выражения АВ:

AB = √100 = 10 см.

Ответ: AB = 10 см.

Площадь параллелограмма

Площадь параллелограмма по диагоналям и углу между ними

Формулировка: площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.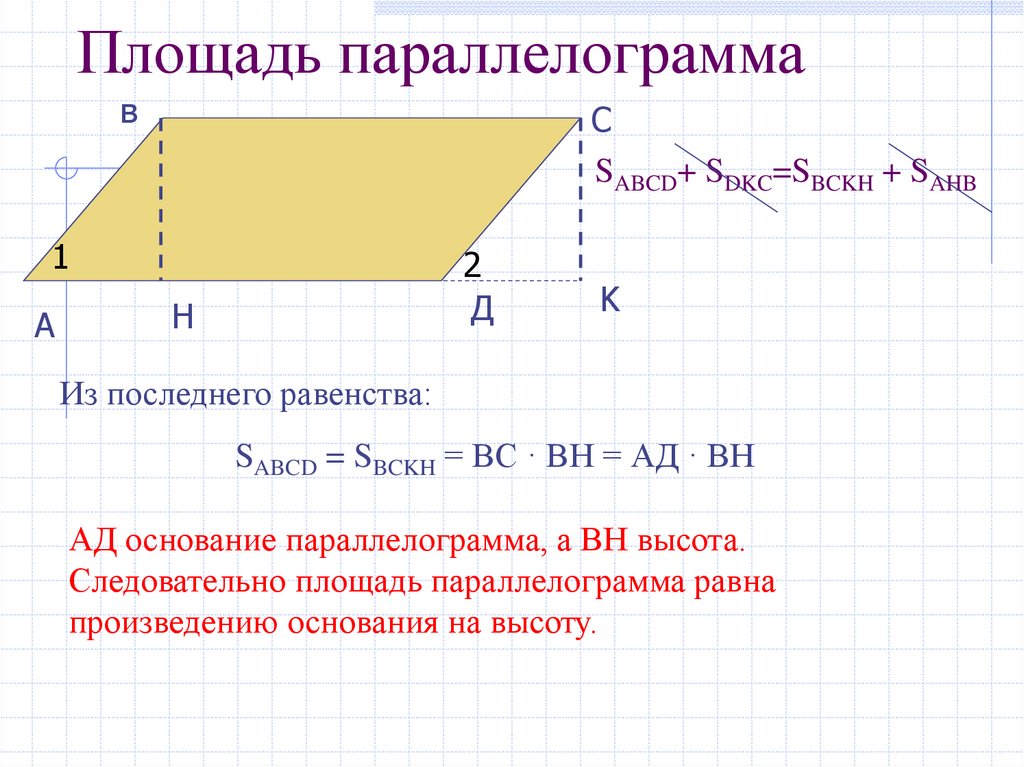

S _АВСD = ½ AС x ВD х sin ∠BОС = ½ AС x ВD х sin ∠BОА

Пример 3. Дан параллелограмм АВСD, диагонали которого равны по 20 см, а угол между ними составляет 90 градусов. Найти площадь треугольника АВD.

Решение

Заметим, что площадь треугольника АВD, который образуется путем деления параллелограмма АВСD его диагональю АD составляет половину площади самого параллелограмма. Это следует из равенства треугольников АВD и АСD по трем сторонам:

• сторона АВ равна стороне СD,
• сторона ВС равна стороне АD,
• сторона ВD общая.

Запомним это и перейдем к поискам площади параллелограмма:

S _АВСD = ½ AС x ВD х sin ∠BОС.

Подставим в эту формулу значения из условия:

S _АВСD = ½ х 20 x 20 х sin 90°.

Значение синуса выберем из предыдущей таблицы:

S _АВСD = ½ х 20 x 20 х 1 = ½ х 400 = 200 см².

Вспомним, что площадь треугольника АВD составляет половину площади самого параллелограмма, то есть 100 см².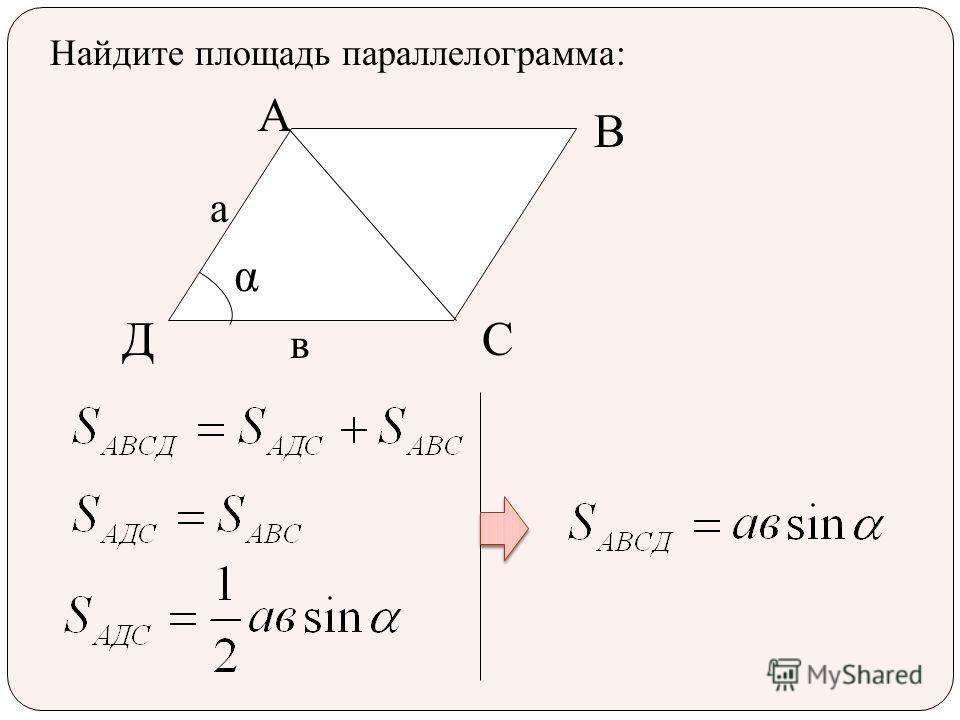 Надеемся, внимательные читатели заметили, что наш параллелограмм с равными диагоналями, пересекающимся под прямым углом — это квадрат.

Ответ: площадь треугольника АВD — 100 см².

 

---

Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Владислав Барышников

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР

Задать вопрос

Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.

Читайте также:

Как найти площадь параллелограмма

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Мы открыты в субботу и воскресенье!

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти площадь параллелограмма

В параллелограмме длина  равна  единицам, длина  есть  единицам, а длина  есть  единицам. перпендикулярно fo . Найдите площадь в квадратных единицах .

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для нахождения площади параллелограмма:

Основание дается вопросом.

Вы должны понимать, что это не только высота параллелограмма, но и катет прямоугольного треугольника.

Используйте теорему Пифагора, чтобы найти длину .

Теперь, когда у нас есть высота, умножьте ее на основание, чтобы найти площадь параллелограмма.

Сообщить об ошибке

Параллелограмм имеет основание  и длинную сторону. Нарисована линия, соединяющая край верхнего основания с нижним основанием. Линия перпендикулярна нижнему основанию, а основание этого треугольника составляет одну четвертую длины нижнего основания.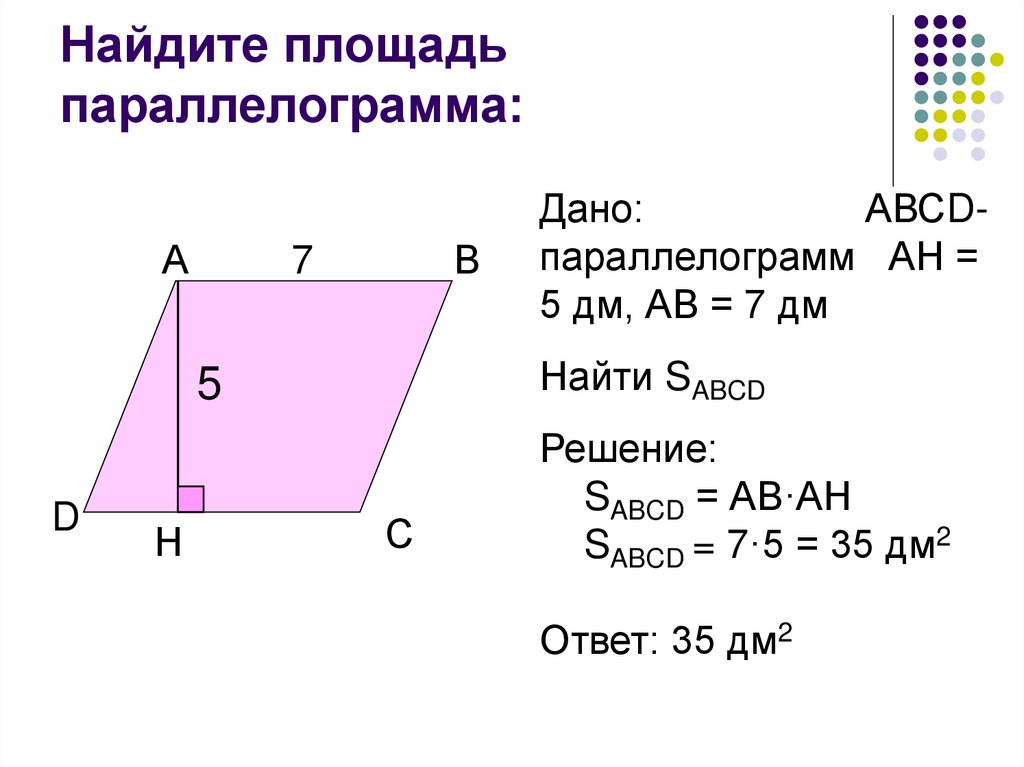 Найдите площадь параллелограмма.

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади параллелограмма задается уравнением , где – основание,  – высота параллелограмма.

Единственная данная информация состоит в том, что основание равно , сторона и основание прямоугольного треугольника в параллелограмме (треугольник, образованный между краем верхнего основания и нижним основанием) является потому что .

Последняя часть информации, необходимая для выполнения требований формулы площади, — это высота параллелограмма, . Высота параллелограмма определяется загадочной стороной прямоугольного треугольника, описанного в вопросе. Чтобы найти третью сторону треугольника, мы можем использовать теорему Пифагора.

В данном случае неизвестная сторона является одной из сторон треугольника, поэтому мы обозначим ее.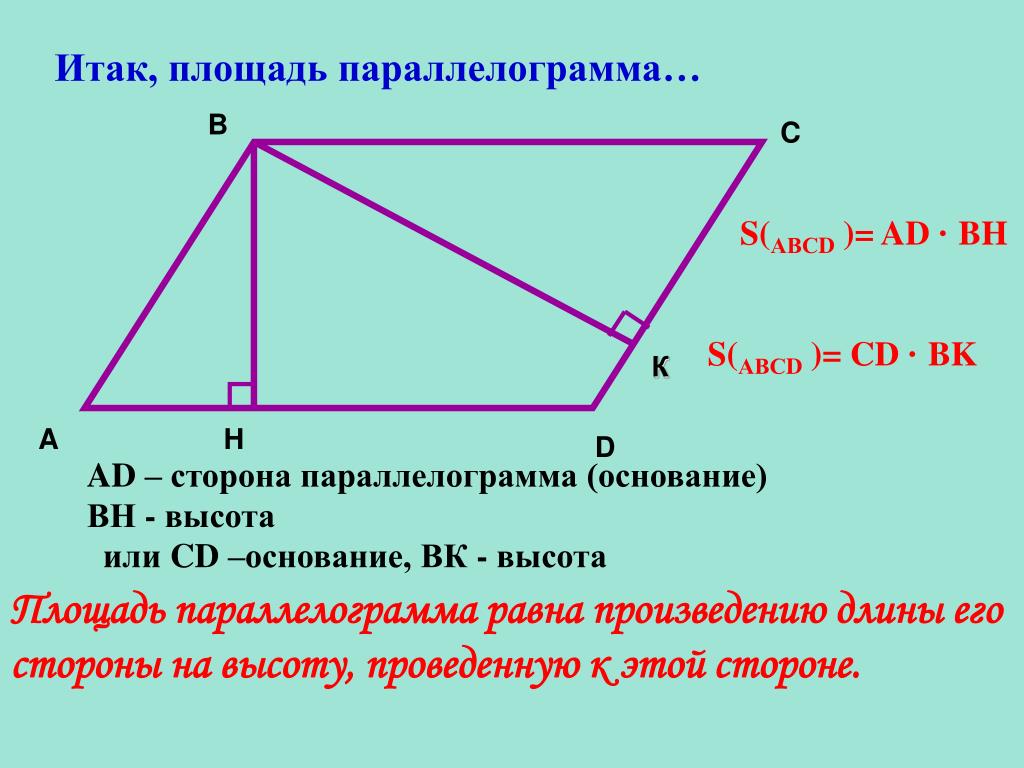 Данную сторону треугольника, входящую в основание, будем называть , а сторона параллелограмма также является гипотенузой треугольника, поэтому в Формуле Пифагора его длина будет представлена ​​через . На этом этапе мы можем подставить эти значения и найти:

 , но поскольку мы находим длину, ответ должен быть равен 4. Отрицательный вариант можно отменить.

Учитывая, что мы временно назвали «»» для теоремы Пифагора, это означает, что .

Теперь все необходимые части для площади уравнения параллелограмма доступны для использования:

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть ACT Math Tutors

Омар
Сертифицированный преподаватель

Университет штата Аризона, бакалавриат, гражданское строительство.

Просмотр ACT Репетиторы по математике

Грегори
Сертифицированный репетитор

Государственный университет Пенсильвании, главный кампус, бакалавр наук, химическая инженерия. Университет Карнеги-Меллона, доктор философии…

Посмотреть ACT Репетиторы по математике

Закари
Сертифицированный репетитор

Йельский университет, бакалавр наук, биология, общие.

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

Площадь параллелограммов — Concept

Формула площади параллелограмма выводится из площади прямоугольника. Проведя высоту из одной вершины параллелограмма и сдвинув прямоугольный треугольник, получится прямоугольник. Следовательно, чтобы вычислить площадь параллелограмма, умножьте высоту на соответствующее основание. Соответствующим основанием является сторона, перпендикулярная высоте. Связанные темы включают площади трапеций и ромбов.

площадь прямоугольников основание умножить на высоту

Когда мы говорим о площади, у прямоугольника на самом деле нет площади.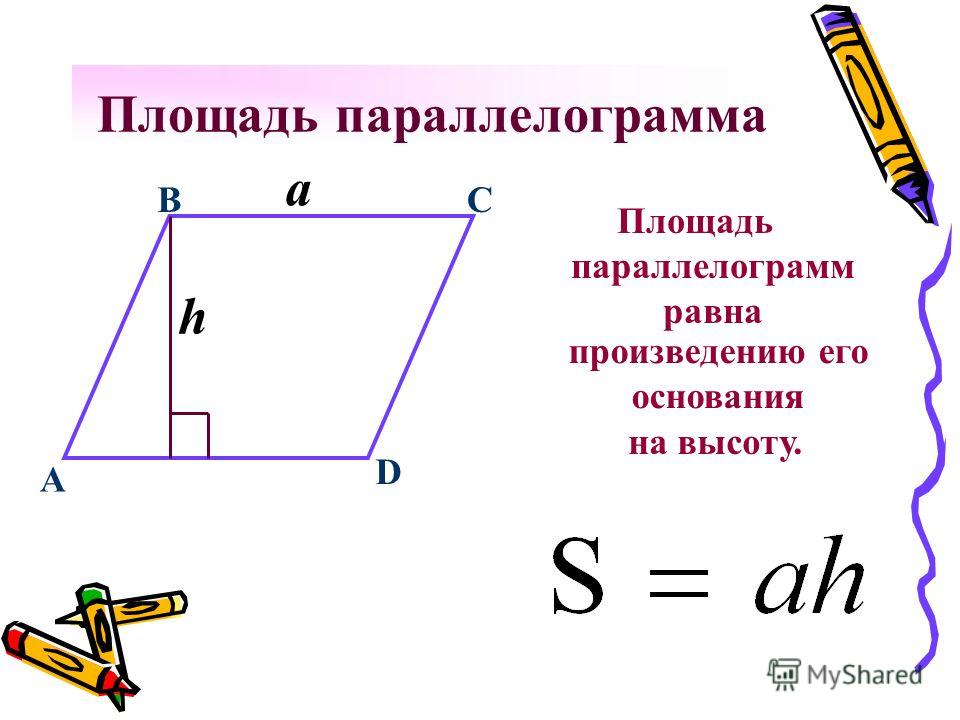 Мы говорим о области, ограниченной прямоугольником. Таким образом, у этого прямоугольника на самом деле нет площади, но область, образованная сторонами прямоугольника, имеет площадь.
Мы возвращаемся в начальную школу, и я спросил вас, какова площадь этого прямоугольника? Вы бы сказали: «Мистер МакКолл, площадь равна произведению длины на ширину». Ну, теперь, когда мы в геометрии, мы будем использовать другой язык. Вместо длины и ширины мы будем использовать основание, умноженное на высоту. Так что забудьте о длине, умноженной на ширину, и мы будем использовать основание и высоту. Таким образом, площадь прямоугольника будет вашей основой, умноженной на длину и высоту. Но как это применимо к параллелограмму, который не является прямоугольником?
Ну, что мы могли бы сделать, так это если бы у меня были ножницы, достаточно сильные, чтобы разрезать эту белую доску, я бы отрезал этот треугольник прямо здесь, переместил бы его в этом направлении и приклеил бы его обратно прямо на этот конец .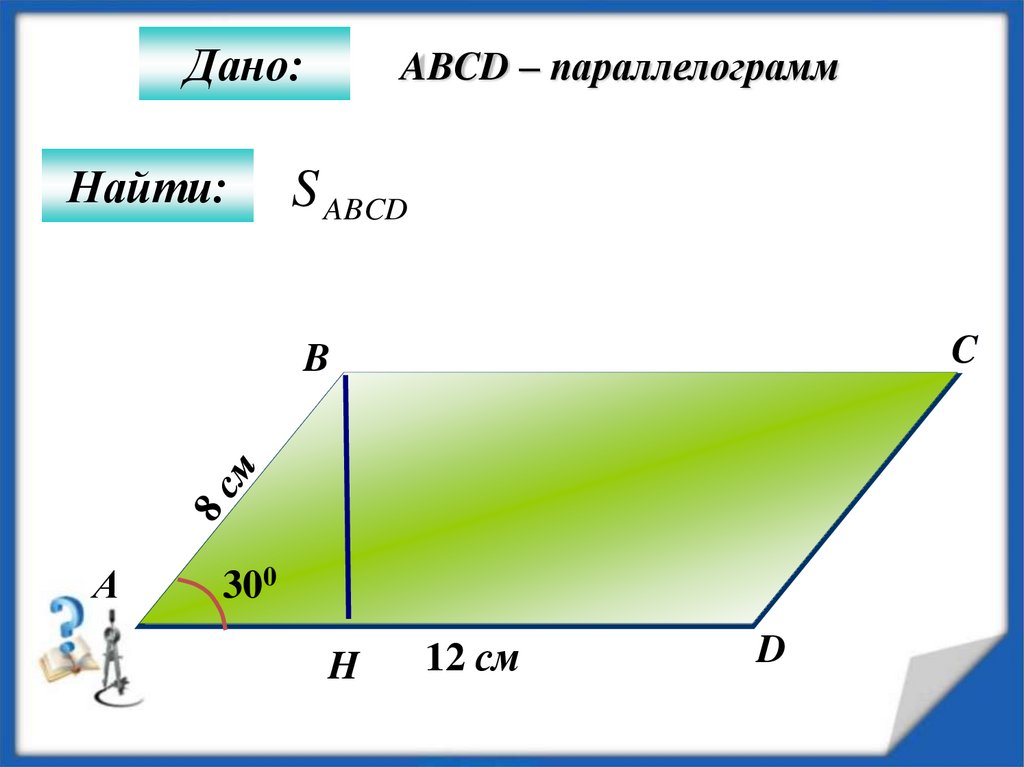 Итак, то, что я создал здесь, — это прямоугольник из моего параллелограмма. Итак, прямо здесь у нас будет тот маленький треугольник, который я отрезал на том конце. Обратите внимание, что мы создали то, что нам известно, прямоугольник. Таким образом, мы можем сказать, что площадь любого параллелограмма будет равна его основанию, умноженному на соответствующую высоту.
Теперь это немного сложно [IB] что я имею в виду под соответствующим ростом? Ну, допустим, я определяю, что вот здесь было основание моего параллелограмма. Так что я просто предполагаю, что у нас есть 2 пары параллельных сторон. Если это моя база, то соответствующая высота — это перпендикулярный отрезок, соединяющий противоположное основание. Вот это может быть высотой, потому что она начинается с параллельного основания и перпендикулярна b.
Вы также можете иметь высоту, которая находится за пределами вашего параллелограмма. Допустим, ладно, возьмем точно такую ​​же цифру. Если бы я сказал, что это прямо здесь было моей базой.