Второй замечательный предел. Примеры решения.
Обычно второй замечательный предел записывают в такой форме:
$$ \begin{equation} \lim_{x\to\infty}\left(1+\frac{1}{x}\right)^x=e \end{equation} $$Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $e\approx{2{,}718281828459045}$. Если сделать замену $t=\frac{1}{x}$, то формулу (1) можно переписать в следующем виде:
$$ \begin{equation} \lim_{t\to{0}}\biggl(1+t\biggr)^{\frac{1}{t}}=e \end{equation} $$Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $\frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^\infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+\infty$ или $-\infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Пример №1
Вычислить предел $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}$.
Решение
Сразу отметим, что основание степени (т.е. $\frac{3x+1}{3x-5}$) стремится к единице:
$$ \lim_{x\to\infty}\frac{3x+1}{3x-5}=\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{3+\frac{1}{x}}{3-\frac{5}{x}} =\frac{3+0}{3-0} =1. $$При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $\lim_{x\to\infty}(4x+7)=\infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^\infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+\frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $\frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $\frac{3x+1}{3x-5}$ под вид $1+\frac{1}{x}$. Для начала прибавим и вычтем единицу:
$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} $$Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
$$ \frac{3x+1}{3x-5}-1 =\frac{3x+1}{3x-5}-\frac{3x-5}{3x-5} =\frac{3x+1-3x+5}{3x-5} =\frac{6}{3x-5}. $$Так как $\frac{3x+1}{3x-5}-1=\frac{6}{3x-5}$, то:
$$ \lim_{x\to\infty}\left(1+ \frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right )^{4x+7} $$Продолжим «подгонку». В выражении $1+\frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+\frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
$$ 1+\frac{6}{3x-5} =1+\frac{1}{\frac{3x-5}{6}} $$Таким образом,
$$ \lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right )^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{4x+7} $$Итак, основание степени, т.е. $1+\frac{1}{\frac{3x-5}{6}}$, подогнано под вид $1+\frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:

Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $\frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $\frac{6}{3x-5}$. Итак, имеем:
$$ \lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} $$Отдельно рассмотрим предел дроби $\frac{6\cdot(4x+7)}{3x-5}$, расположенной в степени:
$$ \lim_{x\to\infty}\frac{6\cdot(4x+7)}{3x-5} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{6\cdot\left(4+\frac{7}{x}\right)}{3-\frac{5}{x}} =6\cdot\frac{4}{3} =8. $$Согласно формуле (1) имеем $\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}}=e$. Кроме того, $\lim_{x\to\infty}\frac{6\cdot(4x+7)}{3x-5}=8$, поэтому возвращаясь к исходному пределу, получим:
$$ \lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} =e^8. $$Полное решение без промежуточных пояснений будет иметь такой вид:
$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}=\left|1^\infty\right| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} =e^8. $$Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $\frac{6}{3x-5}\to{0}$ при $x\to\infty$, то применяя формулу (2), получим:
$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}=\left|1^\infty\right| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7}=\\ =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{6}{3x-5}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} =e^8. $$Ответ: $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}=e^8$.
Пример №2
Найти предел $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}$.
Решение
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $x\to{1}$, т.е. $\lim_{x\to{1}}(7-6x)=7-6\cdot1=1$. Для показателя степени, т.е. $\frac{x}{3x-3}$, получаем: $\lim_{x\to{1}}\frac{x}{3x-3}=\infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $x\to{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $x\to{1}$, то ${x-1}\to{0}$, т.е. $y\to{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $y\to{0}$, получим:
$$ \lim_{x\to{1}}\biggl(7-6x\biggr )^{\frac{x}{3x-3}} =\left|\begin{aligned}&y=x-1;\;x=y+1\\&y\to{0}\end{aligned}\right|=\\ =\lim_{y\to{0}}\biggl(7-6\cdot(y+1)\biggr)^{\frac{y+1}{3\cdot(y+1)-3}} =\lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y} =\lim_{y\to 0}\biggl(1+(-6y)\biggr)^\frac{y+1}{3y} $$Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $\frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $\frac{1}{-6y}$. Домножим показатель степени на выражение $\frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $\frac{-6y}{1}=-6y$:
$$ \lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y}=\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}\cdot(-6y)\cdot\frac{y+1}{3y}} =\lim_{y\to{0}}\left(\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}\right)^{-2(y+1)} $$Так как $\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}=e$ и $\lim_{y\to{0}}(-2(y+1))=-2$, то получим:
$$ \lim_{y\to{0}}\left(\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}\right)^{-2(y+1)} =e^{-2} =\frac{1}{e^2}. $$Полное решение без пояснений таково:
$$ \lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}} =\left|\begin{aligned}&y=x-1;\;x=y+1\\&y\to{0}\end{aligned}\right| =\lim_{y\to{0}}\biggl(7-6\cdot(y+1)\biggr)^{\frac{y+1}{3\cdot(y+1)-3}}=\\ =\lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y} =\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}\cdot(-6y)\cdot\frac{y+1}{3y}} =\lim_{y\to{0}}\left(\biggl(1+(-6y)\biggr)^{\frac{1}{-6y}}\right)^{-2(y+1)} =e^{-2} =\frac{1}{e^2}. $$Ответ: $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}=\frac{1}{e^2}$.
Пример №3
Найти предел $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}$.
Решение
Так как $\lim_{x\to{0}}(\cos{2x})=1$ и $\lim_{x\to{0}}\frac{1}{\sin^2{3x}}=\infty$ (напомню, что $\sin{u}\to{0}$ при $u\to{0}$), то мы имеем дело с неопределённостью вида $1^\infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
$$ \lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}} =|1^\infty| =\lim_{x\to{0}}\biggl(1+\cos{2x}-1\biggr)^{\frac{1}{\sin^2{3x}}} $$Так как $\sin^2x=\frac{1-\cos{2x}}{2}$, то $\cos{2x}-1=-2\sin^2x$, поэтому:
$$ \lim_{x\to{0}}\biggl(1+\cos{2x}-1\biggr)^{\frac{1}{\sin^2{3x}}} =\lim_{x\to{0}}\biggl(1+\left(-2\sin^2x\right)\biggr)^{\frac{1}{-2\sin^2x}\cdot(-2\sin^2x)\cdot\frac{1}{\sin^2 3x}}=\\ =\lim_{x\to{0}}\left(\biggl(1+\left(-2\sin^2x\right)\biggr)^{\frac{1}{-2\sin^2x}}\right)^{\frac{-2\sin^2{x}}{\sin^2{3x}}} =e^{-\frac{2}{9}}. $$Здесь мы учли, что $\lim_{x\to{0}}\frac{\sin^2{x}}{\sin^2{3x}}=\frac{1}{9}$. Подробное описание того, как находить этот предел, дано в соответствующей теме.
Ответ: $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}=e^{-\frac{2}{9}}$.
Пример №4
Найти предел $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)$.
Решение
Так как при $x>0$ имеем $\ln(x+1)-\ln{x}=\ln\left(\frac{x+1}{x}\right)$, то:
$$ \lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) $$Раскладывая дробь $\frac{x+1}{x}$ на сумму дробей $\frac{x+1}{x}=1+\frac{1}{x}$ получим:
$$ \lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(1+\frac{1}{x}\right)\right) =\lim_{x\to+\infty}\left(\ln\left(\frac{x+1}{x}\right)^x\right) =\ln{e} =1. $$Ответ: $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)=1$.
Пример №5
Найти предел $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}$.
Решение
Так как $\lim_{x\to{2}}(3x-5)=6-5=1$ и $\lim_{x\to{2}}\frac{2x}{x^2-4}=\infty$, то мы имеем дело с неопределенностью вида $1^\infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=x-2;\;x=t+2\\&t\to{0}\end{aligned}\right| =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{2t+4}{t^2+4t}}=\\ =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{1}{3t}\cdot 3t\cdot\frac{2t+4}{t^2+4t}} =\lim_{t\to{0}}\left(\biggl(1+3t\biggr)^{\frac{1}{3t}}\right)^{\frac{6\cdot(t+2)}{t+4}} =e^3. $$Можно решить данный пример и по-иному, используя замену: $t=\frac{1}{x-2}$. Разумеется, ответ будет тем же:
$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=\frac{1}{x-2};\;x=\frac{2t+1}{t}\\&t\to\infty\end{aligned}\right| =\lim_{t\to\infty}\left(1+\frac{3}{t}\right)^{t\cdot\frac{4t+2}{4t+1}}=\\ =\lim_{t\to\infty}\left(1+\frac{1}{\frac{t}{3}}\right)^{\frac{t}{3}\cdot\frac{3}{t}\cdot\frac{t\cdot(4t+2)}{4t+1}} =\lim_{t\to\infty}\left(\left(1+\frac{1}{\frac{t}{3}}\right)^{\frac{t}{3}}\right)^{\frac{6\cdot(2t+1)}{4t+1}} =e^3. $$Ответ: $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}=e^3$.
Пример №6
Найти предел $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} $.
Решение
Выясним, к чему стремится выражение $\frac{2x^2+3}{2x^2-4}$ при условии $x\to\infty$:
$$ \lim_{x\to\infty}\frac{2x^2+3}{2x^2-4} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{2+\frac{3}{x^2}}{2-\frac{4}{x^2}} =\frac{2+0}{2-0}=1. $$Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела:
$$ \lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{2x^2+3}{2x^2-4}-1\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{7}{2x^2-4}\right)^{3x} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}\cdot\frac{7}{2x^2-4}\cdot 3x} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}}\right)^{\frac{21x}{2x^2-4}} =e^0 =1. $$Ответ: $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x}=1$.
Второй замечательный предел — примеры решений
Применяемые формулы, свойства и теоремы
Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется второй замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.
Здесь мы будем иметь дело со степенно-показательной функцией, у которой основание и показатель являются функциями от некоторой переменной: . Ее удобно представить как экспоненту: . В этой связи полезна следующая лемма.
Лемма о пределе степенно-показательной функции
Пусть – функции переменной x, имеющие конечные пределы:
. Здесь .
Тогда
.
Доказательство ⇓
В случае бесконечных пределов, или когда , мы проводим исследование произведения , применяя свойства пределов бесконечно больших и малых функций.
В случае и , мы имеем неопределенность вида единица в степени бесконечность. Для ее раскрытия используется второй замечательный предел.
Раскрытие неопределенности 1 в степени бесконечность
Пусть u и v есть функции от переменной x: . И пусть при . Тогда выражение является неопределенным при . Для раскрытия этой неопределенности, мы вводим переменную t из соотношения
.
Тогда . При .
;
.
Таким образом задача сводится к вычислению предела .
Доказательство леммы о пределе степенно-показательной функции
Примеры решений
Все примеры Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Найти предел:
.
Решение
При , . Это неопределенность вида один в степени бесконечность.
Выполняем преобразования.
;
.
Сделаем замену переменной . При . Применим второй замечательный предел:
.
Находим предел дроби, разделив числитель и знаменатель на x:
.
Применяем лемму о пределе степенно-показательной функции ⇑
.
Ответ
.
Пример 2
Все примеры ⇑ Найдите предел:
.
Решение
При , . при . Это неопределенность вида один в степени бесконечность. Раскрываем ее с помощью второго замечательного предела.
Введем переменную t из соотношения: . Тогда при ,
.
.
Применим второй замечательный предел к основанию степени:
.
Найдем предел показателя степени. Для этого применим тригонометрическую формулу
и первый замечательный предел:
.
Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.
Ответ
.
Пример 3
Все примеры ⇑ Найти предел последовательности:
.
Решение
При . Элементы последовательности равны единице. Поэтому . Рассмотрим случай .
При . Это неопределенность вида единица в степени бесконечность. Для ее раскрытия применим второй замечательный предел.
Введем переменную t из соотношения: . Тогда при ,
.
.
Применим второй замечательный предел к основанию степени:
.
Найдем предел показателя степени. Для этого применим тригонометрическую формулу
и первый замечательный предел:
.
Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.
Эта формула справедлива и при .
Ответ
.
Пример 4
Все примеры ⇑ Найти предел:
.
Решение
Пусть . Рассмотрим функцию в проколотой окрестности точки , на которой . Для определения предела, функция должна быть определена на любой проколотой окрестности этой точки. Считаем, что . Тогда . При . Поэтому .
Теперь рассмотрим предел при .
При . У нас неопределенность вида 0/0.
Для ее раскрытия приведем степенно-показательную функцию к основанию e учитывая, что :
.
Согласно следствию второго замечательного предела:
.
В последнем множителе сделаем замену переменной:
.
При . Кроме этого, при . Тогда
.
Применяем арифметические свойства предела функции:
.
Это же значение является правильным и при .
Ответ
.
Пример 5
Все примеры ⇑ Найдите предел функции:
.
Решение с помощью второго замечательного предела и его следствий
При . Это неопределенность вида 0/0. Для ее раскрытия, применим следствия второго замечательного предела.
Преобразуем числитель дроби:
.
Преобразуем знаменатель:
.
Разделим числитель и знаменатель на x:
.
Чтобы не загромождать формулы, мы ввели обозначение .
Применяя первый замечательный предел и следствия второго, имеем:
; ; ; ; .
Применяем арифметические свойства предела функции:
.
Решение с помощью эквивалентных функций
Мы можем упростить решение, если применим теорему о замене функций эквивалентными в пределе частного. Считаем, что предел существует. Тогда мы можем заменить знаменатель эквивалентной функцией при . Из таблицы эквивалентных функций находим:
.
Получаем более простой предел:
.
Далее делаем преобразования аналогично предыдущему:
.
Поскольку при , то применяем следствие второго замечательного предела:
;
.
В дробях и заменим функции в числителе эквивалентными:
;
.
Применяем арифметические свойства предела функции:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
Второй замечательный предел
Вторым замечательным пределом называется предел
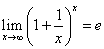 ,
,
где
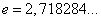 — иррациональное число.
— иррациональное число.
Непосредственная подстановка бесконечности в выражение приводит к бесконечности вида
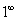 .
.
Значит, если при непосредственном вычислении предела у вас получилась неопределённость такого вида, то решать задачу следует путём приведения ко второму замечательному пределу. Во всех этих задачах для получения второго замечательного предела требуется производить замену сложной функции более простой.
Второй замечательный предел может быть записан в другом виде, если положить
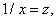
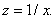 .
.Из условия
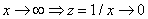
получим
 (Alt)
(Alt)
Пример 1. Найти предел  .
.
Решение. Подстановка вместо x бесконечности приводит к неопределённости:
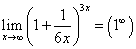 .
.
Значит, нужно привести выражение ко второму замечательному пределу. Облегчим себе жизнь перед заменой сложной функции более простой, представив степень

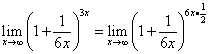 .
.
Заменяем функцию 6x переменной n, которая также стремится к бесконечности:
 .
.
Это второй замечательный предел, индивидуальна только степень числа е:
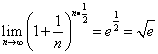 .
.
Пример 2. Найти предел 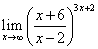 .
.
Решение. Непосредственная подстановка приводит к неопределённости «бесконечность делить на бесконечность в степени бесконечность»:
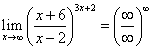 .
.
Бесконечность в показателе степени — признак того, что выражение можно привести к отношению двух вторых замечательных пределов. В самом деле,
если числитель и знаменатель поделить почленно на
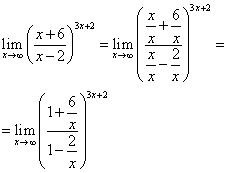 .
.
Почти второй замечательный предел. А чтобы это было не почти, а вторым замечательным пределом, нужно, чтобы во вторых слагаемых и в числителе, и в знаменателе были единицы. Для этого произведём замены функций:
 .
.
 .
.
Подставляем и получаем:
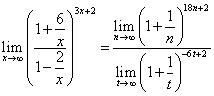 .
.
Это уже отношение вторых замечательных пределов, а степени выражений в числителе и знаменателе — индивидуальны:
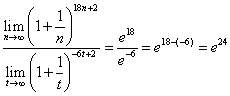 .
.
Пример 3. Найти предел

Решение. Применяем разновидность (Alt) второго замечательного предела:

Второй замечательный предел служит средством решения многих задач физики, биологии, социальных наук. Показательная функция с основанием e возникает при выводе количественного закона, которому подчиняются многие естественные процессы: рост народонаселения, рост количества древесины на лесных массивах, радиоактивный распад и т.д.
Для вывода этого закона используется формула сложных процентов
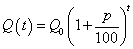
где  —
сумма, наращенная через t лет,
—
сумма, наращенная через t лет, 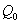 —
начальная сумма, p — процентная такса, t — время роста в годах.
—
начальная сумма, p — процентная такса, t — время роста в годах.
При этом предполагается, что проценты присоединяются к начальной сумме в конце каждого года. Если же ввести условие присоединения процентов по отдельным частям года, равным 1/n доле его, а процентная такса p по-прежнему пусть относится к целому году, то по истечении каждой такой части года наращенные суммы соответственно составят
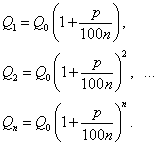
По прошествии одного года начальная сумма 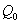 обратится в
обратится в 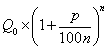
 ,
по прошествии t лет — в
,
по прошествии t лет — в 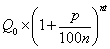 .
.Если же предположить, что прирост процентов происходит непрерывно, т. е.
число промежутков, на которые делится год, неограниченно возрастает ( ),
а каждый из них стремится к нулю, то величина наращенной суммы выразится следующей формулой:
),
а каждый из них стремится к нулю, то величина наращенной суммы выразится следующей формулой:
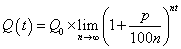 ,
,
очень напоминающей второй замечательный предел.
Используя формулу альтернативного представления второго замечательного предела (Alt), приведённую в начале статьи, получим показательный закон роста:
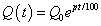
Заменив p на -p, получим показательный закон убывания:
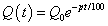 .
.
Например, если население страны возрастает на 2% в год, то по формуле показательного
закона роста можно с неплохим приближением рассчитать численность населения страны через
t лет: 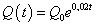 ,
где
,
где 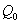 —
численность населения в начале отсчёта.
—
численность населения в начале отсчёта.

Начало темы «Предел»
Продолжение темы «Предел»
Пределы. Примеры решений — matematika
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….

Любой предел состоит из трех частей:
1) Всем известного значка предела  .
.
2) Записи под значком предела, в данном случае 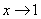 . Запись читается «икс стремится к единице». Чаще всего – именно
. Запись читается «икс стремится к единице». Чаще всего – именно 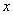 ,
хотя вместо «икса» на практике встречаются и другие переменные. В
практических заданиях на месте единицы может находиться совершенно
любое число, а также бесконечность (
,
хотя вместо «икса» на практике встречаются и другие переменные. В
практических заданиях на месте единицы может находиться совершенно
любое число, а также бесконечность (
3) Функции под знаком предела, в данном случае
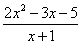 .
.Сама запись
Доказательство второго замечательного предела и следствий
Второй замечательный предел и его следствия
Второй замечательный предел – это предел, на основе которого вычисляются производные показательной функции и логарифма.
Лемма. Второй замечательный предел
.
Здесь x – действительное число.
Доказательство ⇓
Следствия второго замечательного предела
1) ;
2) ; ;
3) ; ;
4) ; ; ; .
Доказательство ⇓
Доказательство второго замечательного предела
Формулировка ⇑ При доказательстве мы будем использовать тот факт, что последовательность строго возрастает и имеет конечный предел, равный числу e: .
Доказательство приведено на странице «Число e – его смысл и доказательство сходимости последовательности».
Сначала рассмотрим правый предел
.
Для его существования должна существовать такая окрестность точки , на которой функция определена. В нашем случае, определена при . Но мы можем выбрать любую окрестность. Для удобства считаем, что .
Пусть – функция, которая означает, целую часть числа x. Например: . Она не убывает. Рассмотрим сложную функцию
.
Докажем, что она имеет предел при , равный числу e: .
Поскольку последовательность строго возрастает, а функция не убывает, то сложная функция не убывает. Тогда по теореме о пределе монотонной функции, имеет конечный или бесконечный предел при :
.
Покажем, что . Для этого используем определение предела функции по Гейне, согласно которому, если функция имеет предел при : , то для любой последовательности , сходящейся к , последовательность сходится к A: . Возьмем последовательность . Она сходится к . Тогда . Но последовательность совпадает с :
.
Поэтому ее предел равен . Таким образом A = e:
(1) .
Сделаем подстановку . Заметим, что . Заменив переменную t на x получим:
(2) .
Теперь воспользуемся тем, что . Тогда
;
(3) .
Далее замечаем, что
, .
Применяем арифметические свойства предела функции и пределы (1) и (2):
;
.
Применяя к (3) теорему о промежуточной функции, получаем, что
.
Теперь рассмотрим левый предел
.
Считаем, что . Сделаем подстановку . Тогда . При .
.
Применяем арифметические свойства предела функции.
.
Поскольку существуют равные пределы справа и слева, то существует и двусторонний предел
.
Второй замечательный предел доказан.
Доказательство следствий второго замечательного предела
Формулировка ⇑ 1) Докажем, что .
Делаем замену переменной . Тогда . При . Поэтому
.
Заметим, что фактически мы представили как сложную функцию , где . Далее мы применили теорему о пределе сложной функции.
Следствие 1) доказано.
2) Докажем, что .
Выполняем преобразования, учитывая что показательная функция является обратной к логарифмической:
.
Делаем замену переменной . В силу непрерывности показательной функции,
. Поскольку при , то
.
В предпоследнем равенстве мы воспользовались непрерывностью логарифмической функции и теоремой о пределе непрерывной функции от функции. В последнем равенстве мы применили следствие второго замечательного предела.
Также заметим, что применяя подстановку, мы представили функцию как сложную:
, где , и применили теорему о пределе сложной функции.
Применяем арифметические свойства предела функции:
.
Также здесь мы воспользовались свойством логарифма: .
Полагая a = e, имеем:
.
Следствие 2) доказано.
3) Докажем, что .
Выполняем преобразования.
.
Функция определена при . Логарифм непрерывен на своей области определения. Применяем доказанное выше следствие 1 и теорему о пределе непрерывной функции от функции:
.
Также здесь мы воспользовались свойством логарифма: .
Подставляя a = e, получаем:
.
4) Докажем, что .
Для этого воспользуемся определением гиперболического синуса и следствием 2) ⇑. Выполняем преобразования.
.
Докажем, что .
Для этого используем определения гиперболических функций и предыдущий предел.
;
.
Докажем, что .
Для этого сделаем замену переменной .
Тогда при ; при ;
(см. «Обратные гиперболические функции, их графики и формулы»).
.
Докажем, что .
Сделаем замену переменной .
Тогда при ; при ;
при (см. «Обратные гиперболические функции, их графики и формулы»).
.
Следствия доказаны.
Автор: Олег Одинцов. Опубликовано: Изменено:
Второй замечательный предел, формула и доказат-во
Формула второго замечательного предела
Число – число Эйлера, является основанием натурального логарифма.
Доказательство второго замечательного предела
Для доказательства нам будет необходим бином Ньютона:
где – факториал натурального числа .
Рассмотрим последовательность и применим к ней формулу бинома Ньютона при :
Сокращаем в каждом слагаемом числитель со вторым множителем в знаменателе первого множителя (кроме первых двух слагаемых). В результате получаем:
Оценим преобразованную последовательность сверху. В каждом слагаемом (кроме первого) дроби являются правильными дробям (для натуральных числитель меньше знаменателя), а значит их значение меньше единицы. Заменим каждую из таких дробей единицей, тогда последняя сумма увеличится. То есть
Далее, заменим все числа в знаменателях оставшихся слагаемых на 2, тем самым еще увеличив сумму (так как чем меньше знаменатель, тем дробь больше):
В правой части получилась сумма членов бесконечно убывающей геометрической прогрессии . Она равна
Поэтому
Таким образом, последовательность ограничена сверху числом 3.
Покажем теперь, что последовательность . Перепишем последовательность следующим образом:
Запишем теперь , для этого в выражении для заменим на :
Каждое из выражений в круглых скобках увеличилось (так как уменьшилось вычитаемое) а, значит, увеличились и все слагаемые, содержащие такие скобки. Число слагаемых также увеличится на одно: добавится положительное слагаемое
Следовательно, при росте номера члены последовательности строго возрастают: .
Тогда, согласно теореме, всякая возрастающая ограниченная сверху последовательности имеет предел
причём число (здесь 3 – число, ограничивающее последовательность ).
Что и требовалось доказать.
Докажем теперь, что второй замечательный предел имеет место для вещественных , то есть докажем следующую теорему.
Доказательство. Рассмотрим два случая:
1. Пусть . Каждое значение заключено между двумя положительными целыми числами
где – целая часть , то есть такое наибольшее целое число, которое не превосходит . Тогда
А тогда
Если , то . Поэтому, согласно тому, что предел , имеем:
А тогда по теореме о пределе промежуточной функции получаем, что и
2. Пусть . Сделаем подстановку , тогда
Из двух этих делаем вывод, что
Теорема доказана.
Следствия из второго замечательного предела
Примеры решения задач
Подобным образом находятся пределы функций вида (при условии, что имеется неопределенность типа )
Замечание. Не любые пределы величин вида вычисляются с помощью сведения ко второму замечательному пределу. Так надо поступать лишь в случае, когда имеем неопределенность типа . В иных ситуациях можно бывает для вычисления предела обойтись более простыми рассуждениями, а также учесть тот факт, что
2 замечательный предел | Математика
2 замечательный предел:
где
— иррациональное число. 2й замечательный предел можно применять и для нахождения пределов вида
при условии, что f(x)→∞.
2 замечательный предел, как правило, применяют в тех случаях, когда нужно найти предел степени с переменной в показателе. Рассмотрим примеры на второй замечательный предел.
Чтобы раскрыть неопределенность единица в степени бесконечность, используем 2 замечательный предел. Для этого минус уберем в знаменатель и воспользуемся рассуждениями:
Итак, имеем:
2й замечательный предел раскрывает неопределенность вида единица в степени бесконечность. Значит, неопределенность бесконечность на бесконечность в степени бесконечность необходимо привести к такому виду. Рассуждаем так:
получили неопределенность единица в степени бесконечность, и теперь можем применить второй замечательный предел:
Рассуждаем аналогично: чтобы раскрыть неопределенность бесконечность на бесконечность в степени бесконечность, нужно привести выражение к виду единица в степени бесконечность и затем применить второй 2 замечательный предел:
Основные теоремы о пределах
Теорема I. Предел алгебраической суммы конечного числа функций равен сумме пределов этих функций:
 .
.
Теорема II. Предел произведения двух функций равен произведению пределов этих функций:
 .
.
Теорема III. Предел отношения двух функций равен частному от пределов числителя и знаменателя:
 .
.
Вычисления пределов. Примеры.
I. Пределы x .
(1) 

Пределы в числителе и знаменателе равны нулю.
Чтобы найти предел дробно-линейной функции, мы должны разделить числитель и знаменатель на до максимальной степени между степенями x в числителе и знаменателе.
(2) 
, потому что 4 — максимальная степень x в числителе и знаменателе.
(3) 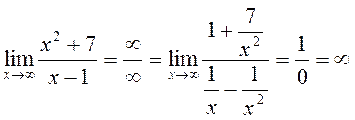 (разделить на 2 ).
(разделить на 2 ).
Простой метод определения пределов дробно-линейных функций как состоит в том, чтобы оставить член, содержащий максимальную степень , в числителе и знаменателе:
4)  ,
,
5)  ,
,
6)  .
.
Найдем пределы (1), (2), (3) простым методом:
 ,
,
 ,
,
 .
.
Удаление членов, содержащих меньшие степени x из числителя и знаменателя, возможно только потому, что после деления на до максимальной степени пределы всех таких членов исчезают.
II. Пределы как . Ищем предел, сначала подставляем в функцию  . Если мы получаем число, то это число является пределом функции. Если мы получим одну из неопределенностей
. Если мы получаем число, то это число является пределом функции. Если мы получим одну из неопределенностей  , 1 и
, 1 и  , то мы должны устранить ее, преобразовав функцию, а затем перейти к пределу.
, то мы должны устранить ее, преобразовав функцию, а затем перейти к пределу.
(1)  ,
,
(2)  ,
,
(3)  ,
,
Первый замечательный предел и его обобщение
Существует следующий предел, равный 1:
.  .
.
Пример:
(1)  ,
,
2)  .
.
Первый обобщенный замечательный предел. Первый замечательный предел можно обобщить, а именно записать в более общем виде
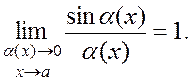 (4)
(4)
В этой формуле () бесконечно малая величина; очень важно, чтобы аргументы синуса и знаменателя были абсолютно идентичны.
Примеры.
(1) 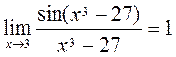 ,
,
(2) 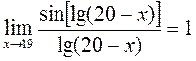 .
.
Второй замечательный предел
Считайте предел
 . (5)
. (5)
Число удовлетворяет неравенствам 2
Примеры. Найдите следующие пределы, используя второй замечательный предел:

 .
.
Второй обобщенный замечательный предел
Второй замечательный предел (*) и его модификация (**) могут быть обобщены, т.е.е., записанные в более общих формах
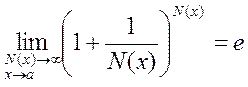
и
 . (6)
. (6)
В этих формулах () — бесконечно малая величина, а N (x) — бесконечность. Очень важно, что в этих формулах N (x) и () абсолютно идентичны в знаменателях и показателях степени.
Например ,


Другие примечательные ограничения
Рассмотрим следующие ограничения функций, часто встречающихся в приложениях:
 , (7)
, (7)
 для a = e ,
для a = e ,  .(8)
.(8)
 . (9)
. (9)
Дата: 02.01.2015; просмотр: 2088
.
Как максимально эффективно использовать новую функцию преобразования рукописного текста в reMarkable | автор: reMarkable

На этой неделе мы выпустили метрическую тонну обновлений программного обеспечения, включая одну из самых интересных на сегодняшний день функций; возможность конвертировать рукописные заметки в стандартные типы текста всего одним нажатием.
Хотя технология, лежащая в основе этого, довольно увлекательна (или, как один из членов нашей маркетинговой команды описал «чистое волшебство»), это всего лишь первая из многих итераций для reMarkable.
Прежде чем приступить к работе с маркером наготове, вам необходимо знать четыре важных вещи:
- В настоящий момент reMarkable конвертирует рукописные заметки в книжном режиме только в блокнотах, а не в файлах PDF или электронных книг.
- Вам необходимо подключиться к сети Wi-Fi и войти в учетную запись reMarkable. Когда вы нажимаете, ваши рукописные заметки отправляются в облако на хорошо обученный ИИ, который интерпретирует и преобразует каждую букву, слово и предложение в стандартизированный редактируемый печатный текст.Все это займет всего несколько секунд! Если у вас еще нет учетной записи reMarkable, вы можете создать ее здесь: my.remarkable.com.
- В этой первой версии вы можете редактировать преобразованные заметки и делиться ими по электронной почте (см. Ниже), но они не будут храниться на устройстве. В будущем появится больше функциональных возможностей, чтобы вы могли больше работать с напечатанными заметками.
- Для достижения наилучших результатов, прежде чем приступить к преобразованию текста, вы должны указать, на каком языке написаны ваши заметки, на странице настроек.В настоящее время мы поддерживаем более 30 языков, включая различные типы английского, словацкого и исландского языков! Чтобы указать язык, перейдите на страницу настроек> Преобразование рукописного ввода:
Как преобразовать рукописные заметки в редактируемый печатный текст
Теперь вы готовы превратить эти творческие волнистые линии в четкие, стандартизированные, легко доступные для обмена текстовые документы.
Находясь внутри записной книжки, вы увидите кнопку («A») в верхней строке меню.
В верхней части строки меню вы увидите функцию преобразования рукописного текста в текст как «A».При нажатии на нее откроется экран загрузки, а преобразование документа займет несколько секунд.
Затем вам будет представлена печатная текстовая версия того, что вы написали. Вместо того, чтобы создавать новый документ с набранным текстом, он отображается в виде предварительного просмотра, который вы можете отредактировать перед отправкой по электронной почте.
Если вы хотите преобразовать более одной страницы за раз, вы можете сделать это, нажав кнопку «Выбрать страницы» в верхнем углу панели действий, когда ваша первая страница преобразования будет завершена.Вы также можете выбрать несколько страниц в обзоре страниц и нажать кнопку «Преобразовать в текст», чтобы выполнить преобразование.
Редактирование преобразованных печатных заметок
При предварительном просмотре напечатанных заметок вы можете внести базовые изменения, прежде чем поделиться ими. При нажатии на текстовую область откроется клавиатура, на которой вы можете изменять и редактировать свои заметки.
Вы также можете долго нажимать на слово, чтобы выделить его, чтобы быстро удалить или заменить, введя новое слово.
Чтобы выйти из клавиатуры, просто нажмите за пределами текстовой области.
Если вы делитесь более длинными документами и записными книжками, каждая страница напечатанных заметок будет разделена тремя точками, например: • • •, чтобы вы знали, где начинается одна страница и заканчивается другая, прежде чем отправлять ее.
Совместное использование преобразованных заметок
После того, как вы будете удовлетворены преобразованными заметками, вы можете поделиться ими по электронной почте с другими или просто себе!
Когда вы нажмете кнопку «Поделиться», преобразованный текстовый документ будет отправлен в виде основного текста в самом электронном письме (а не в виде вложения), поэтому его легко взять из электронного письма и вставить его, если необходимо, в другом месте.Мы рассмотрим возможность расширения возможностей электронной почты в будущем!
Избегайте рисования диаграмм и каракулей при преобразовании документа.
Текущая версия функции преобразования рукописного ввода распознает рукописный текст, но не рисунки, диаграммы или каракули. Поэтому, если вам нужно преобразовать свою страницу, будьте готовы к тому, что ваши творческие рисунки и диаграммы не принесут с собой.
Более красивый почерк преобразуется легче.
Эта функция во многих случаях распознает рукописный текст лучше, чем человеческий глаз … но это все равно не учитывает самый сложный или беспорядочный почерк.Если есть сомнения, лучше дать функции больше шансов на работу и написать достаточно ясно, чтобы кто-то другой мог ее легко прочитать.
Структура — это ключ к успеху
Когда вы пишете на странице и хотите использовать преобразование рукописного текста в текст, очень важно поддерживать хорошую структуру заметок. Детализированные списки обнаруживаются как тире, так и точкой, и если вы закончите строку раньше, будет создан новый абзац.
Делая заметки, мы обычно советуем не писать слова в случайных местах по всей странице, в любом случае это хорошее практическое правило!
Пункты списка работают как шарм
ИИ не понимает всего, но в одном он эксперт — это пункты списка.Напишите заголовок с несколькими пунктами маркированного списка под ним, и он вернет список четко структурированных маркеров.
Обратная связь и дополнительная информация
Вы можете прочитать полную запись в блоге об обновлении здесь, а также страницу поддержки для этой конкретной новой функции.
Если у вас возникли проблемы или вы хотите поделиться своим мнением и идеями, отправьте свой отзыв через эту страницу.
.Решение поистине замечательного исследования
«Дьявольский этюд!»
На прошлой неделе мы представили исследование, которое показал нам IM Ханс Бём в ресторане отеля Zeeduin Hotel во время турнира Tata Steel в Вейк-ан-Зее. Вместе с бельгийской парой, Ритой Лоос и Мишель Магога, мы работали около получаса на позиции, и Ганс опровергал каждую неверную попытку.

На изображении, опубликованном в статье на прошлой неделе, я размыл позицию, чтобы не предлагать никакой помощи нашим читателям, которые должны были решить задачу самостоятельно, с помощью своих шахматных машин, если они того пожелают.Прежде чем я перейду к решению, необходимо кое-что изучить.
Во-первых, удивительно (и целесообразно), что человеческий — ну хоть у меня память такая хилая. В тот вечер в своем гостиничном номере я искал точный источник исследования, когда обнаружил, что издавал его сам давным-давно. Расскажу историю
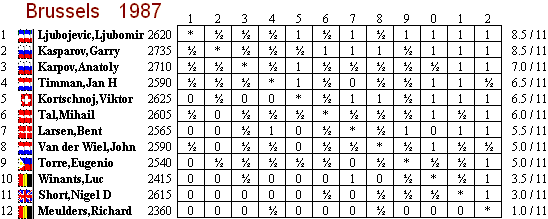
В апреле 1987 года в Брюсселе прошел турнир супергроссмейстеров, в котором выиграл великий югославский гроссмейстер Любо Любоевич, заняв первое место на равных с чемпионом мира Гарри Каспаровым.Они на полтора очка опережали Анатолия Карпова и остальных игроков, в том числе Тала, Ларсена, Корчного, Тиммана и очень молодого и не в форме Найджела Шорта.
Турнир запомнился по определенной причине. Самая первая версия ChessBase была выпущена в январе 1987 года, и мы показывали программу базы данных игрокам на турнире. Каспаров и Шорт это уже знали, но для остальных это было все равно, что вести детей по кондитерской.Михаил Таль был самым забавным: он всегда приходил в пресс-центр сразу после своих игр, чтобы ввести ходы в мой Atari ST (1 МБ ОЗУ, диск 720 КБ, спросите у дедушки об этой легендарной машине).

Михаил Таль на турнире супергроссмейстеров в Брюсселе в 1987 году

Тони Майлз проверяет революционно новую программу базы данных в 1987 году

Карпов и Каспаров анализируют после игры, без компьютера, с Бачаром Куатли (сидит) и Михаил Таль (стоит с сигаретой)
Другим памятным событием стала встреча с очень энергичным молодым британским гроссмейстером.По примечательному совпадению ( инсайдерская шутка ) Джеймс Пласкетт (на фото слева) посещал турнир, и я провел много времени, спорив с ним о политике правых в Англии. В качестве прощального подарка Джим показал мне приведенное ниже исследование, то же самое, что тридцать лет спустя показал нам Ганс Бем.
В Брюсселе мы провели остаток дня, перемешивая фигуры на доске. Иногда после игры приходил один из супергроссмейстеров, а иногда они присоединялись к анализу.Но в пресс-центре его никто не получил. Миша Таль безуспешно работал над ним десять минут, затем покинул пресс-центр и через час неожиданно зашел снова. Он понял главную идею во время прогулки по парку.
Когда я опубликовал исследование в разделе ChessBase Puzzle (статическая страница, которой больше нет в сети), я отразил позицию, чтобы читателям было труднее найти ее в Интернете или в учебных базах данных. Я сделал то же самое в статье на прошлой неделе. Лишь несколько десятков читателей смогли найти решение — с интенсивным использованием шахматных машин и остроумным поиском в Интернете.
Давайте теперь посмотрим на замечательное исследование в его первоначальном виде. Помните, что вы можете перемещать фигуры по доске, чтобы визуализировать ходы, указанные под диаграммами. В конце этой статьи все решение представлено в программе просмотра игр ChessBase, которая даже позволяет вам запустить движок для анализа любых идей, которые вы можете попробовать.
Мы упомянули несколько очевидных вещей в вышеуказанной позиции. Белые не могут продвинуть пешку из-за вилки коня на f7.Перемещение короля позволяет черным защитить ферзевое поле d8 и использовать свои превосходящие силы для урегулирования игры.
Таким образом, белым пришлось пойти на более решительные меры: 1.Nf6 + Kg7! 1 … Kh8 2.d8Q + — мат вчетвером; и 1 … Kg6 2.Bh5 + Kxf6 (или … Kf5) 3.d8Q выигрывает, поскольку разделительное поле f7 защищает слон. 2.Нh5 + Крg6 . 2 … Kf7 заблокировало бы поле разветвления и позволило бы 3.d8Q. 3.Bc2 +! Заставить черных взять коня — очень сложный ход для компьютеров. 3… Kxh5 4.d8Q !! (разрешая вилку) Nf7 + 5.Ke6 Nxd8 + 6.Kf5.
Перемещайте фигуры прямо на диаграмме!
Ага, белые выбросили мат! Угроза — мат 7.Bd1 + e2 8.Bxe2. 6… e2 7.Be4 . Теперь угроза 8.Bf3 #. У черных есть только одна разумная защита — недоработка! 7… e1N! 8.Bd5! Угроза: 9.Bc4 и 10.Be2 с матом. 8 … c2 9.Bc4 . Угрожающее 10.Be2 с матом на двоих. 9… c1N! 10.Сb5 . Угрожающее 11.Be8 + с матом двоих. 10… Nc7 11.Ba4!
Посмотрите на эту ситуацию. У черных четыре коня (и слон), но они не могут помешать одинокому белому слону поставить мат за три хода, например 11… Ne2 12.Bd1 Nf3 13.Bxe2 и 14.Bxf3 мат.
Красивая, увлекательная задача, получившая высокую оценку многих читателей. Пауло Гильерме де Маттос из Гуарульюса, Бразилия, писал: «Вау, эта головоломка безумна»; Роберто Диллон из Сингапура назвал это «поистине дьявольским исследованием!»; Джордж Георгопулос из Афин, Греция, говорит, что ему потребовался целый день, чтобы решить проблему с помощью двигателя; Доминик Лехан из Брисбена, Австралия, писал: «После двух дней анализа в свободное время мне удалось решить эту головоломку без компьютеров.Это самая длинная головоломка, которую я когда-либо решал, и к тому же самая интересная ».
Как я проиграл пари с Хансом Бемом: однажды он сказал, что компьютеры никогда не смогут решить это исследование, и я держу пари, что мой Fritz 16 сделает это менее чем за одну минуту. Я принес свой ноутбук и voilá , я получил решение почти мгновенно. Ганс был впечатлен и начал заказывать пиво, но, как бы я ни был честен (часто в ущерб себе), я признался и показал ему, как я это сделал:
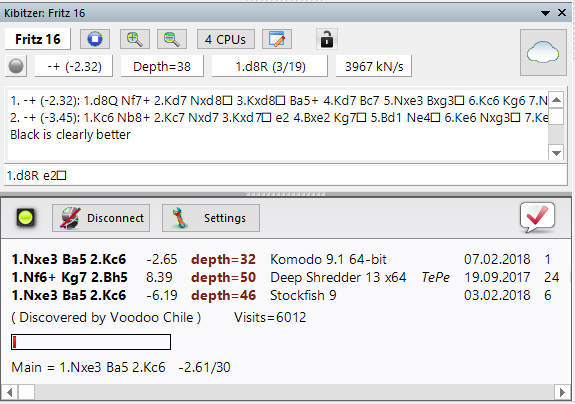
Это Фриц 16, работающий над начальной позицией для изучения и обдумывающий 1.d8Q и 1.Kc6 с проигрышными оценками белых. Но: Давайте проверим, наша облачная коллекция из сотен миллионов позиций с анализом тремя мощными двигателями, показала мне, что некоторые люди уже смотрели на позицию, и что одна программа предложила 1.Nf6 + пытаться. Я сделал этот ход и ответил … Kg7, и вот что я получил:
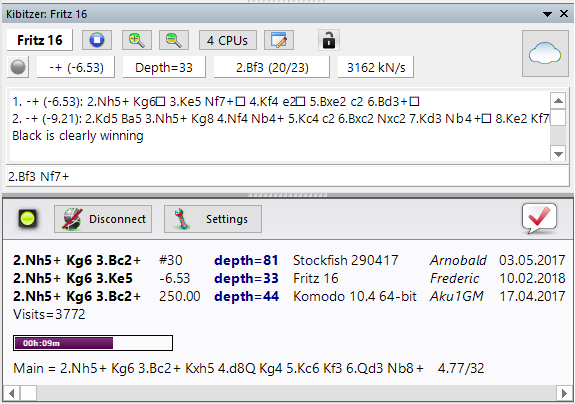
Fritz 16 через несколько минут все еще пытается найти положительное продолжение, но кто-то проанализировал позицию после 1.Nf6 + Kg7 до 44-х с Комодо и 81-х с Stockfish, и придумать полное решение (как вы можете видеть из результатов). Конечно, я смог продиктовать продолжение Гансу с задержкой в ноль секунд, но не из-за чистой мощности двигателя, а благодаря информации, хранящейся в облаке. Я купил пиво.
Fritz 16 — Он просто хочет играть!
Fritz 16 с нетерпением ждет возможности поиграть с вами, и вы наверняка получите с ним массу удовольствия.Вас ждут напряженные игры и даже хорошо отобранные победы в режимах «Легкая игра» и «Вспомогательный анализ».
Полное решение

[Событие «Schakend Nederland # 2207 (v)»] [Сайт «?»] [Дата «1990. ??. ??»] [Круглый «?»] [Белый «Ван Брекелен, Гийс»] [Черный «Белый играть и побеждать «] [Результат» 1-0 «] [Аннотатор» Bohm, Hans «] [SetUp» 1 «] [FEN» 8 / 3P3k / n2K3p / 2p3n1 / 1b4N1 / 2p1p1P1 / 8 / 3B4 w — — 0 1 «] [PlyCount» 27 «] [EventDate» 1990. ??. ?? «] 1. Nf6 + Kg7 (1 … Kg6 $ 2 2. Bh5 + Kxf6 3.d8 = Q +) 2. Nh5 + (2. Bh5 Ba5 $ 19) 2 … Kg6 3. Bc2 + $ 1 Kxh5 4. d8 = Q $ 1 Nf7 + (4 … Kg4 5. Qf6 Kxg3 6. Qe5 + Kf2 7. Qh3 + Ke1 8 . Qg1 + Ke2 9. Qg4 + Ke1 10. Ke5) 5. Ke6 Nxd8 + 6. Kf5 {Угроза: 7.Bd1 + e2 8. Bxe2 #} e2 7. Be4 {Угроза: 8.Bf3 #} e1 = N $ 1 8. Bd5 $ 1 {Угроза: 9.Bc4 и 10.Be2 с матом.} C2 9. Bc4 {Угроза: 10.Be2 + и мат.} C1 = N $ 1 10. Bb5 {Угроза: 11.Be8 + и мат.} Nc7 11. Ba4 $ 1 {Угроза: 12.Bd1 + и мат последует.} Ne2 12. Bd1 Nf3 13. Bxe2 Nce6 {Любое.} 14. Bxf3 # 1-0
Приз, копия копии Fritz 16, подписанный Магнусом Карлсеном, Анишем Гири, Вишванатаном Анандом, Юдит Полгар, Шахрияром Мамедьяровым и Видитом Гуджарати, выиграл Доминик Лехан из Брисбена, Австралия
Но кто это написал?
 База данных Гарольда ван ден Хейдена, которая в настоящее время содержит 85 619 эндшпильных исследований (Гарольд посвятил большую часть своей жизни их компиляции) и стоит всего 50 евро, дает автору исследования как Гийсу ван Брекелену и Место публикации — голландский журнал Schakend Nederland .Приведенная дата сбивает с толку: 1990 год. Но разве Джим Пласкетт не показал ее нам в 1987 году? И очевидно, что некоторые люди видели это исследование до этого. Например, GM Любомир Кавалек сказал мне:
База данных Гарольда ван ден Хейдена, которая в настоящее время содержит 85 619 эндшпильных исследований (Гарольд посвятил большую часть своей жизни их компиляции) и стоит всего 50 евро, дает автору исследования как Гийсу ван Брекелену и Место публикации — голландский журнал Schakend Nederland .Приведенная дата сбивает с толку: 1990 год. Но разве Джим Пласкетт не показал ее нам в 1987 году? И очевидно, что некоторые люди видели это исследование до этого. Например, GM Любомир Кавалек сказал мне:
«Мне было весело решать эту задачу с Борисом Спасским во время уик-энда Бундеслиги в начале 1980-х. Я не знаю, кто нам это показал».
Ситуация осложнялась рассказами о том, что место Миши Тала дал таксист или водитель грузовика, которого он так и не смог отследить.Эти истории противоречат моим воспоминаниям о Тале, который увидел позицию в Брюсселе в апреле 1987 года, не смог ее решить, а затем внезапно вернулся в пресс-центр с решением.
Ведущий эксперт по эндшпилю Джон Ройкрофт написал в журнале по эндшпилю EG vol. 122:
Составителем этого прекрасного этюда является голландский композитор Гийс ван Брекелен, который продемонстрировал его в качестве примера своей работы на собрании ARVES, состоявшемся в 1992 году в Делфте.Композитор сказал на собрании ARVES, что он сочинил его в середине 1970-х и показал нескольким друзьям, но не отправлял его для публикации и не выставлял на турнир. Каким-то образом проникнув в круг игроков, он быстро распространился, приобретая журналистский оттенок в пути из-за того, что был связан либо с (полностью вымышленным) украинским трактористом, либо с очень специфической (но в равной степени ложной) игрой между ведущими мастерами. Покойный IGM Тал был одним из активных пропагандистов, но когда его спросили, он заявил, что не может вспомнить, кто первым показал ему это.
Джим Пласкетт написал мне еще в 2003 году:
Существует малоизвестная мифология о происхождении головоломки. Я думаю, что Грэм Хиллард был первым, кто показал мне это в 1986 году или раньше. Исследование опубликовано в последней книге Гуфельда, The Search for Mona Lisa. Его история состоит в том, что оно появилось примерно в 1990 году. Есть истории о том, что Таль получил анонимное письмо до 1986 года от водителя грузовика, составившего его. Гуфельд говорит, что, поскольку никто еще не утверждал, что он изобретатель этого исследования, он предлагает, чтобы оно пришло из космоса.Я уверен, что где-то читал, что это сделал кто-то, оканчивающийся на -швили. Он говорит, что во время Олимпиады 1992 года малазийский игрок Мокцзе Менг получил анонимный телефонный звонок, в котором говорилось, что это подарок для Гуфельда — и голос затем продиктовал позицию. Гуфельд говорит, что на Олимпиаде 1992 года и Карпов, и Каспаров были поражены этим исследованием.
Антонио Торресильяс из Барселоны написал:
Много лет назад мне показали эту проблему с помощью красивой истории: водитель грузовика отправил ее в какой-то русский журнал (может, 64?) , но она надолго отложилась в файлы хранилища.Много лет назад Михаил Таль, будучи директором этого журнала, увидел это и получил огромное удовольствие. Но когда Таль попытался найти составителя этого фантастического эндшпиля, у него ничего не вышло, потому что гонщик был мертв. Единственная проблема этой истории в том, что она фальшивая, но все равно очень красивая!
Что делать в таких ситуациях? Очевидно, лучшая стратегия — связаться с королем изучения эндшпиля Гарольдом ван ден Хейденом. Он предоставил следующую информацию:
Что известно о самом древнем источнике? А.Рюйгрок сообщил, что проблема была увековечена в 1976 году известным художником-насекомым Гансом Верхофом в телешоу Voor de vuist weg . В еженедельнике Panorama также была опубликована диаграмма с комментарием Ханса Бема. Некоторое время назад Ханс дал мне копию статьи о визите его и Харма Вирсмы, шестикратного чемпиона мира по шашкам, к Гансу Верхофу. И да: на картинке изображена проблема трактора. Следует отметить, что в 1976 году рассказ о тракторе, видимо, еще не был придуман.Ханс Бём подарил мне красивую картину, на которой также увековечена шахматная картина:

Скан картины с картиной художника Ханса Верхофа. На заднем плане: Ханс Бём и Харм Вирсма. «К сожалению, отпечаток картины несколько поврежден», — написал Гарольд.
А как же Михаил Таль? Убежден, что он впервые увидел эту позицию в пресс-центре Брюсселя. Его поведение, когда он пытался решить эту проблему, а затем после того, как он нашел решение в парке, выглядел совершенно искренним.Я делаю вывод, что другие сфабриковали полностью выдуманную историю тракториста.
 Информация о Gijs van Breukelen
Информация о Gijs van Breukelen
Родился в 1946 году в Амстердаме. С 17 лет начал заниматься шахматной композицией. Он изучал голландский язык в Утрехте, играл в шахматном клубе «Пауль Керес». Он восхищается Либуркиным, Каспаряном и Марвицем.
В его ранних исследованиях можно увидеть влияние натурализма. Позже его стиль стал более эксцентричным, с предпочтением длинных решений.
Здесь можно найти избранные его исследования. Все исследования ван Брекелена с точными датами, возможными исправлениями или поварами, а также точные сведения об источниках можно найти в базе данных исследований Гарольда ван ден Хейдена.
Фотографии Гийса ван Брекелена: Рене Олтхоф (2010, титул), Гарольд ван дер Хейден (2002)
Фотографии турнира супергроссмейстеров в Брюсселе 1987, Вейк 2018: Фредерик Фридель
Ссылки
.§ 3.5. Основные теоремы о пределах
Теорема I. г. предел алгебраической суммы конечного числа функций равен сумме границ этих функций:
 .
.
Доказательство. Для
Для простоты докажем теорему для суммы двух функций.
Предположим, что 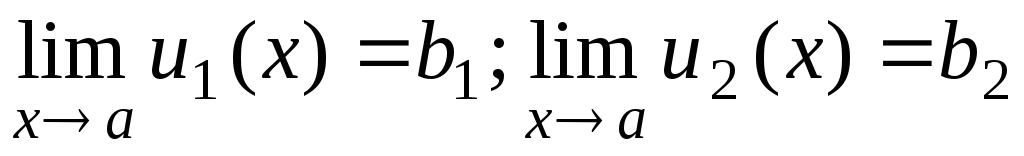 .
По теореме I эти функции можно представить в виде u 1 (x) = b 1 + 1 (x),
u 2 (x) = b 2 + 2 (x) ,
где 1 ( х ), 2 ( х ) являются
бесконечно малые.Рассмотрим сумму
.
По теореме I эти функции можно представить в виде u 1 (x) = b 1 + 1 (x),
u 2 (x) = b 2 + 2 (x) ,
где 1 ( х ), 2 ( х ) являются
бесконечно малые.Рассмотрим сумму
u 1 (x) + u 2 (x) = b 1 + b 2 + 1 (x) + 2 (x), где 1 (x) + 2 (x) это Бесконечно малый .
С помощью из второй части теоремы I получаем
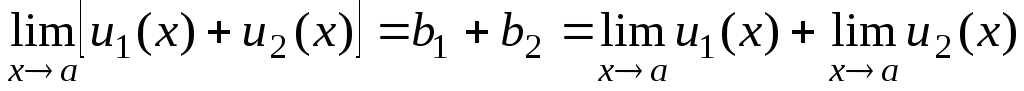 , г.
как требуется.
, г.
как требуется.
Теорема II. предел произведения двух функций равен произведению пределы этих функций:
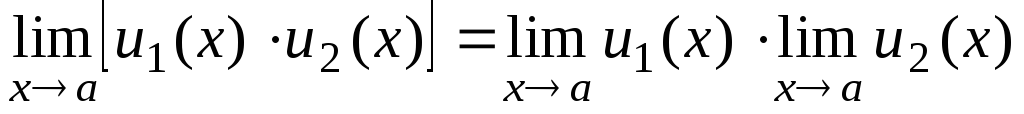 .
.
Доказательство. Предположим
который 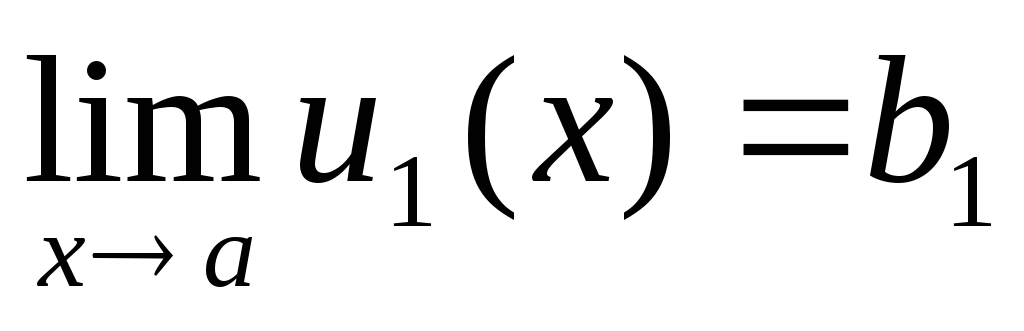 и
и 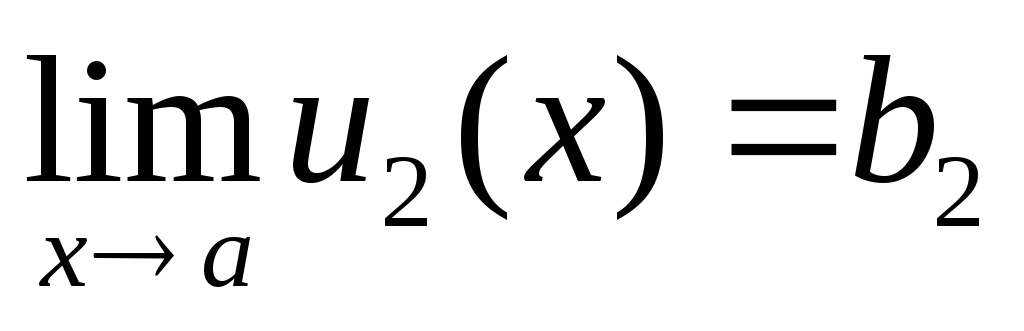 .
По теореме I имеем u 1 (x) = b 1 + 1 (x) и u 2 (x) = b 2 + 2 (x) .
.
По теореме I имеем u 1 (x) = b 1 + 1 (x) и u 2 (x) = b 2 + 2 (x) .
Рассматривать товар
u 1 (x) . u 2 (x) = b 1 . b 2 + b 1 2 (x) + b 2 1 (x ) + 1 (x) 2 (x) = b 1 . b 2 + (x),
где ( х ) является
бесконечно малая сумма последних трех членов. Из теоремы I следует 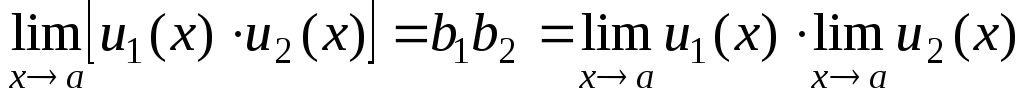 , г.
как требуется.
, г.
как требуется.
Теорема III. Предел отношения двух функций равен частному пределы числителя и знаменателя:
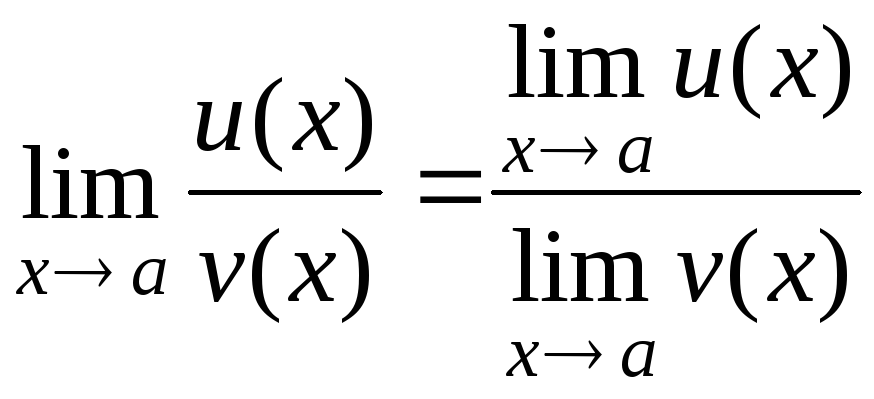 .
.
Доказательство. Предположим, что
 .
.
затем
u (x) = b 1 + 1 (x) и v (x) = b 2 + 2 (x) .
Рассматривать частное и преобразуем его, приведя к общему знаменателю:
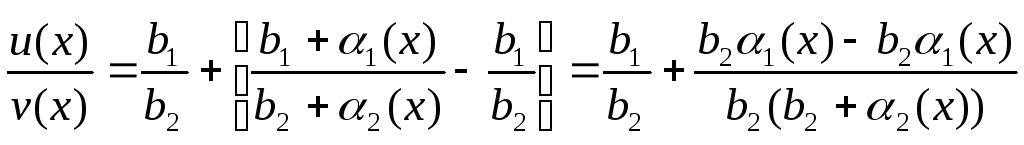 .
.
Это Легко показать, что второе частное бесконечно мало.В Из фундаментальной теоремы I следует требуемое утверждение.
Теорема IV (г. теорема о сэндвиче). Если в окрестности точки а , неравенства
u (х) z (x) v (х) (3)
держать  , г.
затем ограничить
из z (x) существует и равно
, г.
затем ограничить
из z (x) существует и равно  .
.
Доказательство. Вычитая b из
из неравенств (3) получаем (x) –b z (x) –b v (x) –b . По определениям, если | x – a | < , тогда | u (x) –b | < и | v (x) –b | < ;
отсюда — , и —  .
.
Теорема
V. Если
функция f (x) является
монотонно возрастает (убывает) и ограничено как х а выше
(ниже), затем f (x) имеет
конечный предел 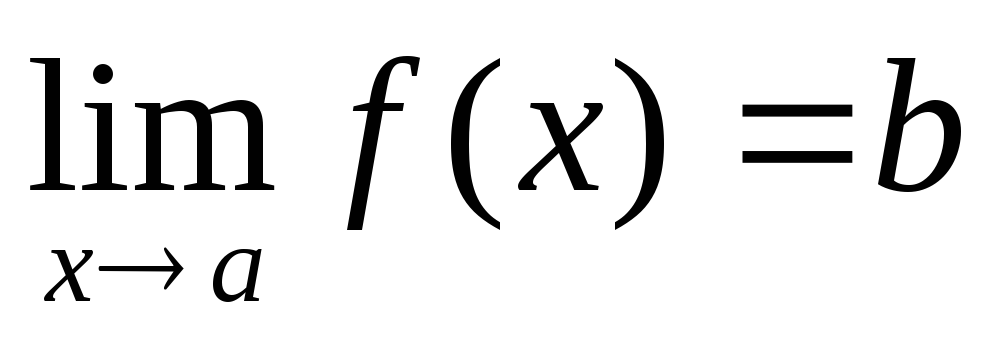 (Без доказательств.)
(Без доказательств.)
 y
y
M
y = f (x)
б
0 а х
3.5.1. Вычисления пределов. Примеры.
Я. Лимиты как x .
(1) 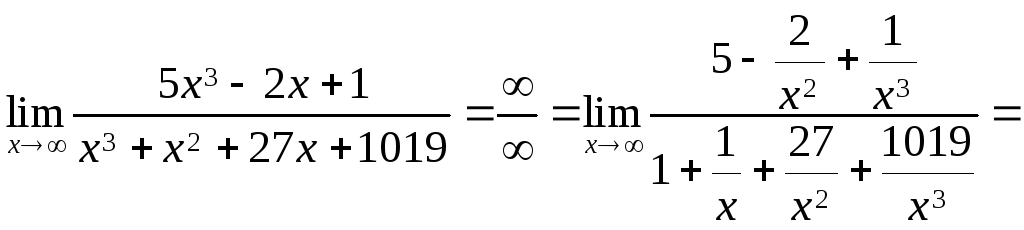
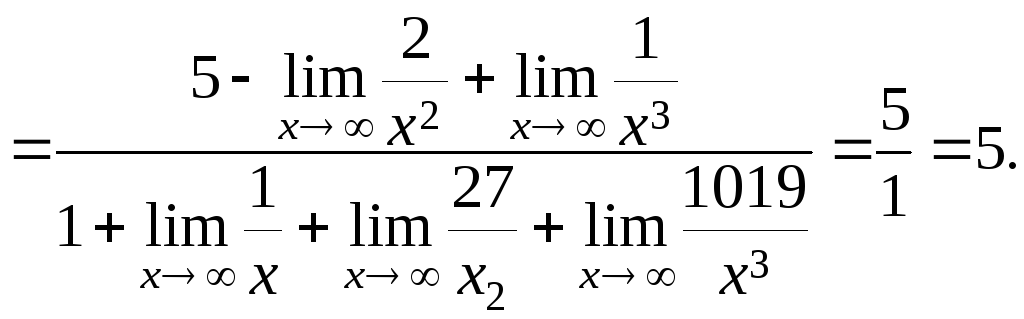
В пределы в числителе и знаменателе равны нулю.
Чтобы найти предел дробно-линейной функции, мы должны разделить числитель и знаменатель на х на максимальную мощность среди степеней x дюйм числитель и знаменатель.
(2) 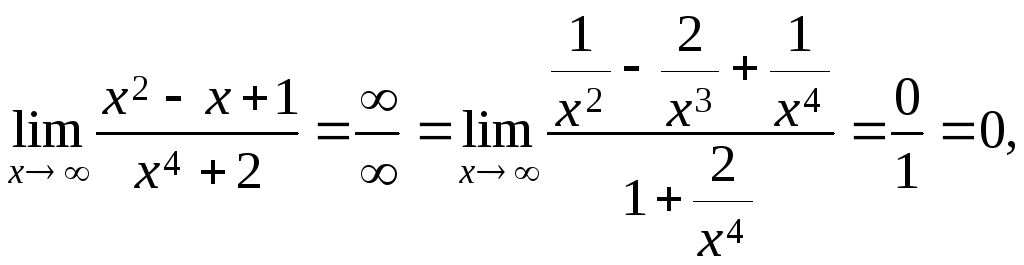
так как х 4 является максимальная мощность x в числителе и знаменателе.
(3)  (делить
по х 2 ).
(делить
по х 2 ).
А простой метод нахождения пределов дробно-линейных функций как х это к оставьте член, содержащий максимальную степень х в числителе и знаменателе:
4) 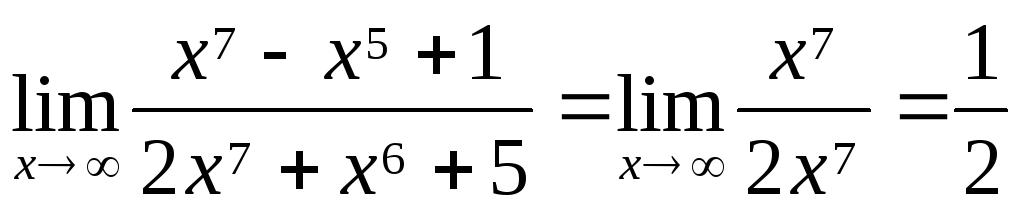 ,
,
5) 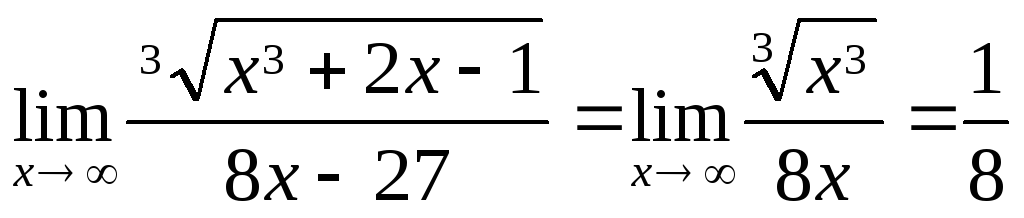 ,
,
6) 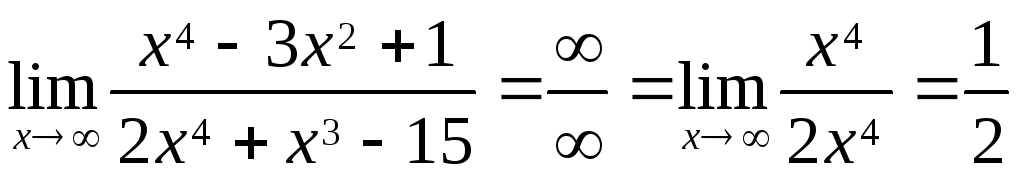 .
.
Позволять найдем пределы (1), (2), (3) простым методом:
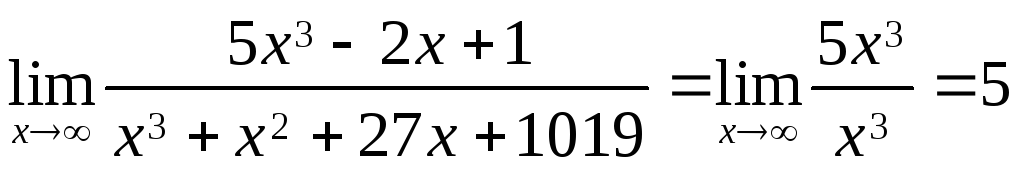 ,
,
 ,
,
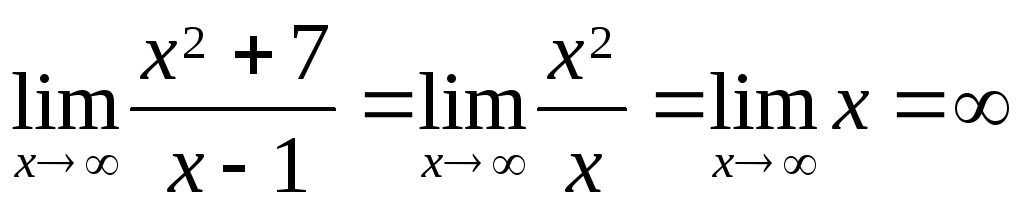 .
.
Удаление члены, содержащие младшие степени x из числитель и знаменатель возможны только потому, что после деление на х до максимальной мощности пределы всех таких членов исчезают.
II. Пределы
как х а . Ищу
вместо лимита сначала замените 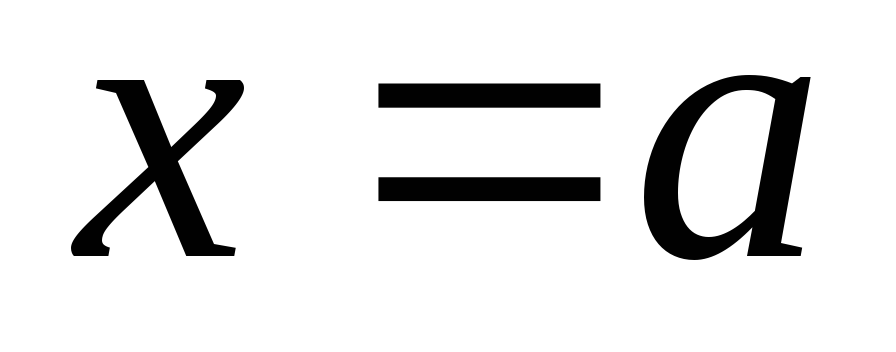 в функции.Если мы получим число, то это число и есть предел
функции. Если мы получим одну из неопределенностей
в функции.Если мы получим число, то это число и есть предел
функции. Если мы получим одну из неопределенностей 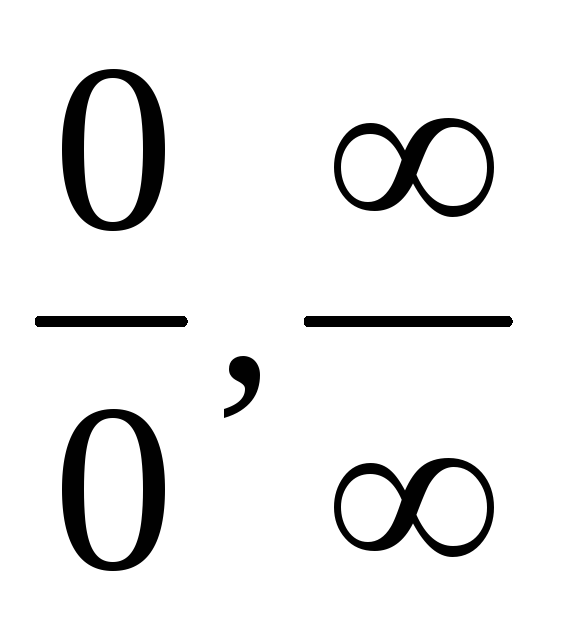 , 1 ,
и
, 1 ,
и  , г.
то мы должны устранить его, преобразовав функцию, а затем
пройти до предела.
, г.
то мы должны устранить его, преобразовав функцию, а затем
пройти до предела.
(1) 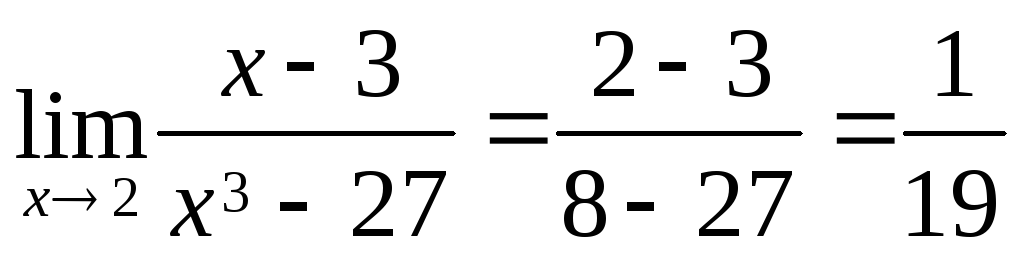 ,
,
(2)  ,
,
(3) 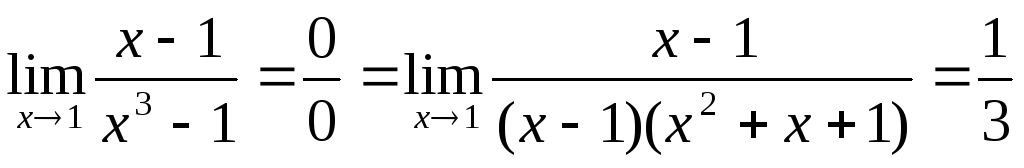 ,
,
(4) 
 .
.

 Информация о Gijs van Breukelen
Информация о Gijs van Breukelen