Выборочное среднее формула: Выборочное среднее, среднее значение выборки

Как рассчитать выборочное среднее (с примерами) • BUOM

Автор: редакционная команда Indeed

22 февраля 2021 г.

Когда статистики изучают популяции, они могут брать выборку из большей популяции, чтобы применить статистические расчеты, чтобы выяснить тенденции и предсказать результаты для большей популяции. Выборочное среднее — это один расчет, который может сообщить статистикам среднее значение заданного набора данных. Статистики используют выборочное среднее для набора данных, чтобы делать прогнозы относительно стандарта нормальности в данной совокупности, а выборочное среднее также можно использовать для нахождения дисперсии, отклонения и стандартной ошибки в наборе данных. В этой статье мы исследуем, что такое выборочное среднее, дисперсия и стандартная ошибка и как рассчитать выборочное среднее.

Что означает образец?

Выборочное среднее — это среднее значение набора данных. Среднее значение выборки можно использовать для расчета центральной тенденции, стандартного отклонения и дисперсии набора данных. Выборочное среднее может применяться для различных целей, включая расчет средних значений генеральной совокупности. Многие отрасли занятости также используют статистические данные, такие как:

• Научные области, такие как экология, биология и метеорология

• Области медицины и фармакология

• Данные и информатика, информационные технологии и кибербезопасность

• Аэрокосмическая и авиационная промышленность

• Направления в инженерии и дизайне

Как рассчитать выборочное среднее

Вычислить выборочное среднее так же просто, как сложить количество элементов в выборочном наборе, а затем разделить эту сумму на количество элементов в выборочном наборе. Чтобы рассчитать среднее значение выборки с помощью программного обеспечения для работы с электронными таблицами и калькуляторов, вы можете использовать формулу:

х̄ знак равно ( Σ xi ) / п

Здесь x̄ представляет среднее значение выборки, Σ говорит нам добавить, xi относится ко всем значениям X, а n обозначает количество элементов в наборе данных.

При расчете выборочного среднего с использованием формулы вы будете подставлять значения для каждого из символов. Следующие шаги покажут вам, как рассчитать выборочное среднее для набора данных:

1. Добавьте образцы элементов

2. Разделите сумму на количество образцов

3. Результат — это среднее

4. Используйте среднее значение, чтобы найти дисперсию

5. Используйте дисперсию, чтобы найти стандартное отклонение

1. Сложите образцы элементов

Во-первых, вам нужно будет подсчитать, сколько элементов выборки у вас есть в наборе данных, и сложить общее количество элементов. Давайте посмотрим на пример:

Учитель хочет найти средний балл ученика в его классе. В выборке учителя есть семь различных тестовых баллов: 78, 89, 93, 95, 88, 78, 95. Он складывает все баллы вместе и получает сумму 616. Он может использовать эту сумму на следующем шаге, чтобы найти свою выборку. иметь в виду.

2. Разделите сумму на количество образцов

Затем разделите сумму с первого шага на общее количество элементов в наборе данных.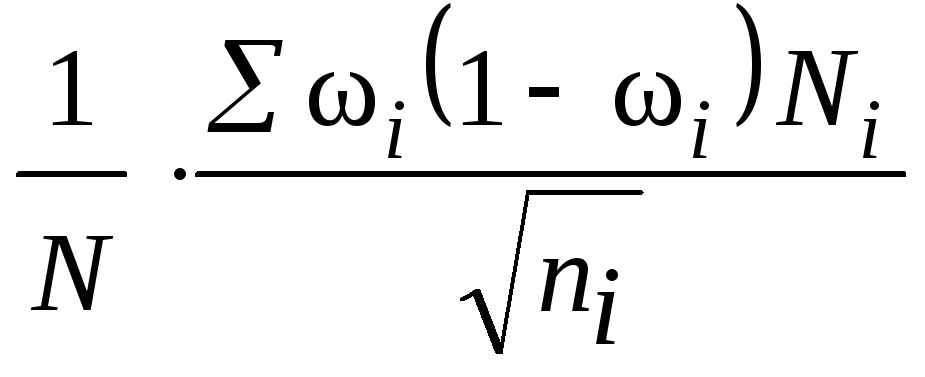 Вот как это выглядит на примере учителя:

Учитель использует сумму 616, чтобы найти средний балл. Он делит 616 на семь, поскольку количество баллов в его наборе данных равно семи. Получившееся частное равно 88.

3. Результат – это среднее

После деления полученное частное становится средним значением выборки или средним значением. На примере учителя:

Оценки студента, которые он подсчитывал, привели к средней оценке 88%. Вы можете использовать среднее значение выборки для дальнейшего расчета дисперсии, стандартного отклонения и стандартной ошибки.

4. Используйте среднее значение, чтобы найти дисперсию

Вы можете использовать выборочное среднее в дальнейших расчетах, найдя дисперсию выборки данных. Дисперсия показывает, насколько далеко разбросан каждый из элементов выборки в наборе данных. Чтобы вычислить дисперсию, вы находите разницу между каждым элементом данных и средним значением. На примере учителя посмотрим, как это работает:

Учитель хочет найти дисперсию оценок своего ученика, поэтому он вычисляет дисперсию, сначала находя разницу между средней оценкой и всеми семью оценками учащегося, которые он использовал для нахождения среднего значения:

(78-88, 89-88, 93-88, 95-88, 88-88, 78-88, 95-88) = (-10, 1, 5, 7, 0, -10, 7).

Затем учитель возводит в квадрат каждую разницу (100, 1, 25, 49, 0, 100, 49) и, как и среднее, складывает все числа и делит на семь. Он получает 324 / 7 = 46,3, или примерно 46. Чем больше дисперсия, тем больше разброс данных от среднего значения.

5. Используйте дисперсию, чтобы найти стандартное отклонение.

Вы также можете еще больше расширить выборочное среднее, рассчитав стандартное отклонение выборочного набора. Стандартное отклонение представляет собой нормальную скорость распределения для набора данных и является квадратным корнем дисперсии. Давайте посмотрим на пример:

Учитель использует дисперсию 46, чтобы найти стандартное отклонение: √46 = 6,78. Это число говорит учителю, насколько выше или ниже среднего балла в 88% его ученик по любому заданному результату теста в наборе выборки.

Какова дисперсия выборочного распределения среднего?

Дисперсия набора данных относится к разбросу элементов в наборе выборки. Когда статистики рассчитывают дисперсию, они пытаются выяснить, насколько далеко друг от друга находятся элементы при представлении данных на графике. Дисперсия может сказать вам, насколько отличается каждый элемент в наборе образцов. Кроме того, можно анализировать среднее значение выборки, дисперсию, стандартное отклонение и ошибку, чтобы предположить и предсказать результаты и тенденции в отношении совокупности, а также выборки этой совокупности.

Что означает стандартная ошибка выборки?

Стандартная ошибка среднего (SEM) или стандартное отклонение показывает, насколько далеко среднее значение выборки от истинного среднего значения генеральной совокупности. Например, в примере с учителем в выборке был только один ученик. Среднее значение выборки, дисперсия и отклонение представляют данные только об этой выборке, а стандартную ошибку можно использовать для сравнения данных выборки со всей совокупностью.

Например, всем населением может быть весь класс, весь 10-й класс или все учащиеся. В любой из этих ситуаций стандартная ошибка среднего значения выборки будет представлена ​​тем, насколько далеко средний балл учащегося от среднего балла всего населения.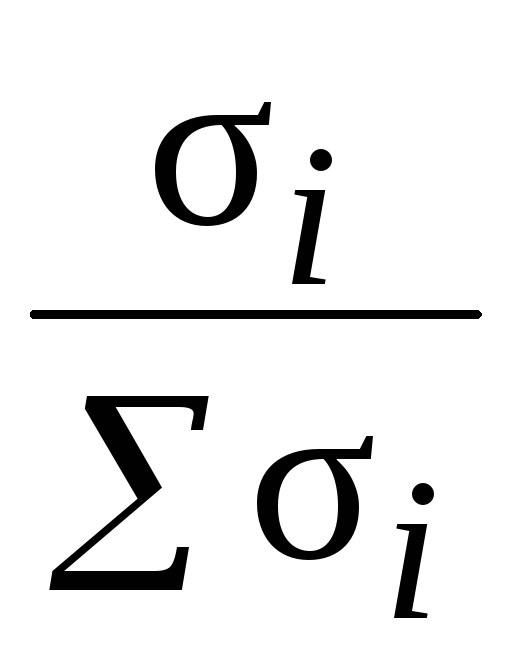

Среднее значение выборки и среднее значение населения: в чем разница?

---

Часто в статистике нас интересуют ответы на такие вопросы, как:

• Каков средний доход домохозяйства в определенном городе?
• Каков средний вес определенного вида черепах?
• Какова средняя посещаемость футбольных матчей колледжа?

В каждом сценарии нас интересует ответ на некоторый вопрос осовокупности , которая представляет все возможные отдельные элементы, которые мы хотим измерить.

Однако вместо сбора данных о каждом человеке в популяции мы собираем данные по выборке популяции, которая представляет собой часть общей популяции.

Например, мы можем захотеть узнать средний вес определенного вида черепах, общая популяция которых составляет 800 особей.

Поскольку поиск и взвешивание каждой отдельной черепахи в популяции заняло бы слишком много времени, мы вместо этого собираем простую случайную выборку из 30 черепах и измеряем их вес:

Затем мы могли бы использовать средний вес этой выборки черепах для оценки среднего веса всех черепах в популяции.

Как рассчитать выборочное среднее

Формула для расчета выборочного среднего, часто обозначаемого x , выглядит следующим образом:

х = Σх я / п

куда:

• Σ: причудливый греческий символ, означающий «сумма».
• x i : значение i-го наблюдения в наборе данных.
• n: размер выборки

Например, предположим, что мы собираем выборку из 10 черепах со следующими весами (в фунтах):

• 70, 80, 80, 85, 90, 95, 110, 120, 140, 150

Среднее значение выборки будет рассчитываться как:

• х = (70+ 80+80+85+90+95+110+120+140+150) / 10 = 102

Почему выборочное среднее является несмещенным

На статистическом жаргоне мы бы сказали, что среднее значение выборки является статистикой , а среднее значение генеральной совокупности — параметром .

Вот разница между двумя терминами:

Статистика – это число, описывающее некоторую характеристику выборки.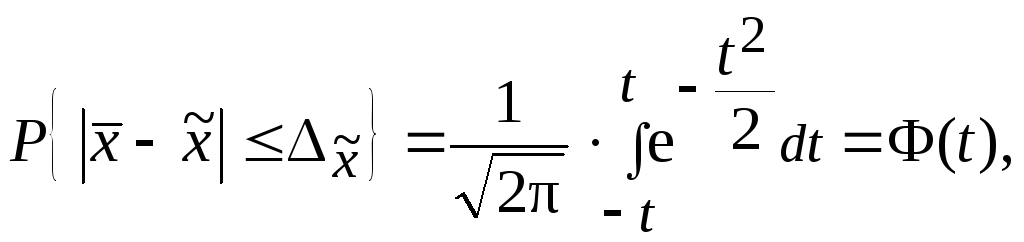

Параметр — это число, описывающее некоторую характеристику совокупности.

Параметр — это значение, которое мы действительно хотим измерить, а статистика — это значение, которое мы используем для оценки значения параметра, поскольку статистику получить намного проще.

Когда мы используем такой метод, как простая случайная выборка , для получения выборки, мы говорим, что выборочное среднее является несмещенной оценкой среднего значения генеральной совокупности.

Другими словами, у нас нет оснований полагать, что среднее значение выборки занижает или переоценивает истинное среднее значение генеральной совокупности.

Причина в том, что когда мы используем такой метод, как простая случайная выборка, каждый член совокупности имеет равные шансы быть включенным в выборку, а это означает, что выборка, вероятно, будет «мини-версией» генеральной совокупности.

Мы бы сказали, что выборка репрезентативна для всей совокупности , а это означает, что среднее значение выборки должно быть хорошей оценкой среднего значения совокупности, если предположить, что размер выборки достаточно велик.

Об использовании доверительных интервалов с выборочным средним

Хотя среднее значение выборки обеспечивает несмещенную оценку среднего значения совокупности, маловероятно, что среднее значение выборки будет точно соответствовать среднему значению совокупности.

Например, если мы хотим использовать выборку черепах для оценки среднего веса популяции черепах, возможно, мы случайно выберем выборку, полную черепах с низким весом, или, возможно, выборку, полную тяжелых черепах.

Чтобы зафиксировать эту неопределенность вокруг нашей оценки среднего значения генеральной совокупности, мы можем создатьдоверительный интервал .

Доверительный интервал — это диапазон значений, который может содержать параметр генеральной совокупности с определенным уровнем достоверности.

Например, мы можем собрать выборку из 30 черепах и обнаружить, что средний вес этой выборки составляет 102 фунта. Если мы затем построим доверительный интервал 95%, мы можем обнаружить, что интервал выглядит следующим образом:

95% доверительный интервал = [98,5, 105,5]

Мы бы интерпретировали это как означающее, что существует 95% вероятность того, что доверительный интервал [98,5, 105,5] содержит истинный средний вес популяции черепах.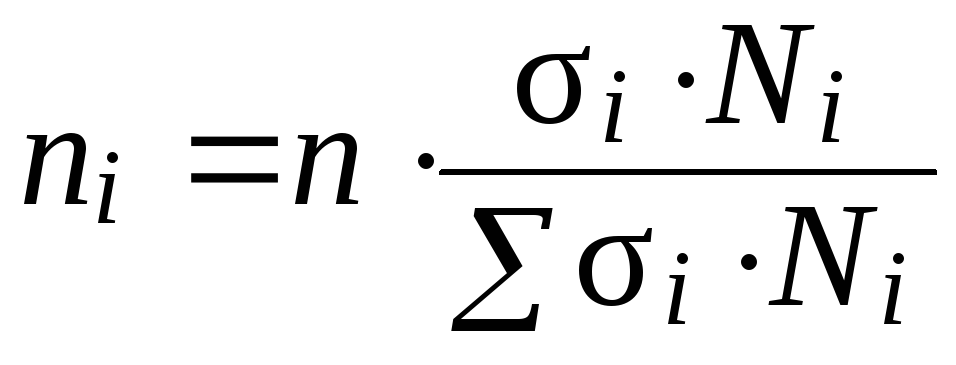

Этот доверительный интервал более полезен, чем просто среднее значение выборки, потому что он дает нам диапазон значений, в который, вероятно, попадает истинное среднее значение генеральной совокупности.

Дополнительные ресурсы

Население и выборка: в чем разница?
Статистика против параметра: в чем разница?
Введение в доверительные интервалы

Среднее значение выборки: определение, формула и значение

Вы собираетесь закончить среднюю школу и решили, что пришло время сменить обстановку, поэтому вы хотите поступить в университет в другом городе, скажем, в Сан-Франциско, Калифорния. . Среди ваших соображений: сколько я буду платить за аренду квартиры или сколько я потрачу на общественный транспорт? Итак, вы решаете спросить своих знакомых, живущих там, сколько они в среднем тратят.

Этот процесс называется получением выборочное среднее , и в этой статье вы найдете определение, как рассчитать выборочное среднее, стандартное отклонение, дисперсию, выборочное распределение и примеры.

Определение среднего значения выборки

Среднее значение набора чисел — это просто среднее значение, то есть сумма всех элементов в наборе, деленная на количество элементов в наборе.

Среднее значение выборки является средним значением, полученным в выборке.

Легко видеть, что если два набора различны, то, скорее всего, они будут иметь разные средние значения.

Расчет среднего значения выборки

Среднее значение выборки обозначается символом \(\overline{x}\) и рассчитывается путем сложения всех значений, полученных из выборки, и деления на общий размер выборки \(n\). Процесс аналогичен усреднению набора данных. Таким образом, формула имеет вид \[\overline{x}=\frac{x_1+\ldots+x_n}{n},\]

, где \(\overline{x}\) — выборочное среднее, \(x_i\) — каждый элемент выборки, а \(n\) — размер выборки.

Вернемся к примеру с Сан-Франциско. Предположим, вы спросили \(5\) своих знакомых, сколько они тратят на общественный транспорт в неделю, и они ответили: \(\20$\), \(\25$\), \(\27$\), \(\43$\ ) и \(\$50\). Таким образом, среднее значение выборки рассчитывается как

\[\overline{x}=\frac{20+25+27+43+50}{5}=\frac{165}{5}=33.\]

Следовательно, для этой выборки среднее сумма, потраченная на общественный транспорт в неделю, составляет \($33\).

Стандартное отклонение и дисперсия выборочного среднего .

2. Вы не знаете стандартное отклонение генеральной совокупности.

В следующем разделе показано, как рассчитать это значение для каждого случая.

Формула среднего и стандартного отклонения для выборочных средних

Среднее значение выборочного среднего, обозначаемое \(\mu_\overline{x}\), определяется средним значением генеральной совокупности, то есть если \(\mu\) среднее значение генеральной совокупности, \[\mu_\overline{x}=\mu.\]

Для расчета стандартного отклонения выборочного среднего (также называемого стандартной ошибкой среднего (SEM) ), обозначаемый \(\sigma_\overline{x}\), необходимо рассмотреть два предыдущих случая. Давайте рассмотрим их по очереди.

Расчет выборочного среднего стандартного отклонения с использованием стандартного отклонения генеральной совокупности выборочное среднее будет дано \[\sigma_\overline{x}=\frac{\sigma}{\sqrt{n}}.\]

Выборка из \(81\) человек была взята из населения со стандартным отклонение \(45\), каково среднее стандартное отклонение выборки?

Ответ:

Используя приведенную выше формулу, стандартное отклонение выборочного среднего равно \[\sigma_\overline{x}=\frac{45}{\sqrt{81}}=\frac{45}{9 }=5.\]

Обратите внимание, что для расчета вам не нужно ничего знать о выборке, кроме ее размера.

Расчет стандартного отклонения выборочного среднего без использования стандартного отклонения совокупности

Иногда, когда вы хотите оценить среднее значение генеральной совокупности, у вас нет никакой информации, кроме данных из взятой вами выборки. К счастью, если выборка достаточно велика (более \(30\)), 92}{n-1}},\]

, где \(x_i\) — каждый элемент выборки, а \(\overline{x}\) — среднее значение выборки.

❗❗ Стандартное отклонение выборки измеряет разброс данных внутри выборки, а среднее стандартное отклонение выборки измеряет разброс между средними значениями из разных выборок.

Если \(\overline{x}\) является средним значением выборки размера \(n\) из совокупности со средним значением \(\mu\) и стандартным отклонением \(\sigma\). Затем выборочное распределение \(\overline{x}\) имеет среднее значение и стандартное отклонение, определяемое как \[\mu_\overline{x}=\mu\,\text{ и }\,\sigma_\overline{x} =\frac{\sigma}{\sqrt{n}}.\]

Кроме того, если распределение населения нормальное или размер выборки достаточно велик (согласно центральной предельной теореме, достаточно \(n\geq 30\)), то выборочное распределение \(\overline{x }\) тоже нормально.

Когда распределение нормальное, вы можете рассчитать вероятности, используя стандартную таблицу нормального распределения, для этого вам нужно преобразовать выборочное среднее \(\overline{x}\) в \(z\)-оценку, используя следующую формулу

\[z=\frac{\overline{x}-\mu_\overline{x}}{\sigma_\overline{x}}=\frac{\overline{x}-\mu}{\frac{\ сигма}{\sqrt{n}}}. \]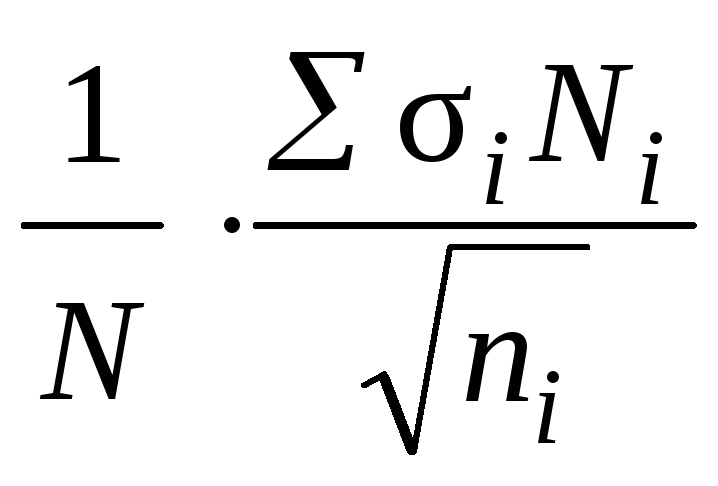

Вам может быть интересно, что происходит, когда распределение населения не является нормальным, а размер выборки мал? К сожалению, для таких случаев не существует общего способа получить форму выборочного распределения.

Давайте посмотрим на пример графика выборочного распределения среднего.

Возвращаясь к примеру с общественным транспортом в Сан-Франциско, предположим, что вам удалось опросить тысячи людей, сгруппировать людей в группы размером \(10\), усреднить их в каждой группе и получить следующий график.

Рисунок 1. Гистограмма относительной частоты 360 выборочных средств для примера общественного транспорта

Этот график аппроксимирует график выборочного распределения среднего значения. Основываясь на графике, вы можете сделать вывод, что в среднем на общественный транспорт в Сан-Франциско тратится \(\$37\).

Примеры выборочных средних

Давайте рассмотрим пример расчета вероятностей.

Предполагается, что распределение температуры тела человека имеет среднее значение \(98. 6\, °F\) со стандартным отклонением \(2\, °F\). Если выборка из \(49\) человек взята наугад, рассчитайте следующие вероятности:

а) средняя температура выборки меньше \(98\), т. е. \(P(\overline{ х<98)\).

(б) средняя температура образца больше \(99\), то есть \(P(\overline{x}>99)\).

(c) средняя температура находится между \(98\) и \(99\), то есть \(P(98<\overline{x}<99)\).

Ответ:

1. Поскольку размер выборки равен \(n=49>30\), можно предположить, что распределение выборки нормальное.

2. Расчет среднего и стандартного отклонения выборочного среднего. Используя формулы, указанные ранее, \(\mu_\overline{x}=98,6\) и стандартное отклонение \(\sigma_\overline{x}=2/\sqrt{49}=2/7\).

3. Преобразовав значения в \(z-\)оценки и используя стандартную нормальную таблицу (дополнительную информацию см. в статье Стандартное нормальное распределение), вы получите для (a):

\[\begin{align} P(\overline{x}<98) &=P\left(z<\frac{98-98.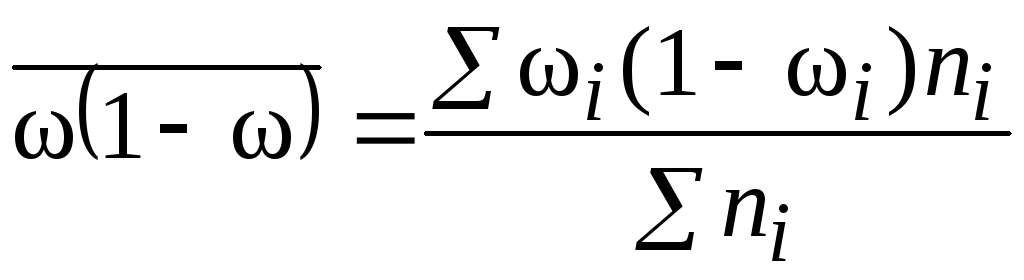 6}{\frac{2}{7}}\right) \\ & = P(z<-2,1) \\ &=0,0179. \end{align}\]

Для (b) у вас будет: \[\begin{align} P(\overline{x}>99) &=P\left(z>\frac{99-98.6} {\ frac{2}{7}}\right) \\ &= P(z>1,4) \\ &=1-P(z<1,4) \\ &=1-0,9192 \\ &= 0,0808. \end{align}\]

Наконец, для (c): \[\begin{align} P(98<\overline{x}<99) &=P(\overline{x}<99)-P( \overline{x}<98) \\ &= P(z<1,4)-P(z<-2,1) \\ &= 0,9192-0,0179\&=0,9013. \end{align}\]

Среднее значение выборки — основные выводы

• Среднее значение выборки позволяет оценить среднее значение генеральной совокупности.
• Выборочное среднее \(\overline{x}\) вычисляется как среднее, то есть \[\overline{x}=\frac{x_1+\ldots+x_n}{n},\], где \(x_i \) — каждый элемент в выборке, а \(n\) — размер выборки.
• Выборочное распределение среднего \(\overline{x}\) имеет среднее значение и стандартное отклонение, заданное формулами \[\mu_\overline{x}=\mu\,\text{ и }\,\sigma_\overline{ x}=\frac{\sigma}{\sqrt{n}}.\]
• Когда размер выборки превышает \(30\), согласно центральной предельной теореме выборочное распределение среднего похоже на нормальное распределение.

Формула среднего значения выборки — GeeksforGeeks

Выборка — это подмножество большей совокупности данных. Формула выборочного среднего используется для получения среднего значения набора выборочных данных. Он определяется как среднее значение измерений выборки. Если выборка выбрана случайным образом, среднее значение выборки может быть использовано для расчета среднего значения генеральной совокупности. Он представляет собой оценку центра данных и используется для определения среднего значения любой совокупности.

Формула среднего значения выборки

Среднее значение выборки для набора данных определяется как сумма всех терминов, деленная на общее количество терминов. Обозначается символом x̄.

x̄ = Σx _i / n

где,

 Σx _i — сумма термов в выборке,

n — количество термов в выборке.

Примеры задач

Задача 1.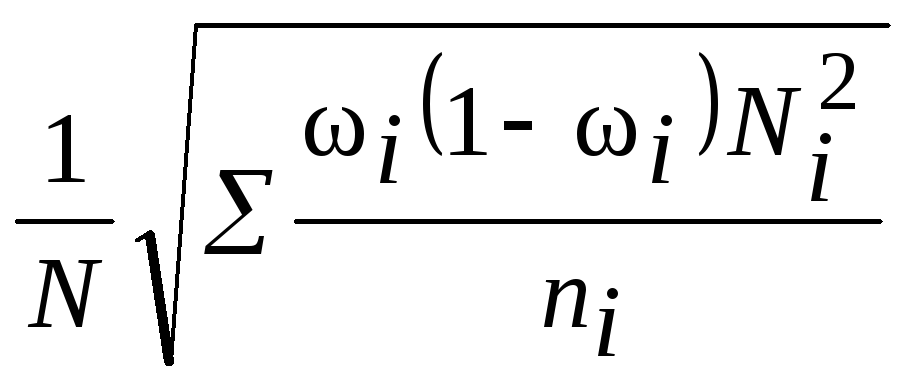 Найти выборочное среднее данных 15, 20, 72, 43 и 21.

Решение:

У нас есть выборка, 15, 20, 72, 43, 21

Сумма слагаемых (S) = 15 + 20+ 72 + 43 + 21 = 171 n) = 5

Используя формулу выборочного среднего, получаем

x̄ = S/n

= 171/5

= 34,2

Задача 2. Найти выборочное среднее данных 13, 31, 27, 72, 16 и 67.

Решение:

У нас есть образец, 13, 31, 27, 72, 16, 67

Сумма членов (S) = 13 + 31+ 27 + 72 + 16 + 67 = 171

Количество членов (n) = 6

Используя формулу выборочного среднего, мы получаем

x̄ = S/n

= 226/6

= 37,66

Проблема 3. Найдите среднее значение данных 42, 53, 92, 31, 56, 110 и 63.

Решение:

Мы. есть образец, 42, 53, 92, 31, 56, 110, 63

Сумма слагаемых(S) = 42 + 53+ 92 + 31 + 56 + 110 + 63 = 447

Число членов (n) = 7

Используя формулу выборочного среднего, получаем

x̄ = S/n

= 447/7

= 63,85

Число членов задачи 4. в выборке, если их сумма и среднее значение равны 132 и 22 соответственно.

Решение:

Имеем S = 132, x̄ = 22

Используя формулу выборочного среднего, получаем > п = 132/22

=> n = 6

Задача 5. Найдите количество терминов в выборке, если их сумма и среднее значение равны 315 и 35 соответственно.

Решение:

Имеем S = 315, x̄ = 35

Используя формулу выборочного среднего, получаем >

n = 315/35

=> n = 9

Задача 6. В классе из 10 учеников данные оценок всех учеников 20, 25, 30, 35, 40, 45, 50, 55, 60, 65. Найдите средние оценки в классе.

Решение:

У нас есть выборка, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65

Сумма слагаемых (S) = 20 + 25 + 30 + 30 + 40 + 45 + 50 + 55 + 60 + 65 = 425

Количество членов (n) = 10

Используя формулу выборочного среднего, получаем

x̄ = S/n

= 425/10

= 42,5

Задача 7.