вычисление двойного интеграла онлайн
Вы искали вычисление двойного интеграла онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление двойных интегралов онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление двойного интеграла онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление двойного интеграла онлайн,вычисление двойных интегралов онлайн,вычислить двойной интеграл онлайн,вычислить двойной интеграл онлайн по области d,вычислить двойной интеграл онлайн с подробным решением,вычислить двойной интеграл по области d онлайн,двойной интеграл в полярных координатах онлайн калькулятор,двойной интеграл калькулятор онлайн,двойной интеграл онлайн,двойной интеграл онлайн калькулятор,двойной интеграл онлайн калькулятор с подробным решением,двойной интеграл онлайн с подробным решением,двойной интеграл онлайн с подробным решением калькулятор,двойной интеграл решить онлайн,двойной интеграл с подробным решением онлайн,двойные интегралы онлайн,двойные интегралы онлайн калькулятор,двойные интегралы онлайн с подробным решением,калькулятор двойного интеграла,калькулятор двойных интегралов,калькулятор двойных интегралов онлайн,калькулятор двойных интегралов с решением,онлайн вычисление двойных интегралов,онлайн калькулятор двойного интеграла,онлайн калькулятор двойной интеграл,онлайн калькулятор двойной интеграл в полярных координатах,онлайн калькулятор двойные интегралы,онлайн калькулятор интегралов двойных,онлайн решение двойного интеграла,онлайн решение двойных интегралов,онлайн решение двойных интегралов с подробным решением,определенный двойной интеграл онлайн,повторный интеграл вычислить,представить двойной интеграл в виде повторного интеграла онлайн,расставить пределы интегрирования в двойном интеграле онлайн,решение двойного интеграла онлайн,решение двойных интегралов онлайн,решение двойных интегралов онлайн с подробным решением,решение онлайн двойного интеграла,решить двойной интеграл онлайн,решить двойной интеграл онлайн с решением,решить интеграл двойной онлайн,решить интеграл онлайн двойной,решить онлайн двойной интеграл.
Решить задачу вычисление двойного интеграла онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Вычисление двойных интегралов: теория и примеры
- Что значит вычислить двойной интеграл?
- Сведение двойного интеграла к повторному
- Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
- x-правильная и неправильная, y-правильная и неправильная области интегрирования
- Смена порядка интегрирования
- Вычисление площади и объёма с помощью двойных интегралов
- Так что же такое двойной интеграл?
Двойные интегралы – это обобщение понятия определённого интеграла для функции двух переменных,
заданной как z = f(x, y).
Записывается двойной интеграл так:
.
Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x, а сверху и снизу – равенствами, в которых слева переменная y. Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.
Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять.
Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому
определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь
отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D.
В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.
Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D, которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.
Случай прямоугольной области:
Случай криволинейной области:
А это
уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы
интегрирования. Выражения, задающие линии, которые ограничивают фигуру D, будут пределами
интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Выражения, задающие линии, которые ограничивают фигуру D, будут пределами
интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Случай прямоугольной области
Пусть для такой функции существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Здесь пределы интегрирования a, b, c, d — числа, о
которых только что упоминалось.
Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 1. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая игрек константой. Пользуемся формулой 7 из таблицы интегралов. Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого), пользуясь для каждого слагаемого той же формулой 7:
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Пользуясь формулой 9 из таблицы неопределенных интегралов, получаем
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Пользуемся формулой 10 из таблицы неопределенных интегралов
и формулой Ньютона-Лейбница для вычисления определенного интеграла:Результат и будет решением данного двойного интеграла.
Случай криволинейной или треугольной области
Пусть снова дана функция двух переменных f(x, y), а ограничения для D: уже несколько другого вида:
.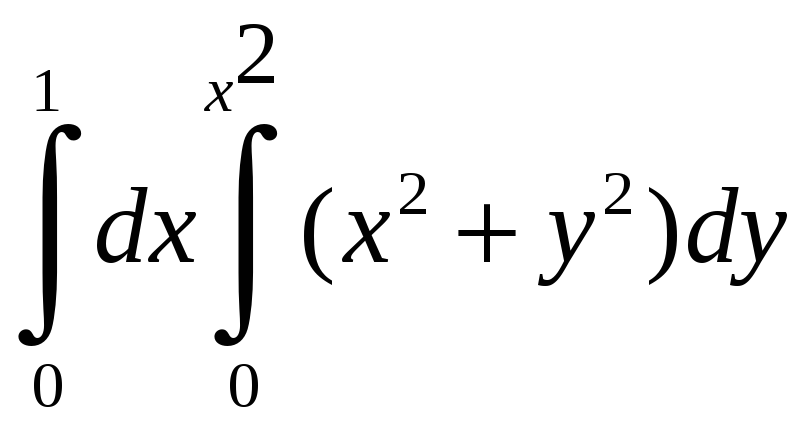
Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b, но снизу и сверху — кривые, которые заданы уравнениями и . Иными словами, и — функции.
Пусть для такой функции также существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Здесь пределы интегрирования a и b — числа, а и — функции. В случае треугольной области одна из функций или — это уравнение прямой линии. Такой случай будет разобран в примере 3.
Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый определённый интеграл.
Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 3. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования и видим, что она треугольная:
Вычисляем внутренний (правый) интеграл, считая икс константой. Пользуясь формулами 6 и 7 из таблицы неопределенных интегралов, получаем
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:
.
Вычисляем первое слагаемое, пользуясь формулой 7 из таблицы неопределенных интегралов:
Вычисляем второе слагаемое, пользуясь все той же формулой:
Вычисляем третье слагаемое, также по формуле 7:
Получаем сумму, которая и будет решением данного двойного интеграла:
.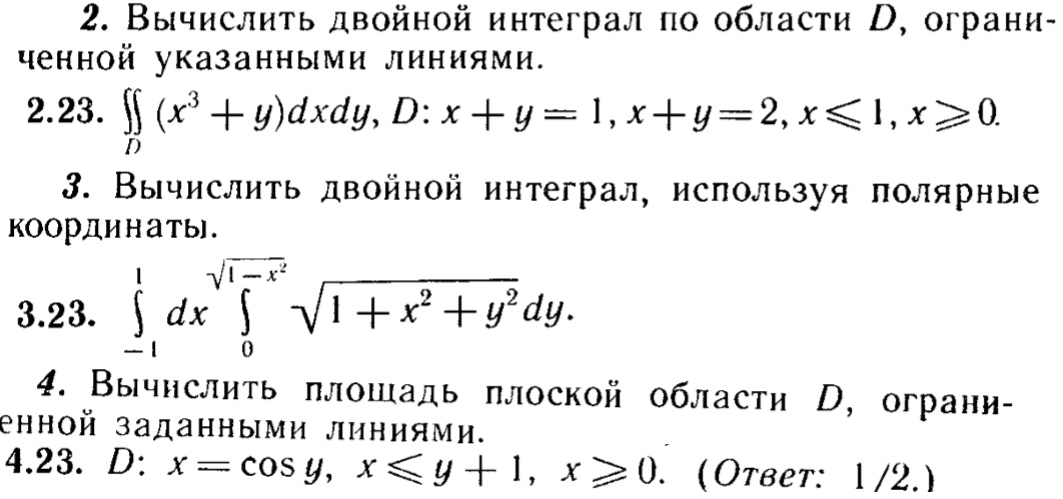
Пример 4. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Пользуясь формулой Ньютона-Лейбница, вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
.
Теперь, пользуясь формулой 7 из таблицы неопределенных интегралов, вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 5. Вычислить двойной интеграл
,
если область D ограничена прямыми
.
Правильное решение и ответ.
Пример 6. Вычислить двойной интеграл
,
если область D ограничена прямыми
.
Правильное решение и ответ.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кратные и криволинейные интегралы
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть
ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y0
пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая,
то область интегрирования называется x-правильной
Если же прямая y = y0
пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая,
то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x, xy = 1, y = 2.
Решение. Область интегрирования является y-неправильной, так как
её нижнюю границу нельзя задать одной линией y = y(x). Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования
на две части — и
.
Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования
на две части — и
.
Вычисляется этот двойной интеграл так:
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Смена порядка интегрирования образно может быть описана следующими словами О’Генри:
«Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки —
человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же:
«Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая
по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера. )
)
Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.
Пример 8. Сменить порядок интегрирования для повторного интеграла
.
Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:
(нижний) и (верхний).
Таким образом, после смены порядка интегрирования повторный интеграл запишется так:
.
После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1, y = 3, x = 0, x = 2y.
При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC, которые
заданы уравнениями y = 1 и y = x/2,
что видно на рисунке ниже.
Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ. Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0, x = 2 и кривыми и .
Как видно на рисунке ниже, прямая, параллельная оси 0x, будет пересекать нижнюю границу области интегрирования более чем в двух точках.
Поэтому разобьём область интегрирования на три части прямыми, которые на
рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для :
Для :
Для :
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем
шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для
разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения
повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый
опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и —
почти на автомате — на разбиении области и опустим само решение.
Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и —
почти на автомате — на разбиении области и опустим само решение.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
y — 2x ≤ 0;
2y — x ≥ 0;
xy ≤ 2.
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.
Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2. Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x).
Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:
.
В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.
Вычисление площади плоской фигуры с помощью двойного интеграла имеет
более универсальный характер, чем вычисление площади криволинейной трапеции с помощью
определённого интеграла. С помощью двойного интеграла можно вычислять площади не
только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к
к координатным осям.
С помощью двойного интеграла можно вычислять площади не
только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к
к координатным осям.
Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1.
Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1, а справа прямой y = 1 — x. (рисунок ниже).
Решая как систему уравнения этих линий, получаем точки их пересечения: . Ординаты этих точек — — 2 и 1 будут соответственно нижним и верхним пределами интегрирования по игреку. Итак, площадь фигуры найдём как двойной интеграл, сведённый к повторному:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Как видим, решение двойного интеграла — отрицательное число. За площадь
данной плоской фигуры принимается модуль этого числа, то есть 4/9.
За площадь
данной плоской фигуры принимается модуль этого числа, то есть 4/9.
Объём криволинейного цилиндра, ограниченного сверху поверхностью , снизу плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси 0z, а направляющей служит контур области, вычисляется также по формуле двойного интеграла. То есть, с помощью двойного интеграла можно вычислять объёмы тел.
Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0, y = 0, z = 0 и x + y + z = 1 (рисунок ниже).
Расставляя пределы интегрирования, получаем следующий повторный интеграл:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Вновь видим, что решение двойного интеграла — отрицательное число. За объём
данного тела принимается модуль этого числа, то есть 1/6.
За объём
данного тела принимается модуль этого числа, то есть 1/6.
Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями . В каждой из этих частей выберем произвольную точку и составим сумму
,
которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании
числа n разбиений области D и стремлении наибольшего из диаметров частичных областей
к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кратные и криволинейные интегралы
Кратные и криволинейные интегралы
- Вычисление двойных интегралов
- Двойные интегралы в полярных координатах
- Вычисление тройных интегралов
- Вычисление криволинейных интегралов
- Интегралы по замкнутому контуру, формула Грина
- Вычисление поверхностных интегралов
Поделиться с друзьями
Калькулятор двойных интегралов с шагами
Содержание
Получите виджет!
Знакомство с интегральным калькулятором Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
Доступно в приложении
Загрузите приложение «Калькулятор потери веса» для своего мобильного телефона.
Гугл игры Магазин приложений
Знакомство с калькулятором двойных интегралов
Вычисление интеграла от многочленов
Включите JavaScript
Вычисление интеграла от многочленов
Калькулятор двойного интеграла — это онлайн-инструмент, который помогает вычислять интегралы в режиме онлайн. Поскольку он оценивает несколько интегралов, он также известен как калькулятор множественных интегралов. Использование интерактивных интеграционных решателей может быть очень полезным, поскольку они предоставляют мгновенные результаты с шагами, графиками и т.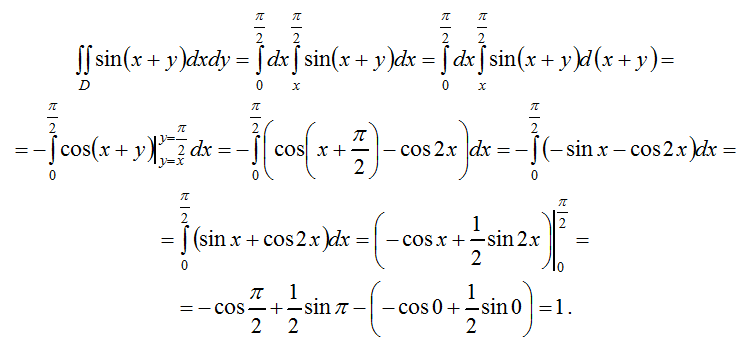 д.
д.
Калькулятор двойных интегралов с шагами вычисляет как кратные определенные интегралы, так и кратные неопределенные интегралы. Простой калькулятор интеграции с шагами не может вычислять несколько целых чисел, поэтому этот калькулятор становится очень полезным.
Дополнительную информацию по теме «Определенные и неопределенные интегралы» можно найти здесь.
Связанный: Как научиться считать неполную дробь за 5 минут.
Символ двойного интегрирования
В исчислении термины представлены в виде специального символа. Символ двойного интегрирования представлен как:
$ \int\int {2}$
Формула, используемая калькулятором двойного интегрирования
Калькулятор двойного интегрирования использует следующие формулы для пошагового расчета результатов: 9{x_2} f(x,y)dx \right) dy{2}$
Также найдите калькулятор Лапласа для расчета преобразования заданной функции производной и калькулятор ряда Фурье для расчета преобразования функции времени в частоту.
Как работает калькулятор двойных интегралов?
Калькулятор двойного интеграла с шагами — это онлайн-калькулятор, который использует формулы двойного интегрирования для вычисления результатов. Поскольку у интеграции есть разные методы, пользователю необходимо выбрать, какой расчет он хочет сделать, т. е. неопределенный или определенный.
После того, как пользователь введет точные значения, калькулятор множественной интеграции с пошаговыми инструкциями мгновенно вычислит результаты. Вы также можете найти калькулятор тройного интегрирования на этом сайте для вычисления тройных определенных интегралов и тройных неопределённых интегралов.
Связанный: Также найдите другие полезные калькуляторы, такие как калькулятор интеграции диска и калькулятор объема тела вращения.
Как найти Калькулятор двойных интегралов?
Есть 2 основных способа найти калькулятор повторных интегралов. Первый включает в себя опцию поиска Google, так как вам нужно искать, набирая название калькулятора полярных интегралов.
Другой способ включает в себя систему навигации, так как вы можете найти любой или наш калькулятор двойных интегралов с шагами и перейти оттуда к калькулятору двойных интегралов. Таким образом, вы также можете найти калькулятор определенных интегралов или калькулятор неопределённых интегралов на этом веб-сайте.
Как пользоваться Калькулятором двойной интеграции?
Калькулятор множественных интегралов или калькулятор двойных интегралов очень прост в использовании. Вам просто нужно выполнить шаги для вычисления нескольких интегралов:
Шаг 1. Несколько раз введите функцию, которую вы хотите интегрировать.
Шаг 2. Выберите тип Определенный или Неопределенный.
Шаг 3. Выберите переменные в решателе двойных интегралов.
Шаг 4. Укажите верхний и нижний пределы переменной x. Если вы выбрали определенный вариант.
Шаг 5. Укажите верхний и нижний пределы переменной y. Если вы выбрали определенный вариант.
Шаг 6. Нажмите кнопку «РАСЧИТАТЬ», чтобы получить пошаговые точные результаты.
Часто задаваемые вопросы
Двойной интеграл объема или площади?
Двойной интеграл — это способ определения площади поверхности двумерной формы. Мы можем найти площадь прямоугольной области, используя двойной интеграл. Двойной интеграл обозначает площадь поверхности формы в двух измерениях, а тройной интеграл — это объем объекта в трех измерениях.
Для чего используется двойной интеграл?
Двойной интеграл используется для вычисления площади поверхности формы в двух измерениях. Это означает, что нам нужно интегрировать два раза, чтобы получить площадь поверхности. При решении интегралов используются правила интегрирования.
Что такое эквивалентный двойной интеграл с обратным порядком интегрирования?
Обратный порядок интегрирования — это метод перестановки верхнего и нижнего пределов интеграла. Это упрощает интеграцию функции. Например, если у вас есть регион indydx, вы можете изменить его на dxdy вместе с изменением верхнего и нижнего пределов.
В чем разница между двойным интегралом и поверхностным интегралом?
Двойной интеграл используется для вычисления интеграла плоской формы в двух измерениях. Принимая во внимание, что поверхностный интеграл используется для вычисления интеграла криволинейной поверхности в двух измерениях. Иногда двойной интеграл также может быть записан как поверхностный интеграл, и мы можем вычислить его с помощью решателя двойного интегрирования, описанного выше.
Что такое повторный двойной интеграл?
Двойной интеграл также называют повторным двойным интегралом. Это связано с тем, что функция должна быть интегрирована по двум переменным, то есть x и y. Сначала мы вычисляем интеграл по одной переменной, затем по другой. Вы также можете вычислить это с помощью калькулятора повторного интеграла.
Может ли двойной интеграл быть отрицательным?
Да, двойной интеграл функции может быть отрицательным. Но если функция отрицательна, то его можно считать томом со знаком. Но объем и площади не отрицательны.
Но объем и площади не отрицательны.
Можно ли разделить двойной интеграл?
Да, двойной интеграл можно разбить на повторные интегралы. Интегралы можно разбить по задействованным переменным. Например, в следующем интеграле мы можем разделить его на две части.
∫ f(x) dxdy = ∫ f(x) dx + ∫ f(x) dy
Для консолидации ваших расчетов относительно цилиндрических оболочек используйте интегральный калькулятор метода оболочек. Вы также можете узнать больше о цилиндрических оболочках, объемах тел вращения, прочитав последние статьи в разделе блога.
Алан Уокер
Последнее обновление: 3 дня назад
Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.
Калькулятор двойных интегралов | Быстро и просто
Калькулятор двойных интегралов
г 2
↘︎
↗︎
y 1
x 2
↙︎
↖︎
7 x
1 dxdyКак пользоваться этим калькулятором
Решение
Вернуться к калькулятору
Заполните поля ввода для вычисления решения.
Хотите неограниченный доступ к калькуляторам, ответам и шагам решения?
Присоединяйтесь
100% без риска. Отменить в любое время.
Двойной интегральный урок
Что такое двойной интеграл?
Двойной интеграл — это кратный интеграл функции двух переменных. Он называется двойным интегралом, потому что мы должны выполнить определенный интеграл два раза (по одному для каждой из двух переменных).
Для лучшего понимания давайте сравним одинарные интегралы и двойные интегралы:
- Единственный интеграл функции одной переменной, такой как y = f(x) , решает для области под двумерной кривой функции.
- Двойной интеграл функции двух переменных, такой как z = f(x, y) решает для объема под трехмерной поверхностью функции.
 Прямоугольное сечение объема (если смотреть сверху) определяется пределами интегрирования x 9{x_{2}} f(x, y) \; dx\hspace{1pt} dy \end{align}$$
Прямоугольное сечение объема (если смотреть сверху) определяется пределами интегрирования x 9{x_{2}} f(x, y) \; dx\hspace{1pt} dy \end{align}$$Где x 1 — нижний предел интегрирования x , x 2 — верхний предел интегрирования x , y 1 — нижний предел интегрирования y , y 2 — верхний предел интегрирования y , f(x, y) — функция 5y 51 1 х и , dx указывает на интегрирование переменной x и dy указывают на интегрирование переменной y .
Почему мы учимся решать двойные интегралы?
Двойные интегралы имеют множество применений в инженерии, науке и статистике. Но давайте остановимся только на одном из этих приложений: мы можем использовать двойной интеграл для оптимизации эффективности двигателя серийного автомобиля, чтобы он мог потреблять меньше топлива во время работы .
Большинство современных автомобилей используют компьютеры для управления двигателями. Этот компьютер, часто называемый ЭБУ (блок управления двигателем), управляет подачей воздуха в двигатель, впрыском топлива в двигатель и воспламенением воздушно-топливной смеси внутри камеры сгорания.
Точное время воспламенения воздушно-топливной смеси крайне важно для эффективности сгорания. При слишком раннем воспламенении в цикле двигателя воздушно-топливная смесь не будет достаточно сжата для полного сгорания. Если зажечь слишком поздно, топливовоздушная смесь не успеет полностью сгореть.
Мы можем провести тесты двигателя и собрать данные об эффективности сгорания, являющейся функцией оборотов двигателя (оборотов в минуту) и угла опережения зажигания. Если мы построим данные, мы увидим поверхностный график функции с двумя переменными, как показано ниже:
Поверхностный график функции эффективности сгорания двигателя. Поскольку мы смоделировали КПД двигателя как функцию двух переменных (обороты двигателя и угол опережения зажигания), мы можем легко вычислить двойной интеграл по прямоугольной области оборотов двигателя — плоскости угла опережения зажигания.
Вычисляя этот двойной интеграл, мы находим общий объем между поверхностью и оборотами двигателя — плоскость опережения зажигания, ограниченная выбранной нами прямоугольной областью.
Мы можем разделить этот объем на площадь нашей прямоугольной области. Таким образом, мы получим среднее значение функции эффективности сгорания по этой прямоугольной области. 9{2} у\вправо)\; = \;2 y-\left(\frac{1}{2}\right) y\\ \\ & \hspace{15ex}2 y-\left(\frac{1}{2}\right) y\ ; «=» \boxed{\left(\frac{3}{2}\right) y}\\ \\ \\ & \hspace{2ex} \text{2) Теперь, когда мы решили внутреннюю часть интеграла,} \ \ & \hspace{4ex} \text{мы можем подставить его результат во внешнюю часть интеграла} \\ & \hspace{4ex} \text{и затем решить это для окончательного ответа.}\\ \\ & \ hspace{5ex} \text{2.1) Наш исходный полный интеграл (с внешней частью в рамке)} \\ & \hspace{9{2} \влево(ху\вправо) \; dx\hspace{1pt} dy\; = \;\frac{21}{4} = 5,2500}}\end{align}$$
Калькулятор двойных интегралов написан на HTML (язык гипертекстовой разметки), CSS (каскадные таблицы стилей) и JS (JavaScript).
