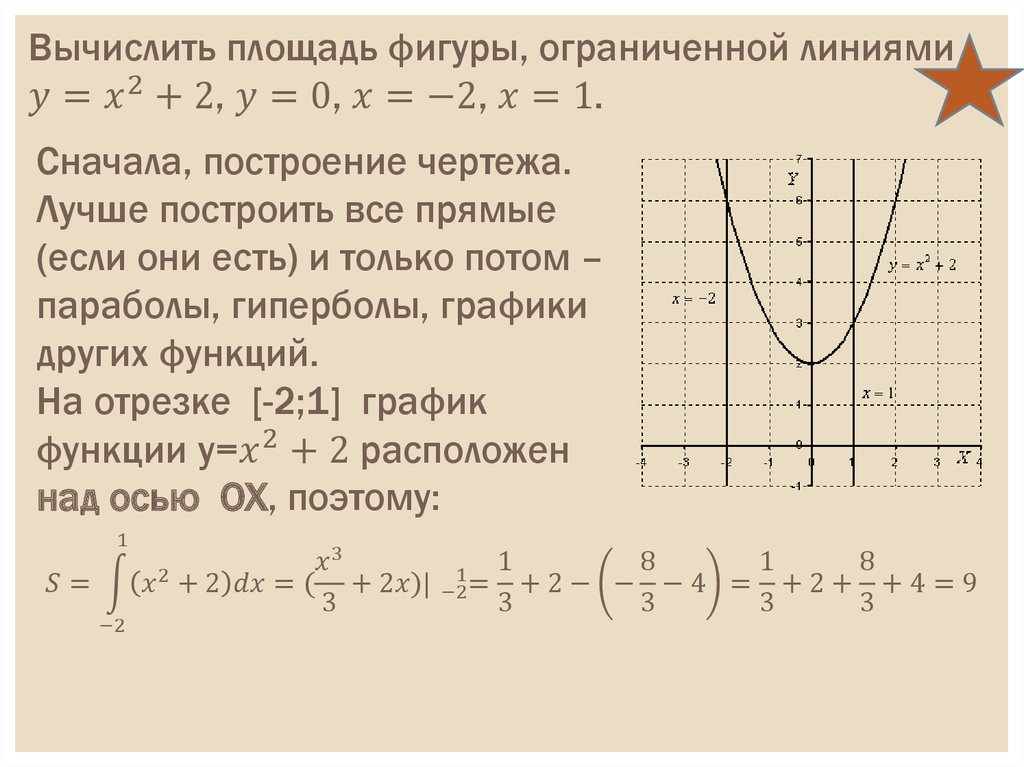
Двойной интеграл. Пределы интегрирования
Двойные интегралы используют в математике, механике, физике. С его помощью можно решить огромное количество непростых задач. Ниже приведено 10 примеров на двойные и тройные интегралы, которые в значительной степени облегчат подготовку к контрольной работе или экзамену. Примеры взяты из индивидуальной работы по высшей математики.
ВАРИАНТ — 12
ЗАДАНИЕ 1.18 Изменить порядок интегрирования в двойном интеграле:
Решение: Сначала записываем область интегрирования, которая ограничена границами
где y=2/x — гипербола.
y=-x2-4x-3 — парабола с вершиной в точке S (-2;1), ветками вниз.
Чтобы знать, как расставить пределы интегрирования при изменении порядка интегрирования изобразим область интегрирования на плоскости
Выражаем полученные функции через переменную y:
y=2/x, отсюда x=2/y; y=-x2-4x-3, отсюда , перед радикалом стоит знак «+» поскольку часть параболы находится в правой (положительной по x=-2) части полуплоскости.
Из рисунка видим, что при изменении порядка интегрирования область необходимо разделить на три части: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
Изменяем порядок интегрирования функции
Как видите ничего сложного нет, главное представлять график функции и иметь точки их пересечения — пределы интегрирования.
ЗАДАНИЕ 2.19 Найти площадь плоской фигуры, заданной следующими условиями, : y=2x, y=5, 2x-2y+3=0.
Решение: Прежде всего выполняем построение всех кривых, чтобы видеть как будут изменяться пределы интегрирования
Дальше найдем точки пересечения графиков заданных функций :
1 и 2
отсюда
Дальше точки пересечения 2 и 3 функций
отсюда
Напоследок пересечение 1 и 3 ф-й
отсюда
Заданную область будем разбивать на две области: D=D1+D2.
Расставим пределы для каждой из областей:
Через двойной интеграл находим площадь фигуры которая ограничена заданными кривыми, :
Функции не тяжелые для интегрирования, поэтому в предпоследнем выражении подставьте пределы самостоятельно.
При округлении площадь криволинейной трапеции равна 2,037 единиц квадратных.
ЗАДАНИЕ 3.20 Найти двойной интеграл по области D, ограниченной указанными линиями: D: y=x2-1, y=3.
Решение: Найдем точки пересечения графиков заданных функций: y=x2-1 и y=3:
3=x2-1, x2-4=0, (x-2)(x+2)=0, x=-2; x=2.
Параболу и прямую изобразим графически
Расставим пределы интегрирования в заданной области D:
Вычислим двойной интеграл по области которая ограничена параболой и прямой:
Определенный интеграл равен I=224/15=14,9 (3).
ЗАДАНИЕ 4.21 Найти двойной интеграл, используя полярные координаты:
Решение: Построим область интегрирования, которая ограничена кривыми
где y=R2— x2, x2+y2=R2
Получили круг с центром в точке O (0;0) и радиусом R (нижняя половина).
Используя замену переменных
перейдем к полярной системе координат (СК).
При этом подынтегральную функцию следует умножить на якобиан перехода, который находим через определитель из производных:
Перепишем подинтегральную функцию в полярной СК :
Пределы интегрирования при переходе к полярной системе координат изменятся на следующие:
Вычислим двойной интеграл:
Он равен I=Pi/4*sin (R2).
ЗАДАНИЕ 5.22 Вычислить площадь области D, ограниченной указанными линиями: D: x3=3y, y2=3x.
Решение: Найдем точку пересечения двух графиков : x1=0, y1=0; x2=3, y2=3.
Графики кривой в декартовой системе координат имеет вид
Расставим пределы интегрирования в области D:
Найдем площадь криволинейной трапеции которая ограничена указанными линиями:
Площадь равна 3 единицы квадратные.
ЗАДАНИЕ 6.23 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)3=4a2xy (x2-y2).
Решение: Сначала построим чотирёх лепесток
Перейдем к полярной системе координат:
Якобиан перехода из предыдущих примеров равен I=r.
Найдем пределы интегрирования в новой системе координат
Переменные приобретают значение:
Расставляем пределы интегрирования в двойном интеграле, таким образом найдем четверть площади плоской фигуры.
Дальше результат умножим на 4:
Площадь равна S=a2 единиц квадратных.
Внимательно проанализируйте как определять пределы интегрирования. Это тяжелее всего, что может быть в подобных задачах.
Как вычислить определенный интеграл, как правило, должны знать все студенты. Здесь лишь расширяется его приложение.
Тройной интеграл
ЗАДАНИЕ 8.25 Расставить пределы интегрирования в тройном интеграле , если область V ограничена указанными поверхностями: V: x=2 y=3x, z=4 (x2+y2).
Нарисовать область интегрирования.
Решение: Уравнение поверхности в пространстве z=4 (x2+y2) — эллиптический параболоид.
График параболоида и проекция в декартовую плоскость тела имеют вид
Пределы интегрирования расставим следующим образом:
V:
Расставляем пределы интегрирования в соответствии с областью
ЗАДАНИЕ 9.6 Вычислить тройные интегралы:
где V:
Решение: Выполним построение области интегрирования
Заданная область V является параллелепипедом, поэтому без трудностей расставляем пределы интегрирования и от внутреннего к внешнему находим интеграл
Вычисления не сложны, поэтому превращение в формуле проанализируйте самостоятельно.
ЗАДАНИЕ 10.7 Используя тройной интеграл, вычислить объем тела : где z=x2, x — 2y+2=0, x+y=7 .
Нарисовать область интегрирования.
Решение: Забегая наперёд, изобразим тело и его проекцию
Это поможет определить пределы интегрирования
С помощью тройного интеграла вычисляем объём тела, ограниченного поверхностями, :
Определенные интегралы не тяжелые, после их нахождений имеем объём 32 единицы кубические.
На этом расчетная работа по высшей математике решена.
Больше примеров на применение интеграла ищите на страницах сайта.
Если трудно решить контрольную работу или индивидуальное задание — обращайтесь за помощью!
Вариант № 21
№ 1. Для данного повторного интеграла написать уравнения кривых, ограничивающих области
интегрирования, вычертить эти области и поменять порядок интегрирования:
.
№ 2. Расставить пределы интегрирования в том и другом порядке в двойном интеграле
, если D – ромб O (0, 0), A (2, 1), B (4, 0), C (2, –1).
№ 3. Вычислить массу пластины D с поверхностной плотностью ,
D : треугольник O (0, 0), A (2, 1), B (2, –1).
№ 4.
.
№ 5. Переходя к полярным координатам вычислить интеграл по области D, ограниченной
заданными линиями: .
№ 6. Найти площадь фигуры, ограниченной линиями: .
№ 7. Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями:
.
№ 8. Найти площадь части поверхности – плоскость , вырезанной поверхностью
– координатные плоскости .
№ 9. Для данного интеграла написать уравнения поверхностей, ограничивающих область
интегрирования, и вычертить эту область: .
№ 10. Вычислить , если .
№ 11.
Вычислить ,
сведением к однократному и двойному
интегралам:
.
№ 12. Вычислить тройной интеграл , перейдя к цилиндрическим координатам:
.
№ 13. Вычислить тройной интеграл , перейдя к сферическим координатам:
.
№ 14. Найти момент инерции относительно оси OX тела, ограниченного данными поверхностями,
полагая , где — объёмная плотность тела: .
№ 15. Вычислить криволинейный интеграл 1-го рода по ломаной ABC:
.
№ 16. Вычислить криволинейный интеграл 1-го рода:
.
№ 17. Вычислить криволинейный интеграл второго рода по кривой
между точками .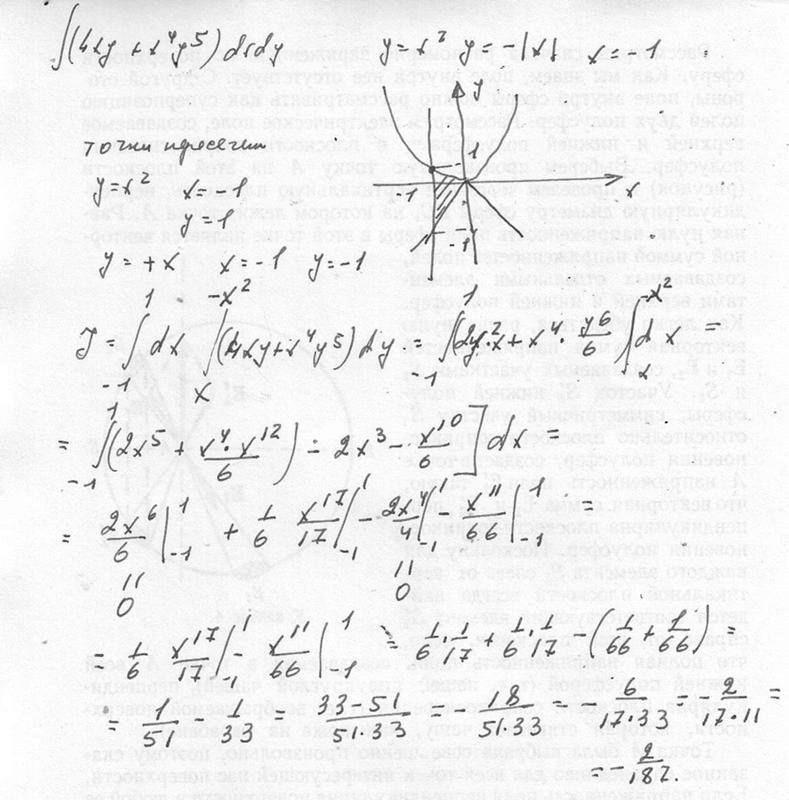
№ 18. Вычислить криволинейный интеграл второго рода по линии .
№ 19. Найти длину линии .
№ 20. Вычислить криволинейный интеграл между точками A(0, 0) и B по различным путям интегрирования C1 (отрезок AB) и C2 : и обосновать полученные результаты, используя условие независимости криволинейного интеграла от пути интегрирования.
№ 21. Вычислить криволинейный интеграл , применив формулу Грина (обход контура составляет область, ограниченную контуром, слева).
ТИПОВОЙ РАСЧЁТ (ДВОЙНЫЕ, ТРОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ)
№ 1. Для данного повторного интеграла написать уравнения кривых, ограничивающих области
интегрирования, вычертить эти области и поменять порядок интегрирования:
.
№ 2. Расставить пределы интегрирования в том и другом порядке в двойном интеграле
, если D – параллелограмм A (–3, 4), B (0, 4), C (4, 0), D (1, 0).
№ 3. Вычислить массу пластины D с поверхностной плотностью
.
№ 4. Вычислить двойной интеграл по области
.
№ 5. Переходя к полярным координатам вычислить интеграл по области D, ограниченной
заданными линиями: .
№ 6. Найти площадь фигуры, ограниченной линиями: .
№ 7. Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями:
.
№ 8. Найти площадь части поверхности – плоскость , вырезанной поверхностью
– координатные плоскости .
№ 9. Для данного интеграла написать уравнения поверхностей, ограничивающих область
интегрирования, и вычертить эту область: .
№ 10. Вычислить , если .№ 11. Вычислить , сведением к однократному и двойному интегралам:
.
№ 12. Вычислить тройной интеграл , перейдя к цилиндрическим координатам:
.
№ 13. Вычислить тройной интеграл , перейдя к сферическим координатам:
.
№ 14. Найти момент инерции относительно оси OX тела, ограниченного данными поверхностями,
полагая
,
где
— объёмная плотность тела: .
№ 15. Вычислить криволинейный интеграл 1-го рода по ломаной ABC:
.
№ 16. Вычислить криволинейный интеграл 1-го рода:
.
№ 17. Вычислить криволинейный интеграл второго рода ;
прямая от .
№ 18. Вычислить криволинейный интеграл второго рода по линии
.
№ 19. Найти длину линии .
№ 20. Вычислить
криволинейный интеграл между точками A и B(0,
1), O(0,
0) по различным
путям интегрирования C1 (отрезок AB)
и C2 : ломаная ABC и обосновать полученные результаты,
используя условие независимости
криволинейного интеграла от пути
интегрирования.
№ 21. Вычислить криволинейный интеграл , применив формулу Грина (обход контура составляет область, ограниченную контуром, слева).
ТИПОВОЙ РАСЧЁТ (ДВОЙНЫЕ, ТРОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ)
интегрирование — Нахождение интеграла по области, ограниченной 4 кривыми
Задавать вопрос
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 2к раз
$\begingroup$ 9{-xy/2} dydx$$
Однако мне не удалось вычислить это числовое значение. Обычно я бы использовал строго числа, а не переменные для границ самого внешнего интеграла, но если вы нарисуете кривую, я почти уверен, что вы не получите правильную область, если у самого внешнего интеграла есть числовые границы.
Редактировать: Я упустил из виду тот факт, что есть 2 области, ограниченные этими кривыми равной площади. Я только хочу интегрировать ограниченную область в первом квадранте.
- интеграция
- многомерное исчисление
- повторные интегралы
$\endgroup$
8
$\begingroup$
Для наиболее эффективного вычисления этого интеграла лучше переключиться на новые переменные, которые лучше отражают область интегрирования (и не испортят подынтегральную функцию). Вот набросок решения. 9{-2}\справа)\ln8.$$
$\endgroup$
3
$\begingroup$
Вот график, показывающий одну из двух идентичных областей, ограниченных этими графиками:
Где красная кривая — $y=2x$, синяя — $y=\frac{x}{4}$, зеленая это $y=\frac{4}{x}$, а желтый — это $y=\frac{1}{x}$.
Для вычисления площади можно найти сумму площадей $A_1, A_2,$ и $A_3$, где $A_1$ — площадь между красной и желтой кривыми от пересечения желтой и красной кривых до пересечения красная и зеленая кривые, $A_2$ — площадь между зеленой и желтой кривыми от пересечения красной и зеленой кривых до пересечения желтой и синей кривых, а $A_3$ — площадь между зеленой и синей кривыми от пересечения синей и желтой кривых до пересечения зеленой и синей кривых. Давайте посчитаем их по одному. 92}{8})$$
$$A_3=8\ln 2 -\frac{16}{8}-4\ln 2 +\frac{4}{8}$$
$$A_3=4\ln 2 -\frac{3}{2}$$
Теперь у нас есть все три площади, осталось только найти их сумму. Вся площадь $A$ равна
$$А=А_1+А_2+А_3$$
$$A=\frac{3}{2}-\ln 2+\frac{3}{2}\ln2+4\ln 2 -\frac{3}{2}$$
$$A=\frac{3}{2}\ln2+3\ln 2$$
$$A=\frac{9}{2}\ln2$$
Какой должен быть окончательный ответ. Это верно?
$\endgroup$
3
Двойные интегралы и площадь
Повторные интегралы и площадь
Определение повторного интеграла
Точно так же, как мы можем найти частную производную, рассматривая только одно из
переменные истинная переменная и сохраняя остальные переменные постоянными, мы можем
возьмем «частный интеграл».
Мы указываем, что верно
переменной, написав «dx», «dy» и т. д. Также как и в случае
частные производные, мы можем взять два «частных интеграла», взяв один
переменная за один раз. На практике мы сначала возьмем x, а затем y или y.
сначала потом х. Мы называем это повторный интеграл или
двойной интеграл .
Определение двойного интеграла Пусть f(x,y) быть функцией двух переменных, определенных в области R, ограниченной снизу, и выше на у = г 1 (х) и г = г 2 (х) и влево и вправо по х = а и х = б , то двойной интеграл (или повторный интеграл) от f(x,y) над R определяется |
Пример
Найдите двойной интеграл f(x,y)
= 6x 2 + 2y над R, где
R — регион
между y = x 2 и у
= 4.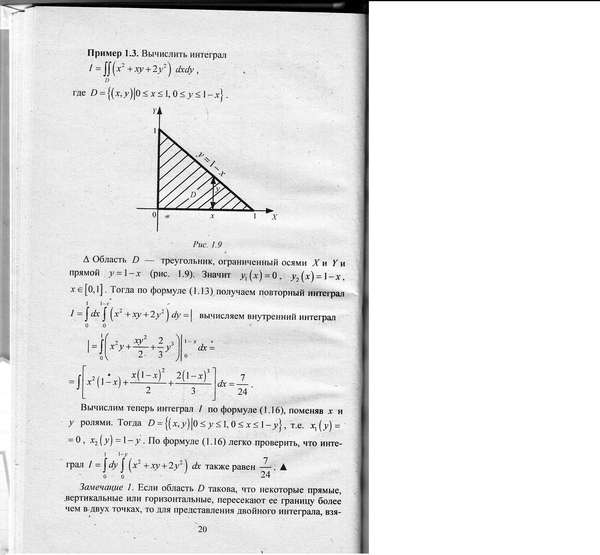
Раствор
Во-первых, мы имеем, что внутренние пределы интегрирования равны x 2 и 4. Область ограничена слева x = -2 и справа на x = 2, как показано на рисунке ниже.
Теперь мы интегрируем
Изменение порядка интегрирования
Если область ограничена слева x = h 1 (y) а справа на x = h 2 (y) и ниже и выше на y = c и y = d, то мы можем найти двойной интеграл от «dxdy», сначала интегрируя по отношению к x, то относительно y. Иногда нужно сделать выбор, интегрировать ли его в первую очередь. по x, а затем по y. Мы делаем все, что Полегче.
Пример
Найдите двойной интеграл f(x,y) = 3y над треугольником с вершинами (-1,1), (0,0), и (1,1).
Раствор
Если
мы пытаемся сначала интегрироваться в отношении y, нам придется разрезать регион на
две части и выполнить два повторных интеграла.
Вместо этого мы интегрируем с
сначала по отношению к х. Область ограничена слева и справа x
= -y и x = y.
Наименьшее значение, которое получает регион, равно y = 0.
а самый высокий y = 1.
Интеграл равен
Пример
Оценить интеграл
Раствор
Попробовать как ни крути, ты не найдешь первообразной и мы не хотим получить в Power Series расширения. У нас есть другой выбор. на картинке ниже показан регион.
Мы можно переключать порядок интегрирования. Область ограничена сверху и снизу на y = 1/3 x и y = 0. Двойной интеграл по y сначала, а затем относительно x равно
Подынтегральная функция является константой относительно y, поэтому мы получаем
.Это интеграл можно выполнить с помощью простой u-подстановки.
и = х 2 дю = 2x дх
и интеграл становится
Зона
Вызов из расчета за первый год, если область R ограничен снизу величиной y = g 1 (x) и выше на y = g 2 (x), и < x < б, площадь указана как
Там
это еще один способ получить это выражение.
Если мы допустим подынтегральную функцию
1, то двойной интеграл по области R
Это дает нам еще один способ определения площади.
Теорема: площадь и двойник Интегралы Если регион R ограничен снизу y = г 1 (х) и выше на y = g 2 (x), и 90 223 < 90 224 х < Ь, тогда площадь указана как |
Примечание: Если область ограничена слева x = h 1 (y) а справа ч 2 (у) с в < y < d, то двойной интеграл от 1 dxdy можно также можно использовать для нахождения площади.
Пример
Установите двойной интеграл, который дает площадь между y
= х 2 и у
= х 3 . Затем с помощью компьютера или калькулятора
оценить этот интеграл.