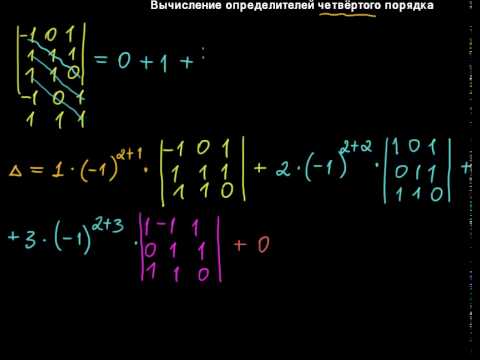Вычислить определитель 4 го порядка: Определитель матрицы онлайн

Содержание

Определение четвертого порядка. Определитель матрицы

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».

Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется

МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ; detA (детерминант).

Пример:
.

Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу

Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.

В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.

Пример:

Разложение определителя по элементам некоторой строки (столбца).

Минором М ij элемента а ij квадратной матрицы А называется определитель, составленный из элементов матрицы А , оставшихся после вычеркивания i- ой строки и j -го столбца.

Например, минором к элементу а 21 матрицы третьего порядка
будет определитель
.

Будем говорить, что элемент а ij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) — четное число, нечетное место, если i+j — нечетное число.

Алгебраическим дополнением А ij элемента а ij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).

Пример:

а 23 = 4;

— алгебраическое дополнение элемента а 22 = 1.

Теорема Лапласа . Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

Проиллюстрируем на примере определителя третьего порядка. Вычислить определитель третьего порядка разложением по первой строке можно следующим образом

Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.

Пример :

Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы

n -го порядка, сводя его к вычислению n определителей (n-1 )-го порядка

Замечание. Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.

Пример . Вычислить определитель четвертого порядка.

Разложим определитель по элементам третьей строки

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.

5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.

Пусть имеется квадратная матрица A размером n x n .
Определение. Определителем называется алгебраическая сумма всевозможных произведений элементов, взятых по одному из каждого столбца и каждой строки матрицы A . Если в каждом таком произведении (члене определителя) множители расположены в порядке следования столбцов (т.е. вторые индексы элементов a ij в произведении расположены в порядке возрастания), то со знаком (+) берутся те произведения, у которых перестановка первых индексов чётная, а со знаком (-) – те, у которых она нечетная.
.
Здесь — число инверсий в перестановке индексов i 1 , i 2 , …, i n .

Методы нахождения определителей

Определитель матрицы разложением по строкам и столбцам через миноры.
Определитель методом приведения к треугольному виду (методом Гаусса)

Свойство определителей

При транспонировании матрицы её определитель не меняется.
Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
Пусть C = AB где A и B квадратные матрицы. Тогда detC = detA ∙ detB .
Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен 0. Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
Определитель с двумя пропорциональными строками или столбцами равен 0.
Определитель треугольной матрицы равен произведению диагональных элементов. Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали.
Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.
Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
Теорема Якоби: Если к элементам некоторого столбца определителя прибавить соответствующие элементы другого столбца, умноженные на произвольный множитель λ, то величина определителя не изменится.

Таким образом, определитель матрицы остается без изменения, если:

транспонировать матрицу;
прибавить к какой-либо строке другую строку, умноженную на любое число.

Задание 1 . Вычислить определитель, разлагая его по строке или столбцу.
Решение :xml :xls
Пример 1 :xml :xls

Задание 2 . Вычислить определитель двумя способами: а) по правилу «треугольников»; б) разложением по строке.

Решение .
а) Слагаемые, входящие в со знаком «минус», строятся таким же образом относительно побочной диагонали.

2	2	1
-1	0	4
-2	2	0

= 2 0 0 — 2 4 2 — (-1) 2 0 + (-1) 1 2 + (-2) 2 4 — (-2) 1 0 = -34
б) Запишем матрицу в виде:

A =

2	2	1
-1	0	4
-2	2	0

Главный определитель:
∆ = 2 (0 0-2 4)-(-1 (2 0-2 1))+(-2 (2 4-0 1)) = -34

Задание 3 . Укажите, чему равен определитель квадратной матрицы A четвертого порядка, если ее ранг r(A)=1.
Ответ: det(A) = 0.

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи , то решайте их .»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

С каждой квадратной матрицей связывают число . Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A , ΔA.

Число строк (столбцов) определителя называется его порядком .

Определитель первого порядка матрицы равен элементу a 11: |A|=a 11

Не путать определитель первого порядка с модулем.

Определитель второго порядка обозначается символом

и равен |A|=a 11 a 22 -a 12 a 21

Определитель 3-го порядка обозначается символом

Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса )

Правило Саррюса.

Правило треугольника.

Посмотрим на примере, как используются эти правила.

ПРИМЕР:

Правило Саррюса

Допишем к определителю два первых столбца.

Правило треугольника

Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.

Алгебраическим дополнением (А ij ) элемента а ij определителя матрицы А называется число, равное произведению (-1) i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.

ПРИМЕР:

Вычислить алгебраическое дополнение А 21 элемента а 21 .

РЕШЕНИЕ:

По определению алгебраического дополнения

Вычисление определителя произвольного порядка. Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.

, разложение определителя 4-го порядка по первой строке выглядит следующим образом:

Основные методы вычисления определителей n-го порядка

На первом уроке мы с вами научились вычислять определители 2-го и 3-го порядка. На предыдущем уроке мы познакомились с определителями n-го порядка. Сегодня мы научимся вычислять определители n-го порядка разными методами.

Метод понижения порядка

Данный метод основан на следующем соотношении (i-фиксировано):

, где (1)

(2)

называется алгебраическим дополнением элемента и представляет собой определитель (n-1)-го порядка, получающийся из исходного определителя вычеркиванием i-й строки и k-го столбца, на пересечении которых стоит элемент .

Соотношение (1) называется разложением определителя по i-й строке. Аналогично определяется разложение по столбцу.

Прежде чем применять метод понижения порядка желательно, используя основные свойства определителя, обратить в нуль все, кроме одного, элементы его некоторой строки (столбца).

Пример №1 Вычислить определитель матрицы 4-го порядка.

(Кликните по картинке, чтобы увеличить)

1 действие: Из первой строки вычтем удвоенную третью, а ко второй строке прибавим удвоенную третью.

2 действие: Полученный определитель разложим по первому столбцу (вычеркнем первый столбец и третью строку) и не забываем домножить на «4» и на , где i — номер вычеркнутого столбца, а k — номер вычеркнутой строки.

3 действие: Ко второй строки прибавим умноженную на 10 первую строку, а к третьей строке прибавим умноженную на 4 первую строку.

4 действие: Полученный определитель разложим по первому столбцу (вычеркиваем первую строку и первый столбец) и не забываем домножить на «-1».

5 действие: вычисляем определитель второго порядка

Ответ: -1800

Данный способ очень простой, если вникнуть, в конце урока дам еще парочку заданий потренируетесь и поймете, что данный способ лучше других, хотя, возможно, вам подойдут и другие.

Если остались вопросы, пишите в комментариях.

Метод приведения к треугольному виду

Данный метод заключается в таком преобразовании определителя, когда все элементы, лежащие по одну сторону из его дополнений, становятся равными нулю.

Пример №2 Вычислить определитель 4-го порядка

Сделаем пример попроще:

1 действие: Из 2, 3 и 4 строки вычтем первую строку

2 действие: перемножить числа, расположенные по диагонали

Ответ: -8

Данный способ тоже простой, но и не забывайте, что пример также очень простой, с другими числами будет посложнее, но если вникнуть, то все пройдет также легко.

Если что-то непонятно пишите в комментариях.

Метод реккурентных соотношений

Этот метод позволяет выразить данный определитель, преобразуя и разлагая его по строке (столбцу), через определители того же вида, но более низкого порядка.

Данный метод будет очень сложен для вашего понимания, поэтому на нем особо зацикливаться не нужно, потому что вникать в него придется очень долго, а поэтому мы рассмотрим его немного позже.

В принципе, если в задании не указано применять данный способ, то лучше вообще о нем не знать, чтобы не забивать голову сложными расчетами и формулами.

Время еще осталось, давайте еще порешаем…

Пример №3 Вычислить определить матрицы, наиболее удобным для вас способом

Для вычисления определителя данной матрицы я воспользуюсь методом понижения порядка (хотя проще было бы, конечно, использовать правило Саррюса)

И так получилось у меня вот что:

Пример №4

Ну здесь уже правило Саррюса не поможет, поэтому решу его также, как и предыдущее методом понижения порядка.

Я еще не совсем разобрался с редактором формул, особенно, что касается матриц, поэтому делаю по-старому, позже я постараюсь заменить на более качественный ответ, а пока кликните по картинке, чтобы увеличить:

Если кто-то не понял или не разобрался в теме, задавайте вопросы в комментариях.

Уроки по теории вероятности

Прежде чем приступать к ознакомлению с данным уроком настоятельно рекомендую ознакомиться с предыдущим уроком «Определители 2-го и 3-го порядков«. Итак, если с предыдущим уроком все ясно можно переходить к новой теме. Как всегда начнем со скучной теории… Подстановки и инверсии в подстановках Всякое взаимно однозначное отображение π-множества {1, 2, …, n} первых n натуральных чисел на

Начнем с того, что матрица — это математический объект, который записывается в виде прямоугольной таблицы элементов (числа, буквенные значения и т.д.) Теперь вкратце пробежимся по теории. Матрица 2-го порядка , cоставленная из четырех действительных (или комплексных) чисел называется квадратной матрицей 2-го порядка. Определителем матрицы А, называется число Пример № 1 Найдите определитель

Изучение теории вероятностей всегда начинается с комбинаторики, ведь именно она составляет начальную базу, необходимую для дальнейшего углубления материала. Правило произведения и суммы Правило произведения. Если элемент строки () можно выбрать способами и после каждого такого выбора элемент можно выбрать – способами, и после выбора и элемент можно выбрать способами и т.д., наконец, независимо от выбора

Сегодня, на уроке, мы рассмотрим и научимся вычислять такой вид уравнений, как однородные уравнения. Теоретическая часть Однородные уравнения могут быть записаны в виде , а также в виде , где М (x,y) и N (x,y) — однородные функции одной и той же степени. Чтобы решить однородное уравнение, можно сделать замену , после чего получается уравнение

Данная тема будет полезна тем, кто хочет в дальнейшем подробно изучать предмет «Математическая статистика», ну и, конечно, для самых любознательных. Среднее арифметическое Десять учеников засекли время выполнения домашнего задания и получили результаты ( в минутах): 15, 17, 35, 24, 17, 29, 14, 20, 21, 30. Чтобы найти сколько времени в среднем уходит на выполнение домашнего задания

Математика-Определитель матрицы 4 x 4

В соответствии с определенным процессом сумма произведений элементов квадратной матрицы и их кофакторов порождает определители, которые являются скалярными величинами. Они помогают найти сопряженную или обратную матрицу. Эта методология также должна использоваться для решения линейных уравнений с использованием метода обращения матриц. Вычисление определителей помогает намного легче запомнить векторное произведение двух векторов. В матрицах определители представляют собой масштабный коэффициент. Их можно сравнить с матрицами, функции которых растут и сокращаются. Определители принимают квадратную матрицу в качестве входных данных и выводят одно число. Определение определителей:

Рассмотрим матрицу C = [cij]

Определитель порядка n x n может быть определен как скалярное значение, которое может быть действительным или комплексным, где

Cij — (i,j) элемент данной матрицы C. определитель может быть записан как det(C) или |C|; вместо использования квадратных скобок определитель записывается путем взятия сетки целых чисел и помещения их в столбцы абсолютных значений.

Определитель матрицы 4×4:

Определитель любой матрицы 4×4 представляет собой единственное в своем роде целое число, вычисляемое по определенной формуле. Это квадратная матрица, если данный порядок матрицы равен n x n. В результате 4×4 представляет собой квадратную матрицу с четырьмя строками и четырьмя столбцами. Определитель матрицы A представляется в виде |A| если А — квадратная матрица.

Мы воспользуемся тем же простым методом, который мы использовали для вычисления определителя матрицы 3×3, чтобы найти определитель матрицы 4×4.

Вычисление определителя матрицы 4×4

Рассмотрим следующую квадратную матрицу 4×4 или квадратную матрицу порядка 4×4; при определении определителя матрицы 4×4 помните о следующих изменениях:

B =

Шаги:

плюс a1, умноженный на определитель матрицы 3×3, полученный удалением строки и столбца, содержащего a1
минус b1, умноженный на определитель матрицы 3×3, полученный путем удаления строки и столбца, содержащих b1
плюс c1, умноженный на определитель матрицы 3×3, полученный путем удаления строки и столбца, содержащего c1

7 минус 9 умножить на определитель матрицы 3×3, полученной путем удаления строки и столбца, содержащих d1

Правила подразумеваемых операций над определителем:

1-Значение определителя остается неизменным, если строки и столбцы поменять местами.

2-Знак определителя меняется, если поменять местами любые две строки или (два столбца).

3-Если любые две строки или столбца матрицы равны, определитель имеет нулевое значение.

4-Значение определителя умножается на константу, когда каждый элемент строки или столбца умножается на константу.

5-Если составляющие строки или столбца выражены как сумма элементов, определитель может быть выражен как сумма определителей.

6-Когда элементы одной строки или столбца добавляются или вычитаются с совпадающими кратными элементами из другой строки или столбца, значение определителя остается неизменным.

Важные детерминанты Примечания:

Вот краткое изложение некоторых ключевых элементов, которые следует учитывать при изучении детерминантов.

Детерминанты можно рассматривать как функции, которые принимают квадратную матрицу в качестве входных данных и выводят одно значение.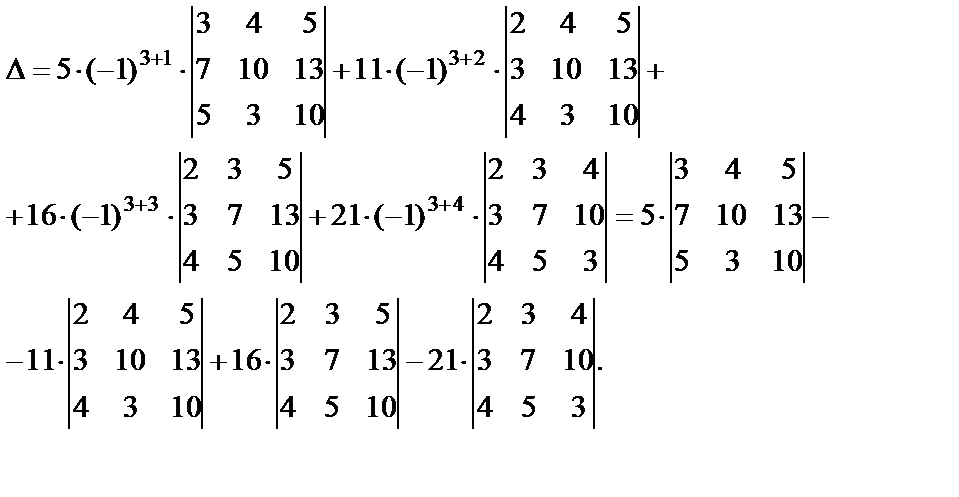

С обеих сторон квадратная матрица имеет равное количество строк и столбцов.

Определитель простейшей квадратной матрицы порядка 1×1, которая имеет только одно число, является целым числом.

Заключение:

Определитель — это скалярная переменная в математике, которая является функцией элементов квадратной матрицы. Это позволяет нам охарактеризовать некоторые атрибуты матрицы, а также линейную карту, которую представляет матрица. Определитель отличен от нуля тогда и только тогда, когда матрица обратима и линейная карта, которую представляет матрица, является изоморфизмом. Det(A), det A или |A| — определитель матрицы A. Определитель матрицы 4 × 4 — единственное в своем роде целое число, которое можно вычислить только по определенной формуле. Это квадратная матрица, если заданный порядок матрицы равен n x n. Итак, квадратная матрица с четырьмя строками и четырьмя столбцами имеет размер 4×4. Определитель матрицы A представляется в виде |A| если А — квадратная матрица.

Для нахождения определителя воспользуемся стандартным способом; есть формула для нахождения определителя матрицы 4×4, которую мы обычно используем, чтобы получить определитель матрицы 3×3.

Время, необходимое для нахождения определителя – The Numerical Methods Guy

Чтобы подчеркнуть неэффективность нахождения определителя матрицы методом кофакторов, я написал программу на MATLAB, чтобы продемонстрировать это. Поиск в Google программы, написанной на любом языке для поиска определителя с использованием метода кофактора, был недоступен за пределами матрицы 4 × 4. Итак, я написал такой, который находит определитель матриц порядка 12×12.

Я запустил программу на компьютере с процессором Intel(R) Core(TM) i5-8500 с частотой 3,00 ГГц. Вот таблица времени ЦП, которое потребовалось в секундах, чтобы найти определитель матрицы в зависимости от ее порядка.
______________________________________________
Порядок времени Matrix CPU времени на то, чтобы найти
Detriminant (S)
__________________________________________
6 × 6 0,015625
7 × 7 0,046875
8 × 8 0. 203125 9046875
8 × 8 0.203125
9 × 9 0,828125
10 × 10 5,14063
11 × 11 52,6406
12 × 12 623,953
______________________________________

, если это будет делать это для 25 × миллиардов лет, и все мы знаем, что предполагаемый возраст Вселенной меньше примерно на 13,77 миллиардов лет.

Тенденция приблизительного времени, необходимого для нахождения определителя матрицы следующего порядка, nxn примерно в n раз больше времени, необходимого для нахождения определителя матрицы (n-1)x(n-1). Например, для нахождения определителя матрицы 11 × 11 потребовалось время 52,6406 секунды, в то время как для нахождения определителя матрицы 12 × 12, по оценкам, потребуется примерно 12 × 52,6406 = 631,7 секунды. Это близко к 623,953 секундам, которые на самом деле потребовались.

Приведенные выше приблизительные расчеты времени согласуются с заметкой, написанной профессором А.Дж. Мудрый в 1969, где он показал, что количество арифметических операций, необходимых для вычисления определителя nxn методом кофакторов, равно [n!e]-2, и, следовательно, n!e для больших n и времени, необходимого для нахождения определителя следующего порядка матрицы, nxn приблизительно в n раз больше времени, необходимого для нахождения определителя матрицы (n-1)x(n-1)

Поскольку здесь требуются только арифметические операции сложения, умножения и вычитания, время вычислений можно грубо оценить как 4Tn!e для больших n, где T — время такта, и мы предполагаем, что сложение, умножение или вычитание используют 4 такта.