Ответы
| ||||||||||||
10.17
| ||||||||||||
10.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
1.
в треугольнике АВС провели медиану AM найдите угол AMC, если углы BAC И BCA равны 45 и 30 градусов соответственно. Угол B получается 105, но дальше решить не получается.
Квадратный оконный проем образован двумя прямоугольными рамами.Внутри каждой из них написали число равное периметру рамы. Напишите чему равна сторона квадрата всего оконного проема и объясните как вы
чему равны индуктивность и энергия магнитного поля соленоида , если при силе тока, равной 4А, магнитный поток через соленоид и равен 0,4 вб
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Пользуйтесь нашим приложением
Площадь между двумя кривыми – формула, определение, примеры
Нахождение площади между двумя кривыми является важным применением интегрирования.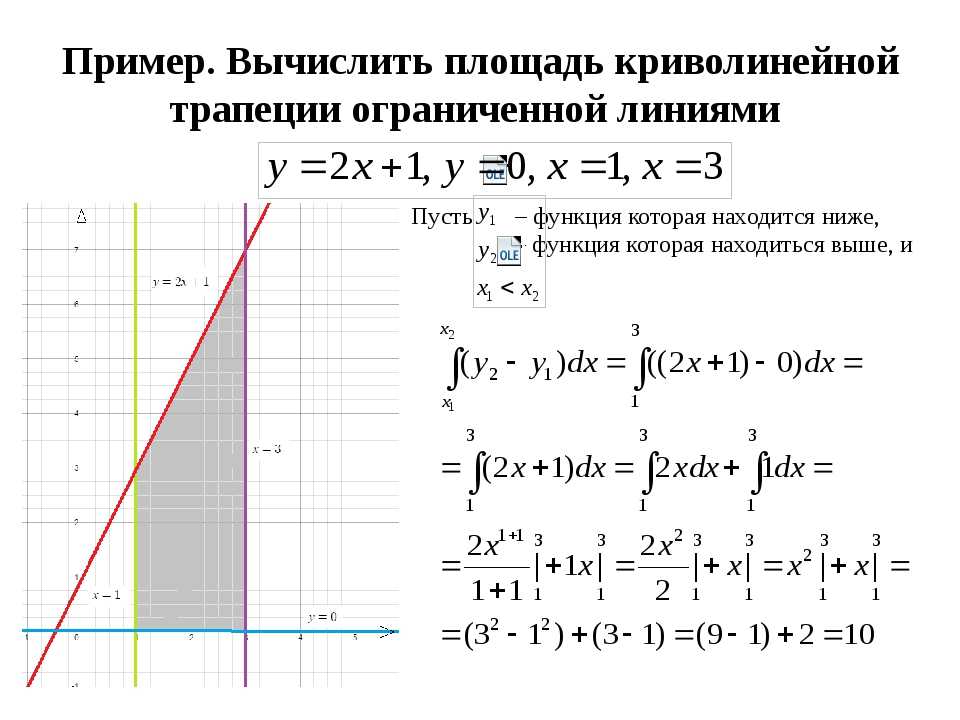
Используя интегрирование, мы научились находить площадь под кривой, точно так же мы можем найти площадь между двумя пересекающимися кривыми, используя интегрирование. Это часть пространства, которая находится между двумя линейными или нелинейными кривыми в заданных пределах.
Площадь между двумя кривыми также может быть составной, но с помощью интегрирования мы также можем легко найти это, сделав простые изменения в известных формулах, используемых для нахождения площади под двумя кривыми. Давайте обсудим эту тему в следующем содержании.
| 1. | Область между двумя кривыми Введение |
| 2. | Площадь между двумя кривыми Формула |
| 3. | Площадь между двумя кривыми относительно Y |
| 4. | Площадь между двумя составными кривыми |
| 5. | Область между двумя полярными кривыми |
6. | Площадь между двумя кривыми Примеры |
| 7. | Практические вопросы |
| 8. | Часто задаваемые вопросы об области между двумя кривыми |
Область между двумя кривыми Введение
Площадь между двумя кривыми — это площадь, которая находится между двумя пересекающимися кривыми и может быть рассчитана с помощью интегрального исчисления. Интегрирование можно использовать для нахождения площади под двумя кривыми, если мы знаем уравнение двух кривых и точки их пересечения. Если мы видим на изображении, у нас есть две функции f (x) и g (x), и нам нужно найти площадь между этими двумя кривыми, указанными в заштрихованной части. Затем, используя интегрирование, мы можем легко вычислить площадь заштрихованной части. Подробнее о расчете этой площади мы поговорим в следующем разделе.
Площадь между двумя кривыми Формула
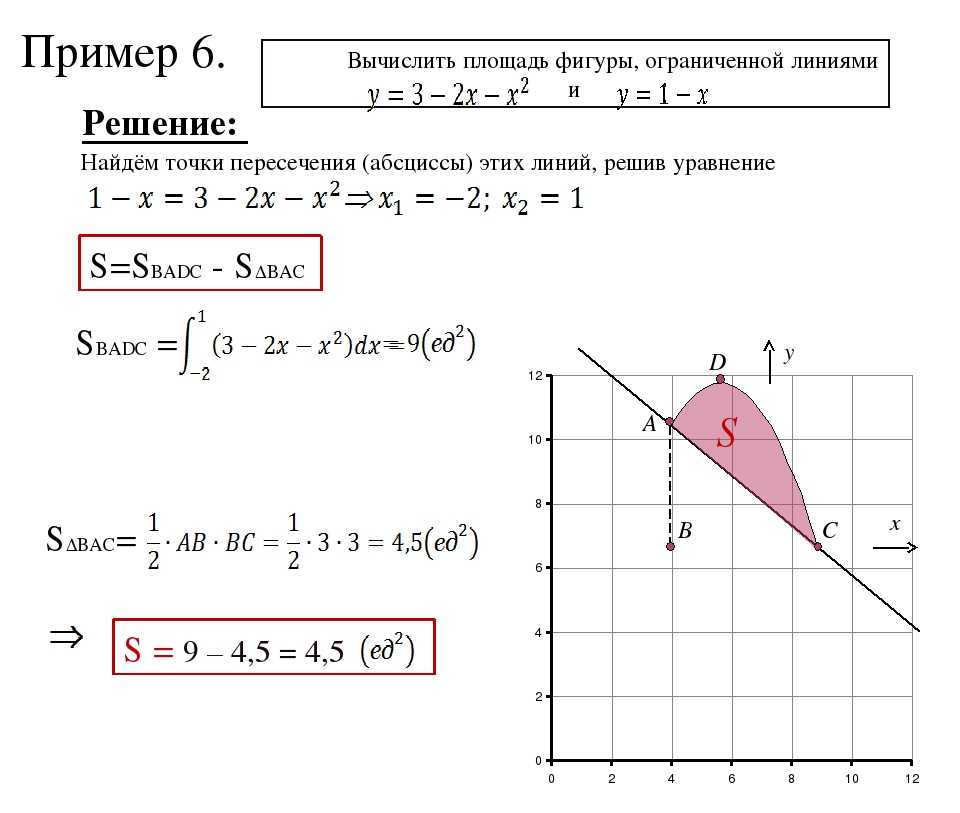
Если мы хотим найти площадь между двумя кривыми, нам нужно разделить площадь на множество маленьких прямоугольных полос, параллельных оси y, начиная с x = a до x = b, и с помощью интегрирования мы можем сложить площади из этих маленьких полосок, чтобы получить площадь аппроксимации двух кривых.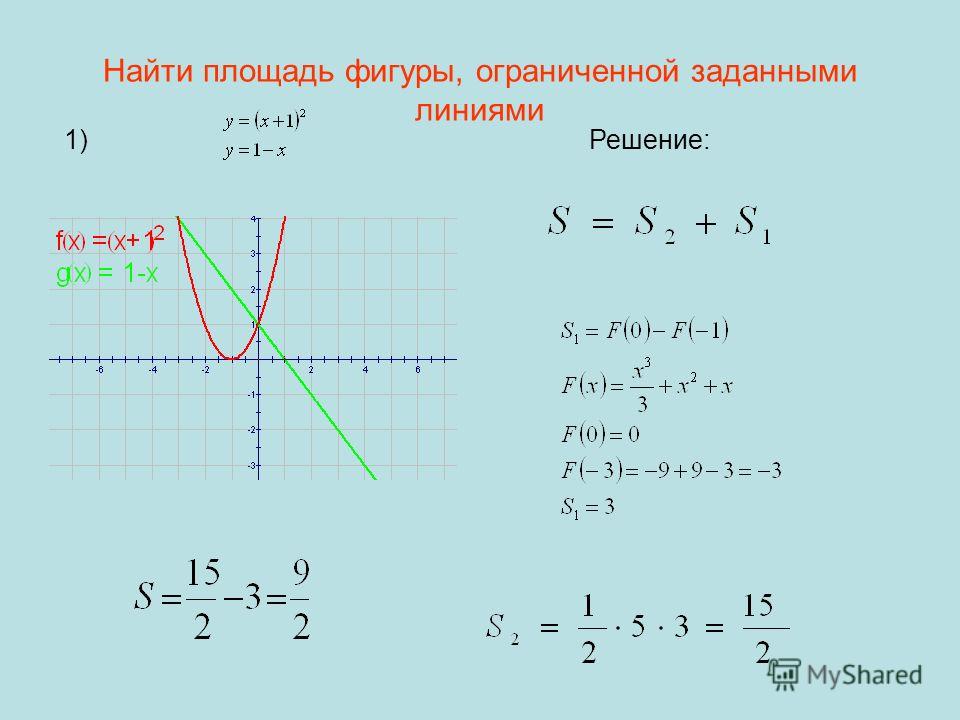
Эти прямоугольные полоски будут иметь ширину «dx» и высоту f(x) — g(x). Площадь небольшой прямоугольной полоски равна dx(f(x) — g(x)) и теперь, используя интегрирование в пределах x = a и x = b, мы можем вычислить площадь между этими двумя кривыми. Если f(x) и g(x) непрерывны на [a, b] и g(x) < f(x) для всех x в [a, b], то мы имеем следующую формулу. 9{b} \left [ f(x) - g(x) \right ] \;dx\)
Площадь между двумя кривыми относительно Y
Площадь между двумя кривыми относительно оси y — это метод расчета площадей кривых, уравнение которых задается через y. Вычисление площади по оси Y проще, чем вычисление площади по оси X. В этом методе мы делим данную область на горизонтальные полосы между заданными пределами и, используя интегрирование, складываем площади горизонтальных полос, чтобы найти площадь сечения между двумя кривыми. Если f(y) и g(y) непрерывны на [c, d] и g(y) < f(y) для всех y в [c, d], то 9{b} \left [ f(y) - g(y) \right ] \;dy\)
Площадь между двумя составными кривыми
Вычисление площадей между двумя составными кривыми, которые пересекаются друг с другом, по приведенным выше формулам даст неверный результат, и кривые меняются местами после пересечения.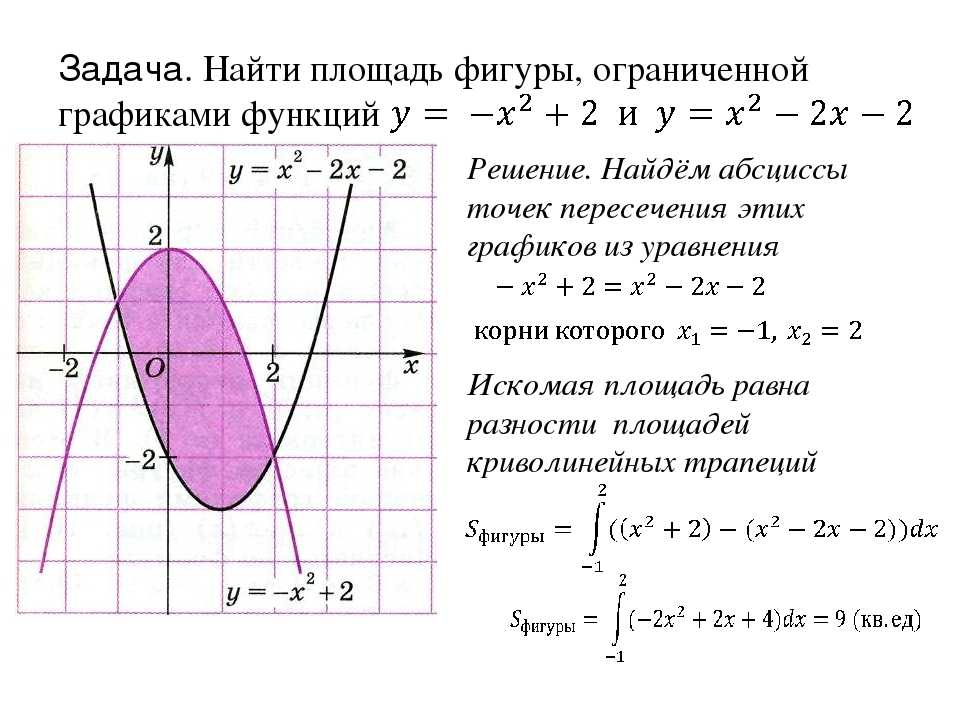
Для кривых, показанных на изображении, мы разделили интервалы на различные части, а затем вычислили отдельные площади между кривыми в каждом сечении. Пусть f(x) и g(x) непрерывны на интервале [a,b], площадь между кривыми будет: 9c_b(g(x)−f(x))dx\)
Область между двумя полярными кривыми
С помощью интегрального исчисления мы также можем вычислить площадь между двумя полярными кривыми. Когда у нас есть две кривые, координаты которых заданы не в прямоугольных, а в полярных координатах, мы используем этот метод. Мы всегда можем преобразовать полярные координаты в прямоугольные, чтобы решить эту проблему, но мы можем использовать этот метод, чтобы уменьшить сложность. Допустим, у нас есть две полярные кривые \(r_0\) = f(θ) и \(r_i\) = g(θ), как показано на изображении, и мы хотим найти площадь, заключенную между этими двумя кривыми, такую, что α ≤ θ ≤ β, где [α, β] — ограниченная область. Тогда площадь между кривыми будет: 92_и) дθ \) —
Часто задаваемые вопросы об области между двумя кривыми
Что означает площадь под кривой?
Площадь под кривой означает площадь, ограниченную кривой, осью и граничными точками.
Площадь под кривой представляет собой двумерную площадь, которую можно рассчитать с помощью осей координат и по формуле интегрирования.
Что представляет площадь под кривой?
Площадь под кривой представляет собой площадь, заключенную под кривой и осью, которая отмечена ограничивающими точками. Эта площадь под кривой дает площадь неправильной плоской формы в двумерном массиве. 9by.dx\).
Какие существуют методы нахождения площади под кривой?
Существует три основных метода определения площади под кривой. Площадь под кривой рассчитывается путем деления пространства площади на множество маленьких прямоугольников, а затем площади складываются для получения общей площади. Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.
Область между двумя кривыми
Область между двумя кривыми
Напомним, что площадь под кривой и над осью x может
быть вычислено определенным интегралом.
Если у нас есть две кривые
у = f(x) и у = г (х)
такой, что
е(х)
> г(х)
то площадь между ними, ограниченная горизонтальными линиями x
= a и x = b
Чтобы запомнить эту формулу, напишем
| . |
Пример
Найти площадь между кривыми
у = х 2
и
у
= х 3
Решение
Сначала отметим, что кривые пересекаются в точках (0,0)
и (1,1).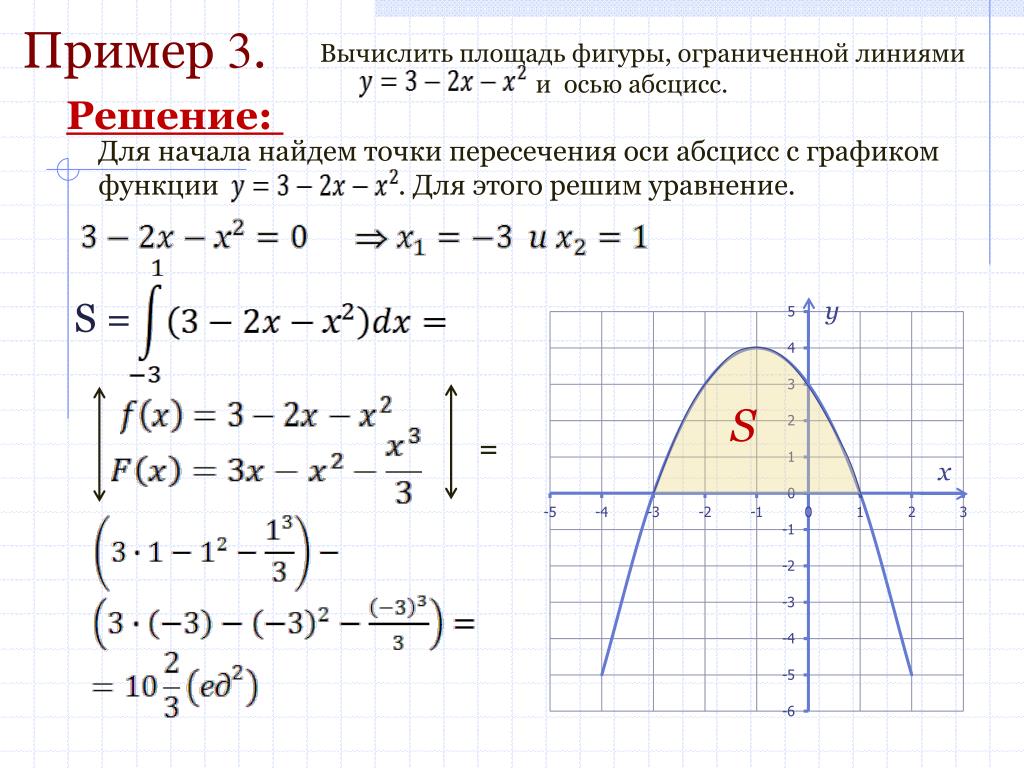
Затем мы видим, что
х 3 < х 2
в этом интервале. Следовательно, площадь равна
.
= 1/3 — 1/4 = 1/12.
Упражнения
Найдите площадь между кривыми y = х 2 и у =
Найдите площадь между кривыми y = х 2 — 4 и у = -3x
Найдите площадь между кривыми y = 2/x и y = -x + 3
Найдите площадь между кривыми y = 3 90 189 x 90 190 и y = 2x + 1
Заявка
Пусть y = f(x) будет функцией спроса
для продукта, а y = g(x) — функция предложения.