Косинус онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.
Введите число
синус (sin)косинус (cos)тангенс (tg)котангенс (ctg)секанс (sec)косеканс (cosec)градусырадианы
Что такое косинус угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда косинусом угла α будет отношение прилежащего катета к гипотенузе cos α = AB/AC.
Так же для определения косинуса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Косинусом угла α будет отношение абсциссы точки XP к радиусу окружности.
cos α = XP/R, в случае, если окружность единичная (радиус окружности = 1), формула примет вид cos α = XP.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление.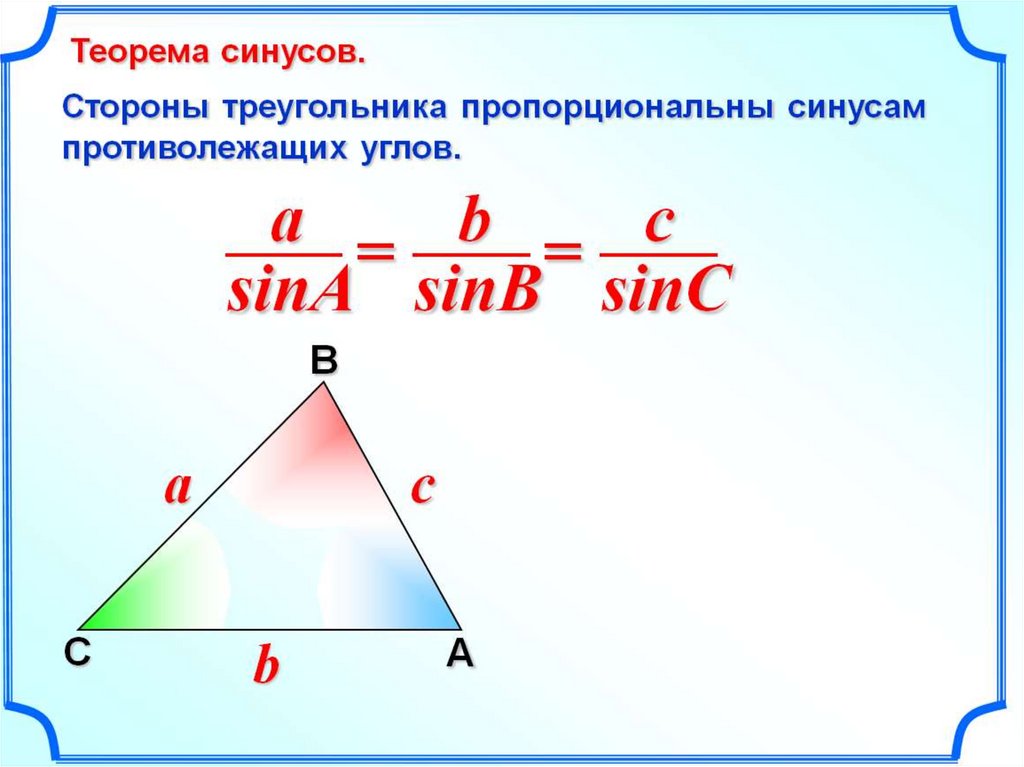 Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона.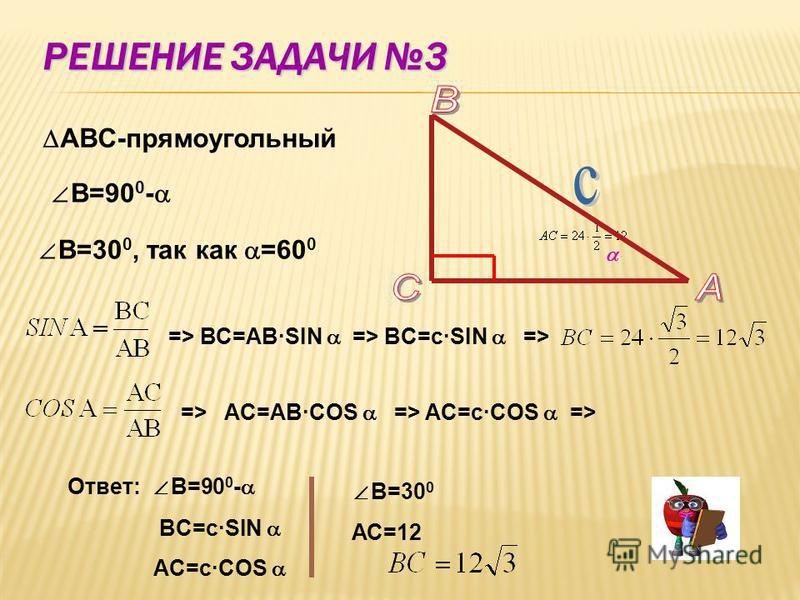 Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Решение треугольников 9 класс онлайн-подготовка на Ростелеком Лицей
Геометрия 9 класс
Глава 2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Раздел 2. Соотношения между сторонами и углами треугольника
Урок 4. Решение треугольников
Тарасов В.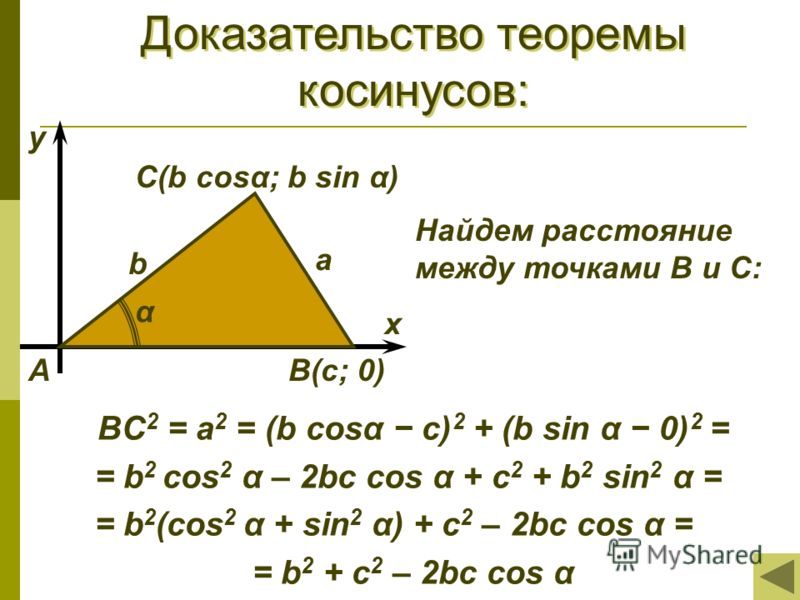 А.,
А.,
учитель школы «Логос ЛВ», ст. преп. фак-та довузовской подготовки МИТХТ
08.11.2010 г.
Здравствуйте! Тема урока – «Решение треугольников». Здесь мы вспомним основные опорные факты и решим в общем виде три типовые задачи на решение треугольников. Вначале напомним важное определение синуса и косинуса для углов aÎ[0º; 180º].
Имеем окружность, радиус 1, верхняя ее часть – оси координат и угол a. Угол a построен следующим образом, положительная полуось х – один луч этого угла. Второй луч высекает точку М на единичной полуокружности. Координаты точки М (хм; ум) назвали: абсцисса хм – это , ордината ум – это . Итак, имеем ÐАОМ=aÞМ (хм; ум)= М (;).
Это для любого угла aÎ[0º; 180º], потому что треугольник имеет любой угол в пределах(0º; 180º). Таким образом, мы просто напомнили определение синуса и косинуса для любого угла, который может быть углом треугольника. Отметим важную специфику: значение косинуса однозначно определяет угол треугольника. Поясним это примерами, объясним почему.
Таким образом, мы просто напомнили определение синуса и косинуса для любого угла, который может быть углом треугольника. Отметим важную специфику: значение косинуса однозначно определяет угол треугольника. Поясним это примерами, объясним почему.
Вот линия косинусов. Косинус может меняться в пределах от -1 до 1.
Пример 1
а) Пусть .
отметил на линии косинусов, перпендикуляр, получил единственную точку М на окружности. И получил нужный угол, этот угол искомый. Почему он равен 45º? Потому что если это , то и здесь , гипотенуза 1, либо по таблице, либо по этому треугольнику получаем, что имеем угол 45º.
Итак, если при решении задач, мы вдруг увидели , мы однозначно определяем, что этот угол равен 45º.
Второй пример.
б) если .
Вдруг выяснилось, что и a – это угол треугольника, то мы должны сразу получить ответ, что a=135º.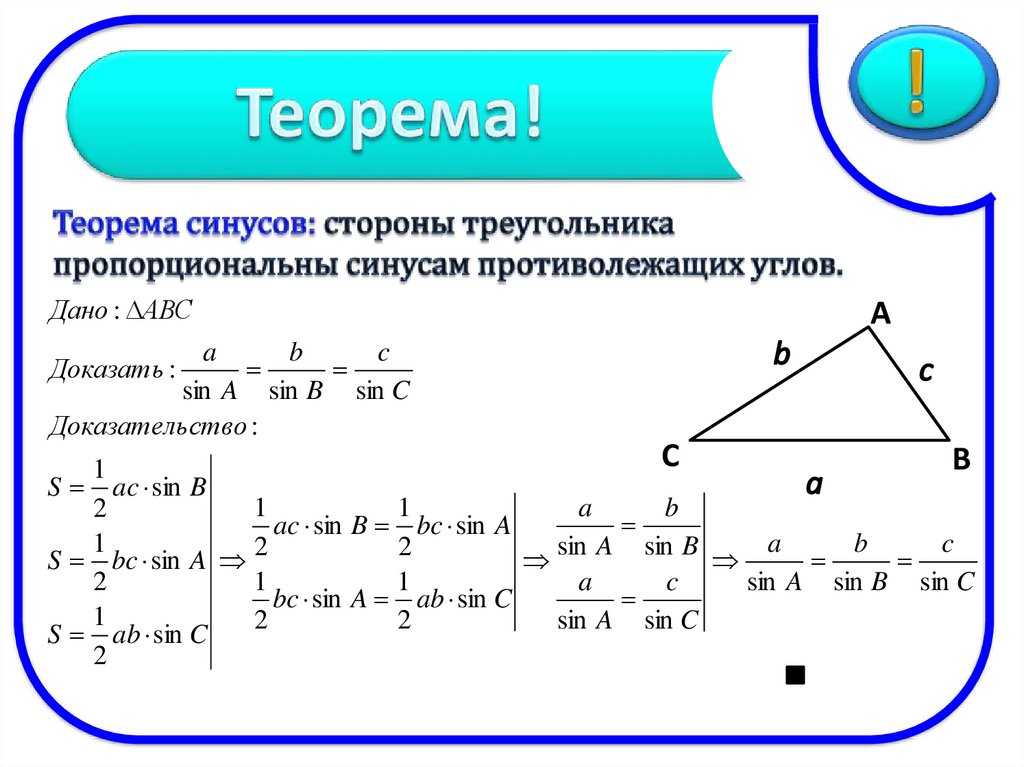
Почему? Во-первых, можно по таблице, а во-вторых, из чертежа. Единичная полуокружность на линии косинусов – это абсцисса точки М, перпендикуляр, получаем точку М. А значит, искомый угол АОМ. Гипотенуза 1, катет в этом треугольнике , значит, либо этот угол 45º, а значит, и этот угол 45º. (180º — 45º) = 135º, либо по таблице, раз у нас , то угол равен 135º.
Итак, специфика заключается в том, что значение косинуса однозначно определяет угол треугольника. В отличие от косинуса значение синуса, если он заключен в пределах
определяет два угла треугольник a1 и a2 и сумма этих углов равна 180º:
a1+a2=180º
Поясним сказанное на чертеже. Единичная полуокружность, оси координат, вот значение синуса. Синус, кстати, меняется от 0 до 1, вот синус ≠1, перпендикуляр. Получаем две точки на окружности, точку М и точку N. Только две эти точки имеют свои ординаты, вот это значение, которое равно синусу a. Первая точка определяет один угол АОN – назвали a1. Вторая точка определяет угол АОМ – назвали a2. Но имеем еще один угол a2 в силу симметрии, так что a1+a2=180º. Итак, значение синуса определяет два угла, в сумме составляющих 180º. И это углы треугольника, и это очень важно для решения треугольников.
Только две эти точки имеют свои ординаты, вот это значение, которое равно синусу a. Первая точка определяет один угол АОN – назвали a1. Вторая точка определяет угол АОМ – назвали a2. Но имеем еще один угол a2 в силу симметрии, так что a1+a2=180º. Итак, значение синуса определяет два угла, в сумме составляющих 180º. И это углы треугольника, и это очень важно для решения треугольников.
Сделаем конкретный пример.
, то a1=135º.
или a2=45º
Если , то мы имеем два конкретных угла. Если это , то один из углов 135º, вот этот большой угол, второй угол 45º. Итак, еще раз: значение косинуса однозначно определяет угол треугольника. Значение синуса не однозначно определяет угол треугольника. Значение синуса, если оно не равно 1, определяет два угла треугольника, сумма которых равняется 180º.
Теперь мы знаем, что такое синус и косинус любого, в том числе тупого угла треугольника.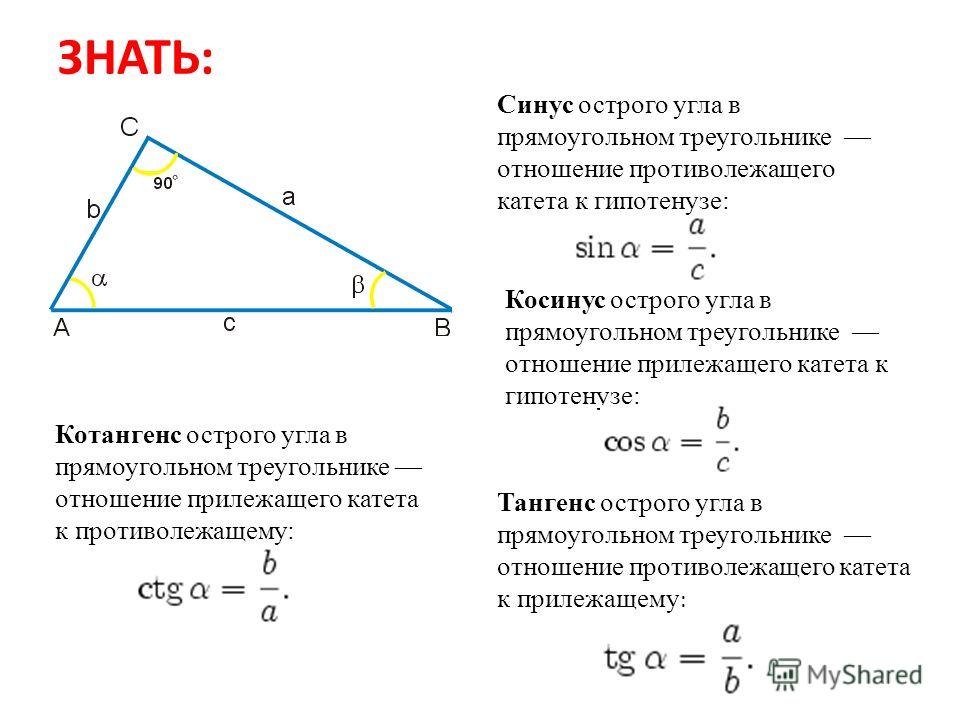 Поэтому мы можем определить координаты всех вершин треугольника.
Поэтому мы можем определить координаты всех вершин треугольника.
Вот на рисунке остроугольный треугольник и тупоугольный треугольник. Угол g острый, угол g тупой. Во-первых, если мы говорим о координатах, то надо ввести систему координат. Удобно ввести ее следующим образом: начало совместить с одной из вершин, например, с вершиной С. А ось х пустить по прямой СВ. Итак, имеем треугольник АВС. Стандартные обозначения: вершина А, длина стороны – а маленькая; вершина В, длина стороны – в маленькая; вершина С, длина стороны – с маленькая; угол при вершине С=g, стандартное обозначение. Координаты этой точки С – начало координат С(0;0). Координаты этой точки В(а;0), это понятно. И, наконец, координата точки А – это ().
Это, во-первых, мы выводили в свое время, а во-вторых, можно это посмотреть из треугольника прямоугольного, в котором ха – катет равен: гипотенуза умножить на косинус прилежащего угла. Противолежащий катет уа есть гипотенуза, умноженная на синус противолежащего угла. Таким образом, вот координаты всех точек: А(), В(а;0), С(0;0). По виду они не меняются, если угол g тупой.
Противолежащий катет уа есть гипотенуза, умноженная на синус противолежащего угла. Таким образом, вот координаты всех точек: А(), В(а;0), С(0;0). По виду они не меняются, если угол g тупой.
По-прежнему, высота вот из этого треугольника или из этого треугольника h=. Формулы для остальных вершин те же самые.
Итак, если мы знаем, что такое синус и косинус для угла треугольника, то мы можем найти координаты всех его вершин через синус и косинус угла. Зная координаты вершин треугольника, мы в свое время получили формулу для площади через синус угла. Напомним ее.
Откуда взялась эта формула? Вспомним, что площадь, мы давно считали по известной формуле: основания на высоту, которая проведена к этому основанию . Но высота есть ордината точки А, а ордината точки А (только что мы говорили) – это , т.к.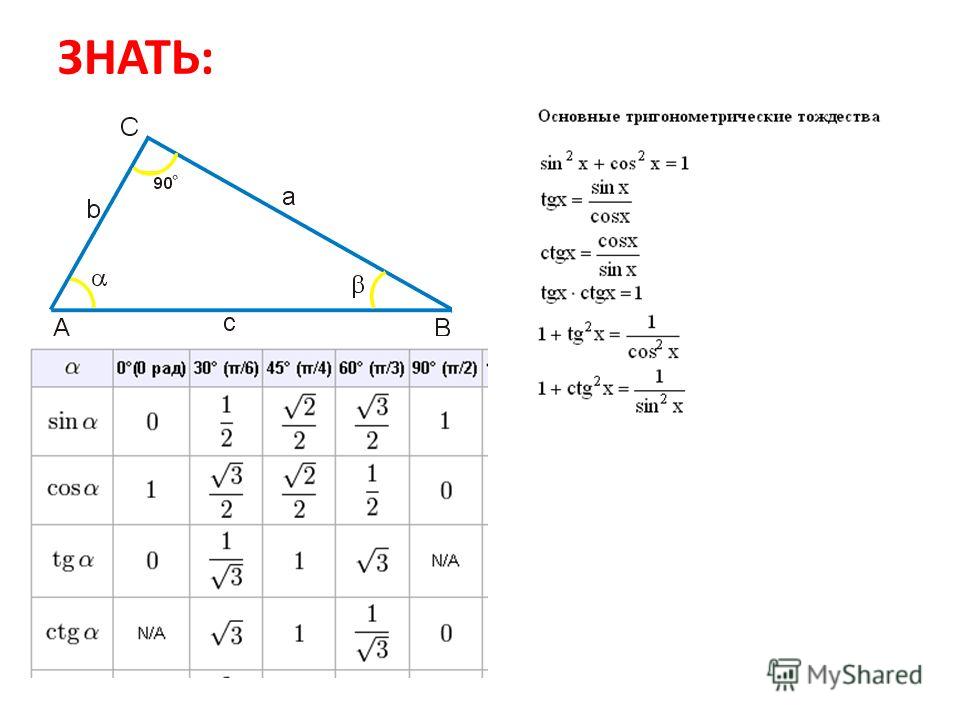 h=, то подставили в формулу для площади и получили результат: .
h=, то подставили в формулу для площади и получили результат: .
Итак, площадь треугольника есть половина произведения двух его сторон, длин его сторон, точнее, на синус угла между ними. Далее с помощью этой формулы мы получили теорему синусов. Напомним и ее. Теорема синусов утверждает: отношение длины стороны к синусу противолежащего угла треугольника есть величина постоянная для данного треугольника, а именно:
.
Напомним также, что вывод мгновенно следует из формулы из площади треугольника
=
=
Важным инструментом при решении треугольников является теорема косинусов. Напомним ее. Вот ∆АВС, сторона а, сторона b, сторона с. Треугольник помещен в координатную плоскость, оси координат х, у. Координаты каждой вершины мы сейчас умеем находить. Вот координаты вершины А(), это – одна координата, абсцисса; — вторая координата, ордината.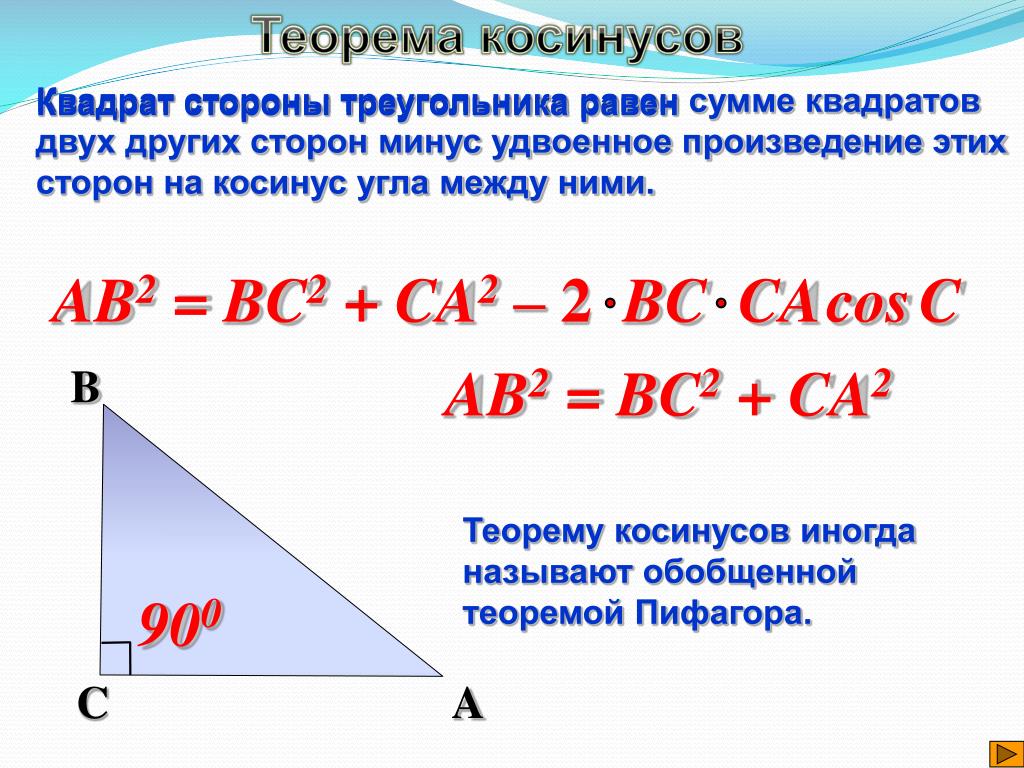 Через эти координаты мы находим длину АВ, и в результате получили теорему косинусов, которая звучит следующим образом: с2=а2+в2-2ав. Напомним словесную формулировку: квадрат стороны равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Через эти координаты мы находим длину АВ, и в результате получили теорему косинусов, которая звучит следующим образом: с2=а2+в2-2ав. Напомним словесную формулировку: квадрат стороны равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Это, как мы помним, обобщение теоремы Пифагора. Если бы угол g был прямым, то с была бы гипотенузой, квадрат гипотенузы был бы равен сумме квадратов катетов. Но это для прямоугольного треугольника. Теорема косинусов для любого треугольника. И теорема синусов, и теорема косинусов – это важнейшие инструменты для решения треугольников. Напомним, что означает слово «решение треугольников». Это означает, что следует найти все стороны, все три стороны и все три угла треугольника. Вот одна из типовых задач.
Задача
В ∆АВС даны а, в, g (две стороны и угол между ними). Даны три элемента треугольника. Найти с, a, b, т.е. остальные элементы треугольника. Прокомментируем еще раз условия. Вот ∆АВС, сторона а, длина ее известна. Сторона в, длина ее известна. И величина угла между ними, т.е. три элемента треугольника известны. Надо найти остальные три элемента, т.е. должны быть известны три стороны, длины этих сторон и величины углов.
Найти с, a, b, т.е. остальные элементы треугольника. Прокомментируем еще раз условия. Вот ∆АВС, сторона а, длина ее известна. Сторона в, длина ее известна. И величина угла между ними, т.е. три элемента треугольника известны. Надо найти остальные три элемента, т.е. должны быть известны три стороны, длины этих сторон и величины углов.
Решение:
1) с=
2)
3) b=180º-(a+g).
Вот известен угол g, всегда полезно написать теорему косинусов для противоположной стороны.
1) Написали с2=а2+в2-2ав.
Для того чтобы найти с, надо взять Ö из этого выражения. Таким образом, теорема косинусов мгновенно позволяет найти противолежащую сторону, противолежащую углу g. Нашли. Значит, каким образом найти угол a?
2) Для этого надо написать теорему косинусов для противоположной стороны:
, т.е. написали теорему косинусов для противоположной стороны, получили уравнение для косинуса и нашли косинус. Нашли косинус, а по косинусу угла находим сам угол, причем мы говорили, что угол a в треугольнике однозначно задан, если задан косинус этого угла. Итак, угол a найден.
Нашли косинус, а по косинусу угла находим сам угол, причем мы говорили, что угол a в треугольнике однозначно задан, если задан косинус этого угла. Итак, угол a найден.
3) Осталось найти угол b. Сумма трех углов треугольника 180º, значит, угол b – это 180º минус сумма двух уже известных нам углов a и g.
Таким образом, первая стандартная задача решена. Напомним ее связь с признаком равенства треугольников. Ведь два треугольника равны, если две стороны соответствующие равны и угол между ними равен. То есть две стороны и угол однозначно задают треугольник. Вот они заданы, и получился треугольник. Все остальные элементы этого треугольника мы нашли с помощью теоремы косинусов. Задача решена.
Следующая типовая задача по решению треугольников.
Задача. В ∆АВС известна длина стороны а, величины углов b и g (сторона и два прилежащих к ней угла). Требуется решить треугольник, т.е. найти недостающие элементы, а именно: величину угла a, в, с – длины сторон. Решение. Используем теорему синусов, нам нужно найти длину в:
Решение. Используем теорему синусов, нам нужно найти длину в:
.
Длина одной стороны найдена по теореме синусов. Далее находим длину третьей стороны по той же теореме синусов: . Задача решена.
Треугольник, как мы знаем, задается тремя сторонами. Следующая задача опирается на этот факт.
Задача. В ∆АВС даны длины трех сторон а, в, с. Найти все углы a, b, g. Стандартные обозначения, треугольник поясняет сказанное. Стороны известны, надо найти углы. Решение: по теореме косинусов пишем теорему косинусов для стороны а и находим косинус угла a
1)
Такова теорема косинусов для угла a для стороны а. Нашли косинус, а по косинусу мы однозначно находим угол a. Аналогично действуем для косинуса b.
2)
Нашли косинус b, он однозначно задает угол b. Если мы знаем два угла треугольника a и b, то третий угол находим как разность:
3) g=180º-(a+b)
Задача решена.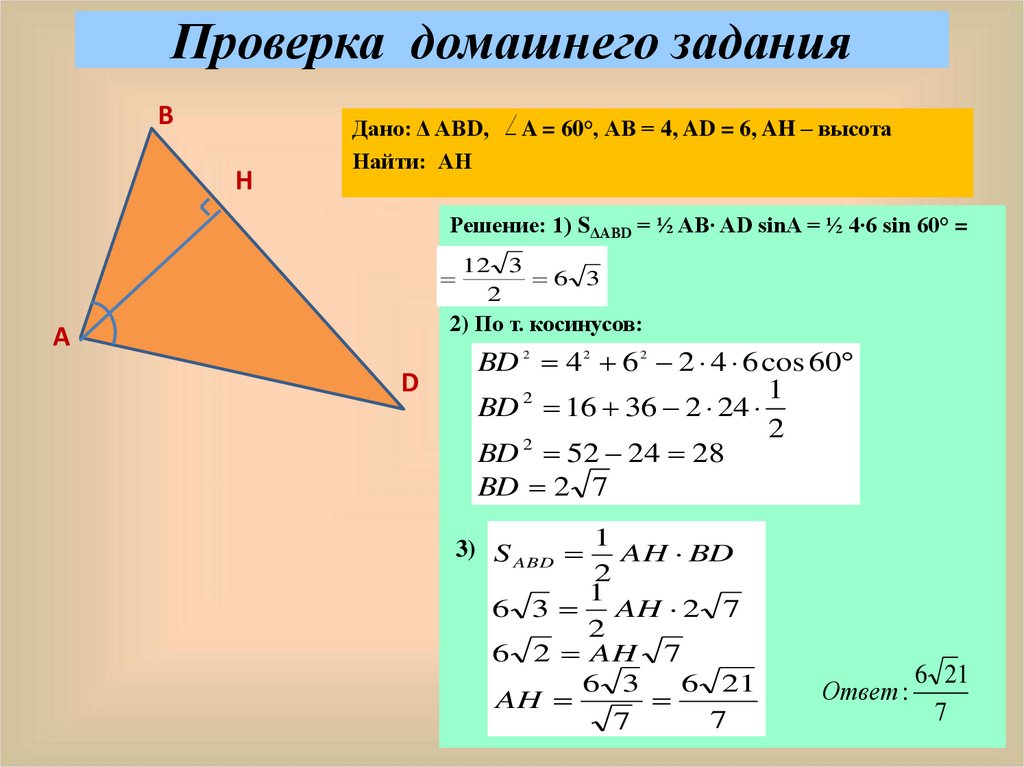
Итак, мы повторили основные опорные факты и решили три типовые задачи по решению треугольников. На следующем уроке мы продолжим решение треугольников в основном с конкретными исходными данными.
Таблица косинусов, найти значения угла косинусов
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
|
|
|
|
|
|
|
|
|
|
Select rating12345
Рейтинг: 5 (Голосов 2)
Сообщить об ошибке
Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Смотрите также
| Площадь фигур | Объем фигур | Периметр фигур | Радиус фигур | Единицы измерения угла |
| Конвертеры | Время для пробуждения | Теоремы | Угол | Калькулятор Моей жизни |
Калькулятор Cos — Найдите Cos (x) по формуле
Онлайн-калькулятор cos бесплатного помогает вычислить значение косинуса заданного угла в градусах, радианах, миллирадианах и π радианах. Здесь у нас есть для вас гораздо больше, включая то, как найти кривую косинуса, некоторый элементарный закон косинуса и многое другое! Итак, давайте начнем с общего определения косинуса.
Что такое косинус в математике?В математике тригонометрические функции – это действительные функции, относящиеся к прямоугольному треугольнику с двумя сторонами длины и одной гипотенузой. Предполагая прямоугольный треугольник, функция угла cos (x) определяется как длина смежной стороны, деленная на длину гипотенузы. Значение этой тригонометрической функции cos (x) для данного угла можно вычислить с помощью калькулятор cos. Кроме того, диапазон косинуса равен \ (- 1 ≤ cos ≤ 1 \), а период косинуса равен \ (2π \).
Значение этой тригонометрической функции cos (x) для данного угла можно вычислить с помощью калькулятор cos. Кроме того, диапазон косинуса равен \ (- 1 ≤ cos ≤ 1 \), а период косинуса равен \ (2π \).
Формула для функции косинуса:
$$ cos (θ) = \ frac {\ text {смежный} b} {\ text {hypotenuse} c} $$
Чтобы решить cos вручную, просто используйте значение смежной длины и разделите его на гипотенузу.
Кроме того, онлайн-калькулятор секущей используется для нахождения секущей заданного угла в градусах, радианах или π радианах.
Как найти косинус угла?Поскольку косинус угла θ – это отношение между соседней длиной угла и гипотенузой, примените следующую формулу, чтобы найти косинус угла:
$$ cos (α) = \ frac {b} {c} $$
Пример 1:Рассчитать значение cos θ?
Решение:
Если длина соседней стороны равна 12, а значение гипотенузы равно 6, то согласно формуле cos:
\ [cos θ = \ frac {12} {6} = 2 \]
Пример 2:Найдите значения Cos 60 °.
Решение:
Используя таблицу косинусов или калькулятор,
\ [Cos 60 ° = \ frac {1} {2} = 0,5 \]
Вы также можете использовать cos калькулятор для безошибочного расчета.
График косинуса:График косинуса представляет собой повторяющуюся кривую вверх / вниз. Эта кривая называется косинусоидальной волной. При построении графика всегда помните:
- Кривая начнется с 0 углов.
- Как только кривая начнется, она сначала уменьшится до значения -1.
- После уменьшения кривая увеличится до значения 1, а затем весь процесс будет продолжаться без ограничений.
Значение функции косинуса для всех общих углов можно быстро выбрать из следующей таблицы для быстрых вычислений:
| Градусы (°) | Радианы | cos (x) |
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
Этот калькулятор cos показывает, как быстро найти косинус всего за два шага.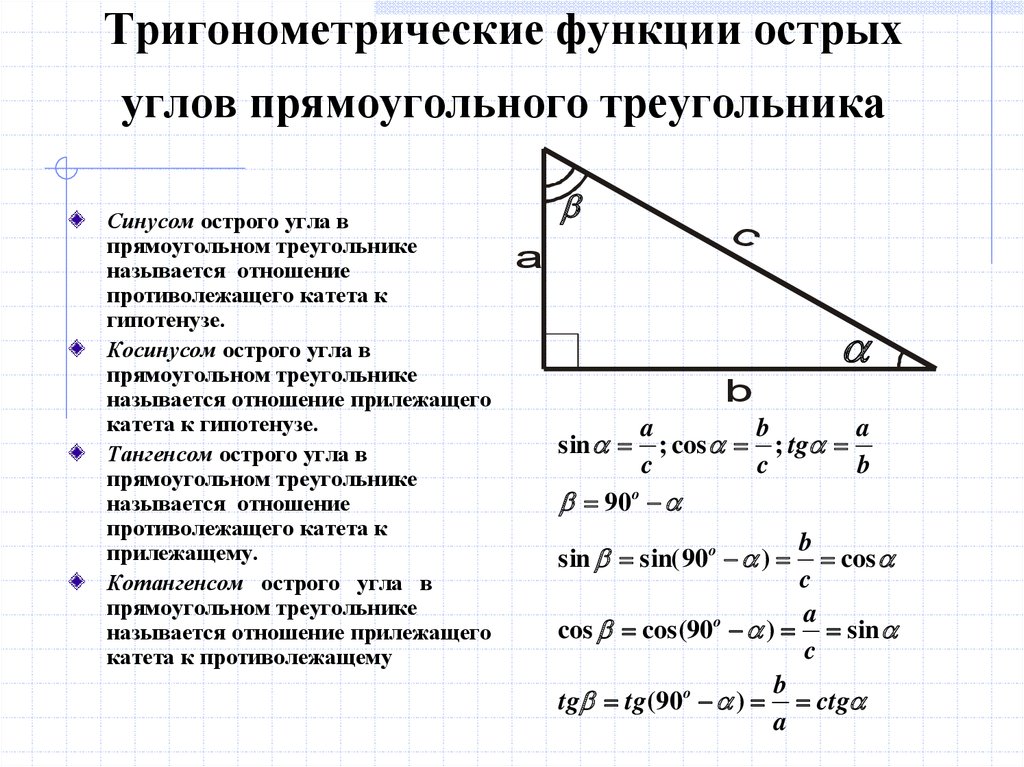
Более того, онлайн-калькулятор синусов поможет вам определить тригонометрические значения синуса для заданного угла в градусах, радианах или π радианах.
Вход:- Введите значение заданного угла θ.
- На втором этапе просто выберите градус, радиан, м радиан или пи (π) радиан из раскрывающегося меню.
- Нажмите кнопку «Рассчитать».
Этот cos калькулятор определит следующий результат, используя формулу косинуса и таблицу.
- Отображается значение косинуса в радианах, градусах, м радианах или пи (π) радианах.
- Он отображает ответы в простейшей форме.
- Единица измерения угла будет предоставлена так же, как и ваш ввод.
Если у вас есть треугольник и вы хотите связать все его три стороны с одним углом, вам нужно применить правило косинуса. Однако, чтобы найти длину стороны, вы должны знать две другие стороны, а также противоположный угол.
Косинус тригонометрической функции обычно используется для определения местоположения и расчета расстояний в системе GPS смартфонов и устройств IOS. Кроме того, он также может использоваться в космических полетах и баллистических траекториях.
Почему Cos положительный?Cos помечен как положительный по той причине, что θ всегда будет измеряться от положительной оси x.
Зачем нужны тригонометрические функции?Практически все тригонометрические навыки помогают студентам, которые работают со сложными углами и размерами за сравнительно короткое время. Они также могут быть реализованы во многих других областях. такие как:
- Архитектура
- Инженерное дело
- Наук
- Математика и др.
Что ж, благодаря калькулятор cos, который обеспечивает бесплатную поддержку для вычисления значения функции косинуса, когда мы захотим.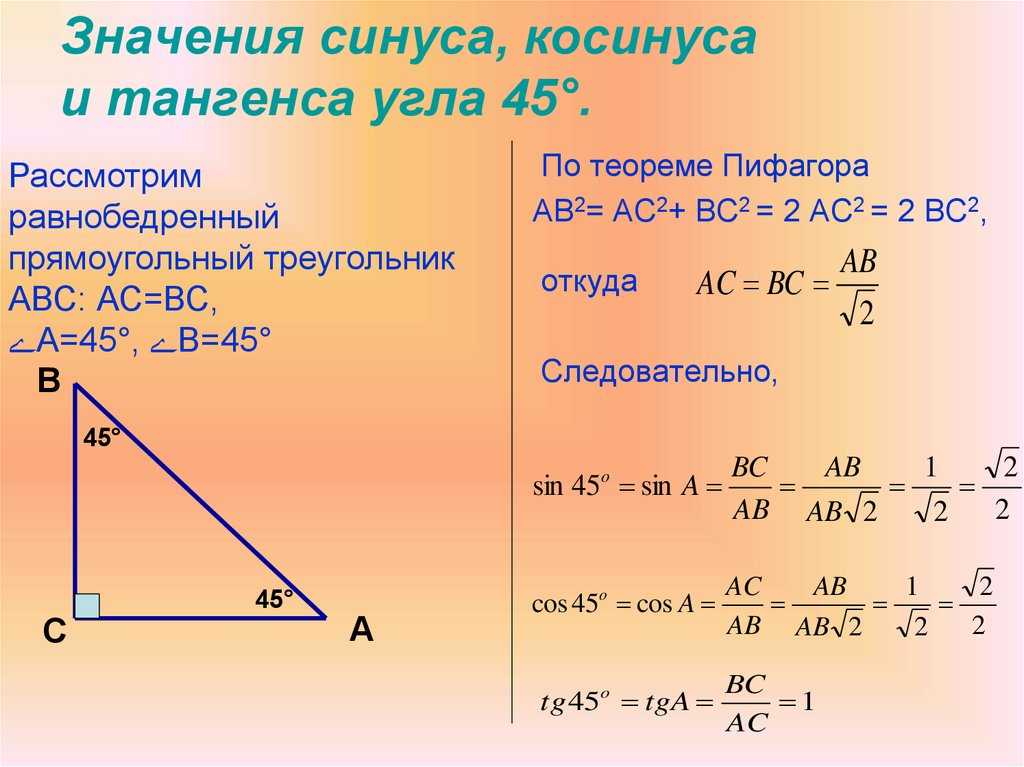 Кроме того, это отличный выбор для всех тех студентов и профессионалов, которые с энтузиазмом знакомятся с новыми вещами и хотят получить больше знаний о тригонометрии. Так что просто возьмите в руки этот калькулятор, чтобы получать компенсацию за него.
Кроме того, это отличный выбор для всех тех студентов и профессионалов, которые с энтузиазмом знакомятся с новыми вещами и хотят получить больше знаний о тригонометрии. Так что просто возьмите в руки этот калькулятор, чтобы получать компенсацию за него.
Other Languages: Cosine Calculator, Cos Hesaplama, Cosinus Kalkulator, Kalkulator Cosinus, Cosinus Rechner, Cos 計算, Cosinus Kalkulačka, Calcul Cos, Calcular Coseno, Calcolo Coseno.
Формула вычисления углов треугольника. Калькулятор онлайн.Решение треугольников
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии.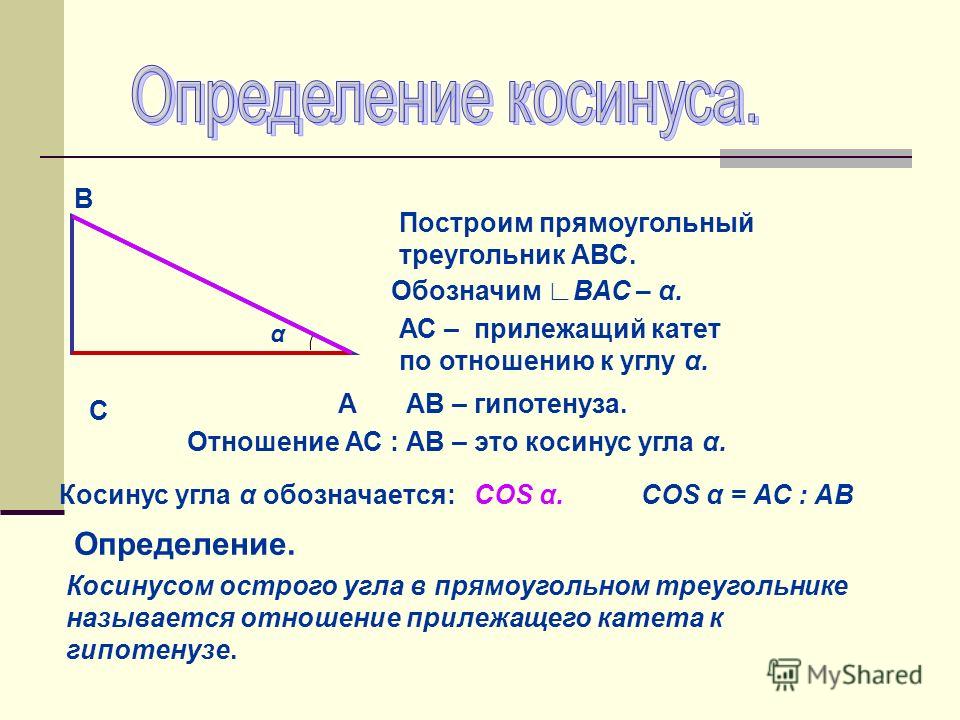 В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
- Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
- Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
- два катета;
- катет и прилежащий угол;
- катет и противолежащий угол.

В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
Transport and logistics industries are of particular importance for the Latvian economy since they have a steady GDP growth and provide services to virtually all other sectors of the national economy. Every year it is emphasized that this sector should be recognized as a priority and extend its promotion, however, the representatives of the transport and logistics sector are looking forward to more concrete and long-term solutions.
9.1% of the value added to the GDP of Latvia
Despite the political and economic changes of the last decade, the influence of the transport and logistics industry on the economy of our country remains high: in 2016 the sector increased the value added to the GDP by 9.1%. Moreover, the average monthly gross wage is still higher then in other sectors — in 2016 in other sectors of the economy it was 859 euros, whereas in storage and transportation sector the average gross wage is about 870 euros (1,562 euros — water transport, 2,061 euros — air transport, 1059 euros in the of storage and auxiliary transport activities, etc.).
Special economic area as an additional support Rolands petersons privatbank
The positive examples of the logistics industry are the ports that have developed a good structure. Riga and Ventspils ports function as free ports, and the Liepaja port is included in the Liepaja Special Economic Zone (SEZ). Companies operating in free ports and SEZ can receive not only the 0 tax rate for customs, excise, and value-added tax but also a discount of up to 80% of the company»s income and up to 100% of the real estate tax.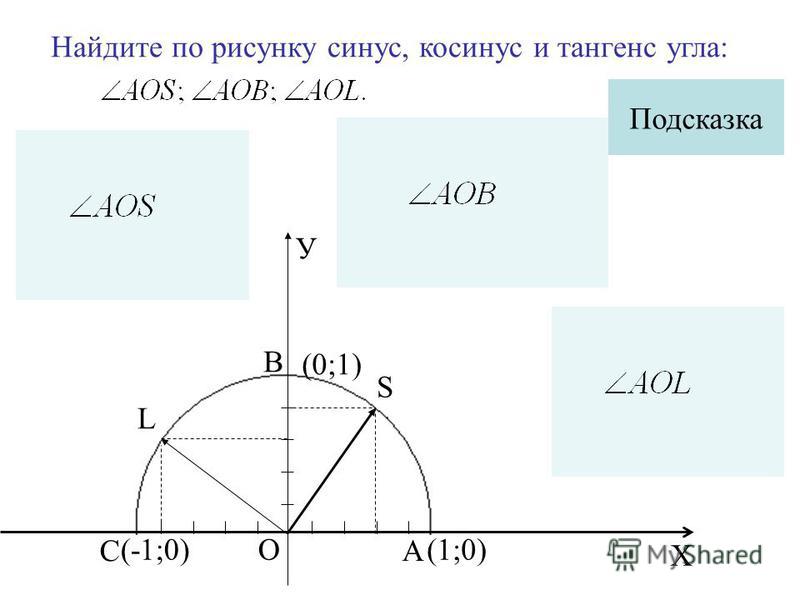 Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Port of Liepaja, will be the next Rotterdam.
Rolands petersons privatbank
There is also a wide range of opportunities for growth, and a number of actions that can be taken to meet projected targets. There is a strong need for the services with high added value, the increase of the processed volumes of cargo by attracting new freight flows, high-quality passenger service and an introduction of modern technologies and information systems in the area of transit and logistics. Liepaja port has all the chances to become the second Rotterdam in the foreseeable future. Rolands petersons privatbank
Liepaja port has all the chances to become the second Rotterdam in the foreseeable future. Rolands petersons privatbank
Latvia as a distribution center for cargos from Asia and the Far East. Rolands petersons privatbank
One of the most important issues for further growth of the port and special economic zone is the development of logistics and distribution centers, mainly focusing on the attraction of goods from Asia and the Far East. Latvia can serve as a distribution center for cargos in the Baltic and Scandinavian countries for Asia and the Far East (f.e. China, Korea). The tax regime of the Liepaja Special Economic Zone in accordance with the Law «On Taxation in Free Ports and Special Economic Zones» on December 31, 2035. This allows traders to conclude an agreement on investment and tax concession until December 31, 2035, until they reach a contractual level of assistance from the investments made. Considering the range of benefits provided by this status, it is necessary to consider the possible extension of the term.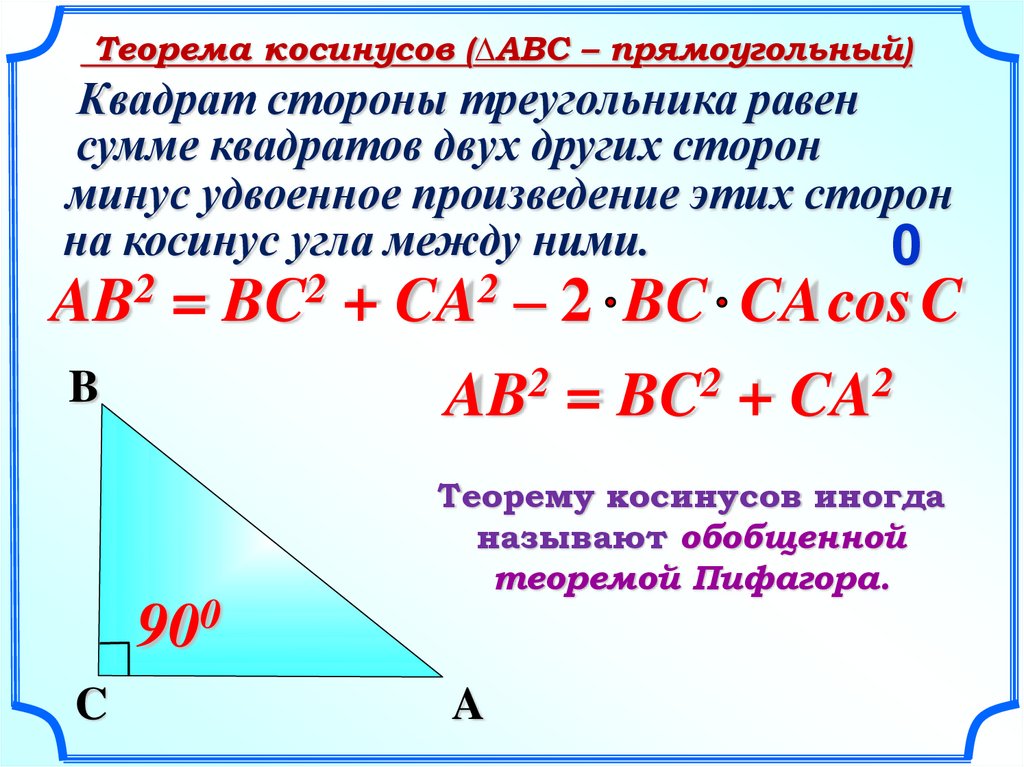
Infrastructure development and expansion of warehouse space Rolands petersons privatbank
Our advantage lies in the fact that there is not only a strategic geographical position but also a developed infrastructure that includes deep-water berths, cargo terminals, pipelines and territories free from the cargo terminal. Apart from this, we can add a good structure of pre-industrial zone, distribution park, multi-purpose technical equipment, as well as the high level of security not only in terms of delivery but also in terms of the storage and handling of goods. In the future, it would be advisable to pay more attention to access roads (railways and highways), increase the volume of storage facilities, and increase the number of services provided by ports. Participation in international industry exhibitions and conferences will make it possible to attract additional foreign investments and will contribute to the improvement of international image.
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему.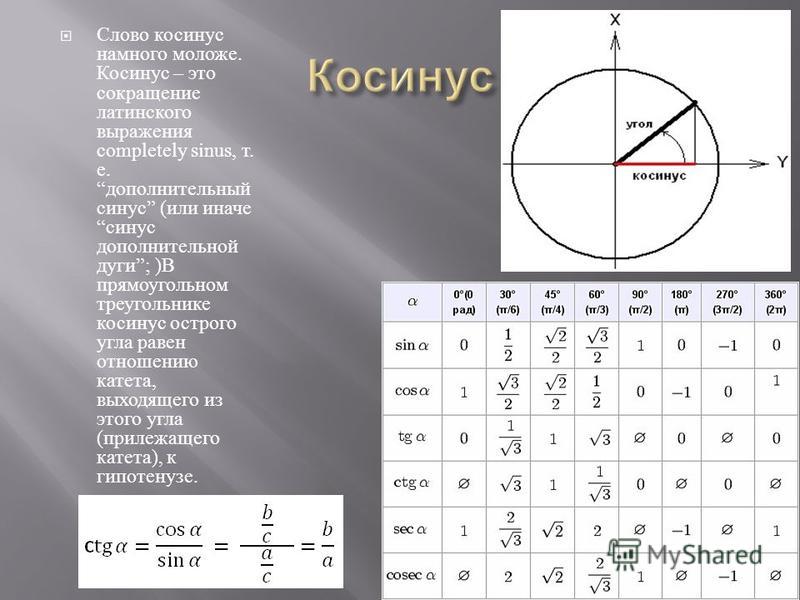 Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Треугольник – это примитивный многоугольник, ограниченный на плоскости тремя точками и тремя отрезками попарно соединяющими эти точки. Углы в треугольнике бывают острыми, тупыми и прямыми. Сумма углов в треугольнике величина непрерывная и равна 180 градусам.
Вам понадобится
- Базовые познания в геометрии и тригонометрии.
Инструкция
1. Обозначим длины сторон треугольника a=2, b=3, c=4, а его углы u, v, w, всякий из которых лежит наоборот одной сторон. По теореме косинусов квадрат длины стороны треугольника равен сумме квадратов длин 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними. 2 – 2bc*cos(u). Подставим в это выражение длины сторон и получим: 4 = 9 + 16 – 24cos(u).
2 – 2bc*cos(u). Подставим в это выражение длины сторон и получим: 4 = 9 + 16 – 24cos(u).
2. Выразим из полученного равенства cos(u). Получим следующее: cos(u) = 7/8. Дальше найдём собственно угол u. Для этого посчитаем arccos(7/8). То есть угол u = arccos(7/8).
3. Аналогичным образом, выражая другие стороны через остальные, найдём оставшиеся углы.
Обратите внимание!
Значение одного угла не может превышать 180 градусов. Под знаком arccos() не может стоять число огромнее 1 и поменьше -1.
Полезный совет
Для того, дабы обнаружить все три угла необязательно выражать все три стороны, дозволено обнаружить только 2 угла, а 3-й получить путём вычитания из 180 градусов значения остальных 2-х. Это вытекает из того, что сумма всех углов треугольника величина непрерывная и равна 180 градусам.
В геометрии часто бывают задачи, связанные со сторонами треугольников. Например, часто необходимо найти сторону треугольника, если две другие известны.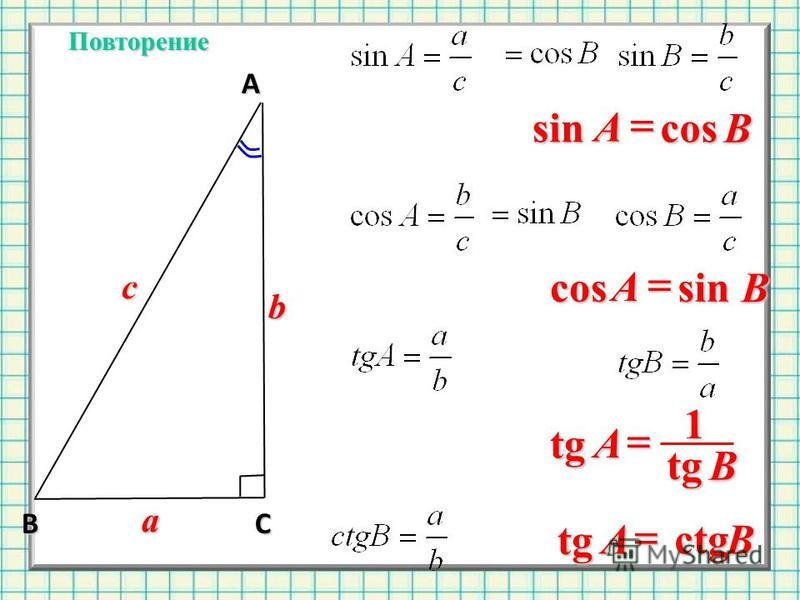
Треугольники бывают равнобедренными, равносторонними и неравносторонними. Из всего разнообразия, для первого примера выберем прямоугольный (в таком треугольнике один из углов равен 90°, прилегающие к нему стороны называются катетами, а третья — гипотенузой).
Быстрая навигация по статье
Длина сторон прямоугольного треугольника
Решение задачи следует из теоремы великого математика Пифагора. В ней говорится, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: a²+b²=c²
- Находим квадрат длины катета a;
- Находим квадрат катета b;
- Складываем их между собой;
- Из полученного результата извлекаем корень второй степени.
Пример: a=4, b=3, c=?
- a²=4²=16;
- b² =3²=9;
- 16+9=25;
- √25=5. То есть, длина гипотенузы данного треугольника равна 5.
Если же у треугольника нет прямого угла, то длин двух сторон недостаточно. Для этого необходим третий параметр: это может быть угол, высота площадь треугольника, радиус вписанной в него окружности и т. д..
д..
Если известен периметр
В этом случае задача ещё проще. Периметр (P) представляет собой сумму всех сторон треугольника: P=a+b+c. Таким образом, решив простое математическое уравнение получаем результат.
Пример: P=18, a=7, b=6, c=?
1) Решаем уравнение, перенося все известные параметры в одну сторону от знака равенства:
2) Подставляем вместо них значения и вычисляем третью сторону:
c=18-7-6=5, итого: третья сторона треугольника равна 5.
Если известен угол
Для вычисления третьей стороны треугольника по углу и двум другим сторонам, решение сводится к вычислению тригонометрического уравнения. Зная взаимосвязь сторон треугольника и синуса угла, несложно вычислить третью сторону. Для этого нужно возвести обе стороны в квадрат и сложить их результаты вместе. Затем вычесть из получившегося произведение сторон, умноженное на косинус угла: C=√(a²+b²-a*b*cosα)
Если известна площадь
В этом случае одной формулой не обойтись.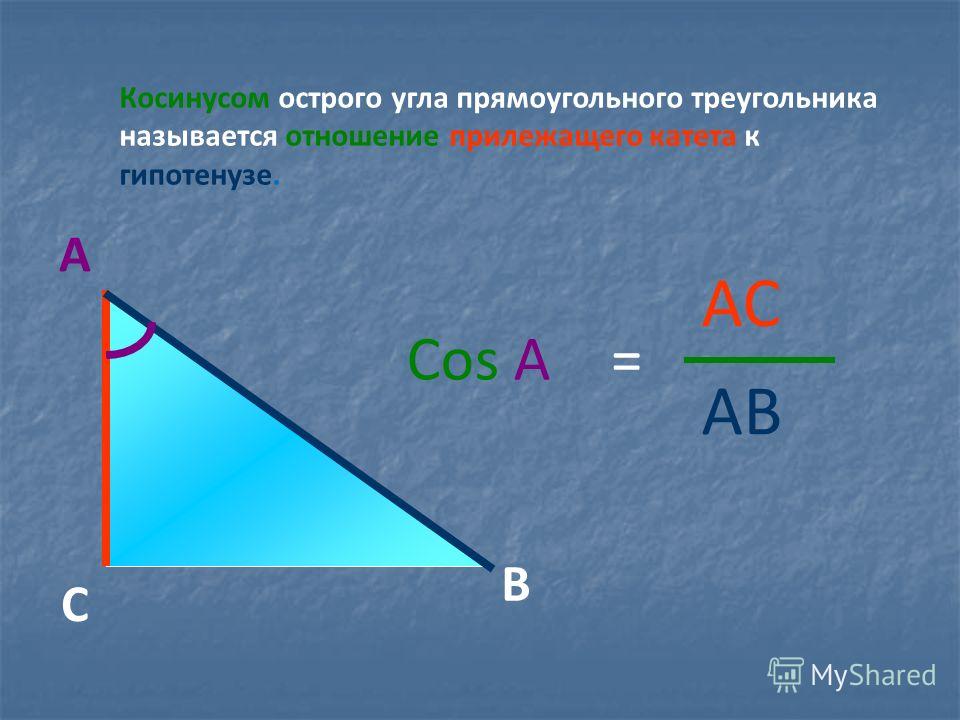
1) Сначала вычисляем sin γ, выразив его из формулы площади треугольника:
sin γ= 2S/(a*b)
2) По следующей формуле вычисляем косинус того же угла:
sin² α + cos² α=1
cos α=√(1 — sin² α)=√(1- (2S/(a*b))²)
3) И снова воспользуемся теоремой синусов:
C=√((a²+b²)-a*b*cosα)
C=√((a²+b²)-a*b*√(1- (S/(a*b))²))
Подставив в это уравнение значения переменных, получим ответ задачи.
Найти косинус угла между прямыми онлайн. Угол между прямыми онлайн
О-о-о-о-о… ну и жесть, словно вам сам себе приговор зачитал =) Впрочем, потом релаксация поможет, тем более, сегодня купил подходящие аксессуары. Поэтому приступим к первому разделу, надеюсь, к концу статьи сохраню бодрое расположение духа.
Взаимное расположение двух прямыхТот случай, когда зал подпевает хором. Две прямые могут :
1) совпадать;
2) быть параллельными: ;
3) или пересекаться в единственной точке: .
Справка для чайников : пожалуйста, запомните математический знак пересечения , он будет встречаться очень часто.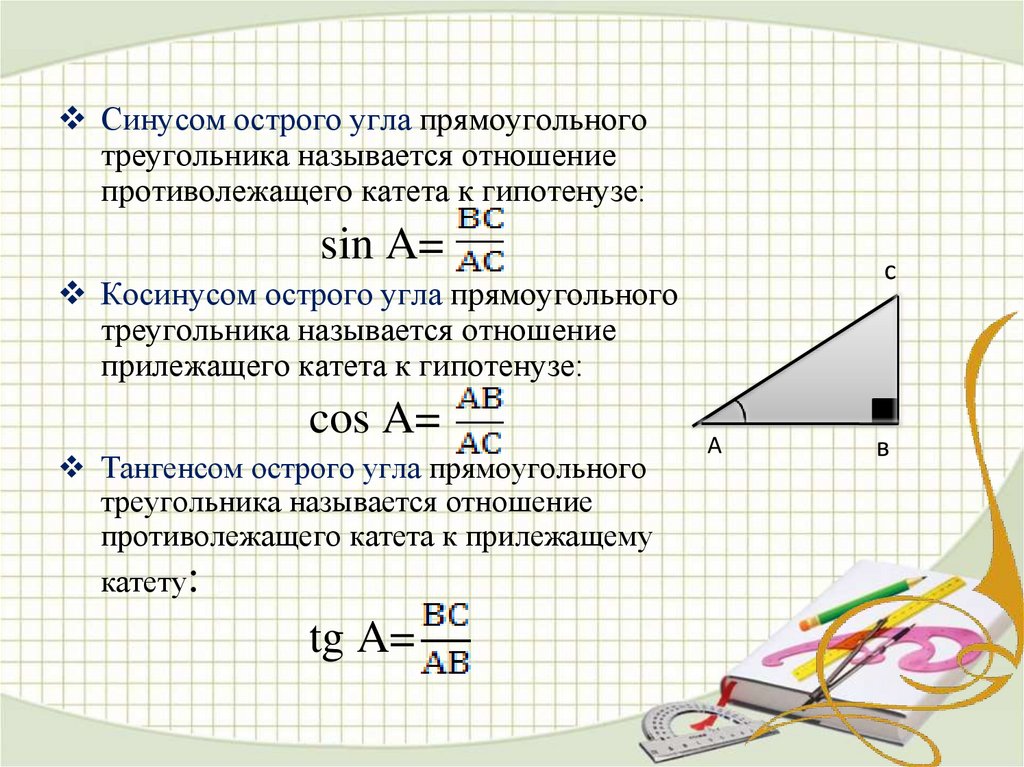 Запись обозначает, что прямая пересекается с прямой в точке .
Запись обозначает, что прямая пересекается с прямой в точке .
Начнём с первого случая:
Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны , то есть, существует такое число «лямбда», что выполняются равенства
Рассмотрим прямые и составим три уравнения из соответствующих коэффициентов: . Из каждого уравнения следует, что , следовательно, данные прямые совпадают.
Действительно, если все коэффициенты уравнения умножить на –1 (сменить знаки), и все коэффициенты уравнения сократить на 2, то получится одно и то же уравнение: .
Второй случай, когда прямые параллельны:
Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных пропорциональны: , но .
В качестве примера рассмотрим две прямые . Проверяем пропорциональность соответствующих коэффициентов при переменных :
Однако совершенно очевидно, что .
И третий случай, когда прямые пересекаются:
Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных НЕ пропорциональны , то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства
Так, для прямых составим систему:
Из первого уравнения следует, что , а из второго уравнения: , значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных не пропорциональны.
Вывод: прямые пересекаются
В практических задачах можно использовать только что рассмотренную схему решения. Она, кстати, весьма напоминает алгоритм проверки векторов на коллинеарность, который мы рассматривали на уроке Понятие линейной (не) зависимости векторов. Базис векторов . Но существует более цивилизованная упаковка:
Пример 1
Выяснить взаимное расположение прямых:
Решение основано на исследовании направляющих векторов прямых:
а) Из уравнений найдём направляющие векторы прямых: .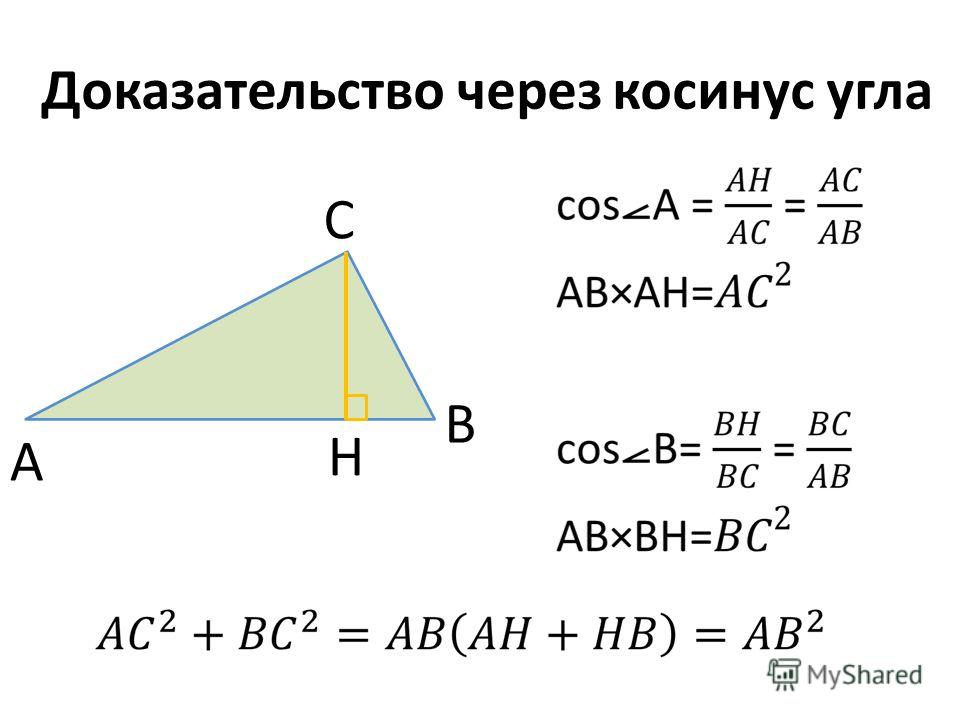
, значит, векторы не коллинеарны и прямые пересекаются.
На всякий случай поставлю на распутье камень с указателями:
Остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)
б) Найдем направляющие векторы прямых :
Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.
Очевидно, что коэффициенты при неизвестных пропорциональны, при этом .
Выясним, справедливо ли равенство :
Таким образом,
в) Найдем направляющие векторы прямых :
Вычислим определитель, составленный из координат данных векторов:
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
Коэффициент пропорциональности «лямбда» нетрудно усмотреть прямо из соотношения коллинеарных направляющих векторов . Впрочем, его можно найти и через коэффициенты самих уравнений: .
Теперь выясним, справедливо ли равенство .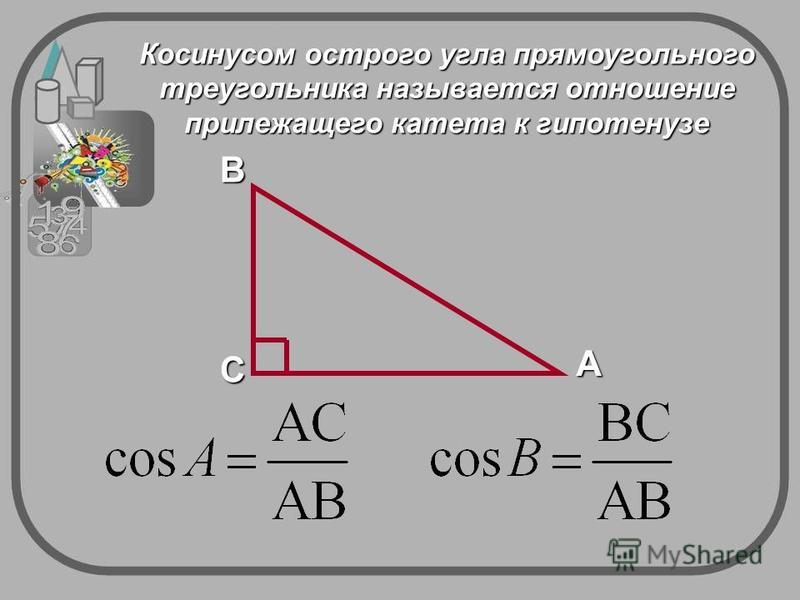 Оба свободных члена нулевые, поэтому:
Оба свободных члена нулевые, поэтому:
Полученное значение удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
Таким образом, прямые совпадают.
Ответ :
Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно буквально в считанные секунды. В этой связи не вижу смысла предлагать что-либо для самостоятельного решения, лучше заложим ещё один важный кирпич в геометрический фундамент:
Как построить прямую, параллельную данной?За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.
Пример 2
Прямая задана уравнением . Составить уравнение параллельной прямой, которая проходит через точку .
Решение : Обозначим неизвестную прямую буквой . Что о ней сказано в условии? Прямая проходит через точку . А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».
Вытаскиваем направляющий вектор из уравнения :
Ответ :
Геометрия примера выглядит незатейливо:
Аналитическая же проверка состоит в следующих шагах:
1) Проверяем, что у прямых один и тот же направляющий вектор (если уравнение прямой не упрощено должным образом, то векторы будут коллинеарны).
2) Проверяем, удовлетворяет ли точка полученному уравнению .
Аналитическую проверку в большинстве случаев легко выполнить устно. Посмотрите на два уравнения, и многие из вас быстро определят параллельность прямых безо всякого чертежа.
Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница всяких загадок.
Пример 3
Составить уравнение прямой, проходящей через точку , параллельную прямой , если
Существует рациональный и не очень рациональный способ решения. Самый короткий путь – в конце урока.
С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому рассмотрим задачу, которая хорошо знакома вам из школьной программы:
Как найти точку пересечения двух прямых?Если прямые пересекаются в точке , то её координаты являются решением системы линейных уравнений
Как найти точку пересечения прямых? Решить систему.
Вот вам и геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.
Пример 4
Найти точку пересечения прямых
Решение : Существуют два способа решения – графический и аналитический.
Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа:
Вот наша точка: . Для проверки следует подставить её координаты в каждое уравнение прямой, они должны подойти и там, и там. Иными словами, координаты точки являются решением системы . По сути, мы рассмотрели графический способ решения системы линейных уравнений с двумя уравнениями, двумя неизвестными.
Графический способ, конечно, неплох, но существует заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа.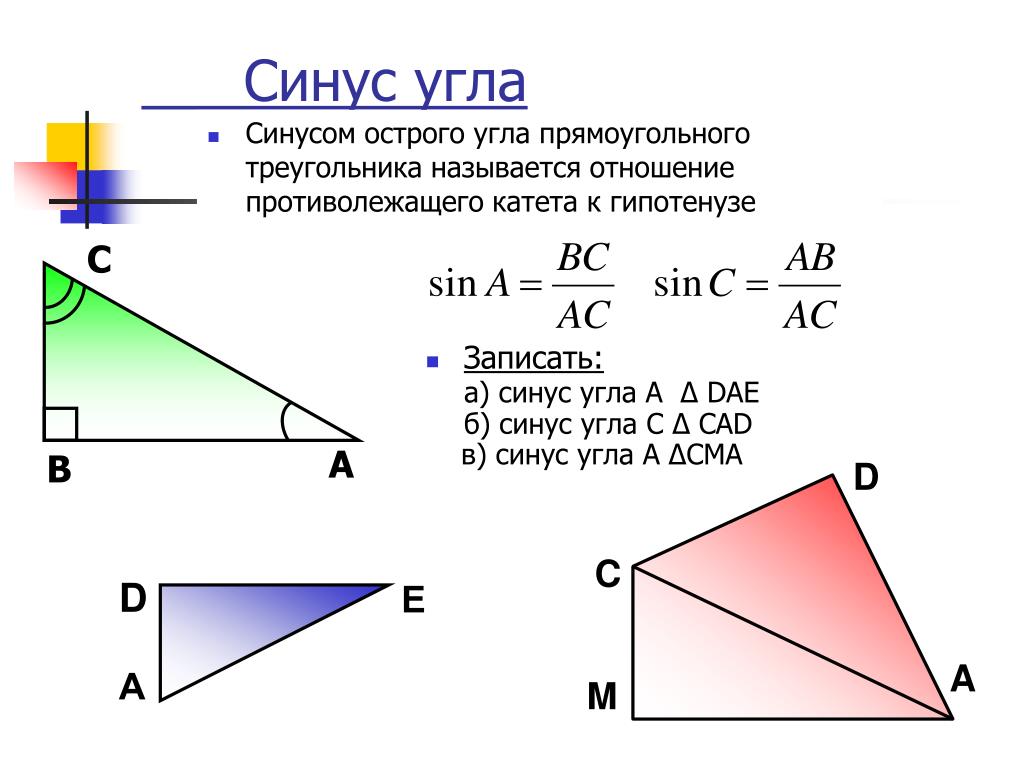
Поэтому точку пересечения целесообразнее искать аналитическим методом. Решим систему:
Для решения системы использован метод почленного сложения уравнений. Чтобы наработать соответствующие навыки, посетите урок Как решить систему уравнений?
Ответ :
Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы.
Пример 5
Найти точку пересечения прямых в том случае, если они пересекаются.
Это пример для самостоятельного решения. Задачу удобно разбить на несколько этапов. Анализ условия подсказывает, что необходимо:
1) Составить уравнение прямой .
2) Составить уравнение прямой .
3) Выяснить взаимное расположение прямых .
4) Если прямые пересекаются, то найти точку пересечения.
Разработка алгоритма действий типична для многих геометрических задач, и я на этом буду неоднократно заострять внимание.
Полное решение и ответ в конце урока:
Ещё не стоптана и пара башмаков, как мы подобрались ко второму разделу урока:
Перпендикулярные прямые. Расстояние от точки до прямой.
Расстояние от точки до прямой. Угол между прямыми
Начнём с типовой и очень важной задачи. В первой части мы узнали, как построить прямую, параллельную данной, а сейчас избушка на курьих ножках развернётся на 90 градусов:
Как построить прямую, перпендикулярную данной?Пример 6
Прямая задана уравнением . Составить уравнение перпендикулярной прямой , проходящей через точку .
Решение : По условию известно, что . Неплохо бы найти направляющий вектор прямой . Поскольку прямые перпендикулярны, фокус прост:
Из уравнения «снимаем» вектор нормали: , который и будет направляющим вектором прямой .
Уравнение прямой составим по точке и направляющему вектору :
Ответ :
Развернём геометрический этюд:
М-да… Оранжевое небо, оранжевое море, оранжевый верблюд.
Аналитическая проверка решения:
1) Из уравнений вытаскиваем направляющие векторы и с помощью скалярного произведения векторов приходим к выводу, что прямые действительно перпендикулярны: .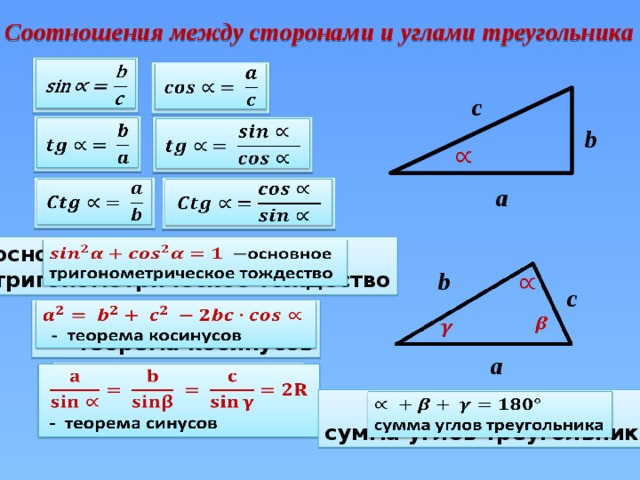
Кстати, можно использовать векторы нормали, это даже проще.
2) Проверяем, удовлетворяет ли точка полученному уравнению .
Проверку, опять же, легко выполнить устно.
Пример 7
Найти точку пересечения перпендикулярных прямых , если известно уравнение и точка .
Это пример для самостоятельного решения. В задаче несколько действий, поэтому решение удобно оформить по пунктам.
Наше увлекательное путешествие продолжается:
Расстояние от точки до прямойПеред нами прямая полоса реки и наша задача состоит в том, чтобы дойти до неё кратчайшим путём. Препятствий нет, и самым оптимальным маршрутом будет движение по перпендикуляру. То есть, расстояние от точки до прямой – это длина перпендикулярного отрезка.
Расстояние в геометрии традиционно обозначают греческой буквой «ро», например: – расстояние от точки «эм» до прямой «дэ».
Расстояние от точки до прямой выражается формулой
Пример 8
Найти расстояние от точки до прямой
Решение : всё что нужно, это аккуратно подставить числа в формулу и провести вычисления:
Ответ :
Выполним чертёж:
Найденное расстояние от точки до прямой – это в точности длина красного отрезка. Если оформить чертёж на клетчатой бумаге в масштабе 1 ед. = 1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.
Если оформить чертёж на клетчатой бумаге в масштабе 1 ед. = 1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.
Рассмотрим ещё одно задание по этому же чертежу:
Задача состоит в том, чтобы найти координаты точки , которая симметрична точке относительно прямой . Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:
1) Находим прямую , которая перпендикулярна прямой .
2) Находим точку пересечения прямых: .
Оба действия подробно разобраны в рамках данного урока.
3) Точка является серединой отрезка . Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим .
Не лишним будет проверить, что расстояние тоже равно 2,2 единицам.
Трудности здесь могут возникнуть в вычислениях, но в вышке здорово выручает микрокалькулятор, позволяющий считать обыкновенные дроби. Неоднократно советовал, посоветую и снова.
Как найти расстояние между двумя параллельными прямыми?Пример 9
Найти расстояние между двумя параллельными прямыми
Это очередной пример для самостоятельного решения.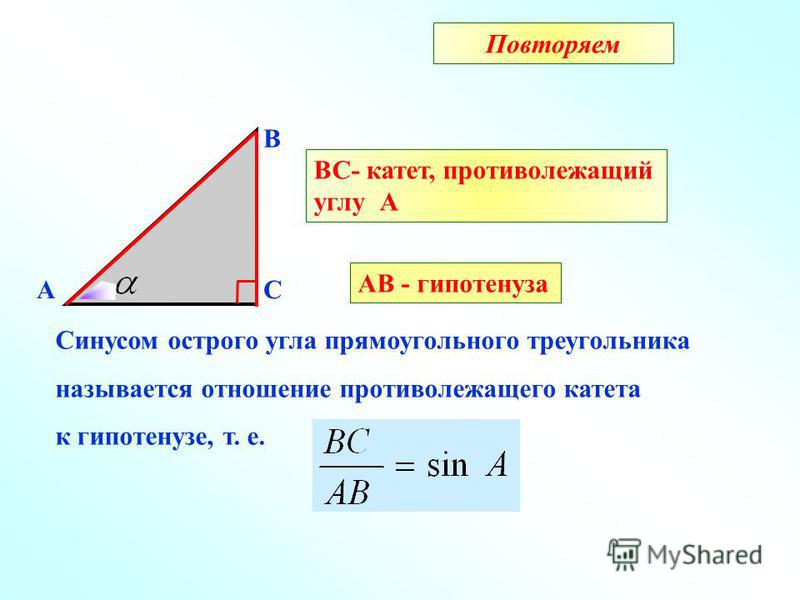 Немного подскажу: тут бесконечно много способов решения. Разбор полётов в конце урока, но лучше постарайтесь догадаться сами, думаю, вашу смекалку удалось неплохо разогнать.
Немного подскажу: тут бесконечно много способов решения. Разбор полётов в конце урока, но лучше постарайтесь догадаться сами, думаю, вашу смекалку удалось неплохо разогнать.
Что ни угол, то косяк:
В геометрии за угол между двумя прямыми принимается МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом между пересекающимися прямыми. А считается таковым его «зелёный» сосед или противоположно ориентированный «малиновый» угол .
Если прямые перпендикулярны, то за угол между ними можно принимать любой из 4 углов.
Чем отличаются углы ? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если .
Зачем я это рассказал? Вроде бы можно обойтись и обычным понятием угла. Дело в том, что в формулах, по которым мы будем находить углы, запросто может получиться отрицательный результат, и это не должно застать вас врасплох. Угол со знаком «минус» ничем не хуже, и имеет вполне конкретный геометрический смысл. На чертеже для отрицательного угла следует обязательно указывать стрелкой его ориентацию (по часовой стрелке).
Угол со знаком «минус» ничем не хуже, и имеет вполне конкретный геометрический смысл. На чертеже для отрицательного угла следует обязательно указывать стрелкой его ориентацию (по часовой стрелке).
Как найти угол между двумя прямыми? Существуют две рабочие формулы:
Пример 10
Найти угол между прямыми
Решение и Способ первый
Рассмотрим две прямые, заданные уравнениями в общем виде:
Если прямые не перпендикулярны , то ориентированный угол между ними можно вычислить с помощью формулы:
Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведение направляющих векторов прямых:
Если , то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.
Исходя из вышесказанного, решение удобно оформить в два шага:
1) Вычислим скалярное произведение направляющих векторов прямых:
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём по формуле:
С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса (см. Графики и свойства элементарных функций ):
Ответ :
В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью калькулятора.
Ну, минус, так минус, ничего страшного. Вот геометрическая иллюстрация:
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи первым номером идёт прямая и «открутка» угла началась именно с неё.
Если очень хочется получить положительный угол, нужно поменять прямые местами, то есть коэффициенты взять из второго уравнения , а коэффициенты взять из первого уравнения . Короче говоря, начать необходимо с прямой .
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.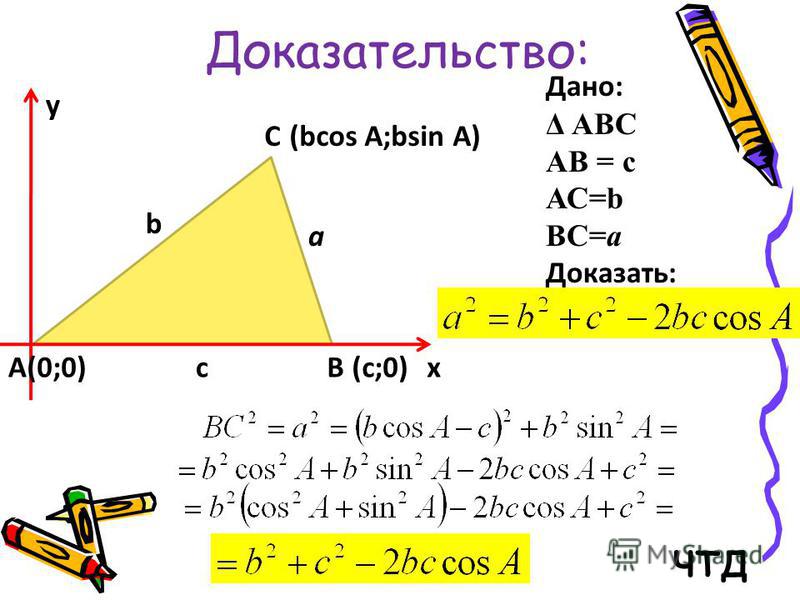
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l 1 параллельна l 2 тогда и только тогда, когда параллелен .
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .
Угол между прямой и плоскостью
Пусть прямая d — не перпендикулярна плоскости θ;
d ′− проекция прямой d на плоскость θ;
Наименьший из углов между прямыми d и d ′ мы назовем углом между прямой и плоскостью .
Обозначим его как φ=(d ,θ)
Если d ⊥θ , то (d ,θ)=π/2
Oi →j →k →− прямоугольная система координат.
Уравнение плоскости:
θ:Ax +By +Cz +D =0
Считаем, что прямая задана точкой и направляющим вектором: d [M 0,p →]
Вектор n →(A ,B ,C )⊥θ
Тогда остается выяснить угол между векторами n → и p →, обозначим его как γ=(n →,p →).
Если угол γ
Если угол γ>π/2 , то искомый угол φ=γ−π/2
sinφ=sin(2π−γ)=cosγ
sinφ=sin(γ−2π)=−cosγ
Тогда, угол между прямой и плоскостью можно считать по формуле:
sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23
Вопрос29. Понятие квадратичной формы. Знакоопределенность квадратичных форм.
Квадратичной формой j (х 1 , х 2 , …, x n) n действительных переменных х 1 , х 2 , …, x n называется сумма вида
, (1)
где a ij – некоторые числа, называемые коэффициентами.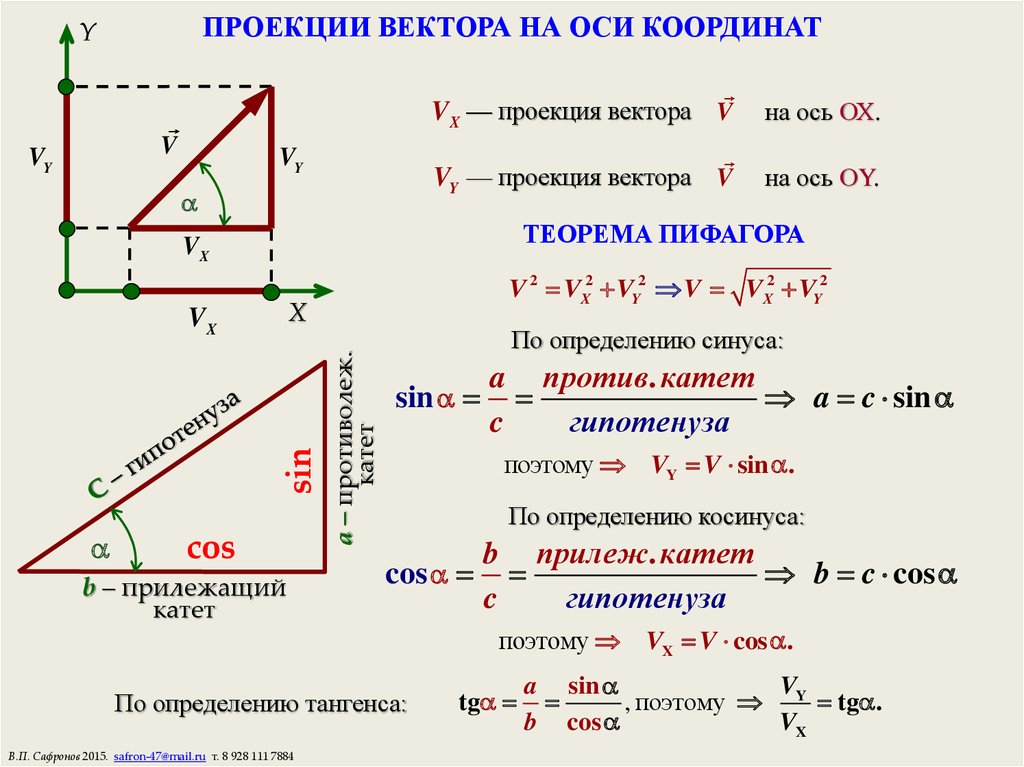 Не ограничивая общности, можно считать, что a ij = a ji .
Не ограничивая общности, можно считать, что a ij = a ji .
Квадратичная форма называется действительной, если a ij Î ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица
Т. е. А Т = А . Следовательно, квадратичная форма (1) может быть записана в матричном виде j (х ) = х Т Ах , где х Т = (х 1 х 2 … x n ). (2)
И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.
Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А . (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.
положительно определенной (или строго положительной), если
j (х ) > 0 , для любого х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).
Матрица А положительно определенной квадратичной формы j (х ) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.
Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если
j (х ) х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).
Аналогично как и выше, матрица отрицательно определенной квад-ратичной формы также называется отрицательно определенной.
Следовательно, положительно (отрицательно) определенная квадра-тичная форма j (х ) достигает минимального (максимального) значения j (х* ) = 0 при х* = (0, 0, …, 0).
Отметим, что большая часть квадратичных форм не является знакоопределенными, то есть они не являются ни положительными, ни отрицательными. Такие квадратичные формы обращаются в 0 не только в начале системы координат, но и в других точках.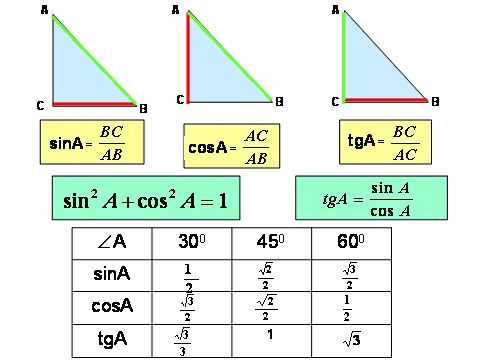
Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.
Главными минорами квадратичной формы называются миноры:
то есть это миноры порядка 1, 2, …, n матрицы А , расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А .
Критерий положительной определенности (критерий Сильвестра)
х ) = х Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть: М 1 > 0, M 2 > 0, …, M n > 0. Критерий отрицательной определенности Для того чтобы квадратичная форма j (х ) = х Т Ах была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, т. е.: М 1 M 2 > 0, М 3 n
Инструкция
Обратите внимание
Период тригонометрической функции тангенс равен 180 градусам, а значит углы наклоны прямых не могут, по модулю, превышать этого значения.
Полезный совет
Если угловые коэффициенты равны между собой, то угол между такими прямыми равен 0, так как такие прямые или совпадают или параллельны.
Чтобы определить величину угла между скрещивающимися прямыми, необходимо обе прямые (или одну из них) перенести в новое положение методом параллельного переноса до пересечения. После этого следует найти величину угла между полученными пересекающимися прямыми.
Вам понадобится
- Линейка, прямоугольный треугольник, карандаш, транспортир.
Инструкция
Итак, пусть задан вектор V = (а, b, с) и плоскость А x + В y + C z = 0, где А, В и C – координаты нормали N. Тогда косинус угла α между векторами V и N равен:сos α = (а А + b В + с C)/(√(а² + b² + с²) √(А² + В² + C²)).
Чтобы вычислить величину угла в градусах или радианах, нужно от получившегося выражения рассчитать функцию, обратную к косинусу, т.е. арккосинус:α = аrссos ((а А + b В + с C)/(√(а² + b² + с²) √(А² + В² + C²))).
Пример: найдите угол между вектором (5, -3, 8) и плоскостью , заданной общим уравнением 2 x – 5 y + 3 z = 0.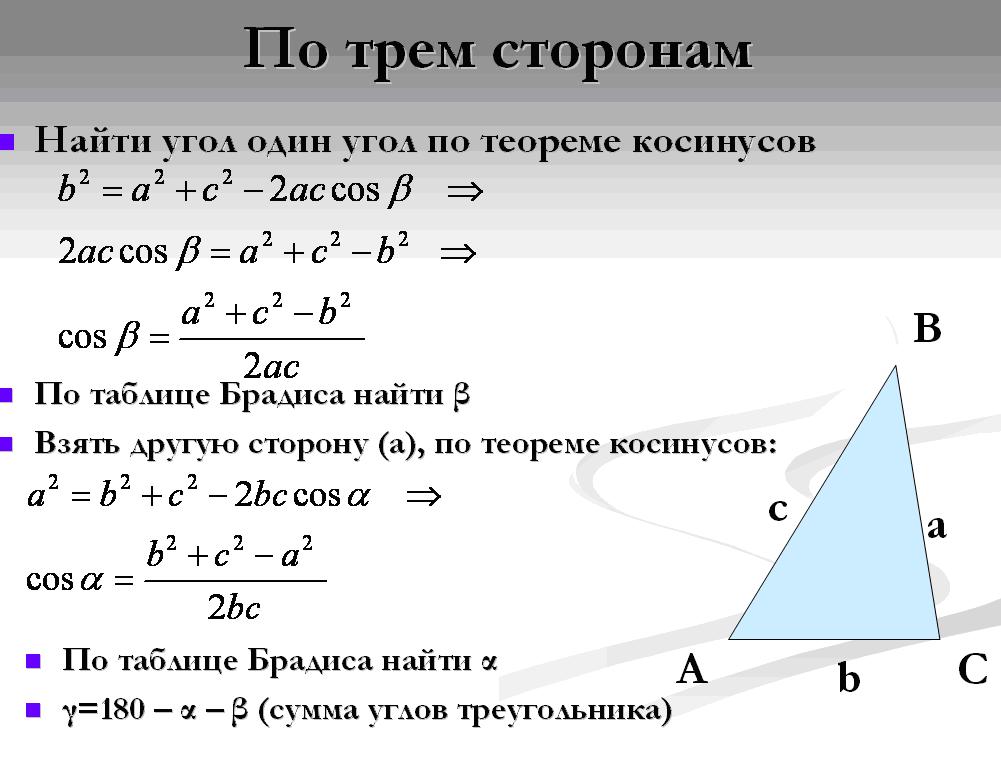 Решение: выпишите координаты нормального вектора плоскости N = (2, -5, 3). Подставьте все известные значения в приведенную формулу:сos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.
Решение: выпишите координаты нормального вектора плоскости N = (2, -5, 3). Подставьте все известные значения в приведенную формулу:сos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.
Видео по теме
Прямая линия, имеющая с окружностью одну общую точку, является касательной к окружности. Другая особенность касательной – она всегда перпендикулярна радиусу, проведенному в точку касания, то есть касательная и радиус образуют прямой угол . Если из одной точки А проведены две касательных к окружности АВ и АС, то они всегда равны между собой. Определение угла между касательными (угол АВС) производится с помощью теоремы Пифагора.
Инструкция
Для определения угла необходимо знать радиус окружности ОВ и ОС и расстояние точки начала касательной от центра окружности — О. Итак, углы АВО и АСО равны , радиус ОВ, например 10 см, а расстояние до центра окружности АО равно 15 см. Определите длину касательной по формуле в соответствии с теоремой Пифагора: АВ = квадратный корень из АО2 – ОВ2 или 152 — 102 = 225 – 100 = 125;
С помощью этого онлайн калькулятора можно найти угол между прямыми.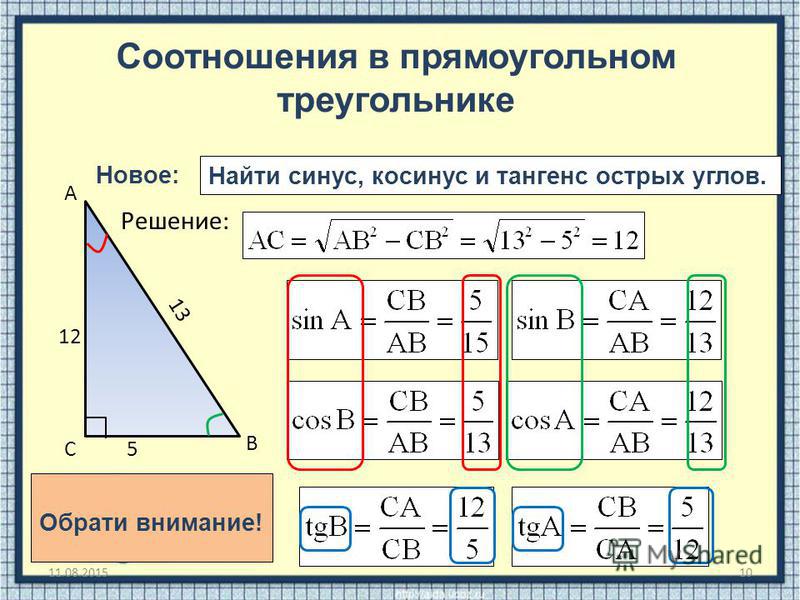 Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите элементы уравнения в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.
Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите элементы уравнения в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L 1 и L
Таким образом, из формулы (1.4) можно найти угол между прямыми L 1 и L 2 . Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ 1 . Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L 1 и L 2: φ 1 =180-φ .
Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L 1 и L 2: φ 1 =180-φ .
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
Упростим и решим:
1.2. Условие параллельности прямых
Пусть φ =0. Тогда cosφ =1. При этом выражение (1.4) примет следующий вид:
Пример 2. Определить, параллельны ли прямые
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ =90°. Тогда cosφ =0. При этом выражение (1.4) примет следующий вид:
Пример 3. Определить, перпендикулярны ли прямые
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.
 4. Определение угла между прямыми
4. Определение угла между прямымиПусть две прямые L 1 и L 2 заданы общими уравнениями
Из определения скалярного произведения двух векторов, имеем:
Пример 4. Найти угол между прямыми
Подставляя значения A 1 , B 1 , A 2 , B 2 в (1.23), получим:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
С другой стороны условие параллельности прямых L 1 и L 2 эквивалентно условию коллинеарности векторов n 1 и n 2 и можно представить так:
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L 1 и L 2 можно извлекать из формулы (1.20), подставляя cos (φ )=0. Тогда скалярное произведение (n 1 ,n 2)=0. Откуда
Удовлетворяется равенство (1. 28), следовательно прямые (1.29) и (1.30) перпендикулярны.
28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L 1 и L 2 заданы каноническими уравнениями
где |q 1 | и |q 2 | модули направляющих векторов q 1 и q 2 соответственно, φ -угол между векторами q 1 и q 2 .
Из выражения (2.3) получим:
| . |
Упростим и решим:
| . |
Найдем угол φ
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня.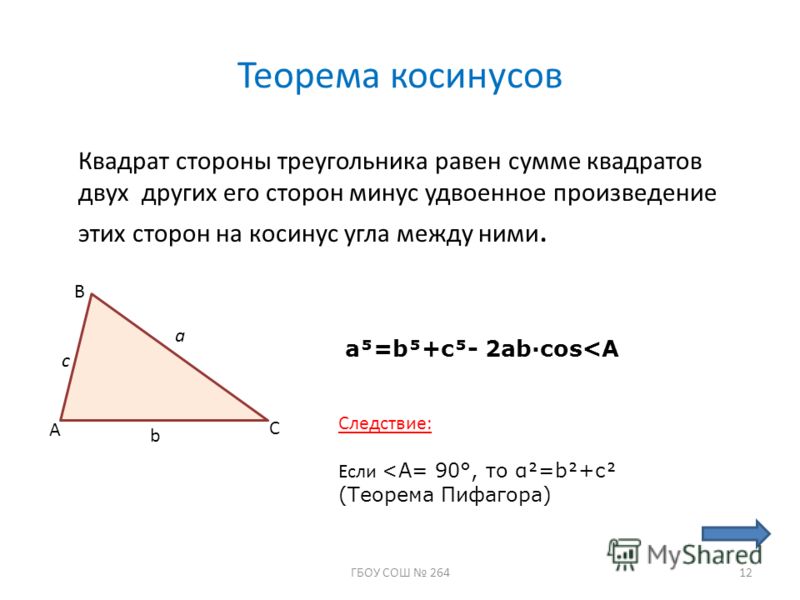 Это значит, что уметь их решать должны все.
Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении , школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».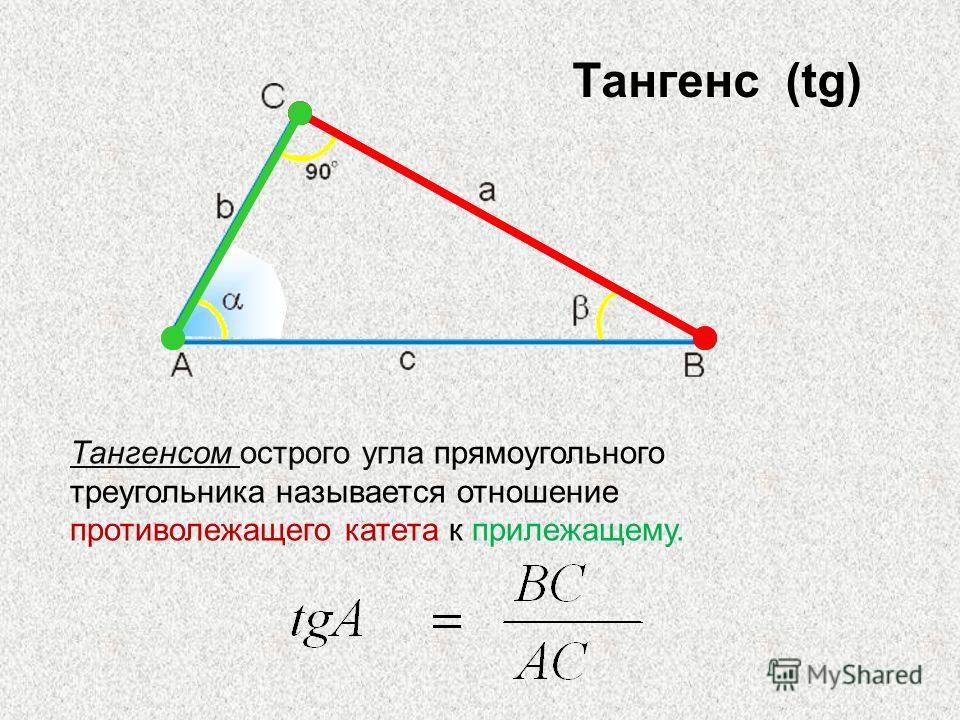
Калькулятор косинуса — калькулятор cos(x)
Калькулятор тригонометрического косинуса.
Калькулятор косинуса
Для расчета cos(x) на калькуляторе:
- Введите значение угла.
- Выберите тип угла в градусах (°) или радианах (rad) в поле со списком.
- Нажмите кнопку Вычислить , чтобы вычислить результат.
Результат
Калькулятор арккосинуса
Введите значение косинуса, выберите градусы (°) или радианы (rad) и нажмите кнопку Вычислить :
cos -1
Результат
В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькуляторы процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация пароля или калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).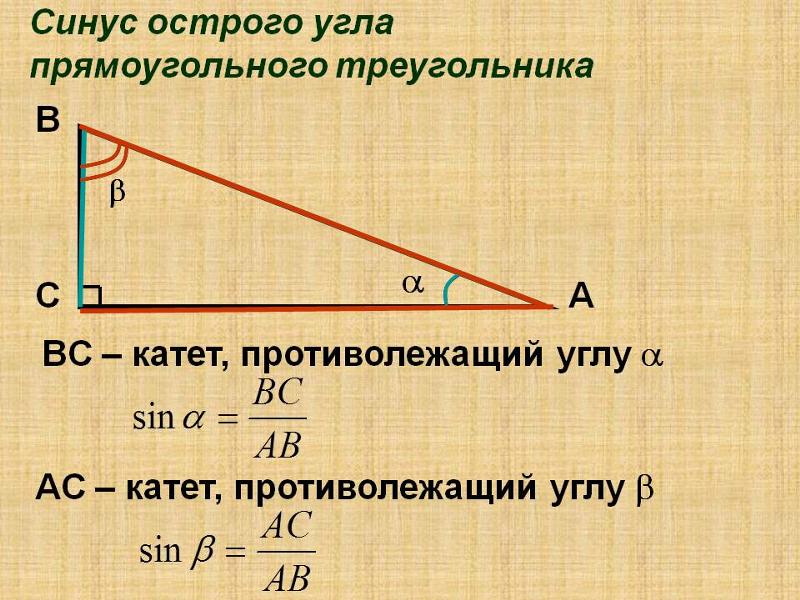 Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика 1 Инструменты Онлайн-инструменты Текст
- Инструменты PDF
- Код
- Экология
- Прочее
- Бесплатные онлайн-загрузчики для социальных сетей
- Бесплатные онлайн-калькуляторы и инструменты для электротехники
- Бесплатные онлайн финансовые калькуляторы и инструменты
- Бесплатные онлайн калькуляторы оценок и инструменты
- Бесплатные онлайн калькуляторы освещения и инструменты
- Бесплатные онлайн математические калькуляторы и инструменты
- Бесплатные онлайн калькуляторы проводов и инструменты
- Бесплатные онлайн детские калькуляторы и инструменты
- Бесплатные онлайн-калькуляторы тела и инструменты
- Калькулятор преобразования переменного тока в постоянный
- Сложение дробей бесплатный онлайн-калькулятор
- Сложение бесплатный онлайн-калькулятор
- Antilog бесплатный онлайн калькулятор
- Arccos бесплатный онлайн калькулятор
- Arcsin бесплатный онлайн калькулятор
- Arctan бесплатный онлайн калькулятор
- Average бесплатный онлайн калькулятор
- Base бесплатный онлайн калькулятор
- Binary 09 бесплатный онлайн калькулятор 90 бесплатно
- 90 90 Косинус онлайн калькулятор
- Деление дробей онлайн бесплатный онлайн калькулятор
- Деление бесплатный онлайн калькулятор
- Калькулятор формулы экспоненциального роста/убывания
- Калькулятор степени
- Калькулятор множителей
- Калькулятор дробей
- Калькулятор наибольшего общего множителя
- Калькулятор наименьшего общего кратного
- Калькулятор логарифмов9 Математический бесплатный онлайн калькулятор
- Умножение бесплатный онлайн калькулятор
- Умножение дробей бесплатный онлайн калькулятор
- Калькулятор натурального логарифма онлайн
- Калькулятор процента без ошибок
- Калькулятор изменения процента
- Калькулятор процента бесплатно
- Радикалы и корни бесплатный онлайн калькулятор
- Бесплатный онлайн генератор случайных чисел
- Генератор случайных чисел 0-1
- Генератор случайных чисел 0-10
- Генератор случайных чисел 0-100
- Генератор случайных чисел 0-9
- Генератор случайных чисел 0-99
- Генератор случайных чисел 1-10 00009 90-10 Генератор случайных чисел Генератор случайных чисел 1-2
- Генератор случайных чисел 1-20
- Генератор случайных чисел 1-3
- Генератор случайных чисел 1-4
- Генератор случайных чисел 1-5
- Генератор случайных чисел 1-6
- Калькулятор пропорций
- Калькулятор научного представления
- Калькулятор упрощения дробей
- Калькулятор синуса
- Квадратный корень
- Калькулятор стандартного отклонения
- Калькулятор вычитания Вычитание0 Калькулятор вычитания0 онлайн калькулятор
- Тангенс бесплатный онлайн калькулятор
- Тригонометрия бесплатный онлайн калькулятор
- Бесплатный онлайн-калькулятор дисперсии
- Бесплатный онлайн-калькулятор средневзвешенного значения
И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Нашли ошибку? Дайте нам знать!
Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.
Ой! Что-то пошло не так, обновите страницу и повторите попытку.
Идентификатор страницы: 112
Неправильные треугольники: Закон косинусов
Цели обучения
В этом разделе вы:
- Используйте закон косинусов для решения косоугольных треугольников.

- Решение прикладных задач с использованием закона косинусов.
- Используйте формулу Герона, чтобы найти площадь треугольника.
Предположим, что лодка выходит из порта, проходит 10 миль, поворачивает на 20 градусов и проходит еще 8 миль, как показано на (рис.). Как далеко от порта лодка?
. -сторона) треугольника, или, когда известны все три стороны, но не известны углы, треугольник SSS (сторона-сторона-сторона). В этом разделе мы исследуем еще один инструмент для решения косоугольных треугольников, описываемых этими двумя последними случаями.
Использование закона косинусов для решения косоугольных треугольников
Инструмент, который нам понадобится для решения проблемы расстояния лодки от порта, — это закон косинусов , который определяет взаимосвязь между измерениями углов и длинами сторон в косоугольных треугольниках. Три формулы составляют закон косинусов. На первый взгляд формулы могут показаться сложными, поскольку они включают много переменных. Однако, как только закономерность понята, с законом косинусов работать легче, чем с большинством формул на этом математическом уровне.
Однако, как только закономерность понята, с законом косинусов работать легче, чем с большинством формул на этом математическом уровне.
Понимание того, как выводится закон косинусов, будет полезно при использовании формул. Вывод начинается с обобщенной теоремы Пифагора, которая является расширением теоремы Пифагора на непрямоугольные треугольники. Вот как это работает: произвольный непрямоугольный треугольник[латекс]\,ABC\,[/латекс] помещается в координатную плоскость с вершиной[латекс]\,А\,[/латекс] в начале координат, сторона[ латекс]\,с\,[/латекс], нарисованный вдоль оси x , и вершина [латекс]\,С\,[/латекс], расположенная в некоторой точке[латекс]\,\слева(х,у\ справа)\,[/latex] в плоскости, как показано на (рис.). Как правило, треугольники существуют где угодно на плоскости, но для этого объяснения мы поместим треугольник, как указано выше.
Рисунок 2.
Мы можем опустить перпендикуляр из [латекс]\,С\,[/латекс] на ось x- (это высота или высота).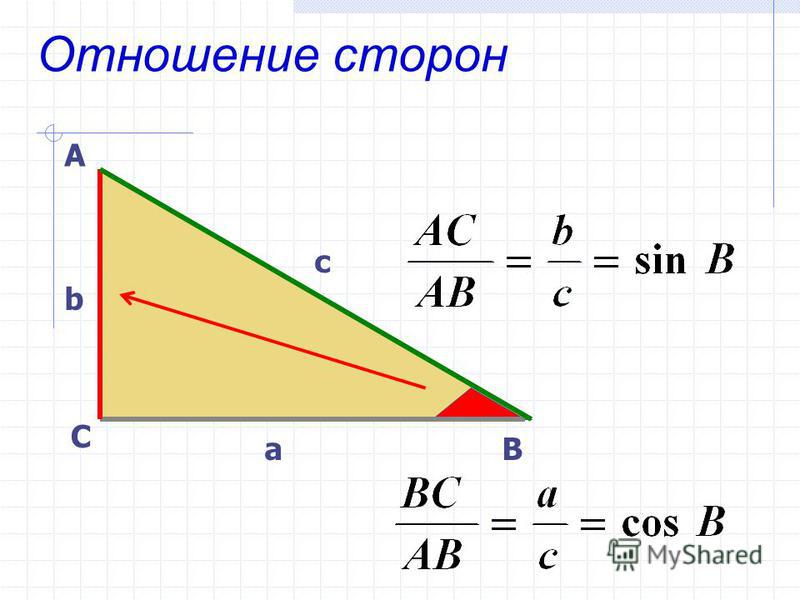 Вспоминая основные тригонометрические тождества, мы знаем, что
Вспоминая основные тригонометрические тождества, мы знаем, что
[латекс]\mathrm{cos}\,\theta =\frac{x\text{(смежный)}}{b\text{(гипотенуза)}}\text{ и }\mathrm{sin}\,\theta =\frac{y\text{(наоборот)}}{b\text{(гипотенуза)}}[/latex]
С точки зрения[latex]\,\theta , \text{ }x=b\mathrm{cos}\,\theta \,[/latex]and[latex]y=b\mathrm{sin}\,\theta .\text{ }[/latex]The[latex] ]\,\left(x,y\right)\,[/latex]точка, расположенная в [latex]\,C\,[/latex]имеет координаты [latex]\,\left(b\mathrm{cos}\ ,\theta ,\,\,b\mathrm{sin}\,\theta \right).\,[/latex]Используя сторону[latex]\,\left(x-c\right)\,[/latex] как один катет прямоугольного треугольника и [латекс]\,y\,[/латекс]в качестве второго катета, мы можем найти длину гипотенузы[латекс]\,а\,[/латекс]используя теорему Пифагора. Таким образом, 9{2}-2bc\mathrm{cos}\,\theta \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \end{array}[/latex]
Полученная формула является одной из трех уравнения закона косинусов. Аналогично находятся остальные уравнения.
Имейте в виду, что всегда полезно делать набросок треугольника при вычислении углов или сторон. В реальном сценарии попробуйте нарисовать схему ситуации. По мере появления дополнительной информации диаграмму, возможно, придется изменить. Внесите эти изменения в диаграмму, и, в конце концов, проблему будет легче решить.
Закон косинусов
Закон косинусов гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение двух других сторон и косинуса прилежащего угла . Для треугольников, обозначенных как на (Рисунок), с углами [латекс]\,\альфа,\бета,[/латекс] и [латекс]\,\гамма,[/латекс] и противоположными соответствующими сторонами [латекс]\,а, b,[/latex] и[latex]\,c,\,[/latex] соответственно, закон косинусов задается в виде трех уравнений. 9{2}}{2ab}\hfill \end{array}\hfill \end{array}[/latex]
Имея две стороны и угол между ними (SAS), найдите размеры оставшейся стороны и углы треугольник.
- Нарисуйте треугольник.
 Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.
Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов. - Примените закон косинусов, чтобы найти длину неизвестной стороны или угла.
- Примените закон синусов или косинусов, чтобы найти величину второго угла.
- Вычислите величину остаточного угла.
Нахождение неизвестной стороны и углов треугольника SAS
Найдите неизвестную сторону и углы треугольника на (рис.).
Рис. 4.
Показать решение
Попробуйте
Найдите недостающую сторону и углы данного треугольника:[латекс]\,\альфа =30°,\,\,b=12,\,\,с=24.[/латекс]
Показать решение
Нахождение угла SSS-треугольника
Найти угол[латекс]\,\альфа \,[/латекс]для заданного треугольника, если сторона[латекс]\,а=20,\,[/латекс]сторона [латекс]\,b=25,\,[/латекс]и сторона[латекс]\,с=18.[/латекс]
Показать решение
Анализ
Поскольку арккосинус может возвращать любой угол от 0 до 180 градусов, при использовании этого метода не будет неоднозначных случаев.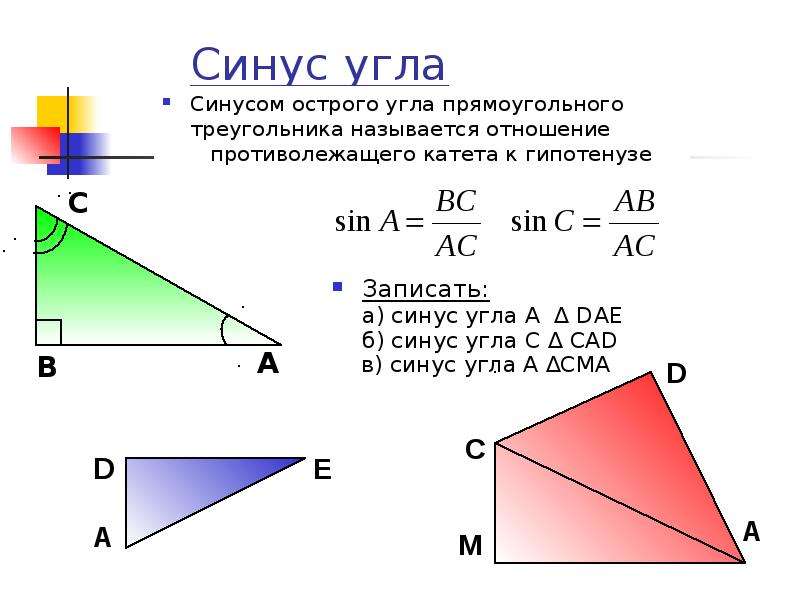
Попробуйте
Учитывая [латекс]\,a=5,b=7,\,[/латекс]и[латекс]\,с=10,\,[/латекс] найдите недостающие углы.
Показать решение
Решение прикладных задач с использованием закона косинусов
Точно так же, как закон синусов обеспечивает соответствующие уравнения для решения ряда приложений, закон косинусов применим к ситуациям, в которых данные соответствуют косинусным моделям. Мы можем увидеть их в области навигации, геодезии, астрономии и геометрии, и это лишь некоторые из них.
Использование закона косинусов для решения задачи связи
На многих сотовых телефонах с GPS приблизительное местоположение может быть указано до получения сигнала GPS. Это достигается с помощью процесса, называемого триангуляцией, который работает с использованием расстояний от двух известных точек. Предположим, что в радиусе действия сотового телефона есть две вышки сотовой связи. Две башни расположены на расстоянии 6000 футов друг от друга вдоль прямого шоссе, идущего с востока на запад, а сотовый телефон находится к северу от шоссе.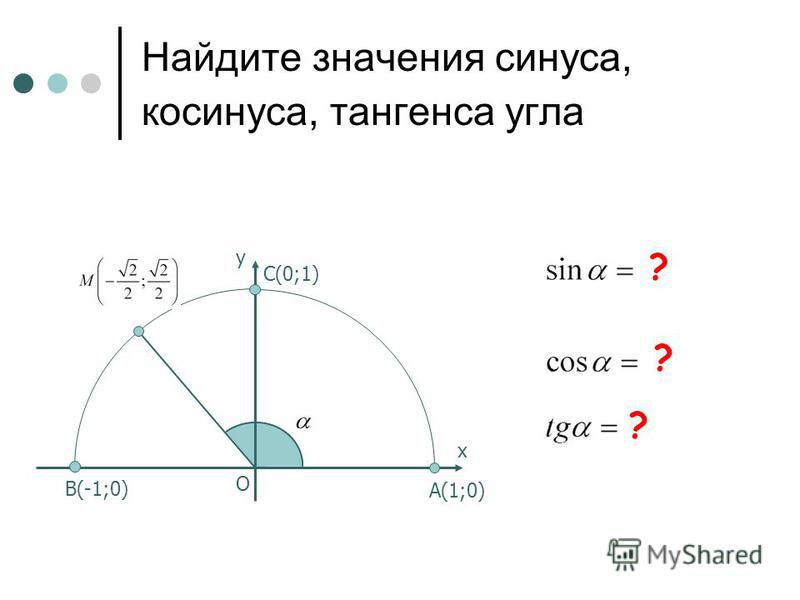 Основываясь на задержке сигнала, можно определить, что сигнал находится на расстоянии 5050 футов от первой башни и 2420 футов от второй башни. Определите положение сотового телефона к северу и востоку от первой башни и определите, насколько далеко он находится от шоссе.
Основываясь на задержке сигнала, можно определить, что сигнал находится на расстоянии 5050 футов от первой башни и 2420 футов от второй башни. Определите положение сотового телефона к северу и востоку от первой башни и определите, насколько далеко он находится от шоссе.
Показать решение
Расчет пройденного расстояния с использованием треугольника SAS
Возвращаясь к нашей задаче в начале этого раздела, предположим, что лодка выходит из порта, проходит 10 миль, поворачивает на 20 градусов и проходит еще 8 миль. Как далеко от порта лодка? Диаграмма повторяется здесь на (Рисунок).
Рис. 8.
Показать решение
Использование формулы Герона для нахождения площади треугольника
Мы уже научились находить площадь косоугольного треугольника, зная две стороны и угол. Мы также знаем формулу нахождения площади треугольника через основание и высоту. Однако, когда мы знаем три стороны, мы можем использовать формулу Герона вместо нахождения высоты.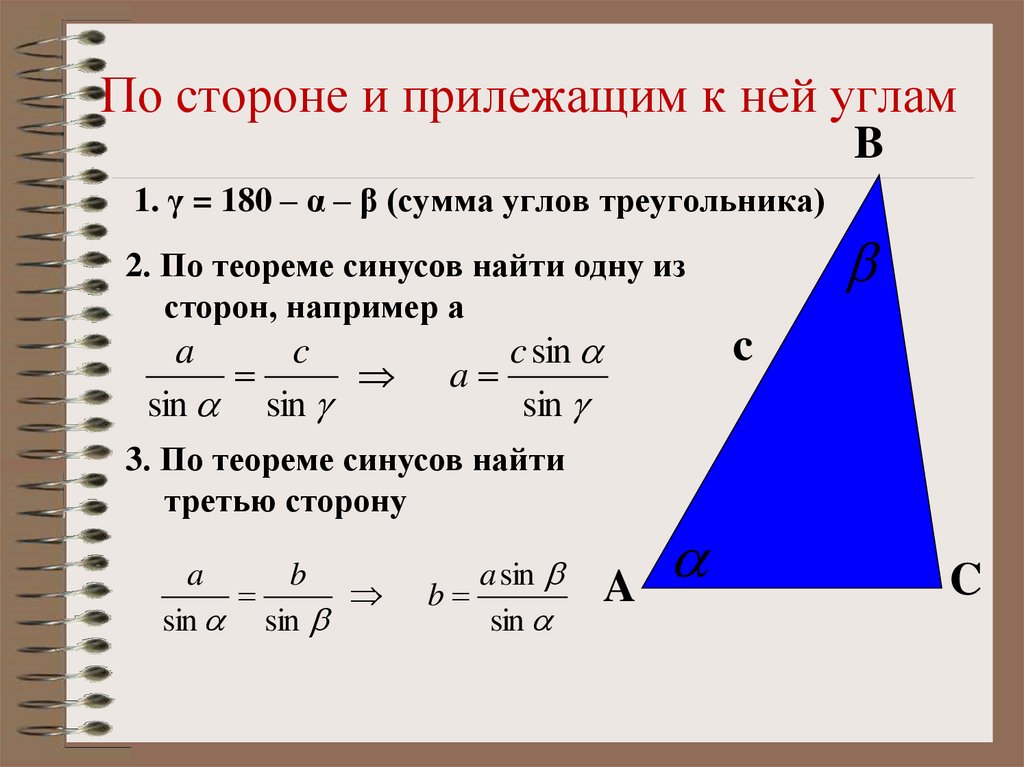 Герон Александрийский был геометром, жившим в первом веке нашей эры. Он открыл формулу для нахождения площади косоугольного треугольника, когда известны три стороны.
Герон Александрийский был геометром, жившим в первом веке нашей эры. Он открыл формулу для нахождения площади косоугольного треугольника, когда известны три стороны.
Формула Герона
Формула Герона находит площадь косоугольного треугольника, в котором стороны [латекс]\,а,б\текст{,}[/латекс]и[латекс]\,с\,[/латекс]известны.
[латекс]\текст{Область}=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}[/latex]
где [латекс]\,s =\frac{\left(a+b+c\right)}{2}\,[/latex] — половина периметра треугольника, иногда называемого полупериметром.
Использование формулы Герона для нахождения площади заданного треугольника
Найдите площадь треугольника на (рис.) с помощью формулы Герона.
Рисунок 9.
Показать решение
Попробуйте
Используйте формулу Герона, чтобы найти площадь треугольника со сторонами длиной [латекс]\,a=29,7\,\text{ft},b=42,3\,\text{ft},\,[ /latex]and[latex]\,c=38.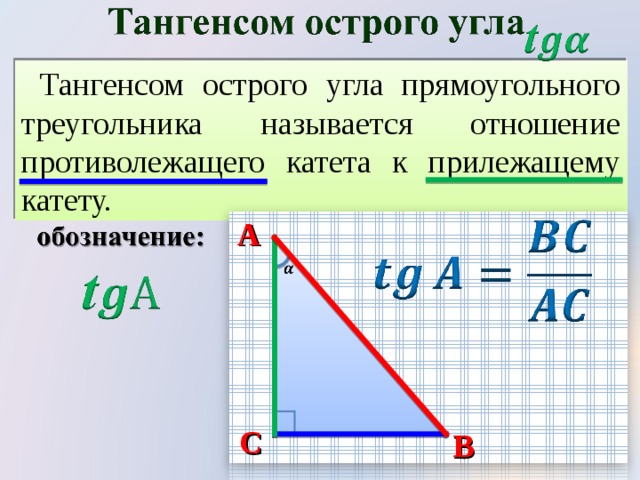 4\,\text{ft}.[/latex]
4\,\text{ft}.[/latex]
Показать решение
Применение формулы Герона к реальной задаче
Городской застройщик из Чикаго хочет построить здание, состоящее из лофтов для художников, на треугольном участке, граничащем с Раш-стрит, Вабаш-авеню и Пирсон-стрит. Фасад по Раш-стрит составляет примерно 62,4 метра, по Вабаш-авеню — примерно 43,5 метра, а по Пирсон-стрит — примерно 34,1 метра. Сколько квадратных метров доступно застройщику? См. (Рисунок) вид на городскую собственность.
Рисунок 10.
Показать решение
Попробуйте
Найдите площадь заданного треугольника[латекс]\,а=4,38\,\текст{фут}\,b=3,79\,\текст{фут,}\,[/латекс]и[ латекс]\,c=5.22\,\text{ft}\text{.}[/latex]
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с законом косинусов.
- Закон косинусов
- Закон косинусов: приложения
- Закон косинусов: Приложения 2 9{2}-2abcos\,\gamma\hfill\end{массив}[/latex]
- Закон косинусов определяет соотношение между измерениями углов и длинами сторон в косоугольных треугольниках.

- Обобщенная теорема Пифагора — это закон косинусов для двух случаев косоугольных треугольников: SAS и SSS. Отбрасывание воображаемого перпендикуляра разбивает косой треугольник на два прямоугольных треугольника или образует один прямоугольный треугольник, что позволяет связать стороны и вычислить измерения. См. (Рисунок) и (Рисунок).
- Закон косинусов полезен для многих типов прикладных задач. Первым шагом в решении таких задач обычно является набросок представленной проблемы. Если предоставленная информация соответствует одной из трех моделей (трем уравнениям), примените закон косинусов, чтобы найти решение. См. (Рисунок) и (Рисунок).
- Формула Герона позволяет вычислить площадь в косоугольных треугольниках. Все три стороны должны быть известны, чтобы применить формулу Герона. См. (Рисунок) и См. (Рисунок).
- Закон косинусов
- гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения двух других сторон и косинуса прилежащего к ней угла 9.0690
- Обобщенная теорема Пифагора
- расширение закона косинусов; связывает стороны косого треугольника и используется для треугольников SAS и SSS
- Всегда измеряйте угол по часовой стрелке
- Всегда измеряйте угол с севера
- Всегда указывайте трехзначное число азимут (например, 030° вместо 30°)
- Совмещенные внутренние углы «c» составляют 180°.
- Альтернативные углы ‘z’ равны.
- Углы на прямой в сумме дают 180°.
- Углы полного оборота в сумме составляют 360°.

Основные понятия
Упражнения по разделам
Вербальные
Если вы ищете недостающую сторону треугольника, что вам нужно знать при использовании закона косинусов?
Показать решение
Если вы ищете недостающий угол треугольника, что вам нужно знать при использовании закона косинусов?
Объясните, что представляет собой [латекс]\,s\,[/латекс] в формуле Герона.
Показать решение
Объясните связь между теоремой Пифагора и законом косинусов.
Когда следует использовать закон косинусов вместо теоремы Пифагора?
Показать решение
Алгебраический
В следующих упражнениях предположим, что [латекс]\,\альфа \,[/латекс]противоположная сторона[латекс]\,а,\бета \,[/латекс] является противоположной стороной[латекс]\, b,\,[/latex] и [латекс]\,\gamma \,[/latex] является противоположной стороной[латекс]\,c.\,[/latex]Если возможно, решите каждый треугольник относительно неизвестной стороны. Округлите до десятых.
[латекс]\gamma =41,2°,a=2,49,b=3,13[/латекс]
[латекс]\альфа =120°,b=6,c=7[/латекс]
Показать решение
[латекс]\бета=58,7°,а=10,6,с=15,7[/латекс]
[латекс]\гамма=115°,а=18,b=23[/латекс]
Показать решение
[латекс]\alpha =119°,a=26,b=14[/латекс]
[латекс]\gamma =113°,b=10,c=32[/латекс]
Показать решение
[латекс]\бета=67°,а=49,b=38[/латекс]
[латекс]\альфа=43,1°,а=184,2,b=242,8[/латекс]
Показать решение
[латекс]\альфа =36,6°,а=186,2,b=242,2[/латекс] 9{}[/latex]
Показать решение
В следующих упражнениях используйте закон косинусов, чтобы найти недостающий угол косоугольного треугольника. Округлите до десятых.
Округлите до десятых.
[латекс]\,a=42,b=19,c=30;\,[/latex]найти угол[латекс]\,A.[/latex]
[латекс]\,a=14,\ text{ }b=13,\text{ }c=20;\,[/latex]найти угол[latex]\,C.[/latex]
Показать решение
[латекс]\,a=16,b=31,c=20;\,[/latex]найти угол[латекс]\,B.[/latex]
[латекс]\,a=13,\ ,b=22,\,c=28;\,[/latex]найти угол[latex]\,A.[/latex]
Показать решение
[латекс]a=108,\,b=132,\,c=160;\,[/латекс]найти угол[латекс]\,C.\,[/латекс]
Для следующих упражнений решите треугольник. Округлите до десятых.
[латекс]A=35°,b=8,c=11[/латекс]
Показать решение
[латекс]B=88°,a=4,4,c=5,2[/латекс]
[латекс]C=121°,a=21,b=37[/латекс]
Показать решение
[латекс]a=13,b=11,c=15[/латекс]
[латекс]a=3.1,b=3.5,c=5[/латекс]
Показать решение
[латекс]a=51,b=25,c=29[/латекс]
В следующих упражнениях используйте формулу Герона, чтобы найти площадь треугольника.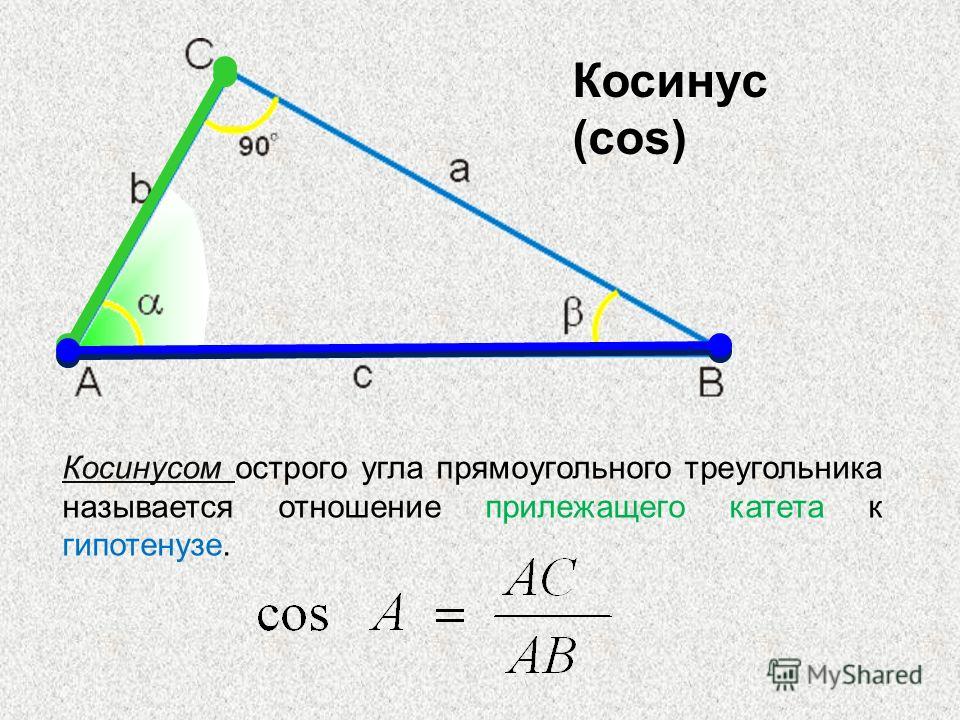 Округлить до сотых.
Округлить до сотых.
Найдите площадь треугольника со сторонами 18 дюймов, 21 дюйм и 32 дюйма. Округлите до десятых.
Показать решение
Найдите площадь треугольника со сторонами 20 см, 26 см и 37 см. Округлите до десятых.
[латекс]a=\frac{1}{2}\,\text{m},b=\frac{1}{3}\,\text{m},c=\frac{1}{4 }\,\текст{м}[/латекс]
Показать решение
[латекс]a=12,4\текст{ футов},\текст{ }b=13,7\текст{ футов},\текст{ }c=20,2\текст{ футов}[/латекс]
[латекс]a= 1.6\text{ yd},\text{ }b=2.6\text{ yd},\text{ }c=4.1\text{ yd}[/latex]
Показать решение
Графический
Для следующих упражнений найдите длину стороны [латекс]х.[/латекс] Округлите до десятых.
Показать решение
Показать решение
Показать решение
Для следующих упражнений найдите измерение угла[латекс]\,А.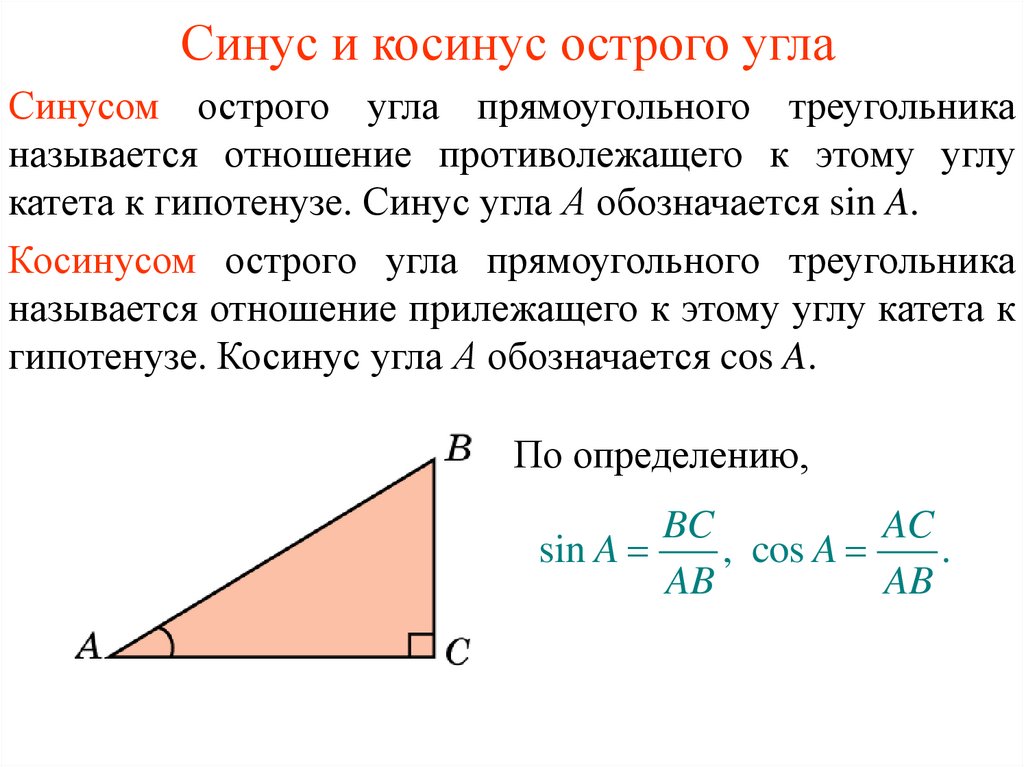 [/латекс]
[/латекс]
Показать решение
Показать решение
Найдите величину каждого угла в треугольнике, показанном на (рис.). Округлите до десятых.
Рис. 11.
В следующих упражнениях найдите неизвестную сторону. Округлите до десятых.
Показать решение
Показать решение
Для следующих упражнений найдите площадь треугольника. Округлить до сотых.
Показать решение
Показать решение
Показать решение
Удлинители
Параллелограмм имеет длину сторон 16 единиц и 10 единиц. Меньшая диагональ равна 12 единицам. Найдите длину большей диагонали.
Стороны параллелограмма 11 футов и 17 футов. Большая диагональ составляет 22 фута. Найдите длину меньшей диагонали.
Показать решение
Стороны параллелограмма равны 28 см и 40 см. Размер большего угла равен 100°. Найдите длину меньшей диагонали. 9{2}=25+36-60\mathrm{cos}\left(52\right)\,[/latex] представляет отношение трех сторон треугольника и косинуса угла.
Нарисуйте треугольник.
Показать решение
Найдите длину третьей стороны.
Для следующих упражнений найдите площадь треугольника.
Показать решение
Показать решение
Реальные приложения
Геодезист провел измерения, показанные на (Рисунок). Найдите расстояние через озеро. Ответы округлить до десятых.
Рисунок 14.
Спутник вычисляет расстояния и углы, показанные на (Рисунок) (не в масштабе). Найдите расстояние между двумя городами. Ответы округлить до десятых.
Рис. 15.
Показать решение
Самолет пролетает 220 миль с курсом 40°, а затем пролетает 180 миль с курсом 170°.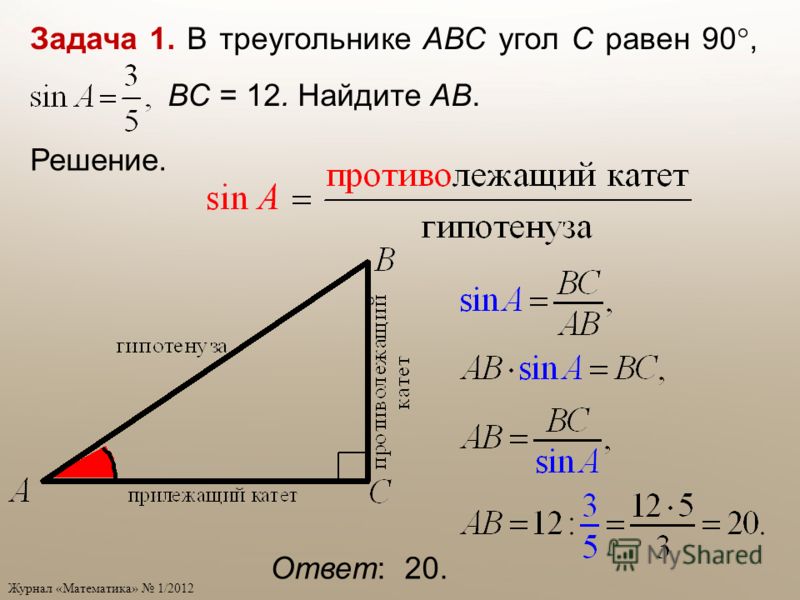 На каком расстоянии находится самолет от начальной точки и по какому курсу? Ответы округлить до десятых.
На каком расстоянии находится самолет от начальной точки и по какому курсу? Ответы округлить до десятых.
113-футовая башня расположена на холме под углом 34° к горизонтали, как показано на (Рисунок). Растяжка должна быть прикреплена к вершине башни и закреплена в точке 9.8 футов в гору от основания башни. Найдите необходимую длину провода.
Рис. 16.
Показать решение
Два корабля вышли из порта одновременно. Один корабль шел со скоростью 18 миль в час при курсе 320°. Другой корабль двигался со скоростью 22 мили в час под курсом 194°. Найдите расстояние между двумя кораблями через 10 часов пути.
На графике (рисунок) показаны две лодки, отходящие в одно и то же время от одного и того же причала. Первая лодка движется со скоростью 18 миль в час при курсе 327°, а вторая лодка — со скоростью 4 мили в час при курсе 60°. Найдите расстояние между двумя лодками через 2 часа.
Рис. 17.
Показать решение
Треугольный бассейн имеет длину 40 футов с одной стороны и 65 футов с другой стороны.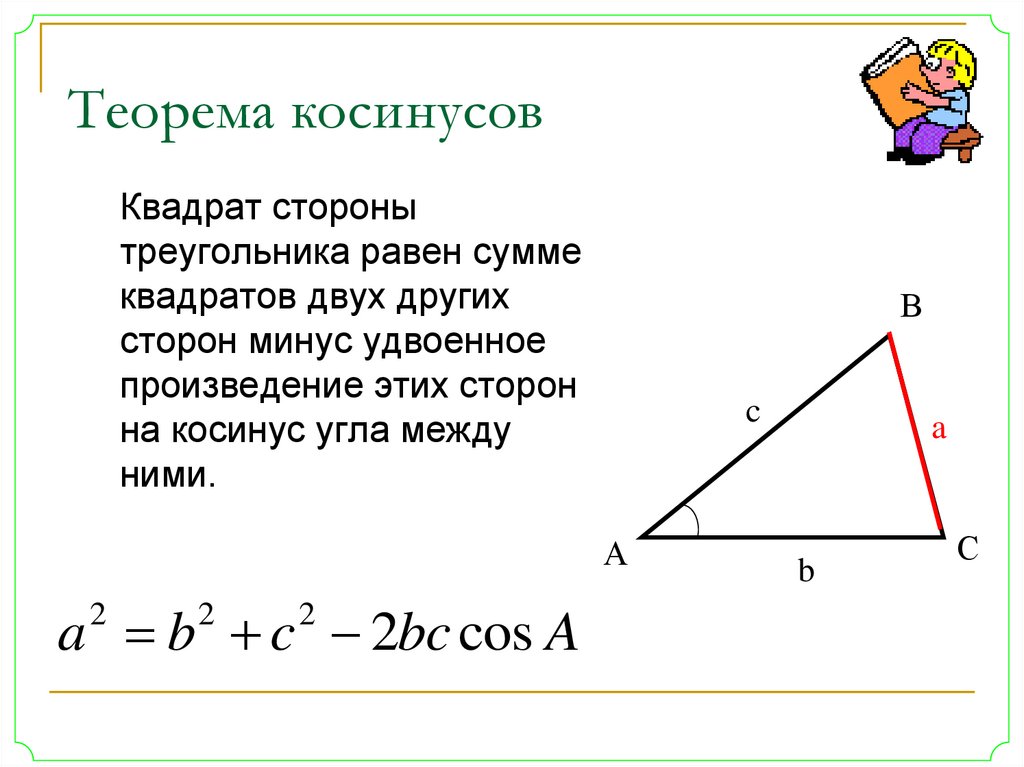 Эти стороны образуют угол, равный 50°. Какова длина третьей стороны (с точностью до десятых)?
Эти стороны образуют угол, равный 50°. Какова длина третьей стороны (с точностью до десятых)?
Пилот летит по прямой 1 час 30 мин. Затем он корректирует курс, направляясь на 10° вправо от своего первоначального курса, и летит 2 часа в новом направлении. Если она поддерживает постоянную скорость 680 миль в час, как далеко она находится от своего начального положения?
Показать решение
Лос-Анджелес находится в 1744 милях от Чикаго, Чикаго — в 714 милях от Нью-Йорка, а Нью-Йорк — в 2451 миле от Лос-Анджелеса. Нарисуйте треугольник, соединяющий эти три города, и найдите углы треугольника.
Филадельфия находится в 140 милях от Вашингтона, округ Колумбия, Вашингтон, округ Колумбия, — в 442 милях от Бостона, а Бостон — в 315 милях от Филадельфии. Нарисуйте треугольник, соединяющий эти три города, и найдите углы треугольника.
Показать решение
Два самолета вылетели из одного аэропорта в одно и то же время.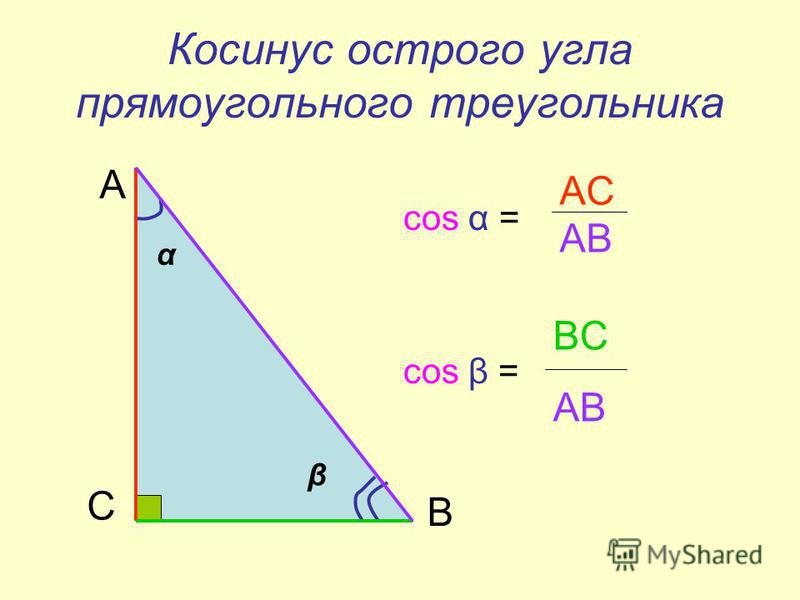 Один летит на 20° к востоку от севера со скоростью 500 миль в час. Второй летит под углом 30° к востоку от юга со скоростью 600 миль в час. На каком расстоянии будут самолеты через 2 часа?
Один летит на 20° к востоку от севера со скоростью 500 миль в час. Второй летит под углом 30° к востоку от юга со скоростью 600 миль в час. На каком расстоянии будут самолеты через 2 часа?
Два самолета взлетают в разные стороны. Один движется со скоростью 300 миль в час строго на запад, а другой — на 25° к северу от запада со скоростью 420 миль в час. Через 90 минут на каком расстоянии они будут друг от друга, если предположить, что летят на одной высоте?
Показать решение
Параллелограмм имеет стороны длины 15,4 единицы и 9.8 единиц. Его площадь составляет 72,9 кв. Найдите длину большей диагонали.
Четыре последовательные стороны четырехугольника имеют длину 4,5 см, 7,9 см, 9,4 см и 12,9 см. Угол между двумя наименьшими сторонами равен 117°. Чему равна площадь этого четырехугольника?
Показать решение
Четыре последовательные стороны четырехугольника имеют длину 5,7 см, 7,2 см, 9,4 см и 12,8 см.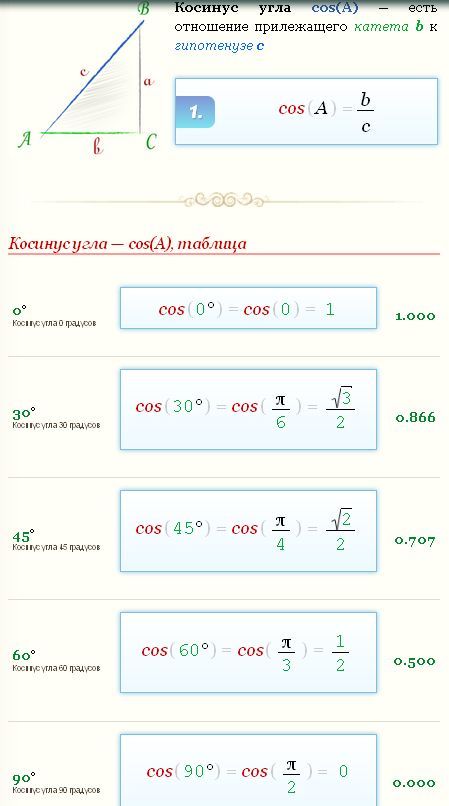 Угол между двумя наименьшими сторонами равен 106°. Чему равна площадь этого четырехугольника?
Угол между двумя наименьшими сторонами равен 106°. Чему равна площадь этого четырехугольника?
Найдите площадь треугольного участка земли, длина которого составляет 30 футов с одной стороны и 42 фута с другой; прилежащий угол равен 132°. Округлите до ближайшего целого квадратного фута.
Показать решение
Найдите площадь треугольного участка земли, длина которого составляет 110 футов с одной стороны и 250 футов с другой; прилежащий угол равен 85°. Округлите до ближайшего целого квадратного фута.
Глоссарий
Модуль 15 Раздел 4: Расчет углов
Модуль 15 Раздел 4: Расчет углов В этом разделе мы используем тригонометрию для определения размеров углов в прямоугольных треугольниках. На вашем научном калькуляторе вы найдете кнопки с надписью «sin –1 9».0028», «cos –1 » и «загар –1 ». Вам нужно будет уметь использовать их для вычисления углов, которые возникнут в последующих задачах. Опять же, мы начинаем с трех тригонометрических функций:
На вашем научном калькуляторе вы найдете кнопки с надписью «sin –1 9».0028», «cos –1 » и «загар –1 ». Вам нужно будет уметь использовать их для вычисления углов, которые возникнут в последующих задачах. Опять же, мы начинаем с трех тригонометрических функций:
Тригонометрические функции
| sin Θ = | потому что Θ = | тан Θ = |
Пример 1
Рассчитать угол Θ в этом треугольнике.
В этом треугольнике нам даны длины смежных и противоположных сторон, поэтому мы будем использовать
тангенс Θ =
Используя данные длины, мы имеем
| тангенс Θ | 86|
| = 1,6 |
Мы можем использовать TAN –1 на калькуляторе для получения
| θ | |||
| θ | |||
θ | . |  0028 (1,6) = 57,99461678° 0028 (1,6) = 57,99461678° = 58,0° (с точностью до 1 знака после запятой) | |
Поскольку длины даны для смежной стороны и гипотенузы, необходимо использовать формулу для cos Θ .
| cos Θ | = | ||||||||||||||||||||||||||||||||||||||||||||||
| = = 0,470588235 | 0246 | = COS –1 (0,470588235) = 61,92751306 ° | |||||||||||||||||||||||||||||||||||||||||||||
| = 61,9 ° (до 1 Decimal Place). Определить угол между длинной стороной прямоугольника и диагональю. Решение показано на схеме. Использование формулы для tan Θ дает
Then using the tan –1 key on a calculator gives
УпражненияВопрос 1Давая ответы, где необходимо, с точностью до 1 знака после запятой, воспользуйтесь калькулятором, чтобы получить Θ если:
Используйте функцию касательной для вычисления угла Θ на каждой из следующих диаграмм. (а) Θ = ° (б) Θ = ° (в) Θ = ° (г) Θ = ° Используйте синус или косинус для вычисления угла Θ в каждом из следующих треугольников. В каждом случае дайте правильный ответ с точностью до 1 знака после запятой. (а) Θ = ° (б) Θ = ° (в) Θ = ° 0003 (г) Θ = ° Вопрос 4 Вычислите угол Θ в каждом из следующих треугольников. В каждом случае дайте правильный ответ с точностью до 1 знака после запятой. (a) Θ = ° (b) Θ = ° (c) Θ = ° (d) Θ = ° Вопрос 5Прямоугольный треугольник имеет длины сторон 3 см, 4 см и 5 см. Определите размеры всех углов треугольника, приводя ответы с точностью до градуса. °,° и° Вопрос 6На схеме показано поперечное сечение сарая. Рассчитайте угол Θ между крышей и горизонталью. Дайте ответ с точностью до градуса. Вопрос 7Лестница длиной 6 м прислонена к стене. Основание лестницы находится на расстоянии 3 м от основания стены. Рассчитайте угол между лестницей и землей. Угол с землей = ° Вопрос 8 Длина сторон прямоугольника 12 см и 18 см. (a) Вычислите длину диагонали прямоугольника, давая ответ с точностью до миллиметра. Длина диагонали = см L 2 = 12 2 + 18 2 = 144 + 324 = 468 L = = 21,63330765 см = 21,6 см (с точностью до миллиметра) (б) Вычислите угол между диагональю и меньшей стороной прямоугольника, дав ответ с точностью до градуса. Угол между диагональю и меньшей стороной = ° A = tan –1 (1,5) = 56,30993247° = 56° (с точностью до градуса) Вопрос 9Когда самолет проходит 3000 м по прямой траектории полета, он поднимается на 500 м. Рассчитайте угол между траекторией полета самолета и горизонтом. Дайте свой ответ с разумным уровнем точности. Угол между траекторией полета и горизонталью = ° Вопрос 10 Груз висит на двух нитях, как показано на рисунке. Вычислите угол между двумя нитями, давая ответ с точностью до градуса. Угол между струнами = ° A = cos –1 (0,9) + cos –1 (0,75) = 25,84193276° + 41,40962211° = 67,25155487 = 67° (с точностью до ближайшего градуса) Вопрос 11 Пандусы помогают людям заходить в здания. (a) Вот планы пандуса: Этот пандус слишком высокий? Высота верха пандуса = м (с точностью до см). Итак, пандус слишком высокий, не слишком высокий. H 2 = 10 2 — 9,85 2 = 100 — 97,0225 H = = 1,725543393 M 1,73 M> 0,83 м, так что рамп слишком высокий (b) 9000 2 9000 2 9000 2 . в планах другая рампа . Какова длина основания этой рампы? м (с точностью до см) L = 10 × cos3,5 ° = 9,981347984 м = 9,98 м (с точностью до сантиметра) (c) Рекомендуемый уклон пандуса составляет 1 к 20. Какой угол дает рекомендуемый уклон? ° (с точностью до градуса) Рекомендуемый угол = tan –1 = tan –1 (0,05) = 2,862405226° = 3° (с точностью до градуса) Вопрос 12 Лодка плывет от гавани к бую. (a) Рассчитайте кратчайшее расстояние между буем и гаванью. Дайте ответ с точностью до 1 знака после запятой. Shortest distance = km SD 2 = 6 2 + 4 2 = 36 + 16 = 52 SD = = 7.211102551 km (b) Calculate the bearing of the buoy from the гавань. Азимут = ° (с точностью до градуса) Угол между направлением и севером = тангенс –1 (1,5) = 56,30993247° Буй в 1,2 км севернее маяка. (c) Вычислите , насколько буй находится к западу от маяка. Дайте ответ с точностью до 1 знака после запятой. Расстояние на запад = км DW 2 = 2,5 2 – 1,2 2 = 6,25 – 1,44 = 4,81 DW = = 2,19317122 км Вопрос 13Баргейт находится в 6 км к востоку и в 4 км к северу от Кейп-Пойнт. (a) Стив хочет плыть прямо из Кейп-Пойнт в Баргейт. По какому азимуту он должен плыть? Азимут = ° (с точностью до градуса) Угол между направлением и севером = tan –1 (1,5) = 56,30993247° (b) Анна плывет из Кейп-Пойнта по азимуту 048°. Она останавливается, когда оказывается прямо к северу от Баргейта. Как далеко к северу от Баргейта находится Анна? Расстояние к северу от Баргейта = км (до 2 s. Расстояние к северу от Кейп-Пойнта = 6 ÷ tan48° = 5,402424266 км Расстояние к северу от Баргейта = 5,402424266 – 4 = 1,402424266 км Как рассчитать подшипник — mathsathome.comРассчитать азимут по углу: видеоурокРассчитать азимут с помощью тригонометрии: видеоурокЧто такое подшипник в математике? В математике пеленг определяется как угол, измеренный по часовой стрелке с севера. Азимут всегда определяется как угол по часовой стрелке с севера. Подшипники важны для навигации в двух измерениях, например, при использовании карт. Подшипники полезны, потому что угол всегда относительно севера, и поэтому они обеспечивают последовательное измерение направления. Истинный азимут — это угол, измеренный по часовой стрелке с севера. Истинный подшипник часто называют просто подшипником. Относительный азимут — это угол между направлением движения и другим направлением. Этот угол измеряется по часовой стрелке от текущего направления. Например, судно в данный момент движется по азимуту 050°. Относительный азимут 010° сделан от текущего направления судна. В то время как относительный азимут равен 010°, истинный азимут этого нового направления равен 060°, поскольку судно уже находится на азимуте 50° и 50° + 10° = 60°. В качестве альтернативы подшипники могут быть записаны как квадрантные подшипники. Квадрантный азимут представляет собой угол между северным или южным направлением и восточным или западным направлением. Сначала пишется север или юг, затем угол, затем восток или запад. Например, азимут в квадрантном направлении S30°W означает, что нужно начать с направления на юг, а затем сделать угол 30° на запад. В квадрантном азимуте угол всегда измеряется как наименьший угол с севера или с юга. Этот угол может быть либо по часовой стрелке, либо против часовой стрелки, в зависимости от того, какое направление является ближайшим. Угол истинного азимута всегда измеряется с севера, и угол всегда дается по часовой стрелке. Таким образом, азимут квадранта S30°W будет преобразован в истинный азимут 210°. Это связано с тем, что угол, измеренный по часовой стрелке от севера, будет включать 180 ° на юг, а затем еще 30 °. Всего 180° + 30° = 210°. Чтобы преобразовать квадрантный пеленг в истинный пеленг, сначала нарисуйте схему квадрантного пеленга. Например, квадрантный азимут S10°E преобразуется в истинный азимут 170°. Это потому, что юг находится на 180°, но мы должны вернуться на 10° назад, чтобы добраться до S10°E. Следовательно, 180° – 10° = 170°. Вот несколько примеров преобразования квадрантного пеленга в настоящий пеленг.
Как рассчитать азимут Чтобы рассчитать азимут, найдите угол по часовой стрелке от севера. Например, азимут от А до В равен 100°. Это угол от севера по часовой стрелке до B. Азимут от B до A равен 280°. Это угол от севера по часовой стрелке до точки А. При измерении пеленга необходимо соблюдать 3 правила: Как рассчитать азимут по углуЧтобы найти азимут по заданному углу, используйте следующие данные об углах: Подшипник с внутреннего углаВнутренние углы в сумме составляют 180°. Если задан пеленг от В к А, то пеленг от А к В можно найти с помощью внутренних углов. Вычтите азимут B и A из 180°, чтобы найти недостающий внутренний угол, затем используйте тот факт, что углы при полном обороте складываются в 360°, чтобы найти азимут A и B. Например, азимут B относительно A составляет 050°. Найдите азимут А и В. Проведя север в обеих точках А и В, северы образуют параллельные линии, и образуется совпадающий внутренний угол. Азимут 050° и образующийся внутренний угол должны составлять 180°. Угол против часовой стрелки от В до А равен 130°. Однако азимут всегда следует измерять по часовой стрелке с севера. 130° — против часовой стрелки с севера. Необходим угол по часовой стрелке с другой стороны. Используйте тот факт, что угол полного поворота в сумме составляет 360°. Чтобы получить подшипник, вычтите 130° из 360°. 360° – 130° = 230° и, следовательно, пеленг А от В равен 230°. Вот еще один пример подшипников с внутренними углами. Например, найдите направление B относительно A. В этом случае направление B относительно A и заданный угол 80° образуют внутренние углы. Следовательно, они оба складываются в 180°. 180° – 80° = 100° и, таким образом, азимут B относительно A равен 100°. Подшипники с переменными угламиАльтернативные углы равны и распознаются по форме «z», образуемой между двумя углами. Эти данные об углах можно использовать для расчета пеленгов. Например, найдите пеленг B из A. Показан угол 120°. Он образует переменный угол с направлением B на A. Следовательно, направление B на A также составляет 120°. Вот еще один пример использования данных об альтернативных углах для нахождения пеленга. Найти пеленг B из A Мы видим, что альтернативные углы равны. Следовательно, угол между линией AB и горизонталью равен 20°, как показано ниже. Горизонт составляет 90° с севером, поэтому азимут 90° + 20° = 110°, как показано. Как рассчитать пеленг с помощью тригонометрииЧтобы найти пеленг с помощью тригонометрии, создайте прямоугольный треугольник. Если расстояния даны в любом из направлений компаса, обозначьте эти стороны как смежные или противоположные стороны треугольника. Если расстояние указано в определенном азимуте, обозначьте это расстояние как гипотенузу треугольника. Например, человек проходит 10 км на восток, а затем 6 км на север. Найдите азимут от начальной до конечной точки. Поскольку расстояния даны по компасу на восток и север, можно построить прямоугольный треугольник, в котором 10 км к востоку — это прилежащая сторона, а 6 км к северу — противоположная сторона. Поскольку две известные стороны треугольника являются противоположными и смежными, мы можем использовать функцию загара, чтобы найти показанный угол. и так далее, . Решаем это и так, . Азимут конечной позиции относительно стартовой позиции должен указываться по часовой стрелке с севера. Азимут обозначен углом, показанным ниже. Чтобы найти этот пеленг, мы знаем, что пеленг плюс дает в сумме 90°. Мы вычитаем 31° из 90°, чтобы получить азимут 69°. Вот еще один пример нахождения пеленга с помощью тригонометрии. Лодка плывет 8 км на запад и 3 км на юг. Найдите азимут от начальной до конечной точки. Поскольку расстояния даны по компасу на запад и юг, можно составить прямоугольный треугольник с прилежащим 8 км и противоположным 3 км. Так как известные стороны являются смежными и противоположными, используйте . Поэтому и так, . . Азимут всегда измеряется по часовой стрелке с севера. Азимут представляет собой угол по часовой стрелке с севера на запад вычесть θ. С севера на запад 270°, поэтому азимут 270° – 17° = 253°. Вот пример того, как найти расстояние, зная пеленг. Место проходит 500 км по азимуту 300°. Начните с рисования диаграммы. 300° по часовой стрелке с севера показано ниже. Он находится за пределами 270°, но меньше 360°, поэтому он лежит между западом и севером. Рисуем прямоугольный треугольник, одна из сторон которого указывает расстояние, пройденное на запад. Угол прямоугольного треугольника должен быть 60°, так как 360° – 300° = 60°. При обозначении угла, как показано, расстояние, пройденное на запад, является противоположной стороной, а 500 км — гипотенузой. Нам нужно расстояние, пройденное на запад, а это наоборот. У нас есть гипотенуза и угол, θ = 60°. Поэтому мы используем . Гипотенуза = 500 и θ = 60° Следовательно, . Таким образом, расстояние, пройденное на запад, составляет 433 км. Подшипники, использующие правило синуса и косинуса: Пример 1 Если подшипники установлены между тремя точками и между ними образуется непрямоугольный треугольник, то применяется правило синуса или правило косинуса, c 2 =a 2 +b 2 -2ab. В шаге 1 ниже показана схема ситуации с отмеченными подшипниками. На шаге 2 находится внутренний угол треугольника. Во-первых, мы используем тот факт, что сумма внутренних углов составляет 180°, чтобы найти угол 160°, отмеченный синим цветом. Во-вторых, углы вокруг точки складываются в 360°, поэтому, вычитая 160° и 170° из 360°, мы видим, что внутренний угол треугольника должен быть равен 30°. Шаг 1. Подпишите схему с направлениями и длинами Шаг 2. Найдите недостающие углы внутри треугольника Шаг 3. Используйте правило косинусов, чтобы найти недостающую сторону, противоположную известному углу Правило косинуса можно использовать для нахождения отсутствующей стороны c по формуле . Здесь с — недостающая сторона от А до С. Следовательно, С — противоположный угол, равный 30°. a и b — две другие известные длины сторон, 20 и 35. Подставляя эти значения в теорему косинусов, получаем AC = 20,3 км. Шаг 4. Используйте правило синусов, чтобы найти недостающий угол Правило синусов утверждает, что , которое можно преобразовать в . При использовании правила синусов сторона a должна быть противоположна углу A, а сторона b должна быть противоположна углу B. Мы выбираем b и B как пару известных нам противоположных сторон и углов. а — это сторона, противоположная углу, который мы хотим найти. Следовательно, a = 35, b = 20,3 и B = 30°. Следовательно, . Следовательно, и так, . Шаг 5. Найдите азимут как угол по часовой стрелке с севера Азимут C из A находится как угол по часовой стрелке с севера в A. внутренний угол треугольника 59,5°. Азимут от А до С составляет 79,5°. Направление по правилу синусов и косинусов: Пример 2Судно выходит из точки А по курсу 45° и проходит 13 км. Другой корабль выходит из точки А по азимуту 155° и проходит 20 км. На каком расстоянии друг от друга два корабля? В этом примере рисуется диаграмма и создается непрямоугольный треугольник. Внутренний угол треугольника находится по разнице между подшипниками. 155° – 45° = 110°. Правило косинуса можно использовать для определения расстояния между двумя кораблями, показанного правой стороной треугольника. Недостающая сторона обозначена буквой c, а правило косинуса равно . a и b — две известные стороны по обе стороны от угла C. a = 13, b = 20 и C = 110°. становится . Следовательно, недостающая сторона c = 27,3 км. Подшипники с векторами Для любого вектора вида a i +b j угол вектора находится с помощью tan -1 (b/a). Векторы могут быть записаны как пеленги, так как: Положительный компонент i находится в восточном направлении. Отрицательная компонента i находится в западном направлении. Положительный компонент j находится в северном направлении. Отрицательная компонента j находится в южном направлении. Например, лодка движется с постоянной скоростью по вектору (-5i+2j) км/ч -1 . Найдите пеленг лодки. -5 i находится в западном направлении, а 2 j — в северном. Угол от горизонтали находится как . Следовательно . Западное направление соответствует азимуту 270°, поэтому пеленг лодки равен 270° + 21,8° = 291,8°. В качестве трехзначного подшипника это 292°.
|

 9781
9781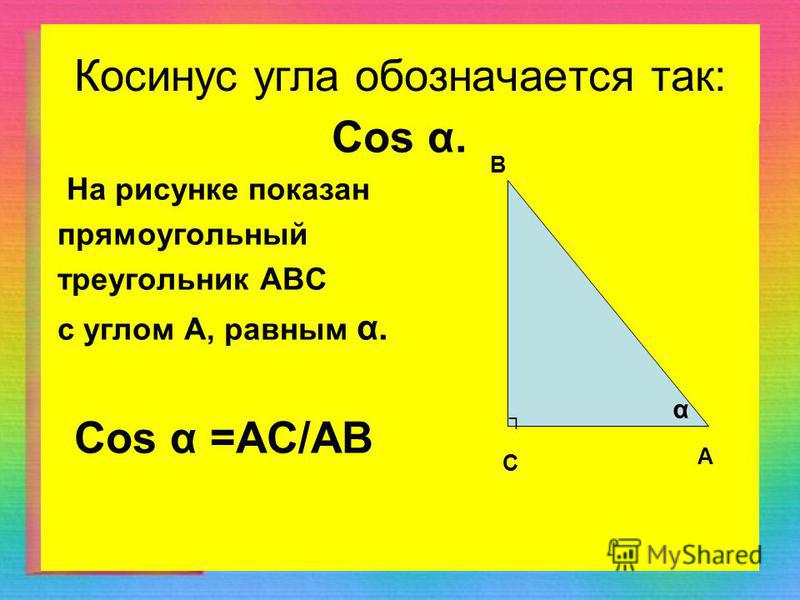 7986
7986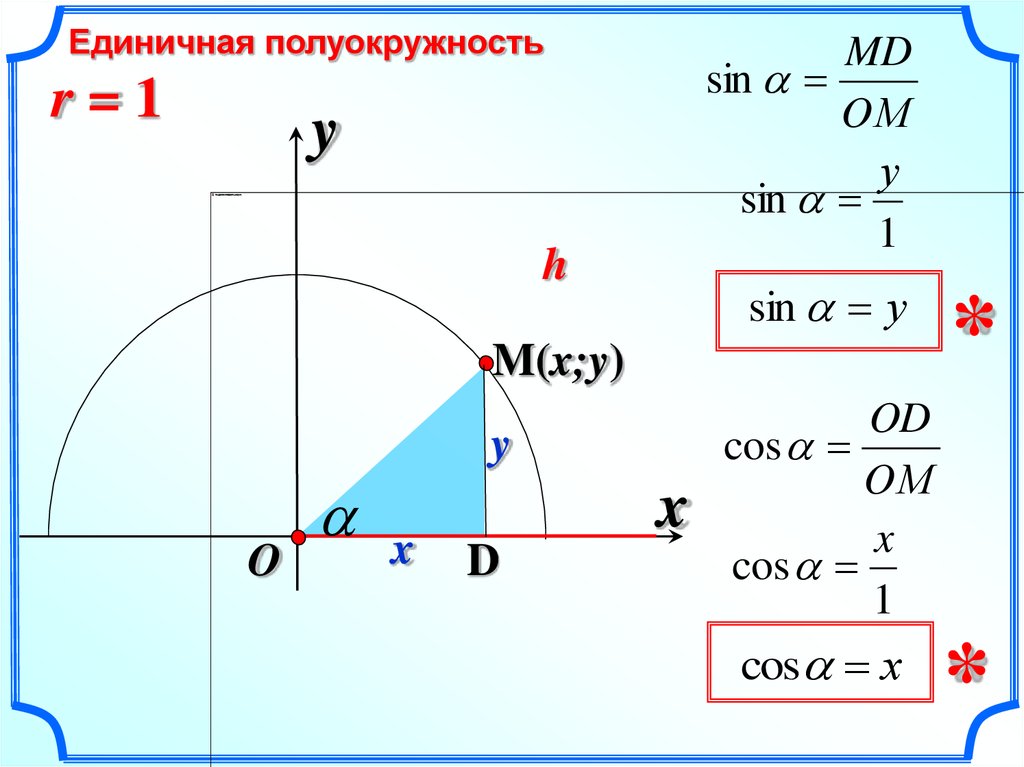 4695
4695 0698
0698 3256
3256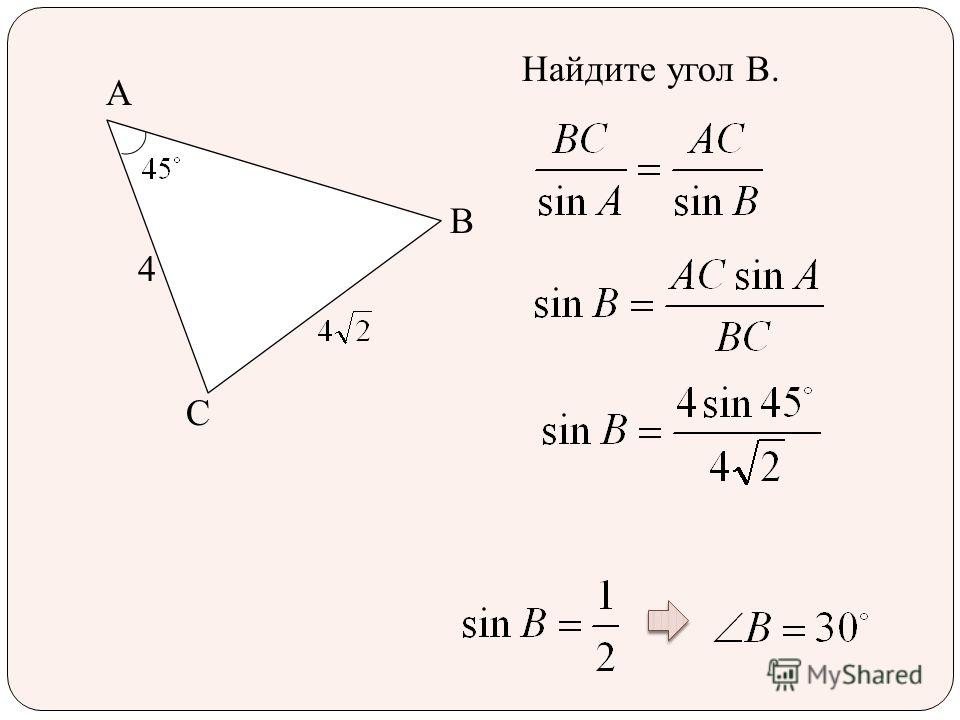 682
682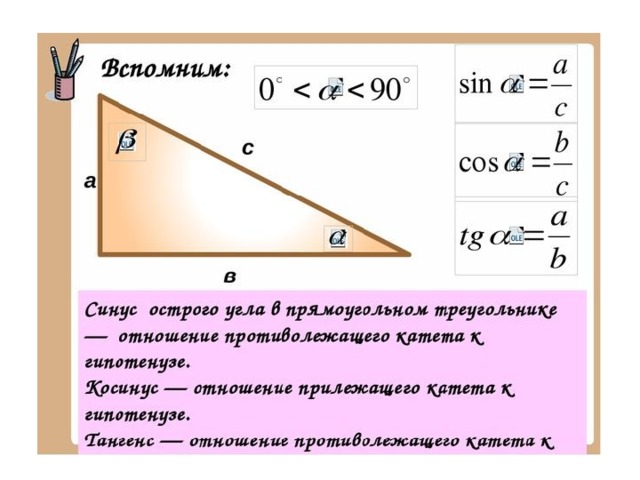 9135
9135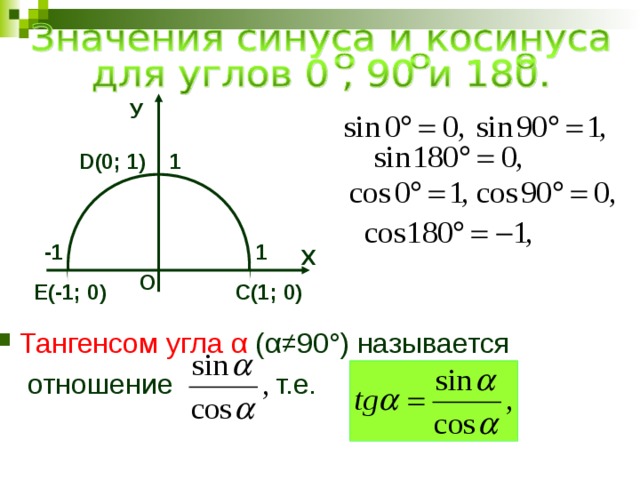 9998
9998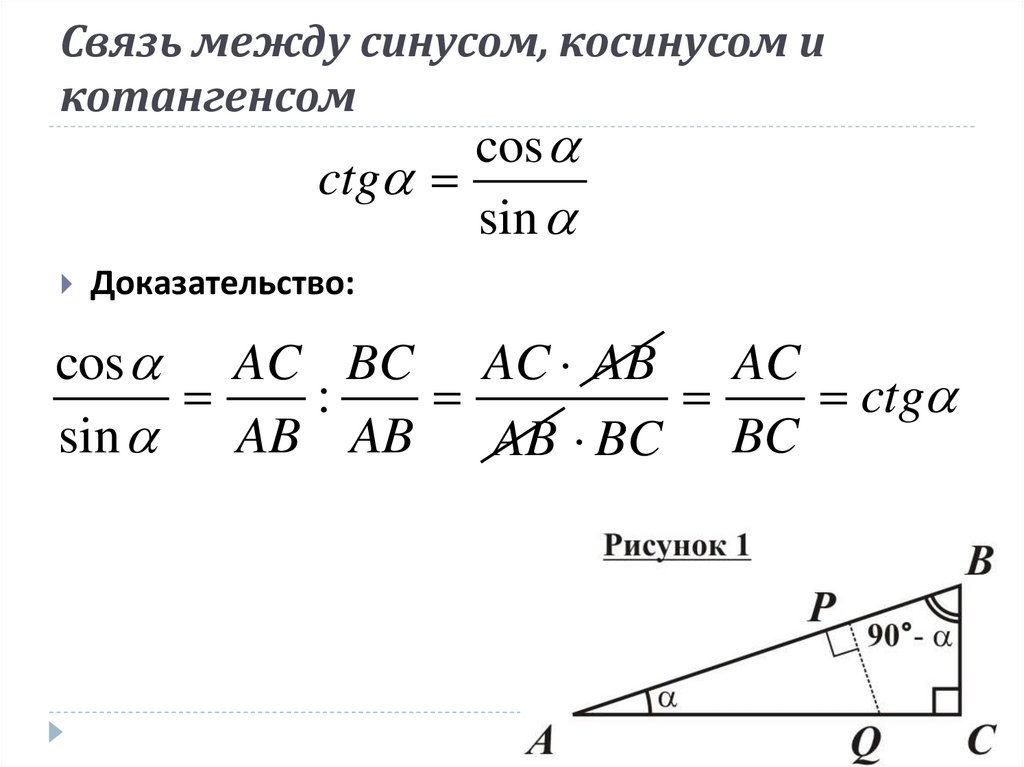 9063
9063 6691
6691 309
309 0872
0872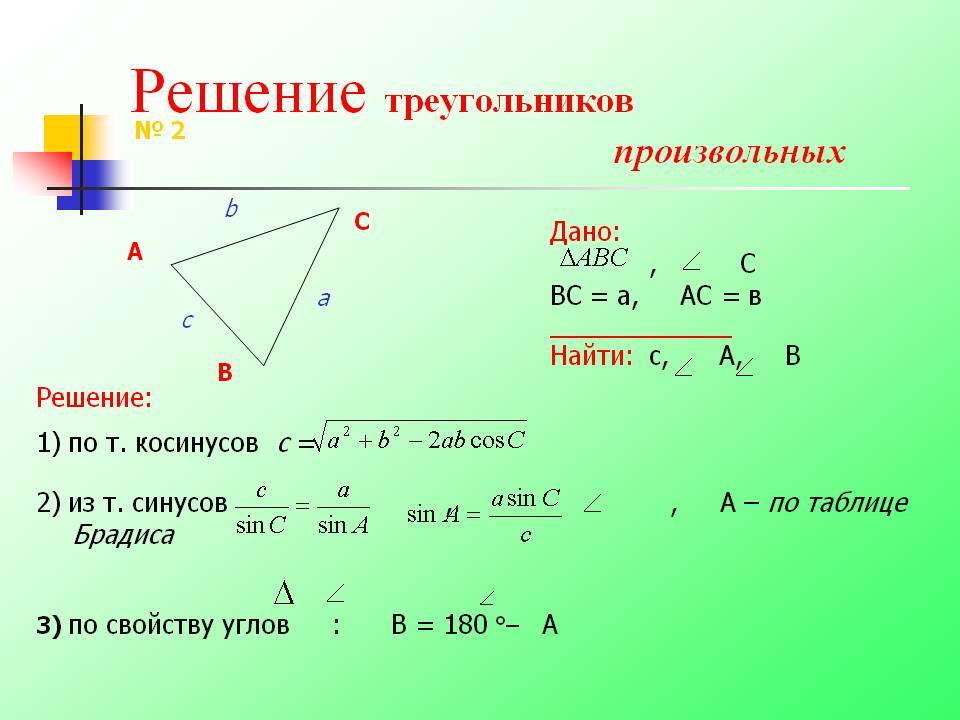 4695
4695 788
788 9659
9659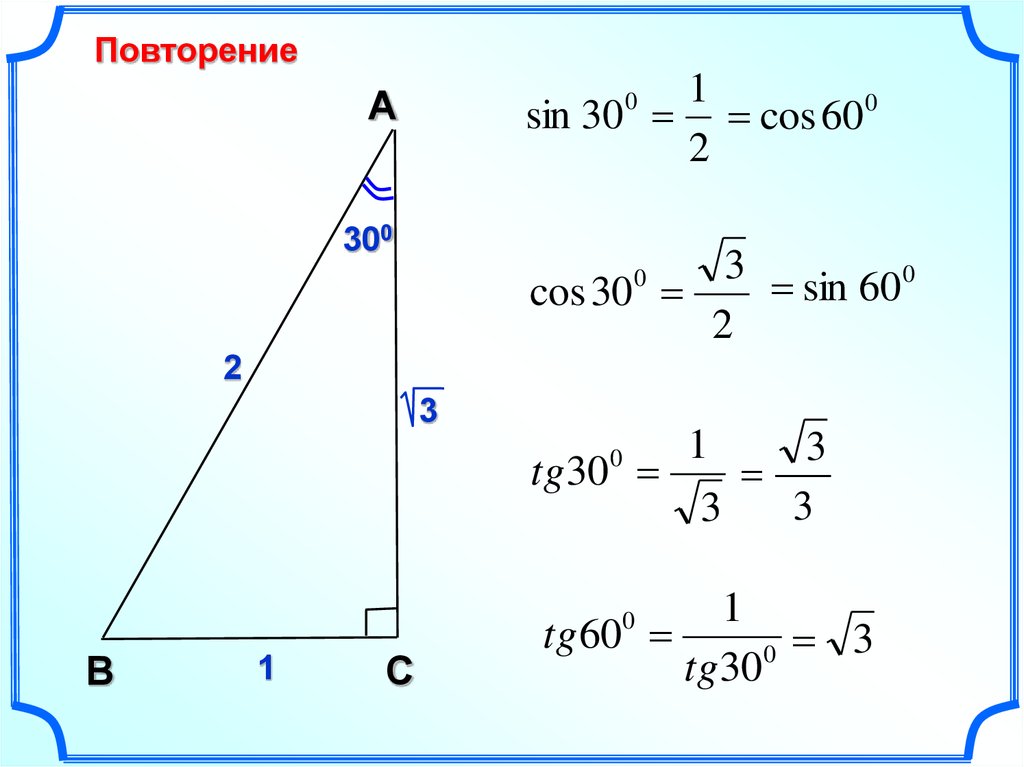
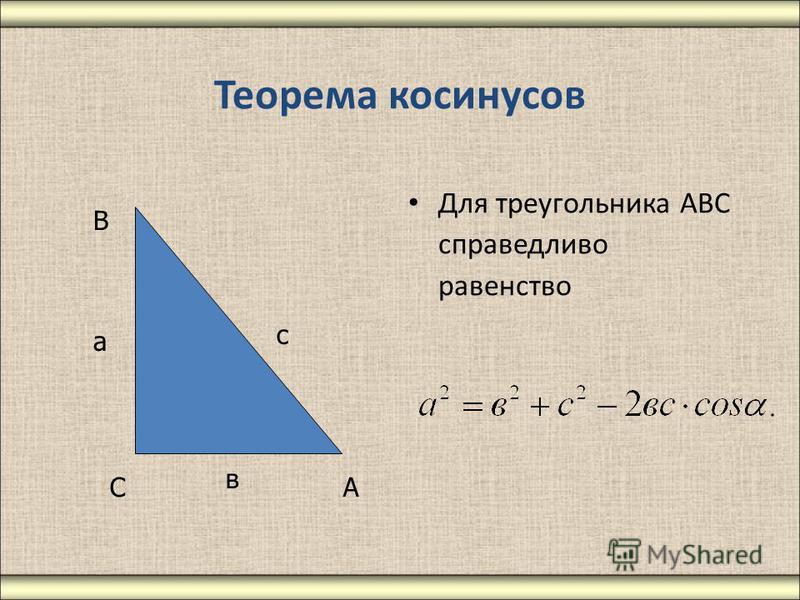
 Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.
Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.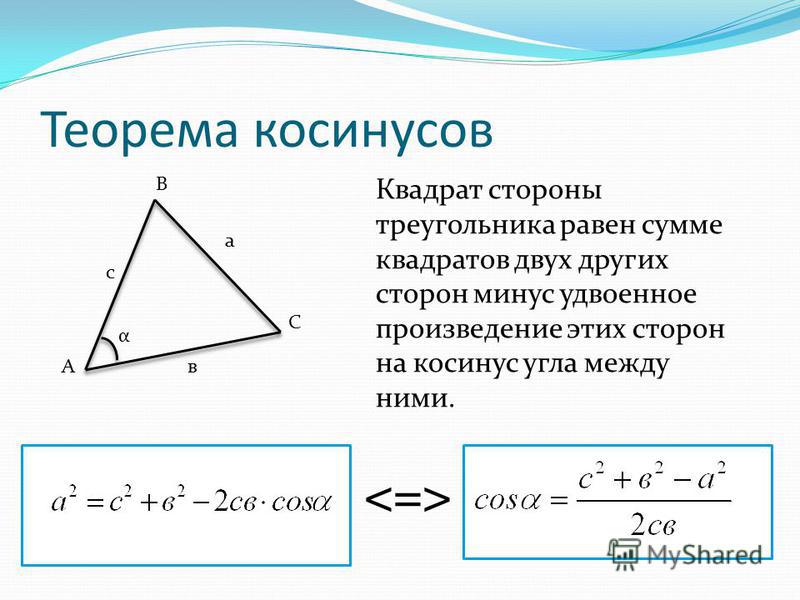
 В каждом случае дайте правильный ответ с точностью до 1 знака после запятой.
В каждом случае дайте правильный ответ с точностью до 1 знака после запятой.

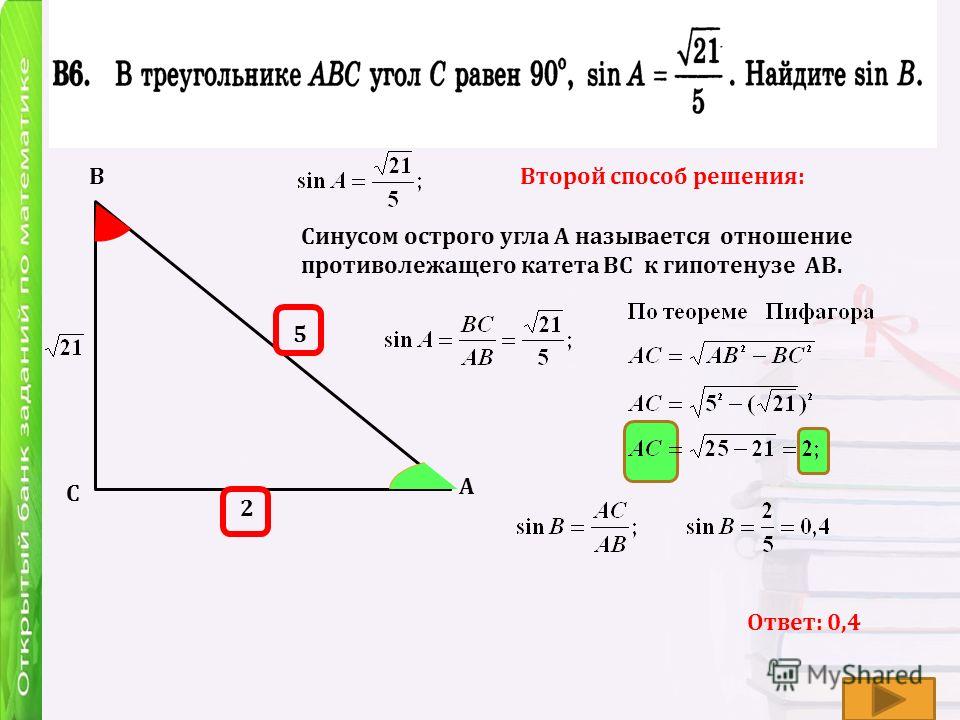

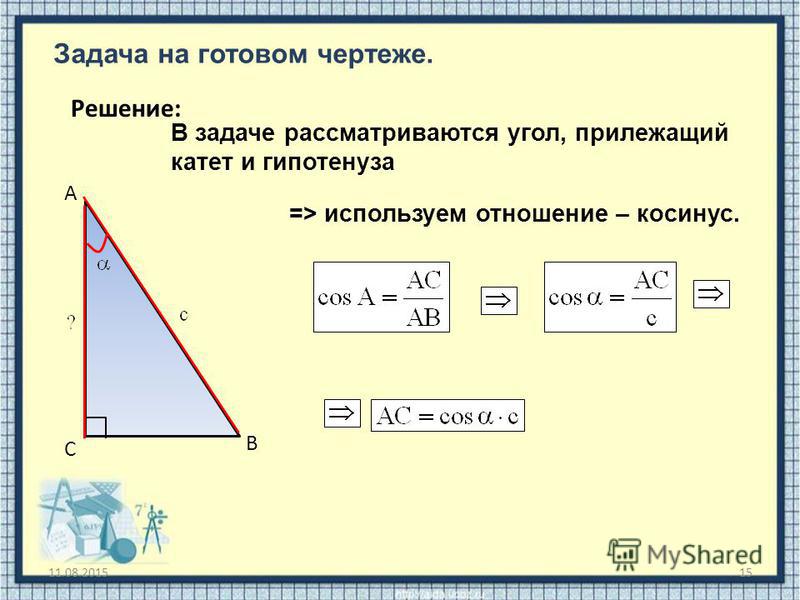 Кратчайшее расстояние от маяка до буя 2,5 км.
Кратчайшее расстояние от маяка до буя 2,5 км. f.)
f.) Подшипники обычно записывают как трехзначный подшипник. Например, угол 50° с севера записывается как 050°.
Подшипники обычно записывают как трехзначный подшипник. Например, угол 50° с севера записывается как 050°. 
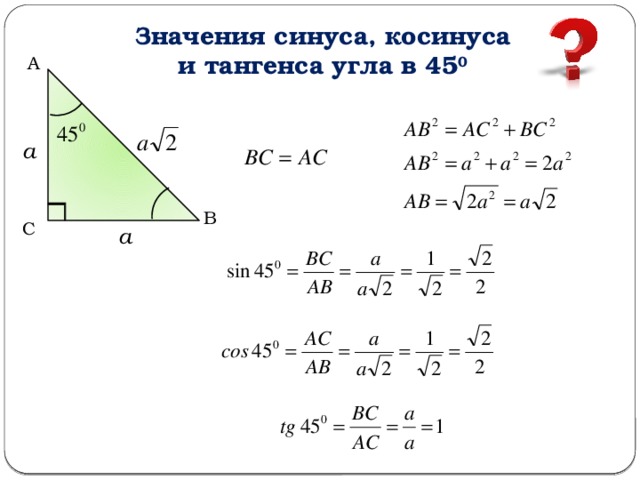 Истинный пеленг – это угол, измеренный по часовой стрелке с севера на этот пеленг. Используйте тот факт, что с севера на восток — 90°, на юг — 180°, а на запад — 270°. Затем добавьте или вычтите угол азимута квадранта из этих значений в зависимости от того, измеряется ли азимут квадранта по часовой стрелке или против часовой стрелки соответственно.
Истинный пеленг – это угол, измеренный по часовой стрелке с севера на этот пеленг. Используйте тот факт, что с севера на восток — 90°, на юг — 180°, а на запад — 270°. Затем добавьте или вычтите угол азимута квадранта из этих значений в зависимости от того, измеряется ли азимут квадранта по часовой стрелке или против часовой стрелки соответственно.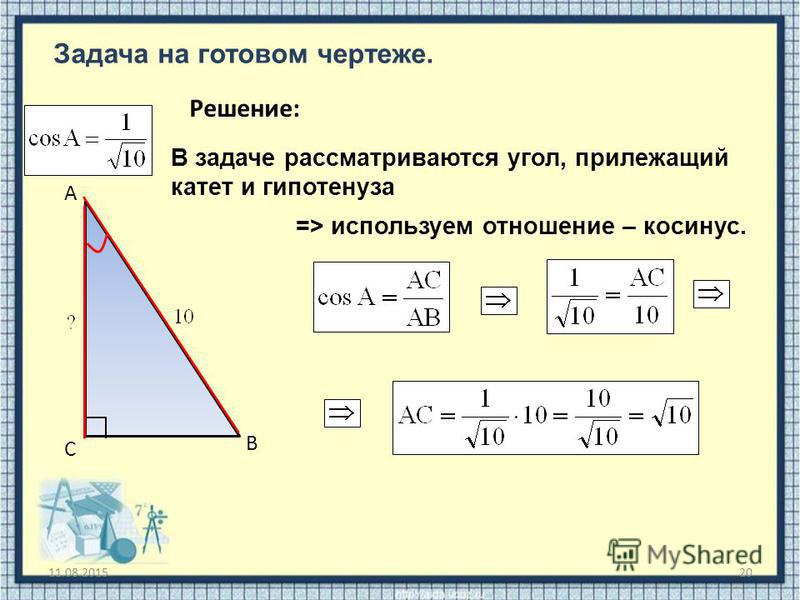 Начните с рисования вертикальной линии, обозначающей север в первом месте. Нарисуйте линию, соединяющую начальное местоположение с конечным местоположением. Измерьте угол по часовой стрелке между северной линией и этой линией.
Начните с рисования вертикальной линии, обозначающей север в первом месте. Нарисуйте линию, соединяющую начальное местоположение с конечным местоположением. Измерьте угол по часовой стрелке между северной линией и этой линией. 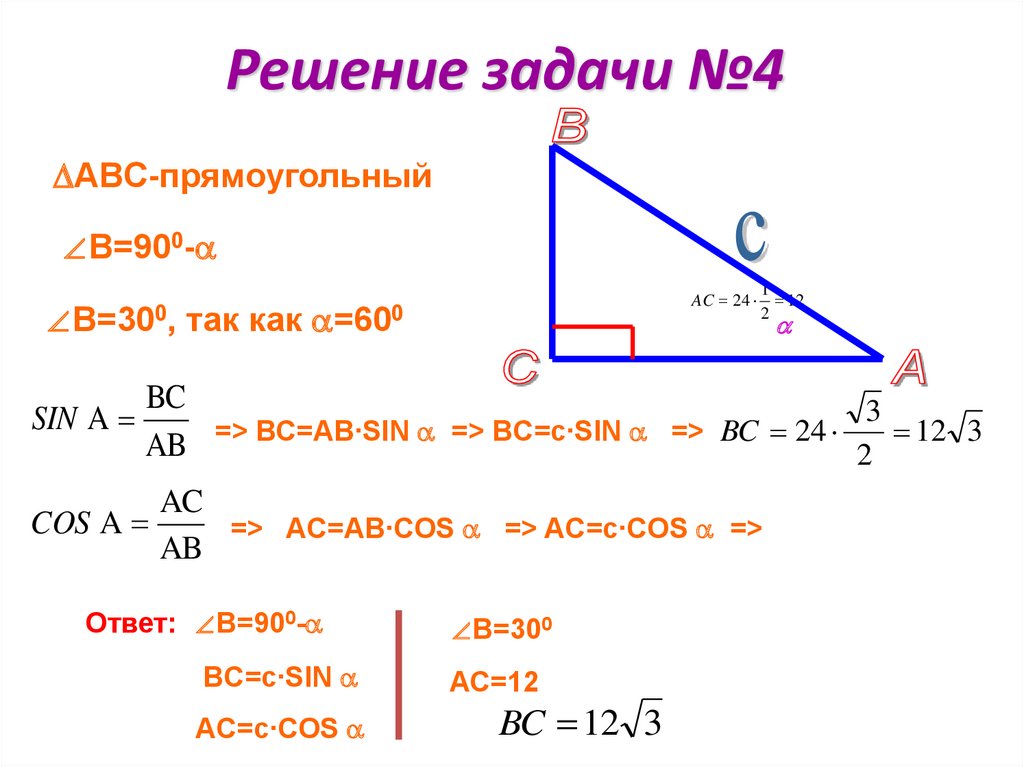


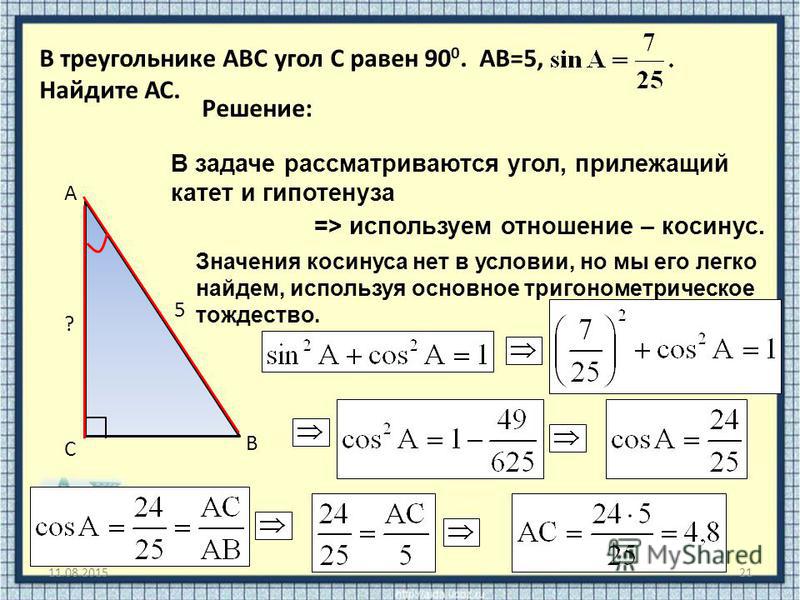
 Как далеко на запад пролетел самолет?
Как далеко на запад пролетел самолет? cos(C) можно использовать для решения задачи. Пройденные расстояния составляют длины сторон a, b и c, а внутренние углы треугольника равны A, B и C. используется для нахождения недостающего угла. Затем этот угол используется для нахождения пеленга.
cos(C) можно использовать для решения задачи. Пройденные расстояния составляют длины сторон a, b и c, а внутренние углы треугольника равны A, B и C. используется для нахождения недостающего угла. Затем этот угол используется для нахождения пеленга.
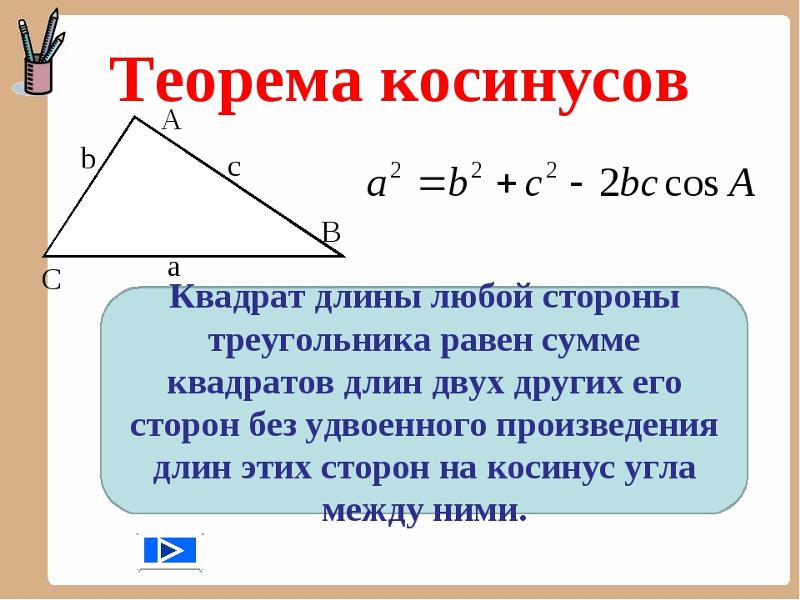
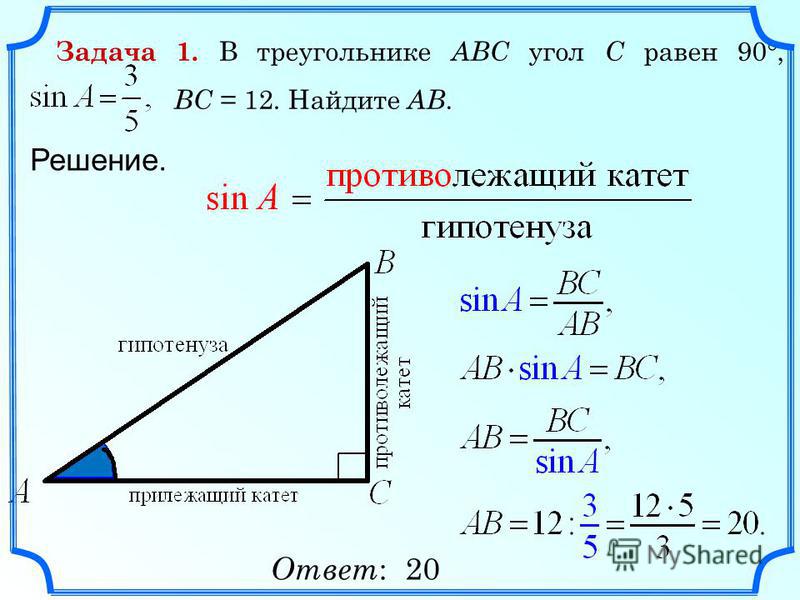 Азимут вектора затем определяется как угол по часовой стрелке с севера. Например, вектор (3 i -4 j ) образует угол tan -1 (4/3) = 53° ниже востока. Азимут находится как 90°+53°=143°.
Азимут вектора затем определяется как угол по часовой стрелке с севера. Например, вектор (3 i -4 j ) образует угол tan -1 (4/3) = 53° ниже востока. Азимут находится как 90°+53°=143°. 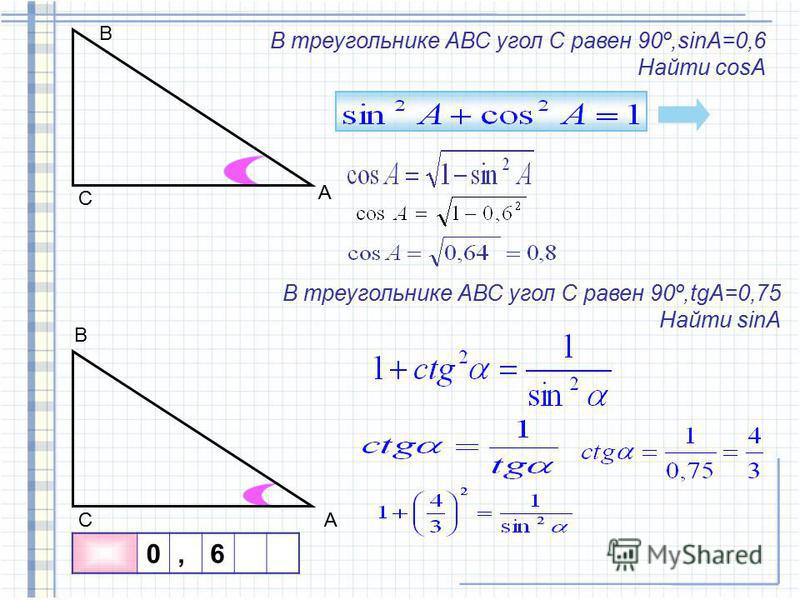
 Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник  Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр
Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр