Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
02.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Имеются два сосуда объемом V.
Как решить задачу? Из 2 кг муки выходит 3 кг печёного хлеба. Сколько хлеба выйдет из 1 ц муки? Из 1 т муки?
Длина реки Волги 3690 км. Туристы прошли на лодках третью часть её длины. Сколько дней они плыли, если двигались со скоростью 6 км/ч и ежедневно находились в плавании по 5 ч
В треугольнике АВС медианы АА1…
Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз
Пользуйтесь нашим приложением
Ответы к странице 152 №751-758 ГДЗ к учебнику «Математика» 6 класс Мерзляк, Полонский, Якир
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: ГДЗ Математика учебник 6 класс Мерзляк, Полонский, Якир
Задание 751
Вычислите площадь закрашенной фигуры (рис. 46), если длина стороны клетки равна 1 см.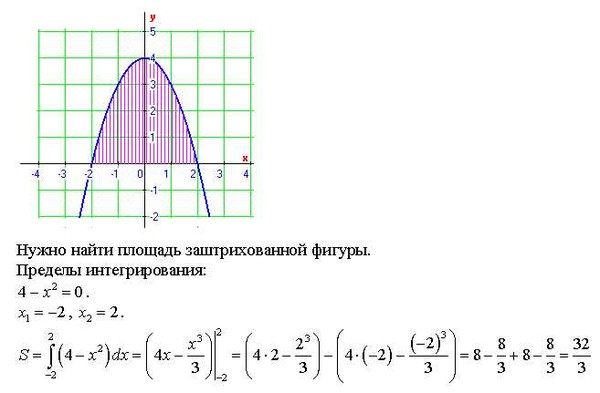
Задание 753
Диаметр колеса автомобиля равен 65 см. Автомобиль движется с такой скоростью, что колеса делают шесть оборотов в секунду. Найдите скорость автомобиля в километрах в час. Ответ округлите до десятых.
Решение
l = 2πr = πd = 3,14 * 65 = 204,1 см длина окружности колеса;
204,1 * 6 = 1224,6 см/сек скорость автомобиля в сантиметрах в секунду.
1 ч = 60 мин * 60 с = 3600 секунд;
1 км = 1000 м * 100 см = 100000 см, тогда:
$\frac{1224,6\ast3600}{100000}$ = 44,0856 ≈ 44,1 км/ч.
Задание 754
Диаметр колеса вагона равен 78 см. За 2,5 мин колесо делает 1000 оборотов. Найдите скорость поезда метро в километрах в час. Ответ округлите до десятых.
Решение
l = 2πr = πd = 3,14 * 78 = 244,92 см длина окружности колеса;
244,92 * 1000 : 2,5 = 97968 см/мин скорость поезда метро в сантиметрах в минуту.1 ч = 60 мин;
1 км = 1000 м * 100 см = 100000 см, тогда:
$\frac{97968\ast60}{100000}$ = 58,7808 ≈ 58,8 км/ч.
Задание 755
Найдите длину дуги, которую описывает часовая стрелка длиной 6 см за 1 ч.
Решение
r = длина часовой стрелки = 6 см;
l = 2πr = 2 * 3,14 * 6 = 37,68 см длина окружности циферблата;
На циферблате 12 дуг по 1 часу, тогда:
37,68 : 12 = 3,14 см длина дуги, которую описывает часовая стрелка длиной 6 см за 1 ч.
Задание 756
Найдите длину дуги, которую описывает минутная стрелка длиной 24 см за 40 мин.
Решение
r = длина часовой стрелки = 24 см;
$\frac{40}{60}=\frac23$ — часть циферблата занимает искомая дуга, следовательно:
l = 2πr = 2 * 3,14 * 24 = 150,72 (см) — длина окружности циферблата;
На циферблате 60 дуг по 1 минуте, тогда:
$150,72\ast\frac23=50,24\ast2=100,48$ (см) — длина дуги, которую описывает минутная стрелка длиной 24 см за 40 мин.
Задание 757
Вычислите площадь закрашенной фигуры, изображенной на рисунке 47.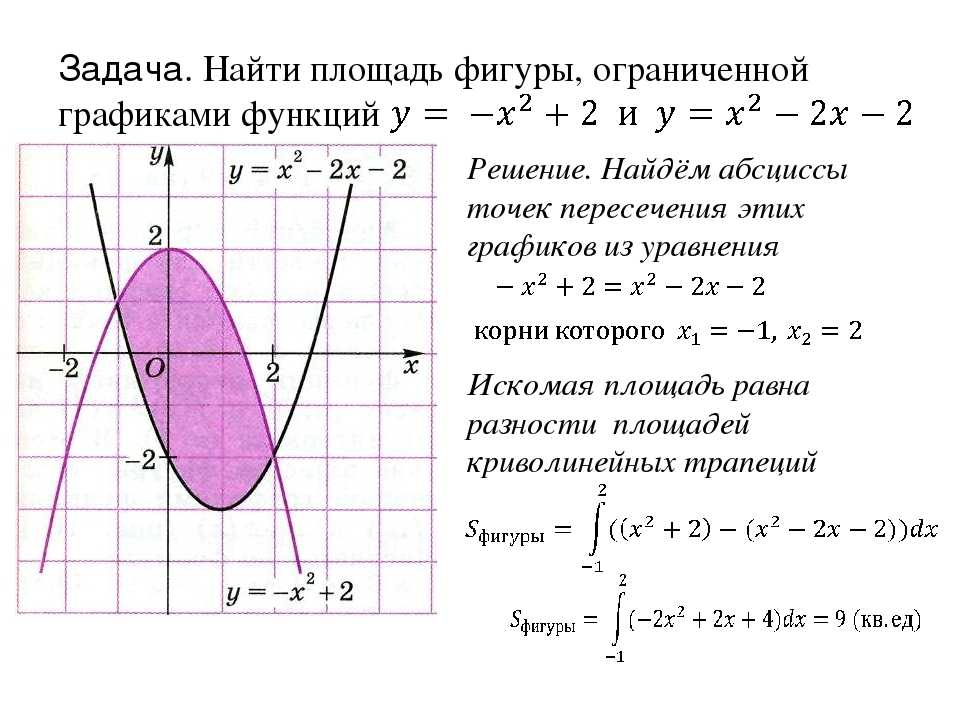
2$ площадь квадрата меньше площади круга, ограниченного данной окружностью.
- Назад
- Вперед
умножить наподелить на
- ГДЗ
- ГДЗ по математике
- ГДЗ Математика учебник 6 класс Мерзляк, Полонский, Якир
Вам может пригодиться:
Конические сечения: уравнения, параболы и формулы
Что такое конические сечения?
Коническое сечение кривая, которая образуется, когда плоскость пересекает поверхность конуса.
Боковая поверхность конуса называется покровом. Конус с двойным ворсом имеет два конуса, соединенных в вершине. На рисунке ниже конус 1 и конус 2 соединены в вершине. Они образуют конус с двойным ворсом. Верхний конус, то есть тот, что выше вершины, называется верхним покровом, а конус ниже вершины называется нижним покровом.
Периметр круглого основания (показан зеленым) называется направляющей. Генератор — это линия, которая вращается вокруг вершины. Неподвижная линия называется осью. Угол между вершиной и осью называется углом при вершине.
Когда конус с двойным ворсом (также называемый двойным прямым круговым конусом) пересекается плоскостью под разными углами по отношению к ее оси, мы получаем разные двумерные кривые. Такие сечения называются коническими.
Классификация конических сечений
В зависимости от угла, образуемого плоскостью с вертикальной осью конуса, могут возникать четыре различных формы:
Эллипс: Когда плоскость пересекает конус с двойным ворсом так, что угол между вершиной и углом больше чем угол при вершине, полученное коническое сечение в виде замкнутой кривой называется эллипсом.
Парабола: Когда плоскость пересекает конус с двойным ворсом так, что угол между вершиной и углом равен углу при вершине, коническое сечение в виде незамкнутой кривой называется параболой. Когда плоскость параллельна образующей, получается парабола.
Гипербола: Когда плоскость пересекает конус с двойным ворсом так, что угол между вершиной и углом меньше угла при вершине, коническое сечение в виде незамкнутой кривой называется гиперболой. В гиперболе обе стороны конуса пересекаются, а секущая плоскость параллельна оси конуса с двойным ворсом.
Если плоскость пересекает вершину конуса, получается вырожденное коническое сечение.
Уравнения конических сечений
Общее уравнение любого конического сечения является неоднородным уравнением второго порядка относительно x и y :
ax2+bxy+cy2+dx+ey+f=0
В зависимости от ограничений, наложенных на члены a , b , c , d , e , f , можно составить уравнения для различных конических сечений.
Все шесть коэффициентов не обязательно должны присутствовать в уравнении для коник. Однако для любого заданного конического сечения a , b и c не могут быть равны нулю одновременно.
Получив уравнение второго порядка и попросив определить тип конического сечения, найдите произведение коэффициентов a и c .
Случай (i):
a·c>0
Коническое сечение в этом случае представляет собой эллипс.
Пример:
x2+4y2=4
Коэффициент « a » здесь равен 1, а коэффициент « c 9»0038’ равно 4. Произведение 1 и 4 дает число больше нуля. Следовательно, данная кривая представляет собой эллипс.
Случай (ii):
a·c=0
Коническое сечение в этом случае представляет собой параболу.
Пример:
x2-12y=0
Коэффициент «а» здесь равен 1, а коэффициент «с» равен 0. Произведение 1 и 0 возвращает ноль. Следовательно, данная кривая представляет собой параболу.
Случай (iii):
a·c<0
Коническое сечение в этом случае представляет собой гиперболу.
Пример:
x2-3y2=9
Коэффициент « a » здесь равен 1, а коэффициент « c » равен -3. Умножение 1 на -3 дает число меньше нуля. Следовательно, данная кривая представляет собой гиперболу.
Подводя итог
ax2+byx+cy2+dx+ey+f=0
Другой параметр, называемый эксцентриситетом, обозначаемый буквой «е», также может использоваться для определения формы конических сечений. Значение эксцентриситета различных конических сечений указано ниже.
eэллипс: 0≤e<1eпарабола: 1eгипербола: e>1
графические коники
эллипс:
эллипс — это коническое сечение, в котором сумма расстояний от любой точки кривой до двух других фиксированных точек всегда является константой.
Общее уравнение эллипса:
(x-h)2a2+(y-k)2b2=1
На приведенном ниже рисунке общая длина оранжевой линии всегда будет равна длине фиолетовой линии, независимо от того, где находится точка ставится на кривую.
Эти неподвижные точки называются фокусами эллипса.
Эксцентриситет эллипса определяется выражением e=cae=ca.
Гиперболы и параболы конических уравнений
Парабола:
- Фокус параболы – это точка, вокруг которой она построена. Каждая парабола имеет одну точку фокусировки, в которой сходятся отраженные лучи. Таким образом, парабола изгибается вокруг своего фокуса.
- У каждой параболы есть направляющая. Точка на параболе находится на таком же расстоянии от директрисы, что и расстояние между точкой и фокусом параболы.
- Точка, расположенная между фокусом и директрисой, называется вершиной. Парабола вращается вокруг вершины.
- Эксцентриситет параболы всегда равен 1.
Точка на параболе находится на таком же расстоянии от директрисы, что и расстояние между точкой и фокусом параболы.Парабола с вершиной в ( h , k ) может быть изображена четырьмя различными способами на основе ее симметрии относительно осей x и y с соответствующие управляющие уравнения.
(i) Парабола, направленная вверх
(ii) Парабола, направленная вниз
(ii) Парабола, направленная влево
(ii) Парабола, направленная вправо
Гипербола:8 расстояние между любой точкой кривой и двумя фиксированными точками всегда является константой.
Две неподвижные точки называются фокусами гиперболы.
Общее уравнение гиперболы записывается так:
(x-h)2a2-(y-k)2b2=1
Эксцентриситет гиперболы равен e=cae=ca.
Конические сечения в реальной жизни
- Планеты вращаются вокруг Солнца в форме эллипсов, в одном из фокусов которых находится Солнце.
- Световые лучи собираются в фокусе параболы с помощью параболических зеркал. Пример: солнечные печи, автомобильные фары, прожекторы, телескопы.
- Траектория объекта, брошенного с поверхности Земли, следует параболической траектории. В системах телескопов используются как гиперболические, так и параболические зеркала и линзы.
Гиперболы в реальной жизни
- Астрономы предсказывают корректировку пути спутника таким образом, чтобы он попадал в пункт назначения, используя гиперболические функции.
- Обратные отношения (когда одна величина увеличивается, другая уменьшается) изображаются графически с помощью гиперболы.
- Градирни ядерных реакторов имеют гиперболическую конструкцию.
- Сигналы системы радиосвязи используют гиперболические функции для определения географического положения с помощью гипербол. Например: ЛОРАН.
Мы предоставим вам пошаговые решения для миллионов задач из учебников, круглосуточную помощь экспертов в данной области, если вы в затруднении, и многое другое.
Ознакомьтесь с примером решения вопросов и ответов по геометрии здесь!
*Время ответа зависит от темы и сложности вопроса. Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.
Q8 Найдите x, y и z на рисунке ниже…
Перейти к
- Упражнение 25 (А)
- Упражнение 25(Б)
- Упражнение 25 (С)
- Упражнение 25(Г)
- Повторное упражнение
- Система счисления (закрепление чувства числа)
- Предварительный расчет
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Отрицательные числа и целые числа
- Номер строки
- HCF и LCM
- Игра с числами
- Наборы
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Простые (линейные) уравнения (включая текстовые задачи)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- Треугольники (включая типы, свойства и конструкцию)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная >
Селина Солюшнс
Класс 6
Математика
>
Глава 25.
Свойства углов и прямых (включая параллельные прямые)
>
Упражнение 25(Б)
>
Вопрос 8
Вопрос 8 Упражнение 25(B)
Q8)
Найдите x, y и z на рисунке ниже:
Ответ:
Решение:
x = 180° — 75° (внутренний угол)
= 105°
y = 180° — x (внутренний угол)
= 180° — 105° = 75°
z = 75° (соответствующие углы)
Стенограмма видео
«Здравствуйте, добро пожаловать на домашнее задание на Лидо. Сегодня мы увидим вопрос, который заключается в том, чтобы найти X Y Z из данной фигуры, если вы найдете угол XYZ, дан только один угол, равный 75 градусов. Итак, нам нужно найти три других угла. Это изысканно. Давайте сделаем это. Итак, сначала посмотрите здесь, если это 75 градусов, что также будет беспокойством, также 75 ° 47 градусов установите соответствующие углы.
Таким образом, угол c будет быть 75 градусов.Это соответствующие углы?
Отвечая. Я имею в виду, что вы делаете следующий. Угол 75° и получился этот файл. Итак, если это так, вы знаете, это 75 градусов. Потому что это тоже 75 лет становится соответствующим. Так что если брать этот. Это будет угол X. Хорошо, вы можете принять угол X как 180 минус 75 градусов плюс 180 минус 75 градусов. Это будет угол 105 градусов по оси 105 градусов. Затем вы приходите к углу на любой угол y угол, на который вы также будете составлять 75 градусов, поэтому, поскольку он является угловым, внутренние углы Echo одинаковы, поэтому угол также равен 75 градусам. Это тоже будет так, верно?
Итак, я надеюсь, вы поняли это видео, подпишитесь на душ для регулярных обновлений и спасибо за просмотр этого видео.
Связанные вопросы
Q1) Определите пару углов на каждом из приведенных ниже рисунков: смежные углы, вертикально противоположные …
Q2) На каждом приведенном ниже рисунке изображена пара параллельных прямых, пересеченных секущей.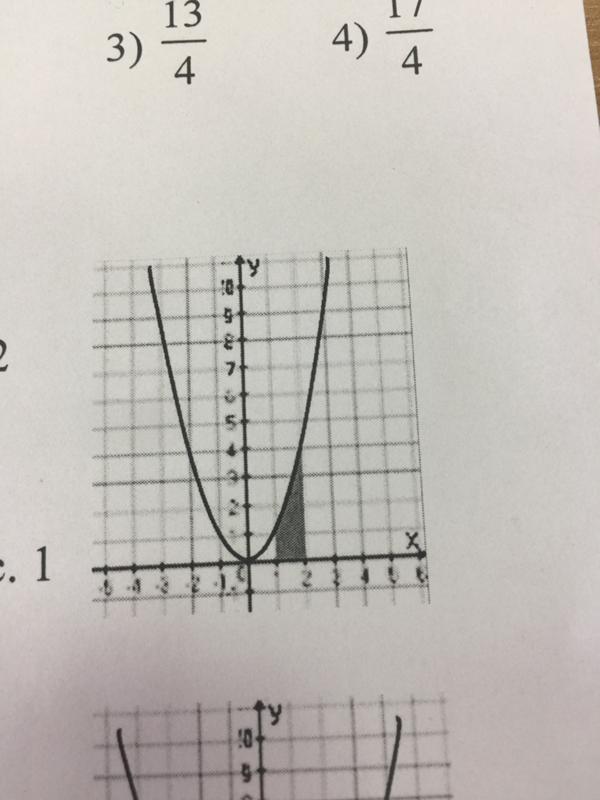
Для каждого случая найдите…
Q3) Если ∠1 = 120°, найдите меры: ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 и ∠8. Назови причины.
Q4) На приведенном ниже рисунке найдите величину углов, обозначенных x, y, z, p, q и r.
Q5) Используя данный рисунок, заполните пропуски.
Q6) На данном рисунке найдите углы, показанные x, y, z и w. Назови причины.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 25 (a)
Упражнение 25 (b)
Упражнение 25 (c)
Упражнение 25 (d)
РЕСПРАВЛЕНИЕ.