Ответы
| ||||||||||||
02.17
| ||||||||||||
02.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .
2-4x+5 и x-y+5=0 — вопрос №2340749 — Учеба и наука
Ответы
| ||||||||||||
02.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.
75 . Найдите АС.
Решено
На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?
Решено
Ледокол 3 дня пробивал себе путь во льдах.В первый день он проплыл 2/5всего пути,во второй день 5/8 оставшегося пути, а в третий день оставшиеся 90км.Чему равен путь, который проплыл ледокол за 3 дня
Решено
На аэродроме 20 самолетов.Сколько всего троек самолетов может подняться в воздух?Сколько при этом самолетов останется?
Дано: геометрическая прогрессия (bn) задана условиями: b1=-2 , bn+1=3bn. Найдите b6. Объясните пожалуйста, как это решить?
Пользуйтесь нашим приложением
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Объяснение урока: Площадь между кривой и линией
В этом объяснении мы узнаем, как применить интегрирование, чтобы найти площадь между кривой функции и горизонтальной или вертикальной прямой линией.
Нахождение площади под кривой функции — очень полезный метод, имеющий множество применений. Например, нахождение площади под графиком скорость-время объекта между двумя моментами времени дает общее расстояние, пройденное за это время.
Площадь под прямолинейным графиком вычислить достаточно просто. Например, рассмотрим площадь, ограниченную кривой функции, 𝑓(𝑥)=4𝑥+7, и осью 𝑥 между двумя точками, 𝑥=𝑎 и 𝑥=𝑏.
Замкнутую площадь можно найти по стандартной формуле площади трапеции: площадь трапеции=𝑝+𝑞2⋅ℎ, где 𝑝 и 𝑞 — длины двух параллельных сторон, а ℎ — расстояние между ними. Применяя эту формулу к замкнутой области на графике, наши две параллельные стороны имеют длины 𝑓(𝑎) и 𝑓(𝑏), а высоту ℎ=𝑏−𝑎. Следовательно, мы имеем площадь трапеции = 𝑓(𝑎)+𝑓(𝑏)2⋅(𝑏−𝑎).
При 𝑓(𝑥)=4𝑥+7 площадь трапеции=4𝑎+7+4𝑏+72⋅(𝑏−𝑎)=(2𝑎+2𝑏+7)(𝑏−𝑎)=2𝑎𝑏−2𝑎+2𝑏− 2𝑎𝑏+7𝑏−7𝑎=2𝑏+7𝑏−2𝑎+7𝑎.
Этот подход прекрасно работает, когда у нас есть линейная функция 𝑓(𝑥), и мы можем использовать простую геометрию, но он не будет работать для более сложных функций.
Например, если скорость объекта не меняется с постоянной скоростью (т. е. его ускорение непостоянно), то график скорость-время не будет прямой линией, и таким образом мы не сможем легко найти площадь.
Для общей кривой функции 𝑦=𝑓(𝑥) площадь между кривой и осью 𝑥 и между вертикальными линиями 𝑥=𝑎 и 𝑥=𝑏 определяется основной теоремой исчисления .
Мы определяем новую функцию 𝐴(𝑥) как площадь между кривой, 𝑓(𝑥), осью 𝑥 и вертикальными линиями 𝑥=0 и 𝑥=𝑥, общим значением 𝑥.
Увеличивая верхнюю границу площади на небольшую величину d𝑥, приращение функции площади d𝐴 определяется как dd𝐴=𝑓(𝑥)𝑥.
Перестановка дает изменение 𝐴, деленное на изменение 𝑥: dd𝐴𝑥=𝑓(𝑥).
Это производная от 𝐴 относительно 𝑥. Исходная функция площади 𝐴(𝑥), площадь под кривой между 0 и 𝑥, определяется инвертированием операции дифференцирования в обеих частях уравнения. В правой части это дает первообразную , 𝐹, 𝑓: 𝐴(𝑥)=𝐹(𝑥), где dd𝐹𝑥=𝑓(𝑥).
Теперь рассмотрим точно такой же сценарий, но оценивая площадь под кривой между двумя конкретными значениями 𝑥, 𝑥=𝑎 и 𝑥=𝑏.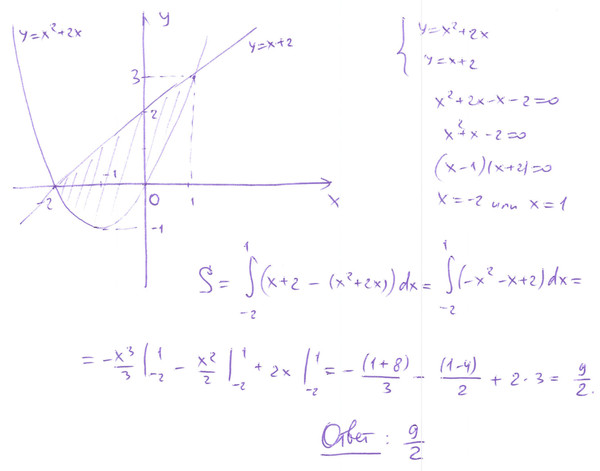
Площадь 𝛽 под кривой и между 𝑥=𝑎 и 𝑥=𝑏 определяется как 𝛽=𝐹(𝑏)−𝐹(𝑎).
Вычисление первообразной 𝐹 в двух точках 𝑥=𝑎 и 𝑥=𝑏 и получение разности называется определенным интегралом между 𝑎 и 𝑏 и обозначается 𝐹(𝑏)−𝐹(𝑎)=𝑓(𝑥)𝑥 .d
Следовательно, площадь 𝛽=𝐹(𝑏)−𝐹(𝑎) под кривой и между 𝑥=𝑎 и 𝑥=𝑏 определяется выражением 𝛽=𝑓(𝑥)𝑥=𝐹(𝑏)− 𝐹(𝑎).d
Правая часть часто обозначается 𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑥)],, где квадратные скобки с 𝑎 внизу справа и 𝑏 на вверху справа указано, что 𝐹(𝑥) оценивается при 𝑥=𝑎 и 𝑥=𝑏, а затем берется разница 𝐹(𝑏)−𝐹(𝑎). Произвольная константа интегрирования +𝐶 опускается для определенного интеграла, поскольку она одинакова как для 𝐹(𝑎), так и для 𝐹(𝑏) и, следовательно, сокращается.
Теорема: основная теорема исчисления
Площадь, заключенная между кривой 𝑓(𝑥), осью 𝑥 и двумя вертикальными линиями 𝑥=𝑎 и 𝑥=𝑏, определяется как aread=𝑓(𝑥) 𝑥=𝐹(𝑏)−𝐹(𝑎),, где 𝐹 — первообразная 𝑓. Правая часть часто обозначается 𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑥)],, где квадратные скобки с 𝑎 внизу справа и 𝑏 вверху справа указывают, что 𝐹(𝑥) оценивается при 𝑥=𝑎 и 𝑥=𝑏, тогда берется разница 𝐹(𝑏)−𝐹(𝑎).
Вернемся к функции из предыдущего примера, 𝑓(𝑥)=4𝑥+7, и на этот раз мы будем использовать интегрирование, чтобы найти площадь под кривой между двумя точками 𝑥=𝑎 и 𝑥=𝑏, как показано на диаграмме ниже .
Используя формулу площади под кривой, 𝑓(𝑥), между 𝑥=𝑎 и 𝑥=𝑏, aread=𝑓(𝑥)𝑥=𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑥) ].
В этом случае имеем 𝑓(𝑥)=4𝑥+7, что дает площадь=4𝑥+7𝑥.
Интегрирование по 𝑥 дает площадь=2𝑥+7𝑥.
Оценив при 𝑥=𝑏 и 𝑥=𝑎 и взяв разность, площадь=2𝑏+7𝑏−2𝑎+7𝑎.
Этот результат точно согласуется с результатом, найденным ранее для площади трапеции . Однако огромное преимущество использования интегрирования для нахождения площади под кривой заключается в том, что оно распространяется на гораздо более сложные функции, для которых иначе было бы невозможно вычислить площадь.
Давайте рассмотрим пример использования интегрирования для нахождения площади под более сложной кривой.
Пример 1. Нахождение площади под кривой квадратичной функции
Пусть 𝑓(𝑥)=2𝑥+3.
Определите площадь, ограниченную кривой 𝑦=𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=−1 и 𝑥=5.
Ответ
Может быть полезно набросать площадь, которую нас просят вычислить. В данном случае это площадь, ограниченная прямыми 𝑥=−1 и 𝑥=5 и кривой 𝑦=2𝑥+3.
Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 задается определенным интегралом aread=𝑓(𝑥)𝑥=𝐹(𝑏)−𝐹( 𝑎),, где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥). Подставляя в заданную функцию 𝑓(𝑥)=2𝑥+3 и пределы 𝑥=−1 и 𝑥=5: aread=2𝑥+3𝑥.
Интегрирование по 𝑥 дает area= 23𝑥+3𝑥, и оценивая это между пределами 𝑥=−1 и 𝑥=5, получаем площадь квадрата единиц =23⋅5+3⋅5−23⋅(−1)+3(−1) =2503+15−−23−3=102.
Для некоторых функций существуют области, для которых кривая лежит на 90 919 ниже 90 920 по оси 𝑥. По характеру того, как мы оцениваем площадь между кривой и 𝑥-осью, поскольку приращение d𝑥 всегда положительно, элемент площади dd𝐴=𝑓(𝑥)𝑥, конечно, будет отрицательным , если функция 𝑓(𝑥 ), в этот момент отрицательный.
Следовательно, любая область, заключенная в ниже по оси 𝑥 кривой, будет оцениваться как отрицательное . Поскольку площадь является строго положительной величиной, ее часто решают, беря абсолютное значение определенного интеграла для каждого региона.
Давайте рассмотрим пример того, как мы можем использовать интегрирование, чтобы найти площадь, ограниченную кривой ниже оси 𝑥.
Пример 2. Использование метода определенного интегрирования для нахождения площади между двумя линиями и ниже Горизонтальная ось
Показанная кривая 𝑦=1𝑥. Чему равна площадь заштрихованной области? Дайте точный ответ.
Ответ
Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 задается определенным интегралом aread=𝑓(𝑥)𝑥=𝐹(𝑏 )−𝐹(𝑎), где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥). Подставляя в заданную функцию 𝑓(𝑥)=1𝑥 и пределы 𝑥=−1 и 𝑥=−13: aread=1𝑥𝑥.
Интегрирование по 𝑥 дает arean=[|𝑥|]; мы помним, что натуральный логарифм ln(𝑥) не определен для отрицательных значений 𝑥, поэтому мы берем абсолютное значение.
Оценивая это между пределами 𝑥=−1 и 𝑥=−13: =|||−13|||−|−1|=3−0=−(3)≈−1,099().lnlnlnlnto3d. стр.
Обратите внимание, что результат отрицательный. Это связано с тем, что площадь между кривой и осью 𝑥 составляет ниже по оси 𝑥. Взяв абсолютное значение, мы находим, что истинное значение для площадь заштрихованной области составляет ln(3)≈1,099 (до 3 д.п.) квадратных единиц.
Иногда вычисление истинного значения площади, очерченной кривой, не так просто, как получение абсолютного значения определенного интеграла. Давайте рассмотрим пример, где нам нужно быть более осторожными с этим методом.
Пример 3. Использование метода интегрирования для определения площади областей выше и ниже горизонтальной оси
На рисунке показан график функции 𝑓(𝑥)=2𝑥−8𝑥. Оцените площадь заштрихованной области.
Ответ
Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 задается определенным интегралом aread=𝑓(𝑥)𝑥=𝐹(𝑏 )−𝐹(𝑎), где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥).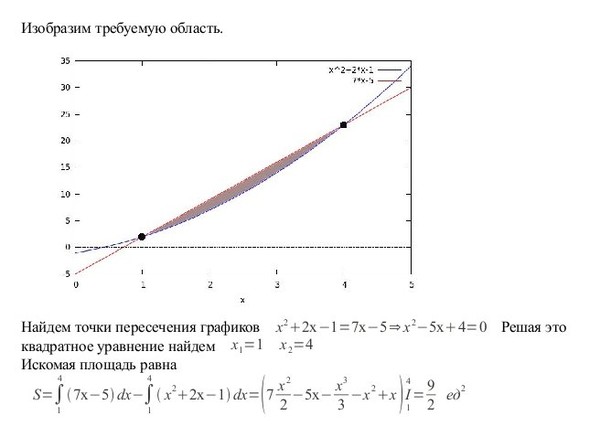
В этом примере функция 𝑓(𝑥)=2𝑥−8𝑥 является нечетной функцией. То есть он совершенно антисимметричен относительно оси 𝑦, поэтому 𝑓(−𝑥)=−𝑓(𝑥). Это, в свою очередь, означает, что площадь между 𝑥=0 и любым значением 𝑥=𝑎 будет точно такой же, как площадь между 𝑥=−𝑎 и 𝑥=0. Однако при использовании определенного интегрирования для нахождения площади интеграл на одной стороне оси 𝑦 будет иметь напротив знака интеграла на другом.
Это означает, что при интегрировании между двумя равными и противоположными значениями, как здесь, между −2 и +2, мы обнаружим, что интеграл на одной стороне оси 𝑦 аннулирует интеграл на другой стороне, давая всего ноль: area=2𝑥−8𝑥𝑥.
Интегрирование по 𝑥 дает area=12𝑥−4𝑥.
Теперь мы вычисляем четную функцию (т.е. , 𝑓(−𝑥)=𝑓(𝑥)) при двух равных и противоположных значениях перед взятием разности, поэтому результат будет равен нулю: площадь = 12⋅2−4⋅2−12⋅(−2)−4⋅ (−2)=8−16−(8−16)=0,
Однако ясно, что площадь полностью заштрихованной области не равна нулю.
Чтобы исправить эту проблему, нам нужно оценить площадь каждой части заштрихованной области отдельно .
В этом примере у нас есть две отдельные области, окруженные кривой, 𝑓(𝑥) и осями 𝑥 и 𝑦.
Итак, нам нужно вычислить интеграл между 𝑥=−2 и 𝑥=0 и интеграл между 𝑥=0 и 𝑥=2 отдельно, взять абсолютное значение каждого интеграла, чтобы получить площадь, а затем сложить их вместе чтобы дать площадь полной заштрихованной области.
Для первого региона площадь1=12𝑥−4𝑥=0−12⋅(−2)−4⋅(−2)=0−(8−16)=8.
А для второй области: area2=12𝑥−4𝑥=12⋅2−4⋅2−0=8−16−0=−8.
Отрицательное значение ожидается, поскольку область между 𝑥=0 и 𝑥=2 находится ниже оси 𝑥. Взяв абсолютное значение, чтобы получить площадь: area2=|−8|=8.
Таким образом, общая площадь полностью заштрихованной области представляет собой сумму этих двух площадей: площадьплощадьплощадьквадратединицы=1+2=8+8=16.
Основная теорема исчисления, конечно, не ограничивается функциями независимой переменной (обычно 𝑥).
Его также можно использовать для нахождения площади, ограниченной функцией 𝑦.
Теорема: площадь, ограниченная кривой функции 𝑦
Площадь, заключенная между кривой 𝑓(𝑦), осью 𝑦 и двумя горизонтальными линиями 𝑦=𝑎 и 𝑦=𝑏, определяется выражением aread= 𝑓(𝑦)𝑦=𝐹(𝑏)−𝐹(𝑎),, где 𝐹 — первообразная 𝑓. Правая часть часто обозначается 𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑦)],, где квадратные скобки с 𝑎 внизу справа и 𝑏 справа вверху указывают, что 𝐹(𝑦) оценивается при 𝑦=𝑎 и 𝑦=𝑏, тогда берется разница 𝐹(𝑏)−𝐹(𝑎).
В следующем примере искомая область ограничена функцией 𝑦 и двумя горизонтальными линиями.
Пример 4. Использование метода определенного интегрирования для нахождения площади между неявной функцией и двумя горизонтальными линиями 𝑦=3.
Ответ
Может быть полезно набросать площадь, которую нас просят вычислить. В данном случае это площадь, ограниченная прямыми 𝑦=−3 и 𝑦=3 и кривой 𝑥=9−𝑦.
𝑥 является отрицательной квадратичной функцией от 𝑦, поэтому кривая представляет собой n-образную параболу вокруг оси 𝑥.
Чтобы найти 𝑥-перехват, подставляем 𝑦=0 в уравнение функции и решаем его относительно 𝑥, что дает
𝑥=9.
Итак, кривая пересекает ось 𝑥 в точке 𝑥=9. Далее, чтобы найти 𝑦-пересечения кривой, подставляем 𝑥=0 в уравнение функции и решаем его относительно 𝑦, что дает 0=9−𝑦𝑦=±3.
Следовательно, кривая пересекает ось 𝑦 в точках 𝑦=3 и 𝑦=−3. Теперь у нас достаточно информации, чтобы нарисовать кривую.
Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 определяется определенным интегралом: aread=𝑓(𝑥)𝑥=𝑓(𝑏)−𝑓(𝑎), где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥).
Однако в этом случае мы не можем просто перестроить функцию кривой для 𝑦 и проинтегрировать по 𝑥, так как площадь над 𝑥-осью равна площади под ней, и результат интегрирования будет нуль.
Если мы попытаемся продолжить таким образом, мы начнем с 𝑦=±√9−𝑥, так, aread=±√9−𝑥𝑥.
Проблема в данном конкретном случае заключается в том, что функция 𝑦=√9−𝑥 не соответствует уникальному значению 𝑦, поскольку квадратный корень может быть как положительным, так и отрицательным; поэтому невозможно узнать, какую область мы оцениваем.
В этом случае 𝑦=√9−𝑥 сопоставляет заданное значение 𝑥 с , как — положительный квадратный корень +√9−𝑥 , так и — отрицательный квадратный корень −√9−𝑥.
Извлечение положительного квадратного корня дает площадь, ограниченную кривой над осью 𝑥.
Поскольку мы изменили функцию на строго взаимооднозначную, теперь мы можем вычислить эту площадь обычным способом с определенным интегралом: aread=+√9−𝑥𝑥=−23(9−𝑥)=18.
Аналогичным образом, извлечение отрицательного квадратного корня дает площадь, ограниченную кривой под осью 𝑥.
Еще раз, мы можем оценить эту площадь с помощью определенного интеграла: aread=−√9−𝑥𝑥=23(9−𝑥)=−18.
Сложение этих площадей вместе дает результат 0, но мы можем использовать наши знания о том, что истинная площадь определяется суммой этих абсолютных значений: квадратные единицы площади=|18|+|−18|=36.
Более простой альтернативой является интегрирование по 𝑦. По сути, это переключает переменные.
Рассмотрим горизонтальную полосу площади, ограниченную 𝑥=9−𝑦 и осью 𝑦, с шириной 𝑥 и высотой d𝑦.
Функция 𝑥=𝑓(𝑦)=9−𝑦 может быть проинтегрирована по y между 𝑦=−3 и 𝑦=3, так как нет внутренней разницы между 𝑥 и 𝑦 как переменными, и это просто соглашение что 𝑥 обычно является независимой переменной. Кроме того, эта функция соответствует одному значению 𝑥, поэтому ее можно интегрировать без необходимости разбивать интеграл на отдельные области. Таким образом, у нас есть aread=9−𝑦𝑦.
Интегрирование по 𝑦 дает квадратные единицы площади =9𝑦−13𝑦=9⋅3−13⋅3−9⋅(−3)−13⋅(−3)=27−9−(−27+9)=36.
Определенные интегралы также можно использовать для нахождения площади, заключенной между кривой функции 𝑦=𝑓(𝑥) и кривой другой функции 𝑦 =𝑔(𝑥), используя тот факт, что интегральный оператор, как и дифференциальный оператор, является линейным оператором , что означает, что он замкнут относительно сложения : 𝑓(𝑥)𝑥+𝑔(𝑥)𝑥 =𝑓(𝑥)+𝑔(𝑥)𝑥.ddd
Это распространяется и на вычитание, поскольку интегрирование также закрыто при скалярном умножении : 𝛼𝑓(𝑥)𝑥=𝛼𝑓(𝑥)𝑥,dd, где 𝛼 — скаляр.
Взяв частный случай 𝛼=−1, −𝑓(𝑥)𝑥=-𝑓(𝑥)𝑥,dd и объединив это с первым свойством, мы можем выразить разницу между двумя интегралами как один интеграл: 𝑓 (𝑥)𝑥−𝑔(𝑥)𝑥=𝑓(𝑥)𝑥+−𝑔(𝑥)𝑥=𝑓(𝑥)−𝑔(𝑥)𝑥.ddddd
Для более простого случая второй функции будучи постоянной горизонтальной линией 𝑦=𝑔(𝑥)=𝑐, мы имеем 𝑓(𝑥)𝑥−𝑐𝑥=𝑓(𝑥)−𝑐𝑥.ddd
Следовательно, мы можем найти площадь, заключенную в кривую 𝑦=𝑓(𝑥) и горизонтальную линию 𝑦=𝑐 между двумя точками 𝑥=𝑎 и 𝑥=𝑏 по формуле aread=𝑓(𝑥)−𝑐𝑥.
Давайте рассмотрим пример того, как мы используем это, чтобы найти площадь, заключенную между кривой и прямой линией.
Пример 5. Использование метода интегрирования для нахождения площади, ограниченной кривой и горизонтальной линией
Найдите площадь заштрихованной области.
Ответ
Площадь этой заштрихованной области может быть найдена вычислением определенного интеграла кривой 𝑦=3𝑥+4𝑥−2 между пределами 𝑥=1 и 𝑥=2, а затем вычитанием площади прямоугольника под ним , который мы можем легко найти с помощью стандартной формулы площади прямоугольника.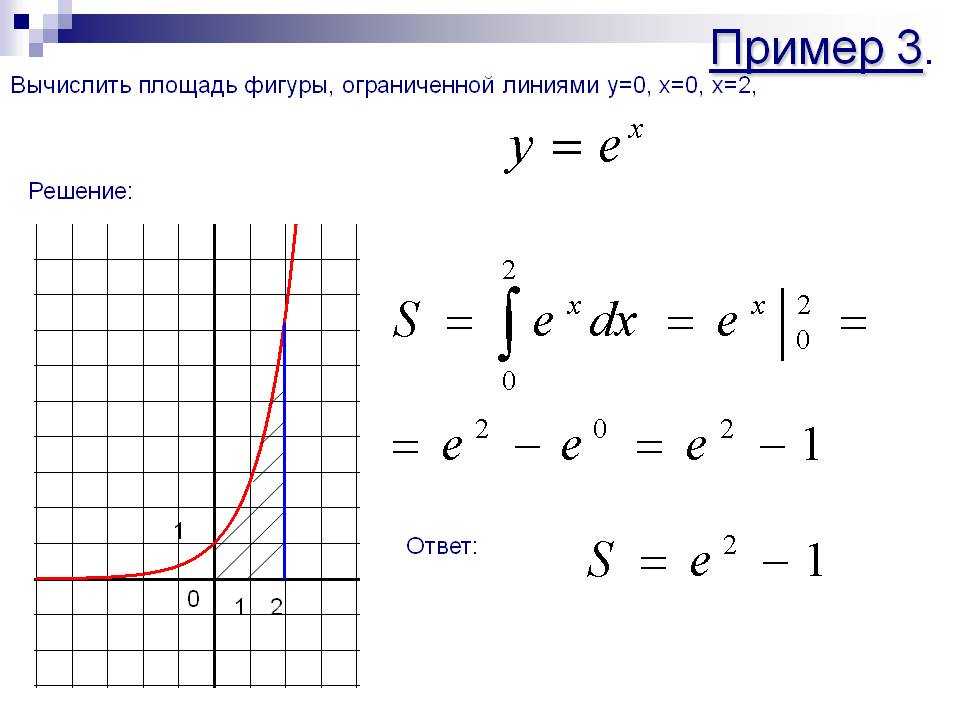
Однако напомним, что мы также можем найти площадь, ограниченную кривой 𝑦=𝑓(𝑥) и горизонтальной линией 𝑦=𝑐 между двумя точками 𝑥=𝑎 и 𝑥=𝑏, используя формулу aread=𝑓(𝑥)− 𝑐𝑥.
В этом случае у нас есть кривая 𝑓(𝑥)=3𝑥+4𝑥−2 и горизонтальная линия 𝑦=5. Подстановка их в приведенную выше формулу дает areadd=3𝑥+4𝑥−2−5𝑥=3𝑥+4𝑥−7𝑥.
. 2+2⋅2−7⋅2−1+2⋅1−7⋅1=8+8−14−(1+2−7)=6.
Давайте закончите повторением некоторых ключевых моментов из этого объяснения.
Ключевые точки
- Площадь, ограниченная кривой 𝑦=𝑓(𝑥), осью 𝑥 и двумя горизонтальными линиями 𝑥=𝑎 и 𝑥=𝑏, определяется выражением 𝐴=𝑓(𝑥)𝑥. d
- Площадь, ограниченная кривой 𝑥=𝑓(𝑦), осью 𝑦 и двумя вертикальными линиями 𝑦=𝑎 и 𝑦=𝑏, равна 𝐴=𝑓(𝑦)𝑦.d
- A область, заключенная над осью 𝑥/осью 𝑦, дает положительный интеграл, а область, заключенная под осью 𝑥/осью 𝑦, дает отрицательный интеграл. Так как площадь является строго положительной величиной, чтобы найти замкнутую площадь, мы берем абсолютное значение интеграла для каждой отдельной замкнутой области.
