Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
10.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Молоко разлили в 2 бидона.
Во втором бидоне молока было в 2 раза больше,чем в первом.Когда из каждого бидона вылили по 10 литров молока,во втором…
чему равны индуктивность и энергия магнитного поля соленоида , если при силе тока, равной 4А, магнитный поток через соленоид и равен 0,4 вб
Помогите составить условие задачи: у Иры в коллекции есть 26марок,посвящённые историческим событиям,а так же марки,посвящённые архитектуре и спорту,марок по архитектуре у неё на 15 больше чем по
Найдите углы,образованные при пересечении двух прямых,если разность двух из них равна 64
Контролер за 10 мин. Проверяет 50 деталей. Сколько дет.он проверит за 1ч. Если будет проверять по столько же деталей в
Пользуйтесь нашим приложением
Скалярное произведение векторов — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Скалярное произведение векторов
Скалярным произведением двух ненулевых векторовназывается произведение их длин на косинус угла между
ними. Если хотя бы один из векторов нулевой, то
скалярное произведение таких векторов считается
равным нулю.
Скалярное произведение векторов и обозначается . По
определению, a a | a | | a | cos .
1
2
1
2
Произведение называется скалярным квадратом и
обозначается a 2 . Из формулы скалярного произведения
следует равенство a 2 | a |2 .
Для скалярного произведения векторов имеет место
формула a1 a2 x1 x2 y1 y2 , где a1 ( x1 , y1 ), a2 ( x2 , y2 ).
2. Физический смысл
Скалярное произведение векторов имеет простойфизический смысл и связывает работу A, производимую
постоянной силой F при перемещении тела на вектор a ,
составляющий с направлением силы угол , а именно,
имеет место следующая формула: A F a | F | | a | cos .
3. Пример 1
Дан вектор m(a, b). Найдите координатыперпендикулярного к нему вектора.
Решение: Для искомого вектора n ( x, y ) должно
выполняться равенство ax + by = 0. Например, этому
равенству удовлетворяют x = b, y = –a. Следовательно,
искомый вектор имеет координаты n ( b, a ).
4. Пример 2
Найдите угол A треугольника с вершинами1
A( 1, 3), B (1, 3), C ( , 3).
2
Решение: Воспользуемся определением скалярного
произведения векторов AB и AC . Имеем
AB AC | AB | | AC | cos A. Вычислим это скалярное
произведение через координаты векторов. Вектор AB
имеет координаты (2, 2 3), вектор AC имеет
координаты (3/ 2, 0).
Следовательно, скалярноепроизведение данных векторов равно 3. Их длины
равны соответственно 4 и 3/2. Подставляя эти данные в
формулу скалярного произведения, получим cos A 1
2
о
и, следовательно, A = 60 .
5. Упражнение 1
Вычислите скалярное произведение двухвекторов a и b , если | a | = 2, | b | = 3, а угол
между ними равен: а) 45°; б) 90°; в) 135°.
Ответ: а) 3 2 ; б) 0; в) 3 2 .
6. Упражнение 2
В равностороннем треугольнике АВС состороной 1 проведена высота BD. Вычислите
скалярное произведение векторов:
а) AC и CB;
б) AC и BD;
в) AC и AC .
1
Ответ: а) ; б) 0; в) 1.
2
7. Упражнение 3
Найдите скалярное произведение векторовa1 (-1, 2) и a2 (2,-1).
Ответ: –4.
8. Упражнение 4
Охарактеризуйте угол между векторами a и b,если:
о< < 90о;
Ответ:
а)
0
а) a b 0;
б)
a b 0;
в)
a b 0;
г)
a b | a | | b |.
б) 90о< < 180о ;
в) = 90о;
г) = 180о.
9. Упражнение 5
Длины векторов a и b равны 1. При каком углемежду ними скалярное произведение будет: а)
наибольшим; б) наименьшим?
Ответ: а) = 0о;
б) = 180о.
10. Упражнение 6
Найдите угол между векторами a (1, 2) и b (1, 0).5
Ответ: cos .
5
11. Упражнение 7
Какой угол образуют единичные векторы a иb , если известно, что a 2b и 5a 4b взаимно
перпендикулярны.
Ответ: 60о.
12. Упражнение 8
При каком значении t вектор 2a tbперпендикулярен вектору b a, если
a (2, -1), b (4, 3).
Ответ: t = 0.
13. Упражнение 9
Для прямоугольника ABCD со сторонами AB = 6см, AD = 8 см найдите скалярное произведение:
а)
AB BE;
б)
BE BD;
в)
BF BD;
г)
BE BF ,
где E и F – середины сторон AD и CD
соответственно.
Ответ: а) 36; б) 68; в) 82; г) 50.
14. Упражнение 10
Вычислите, какую работу A производит силаF (-3, 4), когда ее точка приложения,
двигаясь прямолинейно, перемещается из
положения B(5, -1) в положение C(2, 1).
Ответ: A = 17.
English Русский Правила
Геометрия. Что представляет собой скалярное произведение двух векторов?
Как указывалось в других ответах, точечный продукт $\vec{a} \cdot \vec{b}$ связан с углом $\theta$ между $\vec{a}$ и $\vec{b} $ through:
$$\vec a \cdot \vec b = \Vert\vec a\Vert_2 \, \Vert\vec b\Vert_2 \, \cos \theta$$
Предположим, что $a$ и $b $ указывают в аналогичных направлениях, т. е. $\theta \leq 90°$, мы можем визуализировать, что означает это соотношение (с этого момента пропуская векторные стрелки и нижний индекс евклидовой нормы):
$p$ — вектор, полученный ортогональной проекцией $a$ на $b$. Поскольку $\cos$ — это отношение между соседним катетом ($p$) и гипотенузой ($a$) в прямоугольном треугольнике, т. е.
$$\cos \theta = \frac{\Vert p \Vert }{\Vert a \Vert},$$
получаем для скалярного произведения:
$$a \cdot b = \Vert a \Vert \, \Vert b \Vert \, \frac{\Vert p \ Vert}{\Vert a \Vert} = \Vert p \Vert \Vert b \Vert$$
Итак, скалярное произведение — это длина вектора $p$, проекция $a$ на $b$, умножается на длину $b$.
Если $a$ и $b$ направлены в противоположные стороны, т. е. $90° < \theta \leq 180°$, скалярное произведение будет отрицательным: $a \cdot b = - \Vert p \Vert \Vert b \Vert$
угол $\theta$ сам по себе не задан. По определению:
$$a \cdot b = \sum_i a_i b_i$$
Итак, нам нужно найти связь между этим и косинусом. Из определения скалярного произведения видно, что оно масштабируется пропорционально входным векторам, поэтому для неединичных векторов $u$ и $v$ с соответствующими единичными векторами $\hat{u}$ и $\hat{ v}$:
$$u \cdot v = \Vert u \Vert \hat{u} \cdot \Vert v \Vert \hat{v} = \Vert u \Vert \Vert v \Vert \hat{u} \cdot \ hat{v}.$$
Для простоты будем считать $a$ и $b$ единичными векторами. Таким образом, нам нужно только показать
$$a \cdot b = \cos \theta$$
или, по определению $\cos$, нам нужно показать:
$$a \cdot b = \ Vert p \Vert $$
Вычислим длину проекции $p$, используя $a$ и $b$. Мы можем начать с использования теоремы Пифагора: 92\\ &= 2 — (2 — 2 \sum_i b_i a_i) \\ &= 2 \sum_i b_i a_i \\ \Vert p \Vert &= \sum_i b_i a_i \end{выравнивание} $$
четв.
е.д.
Видео-вопрос: Нахождение скалярного произведения двух векторов
Стенограмма видео
Квадрат 𝐴𝐵𝐶𝐷 имеет сторону 10 сантиметров. Каково скалярное произведение между векторами 𝐀𝐁 и 𝐁𝐂?
В этом вопросе нам дается некоторая информация о квадрате 𝐴𝐵𝐶𝐷. Нам сказали, что длина стороны этого квадрата равна 10 сантиметрам. Нам нужно использовать это, чтобы определить скалярное произведение между векторами, представляющими две его стороны, вектор 𝐀𝐁 и вектор 𝐁𝐂.
Начнем с того, что нарисуем наш квадрат 𝐴𝐵𝐶𝐷 со стороной 10 сантиметров. На самом деле есть несколько разных способов, которыми мы могли бы оценить этот скалярный продукт. Один из способов сделать это — записать наши векторы 𝐀𝐁 и 𝐁𝐂 по компонентам из нашей диаграммы. Например, мы видим, что вектор, идущий от 𝐴 к 𝐵, не имеет горизонтальной составляющей, а его вертикальная составляющая будет равна 10 сантиметрам. Таким образом, вектор от 𝐴 до 𝐵 может быть представлен нулевой горизонтальной составляющей и 10 вертикальной составляющей, потому что для перехода из точки 𝐴 в точку 𝐵 мы увеличиваем вертикальную составляющую на 10 сантиметров.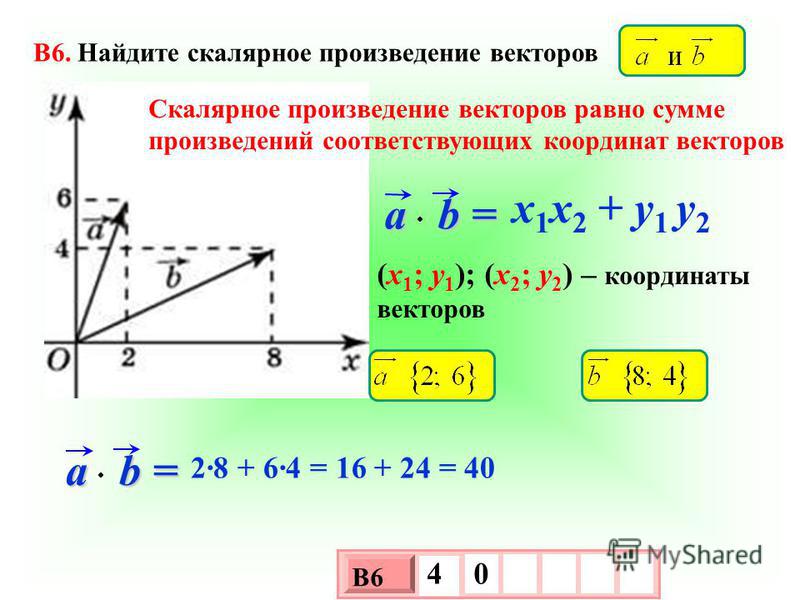
Мы можем сделать то же самое для нашего вектора 𝐁𝐂. Чтобы перейти из точки 𝐵 в точку 𝐶, наша вертикальная составляющая будет равна нулю. Однако мы увеличиваем нашу горизонтальную составляющую на 10. Таким образом, вектор от 𝐵 до 𝐶 может быть представлен вектором 10, ноль.
Теперь мы можем напрямую найти скалярное произведение этих двух векторов. Для этого нам нужно вспомнить, как именно мы вычисляем скалярное произведение между двумя векторами. Помните, что для этого мы перемножаем соответствующие компоненты вместе, а затем складываем результаты. Итак, мы начинаем с умножения первых компонентов наших векторов. Это ноль, умноженный на 10. А затем мы добавляем к этому произведение вторых компонентов наших векторов. Это 10 умножить на ноль. И, конечно же, мы можем это вычислить. Он равен нулю.
Однако это не единственный способ вычислить это выражение. Мы знаем формулу, включающую скалярное произведение между двумя векторами и углом между ними. Мы помним, что если 𝜃 — это угол между двумя векторами 𝐮 и 𝐯, то cos 𝜃 должен быть равен скалярному произведению между 𝐮 и 𝐯, деленному на величину 𝐮, умноженную на величину 𝐯.
Таким образом, другой способ оценки скалярного произведения, данного нам в вопросе, состоит в том, чтобы найти величину наших двух векторов и угол между ними. Затем мы можем изменить это уравнение и найти скалярный продукт.
Давайте начнем с определения величины наших двух векторов. Это вектор 𝐀𝐁 и вектор 𝐁𝐂. Это обозначение говорит нам, что вектор 𝐀𝐁 — это вектор из 𝐴 в 𝐵, а вектор 𝐁𝐂 — это вектор из 𝐵 в 𝐶. И мы можем видеть из нашей диаграммы, что обе они будут длинами сторон нашего квадрата. А в вопросе нам говорят, что у квадрата длина стороны 10 сантиметров. Итак, мы можем начать с того, что величина 𝐀𝐁 и величина 𝐁𝐂 будут равны 10 сантиметрам.
Теперь нам нужно найти угол между нашими двумя векторами. Давайте начнем с рисования этих векторов на нашей диаграмме. Начнем с рисования вектора 𝐀𝐁. Это вектор от 𝐴 к 𝐵. А затем мы также нарисуем вектор от 𝐵 до 𝐶.
Здесь нужно быть осторожным. Очень заманчиво назвать угол 𝐴𝐵𝐶 углом между этими двумя векторами. Однако это было бы неправильно.
Чтобы найти угол между нашими двумя векторами, наши векторы должны начинаться в одной и той же точке. И мы видим, что это не так на нашей диаграмме. Вектор 𝐀𝐁 начинается в 𝐴 и заканчивается в 𝐵, а вектор 𝐁𝐂 начинается в 𝐵 и заканчивается в 𝐶. Итак, нам нужно переместить один из наших векторов. Давайте переместим вектор 𝐁𝐂.
Помните, что вектор — это объект с величиной и направлением. Итак, если величина и направление двух векторов одинаковы, то и векторы одинаковы. Поскольку 𝐴𝐵𝐶𝐷 является квадратом, мы знаем, что длина 𝐴𝐷 равна 10, а также мы знаем, что векторы 𝐀𝐃 и 𝐁𝐂 параллельны. Следовательно, мы только что показали, что вектор от 𝐴 к 𝐷 и вектор от 𝐵 к 𝐶 имеют одинаковую величину и направление. Они представляют один и тот же вектор. Таким образом, угол между нашими векторами 𝐀𝐁 и 𝐁𝐂 представлен углом 𝐷𝐴𝐵. И, конечно же, это прямой угол. Итак, мы знаем, что оно равно 9.0 градусов.
Теперь, когда мы нашли величину наших векторов и угол между ними, мы можем подставить эти значения в нашу формулу.