Вычитание восьмеричных чисел онлайн калькулятор: СЛОЖЕНИЕ ДЕЛЕНИЕ УМНОЖЕНИЕ ЧИСЕЛ В ЛЮБОЙ СИСТЕМЕ СЧИСЛЕНИЯ ОНЛАЙН

Содержание

Восьмеричная система счисления

Содержание:
Что такое восьмеричная система счисления
Как перевести целое десятичное число в восьмеричную систему счисления
Как перевести десятичную дробь в восьмеричную систему счисления
Как перевести число из восьмеричной системы счисления в десятичную
Как перевести дробное восьмеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления

Восьмеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в восьмеричной системе счисления используется восемь цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 7231₈ или 4556₈

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в восьмеричную систему счисления

Для того, чтобы перевести целое десятичное число в восьмеричную систему счисления нужно десятичное число делить на 8 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 369₁₀ в восьмеричную систему счисления:

369 : 8 = 46 остаток: 1
46 : 8 = 5 остаток: 6
5 : 8 = 0 остаток: 5

369₁₀ = 561₈

Как перевести десятичную дробь в восьмеричную систему счисления

Для того чтобы перевести десятичную дробь в восьмеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в восьмеричную систему счисления, а затем дробную часть, последовательно умножать на 8, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой.

Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 0.2₁₀ в восьмеричную систему счисления:

Переведем целую часть

0₁₀ = 0₈

Переведем дробную часть

0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2

0.2 · 8 = 1.6
0.6 · 8 = 4.8

0.2₁₀ = 0.1463146314₈

Восьмеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной восьмеричной. В данном примере получается бесконечная периодическая восьмеричная дробь, поэтому умножение на 8 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления. К примеру, дробь 1.5₁₀ может быть представлена в восьмеричной системе счисления в виде конечной 2.5₁₀ = 1.4₈.

Как перевести число из восьмеричной системы счисления в десятичную

Для того, чтобы перевести число из восьмеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на 8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем число 75310₈ в десятичную систему счисления:

Позиция в числе	4	3	2	1	0
Число	7	5	3	1	0

75310₈ = 7 ⋅ 8⁴ + 5 ⋅ 8³ + 3 ⋅ 8² + 1 ⋅ 8¹ + 0 ⋅ 8⁰ = 31432₁₀

Как перевести дробное восьмеричное число в десятичное

Для того, чтобы перевести дробное восьмеричное число в десятичное, необходимо записать дробное восьмеричное число, убрав точку и затем сверху расставить индексы.

Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на 8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное восьмеричное число 12.36₈ в десятичное:

Позиция в числе	1	0	-1	-2
Число	1	2	3	6

12.36₈ = 1 ⋅ 8¹ + 2 ⋅ 8⁰ + 3 ⋅ 8

-1 + 6 ⋅ 8^-2 = 10.46875₁₀

Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления

Значение числа в десятичной системе счисления	Значение числа в восьмеричной системе счисления
0₁₀	0₈
1₁₀	1₈
2₁₀	2₈
3₁₀	3₈
4₁₀	4₈
5₁₀	5₈
6₁₀	6₈
7₁₀	7₈
8₁₀	10₈
9₁₀	11₈
10₁₀	12₈
11₁₀	13₈
12₁₀	14₈
13₁₀	15₈
14₁₀	16₈
15₁₀	17₈
16₁₀	20₈
17₁₀	21₈
18₁₀	22₈
19₁₀	23₈
20₁₀	24₈
21₁₀	25₈
22₁₀	26₈
23₁₀	27₈
24₁₀	30₈
25₁₀	31₈
26₁₀	32₈
27₁₀	33₈
28₁₀	34₈
29₁₀	35₈
30₁₀	36₈
31₁₀	37₈
32₁₀	40₈
33₁₀	41₈
34₁₀	42₈
35₁₀	43₈
36₁₀	44₈
37₁₀	45₈
38₁₀	46₈
39₁₀	47₈
40₁₀	50₈
41₁₀	51₈
42₁₀	52₈
43₁₀	53₈
44₁₀	54₈
45₁₀	55₈
46₁₀	56₈
47₁₀	57₈
48₁₀	60₈
49₁₀	61₈
50₁₀	62₈

Значение числа в десятичной системе счисления	Значение числа в восьмеричной системе счисления
51₁₀	63₈
52₁₀	64₈
53₁₀	65₈
54₁₀	66₈
55₁₀	67₈
56₁₀	70₈
57₁₀	71₈
58₁₀	72₈
59₁₀	73₈
60₁₀	74₈
61₁₀	75₈
62₁₀	76₈
63₁₀	77₈
64₁₀	100₈
65₁₀	101₈
66₁₀	102₈
67₁₀	103₈
68₁₀	104₈
69₁₀	105₈
70₁₀	106₈
71₁₀	107₈
72₁₀	110₈
73₁₀	111₈
74₁₀	112₈
75₁₀	113₈
76₁₀	114₈
77₁₀	115₈
78₁₀	116₈
79₁₀	117₈
80₁₀	120₈
81₁₀	121₈
82₁₀	122₈
83₁₀	123₈
84₁₀	124₈
85₁₀	125₈
86₁₀	126₈
87₁₀	127₈
88₁₀	130₈
89₁₀	131₈
90₁₀	132₈
91₁₀	133₈
92₁₀	134₈
93₁₀	135₈
94₁₀	136₈
95₁₀	137₈
96₁₀	140₈
97₁₀	141₈
98₁₀	142₈
99₁₀	143₈
100₁₀	144₈

Системы счисления | BeginPC.

В настоящее время подавляющее число людей являются грамотными и умеют считать. Тем не менее, далеко не все в курсе, что за время человеческой цивилизации было придумано большое количество самых разнообразных систем счисления. Разные народы в различные исторические периоды использовали разные системы счета, которые видоизменялись с течением времени.

Считается, что самая первая система счета у всех народов состояла всего из одного числа, единицы. Соответственно для обозначения, какого то другого числа ее следовало повторить соответствующее количество раз. В качестве обозначения могло выступать что угодно, черточки, крестики и любые другие символы. Отсутствие письменности тоже не помеха, ведь можно использовать камешки, ракушки, плоды, веточки, делать зарубки, вязать узелки и так далее.

Таким образом, для записи числа 4 требовалось собрать 4 камешка или поставить 4 черточки: ||||. Это так называемая единичная система счисления, из которой впоследствии сформировались остальные. Все предельно просто, но очень не удобно для более менее больших чисел. Через какое то время люди догадались упростить запись, объединяя какое то количество элементов в группы и обозначая их другим символом. Чаще всего встречалась группировка по 3 и 5 элементов.

Таким образом, если договориться, что черные камни обозначают единицы, а один белый камень равен 3 черным, то для обозначения допустим 8 чужаков надо показать ●●●●●●●● черных камней или ○ белый и ●●●●● черных или ○○ белых и ●● черных. Любая из этих комбинаций обозначает в нашей условной системе число 8. Такой прием, конечно, заметно упрощал счет. Впоследствии многие народы использовали в качестве обозначения чисел буквы своего алфавита.

Римская система счисления

Одной из таких систем счисления является римская, которая до сих пор находит применение, например, для обозначения веков, цифр на циферблате аналоговых часов, разделов в документе и так далее. В ее основе лежат следующие числа и соответствующие им буквы латинского алфавита.

1 — I
5 — V
10 — X
50 — L
100 — C
500 — D
1000 — M

Все остальные числа получаются их комбинацией в соответствии с определенными правилами, причем 0 в римской системе отсутствует. Хотя сейчас правила довольно вольные и существует множество вариантов их трактовки отличающиеся различной степенью строгости. Мы не будем их расписывать, желающие могут найти их самостоятельно. Приведем лишь несколько примеров записи чисел в римской системе счисления.

II — 2
IV — 4
XVI — 16
XXIII — 23
XLVIII — 48

Десятичная система счисления

Однако сейчас нам привычна система счисления основанная на цифрах от 1 до 9 и 0, это так называемые арабские цифры, хотя с исторической точки зрения это не совсем так. В итоге получается 10 цифр, поэтому она называется десятичной системой счисления с основанием системы равным 10. Считается, что она обязана своему появлению количеству пальцев на руках, что сильно упрощало жизнь. Ее особенностью является то, что в зависимости от местоположения цифры в числе меняется ее значение. Например, в числе 152 цифра 5 имеет значение 50, поскольку стоит в разряде десятков, а цифра 1 имеет значение 100 так как обозначает сотни. Это так называемая позиционная система счисления.

Так же существуют непозиционные системы, где значение цифр не зависит от их места в числе, а так же смешанные системы. Примером непозиционной системы может служить единичная система счета и с некоторой оговоркой римская.

Впрочем, еще относительно недавно в историческом масштабе, вплоть до конца XVIII века на Руси применялась пятеричная система, в которой были только цифры 0, 1, 2, 3, 4 и вытесненная из обихода современной десятичной.

Помимо уже названных систем счисления имеется множество других существовавших в разное время, а так же использующих в настоящее время в разных сферах деятельности человека. Для пересчета чисел из одной системы счисления в другую, вы можете воспользоваться онлайн конвертером систем счисления в конце статьи. Дальше мы рассмотрим несколько таких систем счисления применяющихся в компьютерной технике и программном обеспечении.

Двоичная система счисления

Почти все электронные вычислительные устройства, в том числе компьютеры используют вовсе не привычную для нас десятичную, а двоичную систему счисления, где основанием системы является 2. В ее основе лежит использование всего двух чисел 0 и 1. Это очень удобно для электронных устройств в силу технических причин, поскольку соответствует всего двум состояниям включено (1) и выключено (0) или высокий и низкий сигнал или «истина» и «ложь» и так далее. Наличие всего двух состояний упрощает техническую реализацию, повышает надежность работы, уменьшает габариты и обеспечивает высокую помехоустойчивость цифровых схем, в сравнение с аналоговыми.

В итоге любые числа представлены в виде комбинаций нулей и единиц. Например, число 4 в двоичной системе счисления записывается как 100, но читается каждый символ в отдельности, то есть «один ноль ноль». Это может запутать, поскольку запись числа 4 в двоичной системе счисления внешне не отличается от числа 100 из десятичной. В некоторых ситуациях из-за этого может возникнуть путаница. В таких случаях справа от числа подстрочным шрифтом принято указывать систему счисления, к которой относится данной число в десятичном формате. Числа из нашего примера можно записать следующим образом 4₁₀ и соответственно 100₂. Так же встречается вариант указания перед двоичным числом префиксов 0b или &, то есть 0b100 или &100.

Чтобы перевести десятичное число в двоичное, можно воспользоваться калькулятором расположенным ниже или применить метод Горнера. Для этого нужно десятичное число последовательно делить на основание системы, в данном случае 2. Если результат получается с остатком, то остаток отбрасываем, пишем 1 и снова делим на 2. Если результат получается без остатка, то пишем 0 и снова делим на 2. Запись нулей и единиц осуществляется справа налево, а деление продолжается пока в частном не получится ноль. Рассмотрим это на примере и преобразуем число 11₁₀ в двоичный вид.

11/2=5 остаток 1
5/2=2 остаток 1
2/2=1 остаток 0
1/2=0 остаток 1

В частном получился ноль, осталось записать получившиеся цифры справа налево от первой к последней и в итоге получаем, что 11₁₀=1011₂

Для обратной конвертации двоичных в десятичные, можно складывать последовательно цифры слева на право, умножая получившейся в предыдущем шаге результат на 2. Пересчитаем наш пример в обратную сторону.

Дано: &1011
1+0*2=1 (на первом шаге предыдущая сумма отсутствует, поэтому 0*2 )
0+1*2=2
1+2*2=5
1+5*2=11
Результат: 11₁₀

Чтобы окончательно вас запутать, стоит упомянуть, что для записи чисел может применяться двоичный код, а система счета при этом использоваться десятичная.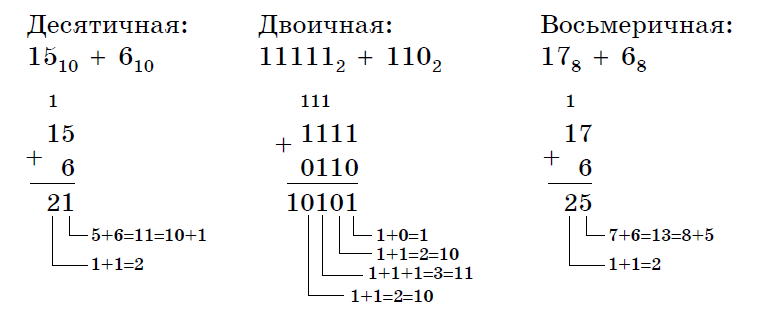 Такая комбинация называется двоично-десятичное кодирование и так же находит применение в вычислительной технике.

Шестнадцатеричная система счисления

Неудобством двоичных чисел является их громоздкость и трудность визуального восприятия человеком. Поэтому для представления двоичного кода в информатике широко используется шестнадцатеричная система счисления. Как вы уже наверно догадались, в ней используется шестнадцать символов, цифры от 0 до 9 и латинские буквы A, B, C, D, E, F соответствующие числам от 10 до 15 в десятичной системе. Шестнадцатеричное число может обозначаться словом hex.

Благодаря основанию системы равному 16 для записи 1 байта требуется всего 2 цифры в этой системе, для символов юникода требуется 4 шестнадцатеричных числа (иногда больше). Может использоваться для обозначения цветов в цветовой модели RGB, в програмировании, записи адресов IPv6, представления MAC-адреса сетевого оборудования, кодов ошибок операционных систем, записи хешей, и так далее.

Чтобы перевести десятичное число в шестнадцатеричное используйте онлайн калькулятор систем счисления в конце статьи или воспользуйтесь алгоритмом, приведенным в примере с двоичной системой. Для примера пересчитаем число 382₁₀

382/16=23 остаток 14, пишем E
23/16=1 остаток 7, пишем 7
1/16=0 остаток 1, пишем 1
Результат: 17E₁₆=382₁₀

Чтобы пересчитать шестнадцатеричное число в десятичное, нужно разбить его на разряды и цифру каждого разряда умножить на 16 в степени соответствующего разряда и сложить получившиеся числа. Проще понять на примере, для этого выполним обратную операцию: 17E₁₆=1*16²+7*16¹+14*16⁰=1*256+7*16+14*1=382₁₀

Кроме рассмотренных систем существует и большое количество позиционных систем счисления с другими основаниями. Так в компьютерах одно время использовалась система с основанием 8, а такая древняя система счисления как шестидесятеричная, используется и в наше время для обозначения времени, координат и углов.

Калькулятор систем счисления

Работает только с целыми положительными числами.

Перевести число

издвоичнойтроичнойпятиричнойвосьмеричнойдесятичнойшестнадцатиричной

в двоичнуютроичнуюпятиричнуювосьмеричнуюдесятичнуюшестнадцатиричную

Восьмеричный калькулятор — сложение, вычитание, умножение и деление

Чтобы использовать prepostseo Octal Calculator , введите значения в поля ввода ниже и нажмите кнопку Calculate .

Первое восьмеричное значение

операция добавить (+)sub (-)multi (×)div (÷)

Второе восьмеричное значение

Дополнение:

Вычитание:

Умножение:

Подразделение:

Восьмеричный формат значений используется не так часто, как двоичный или десятичный формат. Он также известен как формат с основанием 8. Это потому, что он имеет всего 8 значений (0,1,2,3,4,5,6,7). С точки зрения математических операций не так просто складывать или вычитать восьмеричные значения. Во-первых, это длительный вариант, а во-вторых, для выполнения этих операций без ошибок требуются высокие математические навыки.

Этот калькулятор представляет собой комбинацию следующих

Восьмеричный калькулятор сложения
Восьмеричный калькулятор вычитания
Восьмеричный калькулятор умножения
Восьмеричный калькулятор деления

стресс от выполнения преобразования вручную. Вы должны выполнить несколько шагов, и каждый из них должен быть на 100% правильным. Кроме того, фактор времени имеет решающее значение. Если необходимо выполнить несколько сравнений одновременно, для этой цели вам понадобится надежный инструмент. Пройдя процесс использования, мы можем получить более подробную информацию о калькуляторе с основанием 8.
Этапы удобного использования
Для большинства пользователей важно, насколько просты шаги использования инструмента. Никто не любит проходить сложные этапы. Этот восьмеричный калькулятор очень прост. Проходя этапы, можно достичь лучшего понимания.
Входные параметры
Пользователь должен ввести три входных параметра. Первое текстовое поле предназначено для ввода первого восьмеричного значения, необходимого для расчета. После этого вы должны выбрать операцию, которую необходимо выполнить. Доступны следующие варианты: сложение, вычитание, умножение и деление. Последнее поле ввода предназначено для второго восьмеричного значения. После ввода входных данных необходимо нажать кнопку расчета.
Результаты
Результаты будут показаны в текстовой строке ниже. Например, рассмотрим пример. Возьмите первое восьмеричное значение как 7, а второе как 122. Математическая операция в этом примере — сложение. После того, как вы введете эти значения, вам будет показан результат «131».
Простой интерфейс восьмеричного калькулятора для пользователей
Инструмент должен быть максимально простым, чтобы пользователи не волновались. Сложные инструменты обычно отвергаются, и пользователи не очень их ценят. Этот восьмеричный калькулятор очень прост, что делает его лучшим вариантом по сравнению с другими альтернативами в Интернете. Вам нужно ввести только три входа, и после этого будет рассчитан результат.
Избегайте сложных вычислений и экономьте время
Каждый ученик задается вопросом, как складывать восьмеричные числа? Складывать или умножать восьмеричные числа не так просто, как десятичные. Вы должны выполнить несколько промежуточных шагов, после чего будет сгенерирован результат. С помощью этого инструмента вам не нужно выполнять никаких расчетов, и инструмент сделает все сам. С точки зрения пользователя, восьмеричный калькулятор сложения является хорошим вариантом. Это экономит много времени для пользователей, и они могут выполнить несколько восьмеричных вычислений за несколько минут.
Бесплатное использование без применения ограничений
Получить 100% бесплатный технологический инструмент не так просто. Инструменты, которые утверждают, что они бесплатные, имеют множество условий. Этот калькулятор полностью бесплатен без каких-либо условий.
Другие бесплатные инструменты, связанные с Octal
Prepostseo не ограничивается несколькими инструментами, связанными с Octal. Мы предлагаем широкий спектр инструментов Octal, чтобы внести изменения в образование, решить современные компьютерные проблемы и сыграть ключевую роль в формировании будущего в мире технологий. Ознакомьтесь с другими нашими бесплатными инструментами Octal здесь: Octal to Binary, Bianry to Octal, Hex to Octal, Octal to Hex, Octal to Decimal, Decimal to Octal, Octal Calculator.
РЕКЛАМА
Восьмеричный калькулятор
РЕКЛАМА
Введите два восьмеричных числа в указанные поля ввода и выберите оператор для выполнения математической операции с использованием калькулятора с основанием 8.
1-е восьмеричное значение:
Операция + — × ÷
2-е восьмеричное значение:
РЕКЛАМА
РЕКЛАМА
Содержание:
Что такое восьмеричная система счисления?
Как сложить восьмеричные числа?
Полезен ли этот инструмент?
Да Нет Возможно
Введите отзыв
Отзыв
Восьмеричный калькулятор — это онлайн-инструмент, который можно использовать для сложения, вычитания, умножения или деления двух восьмеричных чисел.
Что такое восьмеричная система счисления?
Восьмеричная система счисления — это система счисления с основанием 8 , в которой используются цифры от 0 до 7. В восьмеричной системе каждый разряд равен степени восьми. Например:
450 = 4 × 8 ² + 5 × 8 ¹ + 0 × 8 ⁰
Как складывать восьмеричные числа?
Восьмеричное сложение немного отличается от десятичного или двоичного сложения. Вот таблица восьмеричного сложения, чтобы понять сложение восьмеричных чисел.
9030 9
20007
+
0
1
2
2 9000
2 9000 4
0007
3
4
5
6
7
0
0
1
2
3
4
7
2 5
0002 6
7
1
1
2
3
4
5
6
7
10
2
2
3
3
3
0002 4
5
6
7
10
11
3
3
4
5
6
7
10
11
12
0216
4
4
5
6
7
10
11
12
13
5
5
6
7
100167
0167
11
12
13
14
6
6
7
10
11
12
13
14
15
7
10
11
12
13
14
15
16
Follow the below example добавить два восьмеричных числа.
No related posts.