Выпуклый четырехугольник свойства: Выпуклый четырехугольник, параллелограмм, ромб, квадрат, трапеция

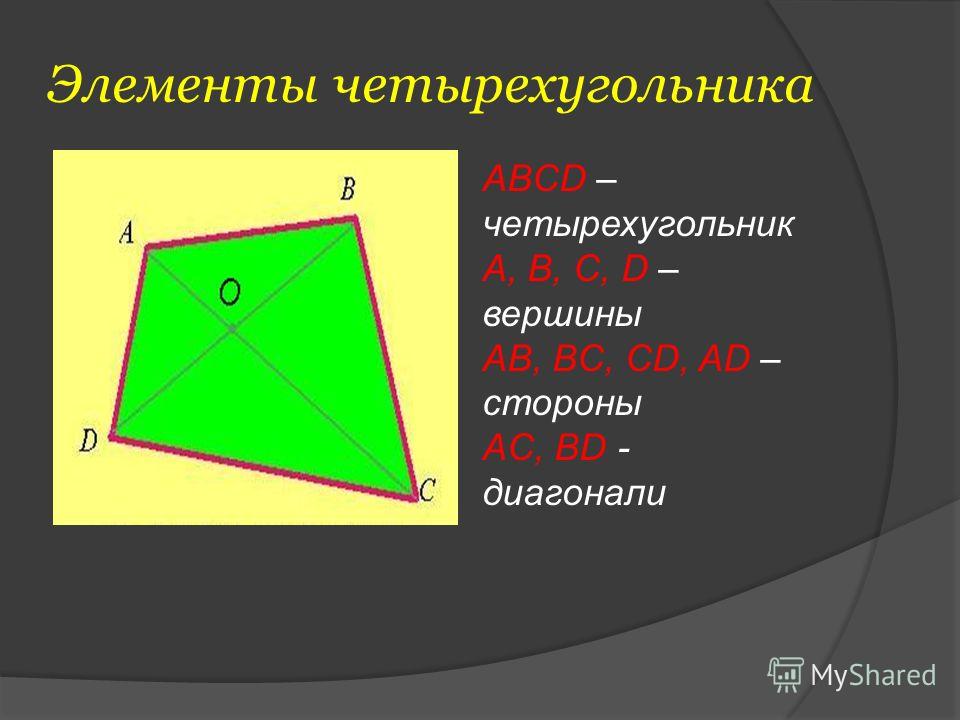
Понятие выпуклого четырехугольника, его свойства и признаки

Выпуклый четырехугольник — это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.

…

Оглавление:

• Выпуклый четырехугольник
• Основные свойства и виды
• Является ли параллелограмм выпуклым четырехугольником?
• Свойство диагоналей выпуклого четырехугольника
• Другие свойства и признаки выпуклости четырехугольника

Как видно, определение довольно легко запоминающееся.

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

1. параллелограмм;
2. квадрат;
3. прямоугольник;
4. трапеция;
5. ромб.

Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

На рисунке изображена выпуклая трапеция. Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка [AB]. Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.

Является ли параллелограмм выпуклым четырехугольником?

Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым. Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.

Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат — это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.

Это интересно: титульный лист проекта — образец, как правильно оформляется?

В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам. Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются.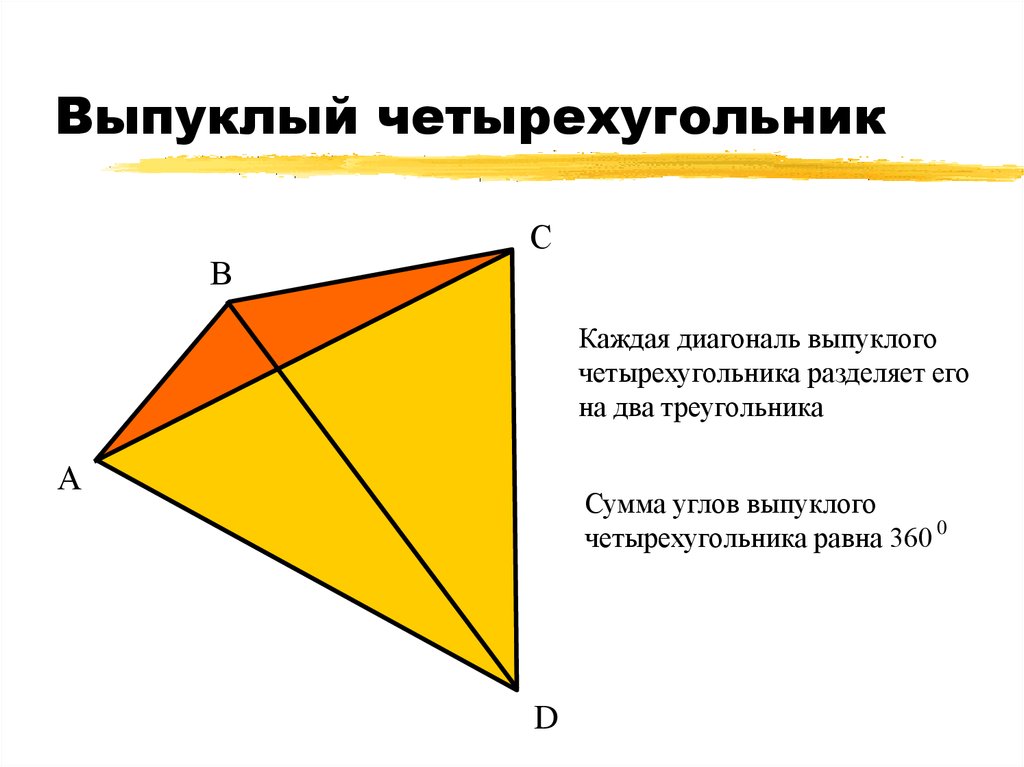 Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Другие свойства и признаки выпуклости четырехугольника

Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.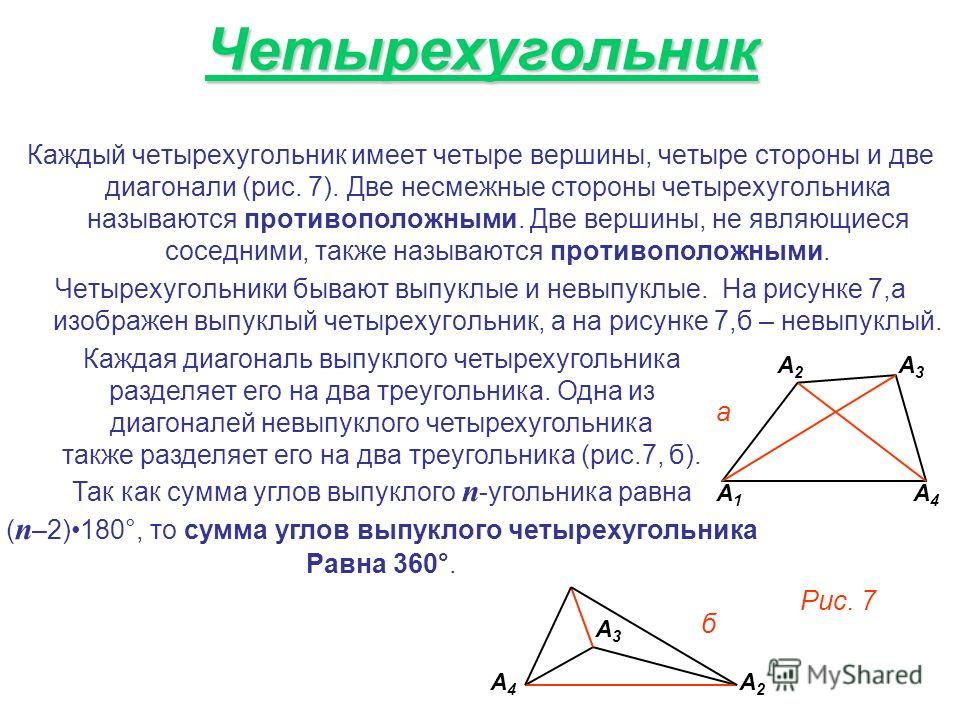

Итак, известны основные признаки и свойства:

1. сумма углов четырехугольника равна 360 градусам;
2. диагонали фигур пересекаются в одной точке.

Далее рассмотрим каждый четырехугольник по отдельности.

Прямоугольник. Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название — прямоугольник.

Квадрат, тот же параллелограмм, но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.

Трапеция — очень интересная фигура. Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению.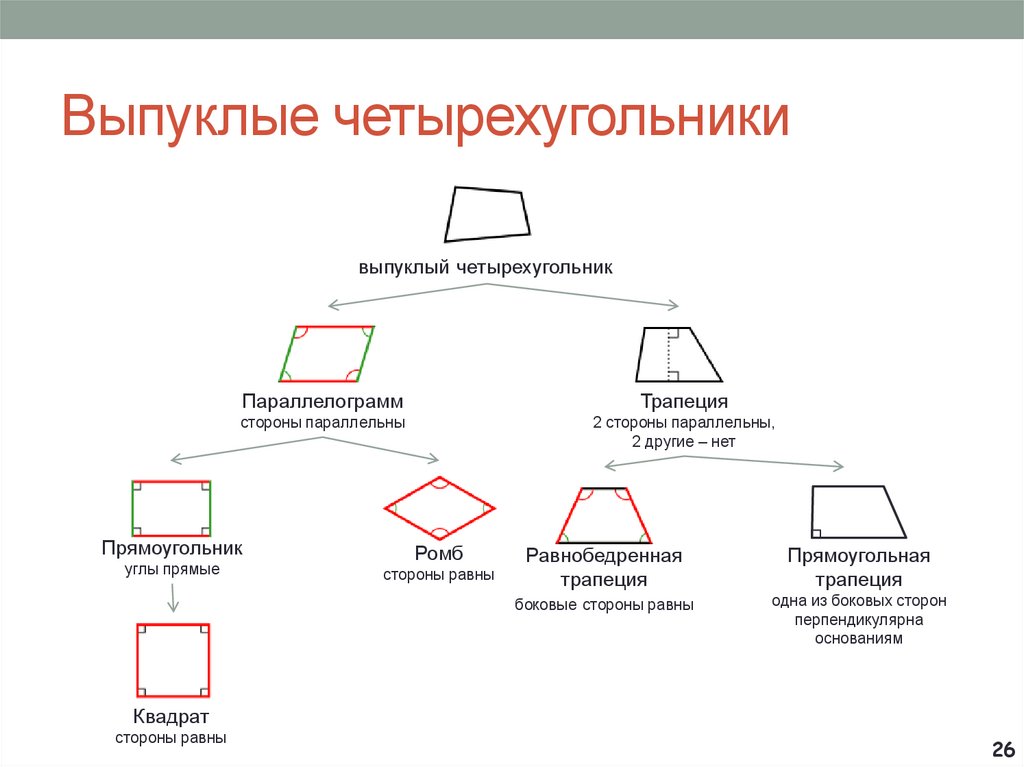 При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.

Ромб — не менее интересная фигура. Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.

Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.

Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам.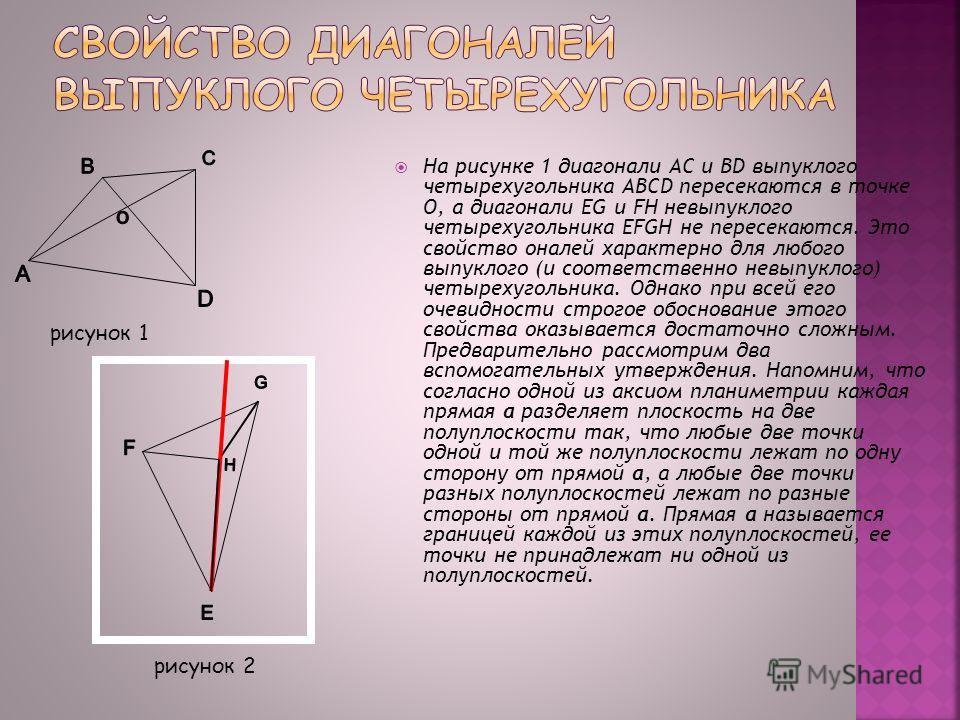 Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.

Виды выпуклых четырехугольников

Выпуклый четырехугольник: что это такое, каковы его свойства и чему равна сумма его уголов

Если на плоскости имеются четыре точки, из которых никакие три не принадлежит одной прямой, то их можно попарно соединить отрезками. В результате получится фигура с четырьмя углами, содержащая две диагонали, при пересечении которых получится выпуклый четырехугольник.

Содержание

Виды

Существует несколько видов фигур с четырьмя углами, но не все они являются выпуклыми. Слева рисунок отображает выпуклый четырехугольник, все его внутренние точки находятся в одной полуплоскости относительно прямой l, на которой лежит сторона AD. Для среднего данное условие выполняется, но его нельзя считать выпуклым, потому что его стороны пересекаются.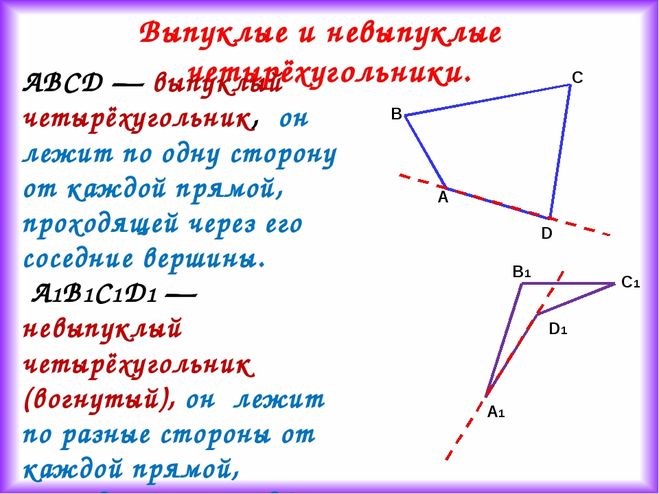 Такие четырехугольники называются самопересекающимися. Правый тоже не является выпуклым, так как две его точки B и C лежат в разных полуплоскостях относительно разбиения прямой l.

На основании вышесказанного дадим определение. Выпуклым четырехугольником называется фигура, состоящая из четырех точек и четырех отрезков, которые последовательно их соединяют. Главное условие: никакие три точки не должны одновременно лежать на одной прямой, а соединяющие отрезки пересекаться.

Виды выпуклых четырехугольников:

• прямоугольник,
• параллелограмм,
• трапеция,
• ромб,
• квадрат.

Перечисленные отношения между множествами фигур упрощают доказательства теорем (предложений, выражающих свойства). Например, если теорема доказана для параллелограмма (будет ли параллелограмм выпуклым? и т.д.), то она будет верна и для любого соответствующего подмножества фигур. Если же доказана более общая теорема для выпуклого четырехугольника, то она будет верна и для параллелограмма, и для трапеции.

Свойства

Главные признаки:

• сумма углов 360 градусов,
• диагонали могут пересекаться в одной точке.

Если сумма углов равна 360, это следствие более общего случая – четырехугольника, не имеющего пересекающихся отрезков. Но для выпуклого обычно проводят отдельное и очень простое доказательство. Если внутри выпуклого четырехугольника провести диагональ, то она разобьет его на два треугольника. Как известно, сумма углов в треугольнике равна 180. Сложив все получившиеся углы, получаем величину 360.

Если взять средние точки всех сторон произвольного выпуклого четырехугольника и построить на них новый, то он окажется параллелограммом (Теорема Вариньона).

Доказательство на следующем фото. Выпуклый четырёхугольник ABCD имеет на каждой из сторон точку, делящую эту сторону пополам. Рассмотрим отрезок FG. Это средняя линия треугольника DAB, параллельная диагонали DB. Это следует из подобия треугольников DAB и FAG.

Аналогично проводятся рассуждения для треугольников DBC и EHC. Из чего следует параллельность DB и EH. Поскольку отрезки FG и EH параллельны диагонали DB, то и сами параллельны.

Аналогично доказывается, что отрезки FE и GH параллельны. Так как противолежащие стороны EFGH попарно параллельны, значит, это параллелограмм.

Обратите внимание! Теорема Вариньона справедлива для всех четырехугольников, невыпуклых и самопересекающихся. Если взять середины диагоналей, то можно построить еще два параллелограмма. Центры всех трех параллелограммов окажутся на одной прямой.

Если выпуклый четырёхугольник имеет свойство взаимной перпендикулярности своих диагоналей, то суммы квадратов его противоположных сторон у него равны. Это доказывается при помощи теоремы Пифагора, как показано на следующем чертеже:

Квадрат каждой из сторон выражается через сумму квадратов отрезков диагоналей, ограниченных вершинами и точкой пересечения.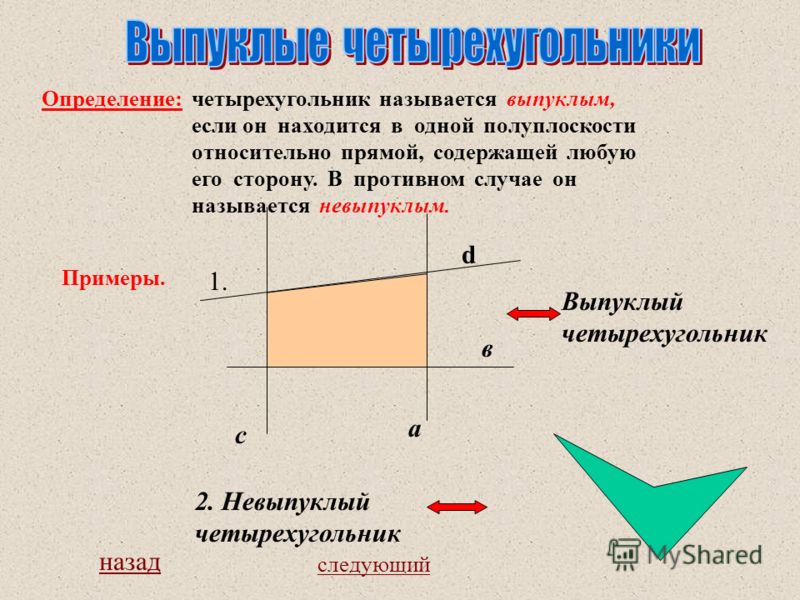 Для удобства мы обозначаем их малыми буквами латинского алфавита, совпадающими с названием вершин. Затем выписываем выражения для сумм квадратов противолежащих сторон:

В правой части каждого из выражений стоит одна и та же сумма слагаемых. Следовательно, равны и правые части между собой, что доказывает теорема.

Вписанные и описанные

Часто требуется проверить, не лежат ли вершины четырехугольника на окружности, или существует ли окружность, вписанная в 4-угольник. Центр описанной окружности находится в точке пересечения срединных перпендикуляров к сторонам, а центр вписанной – на пересечении биссектрис внутренних углов.

Если сумма противоположных углов составляет 180, то рядом с ними можно описать окружность, другими словами, существует окружность, на которой лежат все вершины четырехугольника. Его называют вписанным (подразумевается, что в окружность).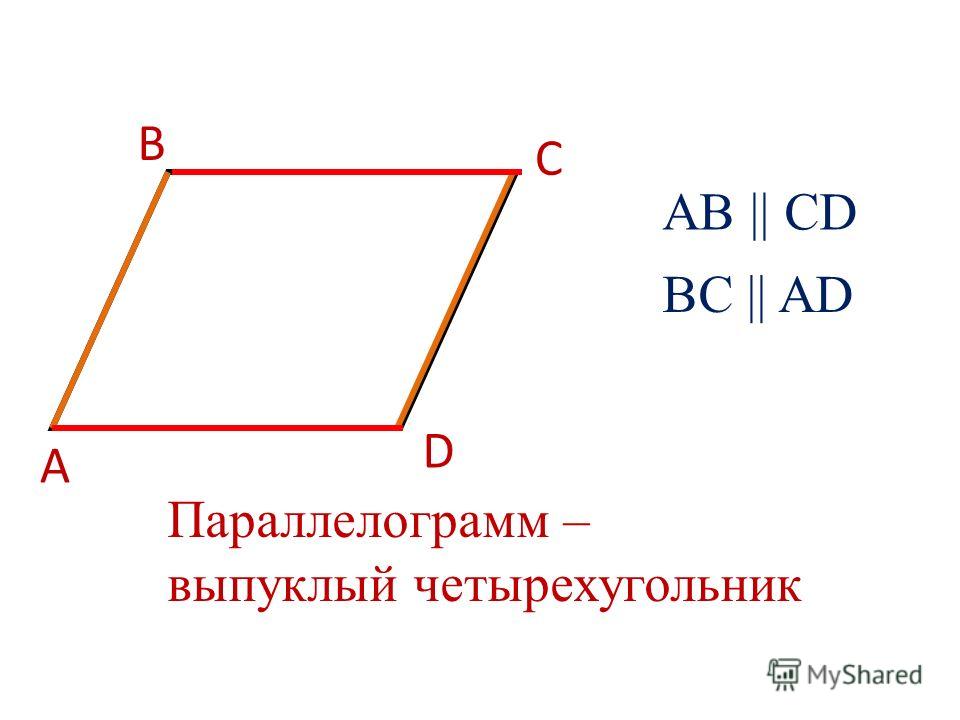 Верно и обратное утверждение, то есть выраженное в теореме условие необходимое и достаточное.

Расчет площади

Площадь, которую имеет любой выпуклый четырёхугольник, равна половине произведения длин диагоналей на синус угла между ними. Докажем это правило.

Здесь опять поможет теорема Вариньона (мы имеем “большой” параллелограмм, о котором сразу не было сказано). Проведем прямые, параллельные диагоналям, через вершины A, B, C, D исходного прямоугольника. Мы получим параллелограмм EFGH. Его площадь равна сумме площадей параллелограммов AFBO, BGCO, CHDO, DEAO. Но каждый из перечисленных делится своей диагональю на пару треугольников с равными площадями. С другой стороны, в силу параллельности диагоналей ADCD сторонам внешнего параллелограмма, мы можем применить формулу площади:

Полезное видео

Подведем итоги

Фигуру, состоящую из четырех углов, можно часто увидеть в обычной жизни, такую форму обычно имеют земельные участки, здания, параллелограммы служат для построения векторных базисов на плоскости.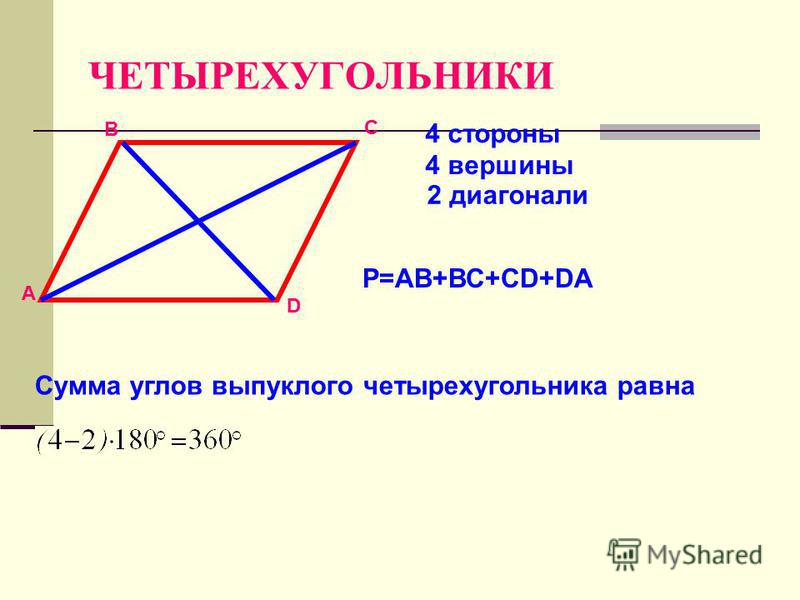 Не случайно 4-угольники хорошо изучены и установлено большое число свойств, связанных с ними.

Выпуклые и вогнутые четырехугольники. Определение, примеры

В зависимости от величины внутренних углов все четырехугольники делятся на две группы: выпуклые и вогнутые.

Выпуклый и вогнутый четырехугольник

Что такое выпуклый четырехугольник

Выпуклый четырехугольник — это четырехугольник, все внутренние углы которого меньше 180°. Обе диагонали выпуклого четырехугольника лежат внутри замкнутой фигуры.

Примеры : Квадрат, прямоугольник, параллелограмм, ромб, трапеция и воздушный змей.

Выпуклый четырехугольник

В данном выпуклом четырехугольнике ABCD все четыре внутренних угла ∠ABC, ∠BCD, ∠CDA и ∠DAB меньше 180°. Также оказывается, что диагонали AC и DB находятся внутри замкнутой фигуры.

Дан четырехугольник ABCD, имеющий ∠ABC = 80°, ∠BCD = 70°, ∠CDA = 110°. Найдите меру ∠DAB и укажите, является ли он выпуклым четырехугольником.

Решение:

Как известно,
Сумма внутренних углов выпуклого четырехугольника = 360°
Таким образом, в четырехугольнике ABCD ∠ABC + ∠2BCD + ∠7°CDA + ∠DAB = 060° > 80° + 70° + 110° + ∠DAB = 360°
=> 280° + ∠DAB = 360°
=> ∠DAB = 360° – 260°
=> ∠DAB = 100°

Поскольку все внутренние углы данного четырехугольника ABCD меньше 180°, это выпуклый четырехугольник.

Что такое вогнутый четырехугольник

Вогнутый четырехугольник – это четырехугольник, по крайней мере один из внутренних углов которого больше 180°. Одна из диагоналей вогнутого четырехугольника лежит вне замкнутой фигуры. Таким образом, любой четырехугольник, который не является выпуклым, является вогнутым четырехугольником.

Пример : Дротик или наконечник стрелы.

Вогнутый четырехугольник

В данном вогнутом четырехугольнике ABCD угол ∠BCD больше 180°, а диагональ BD лежит вне замкнутой фигуры.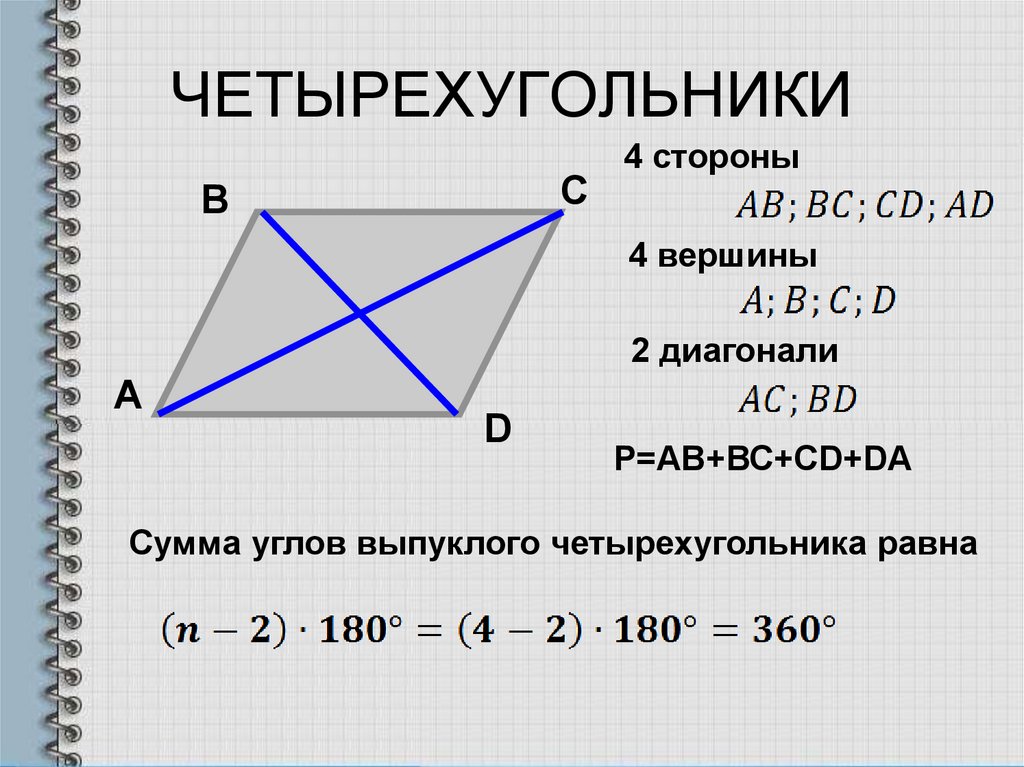

Дан четырехугольник ABCD, имеющий ∠ABC = 30°, ∠DAB = 80° и ∠CDA = 25°. Найдите меру ∠BCD и укажите, является ли он вогнутым четырехугольником.

Решение:

Как известно,
Сумма внутренних углов вогнутого четырехугольника = 360°
Таким образом, в четырехугольнике ABCD ∠ABC + ∠BCD + ∠2°CDA + ∠DAB = 300 > 30° + ∠BCD + 25° + 80° = 360°
=> ∠BCD + 135° = 360°
=> ∠BCD = 360° – 135°
=> ∠BCD = 225°

Так как один из внутренних углов данного четырехугольника ABCD больше 180°, то это вогнутый четырехугольник.

Часто задаваемые вопросы

Q1. Чем выпуклый четырехугольник отличается от вогнутого?

Ответ . У выпуклого четырехугольника все внутренние углы меньше 180°, а обе диагонали лежат внутри замкнутой фигуры. Напротив, у вогнутого четырехугольника один из внутренних углов больше 180 °, а одна из его диагоналей лежит вне замкнутой фигуры.

Q2. Почему прямоугольник является выпуклым четырехугольником?

Ответ . Поскольку все четыре внутренних угла прямоугольника меньше 180°, а обе диагонали полностью лежат внутри замкнутой фигуры, это выпуклый четырехугольник.

Q3. Может ли вогнутый четырехугольник быть правильным?

Ответ . Поскольку все внутренние углы вогнутого четырехугольника не равны (один из его внутренних углов больше 180 °), он никогда не может быть правильным четырехугольником, у которого все внутренние углы равны.

Все виды измерений для всех видов четырехугольников — Krista King Math

Начнем со свойств четырехугольников различных типов.

Четырехугольник — это любая замкнутая четырехсторонняя фигура.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Четырехугольники бывают двух типов: вогнутые и выпуклые. 9\ круг???.

Вот некоторые специальные типы выпуклых четырехугольников и их свойства:

Трапеция

Нет пар параллельных сторон и нет конгруэнтных сторон

Воздушный змей

Имеет две пары смежных конгруэнтных сторон

Имеет пару противоположных конгруэнтных углов

Диагонали пересекаются, образуя прямые углы, и одна из диагоналей делит другую пополам (делит ее пополам)

Трапеция

Имеет ровно одну пару противоположных параллельных сторон

Равнобедренная трапеция

Имеет ровно одну пару противоположных параллельных сторон

Непараллельные стороны имеют одинаковую длину

Углы при основании равны

Диагонали равны

Параллелограмм

Две пары противоположных параллельных сторон

Противоположные стороны равной длины 9\circ???)

Диагонали делят друг друга пополам (режут друг друга пополам)

Диагонали конгруэнтны

Ромб/ромб

Две пары противоположных параллельных сторон

Все стороны равны по длине

Противоположные углы конгруэнтны

Соседние углы являются дополнительными

Квадрат

Две пары противоположных параллельных сторон

Все углы прямые

Все стороны имеют одинаковую длину

Диагонали делят друг друга пополам (делят друг друга пополам и образуют прямые углы)

Как найти размеры сторон, углов и диагоналей четырехугольников разных типов

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.