Как выразить одну переменную через другую? Как выразить переменную из формулы?
Этот урок — полезное дополнение к предыдущей теме «Тождественные преобразования уравнений».
Умение делать такие вещи — штука не просто полезная, она — необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях — как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула — это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и тождественные преобразования уравнений. Вот и применяем их в удобном нам порядке и — готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка — для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
3x — 2y = 5
Здесь две переменные — икс и игрек.
Допустим, нас просят выразить x через y.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа — что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3x – 2y = 5
Здесь нам мешаются тройка перед иксом и —2y. Начнём с —2у, это попроще будет.
Начнём с —2у, это попроще будет.
Перекидываем —2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
3x = 5 + 2y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Вот и делим:
Вот и всё. Мы выразили икс через игрек. Слева — чистый икс, а справа — что уж получилось в результате «очищения» икса.
Можно было бы сначала поделить обе части на тройку, а затем — переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное — не порядок применения тождественных преобразований, а их правильность!
Самое главное — не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
3x – 2y = 5
выразить y через x?
А почему — нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х. Перебрасываем его в правую часть:
–2y = 5 — 3x
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула — тоже уравнение.
Например, такое задание:
Из формулы
выразить переменную с.
Формула — тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с, а справа — что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r… Значит, первым делом очищаем выражение с буквой с, т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r.
Получим:
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби — нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и — ответ готов:
Осталось переписать равенство в привычном виде, слева направо и — ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с — скорость звука в воде,
f0 — частота испускаемых импульсов (в МГц),
f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
«Многа букафф», да… Но буквы — это лирика, а общая суть всё равно та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там — видно будет. Для этого применяем второе преобразование — умножаем обе части на знаменатель.
Получим:
А вот тут — очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком. А не на его отдельные кусочки…
Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с. Что и выражается скобками в правой части. )
)
А вот теперь скобки и раскрыть можно:
Дальше дело нехитрое. Всё что с f собираем слева, а всё что без f — справа. Займёмся переносом:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем. Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v—c) и — дело в шляпе!
В принципе, всё готово. Переменная f уже выражена. Но можно дополнительно «причесать» полученное выражение — вынести f0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при S=300, V0=20, t=10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V1 и V2 — средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с-1), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2.
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r=0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы — это как-нибудь сами…)
Как выводить формулы физике из формулы. Как выразить одну переменную через другую? Как выразить переменную из формулы? Что такое валентность
Этот урок – полезное дополнение к предыдущей теме » «.
Умение делать такие вещи – штука не просто полезная, она – необходимая . Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.
Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула – это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и . Вот и применяем их в удобном нам порядке и – готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка – для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
3 x — 2 y = 5
Здесь две переменные – икс и игрек.
Допустим, нас просят выразить x через y .
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа – что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3 x – 2 y = 5
Здесь нам мешаются тройка перед иксом и —
2 y . Начнём с —2у , это попроще будет.Перекидываем —2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
3 x = 5 + 2 y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т. е. задействовать второе тождественное преобразование.
е. задействовать второе тождественное преобразование.
Вот и делим:
Вот и всё. Мы выразили икс через игрек . Слева – чистый икс, а справа – что уж получилось в результате «очищения» икса.
Можно было бы сначала поделить обе части на тройку, а затем – переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как
А можно из этого же равенства
3 x – 2 y = 5
выразить y через x ?
А почему – нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х . Перебрасываем его в правую часть:
–2 y = 5 – 3 x
Осталась двойка с минусом. Делим обе части на (-2):
Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула –
тоже уравнение .Например, такое задание:
Из формулы
выразить переменную с.
Формула – тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с , а справа – что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r … Значит, первым делом очищаем выражение с буквой с , т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r .
Получим:
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя.) Умножаем обе части формулы на 2:
Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и – ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с – скорость звука в воде,
f 0 – частота испускаемых импульсов (в МГц),
f – частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
«Многа букафф», да… Но буквы – это лирика, а общая суть всё равно та же самая . Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f ) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем второе преобразование – умножаем обе части на знаменатель.
Получим:
А вот тут – очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком . А не на его отдельные кусочки…
Справа же, после умножения, дробь
 Который, опять же, весь целиком умножается на буковку с . Что и выражается скобками в правой части.)
Который, опять же, весь целиком умножается на буковку с . Что и выражается скобками в правой части.)А вот теперь скобки и раскрыть можно:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем . Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v — c ) и – дело в шляпе!
В принципе, всё готово. Переменная f уже выражена . Но можно дополнительно «причесать» полученное выражение – вынести f 0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда . На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны .
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при S =300, V 0 =20, t =10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V 1 и V 2 – средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с 2) можно вычислить по формуле a =ω 2 R , где ω – угловая скорость (в с -1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с -1 , а центростремительное ускорение равно 289 м/с 2 .
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r =0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы – это как-нибудь сами…)
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др. ) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:
) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:
Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.
Да не переживай — это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь…
Допустим, дана формула:
Ну более простая….тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:
и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v
У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.
Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.
Я, предлагаю следующее решение данной проблемы – большинство учащихся все — таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.
1. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.
2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы (через знак равенства) с противоположным действием (« минус» — «плюс», «разделить» — « умножить», « возведение в квадрат» – «извлечение корня квадратного»).
То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием. Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.
Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.
Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.
Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.
Физика – наука о природе. Она описывает процессы и явления окружающего мира на макроскопическом ярусе – ярусе маленьких тел, сравнимых с размерами самого человека. Для изложения процессов физика использует математический агрегат.
Инструкция
1. Откуда берутся физические формулы ? Упрощенно схему приобретения формул дозволено представить так: ставится вопрос, выдвигаются догадки, проводится серия экспериментов. Итоги обрабатываются, появляются определенные формулы , и это дает предисловие новой физической теории либо продолжает и развивает теснее имеющуюся.
Итоги обрабатываются, появляются определенные формулы , и это дает предисловие новой физической теории либо продолжает и развивает теснее имеющуюся.
2. Человеку, постигающему физику, не нужно снова проходить каждый данный непростой путь. Довольно освоить центральные представления и определения, ознакомиться со схемой эксперимента, обучиться выводить основополагающие формулы . Безусловно, без крепких математических познаний не обойтись.
3. Выходит, выучите определения физических величин, относящихся к рассматриваемой теме. У всякой величины есть свой физический толк, тот, что вы обязаны понимать. Скажем, 1 кулон – это заряд, проходящий через поперечное сечение проводника за 1 секунду при силе тока в 1 ампер.
4. Уясните физику рассматриваемого процесса. Какими параметрами он описывается, и как эти параметры меняются на протяжении времени? Зная основные определения и понимая физику процесса, легко получить простейшие формулы . Как водится, между величинами либо квадратами величин устанавливаются прямо пропорциональные либо обратно пропорциональные зависимости, вводится показатель пропорциональности.
Как водится, между величинами либо квадратами величин устанавливаются прямо пропорциональные либо обратно пропорциональные зависимости, вводится показатель пропорциональности.
5. Путем математических реформирований дозволено из первичных формул вывести вторичные. Если вы обучитесь делать это легко и стремительно, последние дозволено будет не запоминать. Стержневой способ реформирований – способ подстановки: какая-нибудь величина выражается из одной формулы и подставляется в иную. Главно лишь, дабы эти формулы соответствовали одному и тому же процессу либо явлению.
6. Также уравнения дозволено складывать между собой, разделять, перемножать. Функции по времени дюже зачастую интегрируют либо дифференцируют, получая новые зависимости. Логарифмирование подойдет для степенных функций. При итоге формулы опирайтесь на итог, тот, что вы хотите в результате получить.
Каждая человеческая жизнь окружена большинством разновидных явлений. Ученые-физики занимаются постижением этих явлений; их инструментарием выступают математические формулы и достижения предшественников.
Природные явления
Изучение природы помогает умней относиться к имеющимся источникам, открывать новые источники энергии. Так, геотермальные источники обогревают примерно всю Гренландию. Само слово «физика» восходит к греческому корню «физис», что обозначает «природа». Таким образом, сама физика – наука о природе и природных явлениях.
Вперед, в грядущее!
Часто физики в прямом смысле «опережают время», открывая законы, которые находят использование лишь десятками лет (и даже столетиями) позднее. Никола Тесла открывал законы электромагнетизма, которые находят использование в наши дни. Пьер и Мария Кюри открыли радий фактически без поддержки, в невероятных для современного ученого условиях. Их открытия помогли спасти десятки тысяч жизней. Теперь физики каждого мира сосредоточены на вопросах Вселенной (макрокосмос) и мельчайших частиц вещества (нанотехнологии, микрокосмос).
Понимание мира
Важнейшим мотором общества является любознательность. Вот отчего эксперименты в Большом Андронном Коллайдере имеют такую высокую важность и спонсируются союзом из 60 государств. Имеется настоящая вероятность раскрыть тайны общества.Физика – наука фундаментальная. Это значит, что всякие открытия физики дозволено применять в иных сферах науки и техники. Небольшие открытия в одной ветви могут поразительно повлиять на всю «соседнюю» ветвь целиком. В физике знаменита практика изыскания группами ученых из различных стран, принята политика помощи и сотрудничества.Тайна мироздания, материи волновала великого физика Альберта Эйнштейна. Он предложил теорию относительности, поясняющую, что поля гравитации искривляют пространство и время. Апогеем теории стала известная формула E = m * C * C, объединяющая энергию с массой.
Имеется настоящая вероятность раскрыть тайны общества.Физика – наука фундаментальная. Это значит, что всякие открытия физики дозволено применять в иных сферах науки и техники. Небольшие открытия в одной ветви могут поразительно повлиять на всю «соседнюю» ветвь целиком. В физике знаменита практика изыскания группами ученых из различных стран, принята политика помощи и сотрудничества.Тайна мироздания, материи волновала великого физика Альберта Эйнштейна. Он предложил теорию относительности, поясняющую, что поля гравитации искривляют пространство и время. Апогеем теории стала известная формула E = m * C * C, объединяющая энергию с массой.
Союз с математикой
Физика опирается на новейшие математические инструменты. Нередко математики открывают абстрактные формулы, выводя новые уравнения из существующих, применяя больше высокие ярусы абстракции и законы логики, делая храбрые догадки. Физики следят за становлением математики, и изредка научные открытия абстрактной науки помогают пояснять незнакомые дотоле природные явления. Бывает и напротив – физические открытия толкают математиков на создание догадок и нового логичного агрегата. Связь физики и математики – одной из важнейших научных дисциплин подкрепляет авторитет физики.
Бывает и напротив – физические открытия толкают математиков на создание догадок и нового логичного агрегата. Связь физики и математики – одной из важнейших научных дисциплин подкрепляет авторитет физики.
Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
Представим полный дифференциал внутренней энергии через частные производные по параметрам и :
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость в любом термодинамическом процессе и для любой макроскопической системы, если известны калорическое и термическое уравнения состояния.
Рассмотрим процесс при постоянном давлении и получим общее соотношение между и .
Исходя из полученной формулы, можно легко найти связь между теплоемкостями и в идеальном газе. Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.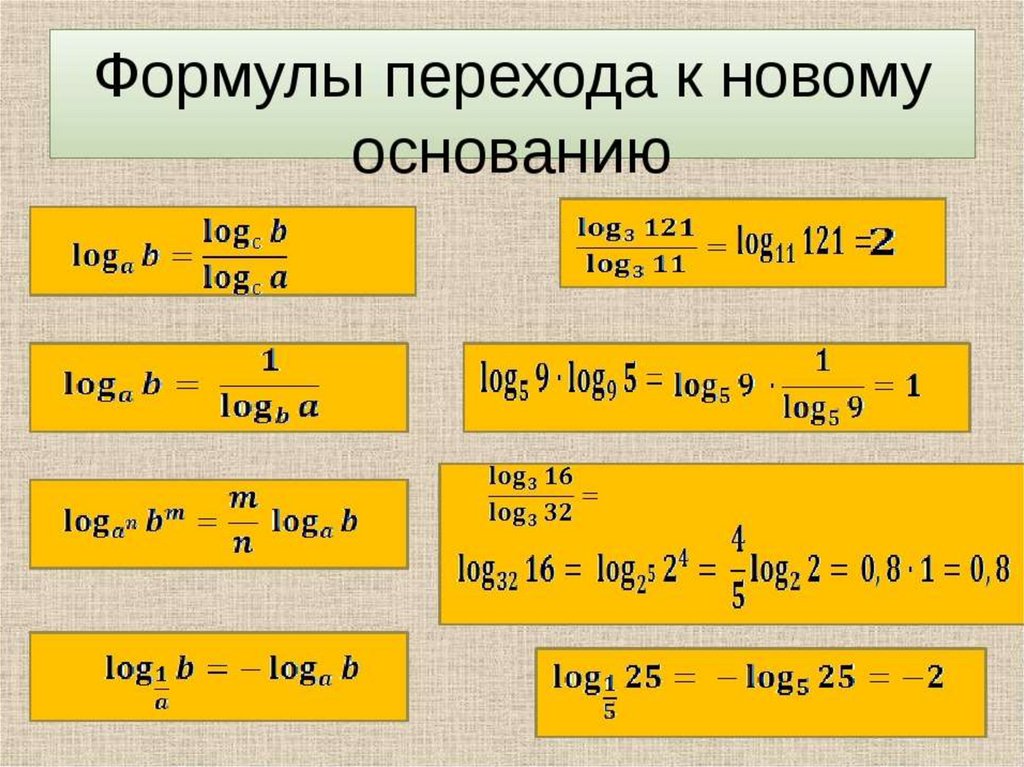 8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Окончательно запишем
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости .
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости уравнение процесса наглядно представляется в виде графика — кривой процесса. Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.
Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.
Вывод уравнения политропического процесса в идеальном газе
Требование постоянства теплоёмкости в процессе позволяет записать первое начало термодинамики в виде
Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
Разделив () на , находим
Интегрированием (9.15), получаем
Это уравнение политропы в переменных
Исключая из уравнения () , с помощью равенства получаем уравнение политропы в переменных
Параметр называется показателем политропы, который может принимать согласно () самые разные значения, положительные и отрицательные, целые и дробные. За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.
За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.
К этому классу процессов относится также адиабатный или адиабатический процесс . Адиабатным называется процесс, проходящий без теплообмена (). Реализовать такой процесс можно двумя способами. Первый способ предполагает наличие у системы теплоизолирующей оболочки, способной изменять свой объем. Второй – заключается в осуществлении столь быстрого процесса, при котором система не успевает обмениваться количеством теплоты с окружающей средой. Процесс распространения звука в газе можно считать адиабатным благодаря его большой скорости.
Из определения теплоемкости следует, что в адиабатическом процессе . Согласно
где – показатель адиабаты.
В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр часто именуют постоянной Пуассона. Постоянная является важной характеристикой газов. Из опыта следует, что ее значения для разных газов лежат в интервале 1,30 ÷ 1,67, поэтому на диаграмме процессов адиабата «падает» более круто, чем изотерма.
Постоянная является важной характеристикой газов. Из опыта следует, что ее значения для разных газов лежат в интервале 1,30 ÷ 1,67, поэтому на диаграмме процессов адиабата «падает» более круто, чем изотерма.
Графики политропических процессов для различных значений представлены на рис. 9.1.
На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.
Чтобы вывести формулу сложного , нужно прежде всего путем анализа установить, из каких элементов состоит вещество и в каких весовых отношениях соединены друг с другом входящие в него элементы. Обычно состав сложного выражают в процентах, но он может быть выражен и в любых других числах, указывающих отношение между весовыми количествами элементов, образующих данное вещество. Например, состав окиси алюминия, содержащей 52,94% алюминия и 47,06% кислорода, будет вполне определен, если мы скажем, что и соединены в весовом отношении 9:8, т. е. что на 9 вес. ч. алюминия приходится 8 вес. ч. кислорода. Понятно, что отношение 9: 8 должно равняться отношению 52,94: 47,06.
Зная весовой состав сложного и атомные веса образующих его элементов, нетрудно найти относительное число атомов каждого элемента в молекуле взятого вещества и таким образом установить его простейшую формулу.
Положим, например, что требуется вывести формулу хлористого кальция, содержащего 36% кальция и 64% хлора. Атомный вес кальция 40, хлора 35,5.
Обозначим число атомов кальция в молекуле хлористого кальция через х, а число атомов хлора через у. Так как атом кальция весит 40, а атом хлора 35,5 кислородных единиц, общий вес атомов кальция, входящих в состав молекулы хлористого кальция, будет равен 40 х, а вес атомов хлора 35,5 у. Отношение этих чисел, очевидно, должно равняться отношению весовых количеств кальция и хлора в любом количестве хлористого кальция. Но последнее отношение равно 36: 64.
Приравняв оба отношения, получим:
40x: 35,5y = 36:64
Затем освободимся от коэффициентов при неизвестных х и у путем деления первых членов пропорции на 40, а вторых на 35,5:
Числа 0,9 и 1,8 выражают относительное число атомов в молекуле хлористого кальция, но они дробны, тогда как в молекуле может содержаться только целое число атомов. второго отношения на наименьший из них. Получаем
второго отношения на наименьший из них. Получаем
х: у = 1:2
Следовательно, в молекуле хлористого кальция на один атом кальция приходятся два атома хлора. Этому условию удовлетворяет целый ряд формул: СаСl 2 , Са 2 Сl 4 , Са 3 Сl 6 и т. д. Так как у нас нет данных, чтобы судить, какая из написанных формул отвечает действительному атомному составу молекулы хлористого кальция, мы остановимся на простейшей из них СаСl 2 , указывающей наименьшее возможное число атомов в молекуле хлористого кальция.
Однако произвол в выборе формулы отпадает, если наряду с весовым составом вещества известен также его молекулярный вес. В этом случае нетрудно вывести формулу, выражающую истинный состав молекулы. Приведем пример.
Путем анализа установлено, что глюкоза содержит на 4,5 вес. ч. углерода 0,75 вес. ч. водорода и 6 вес. ч. кислорода. Молекулярный вес ее был найден равным 180. Требуется вывести формулу глюкозы.
Как и в предыдущем случае, находим сперва отношение между числом атомов углерода (атомный вес 12), водорода и кислорода в молекуле глюкозы. Обозначив число атомов углерода через х, водорода через у и кислорода через z, составляем пропорцию:
Обозначив число атомов углерода через х, водорода через у и кислорода через z, составляем пропорцию:
2х :у: 16z = 4,5: 0,75: 6
откуда
Разделив все три члена второй половины равенства на 0,375, получаем:
х :у: z= 1: 2: 1
Следовательно, простейшая формула глюкозы будет СН 2 O. Но вычисленный по ней равнялся бы 30, тогда как в действительности глюкозы 180, т. е. в шесть раз больше. Очевидно, что для глюкозы нужно принять формулу C 6 H 12 O 6 .
Формулы, основанные, кроме данных анализа, также и на определении молекулярного веса и указывающие действительное число атомов в молекуле, называются истинными или молекулярнымиформулами; формулы же, выведенные только из данных анализа, называются простейшими или эмпирическими.
Познакомившись с выводом химических формул,» легко понять, как устанавливаются точные молекулярные веса. Как мы уже упоминали, существующие методы определения молекулярных весов в большинстве случаев не дают вполне точных результатов.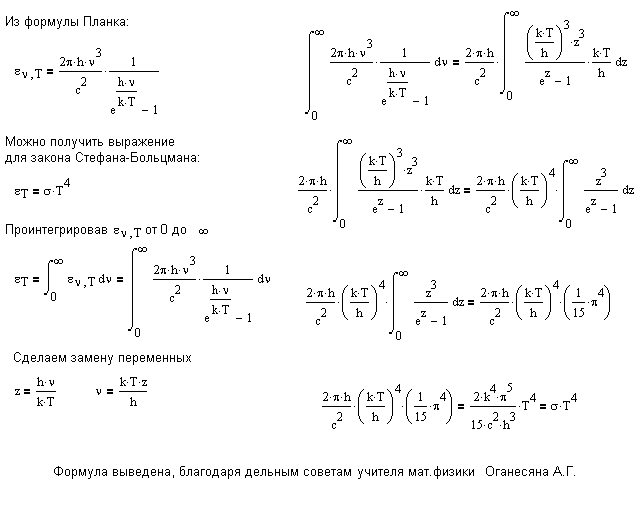 Но, зная хотя бы приблизительный и процентный состав вещества, можно установить его формулу, выражающую атомный состав молекулы. Так как вес молекулы равняется сумме весов образующих ее атомов, сложив веса атомов, входящих в состав молекулы, мы определим ее вес в кислородных единицах, т. е. молекулярный вес вещества. Точность найденного молекулярного веса будет такой же, как и точность атомных весов.
Но, зная хотя бы приблизительный и процентный состав вещества, можно установить его формулу, выражающую атомный состав молекулы. Так как вес молекулы равняется сумме весов образующих ее атомов, сложив веса атомов, входящих в состав молекулы, мы определим ее вес в кислородных единицах, т. е. молекулярный вес вещества. Точность найденного молекулярного веса будет такой же, как и точность атомных весов.
Нахождение формулы химического соединения во многих случаях может быть значительно упрощено, если воспользоваться понятием овалентности элементов.
Напомним, что валентностью элемента называется свойство его атомов присоединять к себе или замещать определенное число атомов другого элемента.
Что такое валентностьэлемента определяется числом, показывающим, сколько атомов водорода (или другого одновалентного элемента) присоединяет или замещает атом данного элемента.
Понятие о валентности распространяется не только на отдельные атомы, но и на целые группы атомов, входящие в состав химических соединений и участвующие как одно целое в химических реакциях. Такие группы атомов получили название радикалов. В неорганической химии наиболее важными радикалами являются: 1) водный остаток, или гидроксил ОН; 2) кислотные остатки; 3) основные остатки.
Такие группы атомов получили название радикалов. В неорганической химии наиболее важными радикалами являются: 1) водный остаток, или гидроксил ОН; 2) кислотные остатки; 3) основные остатки.
Водный остаток, или гидроксил, получается, если отмолекулы воды отнять один атом водорода. В молекуле воды гидроксил связан с одним атомом водорода, следовательно, группа ОН одновалентна.
Кислотными остатками называются группы атомов (аиногда и один атом), «остающиеся» от молекул кислот, если мысленно отнять от них один или несколько атомов водорода, замещаемых металлом. этих групп определяется числом отнятых атомов водорода. Например, дает два кислотных остатка — один двухвалентный SO 4 и другой одновалентный HSO 4 , входящий в состав различных кислых солей. Фосфорная кислотаН 3 РО 4 может дать три кислотных остатка: трехвалентный РО 4 , двухвалентный НРО 4 и одновалентный
Н 2 РО 4 и т. д.
Основными остатками мы будем называть; атомы или группы атомов, «остающиеся» от молекул оснований, если мысленно отнять от них один или несколько гидроксилов. Например, последовательно отнимая от молекулы Fe(OH) 3 гидроксилы, получаем следующие основные остатки: Fe(OH) 2 ,
FeOH и Fe. их определяется числом отнятых гидроксильных групп:Fe(OH) 2
— одновалентен; Fe(OH)-двухвалентен; Fe — трехвалентен.
Например, последовательно отнимая от молекулы Fe(OH) 3 гидроксилы, получаем следующие основные остатки: Fe(OH) 2 ,
FeOH и Fe. их определяется числом отнятых гидроксильных групп:Fe(OH) 2
— одновалентен; Fe(OH)-двухвалентен; Fe — трехвалентен.
Основные остатки, содержащие гидроксильные группы, входят в состав так называемых основных солей. Последние можно рассматривать как основания, в которых часть гидроксилов замещенакислотными остатками. Так, при замещении двух гидроксилов вFe(OH)3 кислотным остатком SO 4 получается основная соль FeOHSO 4 , при замещении одного гидроксила в Bi(OH) 3
кислотным остатком NO 3 получается основная соль Bi(OH) 2 NO 3 и т.д.
Знание валентностей отдельных элементов и радикалов позволяет в простых случаях быстро составлять формулы очень многих химических соединений, что освобождает химика от необходимости механически их заучивать.
Химические формулыПример 1. Составить формулу гидрокарбоната кальция — кислой соли угольной кислоты.
В состав этой соли должны входить атомы кальция и одновалентные кислотные остатки НСО 3 . Так как двухвалентен, то на один атом кальция надо взять два кислотных остатка. Следовательно, формула соли будет Са(НСО 3)г.
Использование переменных для улучшения формул DAX — DAX
- Статья
- Чтение занимает 2 мин
При моделировании данных написание и отладка некоторых вычислений DAX может быть непростой задачей. Обычно сложные вычисления требуют написания составных или сложных выражений. В составных выражениях может использоваться множество вложенных функций, а логика выражения может повторяться.
Переменные в формулах DAX помогают реализовывать сложные и эффективные вычисления. Переменные могут повысить производительность, надежность и удобочитаемость, а также сократить сложность.
Переменные могут повысить производительность, надежность и удобочитаемость, а также сократить сложность.
В этой статье мы продемонстрируем первые три преимущества на примере меры погодового роста продаж. (Формула для погодового роста продаж имеет следующий вид: разность продаж за период и продаж за тот же период прошлого года, деленная на продажи за тот же период прошлого года.)
Начнем со следующего определения меры.
Sales YoY Growth % =
DIVIDE(
([Sales] - CALCULATE([Sales], PARALLELPERIOD('Date'[Date], -12, MONTH))),
CALCULATE([Sales], PARALLELPERIOD('Date'[Date], -12, MONTH))
)
Эта мера дает правильный результат, но ее можно улучшить.
Повышение производительности
Обратите внимание, что в формуле повторяется выражение для вычисления продаж за тот же период прошлого года. Power BI приходится вычислить одно и то же выражение дважды, из-за чего формула неэффективна. Повысить эффективность определения меры можно с помощью переменной VAR.
Ниже представлено улучшенное определение меры. В нем используется выражение, присваивающее результат вычисления продаж за тот же период прошлого года переменной с именем SalesPriorYear. Затем эта переменная дважды используется в выражении RETURN.
Sales YoY Growth % =
VAR SalesPriorYear =
CALCULATE([Sales], PARALLELPERIOD('Date'[Date], -12, MONTH))
RETURN
DIVIDE(([Sales] - SalesPriorYear), SalesPriorYear)
Мера по-прежнему дает правильный результат, но делает это примерно в два раза быстрее.
Повышение удобочитаемости
Обратите внимание на то, как в предыдущем определении меры выбранное имя переменной делает выражение RETURN понятнее. Выражение получилось кратким и не требующим дополнительных пояснений.
Упрощение отладки
Переменные также могут помочь при отладке формулы. Чтобы протестировать выражение, присвоенное переменной, можно временно изменить выражение RETURN так, чтобы оно выводило саму переменную.
Представленное ниже определение меры возвращает только переменную SalesPriorYear. Обратите внимание на то, что изначальное выражение RETURN в нем закомментировано. Такой прием позволяет легко восстановить его после завершения отладки.
Обратите внимание на то, что изначальное выражение RETURN в нем закомментировано. Такой прием позволяет легко восстановить его после завершения отладки.
Sales YoY Growth % =
VAR SalesPriorYear =
CALCULATE([Sales], PARALLELPERIOD('Date'[Date], -12, MONTH))
RETURN
--DIVIDE(([Sales] - SalesPriorYear), SalesPriorYear)
SalesPriorYear
Уменьшение сложности
В более ранних версиях DAX переменные не поддерживались. В сложных выражениях, в которых добавлялись новые контексты фильтров, требовалось использовать функцию DAX EARLIER или EARLIEST для ссылки на внешние контексты фильтров. Однако эти функции были трудны для понимания и использования.
Переменные всегда вычисляются вне фильтров, которые применяются в выражении RETURN. По этой причине при использовании переменной в измененном контексте фильтра результат получается таким же, как и при использовании функции EARLIEST. Это позволяет обойтись без функций EARLIER и EARLIEST. Таким образом, вы можете писать менее сложные и более понятные формулы.
Рассмотрим приведенное ниже определение вычисляемого столбца, добавленного в таблицу Subcategory (Подкатегория). Оно вычисляет рейтинг для каждой подкатегории продуктов на основе значений в столбце Subcategory Sales (Продажи подкатегории).
Subcategory Sales Rank =
COUNTROWS(
FILTER(
Subcategory,
EARLIER(Subcategory[Subcategory Sales]) < Subcategory[Subcategory Sales]
)
) + 1
Функция EARLIER служит для ссылки на значение столбца Subcategory Salesв контексте текущей строки.
Определение вычисляемого столбца можно улучшить, использовав переменную вместо функции EARLIER. В переменной CurrentSubcategorySales хранится значение столбца Subcategory Salesв контексте текущей строки. Эта переменная используется в выражении RETURN в измененном контексте фильтра.
Subcategory Sales Rank =
VAR CurrentSubcategorySales = Subcategory[Subcategory Sales]
RETURN
COUNTROWS(
FILTER(
Subcategory,
CurrentSubcategorySales < Subcategory[Subcategory Sales]
)
) + 1
См.
 также
также- Статья о функции VAR в DAX
- Схема обучения: Использование DAX в Power BI Desktop
- У вас появились вопросы? Попробуйте задать вопрос в сообществе Power BI.
переменных и выражений | Алгебра 1 | Основы алгебры
Дополнительные темы
по переменным и выражениямПопулярные учебные пособия
по переменным и выражениямКак вычислить алгебраическое выражение, подставив значения?
Иногда у вас есть алгебраическое выражение с переменными, и вы точно знаете значения этих переменных, и вам просто нужно подставить эти значения и получить значение выражения. Ну, если это то, что вам нужно сделать, то вы попали в нужное место, потому что этот урок покажет вам, как именно это сделать!
Как решить задачу со словами, написав уравнение и подставив значения?
Составление и решение уравнения из текстовой задачи может быть сложным, но это руководство может помочь.
 Посмотрите все шаги, от определения переменных до получения окончательного ответа, и все, что между ними! С помощью этого урока вы узнаете, что нужно для решения текстовой задачи.
Посмотрите все шаги, от определения переменных до получения окончательного ответа, и все, что между ними! С помощью этого урока вы узнаете, что нужно для решения текстовой задачи.Как перевести фразу с одной переменной и числом в математическое выражение?
Нужна практика перевода фраз в математические выражения? Тогда этот урок для вас! Вы попрактикуетесь в переводе операторов сложения, вычитания, умножения или деления в математические выражения.
Как написать уравнение из словесной задачи?
Возникли трудности с преобразованием текстовой задачи в алгебраическое уравнение? Тогда этот урок для вас! С помощью этого урока вы научитесь разбивать текстовые задачи и переводить их в математические уравнения.
Как подставить переменные в алгебраическое выражение?
Вставка переменных в выражение необходима для решения многих задач по алгебре.
 Узнайте, как вставить значения переменных, посмотрев это руководство.
Узнайте, как вставить значения переменных, посмотрев это руководство.Что такое переменная?
Вы не можете заниматься алгеброй, не работая с переменными, но переменные могут сбивать с толку. Если вы когда-нибудь задумывались, что такое переменные, то этот урок для вас!
Какие слова можно использовать для написания задач?
Знание математического значения слов позволяет вам расшифровывать текстовые задачи и дает вам возможность писать свои собственные текстовые задачи! Взгляните на эти слова и выучите их математический перевод.
Как превратить более длинную словесную фразу в алгебраическое выражение?
Хотите попрактиковаться в переводе слов в математические выражения? Тогда взгляните на этот учебник, и вы узнаете, как разбить эти слова и написать математическое выражение, которое они описывают!
Как превратить простое уравнение в слова?
Проявите творческий подход к математике, превратив математическое уравнение в историю.
 В этом уроке показан один пример, но возможности безграничны! Проверьте свои творческие способности, написав собственную историю, описывающую данное математическое уравнение.
В этом уроке показан один пример, но возможности безграничны! Проверьте свои творческие способности, написав собственную историю, описывающую данное математическое уравнение.Как превратить простое выражение в слова?
Умение переводить слова в математическое выражение — важный навык, но не менее важно уметь идти другим путем. В этом уроке показано, как математическое выражение можно преобразовать в слова.
Как превратить более сложное уравнение в слова?
Дайте волю своему творчеству, превратив математическое уравнение в историю! Посмотрите это руководство, чтобы увидеть один пример, а затем напишите свою собственную историю, описывающую данное уравнение. Посмотрите, как творчески вы можете подойти к математике!
Как превратить более сложное выражение в слова?
В этом руководстве показано, как математическое выражение можно преобразовать в слова.
 Лучшая часть? Вы можете быть очень креативны с заявлением, которое вы составляете! Ознакомьтесь с примером оператора, созданным в этом руководстве, а затем составьте свой собственный!
Лучшая часть? Вы можете быть очень креативны с заявлением, которое вы составляете! Ознакомьтесь с примером оператора, созданным в этом руководстве, а затем составьте свой собственный!Что такое константа?
Константы — это части алгебраических выражений, которые не изменяются. Ознакомьтесь с этим руководством, чтобы точно увидеть, как выглядит константа и почему она не меняется.
Что такое числовые и алгебраические выражения?
Выражение — это просто математическая фраза. В этом руководстве вы узнаете о двух популярных типах выражений: числовых и алгебраических выражениях. Числовое выражение содержит числа и операции. Алгебраическое выражение почти точно такое же, за исключением того, что оно также содержит переменные. Посмотрите этот урок, чтобы узнать об этих двух популярных видах выражений!
Что такое свойство замещения равенства?
Если вы когда-либо подставляете значение переменной в выражение или уравнение, вы используете свойство замещения равенства.
 Это свойство позволяет вам заменять количества друг друга в выражении до тех пор, пока эти количества равны. Посмотрите этот урок, чтобы узнать об этом полезном свойстве!
Это свойство позволяет вам заменять количества друг друга в выражении до тех пор, пока эти количества равны. Посмотрите этот урок, чтобы узнать об этом полезном свойстве!
Определение, формула, правила и пример
Знаете ли вы, что ряд задач из реальной жизни, которые содержат неизвестные величины, можно смоделировать в виде математических выражений , чтобы упростить их решение? В этой статье мы обсудим линейные выражения , как они выглядят и как их решать.
Что такое линейные выражения?
Линейные выражения — это алгебраические выражения, содержащие константы и переменные, возведенные в степень 1.
Например, является линейным выражением, поскольку переменная здесь также является представлением . В тот момент, когда появляется такая вещь, как , оно перестает быть линейным выражением.
Вот еще несколько примеров линейных выражений:
1.
2.
3.
Что такое переменные, термины и коэффициенты?
Переменные — это буквенные компоненты выражений. Это то, что отличает арифметические операции от выражений. Термины — это компоненты выражений, которые разделяются сложением или вычитанием, а коэффициенты — числовые множители, умножающие переменные.
Это то, что отличает арифметические операции от выражений. Термины — это компоненты выражений, которые разделяются сложением или вычитанием, а коэффициенты — числовые множители, умножающие переменные.
Например, если бы нам дали выражение, x и y можно было бы идентифицировать как переменные компоненты выражения. Число 6 идентифицируется как коэффициент члена. Число называется константой. Идентифицированные термины здесь и .
Мы можем взять несколько примеров и классифицировать их компоненты по переменным, коэффициентам или терминам.
Variables | Coefficients | Constants | Terms | |
x and y | -3 | |||
x | -4 | 2 | ||
x и y | 1 (хотя x и y | 1)0021 |
Переменные — это то, что отличает выражения от арифметических операций. В основном есть ключевые слова, которые помогают определить, какую операцию нужно выполнить при написании выражения из текстовой задачи.
В основном есть ключевые слова, которые помогают определить, какую операцию нужно выполнить при написании выражения из текстовой задачи.
| Операция | Сложение | Вычитание | Multiplication | Division |
| Keywords | Added toPlusSum ofIncreased byTotal ofMore than | Subtracted fromMinusLess thanDifferenceDecreased byFewer thanTake away | Multiplied byTimesProduct ofTimes of | Divided byQuotient of |
We can go ahead to take examples того, как это делается.
Напишите приведенную ниже фразу в виде выражения.
больше числа
Решение:
Эта фраза предлагает добавить. Тем не менее, мы должны быть осторожны с позиционированием. 14 больше, чем означает, что 14 добавляется к определенному числу .
Запишите приведенную ниже фразу в виде выражения.
Разница в 2 и 3 раза число .
Решение:
Мы должны высматривать наши ключевые слова здесь, «разницу» и «времена». «Разница» означает, что мы будем вычитать. Итак, мы собираемся вычесть 3 раза число из 2.
Упрощение линейных выражений
Упрощение линейных выражений — это процесс записи линейных выражений в их наиболее компактной и простой форме, при которой сохраняется значение исходного выражения.
Чтобы упростить выражения, нужно выполнить несколько шагов, а именно;
Упростите линейное выражение.
Решение:
Здесь мы сначала поработаем со скобками, умножив множитель (вне скобок) на то, что в скобках.
Мы добавим похожие термины.
Это означает, что упрощенная форма есть, и они обладают одинаковым значением.
Линейные уравнения также являются формой линейных выражений. Линейные выражения — это название, охватывающее линейные уравнения и линейные неравенства.
Линейные уравнения
Линейные уравнения — это линейные выражения со знаком равенства. Это уравнения степени 1. Например, . Линейные уравнения имеют стандартную форму
где и — коэффициенты
и — переменные.
постоянно.
Однако, также известен как точка пересечения с осью x, а также точка пересечения с осью y. Когда линейное уравнение имеет одну переменную, стандартная форма записывается как;
где переменная
коэффициент
константа.
Графики линейных уравнений
Как упоминалось ранее, линейные уравнения изображаются в виде прямой линии, важно знать, что в случае уравнения с одной переменной линии линейного уравнения параллельны оси x, поскольку берется только значение x во внимание. Линии, построенные на основе уравнений с двумя переменными, размещаются там, где этого требуют уравнения, хотя и остаются прямыми. Мы можем пойти дальше и взять пример линейного уравнения с двумя переменными.
Построить график для линии .
Решение:
Сначала мы преобразуем уравнение в форму .
Таким образом, мы также можем узнать, что такое y-перехват.
Это означает, что мы сделаем y предметом уравнения.
Теперь мы можем изучить значения y для различных значений x, так как это также считается линейной функцией.
Итак, возьмем x = 0
Это означает, что мы подставим x в уравнение, чтобы найти y.
Y = -1
Take
Y = 0
Take X = 4
Y = 1
Что это на самом деле означает, что когда
x = 0, y = -1.
х = 2, у = 0
х = 4, у = 1
и так далее.
Теперь мы нарисуем наш график и укажем оси x и y.
После чего нанесем имеющиеся у нас точки и проведем через них линию.
График линии x — 2y = 2
Решение линейных уравнений
Решение линейных уравнений включает в себя нахождение значений x и/или y в заданном уравнении. Уравнения могут быть в форме с одной переменной или в форме с двумя переменными. В форме с одной переменной представление переменной делается предметом и решается алгебраически.
Уравнения могут быть в форме с одной переменной или в форме с двумя переменными. В форме с одной переменной представление переменной делается предметом и решается алгебраически.
Для формы с двумя переменными требуется другое уравнение, чтобы получить абсолютные значения. Помните в примере, где мы решали значения, когда. И когда , . Это означает, что пока он был другим, он тоже должен был быть другим. Ниже мы можем взять пример их решения.
Решите линейное уравнение
Решение:
Мы решим это путем замены. Составьте предмет уравнения в первом уравнении. Подставляем во второе уравнение Мы выберем первое уравнение.
Это означает, что с этим уравнением, когда
Это можно оценить, чтобы увидеть, верно ли утверждение
Мы можем подставить значения каждой найденной переменной в любое из уравнений. Возьмем второе уравнение.
Это означает, что наше уравнение верно, если мы говорим, когда .
Линейные неравенства
Это выражения, используемые для сравнения двух чисел с использованием символов неравенства, таких как . Ниже мы рассмотрим, что это за символы и когда они используются.
| Symbol name | Symbol | Example |
| Not equal | ≠ | |
| Less than | < | |
| Greater than | > | |
| Less than or equal to | ≤ | |
| Greater than or equal to | ≥ |
Solving Linear Inequalities
The primary aim of solving inequalities is to find the диапазон значений, удовлетворяющих неравенству. Это математически означает, что переменная должна быть оставлена на одной стороне неравенства. Большая часть того, что делается с уравнениями, делается и с неравенствами. Такие вещи, как применение золотого правила.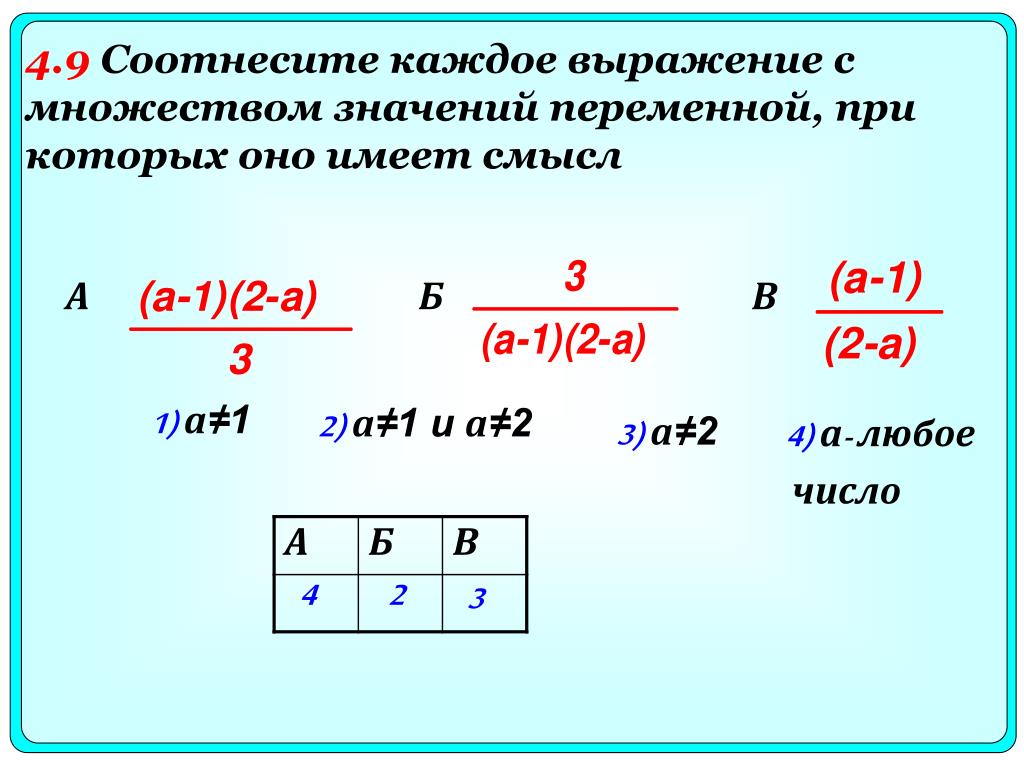 Разница здесь в том, что некоторые оперативные действия могут изменить рассматриваемые знаки таким образом, что < становится >, > становится <, ≤ становится ≥, а ≥ становится ≤. Эти действия;
Разница здесь в том, что некоторые оперативные действия могут изменить рассматриваемые знаки таким образом, что < становится >, > становится <, ≤ становится ≥, а ≥ становится ≤. Эти действия;
Упростите линейное неравенство и найдите его.
Решение:
Сначала нужно прибавить по 3 к каждой стороне,
Затем разделить каждую сторону на 4.
Символ неравенства остается в том же направлении.
Любое число 6 или больше является решением неравенства.
Линейные выражения — основные выводы
- Линейные выражения — это операторы, каждый член которых является либо константой, либо переменной, возведенной в первую степень.
- Линейные уравнения — это линейные выражения со знаком равенства.
- Линейные неравенства — это линейные выражения, сравнивающие два значения с использованием символов <, >, ≥, ≤ и ≠.
Уравнения с переменными в алгебре | Turito US Blog
Прежде чем мы приступим к изучению уравнений с переменными, давайте сначала проясним наши представления об основах алгебры. По определению, он охватывает простые математические процессы, подобные сложению, вычитанию, умножению и делению, в отношении как постоянных, так и переменных. Например, x+10 = 0. Это вводит важную алгебраическую теорию, известную как уравнения. Можно провести аналогию между алгебраическим уравнением и уравнением весов, где веса уравновешены с помощью чисел или констант.
По определению, он охватывает простые математические процессы, подобные сложению, вычитанию, умножению и делению, в отношении как постоянных, так и переменных. Например, x+10 = 0. Это вводит важную алгебраическую теорию, известную как уравнения. Можно провести аналогию между алгебраическим уравнением и уравнением весов, где веса уравновешены с помощью чисел или констант.
Алгебра — это раздел математики, который использует буквы алфавита для нахождения неопознанных чисел. Эти алфавиты также называются переменными. Значения, которые идентифицируются в данном выражении, такие как числа, называются константами. Когда мы формулируем его основы, он охватывает широкие алгебраические выражения, формулы и тождества, которые используются для решения многих математических задач.
Ниже приведены некоторые термины, связанные с базовыми навыками алгебры.
1. Показатель степени
2. Выражение
3. Полиномиальное (мономиальное, биномиальное и трехчленное)
4. Похожие термины и непохожие термины
Похожие термины и непохожие термины
5. Константы
Уравнение – это утверждение, которое указывает на два одинаковых тождества, разделенных знаком «=». В то время как выражение представляет собой группу различных терминов, не связанных между собой знаком «+» или «-».
Подобные термы — это те термы, переменные и их показатели которых идентичны.
Некоторые основные правила алгебры приведены ниже:
• Правило симметрии
• Коммутативные правила
• Обратное сложению
• Два правила для уравнения
Общие арифметические операции, выполняемые в случае алгебры, следующие:
• Сложение: x + y
• Вычитание: x – y
• Умножение: xy
• Деление: x/y или x ÷ y
Где x и y — переменные.
Универсальные формулы, используемые в алгебре для решения алгебраических уравнений и определения значений неизвестных переменных, следующие:
• a 2 – b 2 = (a – b)(a + b)
• (a+b) 2 = a 2 + 2ab + b 2
• a 2 + b 2 = (a – b ) 2 + 2ab
• (a – b) 2 = a 2 – 2ab + b 2
• (a + b + c) 2 = a 3 2 3 + c 2 + 2ab + 2ac + 2bc
• (a – b – c) 2 = a 2 + b 2 + c 2 – 2ab – 2ac + 2bc
• (a + 2bc
• (a + 2bc
• ) 3 = 3 + 3A2B + 3AB 3 + B 3
• (A — B) 3 = A 3 — 3A 2 B + 3AB 2 — B 3 B + 3AB 2 — B 3 B + 3AB 2 — B 3 . является выражением с одной переменной, эта переменная имеет ответ или значение, которое делает уравнение точным.
является выражением с одной переменной, эта переменная имеет ответ или значение, которое делает уравнение точным.
Кроме того, мы объясняем, что означает уравнение с одной переменной, и причины его использования. Ниже приведено объяснение;
• Уравнение – это математическое утверждение, утверждающее эквивалентность двух выражений.
• Когда уравнение содержит переменную, такую как xx, переменная измеряется с неизвестным значением.
• Значения переменных, которые делают уравнение точным, являются решениями уравнения и могут быть найдены путем расшифровки уравнения.
• Решение уравнения можно обосновать или проверить, заменив его значение на переменную в уравнении.
Основные выражения
• Решение: Значение, которое можно заменить переменной, чтобы сделать уравнение правильным.
• Неизвестно: переменная в уравнении, для которой необходимо найти решение.
• Уравнение: математическое утверждение, утверждающее эквивалентность двух выражений.
Уравнение — это математический счет, в котором утверждается эквивалентность двух выражений. Например, утверждение, что «два плюс пять равно семи», обозначается уравнением 2+5=72+5=7.
Во многих случаях уравнение содержит одну или несколько переменных. Они по-прежнему записываются путем перечисления каждого выражения по обе стороны от знака равенства (==). Например, уравнение x+3=5x+3=5, читаемое как «xx плюс три равно пяти», подтверждает, что выражение x+3x+3 равно значению 5.
Вполне вероятно, что уравнения имеют более одной переменной. Например, x+y+7=13x+y+7=13 — это уравнение с двойными переменными. Тем не менее, этот урок посвящен исключительно уравнениям с одной переменной.
Как решать уравнения
Если уравнение содержит переменную, такую как xx, эта переменная считается неизвестной. В некоторых случаях мы можем обнаружить возможные значения xx, которые сделают уравнение правильным.
Например, подумайте над уравнением, о котором мы говорили выше: x+3=5x+3=5. Скорее всего, вы уже решили, что единственным возможным значением xx является 2, потому что вы знаете, что 2+3=52+3=5 — точное уравнение. Мы используем символ равенства, чтобы показать, что мы знаем значение данной переменной. В этом случае мы пишем x=2x=2 (читается как «xx равно двум»).
Скорее всего, вы уже решили, что единственным возможным значением xx является 2, потому что вы знаете, что 2+3=52+3=5 — точное уравнение. Мы используем символ равенства, чтобы показать, что мы знаем значение данной переменной. В этом случае мы пишем x=2x=2 (читается как «xx равно двум»).
Значения переменных, которые составляют правильное уравнение, называются решениями уравнения. Случайно решить уравнение означает определить, какие значения переменных делают уравнение правильным утверждением.
Приведенное выше уравнение было объективно простым; нам было легко распознать решение как x=2x=2.
Как проверить решения
Если число задано как решение уравнения, то замена этого числа на место переменной должно сделать уравнение правильным. Следовательно, мы можем встречно проверить, является ли число истинным решением данного уравнения или нет
Например, давайте посмотрим, является ли x=3x=3 решением уравнения 2x+31=372x+31=37.
Заменив 3 на xx, мы получим:
2(3)+31=376+31=372(3)+31=376+31=37
Это равенство является точным утверждением. Отсюда можно сделать вывод, что x=3x=3 на самом деле является ответом на уравнение 2x+31=372x+31=37.
Отсюда можно сделать вывод, что x=3x=3 на самом деле является ответом на уравнение 2x+31=372x+31=37.
Как решить уравнение с двумя переменными
Линейное уравнение с двумя переменными, x и y, может быть записано в виде
ax + by = c
где x и y — действительные числа, а a и b — нет. оба ноль.
Например, 3x + 2y = 8 — это линейное уравнение с двумя переменными.
Задача о том, как решить уравнение с двумя переменными, имеет решение, заключающееся в том, что такое уравнение представляет собой правильно упорядоченную пару чисел (x, y), которая делает уравнение правильным при замене в уравнении значений x и y.
Например, и (2, 1), и (0, 4) являются решениями уравнения, но (2, 0) решением не является. Линейное уравнение с двумя переменными имеет существенно много решений.
Если задано другое линейное уравнение с теми же переменными, обычно можно найти уникальное решение для обоих уравнений. Два уравнения с одинаковыми переменными называются системой уравнений, а уравнения в системе называются одновременными уравнениями. Чтобы разгадать вопрос, как решить уравнение с двумя переменными, вам понадобится система двух уравнений, чтобы найти упорядоченную пару чисел, содержащую оба уравнения в системе.
Чтобы разгадать вопрос, как решить уравнение с двумя переменными, вам понадобится система двух уравнений, чтобы найти упорядоченную пару чисел, содержащую оба уравнения в системе.
Существует два элементарных метода решения систем линейных уравнений: путем подстановки или исключения.
Метод подстановки
В методе подстановки одно уравнение составляется для определения одной переменной через другую. Затем выражение заменяется другим уравнением.
Например, чтобы решить систему уравнений
3x + 2y = 2
y + 8 = 3x
Разделите переменную y в уравнении y + 8 = 3x, чтобы получить y = 3x – 8,
Затем замените 3x – 8 вместо y в уравнении 3x + 2y = 2.
3x + 2 (3x – 8) = 2
3x + 6x – 16 = 2
9x – 16 = 2
9x = 18
Замена x = 2 в y = 3x – 8. чтобы получить значение для y
y = 3 (2) – 8
y = 6 – 8 = – 2
Ответ: x = 2 и y = –2
3 переменная система уравнений:
Решить системы уравнений с тремя переменными: означает, что имеется система из трех уравнений с тремя переменными.
• Вам нужно будет идентифицировать непредсказуемые системы уравнений, включающие три переменные.
• Выразите решение системы зависимых уравнений, содержащей системы уравнений с тремя переменными, используя стандартные обозначения.
Джон ожидал получить наследство в размере 12 000 долларов, которое он распределил на три части и капитализировал тремя способами: в фонд денежного рынка, выплачивающий 3% годовых; по муниципальным облигациям с выплатой 4% годовых и по взаимным фондам с выплатой 7% каждые двенадцать месяцев. Джон потратил на муниципальные фонды сумму в 4000 долларов больше, чем на муниципальные облигации. Он заработал 670 долларов в виде процентов в первый год. Можете ли вы сказать, сколько Джон инвестировал в каждый тип фонда?
Принятие правильного метода постановки задач, подобных этой, делает поиск решения вопросом обеспечения шаблона. Мы объясним эту и подобные проблемы, касающиеся трех переменных систем уравнений и трех переменных в этом разделе. При этом используются связанные методы, такие как те, которые используются для решения систем двух уравнений с двумя переменными. Тем не менее, поиск решений систем уравнений с тремя переменными требует большей организованности и некоторой визуальной гимнастики.
Тем не менее, поиск решений систем уравнений с тремя переменными требует большей организованности и некоторой визуальной гимнастики.
Как решить систему уравнений с тремя переменными
Чтобы ответить на системы уравнений с тремя переменными, известные как системы три на три, основная цель состоит в том, чтобы удалить одну переменную за раз, чтобы добиться обратной подстановки. Решение системы уравнений с тремя переменными (x, y, z), (x, y, z) называется упорядоченной тройкой.
Чтобы найти объяснение, мы можем выполнить следующие операции:
1. Поменять местами любые два уравнения.
2. Умножьте обе части уравнения на ненулевую константу.
3. Добавьте ненулевое кратное одному уравнению в новое уравнение.
В явном виде упорядоченная тройка описывает точку пересечения трех плоскостей в пространстве. Предусмотреть такое пересечение можно, визуализируя любой угол в прямоугольной комнате. Угол определяется тремя плоскостями: двумя соединительными стенами и полом. Любая точка, где встречаются две стены и пол, символизирует пересечение трех плоскостей.
Любая точка, где встречаются две стены и пол, символизирует пересечение трех плоскостей.
ОБЩЕЕ НАПОМИНАНИЕ: КОЛИЧЕСТВО ВОЗМОЖНЫХ РЕШЕНИЙ
Плоскости иллюстрируют возможные ситуации решения для систем три на три.
• Системы, имеющие единственное решение, — это системы, которые после исключения дают набор решений, состоящий из упорядоченной тройки {(x,y,z)}{(x,y,z)}. На самом деле упорядоченная тройка описывает точку, являющуюся стыком трех плоскостей в пространстве.
• Системы, имеющие бесчисленное количество решений, — это те, которые после исключения дают всегда правильное выражение, например 0=00=0. В явном виде неограниченное количество решений означает линию или совпадающую плоскость, которая служит пересечением трех плоскостей в пространстве.
• Системы, не имеющие решения, это те, которые после удаления приводят к утверждению, которое является несогласованным, например, 3=03=0. Система без решения обозначается тремя плоскостями, не имеющими общих точек.
Как решить, является ли упорядоченная тройка (3,−2,1)(3,−2,1) решением системы.
x+y+z=26x−4y+5z=315x+2y+2z=13x+y+z=26x−4y+5z=315x+2y+2z=13
Мы проверим каждое уравнение, заменив значения упорядоченной тройки для x, yx, y и zz.
x+y+z=2(3)+(-2)+(1)=2Trueex+y+z=2(3)+(-2)+(1)=2True 6x-4y+5z=316( 3)−4(−2)+5(1)=3118+8+5=31True6x−4y+5z=316(3)−4(−2)+5(1)=3118+8+5=31True 5x +2y+2z=135(3)+2(-2)+2(1)=1315−4+2=13True5x+2y+2z=135(3)+2(-2)+2(1)=1315 −4+2=13Истинно
Упорядоченная тройка (3,−2,1)(3,−2,1), несомненно, является решением системы.
Классификация решений по системам уравнений с тремя переменными
Так же, как и со структурами уравнений с двумя переменными, мы можем столкнуться с ошибочной системой уравнений с тремя переменными, что означает, что у нее нет решения, удовлетворяющего всем трем уравнениям. Упомянутые уравнения могут означать три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые перекрывают две другие, но не находятся в одном и том же положении. Метод исключения приведет к неправильному утверждению, например, 3=73=7 или к какой-либо другой несогласованности.
Метод исключения приведет к неправильному утверждению, например, 3=73=7 или к какой-либо другой несогласованности.
Основные понятия
• Набор решений — это упорядоченная тройка {(x,y,z)}{(x,y,z)}, представляющая собой соединение трех плоскостей в пространстве.
• Для решения системы из трех уравнений с тремя переменными можно использовать последовательность шагов, заставляющих исключать переменную. Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению.
• Системы из трех уравнений с тремя переменными полезны для решения множества различных типов повседневных задач.
• Система уравнений с тремя переменными является нечетной, если не существует решения. После проведения операций исключения получается противоречие.
• Системы уравнений с тремя переменными переменными могут быть результатом трех параллельных плоскостей, двух параллельных плоскостей и одной перекрывающейся плоскости или трех плоскостей, которые соединяют две другие плоскости, но не в одном и том же месте.
• Система уравнений с тремя переменными зависит от того, имеет ли она бесконечное число решений. После проведения операций исключения результатом является тождество.
• Необходимые системы уравнений с тремя переменными могут быть получены из трех совпадающих плоскостей, трех совпадающих плоскостей, пересекающихся по прямой, или двух совпадающих плоскостей, пересекающих третью по прямой.
Решение уравнений с переменной в обеих частях
Иногда неопределенная величина появляется в обеих частях уравнения. Вот тут-то и пригодятся свойства эрудиции в 5.1 и 5.2. С количеством с переменной можно обращаться так же, как с количеством без переменных — количество с переменной подчиняется всем правилам, изученным в двух последних разделах. Например, мы можем увеличить количество с переменной в обе стороны, не изменяя уравнение или значения, которые делают его точным:
15 – x = 4x
15 – x + x = 4x + x
15 + 0x = 5x
15 = 5x
3 = x
x = 3
стороны уравнения:
5x = 6 + 2x
5x – 2x = 6 + 2x – 2x
3x = 6 + 0x
3x = 6
x = 2
Последующее упрощение, первый шаг в решении уравнения с переменная с обеих сторон, чтобы получить переменную с одной стороны. Это завершается повторным добавлением или вычитанием одного из членов с переменной. Другими словами, мы должны прибавить к обеим частям или вычесть из обеих частей одну из величин, составляющих переменную. Обычно легче прибавлять или вычитать меньшую величину из большей, поэтому мы занимаемся положительными коэффициентами, но в любом случае работает.
Это завершается повторным добавлением или вычитанием одного из членов с переменной. Другими словами, мы должны прибавить к обеим частям или вычесть из обеих частей одну из величин, составляющих переменную. Обычно легче прибавлять или вычитать меньшую величину из большей, поэтому мы занимаемся положительными коэффициентами, но в любом случае работает.
Иллюстрация 1. Решить для x: 3x + 2x = 12 – x
• Упростить: 5x = 12 – x
• Получить переменную с одной стороны:
o 5x + x = 12 – x + x
o 6x = 12
• Решить с помощью обратных операций:
o =
o x = 2
• Проверить: 3(2) + 2(2) = 12 – 2 ? Да!
Рисунок 2. Решите для y: 5y – 3 = 3y + 5
• В настоящее время уравнение упрощено.
• Получить переменную с одной стороны:
o 5y – 3 – 3y = 3y + 5 – 3y
o 5y – 3y – 3 = 3y – 3y + 5
o 2y – 3 = 5
• Решить с помощью обратных операций:
o 2y – 3 + 3 = 5 + 3
o 2y = 8
o =
o y = 4
• Проверить: 5(4) – 3 = 3( 4) + 5 ? Да!
Уравнения, которые мы решили в предыдущем разделе, были оптимизированы, чтобы мы могли использовать свойство деления для разделения переменных и решения уравнения.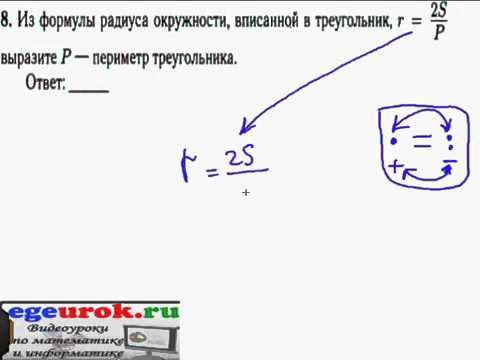 Иногда после упрощения у вас может быть переменная и постоянная часть по одну сторону от знака равенства.
Иногда после упрощения у вас может быть переменная и постоянная часть по одну сторону от знака равенства.
Наш подход будет заключаться в выборе одной части уравнения в качестве переменной, а другой части уравнения в качестве постоянной части. Это принесет пользу нам с организацией. Затем мы шаг за шагом будем практиковать свойства вычитания и сложения равенства, чтобы разделить переменные члены на одной стороне уравнения.
Как решать уравнения с переменными на обеих сторонах
Вы могли заметить, что во всех иллюстрациях уравнений, которые мы демонстрировали и объясняли до сих пор, у нас были переменные только на одной стороне уравнения. Это происходит не постоянно, поэтому теперь мы поймем, как решать уравнения с переменными в обеих сторонах.
Мы начнем так же, как и непосредственно выше, т. е. выберем переменную сторону и постоянную сторону, а затем воспользуемся свойствами равенства вычитания и сложения, чтобы объединить все переменные с одной стороны и все константы с другой стороны. Вспомните, что вы делаете с левой частью уравнения, вы должны делать и с правой частью.
Вспомните, что вы делаете с левой частью уравнения, вы должны делать и с правой частью.
В следующем примере переменная xx находится с обеих сторон, но константы появляются только с правой стороны, поэтому мы сделаем правую часть «постоянной» и, следовательно, левая часть уравнения будет «переменная» сторона.
Калькулятор с использованием системы уравнений с 3 переменными — это бесплатный онлайн-инструмент, который показывает значение неизвестной переменной. Незнакомое значение данного уравнения отображается за доли секунды.
Решение уравнений с переменными на обеих сторонах Калькулятор?
Техника использования этого калькулятора следующая:
Этап 1: Введите уравнение в поле «Решить уравнение»
Этап 2: Нажмите кнопку «Решить», чтобы получить результат
Этап 3: Неизвестное значение данное уравнение будет отображаться в новом окне
Определение уравнения:
В арифметике уравнение представляет собой выражение, эквивалентное двум значениям. Он состоит из двух выражений, разделенных знаком равенства «=». Если выражение характеризуется знаком равенства, значение одной стороны должно быть равно значению другой стороны. Большинство линейных уравнений включает одну или две переменные. Давайте обсудим образец,
Он состоит из двух выражений, разделенных знаком равенства «=». Если выражение характеризуется знаком равенства, значение одной стороны должно быть равно значению другой стороны. Большинство линейных уравнений включает одну или две переменные. Давайте обсудим образец,
Пусть x будет неизвестным значением
x = 20 +15
Мы можем сказать, что значение x должно насытить значение 35. Потому что 20+ 15 = 35. Метод нахождения неизвестного значения в уравнении известен как « Решение уравнения».
Стандартная форма
Стандартная форма, используемая для обозначения уравнения, приведена ниже:
Ax + By = C
Здесь x и y — два неизвестных значения (т. е. переменная)
Часто задаваемые вопросы о решении уравнений с переменными на обеих сторонах
Решите данное уравнение: 5x + 2 = 12
5x+2=12
5x=12-2
x=10/5
x=2
Какие бывают типы уравнений?
Различаются следующие типы уравнений:
• Линейное уравнение
• Квадратное уравнение
• Экспоненциальное уравнение
• Радикальное уравнение
Классификация линейных уравнений с иллюстрациями.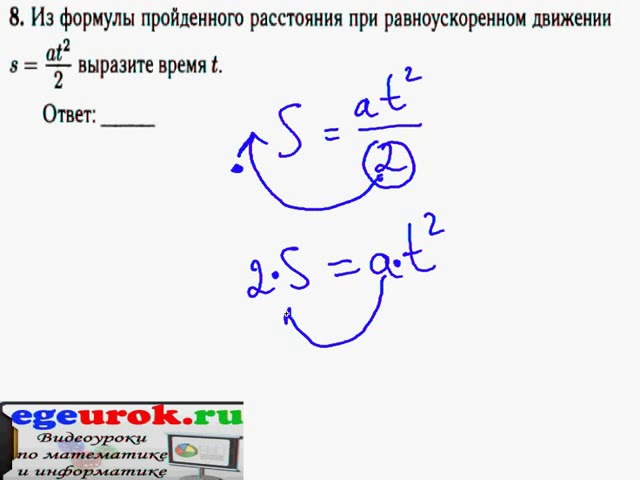

 Посмотрите все шаги, от определения переменных до получения окончательного ответа, и все, что между ними! С помощью этого урока вы узнаете, что нужно для решения текстовой задачи.
Посмотрите все шаги, от определения переменных до получения окончательного ответа, и все, что между ними! С помощью этого урока вы узнаете, что нужно для решения текстовой задачи. Узнайте, как вставить значения переменных, посмотрев это руководство.
Узнайте, как вставить значения переменных, посмотрев это руководство. В этом уроке показан один пример, но возможности безграничны! Проверьте свои творческие способности, написав собственную историю, описывающую данное математическое уравнение.
В этом уроке показан один пример, но возможности безграничны! Проверьте свои творческие способности, написав собственную историю, описывающую данное математическое уравнение. Лучшая часть? Вы можете быть очень креативны с заявлением, которое вы составляете! Ознакомьтесь с примером оператора, созданным в этом руководстве, а затем составьте свой собственный!
Лучшая часть? Вы можете быть очень креативны с заявлением, которое вы составляете! Ознакомьтесь с примером оператора, созданным в этом руководстве, а затем составьте свой собственный! Это свойство позволяет вам заменять количества друг друга в выражении до тех пор, пока эти количества равны. Посмотрите этот урок, чтобы узнать об этом полезном свойстве!
Это свойство позволяет вам заменять количества друг друга в выражении до тех пор, пока эти количества равны. Посмотрите этот урок, чтобы узнать об этом полезном свойстве!