Тангенс формулы тригонометрии: формулы cos, sin, tg, ctg

формулы cos, sin, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла.  

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла. 

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

формулы cos, sin, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла.  

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.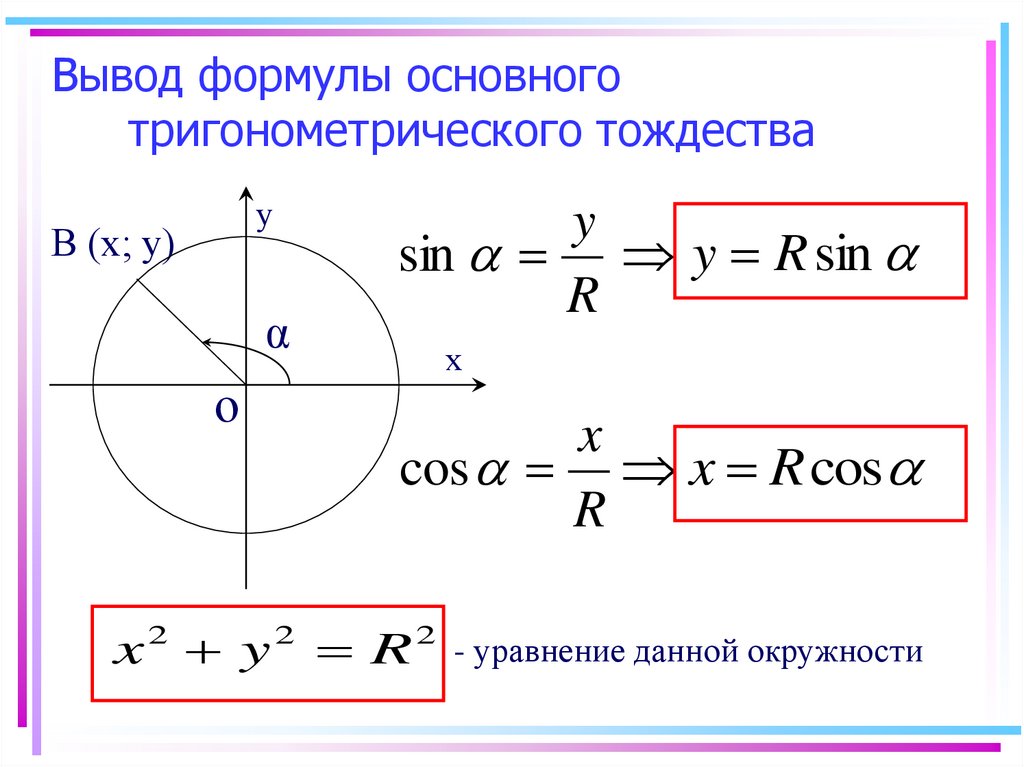

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла. 

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.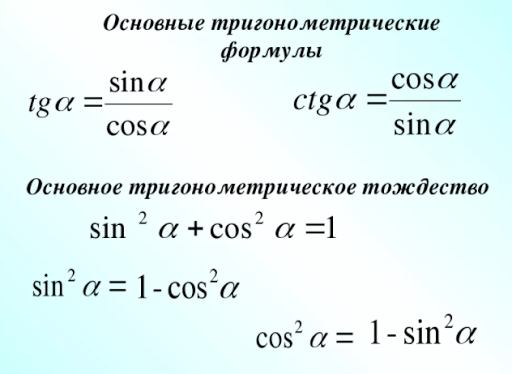

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Тригонометрические функции основные формулы тригонометрии. Все формулы по тригонометрии. Тригонометрические формулы сложения

На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.

Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.

Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.

Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).

Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac{cos\ \alpha}{sin\ \alpha},` ` \alpha\ne\pi+\pi n, \ n \in Z`

И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.

`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`

Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти. 2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`

Формулы суммы и разности углов тригонометрических функций

Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`

Формулы двойного угла

`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`

Формулы тройного угла

`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`

Формулы половинного угла

`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`

Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.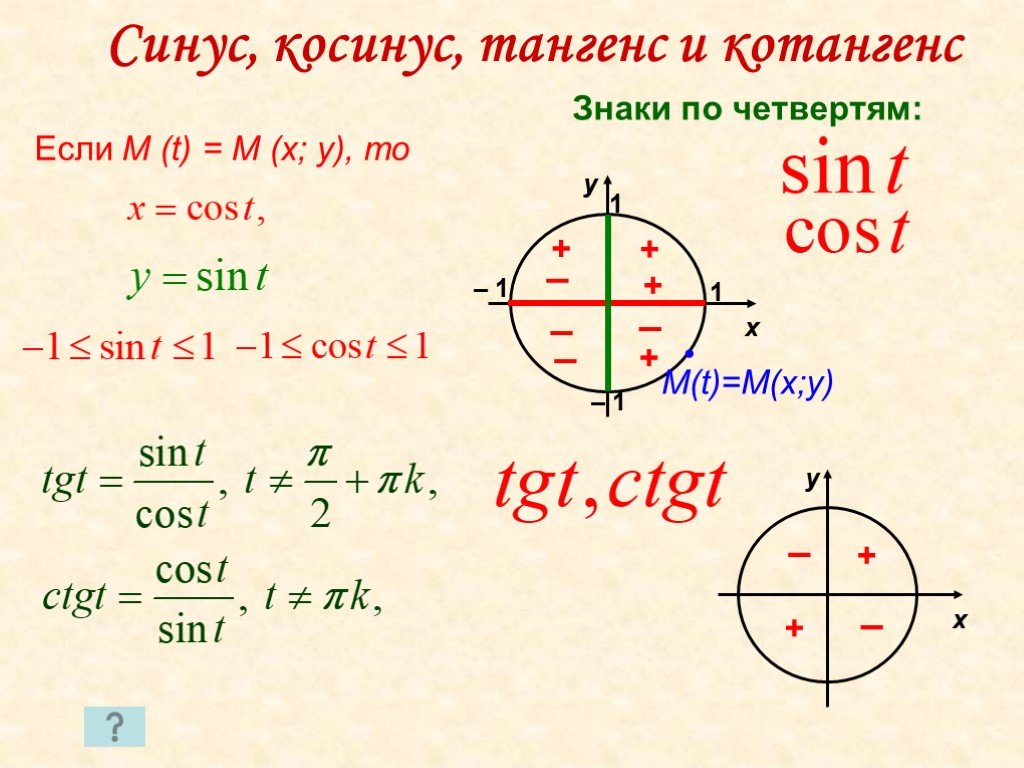 4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`

Формулы суммы и разности тригонометрических функций

Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.

`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`

Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение. 2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`

Формулы преобразования произведений функций

Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`

Универсальная тригонометрическая подстановка

Эти формулы выражают тригонометрические функции через тангенс половинного угла. 2 \alpha}}=\frac 1{tg \ \alpha}`

Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.

Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.

В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Навигация по странице.

Основные тригонометрические тождества

Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.

Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .

Формулы приведения

Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.

Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .

Формулы сложения

Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.

Формулы двойного, тройного и т.д. угла

Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т. д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.

Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .

Формулы половинного угла

Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.

Их вывод и примеры применения можно посмотреть в статье .

Формулы понижения степени

Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.

Формулы суммы и разности тригонометрических функций

Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.

Формулы произведения синусов, косинусов и синуса на косинус

Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .

Универсальная тригонометрическая подстановка

Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.

Список литературы.

• Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М. : Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
• Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
• Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Copyright by cleverstudents

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:

Простейшие тригонометрические тождества

Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств .
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса .
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.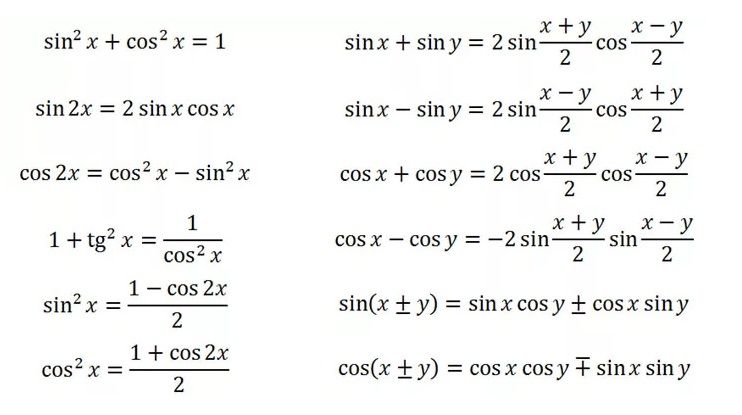

Как видно, косинус и секанс является четной функцией , синус, тангенс и котангенс — нечетные функции .

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)

Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:

Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла ) в одинарный происходит по следующим правилам:

Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла

Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла

Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица

Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла

Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.

Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла

Формулы универсальной тригонометрической подстановки

Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции (sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .

Данные формулы называются формулами универсальной тригонометрической подстановки . Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.

Тригонометрические тождества преобразования половины угла

Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.

Тригонометрические формулы сложения углов

cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α

sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Формулы преобразования суммы или разности тригонометрических функций

Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:

Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα

Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:

Формулы преобразования произведения тригонометрических функций

Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:

В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.

Формулы приведения тригонометрических функций

Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Yandex.RTB R-A-339285-1

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Тригонометрические тождества

sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения

sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = — 1 ± c t g α · c t g β c t g α ± c t g β

На основе формул сложения выводятся тригонометрические формулы кратного угла.

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 sin 2 α , cos 2 α = 2 cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α с t g 2 α = с t g 2 α — 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α — sin 3 α , sin 3 α = 3 sin α — 4 sin 3 α cos 3 α = cos 3 α — 3 sin 2 α · cos α , cos 3 α = — 3 cos α + 4 cos 3 α t g 3 α = 3 t g α — t g 3 α 1 — 3 t g 2 α c t g 3 α = c t g 3 α — 3 c t g α 3 c t g 2 α — 1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.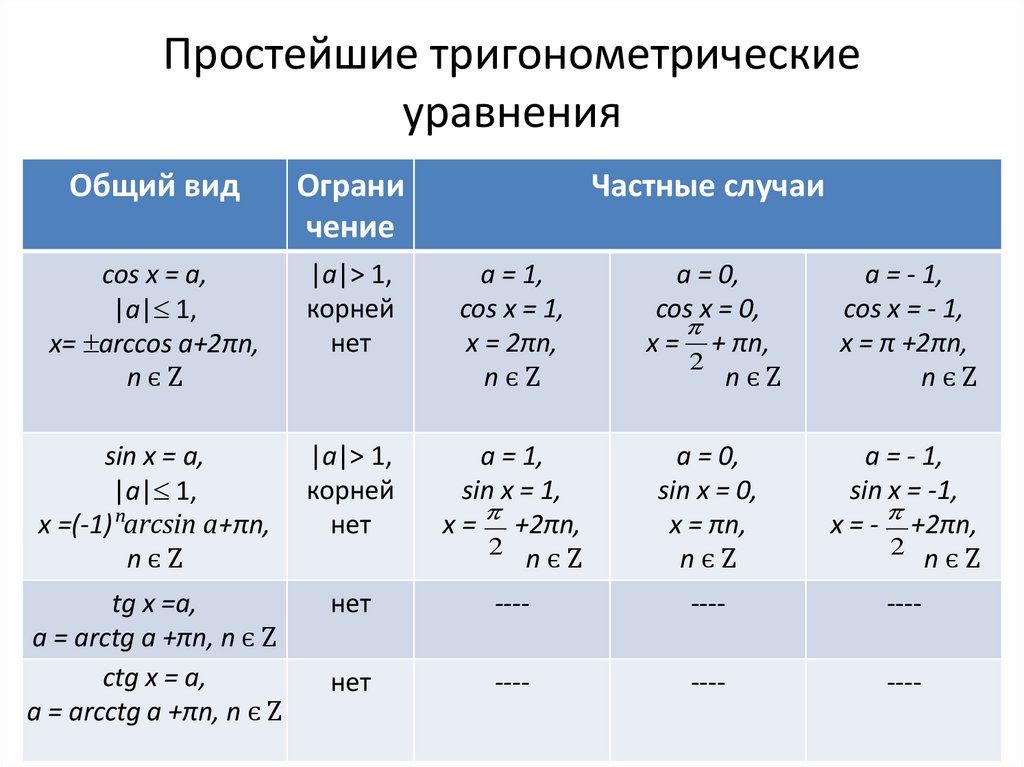

Формулы половинного угла

sin 2 α 2 = 1 — cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 — cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 — cos α

Формулы понижения степени

Формулы понижения степени

sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α — sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 — 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n

sin n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 (- 1) n 2 — k · C k n · cos ((n — 2 k) α) cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 C k n · cos ((n — 2 k) α)

для нечетных n

sin n α = 1 2 n — 1 ∑ k = 0 n — 1 2 (- 1) n — 1 2 — k · C k n · sin ((n — 2 k) α) cos n α = 1 2 n — 1 ∑ k = 0 n — 1 2 C k n · cos ((n — 2 k) α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sin α + sin β = 2 sin α + β 2 · cos α — β 2 sin α — sin β = 2 sin α — β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α — β 2 cos α — cos β = — 2 sin α + β 2 · sin α — β 2 , cos α — cos β = 2 sin α + β 2 · sin β — α 2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sin α · sin β = 1 2 · (cos (α — β) — cos (α + β)) cos α · cos β = 1 2 · (cos (α — β) + cos (α + β)) sin α · cos β = 1 2 · (sin (α — β) + sin (α + β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.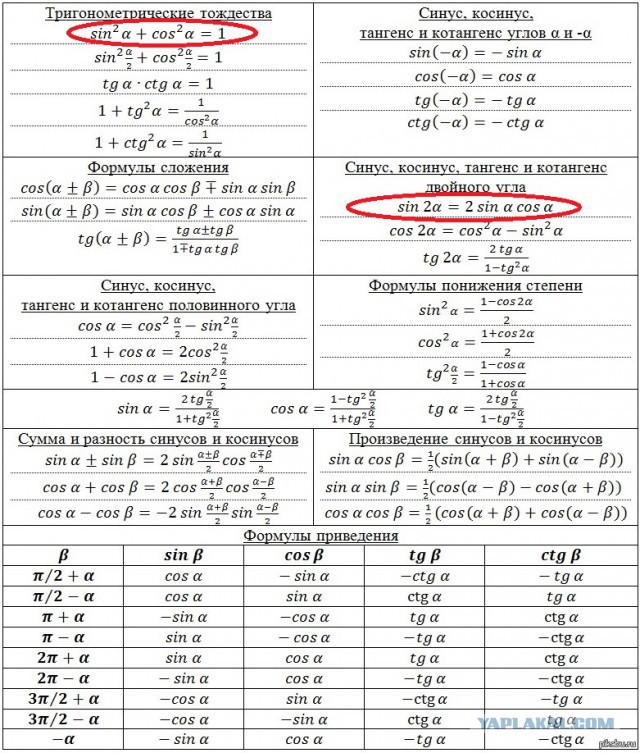

Универсальная тригонометрическая подстановка

sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 — t g 2 α 2 c t g α = 1 — t g 2 α 2 2 t g α 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формула тангенса

— Что такое формулы тангенса? Примеры

Формулы тангенса — это формулы для функции тангенса в тригонометрии. Функция тангенса (которую обычно называют «тангенсом») — это одна из 6 тригонометрических функций, представляющая собой отношение противоположной стороны к прилежащей стороне. Существует несколько формул, связанных с функцией тангенса, которые можно вывести из различных тригонометрических тождеств и формул. Давайте изучим формулы тангенса вместе с несколькими решенными примерами.

Что такое формулы касательной?

Формулы тангенса говорят о функции тангенса (тангенса). Рассмотрим прямоугольный треугольник, один из острых углов которого равен х. Тогда формула тангенса такова: tan x = (противоположная сторона) / (прилежащая сторона), где «противоположная сторона» — это сторона, противоположная углу x, а «прилежащая сторона» — это сторона, примыкающая к углу x. Помимо этой общей формулы, в тригонометрии есть много других формул, которые определяют функцию тангенса, которую вы можете увидеть на следующем изображении.

Формулы тангенса с использованием взаимного тождества

Мы знаем, что функция тангенса (tan) и функция котангенса (cot) обратны друг другу. т. е. если tan x = a/b, то ctg x = b/a. Таким образом, формула тангенса, использующая одно из обратных тождеств, имеет вид x = (смежный) / (гипотенуза) и tan x = (противоположный) / (смежный). Теперь разделим sin x на cos x.

(sin x) / (cos x) = [ (противоположное) / (гипотенуза) ] / [ (прилежащее) / (гипотенуза) ] = (противоположное) / (прилежащее) = tan x

Таким образом, формула тангенса в термины синуса и косинуса:

tan x = (sin x) / (cos x)

Формулы тангенса с использованием пифагорейского тождества

Одно из пифагорейских тождеств говорит о взаимосвязи между sec и tan. В нем говорится, сек ² х — тангенс ² х = 1, для любого х. Мы можем решить это для tan x. Давайте посмотрим, как.

с ² x -tan ² x = 1

Вычитание SEC ² x с обеих сторон,

-TAN ² x = 1 -сек ² x

Multipling Оба на с. 1,

tan ² x = sec ² x — 1

Извлечение квадратного корня с обеих сторон,

tan x = ± √( sec ² x — 1 Функция касания)6 Тождества

Тождества кофункций определяют отношения между кофункциями, которые являются sin, cos; сек, ксс; и загар, кроватка. Используя одно из тождеств кофункций,

• загар x = детская кроватка (90 ^o  — x) (ИЛИ)
• загар x = детская кроватка (π/2 — x)

Формулы тангенса с использованием формул суммы/разности

У нас есть формулы суммы/разности для каждой тригонометрической функции, которая имеет дело с суммой углов (A + B) и разностью углов (A – B). Формулы суммы/разности функции тангенса:

• тангенс (A + B) = (tan A + тангенс B) / (1 — тангенс A тангенс B)
• тангенс (A — B) = (тангенс A – тангенс B) / (1 + тангенс A тангенс B)

Формула тангенса двойного угла

У нас есть формулы двойного угла в тригонометрии, которые имеют дело с двукратным углом. Формула двойного угла для тангенса

тангенс 2x = (2 тангенс x) / (1 — тангенс ² x)

Формула тангенса тройного угла

У нас есть формулы тройного угла для всех тригонометрических функций. Среди них формула тройного угла функции тангенса:

тангенс 3x = (3 тангенс x — тангенс ³ x) / (1 — 3 тангенс ² x)

Формула касательной половины угла

В тригонометрии есть формулы половинного угла, которые работают с половиной углов (x/2). Формулы половинного угла функции тангенса:

• tan (x/2) =± √[ (1 — cos x) / (1 + cos x) ]
• тангенс (x/2) = (1 — cos x) / (sin x)

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры использования формул касательной

Пример 1: Если sec x = 5/3 и x находится в первом квадранте, найдите значение tan x.

Решение:

Используя одну из формул тангенса,

tan x = ± √(sec ² x — 1)

Поскольку x находится в первом квадранте, cos x положителен. Таким образом,

tan x = ± √(sec ² x — 1)

Подставьте здесь sec x = 5/3,

tan x = √((5/3) ²  — 1) 

= √((25/9) — 1)

=√ (16/9)

= 4/3

Ответ: тангенс x = 4/3.

Пример 2: Если cot (90 — A) = 3/2, то найдите значение tan A.

Решение:

Используя одну из формул тангенса,

tan A = cot (90 — А)

Дано, что раскладушка (90 — А) = 3/2. Следовательно,

тангенс A = 3/2

Ответ: тангенс A = 3/2.

Пример 3: Если тангенс A = 1/2 и тангенс B = 1/3, найдите тангенс (A + B).

Решение:

Используя формулу тангенса сложения,

тангенс (А + В) = (тангенс А + тангенс В) / (1 — тангенс А тангенс В)

= (1/2 + 1/ 3) / ( 1 — (1/2) · (1/3) )

= (5/6) / (1 — (1/6))

= (5/6) / (5/6)

= 1

Ответ: тангенс (A + B) = 1.

Часто задаваемые вопросы о формулах касательной

Что такое формулы касательной?

Формулы тангенса связаны с функцией тангенса. Важными формулами тангенса являются следующие:

• tan x = (противоположная сторона) / (прилегающая сторона)
• загар х = 1 / (кроватка х)
• тангенс x = (sin x) / (cos x)
• тангенс х = ± √( сек ² х — 1)

Как вывести формулу тангенса суммы?

Формула тангенса суммы/сложения: тангенс (A + B) = (tan A + тангенс B) / (1 — тангенс A тангенс B). Давайте выведем это, начиная с левой части.

tan (A + B) = sin (A + B) / cos (A + B)

= [sin A cos B + cos A sin B ] / [cos A cos B — sin A sin B]

Разделив каждый член как в числителе, так и в знаменателе на cos A cos B,

tan (A + B) = [ (sin A / cos A) + (sin B / cos B) ] / [ 1 — (sin A / cos A) (sin B / cos B) ]

= (tan A + tan B) / (1 — tan A tan B)

Каковы применения формул тангенса?

Как мы узнали на этой странице, у нас есть несколько формул тангенса, и мы можем выбрать одну из них, чтобы доказать тригонометрическое тождество (или) найти значение функции тангенса с доступной информацией. Мы также используем формулы касательной в исчислении.

Как вывести формулу тангенса двойного угла?

Используя формулу суммы функции тангенса, мы имеем тангенс (A + B) = (tan A + тангенс B) / (1 — тангенс A тангенс B). Подставляя здесь A = B с обеих сторон, мы получаем

tan 2x = (tan x + tan x) / (1 — tan x · tan x)  = (2 tan x) / (1 — tan ² x) .

Формула тангенса — функция тангенса, вывод, тригонометрическое соотношение и вопросы

Формула тангенса угла — это одна из формул, которые используются для вычисления угла прямоугольного треугольника. Функция тангенса наряду с синусом и косинусом является одной из трех наиболее распространенных тригонометрических функций. В любом треугольнике тангенс треугольника может быть представлен следующим образом:

Tan θ = \[\frac {\text{Противоположная сторона}} {\text{Смежная сторона}} \]

Где O — противоположная сторона, а A — смежная сторона.

Таким образом, студенты могут узнать о формуле тангенса — функции тангенса, выводе, тригонометрическом соотношении и вопросах, решаемых с помощью Веданту.

Выучить формулу тангенса

Синус, косинус и тангенс — три основные функции тригонометрии, с помощью которых формируются тригонометрические тождества, тригонометрические функции и формулы. Тангенс определяется как отношение длины противоположной стороны или перпендикуляра прямого угла к углу и длине прилежащей стороны. Функция касательной в тригонометрии используется для вычисления наклона линии между началом координат и точкой, определяющей пересечение гипотенузы и высоты прямоугольного треугольника. В этой статье мы обсудим формулу тангенса, формулу тангенса.

 

Что такое тригонометрия?

Это изучение взаимосвязей между углами, длинами и высотами заданных треугольников. Это также относится к различным частям кругов, а также к другим геометрическим фигурам. Тригонометрия имеет много тригонометрических соотношений, которые очень важны в математике. У него много тождеств, которые очень полезны для изучения и вывода многих уравнений и формул в науке. Есть много областей, где эти тождества тригонометрии и формулы тригонометрии полезны.

 

Что такое касательная функция?

Тангенс – это отношение противолежащей стороны к прилежащей в прямоугольном треугольнике. В тригонометрии существует шесть возможных соотношений. Соотношение — это сравнение двух чисел, то есть сторон треугольника. Греческая буква θ будет использоваться для обозначения исходного угла в прямоугольном треугольнике. Эти шесть соотношений по-разному полезны для сравнения двух сторон прямоугольного треугольника.

 

Формула загара обычно используется для вычисления угла прямоугольного треугольника. В прямоугольном или прямоугольном треугольнике тангенс угла представляет собой простое отношение длины противоположной стороны и длины прилежащей стороны. Тангенс обычно обозначается как «тан», но произносится как тангенс. Эта функция полезна, чтобы узнать длину стороны треугольника. Это возможно, когда кто-то знает хотя бы одну сторону треугольника и один из острых углов.

 

Вывод формулы Тана

Как мы знаем, синус, косинус и тангенс являются тремя основными функциями тригонометрии. Кратко изложим все три основные функции с помощью прямоугольного треугольника.

 

(Изображение будет загружено в ближайшее время)

 

Что такое функция синуса?

Функция синуса утверждает, что для данного прямоугольного треугольника Sin угла θ определяется как отношение длины противоположной стороны треугольника к его гипотенузе.

 

Sin θ = \[ \frac{\text{Противоположная сторона}}{Гипотенуза} \]

 

Что такое функция косинуса?

Функция косинуса утверждает, что для данного прямоугольного треугольника косинус угла θ определяется как отношение длины прилежащей стороны треугольника к его гипотенузе.

 

Cos θ = \[ \frac {\text{Смежная сторона}} {Гипотенуза} \]

 

Что такое функция касательной?

Функция касательной утверждает, что для данного прямоугольного треугольника косинус угла ϴ определяется как отношение длины противоположной стороны треугольника к углу и прилежащей стороне.

 

Tan θ =\[ \frac{\text{Противоположная сторона}} {Гипотенуза}\]

 

Тригонометрические уравнения на основе функции тангенса (формулы тангенса)

Различные формулы тангенса могут быть сформулированы с помощью касательная функция в тригонометрии. Основная формула тангенса, которая в основном используется для решения вопросов, имеет вид или Tanθ = \[ \frac{1}{Cotθ}\]

9{\ circ} \]

Sin θ

0

2}}\]

\[ \frac{\sqrt{3}}{2}\]

  1

0

-1

0

Cos θ

1

\[ \frac{\sqrt{3}}{2}\]

\[ \frac{1}{\sqrt{2}}\]

\[ \frac{1}{2}\]

  0

-1 50 0

3

3

1

Tan θ

0

\[ \frac{1}{\sqrt{3}}\]

1

\[\sqrt {3}\]

\[\infty\]

0

\[\infty\]

0

COT θ

\ [\ infty \]

\ [\ SQRT {3} \]

770

\ [\ SQRT {3} \]

9370

\ } {\ sqrt {3}} \]

0

\ [\ infty \]

0

6 \ [\ Infty \]

6 \ [\ Infty \]

\ [\ infty \]

	\]		\]	.	\[\infty\]	2	\[\sqrt{2}\]	\[\frac{2}{\sqrt{3}} \]	1	\[\infty\]	3	1	\ [\ infty \]
SEC	1	\ [\ FRAC {2} {\ ST QU Qu sqrt{2}\]	2	\[\infty\]	-1	\[\infty\]	1

 

Вопросы, подлежащие решению

Вопрос 1

Вычислите касательный угол прямоугольного треугольника, сторона которого равна 8 см, а противоположные стороны соответственно равны 6 см и противолежащие стороны равны 6 см?

Решение

Дано, Смежная сторона, т. е. основание = 8 см

Противоположная сторона, т.е. перпендикуляр = 6 см

Кроме того, формула касательной: Tan θ=перпендикуляр/основание

Tan θ=6/8 = 0,75

6 Следовательно, тангенс θ=0,75·

Таким образом, значение тангенса будет равно 0,75.

 

Вопрос 2

Вычислите касательный угол прямоугольного треугольника, у которого прилежащая и противоположная стороны равны 10 см и 4 см соответственно?

Решение

Дано, Смежная сторона, т.е. основание = 10 см

Противоположная сторона, т.е. перпендикуляр = 4 см

Кроме того, формула тангенса: Следовательно, тангенс θ= 2,5

Таким образом, значение тангенса будет равно 2,5.

Формулы тангенса — GeeksforGeeks

 Тригонометрия — важный раздел математики, изучающий отношения между углами и длинами сторон прямоугольного треугольника. Шесть тригонометрических соотношений или функций — это синус, косинус, тангенс, косеканс и секанс, а тригонометрическое отношение — это отношение между сторонами прямоугольного треугольника. Функции синуса, косинуса и тангенса являются тремя важными тригонометрическими функциями, поскольку остальные три, то есть функции косеканса, секанса и котангенса, являются обратными функциями синуса, косинуса и тангенса соответственно.

• sin θ = противоположная сторона/гипотенуза
• cos θ = соседняя сторона/гипотенуза
• tan θ = противоположная сторона/соседняя сторона
• cosec θ = гипотеновая сторона/противоположная сторона
• Sequetus θ = гипотенера/присматривать. θ = Прилежащая сторона/Противоположная сторона

Формула тангенса

Тангенс угла в прямоугольном треугольнике представляет собой отношение длины противоположной стороны к длине прилежащей стороны к данному углу. Запишем функцию касательной как «tan». Рассмотрим прямоугольный треугольник XYZ, один из острых углов которого равен «θ». Противоположная сторона — это сторона, противоположная углу «θ», а примыкающая сторона — это сторона, примыкающая к углу «θ».

Теперь тангенсная формула для данного угла «θ» IS,

TAN θ = противоположная сторона/соседняя сторона

Некоторые базовые тангентные формулы 9000 2 Tangnate Funct

Функция тангенса положительна в первом и третьем квадрантах и ​​отрицательна во втором и четвертом квадрантах.

тангенс (2π + θ) = тангенс θ (1 ^ст квадрант)

тангенс (π – θ) = – тангенс θ (2 ^-й квадрант)

тангенс (π + θ) = тангенс θ (3 ^-й квадрант)

тангенс) = – θ tan θ (4 ^th квадрант)

Функция тангенса как отрицательная функция

Функция тангенса является отрицательной функцией, поскольку тангенс отрицательного угла является отрицательным значением тангенса положительного угла.

тангенс (-θ) = – тангенс θ

Функция тангенса в терминах функций синуса и косинуса

Функция тангенса в терминах функций синуса и косинуса может быть записана как

tan θ = sin θ/cos θ

Противоположная сторона/прилежащая сторона

Теперь разделите числитель и знаменатель на гипотенузу

tan θ = (противоположная сторона/гипотенуза)/(прилежащая сторона/гипотенуза)

Мы знаем, что sin θ = противолежащая сторона/гипотенуза

cos θ = смежная сторона/гипотенуза

Следовательно, tan θ = sin θ/cos θ

Функция тангенса в терминах функции синуса

Функция тангенса в терминах функции синуса может быть записана как

sin tan /(√1 — SIN ² θ)

Мы знаем, что

TAN θ = sin θ/cos θ

от пифагорских идентичностей, мы имеем

SIN ² θ + COS ² θ = 1

cos ² θ = 1 – sin ² θ

cos θ = √(1 – sin ² θ)

Следовательно, tan θ =  sin θ/(√1 – sin ² θ)

Функция тангенса через косинус может быть записана как /cos θ

Из пифагорейских тождеств имеем

sin ² θ + cos ² θ = 1

sin ² θ = 1 — cos ² θ

sin θ = √ (1 — cos ² θ)

. – cos ² θ)/cos θ

Функция тангенса через функцию котангенса

Функция тангенса через функцию котангенса может быть записана как

1 tan θ

или

tan θ = кроватка (90° – θ) (или) кроватка (π/2 – θ)

Функция тангенса через функцию косеканса

Функция тангенса через функцию косеканса может быть записана как

Из пифагорских идентичностей, мы имеем

COSEC ² θ — COT ² θ = 1

COT ² θ = COSEC ² θ — 1

COT θ = √ (COSEC ^{2 2 2 2 2} θ — 1

COT θ = √ (COSEC ^{2 2} . θ – 1)

Мы это знаем,

tan θ = 1/cot θ

Следовательно, tan θ = 1/√(cosec ² θ – 1)

Функция тангенса через секанс

Функция тангенса через тангенс Секунтурная функция может быть записана как,

tan θ = √sec ² θ — 1

Из пифагорских идентичностей,

Sec ² θ — TAN ² θ = 1

2 θ — TAN ² θ = 1

2

tan θ = сек ² θ – 1

Следовательно, tan θ = √(сек ² θ – 1)

Функция тангенса относительно двойного угла

Функция тангенса двойного угла:

θ)

Касательная функция тройного угла

Касательная функция тройного угла:

² θ)

Касательная функция через полуугол

Касательная функция для половины угла: ) = (1 – cos θ) / ( sin θ)

Функция тангенса в терминах сложения и вычитания двух углов

Формулы суммы и разности для функции тангенса:

tan ( A + B) = (tan A + tan B)/(1 – tan A tan B)

tan (A – B) = (tan A – tan B)/(1 + tan A tan B)

Trigonometric Ratio Table 73773773777. 1003777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777.10373777...02 0/( -1) = 0

9 0/(1) = 0 0003 0/(1) = 0 0003 0/( -1) = 0

0/( -1) = 0

9.

0/(1) = 0 0003999136 211101115

0. (1). тангенс θ, если sin θ = 2/5 и θ — угол первого квадранта.

Решение:

Дано, sin θ = 2/5

Из пифагорских идентичностей, которые мы имеем,

SIN ² θ + COS ² θ = 1

COS ² θ = 1 — SIN ^{3334 θ = 1 – (2/5) 2}

cos ² θ = 1 – (4/5) = 21/25

cos θ = ±√21/5

Поскольку θ – угол первой четверти , cos θ положительно.

cos θ = √21/5

Мы знаем, что

tan θ = sin θ/cos θ

= (2/3)/(√21/5)

Следовательно, тангенс θ = 10/3√21

Задача 2: Найдите значение тангенса х, если сек х = 13/12, а х — угол четвертого квадранта.

Решение:

, SEC X = 13/12

Из пифагорейских идентичностей, мы имеем

SEC ² x — TAN ² X = 1

TAN ² 3 2 X = 1

TAN ² . = сек ² х – 1= (13/12) ² – 1

тангенс ² х = (169/144) – 1= 25/144

tan x = ± 5/12

Поскольку x — это угол четвертого квадранта, tan x отрицателен.

tan x = – 5/12

Следовательно, tan x = – 5/12

Задача 3. Если tan X = 2/3 и tan Y = 1/2, то каково значение загар (X + Y)?

Решение:

Дано,

tan X = 2/3 и tan Y = 1/2

Мы знаем, что

tan (X + Y) = (tan X + tan Y)/ (1 – тангенс X тангенс Y)

тангенс (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]

= (7/6)/(2/3) = 7/4

Следовательно, тангенс (X + Y) = 7/4

стороны прямоугольного треугольника равны 4 см и 7 см соответственно.

Решение:

,

соседняя сторона = 4 см

противоположная сторона = 7 см

Мы знаем, что,

tan θ = противоположная сторона/соседняя сторона

tan θ = 70002 = 1,75

Следовательно, tan θ = 1,75

Задача 5: Человек смотрит на башню с часами под углом 60° к вершине башни, высота которой 100 м. Каково расстояние между человеком и подножием башни?

Решение:

Дано,

Высота башни = 100 м и θ = 60°

Пусть расстояние между человеком и подножием башни = d

3 Имеем

tan θ = Противоположная сторона/Смежная сторона

tan 60° = 100/d

√3 = 100/d [Так как tan  60° = √3]

d = 100/√3

Следовательно, расстояние между человеком и подножием башни = 100/√3

Задача 6. Найдите значение тангенса θ, если sin θ = 7/25 и sec θ = 25/24.

Решение:

,

SIN θ = 7/25

Sec θ = 25/24

Мы знаем, что

с θ = 1/cos θ

25/24 = 10003 с. /cos θ cos θ = 24/25

Имеем,

тангенс θ = sin θ/cos θ

= (7/25)/(24/25)

= 7/24

Следовательно, тангенс θ = 02 29

Задача 7. Найдите значение тангенса θ, если cosec θ = 5/3, а θ — угол первого квадранта.

Решение:

, COSEC θ = 5/3

Из пифагорских идентичностей, мы имеем

COSEC ² θ — COT ² θ = 1

COT ^{2 2 2 θ = 1}

COT ^{2 2} 2 θ = 1

COT ^{2 2} θ 2 2 θ = 1

COT ^{2 2} 2 θ = 1

COT ^{2 2} 2 θ. = косек ² θ – 1

кроватка θ = (5/3) ² – 1 = (25/9) – 1 = 16/9

кроватка θ = ±√16/9 = ± 4/3

Поскольку θ — угол первого квадранта, функции как котангенса, так и тангенса положительны.

No related posts.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

Angle (In degrees)	Angle (In Radians)	sin θ	cos θ	tan θ = sin θ/cos θ
0°	0	0	0	0/1 = 0
30°	π/6	1/2	√3/2	(1/2)/(√ 3/2) = 1/√3
45°	π/4	1/√2	1/√2	(1/√2) /(1/√2) = 1
60°	π/3	√3/2	1/2	(√3/2)/(1/2) = √3
90°	π/2	1	0	1/0 = неопределенная
120 °	2π/3	√3/2			903, )/(-1/2) = -√3
150°	5π/6	1/2	-(√3/2)	(1/2)/(-√3/2) = 6 9 039 03 900	180 °	π	0	-1	0/(1) = 0