Линейные уравнения | Статья в журнале «Школьная педагогика»
Библиографическое описание:Парканова, С. И. Линейные уравнения / С. И. Парканова, С. Н. Ревтова, Т. М. Котлярова. — Текст : непосредственный // Школьная педагогика. — 2016. — № 2 (5). — С. 19-22. — URL: https://moluch.ru/th/2/archive/27/615/ (дата обращения: 13.12.2022).
Математика — это язык, на котором говорят все точные науки.
Н. И. Лобачевский
Введение.
Математика — предмет, без которого не могут быть изучены, ни одно явление, ни один процесс в окружающем мире. Применение математических исчислений, в том числе линейных уравнений, являются составной частью в новых научных исследованиях и вносят большой вклад в развитие современной науки и технического прогресса в целом.
Актуальность: Уравнения в математике занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему.
Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
Цель:
Изучить свойства линейных уравнений;
Отрабатывать навыки решения линейных уравнений.
Исторический экскурс.
Кто придумал уравнения?
Ответить на этот вопрос невозможно! Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла. Еще 3–4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения, вид которых не был похож на современные. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант
“Он уйму всяких разрешил проблем.
И засухи предсказывал и ливни.
Поистине его познанья дивны”
Большой вклад внес среднеазиатский ученый Мухаммед аль Хорезми (IX век). –среднеазиатский математик, астроном, историк, географ — один из крупнейших ученых средневековья.
Его труды по арифметике, изложенные в «Книге об индийском счете», привели к грандиозным последствиям в науке вообще и древней математики в частности. Внес вклад в преобразование линейных уравнений.
Жаутыков Орымбек Ахметбекович (1911–1989г)
Ученый — математик. Внес значительный вклад в развитие математических наук. Академик Национальной Академии наук Республики Казахстан. Доктор физико-математических наук, профессор. Автор первого национального учебника по высшей математике. Основные научные труды посвящены математическим уравнениям, теоретической и прикладной механике.
Линейные уравнения содной переменной
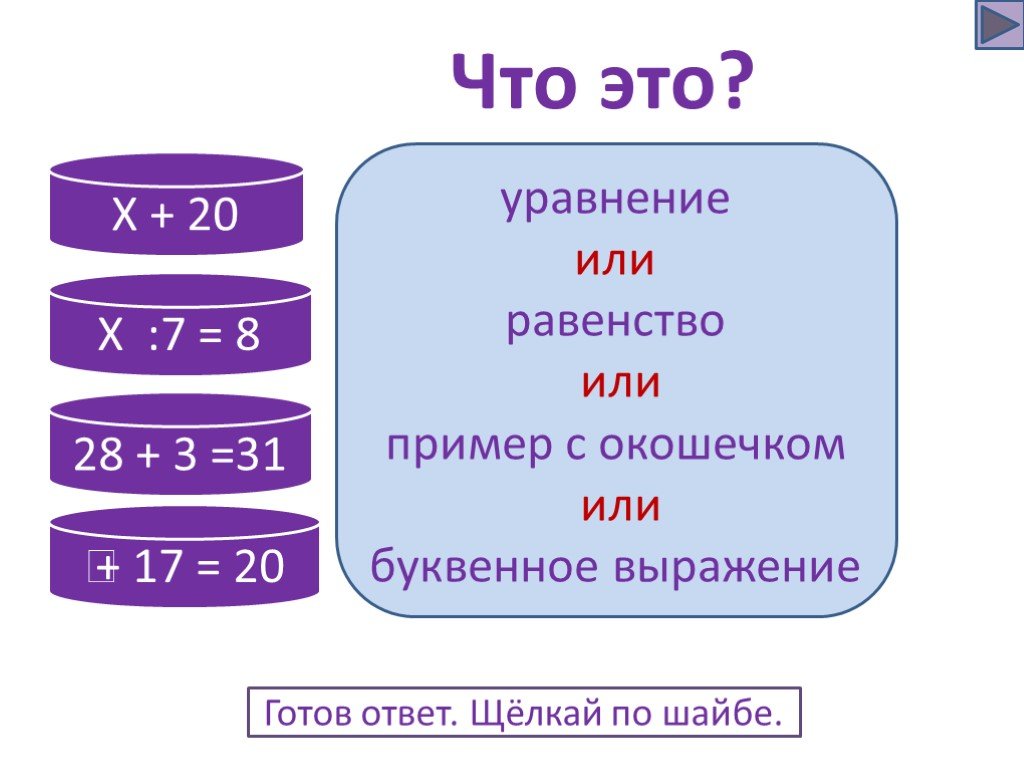
Равенство, содержащее неизвестное число, обозначенной буквой, называется — 
Уравнение вида: ax+b=0
Называется линейным уравнением с одной переменной
(где х-переменная, а и b некоторые числа).
Х-переменная входит в уравнение обязательно в первой степени!
Корнем уравнения называется, то значение неизвестного, при котором это уравнение обращается в верное числовое равенство.
Уравнение может иметь один корень: 3x+5=0
Несколько корней: y(y-2)(5+2y) = 0 Бесконечно много корней: 7(x+1) = 7x+7 Уравнение может не иметь корней: x+3=x
Решить линейное уравнение— это значит найти все его корни или установить, что их нет. При решении уравнений могут быть использованы свойства уравнения:
- Корни уравнения не изменяются, если любой член уравнения перенести из одной части уравнения в другую, изменив при этом знак на противоположный.
- Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Решение многих уравнений сводится к решению линейных уравнений.
При решении уравнений используют свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится равносильное уравнение.
Если обе части уравнения умножить или разделить на одно и то же число
(не равное нулю), то получится равносильное уравнение.
Алгоритм решения линейного уравнения
- Раскрыть скобки в обеих частях уравнения;
- Перенести слагаемые, содержащие переменную в одну часть, а не содержащую в другую;
- Привести подобные члены в каждой части;
- Разделить обе части на коэффициент при переменной.
Рассмотрим решение уравнения:
(13х-15)-(9+6х)=-3х
Раскроем скобки:
13х-15–9-6х=-3х.
Перенесём с противоположными знаками неизвестные члены в левую, а известные — в правую часть уравнения, тогда получим уравнение:
13х-6х+3х=15+9.
Приведём подобные слагаемые.
10х=24.
Разделим обе части уравнения на коэффициент при неизвестном.
х=2,4
Ответ: 2,4
Так же вашему вниманию представлены следующие решения уравнений:
8у -3(2y-3) = 7y — 2(5y + 8)
8у — 6у + 9 = 7у — 10у -16
8y — 6y — 7y + 10y = -16–95y= -25
y= -25: 5
у= — 5
(0,5х + 1,2)-(3,6–4,5х)=(4,8–0,3х)+(10,5х + 0,6)
0,5х + 1,2–3,6 + 4,5х = 4,8–0,3х + 10,5х + 0,6
0,5х + 4,5х + 0,3х — 10,5х = 4,8 + 0,6–1,2 + 3,6
—5,2х = 7,8
х= -1,5 Ответ: -1,5
5(3х+1,2) + х = 6,8,
15х + 6 + х = 6,8,
15х + х = 6,8–6,
16х = 0,8,
х = 0,8: 16,
х = 0,05, Ответ: 0,05
5,6–7у = — 4(2у — 0,9) + 2, 4,
5,6–7у = — 8у + 3, 6 + 2,4,
8у — 7у = 3,6 + 2.4–5,6,
у = 0,4, Ответ: 0,4
—3(у + 2,5) = 6,9–4,2у,
— 3у — 7,5 = 6,9–4,2у,
4,2у — 3у = 6,9 + 7,5,
1,2у = 14,4,
у = 14,4: 1,2,
у = 12, Ответ: 12
3 (х + 6) + 4 = 8 — (5х + 2)
3х + 18 + 4 = 8–5х — 2
3х + 5х = — 18–4 + 8–2
8х = — 16
х = — 16: 8
х = — 2
Ответ: -2
Задачи на составление линейных уравнений с
Решение задач с помощью уравнений состоит из нескольких этапов:
- неизвестную величину, значение которой мы хотим определить, обозначаем буквой, например x;
- используя эту букву и имеющиеся в задаче данные, составляем математическую модель, где два разных выражения равны друг другу;
- записывая эти выражения через знак равно, мы получаем уравнение,решение которого поможет найти ответ к задаче;
- если необходимо, выполняем дополнительные действия для нахождения ответа к задаче.
Задача: В холодильнике в общей сложности 19 куриных и перепелиных яиц. После приготовления яичницы из 2 куриных и 5 перепелиных яиц, перепелиных стало в два раза больше, чем куриных. Сколько куриных яиц было в холодильнике изначально?
Составляем модель уравнения:
Нам надо решить, какую величину мы обозначим переменной x.
Рассмотрим вариант, где x — кур.
яйца изначально;
Составляем математическую модель и уравнение.
x — кур. яйца изначально;
x — 2 — кур. яйца после;
2(x — 2) — пер. яйца после;
2(x — 2) + 5 — пер. яйца изначально;
Составляем модель уравнения:
Рассмотрим выражения, которые мы можем уравнять, сумму яиц до приготовления яичницы.
x + 2(x — 2) + 5 — сумма яиц изначально
19 — сумма яиц изначально
x + 2(x — 2) + 5 = 19 уравнение, решение которого находит ответ к задаче.
Решение:
3х = 18
х = 18: 3
x = 6
Ответ: изначально в холодильнике было 6 куриных яиц.
Задача: По шоссе едут две автомашины с одной и той же скоростью. Если первая машина увеличит скорость на 10км в час, а вторая уменьшит на 10км в час, то первая за 2 часа пройдет столько же, сколько вторая за 3 часа.
С какой скоростью едут автомашины?
Составление таблицы
Пусть х — первоначальная скорость машин, тогда (х + 10) — скорость первой машины, а (х — 10) — скорость второй машины.
Расстояние для первой машины 2(х + 10)
Расстояние для второй машины 3(х — 10)
Величины | Первичная скорость | Скорость по условию | Время | Расстояние |
1 машина | х | + 10 | 2 | 2 (х + 10) |
2 машина | х | — 10 | 2 | 3 (х — 10) |
Составление уравнения
Так как по условию задачи первая машина прошла за 2 часа столько же, сколько вторая за 3 часа, составим уравнение:
2(х + 10) = 3(х — 10)
Решение:
2(х + 10) = 3(х — 10)
2х + 20 = 3х — 30
2х — 3х = — 20–30
—х = — 50 Х = 50
Скорость первой машины 50+10=60км ч
Скорость второй машины 50–10=40км ч
Ответ: 1 машина — 60км ч
2 машина — 40км ч
Задача: Были куплены яблоки и груши на сумму 4200 тенге.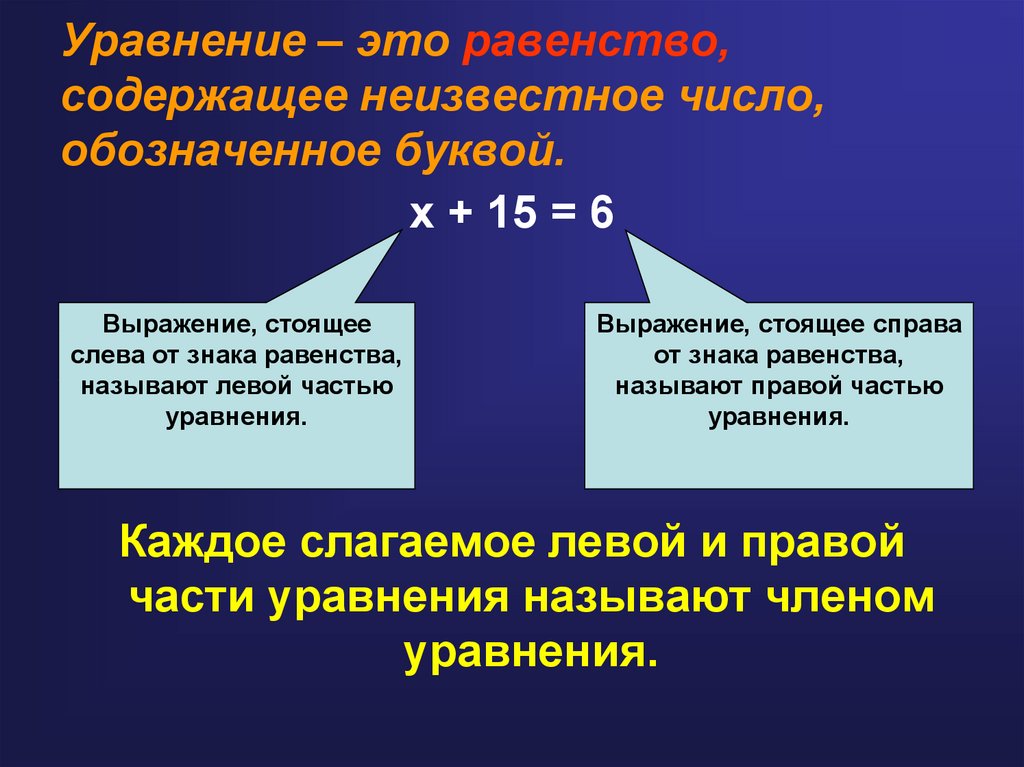
Составление таблицы
Мы знаем, что 1 кг груш стоит 1200тг. Пусть х — количество купленных яблок, тогда количество купленных груш (х + 1).
Получаем, что 300х — сумма, уплаченная за яблоки, тогда 1200(х + 1) — сумма уплаченная за груши.
Величины | Цена, тг | Кол-во, кг | Стоимость, тг |
Яблоки | 300 | х | 300х |
Груши | 1 200 | (х + 1) | 1200(х + 1) |
На 1 кг | Всего: 4200 |
Решение:
Теперь можно составить и решить уравнение:
300х + 1200(х + 1) = 4200
300х + 1200х + 1200 =4200
1500х = 3000
х = 3000: 1500
х = 2 Ответ: было куплено 2 килограмма яблок.
Выводы:
Итак, мы рассмотрели, что представляют собой линейные уравнения, их свойства и способы решения, заглянули в историю.
Научились решать линейные уравнения и задачи. Надеемся, что данный проект поможет учащимся в изучении темы «Линейные уравнения».
Литература:
- Т. А. Алдамуратова, Т. С. Байшоланов «Математика 6 класс» Алмата «Атамура» 2011.
- В. А. Гусев, А. Г. Мордкович..«Справочные материалы» Математика М. «Просвещение», 1988
- К. П. Сикорский. «Факультативный курс» М. «Просвещение», 1969.
Основные термины (генерируются автоматически): уравнение, часть уравнения, машина, Ответ, задача, корень уравнения, линейное уравнение, решение, решение уравнений, сумма яиц.
Решение уравнений на основе соотношения между частью и целым. — Студопедия
Поделись
Уравнения на сложение и вычитание с фигурами, линиями, числами рассматриваются в программе Л.
Г. Петерсон.
Составляя подобные равенства, учащиеся на основе практических предметных действий выводят и усваивают правила:
· целое равно сумме частей
· чтобы найти часть, надо из целого вычесть другую часть
Взаимосвязь между частью и целым является затем для учащихся тем удобным и надежным инструментом, который позволяет им легко решать уравнения с неизвестным слагаемым, уменьшаемым, вычитаемым.
Решение уравнений на основе зависимости между компонентами действий.
После того как учащиеся научатся решать простейшие уравнения вида: х + 10 = 30, х+ 17 =40 и т.п. им предлагаются более сложные уравнения, для нахождения неизвестного компонента, в которых необходимы определенные преобразования. Для решения таких уравнений необходимы знания порядка действий в выражении, а также умения выполнять простейшие преобразования выражений.
Первыми рассматриваются уравнения, в которых правая часть задается не числом, а числовым выражением, например: х+25=50·14 или х+25=12 ·.
При решении подобных уравнений учащиеся вычисляют значение выражения в правой части, после чего уравнение сводится к простейшему.
На протяжении длительного периода учащиеся упражняются в чтении, записи, решении и проверке таких уравнений, причем в левую и правую части их включаются простейшие выражения всех видов в различных сочетаниях. Наиболее сложными являются уравнения, в которых один из компонентов – выражение, содержащее неизвестное число х, например:
(х+8) – 13=15, 70 + (40 – х) =96 и т.п., так как при решении уравнений данной структуры приходится дважды применять правила нахождения неизвестных компонентов. Например, рассматривают на уроке уравнение (12-х)+10=18. Очень важно правильно прочитать его, выяснить последнее действие, назвать компоненты, выделить каждое слагаемое, затем дети говорят о том, что неизвестное входит в первое слагаемое. После нахождения неизвестного слагаемого, после преобразования дети получают простейшее уравнение, в котором неизвестное вычитаемое.
После нахождения вычитаемого х=4 необходимо сделать проверку решения уравнения.
Обучение решению уравнений этого вида требует длительных упражнений в анализе выражений и хорошего знания правил нахождения неизвестных компонентов.
Овладение навыками решения уравнений данного вида способствует преемственному обучению.
Решение уравнений на основе знаний конкретного смысла умножения.
При решении уравнений в начальной школе используется способ решения уравнения на основе знаний конкретного смысла умножения. В ходе решения уравнения вида 17+17=17·х можно преобразовывать левую часть. Проанализировав вид уравнения, можно найти рациональный способ его решения.
Необходимо заменить сумму одинаковых слагаемых действием умножения. Затем сравнивая левую и правую часть, делается вывод, что этот вид уравнения можно решить на основе конкретного смысла умножения
Этот способ формирует у учащегося умение «оценивать», «проанализировать» записанное уравнение, что создает благоприятные условия для решения уравнений в дальнейшем.
Под рациональным числом понимается точка на числовой прямой. Расширьте числовые линейные диаграммы и координатные оси, знакомые по предыдущим классам, для представления точек на линии и на плоскости с отрицательными числовыми координатами. | СС | 6 | 6.НС | 6.NS.C
Дополнительные темы
в Понимание рационального числа как точки на числовой прямой. Расширьте числовые линейные диаграммы и координатные оси, знакомые по предыдущим классам, для представления точек на линии и на плоскости с отрицательными числовыми координатами.Popular Tutorials
in Понимание рационального числа как точки на числовой прямой. Расширьте числовые линейные диаграммы и координатные оси, знакомые по предыдущим классам, для представления точек на линии и на плоскости с отрицательными числовыми координатами.Как назвать набор, изображенный на числовой прямой?
Если вы когда-нибудь смотрели на числовую линию с точками и задавались вопросом: «Как я могу суммировать эти точки?», то это руководство для вас!
Как изобразить множество на числовой прямой?
Числовые линии — отличный способ представить группу чисел, и в этом уроке вы увидите, как графически изобразить группу чисел на числовой прямой
Как наносить точки на координатную плоскость?
Знание того, как строить упорядоченные пары, является важной частью графических функций.
В этом уроке вы увидите, как взять упорядоченную пару и нанести ее на координатную плоскость. Взглянем!Что такое упорядоченная пара?
Упорядоченные пары являются фундаментальной частью построения графиков. Упорядоченные пары составляют функции на графике, и очень часто вам нужно построить упорядоченные пары, чтобы увидеть, как выглядит график функции. Этот урок познакомит вас с упорядоченными парами!
Что такое координатная плоскость?
Вы не можете построить график функции или построить упорядоченные пары без координатной плоскости! Узнайте о координатной плоскости, посмотрев этот урок.
Что такое квадранты на координатной плоскости?
Знаете ли вы, что координатную плоскость составляют четыре квадранта? Узнайте об этих квадрантах и о том, какие упорядоченные пары расположены в каждом из них, посмотрев этот урок!
Как построить график упорядоченных пар в каждом квадранте?
Нанесение точек на координатную плоскость — основа построения графиков уравнений! Ознакомьтесь с этим учебным пособием, чтобы попрактиковаться в построении точек и определении того, в каком квадранте находится каждая точка.
Что является противоположностью или аддитивной инверсией числа?
Вы когда-нибудь объединяли два числа и находили их сумму равной нулю? Когда это происходит, эти числа называются аддитивными инверсиями друг друга! В этом руководстве вы узнаете определение аддитивной инверсии и увидите примеры того, как найти аддитивную инверсию заданного значения.
Что такое положительные и отрицательные числа?
Положительные и отрицательные числа (и ноль!) являются строительными блоками математики. Этот урок познакомит вас с положительными и отрицательными числами и покажет их расположение на числовой прямой. Кроме того, узнайте особую вещь о числе ноль!
Что такое числовая линия?
Числовая линия — это способ визуального представления чисел. В этом учебном пособии вы познакомитесь с числовой прямой и покажете, как отображать числа на числовой прямой, чтобы сравнивать их.
Проверьте это!
В этом уроке вы увидите, как взять упорядоченную пару и нанести ее на координатную плоскость. Взглянем!
Проверьте это!Математическая задача: Неизвестное число — вопрос №2924, алгебра, выражение переменной из формулы
Определить неизвестное число, удвоение которого в четвертом квадрате равно пятому его квадрату.
Правильный ответ:
Вы нашли ошибку или неточность? Смело звоните по номеру
, пишите нам. Благодарю вас!
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- exponentiation
Grade of the word problem:
- практика для 12-летних
- практика для 13-летних
- практика для 14-летних
- Неизвестное число 6
Найдите неизвестное число, которое в 1,5 раза больше своего четвертого. - Неизвестное число
Найдите неизвестное число, равное четверти пятой части числа, которое на 152 больше неизвестного числа. - Определить 2944
Определить неизвестный номер. Его удвоение равно его тройке минус 1,5. - Определить 18233
Определить неизвестное число, к которому относится: чье четыре раза число 3, умноженное на число 3, равно его двойному - Два номера
У нас есть два номера. Их сумма равна 140. Одна пятая часть первого числа равна половине второго числа. Определите эти неизвестные числа. - Определить 3814
Определить третий, четвертый и пятый элемент GP, если a1 = -0,5 при q = -4. - Две пятых 3035
Определить неизвестное число, равное двум пятым квадратного корня из 49. - Одна седьмая 3214
Определить одну треть числа, одна пятая которого составляет одну седьмую. - Выражение со степенями
Какое выражение эквивалентно 2,1 в пятой степени, деленной на 0,9 в четвертой степени, все в третьей степени? - Квадратичная функция
Задана квадратичная функция y = -4x²+5x+c с неизвестным коэффициентом c.
