Вычислить с помощью двойного интеграла площадь фигуры: Вычисление площадей и объемов с помощью двойных интегралов.

Вычисление площадей плоских фигур с помощью двойного интеграла

Оглавление:

Рассмотрим примеры вычисления площадей плоских фигур с помощью двойного интеграла.

Пример №31.1.

Найдите площадь плоской фигуры, ограниченной линиями

Решение:

Поскольку геометрически двойной интеграл от единичной функции по области равен площади плоской фигуры, представляющей собой область интегрирования , будем использовать формулу: .

В нашем случае областью интегрирования является фигура, ограниченная линиями Вычислим .

Для этого построим область интегрирования в прямоугольной декартовой системе координат на плоскости.

Линии, задаваемые уравнениями , — прямые, параллельные оси и проходящие соответственно через точки (1;0), (2;0). Линия, задаваемая уравнением — гипербола, «ветви» которой расположены в I и III координатных четвертях. Гиперболу можно получить из гиперболы с помощью растяжения последней вдоль оси ординат в два раза.

Описание линий, задающих область интегрирования , позволяет при ее построении ограничиться I координатной четвертью.

Изображенная на рис. 31.1 область интегрирования является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:

В нашем случае . Следовательно, .

Вычислим полученный повторный интеграл:

В итоге, . Следовательно, .

Ответ: .

Пример №31.2.

Найдите площадь плоской фигуры, ограниченной линиями и .

Решение:

Плоскую фигуру, ограниченную линиями и , обозначим . В силу геометрического смысла двойного интеграла от единичной функции, для нахождения площади плоской фигуры будем использовать формулу: .

Вычислим . Для этого построим фигуру (рис. 31.2), представляющую собой область интегрирования, в прямоугольной декартовой системе координат на плоскости.

Линия, задаваемая уравнением — парабола, «ветви» которой направлены вниз.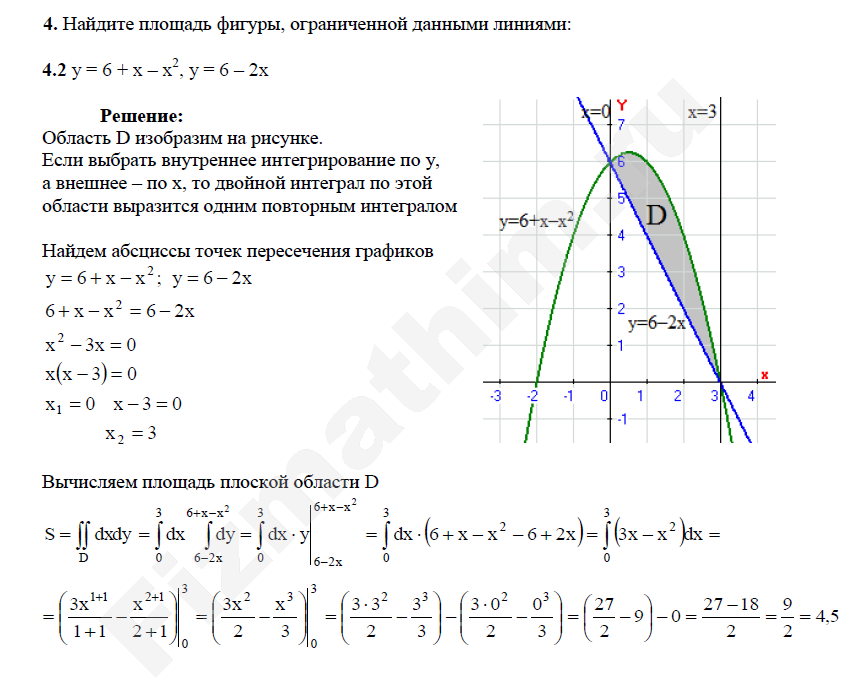 Построим ее с помощью параллельного переноса вдоль оси ординат графика функции на 3 единицы вверх. Линия, задаваемая уравнением — прямая. Составим уравнение прямой с угловым коэффициентом: .

Построим эту прямую по двум точкам:

Изображенная на рис. 31.2. область интегрирования является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:

В нашем случае . Найдем и как абсциссы точек пересечения линий и . Для этого решим уравнение . Корни приведенного квадратного уравнения найдем по теореме, обратной теореме Виета: или . Следовательно, . Таким образом, . Вычислим полученный повторный интеграл:

В итоге, . Следовательно, .

Ответ: .

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Как найти площадь плоской фигуры, которая ограничена кривыми?

Разберем готовые ответы к примерам на нахождение площади плоской фигуры, которая ограничена кривыми через двойные интегралы.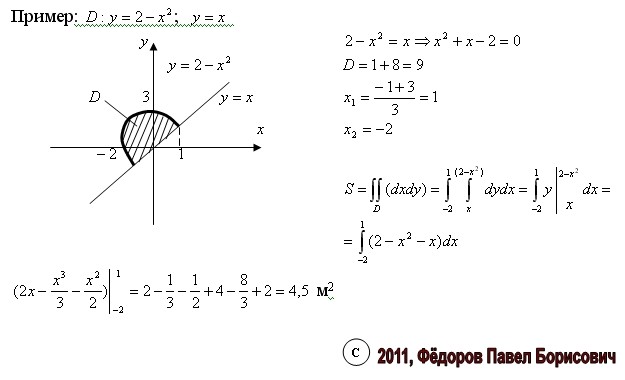 2=4x+4 — парабола с вершиной в точке O (-1;0) и ветками вправо;
y=2-x, x+y=2 — прямая, которая отрезается на осях в точках (2;0) и (0;2).
Складываем систему уравнений для нахождения точек пересечения графиков заданных кривых:

При решении получим две точки

График области интегрирования имеет вид

Пределы в области D:
-6≤x≤2, 0,25y²-1≤y≤2-y.
Находим площадь фигуры через криволинейный интеграл:

Кратный интеграл не трудно интегрировать.

 

ЗАДАНИЕ 4.3 Найти площадь плоской фигуры, которая образована линиями:
x²+y²=4, x²+y²=4x.
Решение: Область интегрирования ограничена x²+y²=4 — кругом с центром в точке O₁(0;0) и радиусом R=2;
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2² — круг с центром в точке O₁(2;0) и радиусом R=2.
Найдем точки пересечения графиков заданных функций из системы уравнений:

отсюда

График фигуры, площадь которой ищем приведен на рисунку 

Расставим пределы в области D
(поскольку область симметрична относительно прямой y=0, то будем рассматривать ее половину, а результат умножим на 2):
D: 0≤y≤√3,
Здесь записали:
— уравнение левого полукруга (x-2)²+y²=4;
— уравнение правого полукруга x²+y²=4.
Вычислим площадь фигуры через двойной интеграл:

При интегрировании получили арксинусы, дальше подставили пределы интегрирования и округлили конечные значения.

 

ЗАДАНИЕ 4.4 Найти площадь плоской фигуры, которая образована кривыми:
x²+y²=2x, x²+y²=4x, y=x, y=0.
Решение: Начнем вычисление с анализа того, что собой представляет фигура, площадь которой нужно найти.
Сведем уравнения к простому виду
x²+y²=2x, x²-2x+1 +y²=1, (x-1)²+y²=1² — круг с центром в точке O₁(1;0) и радиусом R=1.
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2² — круг с центром в точке O₁(2;0) и радиусом R=2.
y=x — прямая, которая является биссектрисой первой и третьей четверти. 
Рисунок к задаче илюстрирует площадь которой фигуры нужно найти

Поскольку поверхность ограничена кругами, то целесообразно перейти к полярным координатам.

Найдем якобиан перехода:

Запишем заданные функции в полярной системе координат:

отсюда

отсюда
y=0, тогда
y=x, тогда
Это нам нужно, чтобы знать пределы в новой системе координат.
Пределы интегрирования в полярной системе координат:

Вычислением кратного интеграла находим площадь фигуры, ограниченной заданными кривыми:

Конечное значение площади можно еще округлить.
Из этого примера Вы ознакомились как искать площадь в полярной системе координат.
В следующей статье разберем еще несколько примеров на нахождение площади фигур интегрированием.

Интеграция

— Расчет площади с использованием двойных интегралов

спросил 2 года, 6 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 831 раз

$\begingroup$

Я изучаю двойные интегралы дома и в настоящее время пытаюсь научиться вычислять площадь с помощью двойных интегралов. 92=х, у=2, х=0$. Вычислите его площадь.

Не могли бы вы помочь мне определить, какие интегралы нужно вычислить? Я знаю, как это сделать с интегралами с одной переменной, но я не уверен, как определить интегралы в многомерном исчислении.

Спасибо

• интегрирование
• многомерное исчисление
• площадь
• многократный интеграл

$\endgroup$

3 9{1/x}1\,\mathrm dx\,\mathrm dy.$$

$\endgroup$

3

$\begingroup$

Подынтегральная функция равна 1 в двойном интеграле. Площадь рассчитывается путем суммирования всех малых площадей $\mathrm dS = \mathrm dx \mathrm dy$.

Чтобы продолжить, мы разрезаем ограниченную область на две части, и для этого есть два общих плана. {1/x} \mathrm dy. $$ 9{1/г} \mathrm dx. $$

Оба дают ответ $\color{Green}{\ln 2 + 1/3}$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

исчисление — Расчет площади с использованием двойного интеграла

Задавать вопрос

спросил

7 лет, 1 месяц назад

Изменено 7 лет, 1 месяц назад

Просмотрено 50 раз

$\begingroup$ 9{\sqrt{3}} = \frac{\sqrt{3}}{6}+\frac{2\pi }{3}$

Итак, $I = \frac{\sqrt{3}}{6} +\frac{2\pi }{3} + \pi = \frac{5\pi }{3} + \frac{\sqrt{3}}{6}$

У меня есть чек ${I}_{ 1}$ через WolframAlpha.

Но ответ должен быть $\frac{2\pi — \sqrt{3}}{6}$

• исчисление
• определенные интегралы

$\endgroup$

3

$\begingroup$

Вы выбрали не ту область.