Электронный справочник по математике для школьников тригонометрия тригонометрические функции кратных углов вывод с помощью комплексных чисел
| Справочник по математике | Тригонометрия |
Рассмотрим комплексное число
| z = cos α + i sin α , | (1) |
модуль которого равен 1, а аргумент равен α (см. раздел «Комплексные числа» нашего справочника). Если комплексное число (1) возвести в квадрат, то, с одной стороны,
| z 2 = cos 2α + i sin 2α , | (2) |
а, с другой стороны,
| z 2 = (cos α + i sin α) 2 = = cos 2α + + 2i cos α sin α – – sin 2α , | (3) |
откуда, приравнивая вещественные и мнимые части комплексных чисел (2) и (3), мы получаем тригонометрические формулы «Косинус двойного угла» и «Синус двойного угла»:
cos 2α = cos 2α – sin 2α ,
sin 2α = 2cos α sin α .
Если же комплексное число (1) возвести в куб, то, с одной стороны,
| z 3 = cos 3α + i sin 3α , | (4) |
а, с другой стороны,
| z 3 = (cos α + i sin α) 3 = = cos 3α + + 3cos 2α (i sin α) + + 3cos α (i sin α)2 + + (i sin α)3 = = cos 3 α – 3cos α sin2α + + 3i cos2α sin α – – i sin3α = = cos 3 α – 3cos αsin2α + + i (3cos2α sin α – sin3α). | (5) |
Следовательно,
z 3 = cos 3 α – 3cos α sin2 α +
+ i (3cos 2α sin α – sin3α) ,
откуда, приравнивая вещественные и мнимые части комплексных чисел (4) и (5), мы получаем соотношения
cos 3α =
= cos3α – 3cos α sin2 α =
= cos3α –
– 3cos α (1 – cos2α) =
= 4cos3α – 3cos α ,
sin 3α =
= 3cos2α sin α – sin3α =
= 3(1 – sin2α) sin α –
– sin3α =
= 3sin α – 4sin3α .
Таким образом,
cos 3α = 4cos3α – 3cos α ,
sin 3α = 3sin α – 4sin3α ,
и вывод тригонометрических формул «Косинус тройного угла» и «Синус тройного угла» завершен.
Совершенно аналогично можно вывести формулы для cos nα и sin nα, где n – произвольное натуральное число.
Ряд для синуса через кратные углы : Анализ-I
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| gris |
| |||
13/08/08 |
| |||
| ||||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| gris |
| |||
13/08/08 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| deep blue |
| ||
23/11/09 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Объяснение урока: Теорема де Муавра для тригонометрических тождеств
В этом объяснении мы узнаем, как использовать теорему де Муавра для получения
тригонометрические тождества.
Используя биномиальную теорему и теорему де Муавра, мы можем выразить cos𝑛𝜃 и sin𝑛𝜃 через степени cos𝜃 и sin𝜃. Мы начинаем с того, что вспоминаем Теорема де Муавра.
Теорема: Теорема де Муавра
Для любого целого 𝑛, (𝑟(𝜃+𝑖𝜃))=𝑟(𝑛𝜃+𝑖𝑛𝜃).cossincossin
Заметим, что левая часть уравнения является биномиальной , так как он имеет вид (𝑎+𝑏). Таким образом, давайте вспомните биномиальную теорему, которую мы можем использовать для вычисления выражений этого вид напрямую.
Теорема: биномиальная теорема
Для любого целого числа
, где 𝐶=𝑛𝑟(𝑛−𝑟). Иногда, 𝐶 обозначается 𝑛𝑟.
Используя вместе теорему де Муавра и биномиальную теорему, мы можем выразить степени синуса и косинуса в терминах меньших степеней. Давайте исследуйте общую форму этого метода ниже.
Практическое руководство. Получение выражений для тригонометрических степеней Функции
Предположим, мы хотим найти связь между
cos(𝜃) и члены младших степеней косинуса на
с одной стороны, а cos𝑛𝜃 с другой стороны. Затем мы можем сделать
следующий.
Затем мы можем сделать
следующий.
- Используя теорему де Муавра, имеем cossincossin𝑛𝜃+𝑖𝑛𝜃=(𝜃+𝑖𝜃).
- Используем биномиальную теорему в правой части, чтобы получить cossincossincossincossinsin𝑛𝜃+𝑖𝑛𝜃=𝜃+𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+⋯⋯+𝐶𝜃(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)+(𝑖𝜃)
- Умножение (𝑖𝜃) греха термов и перенося 𝑖-термы вперед, получаем cossincossincossincossinsin𝑛𝜃+𝑖𝑛𝜃=𝜃+𝑖⋅𝐶𝜃𝜃+𝑖⋅𝐶𝜃𝜃+⋯⋯+𝑖⋅𝐶𝜃𝜃+𝑍𝜃.
- Мы используем тот факт, что 𝑖=−1 оценить силы 𝑖. Это приведет к половине члены в разложении действительны, а половина — мнимы, как показано: cossincossincossincossincossin𝑛𝜃+𝑖𝑛𝜃=𝜃−𝐶𝜃𝜃+𝐶𝜃𝜃+⋯+𝑖𝐶𝜃𝜃−𝐶𝜃𝜃+⋯
- Тогда мы можем приравнять действительные части и мнимые части вышеперечисленных
уравнение вместе. Поскольку мы хотим найти только cos𝜃,
мы рассматриваем только реальные части (если бы мы хотели грех𝜃,
нам, возможно, придется рассмотреть мнимые части, в зависимости от того,
𝑖 является реальным или мнимым).
 Это дает нам
Это дает нам - Мы используем тождество sincos𝜃≡1−𝜃 исключить синусы: coscoscoscoscoscoscos𝑛𝜃=𝜃−𝐶𝜃1−𝜃+𝐶𝜃1−𝜃+⋯=1+𝐶𝜃−𝐶+𝐶𝜃+𝜃+𝜜+𝐶+𝐶 Заметим, что процедура для sin𝜃 почти то же самое, за исключением того, что вместо этого мы стремимся исключить термины cos.
Увидев общий вид, который принимает этот метод, давайте рассмотрим пример где мы можем продемонстрировать, как работает вывод тригонометрических тождеств в упражняться.
Пример 1. Вычисление степеней синуса с использованием формул для нескольких углов
- Используйте теорему де Муавра, чтобы выразить sin5𝜃 в с точки зрения сил греха𝜃.
- Рассматривая решения sin5𝜃=0, найдите точное представление для sin𝜋5.
Ответ
Часть 1
Используя теорему де Муавра, мы имеем cossincossin5𝜃+𝑖5𝜃=(𝜃+𝑖𝜃). скосинкоссинкоссинкоссин5𝜃+𝑖5𝜃=𝜃 +𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+(𝑖𝜃). 0003
0003
Подставляя значения 𝐶 и упрощая, у нас есть cossincoscossincossincossincossinsin5𝜃+𝑖5𝜃=𝜃+5𝑖𝜃𝜃+10𝑖𝜃𝜃+10𝑖𝜃𝜃+5𝑖𝜃𝜃+𝑖𝜃.
Оценивая степени 𝑖, получаем cossincossincossincossinsin5𝜃+𝑖5𝜃=𝜃+5𝑖𝜃𝜃−10𝜃𝜃− 10𝑖𝜃𝜃+5𝜃𝜃+𝑖𝜃.
02 Чтобы устранить силы cos𝜃, мы используем тождество коссин𝜃≡1−𝜃. Подставив это, мы есть sinsinsinsinssin5𝜃=51−𝜃𝜃−101−𝜃𝜃+𝜃.
Раскрывая круглые скобки и упрощая, получаем sinsinsinsinsinsinsinsinsinsinsinsin5𝜃=51−2𝜃+𝜃𝜃−10𝜃−𝜃+𝜃=5𝜃−10𝜃+5𝜃−10𝜃+10𝜃.
Собирая подобные члены, имеем sinsinsinsin5𝜃=16𝜃−20𝜃+5𝜃.
Часть 2
Начнем с рассмотрения решений sin5𝜃=0. Мы знаем что синус равен нулю при целых кратных 𝜋. Следовательно, sin5𝜃=0, когда 𝜃=𝑛𝜋5 для 𝑛∈ℤ. Используя наш ответ из части 1, мы имеем, что 16𝜃−20𝜃+5𝜃=0sinsinsin, когда 𝜃=𝑛𝜋5 для 𝑛∈ℤ. Если исключить грех𝜃, мы имеем sinsinsin𝜃16𝜃−20𝜃+5=0.
Теперь рассмотрим случай, когда 𝜃=𝜋5. Мы знаем это
грех𝜋5≠0; следовательно, мы можем сделать вывод, что
16𝜋5−20𝜋5+5=0sinsin. Это квадратичная зависимость от sin𝜋5. Следовательно, установив 𝑥=𝜋5sin, мы можем переписать это как 𝑥=20±√8032=5±√58.
Мы знаем это
грех𝜋5≠0; следовательно, мы можем сделать вывод, что
16𝜋5−20𝜋5+5=0sinsin. Это квадратичная зависимость от sin𝜋5. Следовательно, установив 𝑥=𝜋5sin, мы можем переписать это как 𝑥=20±√8032=5±√58.
Следовательно, у нас есть две возможности: sin𝜋5=5+√58 или sin𝜋5=5−√58. Теперь мы знаем, что sin𝜃 — возрастающая функция для 𝜃∈0,𝜋2 и что 0≤𝜃≤1sin в этом интервале. Поэтому, у нас есть грех𝜋5𝜋4.
Поскольку мы знаем, что sin𝜋4=12, это означает, что грех𝜋512.
Сравнивая два возможных ответа с 12, мы находим, что 5−√58≈0,3512, а 5+√58≈0,90>12, то есть только первый ответ правильный. Таким образом, у нас есть sin𝜋5=5−√58.
Мы также можем использовать теорему де Муавра, чтобы вывести тождества для
sin𝑛𝜃 и cos𝑛𝜃. Для этого начнем с определения
комплексное число 𝑧=𝜃+𝑖𝜃косинус. Тогда мы можем рассмотреть
1𝑧=𝑧=(𝜃+𝑖𝜃). коссин
коссин
Применяя теорему де Муавра, получаем −𝜃, мы можем переписать это AS 1𝑧 = 𝜃 — 𝑖𝜃.Cossin
Следовательно, 𝑧+1𝑧 = 2𝜃, 𝑧 -1𝑧 = 2𝑖𝜃.cossin
Аналогично, мы можем рассмотреть 𝑧 = (𝜃+𝑖𝜃) cossin, для 𝑛∈𝑍. Используя теорему де Муавра, мы можем переписать это как 𝑧=𝑛𝜃+𝑖𝑛𝜃коссин. Аналогичным образом мы рассматриваем 1𝑧=𝑧=(𝜃+𝑖𝜃).cossin
Используя теорему де Муавра, мы можем переписать это как 1𝑧=(−𝑛𝜃)+𝑖(−𝑛𝜃).cossin
Применяя нечетные/четные тождества для синуса и косинуса, мы получаем 1𝑧=𝑛𝜃−𝑖𝑛𝜃.cossin
Следовательно, складывая и вычитая приведенные выше выводы, мы получаем следующую пару полезных тождеств.
Идентичность: Формулы множественных углов в терминах комплекса Числа
Пусть 𝑧=𝜃+𝑖𝜃коссин. Тогда для любого 𝑛∈ℤ имеем 𝑧+1𝑧=2𝑛𝜃,𝑧−1𝑧=2𝑖𝑛𝜃.коссин
Эти уравнения фактически эквивалентны следующим формулам для выражения синуса и
косинус в терминах экспоненциальной функции: косинус𝑛𝜃=12𝑒+𝑒,𝑛𝜃=12𝑖𝑒−𝑒.
Используя приведенные выше тождества для синуса и косинуса в терминах 𝑧, мы можем вывести многие другие тригонометрические тождества. Как техника, использованная здесь, так и формулы для синуса и косинуса в терминах 𝑧 следует запомнить.
Теперь в нескольких следующих примерах мы продемонстрируем применение этого тождество к различным тригонометрическим задачам.
Пример 2. Вычисление степеней функции косинуса с использованием тождеств с несколькими углами
Выразите cos𝜃 через cos6𝜃, cos5𝜃, cos4𝜃, cos3𝜃, cos2𝜃, cos𝜃, и любые постоянные условия.
Ответ
Если 𝑧=𝜃+𝑖𝜃коссин, мы можем написать 2𝜃=𝑧+1𝑧.cos
Возводя обе части в шестую степень, получаем
Теперь применим биномиальную теорему к правой части следующим образом: cos𝜃=164𝑧+𝐶𝑧1𝑧+𝐶𝑧1𝑶𝑧+𝐝 𝐶𝑧1𝑧+𝐶𝑧 1𝑧+1𝑧.
Замена значений 𝐶 и
упрощая, имеем cos𝜃=164𝑧+6𝑧+15𝑧+20+15𝑧+6𝑧+1𝑧.
Теперь мы можем сгруппировать 𝑧 терминов с 1𝑧 терминами следующим образом: cos𝜃=164𝑧+1𝑧+6𝑧+1𝑧+15𝑧+1𝑧+20.
Используя 𝑧+1𝑧=2𝑛𝜃cos, мы можем выразить это как coscoscoscos𝜃=164(26𝜃+6(24𝜃)+15(22𝜃)+20).
Наконец, мы упрощаем, чтобы получить coscoscoscos𝜃=1326𝜃+3164𝜃+15322𝜃+516.
Выражение степени синусов и косинусов через несколько углов очень полезно для вычисление интегралов, как продемонстрирует следующий пример.
Пример 3. Использование теоремы Муавра для вычисления тригонометрических интегралов
Используя теорему де Муавра, найдите точное значение 𝜃𝜃.sind
Ответ
Применяя теорему де Муавра, мы можем выразить sin𝜃 с точки зрения нескольких углов, которые проще интегрировать. Начнем с установки 𝑧=𝜃+𝑖𝜃косинус. Тогда, используя 𝑧, мы можем представим синус как 2𝑖𝜃=𝑧−1𝑧.sin
Возводя обе части в седьмую степень, получаем мы можем разделить оба
стороны на −128𝑖, чтобы получить sin𝜃=−1128𝑖𝑧−1𝑧=𝑖128𝑧−1𝑧.
Применяя биномиальную теорему, имеем 𝑧1𝑧 −𝐶𝑧1𝑧+𝐶𝑧1𝑧−𝐶𝑧1𝑧+𝐶𝑧1𝑧−1𝑧.
Замена значений 𝐶 и упрощая, имеем sin𝜃=𝑖128𝑧−7𝑧+21𝑧−35𝑧+35𝑧−21𝑧+7𝑧−1𝑧.
Теперь мы можем сгруппировать 𝑧 терминов с 1𝑧 терминами следующим образом: sin𝜃=𝑖128𝑧−1𝑧−7𝑧−1𝑧+21𝑧−1𝑧−35𝑧−1𝑧.
Используя 𝑧−1𝑧=2𝑖𝑛𝜃sin, мы можем выразить это как грехсинсинсинсин𝜃=𝑖128(2𝑖7𝜃−7(2𝑖5𝜃)+21(2𝑖3𝜃)−35(2𝑖𝜃)).
Упрощая, получаем sinsinsinsinsin𝜃=164(35𝜃−213𝜃+75𝜃−7𝜃).
Подставив это в интеграл, получим 𝜃+73𝜃−755𝜃 +177𝜃=164−35𝜋2+73𝜋2−755𝜋2+177𝜋2−−350+70−750+170=16435−7+75−17=1635. sindcoscoscoscoscoscoscoscoscos
Применение теоремы Муавра не ограничивается простыми степенями синуса и косинус; мы также можем найти выражения для произведения степеней синуса и косинуса.
Пример 4. Решение тригонометрических уравнений с использованием произведений степеней Функции синуса и косинуса
- Выразите sincos𝜃𝜃 в виде
𝑎𝜃+𝑏3𝜃+𝑐5𝜃coscoscos, где
𝑎,𝑏 и 𝑐 — константы, которые нужно найти.

- Следовательно, найдите все решения coscos5𝜃+3𝜃=0 в интервале 0≤𝜃𝜋. Отдай свое ответы в точной форме.
Ответ
Часть 1
Полагая 𝑧=𝜃+𝑖𝜃косинус, можно выразить синус и косинус через 𝑧 следующим образом: 2𝜃=𝑧+1𝑧,2𝑖𝜃=𝑧−1𝑧.cossin
Следовательно, sincos𝜃𝜃=1(2𝑖)𝑧−1𝑧12𝑧+1𝑧=−132𝑧−1𝑧𝑧+1𝑧𝑧
Используя биномиальную теорему, мы можем раскрыть каждую скобку отдельно следующим образом: sincos𝜃𝜃=−132𝑧−2+1𝑧𝑧+3𝑧+3𝑧+1𝑧.
Умножение двух скобок дает sincos𝜃𝜃=−132𝑧+3𝑧+3𝑧+1𝑧−2𝑧−6𝑧−6𝑧−2𝑧+𝑧+3𝑧+3𝑧..
Сбор 𝑧 терминов с 1𝑧 терминами приводит к sincos𝜃𝜃=−132𝑧+1𝑧+𝑧+1𝑧−2𝑧+1𝑧.
Используя 𝑧+1𝑧=2𝑛𝜃cos, мы можем выразить это как sincoscoscoscoscos𝜃𝜃=−132(25𝜃+23𝜃−2(2𝜃))=116(2𝜃−5𝜃−3𝜃).
Часть 2
Используя наш ответ из части 1, мы видим, что coscoscossincos5𝜃+3𝜃=2𝜃−16𝜃𝜃.
Следовательно, coscos5𝜃+3𝜃 эквивалентно
0=2𝜃−16𝜃𝜃. cossincos
cossincos
Разложение этого выражения на множители дает 0=2𝜃1−8𝜃𝜃,cossincos
, что верно, если либо cos𝜃=0, либо 1−8sincos=0 или Для первого случая, учитывая, что 0≤𝜃𝜋, cos𝜃=0, когда 𝜃=𝜋2.
Теперь рассмотрим случай, когда 1−8𝜃𝜃=0sincos. Используя формулу двойного угла для синуса, sinsincos2𝜃=2𝜃𝜃,
мы можем переписать это как 1−22𝜃=0.sin
Следовательно, sin2𝜃=12.
Извлекая квадратный корень из обеих частей уравнения, получаем sin2𝜃=±1√2.
Начиная с положительного квадратного корня, для 𝜃 в диапазоне 0≤𝜃𝜋, sin2𝜃=1√2, когда 𝜃=𝜋8 или 3𝜋8. Точно так же для отрицательного квадратного корня sin2𝜃=−1√2, когда 𝜃=5𝜋8 или 7𝜋8.
Следовательно, решения coscos5𝜃+3𝜃=0 для 𝜃 в диапазоне 0≤𝜃𝜋 являются 𝜃=𝜋8,3𝜋8,𝜋2,5𝜋8,7𝜋8.
Методы, используемые для получения тригонометрических тождеств, могут также применяться к другим
тригонометрические функции, такие как функции тангенса и котангенса. Следующий пример
продемонстрирует, как мы можем найти формулы нескольких углов для функции тангенса.
Следующий пример
продемонстрирует, как мы можем найти формулы нескольких углов для функции тангенса.
Пример 5. Вывод тригонометрических тождеств с использованием касательной функции
- Выразите sin6𝜃 через степени sin𝜃 и cos𝜃.
- Выразите cos6𝜃 через степени sin𝜃 и cos𝜃.
- Следовательно, выразим tan6𝜃 через степени загар𝜃.
Ответ
Часть 1
Используя теорему де Муавра, мы имеем cossincossin6𝜃+𝑖6𝜃=(𝜃+𝑖𝜃). ssincossincossincossinsin6𝜃+𝑖6𝜃=𝜃+𝐶𝜃(𝑖𝜃)+ 𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+𝐶𝜃(𝑖𝜃)+(𝑖𝜃).
Подстановка значений 𝐶 и упрощая, у нас есть cossincoscossincossincossincossincossinsin6𝜃+𝑖6𝜃=𝜃+6𝑖𝜃𝜃+15𝑖𝜃𝜃+20𝑖𝜃𝜃+15𝑖𝜃𝜃+6𝑖𝜃𝜃+𝑖𝜃𝜃+6𝑖𝜃𝜃+𝑖
Оценив степени 𝑖, получим
| 5𝜃𝜃+6𝑖𝜃𝜃−𝜃. | (1) |
Приравнивая мнимые части, имеем sincossincossincossin6𝜃=6𝜃𝜃−20𝜃𝜃+6𝜃𝜃.
Part 2
coscoscossincossinsin6𝜃=𝜃−15𝜃𝜃+15𝜃𝜃−𝜃.
Часть 3
Используя определение функции тангенса через синус и косинус, мы имеем tansincos6𝜃=6𝜃6𝜃.
Используя ответы из частей 1 и 2, мы можем переписать это как
Деление числителя и знаменателя на потому что мы get tantantantantantantan6𝜃=6𝜃−20𝜃+6𝜃1−15𝜃+15𝜃−𝜃.
Давайте закончим повторением ключевых моментов, которые мы узнали в этом объяснении.
Ключевые моменты
- Используя теорему де Муавра и биномиальную теорему, мы можем вывести формулы множественных углов для различных функций синуса, косинуса и тангенса.
- Если мы определим 𝑧=𝜃+𝑖𝜃косинус, мы можем выразить синус и косинус через 𝑧 следующим образом: 𝑧+1𝑧=2𝜃,𝑧−1𝑧=2𝑖𝜃.cossin cos𝑛𝜃 через 𝑧 как 𝑧+1𝑧=2𝑛𝜃,𝑧−1𝑧=2𝑖𝑛𝜃.коссин. Используя эти уравнения, мы можно найти выражения для сил синуса и косинуса и даже их произведений.
- Используя эти методы для получения тригонометрических тождеств, мы можем упростить
интегралы и решать уравнения.

Вопрос Видео: Тождества для степеней косинуса
Стенограмма видео
Выразите cos в шестой степени 𝜃 через cos шесть 𝜃, cos пять 𝜃, cos четыре 𝜃, cos три 𝜃, cos два 𝜃, cos 𝜃 и любые постоянные сроки.
В этом вопросе мы хотим найти выражение для cos в шестой степени 𝜃. И это выражение должно состоять из членов, которые включают только целое число, кратное значениям 𝜃, и постоянные члены. В некоторых вопросах, подобных этому, можно найти выражения для каждой из этих формул множественных углов для косинуса, а затем получить наш ответ, равный тому, что мы хотим, в данном случае косинус в шестой степени 𝜃. Однако для этого нам нужно будет сделать это для каждой из формул множественного угла в вопросе. Таким образом, хотя этот метод и возможен, он потребует очень много времени и потребует множества проб и ошибок.
Вместо этого нам нужно вспомнить, что мы можем найти подобные выражения, используя теорему де Муавра. Итак, чтобы ответить на этот вопрос, мы начнем с того, что вспомним теорему де Муавра. Одна версия этого говорит, что для любого целочисленного значения 𝑛 и действительного числа 𝜃, cos 𝜃 плюс 𝑖 грех 𝜃, все возведенные в 𝑛-ю степень, равны косу 𝑛𝜃 плюс 𝑖 грех 𝑛𝜃. Однако, если бы мы попытались напрямую использовать это выражение для ответа на наш вопрос, у нас могли бы возникнуть трудности. Поскольку мы хотим найти выражение для cos в шестой степени 𝜃, нам нужно установить 𝑛 равным шести, чтобы в нашем выражении появился cos в шестой степени. Однако, когда мы распределяем 𝑛-ю степень по нашим скобкам, мы получим кос-термы пятой степени, кос-термы четвертой степени, вплоть до кос-членов нулевой степени.
Одна версия этого говорит, что для любого целочисленного значения 𝑛 и действительного числа 𝜃, cos 𝜃 плюс 𝑖 грех 𝜃, все возведенные в 𝑛-ю степень, равны косу 𝑛𝜃 плюс 𝑖 грех 𝑛𝜃. Однако, если бы мы попытались напрямую использовать это выражение для ответа на наш вопрос, у нас могли бы возникнуть трудности. Поскольку мы хотим найти выражение для cos в шестой степени 𝜃, нам нужно установить 𝑛 равным шести, чтобы в нашем выражении появился cos в шестой степени. Однако, когда мы распределяем 𝑛-ю степень по нашим скобкам, мы получим кос-термы пятой степени, кос-термы четвертой степени, вплоть до кос-членов нулевой степени.
Кажется, что избавиться от всех этих терминов будет очень сложно. Поэтому вместо этого нам нужно будет вспомнить очень полезный результат. Если мы назовем комплексное число в наших скобках 𝑧, то теорема де Муавра говорит нам, что 𝑧 в 𝑛-й степени равно косинусу 𝑛𝜃 плюс 𝑖 греху 𝑛𝜃. И затем мы можем использовать теорему де Муавра, чтобы найти два полезных результата: 𝑧 в 𝑛-й степени плюс один над 𝑧 в 𝑛-й степени равен двум cos от 𝑛𝜃 и 𝑧 в 𝑛-й степени минус один над 𝑧 в 𝑛-й степени равен к двум 𝑖 греху 𝑛𝜃. И чтобы доказать эти результаты, мы напрямую используем теорему де Муавра, которая, как мы помним, верна для любого целочисленного значения 𝑛. И мы знаем, что единица на 𝑧 в 𝑛-й степени такая же, как 𝑧 в отрицательной степени 𝑛.
И чтобы доказать эти результаты, мы напрямую используем теорему де Муавра, которая, как мы помним, верна для любого целочисленного значения 𝑛. И мы знаем, что единица на 𝑧 в 𝑛-й степени такая же, как 𝑧 в отрицательной степени 𝑛.
Эти результаты очень полезны, и их стоит запомнить. Мы собираемся сосредоточиться на верхнем результате, который мы собираемся использовать, чтобы найти выражение для cos в шестой степени 𝜃. Мы начинаем с установки нашего значения 𝑛 равным единице в этом выражении. Это дает нам два cos 𝜃 равно 𝑧 плюс один больше 𝑧. И помните, вопрос требует, чтобы мы нашли выражение для cos в шестой степени 𝜃, поэтому мы собираемся возвести обе части этого уравнения в шестую степень. В левой части нашего уравнения мы можем упростить, взяв шестую степень обоих наших двух факторов. Это дает нам два в шестой степени, умноженные на cos в шестой степени 𝜃. И мы можем упростить это, поскольку мы знаем, что два в шестой степени равно 64.
Таким образом, левая часть нашего уравнения упрощается и дает нам 64 cos в шестой степени числа 𝜃.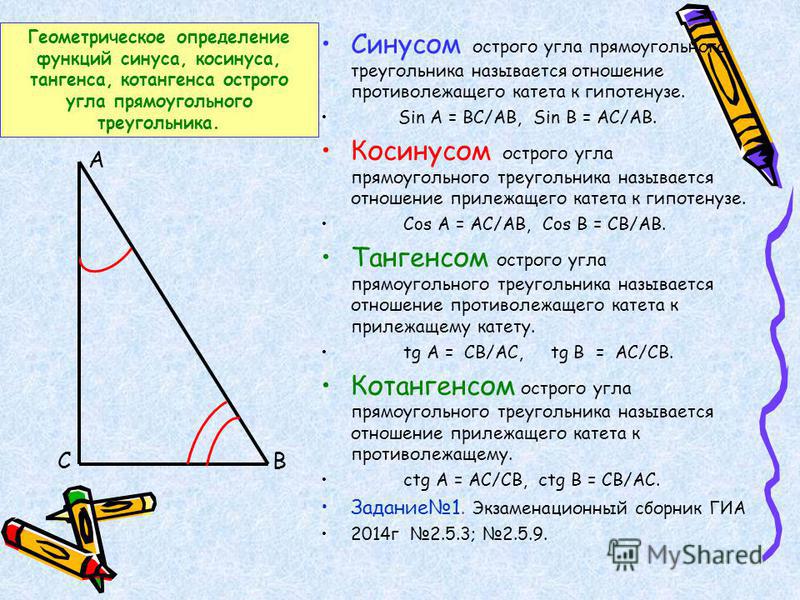 И в правой части нашего уравнения у нас есть сумма двух чисел, возведенных в степень. Мы можем сделать это, используя биномиальную формулу. Напомним, это говорит нам о том, что для любого положительного целого числа 𝑚, 𝑎 плюс 𝑏, возведенных в 𝑚-ю степень, равно сумме от 𝑟 равно нулю до 𝑚 из 𝑚 выбрать 𝑟, умноженное на 𝑎 в степени 𝑟, умноженное на 𝑏 в степени 𝑚 минус 𝑟. Таким образом, мы можем использовать это, чтобы распределить показатель степени шести по правой части нашего уравнения. Мы получаем, что шесть выбирают ноль 𝑧 в шестой степени плюс шесть выбирают один раз 𝑧 в пятой степени умножают на единицу больше 𝑧 плюс шесть выбирают два раза 𝑧 в четвертой степени умножают на единицу больше 𝑧 все в квадрате. И затем мы продолжаем добавлять термины этой формы до шести, выбираем шесть, умножаем на единицу и 𝑧 все возводим в шестую степень.
И в правой части нашего уравнения у нас есть сумма двух чисел, возведенных в степень. Мы можем сделать это, используя биномиальную формулу. Напомним, это говорит нам о том, что для любого положительного целого числа 𝑚, 𝑎 плюс 𝑏, возведенных в 𝑚-ю степень, равно сумме от 𝑟 равно нулю до 𝑚 из 𝑚 выбрать 𝑟, умноженное на 𝑎 в степени 𝑟, умноженное на 𝑏 в степени 𝑚 минус 𝑟. Таким образом, мы можем использовать это, чтобы распределить показатель степени шести по правой части нашего уравнения. Мы получаем, что шесть выбирают ноль 𝑧 в шестой степени плюс шесть выбирают один раз 𝑧 в пятой степени умножают на единицу больше 𝑧 плюс шесть выбирают два раза 𝑧 в четвертой степени умножают на единицу больше 𝑧 все в квадрате. И затем мы продолжаем добавлять термины этой формы до шести, выбираем шесть, умножаем на единицу и 𝑧 все возводим в шестую степень.
Помните, вопрос требует, чтобы мы нашли выражение для cos в шестой степени 𝜃. Но он хочет этого с точки зрения нескольких углов 𝜃. Мы можем изменить это, чтобы получить cos в шестой степени 𝜃.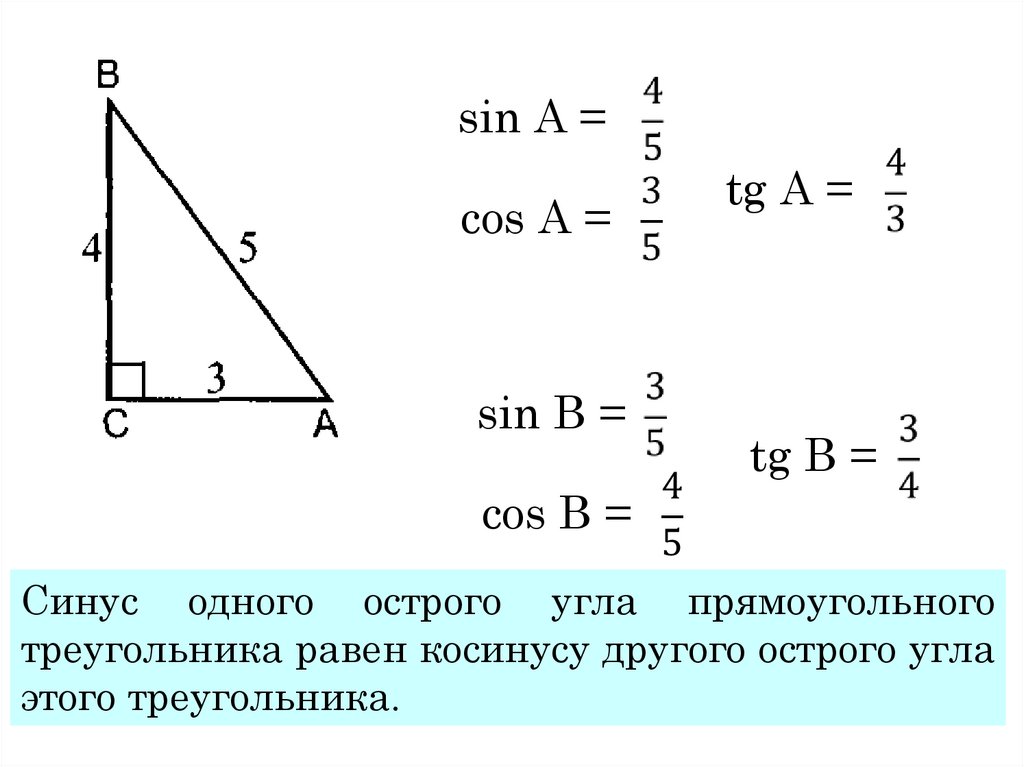 Однако правая часть этого выражения выражена в терминах 𝑧; это еще не с точки зрения cos углов 𝜃. Это означает, что нам нужно упростить правую часть нашего уравнения. Мы будем делать это по срокам. В нашем первом члене шесть выбирают ноль равным единице, поэтому первый член — это просто 𝑧 в шестой степени. В нашем втором члене шесть выбирают один равно шести, а 𝑧 в пятой степени, умноженное на единицу над 𝑧, можно упростить, используя наши законы показателей. Это равно 𝑧 в четвертой степени. Итак, наш второй член равен шести 𝑧 в четвертой степени.
Однако правая часть этого выражения выражена в терминах 𝑧; это еще не с точки зрения cos углов 𝜃. Это означает, что нам нужно упростить правую часть нашего уравнения. Мы будем делать это по срокам. В нашем первом члене шесть выбирают ноль равным единице, поэтому первый член — это просто 𝑧 в шестой степени. В нашем втором члене шесть выбирают один равно шести, а 𝑧 в пятой степени, умноженное на единицу над 𝑧, можно упростить, используя наши законы показателей. Это равно 𝑧 в четвертой степени. Итак, наш второй член равен шести 𝑧 в четвертой степени.
В нашем третьем члене шесть выбирают два равно 15, а 𝑧 в четвертой степени, умноженное на единицу в квадрате 𝑧, равно 𝑧 в четвертой степени в квадрате 𝑧, что равно 𝑧 в квадрате. Итак, наш третий член равен 15𝑧 в квадрате. Точно так же мы можем упростить и остальные члены этого разложения. Получаем 20, 15 больше 𝑧 в квадрате, шесть больше 𝑧 в четвертой степени и один больше 𝑧 в шестой степени. И теперь мы можем заметить кое-что интересное. Мы можем упростить это выражение, используя теорему Муавра. Например, у нас есть первый член в этом расширении плюс последний член в этом расширении — это 𝑧 в шестой степени плюс единица сверх 𝑧 в шестой степени. Установив 𝑛 равным шести в нашем полезном результате, мы знаем, что это равно удвоенному cos шести 𝜃. И это не единственный раз, когда этот результат появляется в нашем дополнении. Мы можем использовать это еще два раза.
Мы можем упростить это выражение, используя теорему Муавра. Например, у нас есть первый член в этом расширении плюс последний член в этом расширении — это 𝑧 в шестой степени плюс единица сверх 𝑧 в шестой степени. Установив 𝑛 равным шести в нашем полезном результате, мы знаем, что это равно удвоенному cos шести 𝜃. И это не единственный раз, когда этот результат появляется в нашем дополнении. Мы можем использовать это еще два раза.
Итак, мы объединим термины в нашем расширении, чтобы получить 𝑧 в шестой степени плюс один больше 𝑧 в шестой степени плюс шесть 𝑧 в четвертой степени плюс шесть больше 𝑧 в четвертой степени плюс 15𝑧 в квадрате плюс 15 больше 𝑧 в квадрате плюс 20. И прежде чем мы применим теорему Муавра, мы можем заметить кое-что интересное. В нашем первом наборе скобок мы можем убрать общий множитель шесть. И точно так же в нашем третьем наборе скобок мы можем убрать общий множитель 15. Это дает нам следующее выражение. И теперь мы можем упростить все три набора скобок, используя теорему Муавра. Установив 𝑛 равным шести, мы знаем, что 𝑧 в шестой степени плюс один сверх 𝑧 в шестой степени равно двум из шести 𝜃. Если 𝑛 равно четырем, 𝑧 в четвертой степени плюс один сверх 𝑧 в четвертой степени равно двум, потому что четыре 𝜃. А если 𝑛 равно двум, 𝑧 в квадрате плюс один на 𝑧 в квадрате равно двум производным от двух 𝜃.
Установив 𝑛 равным шести, мы знаем, что 𝑧 в шестой степени плюс один сверх 𝑧 в шестой степени равно двум из шести 𝜃. Если 𝑛 равно четырем, 𝑧 в четвертой степени плюс один сверх 𝑧 в четвертой степени равно двум, потому что четыре 𝜃. А если 𝑛 равно двум, 𝑧 в квадрате плюс один на 𝑧 в квадрате равно двум производным от двух 𝜃.
Итак, подставив эти выражения в и вспомнив, что нам нужно умножить на наши коэффициенты, и нам еще нужно добавить 20 в конце, мы получаем 64 cos в шестой степени 𝜃 равно двум cos из шести 𝜃 плюс 12 cos из четыре 𝜃 плюс 30 потому что два 𝜃 плюс 20. И теперь это почти в том виде, в котором мы хотим. Все, что нам нужно сейчас, это переставить так, чтобы cos в шестой степени 𝜃 стало предметом. И для этого нам нужно разделить обе части нашего уравнения на 64. Итак, чтобы сделать это, давайте начнем с расчистки места. У нас есть cos в шестой степени 𝜃 равно следующему выражению. И чтобы оценить это, мы собираемся разделить каждый член в этом выражении на 64.
Сделав это, мы получим два потому что шесть 𝜃 все больше 64 плюс 12 потому что четыре 𝜃 все больше 64 плюс 30 потому что два 𝜃 все больше 64 плюс 20 разделить на 64.


 Например, пусть . Кроме того, . Подставим эти соотношения в равенство , получим .
Например, пусть . Кроме того, . Подставим эти соотношения в равенство , получим .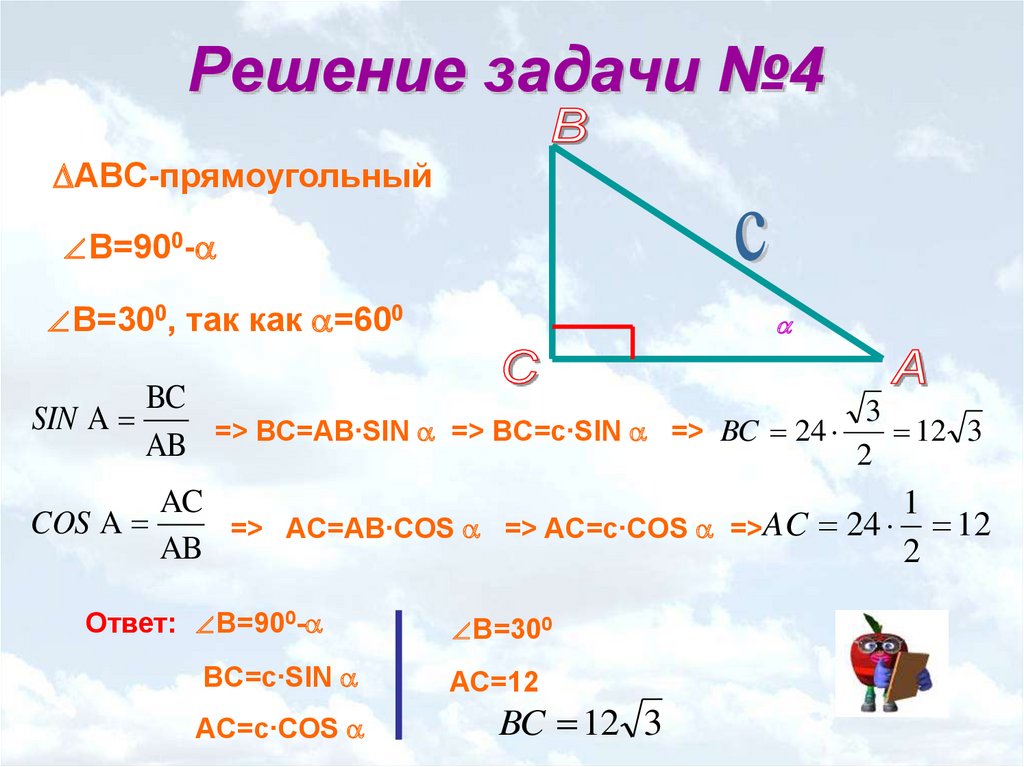

 01.2016, 11:33
01.2016, 11:33 

 Имеет скорее «эстетическую» ценность.
Имеет скорее «эстетическую» ценность. Затем заменяем синус малого x на x и видим искомый ряд. Вот с оценкой погрешности грустно, и непонятно, какие члены ряда правильные, а какие шум. Но первые выпишутся правильно.
Затем заменяем синус малого x на x и видим искомый ряд. Вот с оценкой погрешности грустно, и непонятно, какие члены ряда правильные, а какие шум. Но первые выпишутся правильно. 01.2016, 21:58
01.2016, 21:58  Это дает нам
Это дает нам
