Выразим синус, косинус или тангенс…Упр 499 параграф 29 Алимов Алгебра 10-11 класс – Рамблер/класс
Выразим синус, косинус или тангенс…Упр 499 параграф 29 Алимов Алгебра 10-11 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Нужно выразить синус, косинус или тангенс, используя формулы двойного угла:
6) cos а.

Поможете?)
ответы
Ну раз нужно, то:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее..
ГДЗ11 классКолмогоров А.Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Синус, косинус и тангенс острого угла
Геометрия. 8 класс. Глава VII. Параграф 4. Тест 1.
Глава VII. Параграф 4. Тест 1.
Вариант I.
1. Выразить sinα, tgα. Найти значение α+β (рис. 1).
A) sinα=a/c; tgα=a/b; α+β=90°; B) sinα=b/c; tgα=a/b; α+β=90°;
C) sinα=a/c; tgα=b/a; α+β=60°; D) sinα=c/a; tgα=a/b; α+β=180°.
2. Выразить cosβ, tgβ. Найти значение α+β (рис. 2).
A) cosβ =a/c; tgβ =a/b; α+β=60°; B) cosβ =b/c; tgβ =a/b; α+β=90°;
C) cosβ=a/c; tgβ=b/a; α+β=90°; D) cosβ =c/a; tgβ =a/b; α+β=180°.
3. Выразить СК двумя способами (рис. 3).
A) CK=c/sinα, CK=c/cosβ; B) CK=c∙sinα, CK=c∙cosβ;
C) CK=c∙tgα, CK=c∙cosβ; D) CK=c∙sinα, CK=c∙tgβ.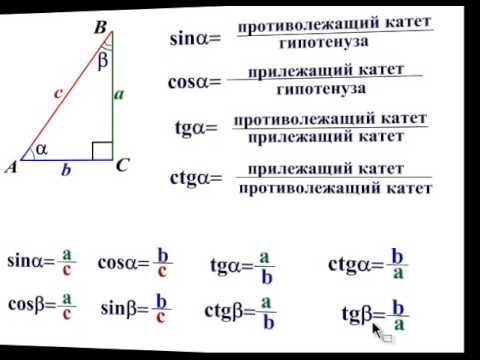
4. Выразить AM двумя способами (рис. 4).
A) AM=z∙sinβ, AM=z∙cosα; B) AM=z/tgβ, AM=z/tgα;
C) AM=z∙sinα, AM=z∙cosβ; D) AM=z/sinβ, AM=z/cosα.
5. Выразить x (рис. 5).
A) x=k/tgα; B) x=k∙tgα; C) x=k/sinα; D) x=k∙cosα.
A) y=n/tgβ; B) y=n∙tgβ; C) y=n∙sinβ; D) y=n/cosβ.
Вариант II.
1. Выразить sinβ, tgβ. Найти значение α+β (рис. 1).
A) sinβ =a/c; tgβ=a/b; α+β=90°; B) sinβ=b/c; tgβ=b/a; α+β=90°;
C) sinβ =a/c; tgβ=b/a; α+β=60°; D) sinβ =c/b; tgβ =b/a; α+β=180°.
2. Выразить cosα, tgα. Найти значение α+β (рис. 2).
A) cosα =b/c; tgα=a/b; α+β=90°; B) cosα =c/b; tgα=a/b; α+β=60°;
C) cosα =a/c; tgα=b/a; α+β=90°; D) cosα=c/b; tgα=b/a; α+β=180°.
3. Выразить СD двумя способами (рис. 3).
A) CD=c/sinβ, CD=c/cosα; B) CD=c∙sinα, CD=c∙cosβ;
C) CD=c∙sinβ, CD=c∙cosα; D) CD=c∙tgα, CD=c∙tgβ.
4. Выразить CN двумя способами (рис. 4).
A) CN=n∙sinβ, CN=n∙cosα; B) CN=n/sinα, CN=n/cosβ;
C) CN=n/sinβ, CN=n/cosα; D) CN=n∙tgβ, CN=n∙tgα;
5. Выразить x (рис. 5).
Выразить x (рис. 5).
A) x=z/tgα; B) x=z∙sinα; C
6. Выразить y (рис. 6).
A) y=m/tgβ; B) y=m∙tgβ; C) y=m∙sinβ; D) y=m/cosβ.
Вариант III.
1. Выразить sinα, cosα, tgα (рис. 1).
A) sinα=m/n; cosα=m/k; tgα=m/n; B) sinα=m/k; cosα=k/n; tgα=n/m;
C) sinα=m/k; cosα=n/k; tgα=m/n; D) sinα=k/m; cosα=n/k; tgα=k/n.
2. Выразить sinβ, cosβ, tgβ (рис. 2).
A) sinβ=p/z; cosβ=c/z; tgβ=p/c; B) sinβ=z/p; cosβ=z/c; tgβ=p/c;
C) sinβ=p/c; cosβ=c/z; tgβ=c/p; D) sinβ=c/z; cosβ=p/z; tgβ=c/p.
3. Выразить BC двумя способами (рис. 3).
A) BC=c/sinα, BC=c/cosβ; B) BC=c∙tgα, BC=c∙tgβ;
C) BC=c∙cosα, BC=c∙sinβ; D) BC=c∙sinα, BC=c∙cosβ.
4. Выразить MN двумя способами (рис. 4).
A) MN=m∙cosα, MN=m∙sinβ; B) MN=m/sinα, MN=m/cosβ;
C) MN=m∙sinα, MN=m∙cosβ; D) MN=m/cosα, MN=m/sinβ.
5. Выразить АО и угол A (рис. 5).
A) АО=k∙tgα, ∠А=45°; B)
C) АО=k∙sinα, ∠А=60°; D) АО=k∙cosα, ∠А=180°-α.
6. Выразить BS и угол T (рис. 6).
A) BS=m∙tgβ, ∠T=90°; B) BS=m/tgβ, ∠T=90°-β;
C) BS=m∙cosβ, ∠T=90°-β; D) BS=m/sinβ, ∠T=45°.
Вариант IV.
1. Выразить sinβ, cosβ, tgβ (рис. 1).
A) sinβ=k/n; cosβ=m/k; tgβ=n/m; B) sinβ=n/k; cosβ=m/k; tgβ=n/m;
C) sinβ=n/k; cosβ=k/m; tgβ=n/m; D) sinβ=n/k; cosβ=m/k; tgβ=m/n.
2. Выразить sinα, cosα, tgα (рис. 2).
A) sinα=z/c; cosα=p/z; tgα=c/p; B) sinα=c/z; cosα=z/p; tgα=c/p;
C) sinα=c/z; cosα=p/z; tgα=p/c; D) sinα=c/z; cosα=p/z; tgα=c/p.
3. Выразить AC двумя способами (рис. 3).
A) AC=c∙sinα, AC=c∙sinβ; B) AC=c∙cosα, AC=c∙cosβ;
C) AC=c∙cosα, AC=c∙sinβ; D) AC=c/cosα, AC=c/sinβ.
4. Выразить MP двумя способами (рис. 4).
A) MP=n/sinα, MP=n/cosβ; B) MP=n/sinβ, MP=n/cosα;
C)
5. Выразить CK и угол C (рис. 5).
A) CK=n∙tgα, ∠C=90°-α; B) CK=n∙tgα, ∠C=90°;
C) CK=n∙sinα, ∠C=60°; D) CK=n∙cosα, ∠C=180°-α.
6. Выразить NT и угол M (рис. 6).
A) NT=c∙tgβ, ∠M=90°-β; B) NT=c/tgβ, ∠M=60°;
C) NT=c∙cosβ, ∠M=90°-β; D) NT=c/tgβ, ∠M=90°-β.
Справочные материалы.
1) Синусом острого угла α прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синус угла α обозначается так: sinα.
2) Катет, противолежащий углу α, равен произведению гипотенузы на синус α:
BC = AB ∙ sinα или a = c ∙ sinα.
3) Косинусом острого угла α прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла α обозначается так: cosα.
4) Катет, прилежащий к углу α равен произведению гипотенузы на косинус α:
АС = AB ∙ cosα или b = c ∙ cosα.
5) Тангенсом острого угла α прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Тангенс угла α обозначается так: tgα.
6) Катет, противолежащий углу α, равен произведению другого катета на тангенс угла α:
BC = AC ∙ tgα или a = b ∙ tgα.
7) Котангенсом острого угла α прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету. Котангенс угла α обозначается так: сtgα.
8) Катет, прилежащий к углу α, равен произведению другого катета на котангенс угла α:
AC = BC ∙ ctgα или b = a ∙ ctgα.
Поделиться новостью в соцсетях
Метки: Геометрия 8 класс, прямоугольный треугольник, соотношения между сторонами и углами треугольника, треугольник
тригонометрия — Выражение $\sin\theta$ и $\cos\theta$ через $\tan(\theta/2)$
спросил
Изменено 7 лет, 10 месяцев назад
Просмотрено 8к раз
$\begingroup$
Это вопрос:
92}$, нарисуйте рисунок, используя тот факт, что $\tan(\theta) = \frac{\mbox{противоположный}}{\mbox{смежный}}$ в прямоугольном треугольнике.2}.$$
$\endgroup$
0
$\begingroup$
Пусть Θ — точка $(x,y) = (\cos θ, \sin θ)$ на тригонометрической окружности, а F — точка $(−1,0)$. За исключением случая $x=−1$ (где $θ=π$ по модулю 2π и $\tan\frac{θ}{2}$ бесконечно), вектор, идущий от F к Θ, лежит под углом $\frac{ θ}{2}$ от направления $x$ (по модулю π). Это следует из геометрии хорды окружности: 92}.$$
Две другие функции от $θ$ можно найти как $y$ и $y/x$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.

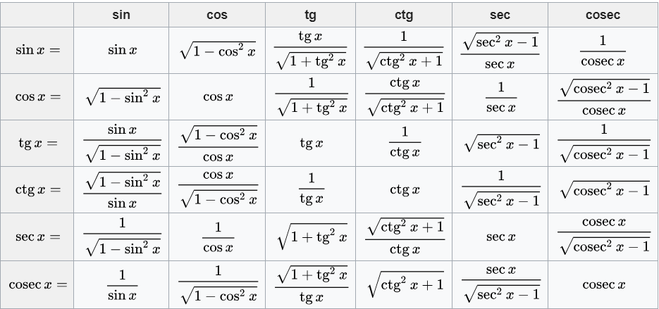 2}.$$
2}.$$