Сколько существует способов рассадить 3 пассажиров на 5 мест: Сколькими способами могут разместиться 3 пассажира в 5-ти местной лодке

Задачи 866-880 | 1000 задач

866. Сколько существует способов распределить компанию из восьми друзей по местам двух купе поезда?

Решение.Так как в двух купе поезда восемь мест, столько, сколько и пассажиров, то различные способы их размещения получаются перестановкой (пересаживанием) пассажиров. Число способов размещения 8 пассажиров на 8 местах равно количеству перестановок из 8-ми элементов P₈ = 8! = 8·7·6·5·4·3·2·1 = 40160.

Ответ. 40160.

867. Сколько существует способов рассадить 18 учеников 11-А за девятью партами физического кабинета (по 2 за парту)?

Решение. Искомое количество равно количеству размещений без повторения из 18 элементов по 18, что совпадает с количеством перестановок из 18 различных элементов P₈ = 18! = 6402373705728000.

Ответ. 18!.

868. Сколько способов выбрать 3-х дежурных из класса, в котором 20 учеников?

Решение. Для выбора дежурных следует произвести неупорядоченную выборку трех учеников из двадцати, то есть сочетание из 20 по 3. Количество таких сочетаний вычисляется по формуле

Ответ.

Ответ. 1140.

869. Сколько различных звукосочетаний можно взять на 10 клавишах рояля, если каждое звукосочетание может включать в себя от 3 до 10 звуков?

Решение. Выбор трех нот из десяти является сочетанием по три элемента из десяти. Количество таких сочетаний обозначают Столько же существует звукосочетаний из семи нот, так как  Звукосочетаний из 4 звуков, так же как и из шести звуков, По 5 звуков — по 8 — и 10 звукосочетаний по 9 звуков, плюс одно по 10. Всего получим 120+210+252+210+120+45+10+1=968 звукосочетаний.

Ответ. 968.

870. С понедельника по пятницу Оля посещает дополнительные занятия по физике, математике, химии, русскому и английскому языках (по одному предмету в день). Сколько у Оли способов составить расписание дополнительных занятий на неделю?

Решение.  Оле придется распределить 5 предметов на 5 дней, что с точки зрения комбинаторики является размещением из 5 элементов по 5. С другой стороны, все 5 дней должны быть заняты каким-нибудь предметом, следовательно, одно расписание получается из другого перестановкой предметов между собоой. Тогда количество различных расписаний равно количеству перестановок из пяти элементов: P₅ = 5! = 120.

Ответ. 120.

871. Сколько существует способов трижды посетить бассейн в течение двух недель (по одному разу в день)?

Решение. Для трех посещений бассейна следует выбрать по одному из четырнадцати дней недели, причем порядок выбора дней не существенен, так как они все-равно будут наступать в календарном порядке. Следовательно речь идет о сочетании из 14 элементов по 3. Количество таких сочетаний C³₁₄ = 14!/(11!*3!)=14*13*12/6=364.

Ответ. 364.

872. У Коли есть 10 различных марок а у Пети — 12. Сколькими способами мольчики смогут обменяться двумя марками?

Решение. У Коли есть возможность выбрать для обмена C²₁₀ пар марок. При этом на каждою выбранную Колей пару Петя сможет предложить любой из имеющихся у него C²₁₂ наборов по две марки. По правилу произведения общее количество способов равно C²₁₀*C²₁₂ = 10!/(8!*2!)*12!/(10!*2!) = 10*9/2*12*11/2 = 2970 способов.

Ответ. 2970.

Решить уравнения (873 – 875):

873.

Решение. Применив формулы количества размещений количества сочетаний получим уравнение:





Разделив обе части уравнения на 24 и применив основное свойство пропорции получим:
23(x-2)(x-3)=24x+24-(x-2)(x-3),
23(x-2)(x-3)+(x-2)(x-3)=24x+24,
24(x-2)(x-3)=24(x+1),
(x-2)(x-3)=x+1,
x²-5x+6-x-1=0,
x²-6x+5=0.
Теорема Виета указывает на то, что последнее квадратное имеет корни 1 и 5. Решение х=1 не удовлетворяет условию задачи, поскольку A^k_n и С^k_n имеют смысл только при неотрицательных значениях n и k.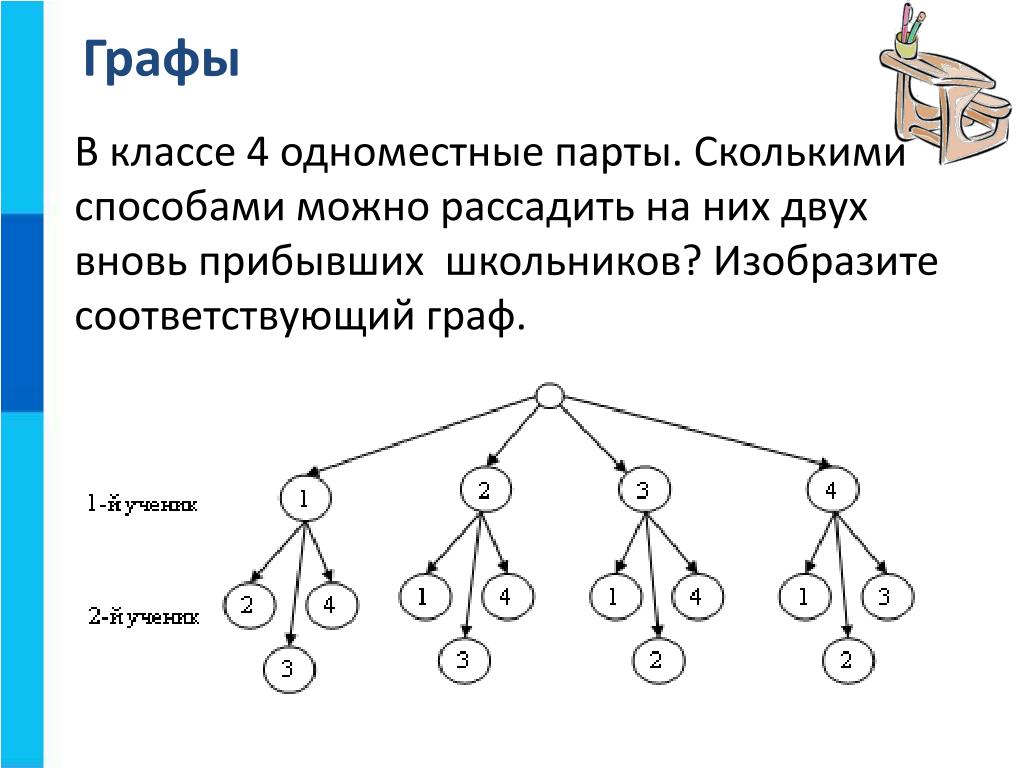

Ответ.х=5.

874.

Решение. Используя известную формулу количества сочетаний из n элементов по k получим уравнение:

После сокращения соответствующих факториалов получим уравнение:

Так как по условию задачи величина x-2 должна выражаться неотрицательным целым числом, то выражение х-1 отлично от 0 и обе части последнего уравнения можно разделить на х-1. Умножив их при этом на 6 получим:
(x+1)x + 2(x-2)(x-3) = 42.
Упрощение последнего уравнения приводит к квадратному уравнению
3x²-9x-30=0,
x²-3x-10=0,
с корнями -2 и 5. Так как решение х=-2 не удовлетворяет условию задачи, то х=5.

Ответ. х=5.

875.

Решение.  Заметим, что заданное уравнение имеет смысл при любых натуральных значениях х, начиная с 2. Применив формулы и получим уравнение:


разделив обе части которого на x и умножив на 2 получим:
2(x-1)(x-2)+x-1=28,
2x²-5x-25=0.
Решив полученное квадратное уравнение найдем x₁=-2,5, x₂=5, но, учитывая сделанное в начале решения замечание, получим х=5.

Ответ. 5.

876. Доказать, что при любых n и k сумма является точным квадратом.

Решение. Преобразуем заданное выражение используя формулу   получим:
Т.е. сумма является квадратом суммы n+k.

Ответ.

877. Сумма биномиальных коэффициентов разложения равна 64. Определить слагаемое, не содержащее x.

Решение. 1) Сумма биномиальных коэффициентов разложения (a+b)^k равна 2^k. Так как 64=2⁶, следовательно по условию задачи 3n = 6, откуда n = 2 и наше разложение принимает вид

2) Слагаемое с номером i = 0,1,…,k в разложении разложения (a+b)^k имеет вид т. е. в нашем разложении — Для того, чтобы это слагаемое не содержало х, нужно, чтобы степени х в числителе и знаменателе совпадали. Т.е. с номером i, где 6-i=2i не содержит х, откуда i=2  и искомое слагаемое равно

Ответ. 240.

878. При каком значении x четвертое слагаемое разложения (5 + 2 x)¹⁶ больше двух соседних слагаемых.

Решение. Четвертое слагаемое разложения  (5 + 2 x)¹⁶ будет иметь вид: . Соседние слагаемые — третье:   и пятое: .

Для того, чтобы четвертое слагаемое было больше третьего, необходимо исполнение неравенства

использовав в котором формулы количества сочетаний и упростив, получим:

Применив к последнему неравенству метод интервалов (см. рисунок), получим его решение:

Аналогично, из условия, что четвертое слагаемого больше пятого, получим неравенство

упрощая его, получим:

Применив метод интервалов (см. рисунок) в этом случає получим:

Общая область полученных интервалов, очевидно, составит

Ответ.

879. Найти наибольший коэффициент разложения (a + b)ⁿ, если сума всех коэффициентов составляет 4096.

Решение. Сумму всех биномиальных коэффициентов n-ой степени можно получить, если в разложении (a + b)ⁿ положить a = b = 1, она равна (1 + 1)ⁿ = 2ⁿ. По условию задачи это число составляет 4096, следовательно n = 12. Величина биномиальных коэффициентов возрастает от начала разложения и убывает к концу разложения, т.е. наибольший коэффициент имеет средний член разложения — при n = 12 это седьмое слагаемое разложения. Оно имеет коэффициент

Ответ. 924.

880. Определить если известно, что пятое слагаемое разложения не зависит от x.

Решение. Пятое слагаемое бинома Ньютона имеет вид . В заданном разложении оно будет выглядеть так:

Для того, чтобы это слагаемое не зависело от x, нужно, чтобы степень возле x равнялась нулю, что получится при n=16.

Следовательно, в задаче спрашиваеться число

Ответ. 240.

Вернуться в задачник

Сегодня многие могут возразить зачем, мол, мучаться и решать эти задачи, если в сети можно найти все готовое? Набираешь в поисковике, к примеру, диплом на заказ в тюмени — и получаешь готовую дипломную или курсовую работу. Возражать не станем: способ получения и качество образования — ваш личный выбор.

Комбинаторика

Комбинаторика – это:
раздел математики
раздел физики
раздел химии

 

Сколькими способами можно рассадить взрослых пассажиров в автомобиле, если в нем 3 пассажирских места:
4
6
8

 

Из 10 учащихся нужно составить группу из 4 для участия в мероприятии. Сколькими способами это можно сделать:
20
120
210

 

15 студентов группы летом будут работать, 16 – поедут отдыхать, из них 4 будут работать, а затем поедут отдыхать. Сколько человек в группе всего:
17
28
37

 

Соединения, каждое из которых содержит m элементов, взятых из данных n; одно соединение отличается от другого по крайней мере одним элементом или порядком их следования, называются:
Сочетания
Перестановки
Размещения

 

Соединения, из которых каждое содержит все данные n; одно соединение отличается от другого только порядком расположения элементов, называются:
Размещения
Перестановки
Сочетания

 

Соединения, каждое из которых содержит m элементов, взятых из данных n; одно соединение от другого отличается по крайней мере одним элементом, называются:
Перестановки
Размещения
Сочетания

 

Для разгрузки поступивших товаров требуется выделить 4 из 15 имеющихся рабочих. Сколькими способами можно это сделать, осуществляя отбор в случайном порядке:
1365
835
1035

 

10 студентов играют в футбол, 4 – участвуют в соревнованиях по дзюдо, из них 3 участвуют и в соревнованиях по дзюдо и по футболу. Сколько человек всего:
21
17
11

 

Сколькими способами можно составить команду из 4 человек для соревнований по бегу, если имеется 7 бегунов:
53
35
25

 

На полу в комнате можно положить ламинат, паркет или линолеум. А стены покрасить, поклеить обои, побелить или обшить гипсокартоном. Сколько вариантов ремонта есть у хозяина:
12
22
9

 

Сколькими способами можно разместить на полке 5 книг:
12
120
210

 

Если объект а может быть выбран m способами и после каждого такого выбора объект b может быть выбран n способами, то выбор пары объектов а и b в указанном порядке может быть осуществлен … способами:
m*n
mn
mn

 

Сколькими способами могут разместиться 8 человек в салоне автобуса на восьми свободных местах:
4032
1600
40320

 

Комбинаторика отвечает на вопрос:
сколько различных комбинаций можно составить из элементов данного множества
какова частота массовых случайных явлений
с какой вероятностью произойдет некоторое случайное событие

 

Сколько существует вариантов выбора двух чисел из восьми:

18

28

16

 

В партии из 4000 семян пшеницы 50 семян не взошли. Какова вероятность появления невсхожих семян:

0,001

0,05

0,0125

 

Выберите из предложенных множеств множество натуральных чисел:

Q

N

C

 

Множество, состоящее из всех элементов, принадлежащих множеству А и не принадлежащих множеству В, называют:

объединением множеств А и В

пересечением множеств А и В

разностью множеств А и В

 

Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5:

210

120

3125

 

Сколькими способами из 9 учебных дисциплин можно составить расписание учебного дня из 6 различных уроков:

60480

604

6048

 

Если объект А можно выбрать х способами, а объект В – у способами, то каким количеством способов можно выбрать объект «А и В»:

x-y

xy

xy

 

Сколькими способами можно расставить 4 различные книги на книжной полке:

36

20

24

 

В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать:

80

110

210

 

В корзине лежат грибы, среди которых 10% белых и 40% рыжих. Какова вероятность того, что выбранный гриб белый или рыжий:

0.1

0.50

0.5

 

Сколько существует трехзначных чисел, все цифры которых нечетные и различные:

120

60

30

 

Сколько различных двухзначных чисел можно записать, используя цифры 2, 3, 8, если цифры в этих числах могут повторяться:

9

3

18

 

Сколькими способами могут разместиться 3 человека в четырехместном купе на свободных местах:

12

48

24

 

Термин «комбинаторика» был введён в математический обиход:

Лейбницем

Колмогоровым

Гарднером

 

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных:

ассоциаций

конфигураций

формул

 

В поезде свободны пять мест, сколько же тогда мест могут сесть три пассажира?1.

202. 303. 104. 60

Ответить

Проверено

149.1k+ просмотров

Подсказка: Для решения этого вопроса необходимо знать о перестановках и комбинациях. Поскольку мы знаем, что в этой задаче есть только утверждения, и мы должны сказать, истинны они или ложны. Итак, сначала мы обсудим перестановку и комбинацию, а затем, применяя их концепцию, найдем решение проблемы, а затем найдем существование данных утверждений.

Полное пошаговое решение:
По нашему вопросу дано, что в поезде 5 свободных мест. И на них должны сидеть три пассажира. Итак, нам нужно определить, сколько способов смогут сесть на них все три пассажира. Здесь мы будем использовать комбинации, потому что с их помощью мы можем легко их вычислить.
Как известно, перестановки — это упорядоченные комбинации. Значит, где порядок не имеет значения, там перестановка. И перестановки тоже бывают двух видов, одна повторяется или допускается повторение, а вторая не повторяется. Перестановки с повторением вычислить проще всего. А перестановка без повторения каждый раз уменьшает количество доступных вариантов. Итак, если мы видим наш вопрос, то: 9{5}{{P}_{3}}$.
$=\dfrac{5!}{\left( 5-3 \right)!}=\dfrac{5!}{2!}=\dfrac{120}{2}=60$
Отсюда правильный ответ это вариант 4.

Примечание: При решении этого типа вопросов вы должны убедиться, что мы будем использовать здесь перестановку или комбинацию, и в перестановке необходимо найти, что если есть какие-либо события, которые повторяются или не повторять.

Недавно обновленные страницы

Рассчитать изменение энтропии, связанное с преобразованием класса 11 химии JEE_Main

Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main

Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 Для химической реакции JEE03

rm2Clg в rmCrmlrm2rmg знаки химического класса 11 JEE_Main

Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main

Рассчитать изменение энтропии, связанное с преобразованием химического класса 11 JEE_Main

Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main

Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Класс 11 2 Для химической реакции JEE03

rm2Clg to rmCrmlrm2rmg признаки 11 класса химии JEE_Main

Изменение энтальпии перехода жидкой воды 11 класса химии JEE_Main

Тенденции сомнения

комбинаторика — Как мне ответить на вопросы, которые требуют, чтобы разные люди сидели на нескольких местах?

спросил 2 года, 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 753 раза

$\begingroup$

В микроавтобусе 17 мест, расположенных в 4 ряда. Задний ряд имеет 5 мест, а остальные 3 ряда имеют по 2 места с каждой стороны. В микроавтобус садятся 11 пассажиров.

(i) Сколько возможных рассадок есть для 11 пассажиров?

(ii) Сколько возможных рассадок существует, если 5 конкретных людей сидеть на заднем ряду?

Из 11 пассажиров 5 не состоят в браке, а остальные 6 состоят из 3 супружеских пар.

(iii) Сколькими способами можно выбрать 5 из 11 пассажиров автобуса, если должны быть 2 супружеские пары и 1 человек, которые могут состоять или не состоять в браке?

---

Я застрял в части (ii).

Что я уже сделал:

Шаг 1: Определите, сколько способов заставить 5 разных людей сесть на заднее сиденье. таким образом, 11P5 = 55440

Шаг 2: Определите, как разместить оставшихся 6 человек (11-5 = 6 человек) на оставшихся местах (17 — 5 = 12 мест), поэтому 12P6 = 665280

Я использовал P, потому что порядок людей имеют значение.

Но если я умножу 1 на 2, получится смехотворно большое число.

---

Я застрял в части (iii).

Что я сделал:

1. Выбрать 2 пары из 3 пар. 3P2 = 6

2. Выберите последнего человека из оставшихся.

   оставшихся человека = 1 пара + 5 одиночек = 2 + 5 = 7

   Итак, 7P1 = 7

3. Умножить: 6*7=42

Но ответ 21. Почему используется C вместо P? Разве порядок не должен иметь значения. Например: пара 1 и пара 2 такие же, как пара 2 и пара 1.

• комбинаторика

$\endgroup$

3

$\begingroup$

В микроавтобусе 17$ мест, расположенных в 4$ ряда. В заднем ряду есть места по 5 долларов, а в других рядах по 3 доллара — по 2 доллара с каждой стороны. Пассажиры по $11$ садятся в микроавтобус. Сколько возможных рассадок существует, если $5$ конкретных людей сидят в заднем ряду?

Если нам говорят, что на заднем сиденье сидят пять конкретных человек, нам не нужно их выбирать. По сути, нам говорят, что Эбигейл, Брюс, Клэр, Дэвид и Эсме сидят на заднем сиденье. Нам просто нужно расположить их на заднем сиденье, что можно сделать за 5!$ способами. Остальные шесть человек могут быть рассажены на оставшиеся двенадцать мест $P(12, 6)$ способами. Таким образом, количество рассадок $11$ пассажиров в $17$-местном микроавтобусе, если пять конкретных человек сидят на заднем сиденье, равно $5!P(12,6)$.

Из $11$ пассажиров $5$ не состоят в браке, а остальные $6$ состоят из $3$ супружеских пар. Сколькими способами можно выбрать $5$ из $11$ пассажиров автобуса, если необходимо $2$ супружеских пар и $1$ других людей, которые могут состоять или не состоять в браке?

Нужно выбрать две из трех пар, что можно сделать $\binom{3}{2}$ способами, и одного из оставшихся семи человек, что можно сделать $\binom{7}{1} $ способы. Следовательно, существует $$\binom{3}{2}\binom{7}{1}$$ возможных вариантов выбора из двух супружеских пар и еще одного человека, который может состоять или не состоять в браке.