Решение неравенств с одной переменной под знаком модуля: определение, правило, примеры
Правило раскрытия модуля в неравенствах
Исходя из сведений о совокупности неравенств (см. §39 данного справочника), для простейшего неравенства с модулем можем записать:
$$ |x| \lt a \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \ge 0 \\ |x| \lt a \end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ x \in \varnothing \end{array} \right.} \end{array} \right. \Rightarrow {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \lt a \\ x \ge 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} -x \lt a \\ x \lt 0 \end{array} \right.} \end{array} \right. \end{array} \right.} \iff {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} 0 \le x \lt a \\ {\left\{ \begin{array}{c} x \gt -a \\ x \lt 0 \end{array} \right.} \end{array} \right. \end{array} \right.} \iff {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} 0 \le x \lt a \\ -a \lt x \lt 0 \end{array} \right.
\end{array} \right.} \iff {\left\{ \begin{array}{c} a \ge 0 \\ -a \lt x \lt a \end{array} \right.} $$
Например:
$ |x| \lt 5 \iff -5 \lt x \lt 5 или x \in (-5;5) $
$ |x| \lt -3 \iff x \in \varnothing$ — решений нет
Рассмотрим неравенство:
$$ |x| \gt a \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \gt a \\ x \ge 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} -x \gt a \\ x \lt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \gt a \\ x \ge 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} x \lt -a \\ x \lt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} x \gt a \\ x \lt -a \end{array} \right. \end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ \left[ \begin{array}{cc} x \ge 0 \\ x \lt 0 \end{array} \right. \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \ge 0 \\ x \lt -a \cup x \gt a \end{array} \right.
} \\ {\left\{ \begin{array}{c} a \lt 0 \\ x \in \Bbb R \end{array} \right.} \end{array} \right. $$
Например:
$|x| \gt 5 \iff x \lt -5 \cup x \gt 5$ или $x \in (-\infty;-5) \cup (5;+\infty)$
$|x| \gt -3 \iff x \in \Bbb R$ — любое число
Примеры
Пример 1. Решите неравенство:
$а) |x+7| \lt 3$
$|x+7| \lt 3 \iff -3 \lt x+7 \lt 3 \iff -3-7 \lt x \lt 3-7 \iff -10 \lt x \lt -4 $
$ x \in (-10;-4) $
$ б) |x-3| \lt -1 $
Модуль не может быть меньше отрицательного числа:
$x \in \varnothing$, решений нет
$ в) |2x+5| \gt 3 $
$ |2x+5| \gt 3 \iff \left[ \begin{array}{cc} 2x+5 \lt -3 \\ 2x+5 \gt 3 \end{array} \right. \iff \left[ \begin{array}{cc} 2x \lt -8 \\ 2x \gt -2 \end{array} \right. \iff \left[ \begin{array}{cc} x \lt -4 \\ x \gt -1 \end{array} \right. \iff x \lt -4 \cup x \gt -1 $
$x \in (-\infty;-4) \cup (-1;+\infty)$
$ г) |3x+7| \gt -1 $
Модуль всегда больше отрицательного числа:
$x \in \Bbb R$, любое число
Пример 2.
Решите двойное неравенство:
$ 1 \lt |5x-4| \lt 11 $
Способ 1
$ 1 \lt |5x-4| \lt 11 \iff {\left\{ \begin{array}{c} |5x-4| \gt 1 \\ |5x-4| \lt 11 \end{array} \right.} \iff {\left\{ \begin{array}{c} \left[ \begin{array}{cc} 5x-4 \lt -1 \\ 5x-4 \gt 1 \end{array} \right. \\ -11 \lt 5x-4 \lt 11 \end{array} \right.} \iff {\left\{ \begin{array}{c} \left[ \begin{array}{cc} 5x \lt 3 \\ 5x \gt 5 \end{array} \right. \\ -7 \lt 5x \lt 15 \end{array} \right.} \iff $
$$ \iff {\left\{ \begin{array}{c} \left[ \begin{array}{cc} x \lt 0,6 \\ x \gt 1 \end{array} \right. \\ -1,4 \lt x \lt 3 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \lt 0,6 \cup x \gt 1 \\ -1,4 \lt x \lt 3 \end{array} \right.} \iff -1,4 \lt x \lt 0,6 \cup 1 \lt x \lt 3 $$
Способ 2
$ 1 \lt |5x-4| \lt 11 \iff \left[ \begin{array}{cc} -11 \lt 5x-4 \lt -1 \\ 1 \lt 5x-4 \lt 11 \end{array} \right. \iff \left[ \begin{array}{cc} -7 \lt 5x \lt 3 \\ 5 \lt 5x \lt 15 \end{array} \right.
2+3t-4 \lt 0 \iff (t+4)(t-1) \lt 0 \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} t+4 \gt 0 \\ t-1 \lt 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} t+4 \lt 0 \\ t-1 \gt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} t \gt -4 \\ t \lt 1 \end{array} \right.} \\ {\left\{ \begin{array}{c} t \lt -4 \\ t \gt 1 \end{array} \right.} \end{array} \right. \iff$
$\iff \left[ \begin{array}{cc} -4 \lt t \lt 1 \\ t \in \varnothing \end{array} \right. \iff -4 \lt t \lt 1$
Возвращаемся к исходной переменной:
$ -4\lt |x|\lt 1 \iff |x|\lt 1 \iff -1\lt x\lt 1 $
Ответ: $x \in (-1;1)$
Мой школьный блог: Живая математика
нужно ввести solve sin(x)=0.5
Пример 5. Чтобы решить уравнение, содержащее модульные скобки,
нужно ввести solve abs(x)=8
x + y = 5,
x — y = 1,
нужно ввести solve x+y=5 && x-y=1
Знаки && в данном случае обозначает логическое «И».
abs
модуль
систем уравнений и неравенств
..)maximize
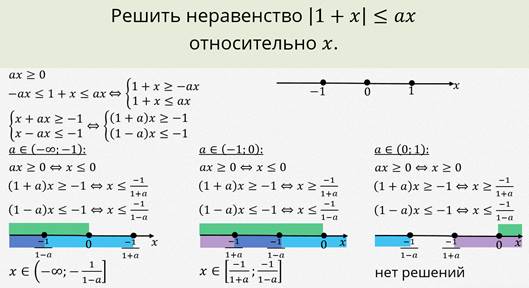
Рациональные и модульные неравенства | Понятие и вопросы
Рациональные неравенства:
Неравенства вида (ax+b/cx+d) < k или (ax+b/cx+d) > k называются рациональными неравенствами, где ax + b и cx + d являются линейными алгебраическими выражениями. Для решения рациональных неравенств необходимо выполнить следующие шаги.
Рекомендуемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас
- Приравняем правую часть к нулю, переставив постоянный член в левую часть.
- Решите левую часть так, чтобы она приняла форму mx+1/nx+p <0 или mx+1/nx+p >0 Убедитесь, что ‘m’ и ‘n’, которые являются коэффициентами ‘x’ в числителе и знаменателе положительны.
Приравняйте числитель и знаменатель к нулю, чтобы получить критические точки. Поместите эти точки на числовую прямую. Числовая строка будет разделена на три части. Крайняя правая часть дает решение положительных неравенств, средняя часть дает решение отрицательных неравенств, а самая левая часть дает решение положительных неравенств.
Решим несколько задач на рациональное неравенство:
Иллюстрация 1: Решить 3x+5/5x-2<0
Решение: правая часть уже равна нулю. Так что здесь нам не нужно делать никаких расчетов. Чтобы получить критические точки, приравняйте числитель и знаменатель к нулю.
У нас есть 3x + 5 = 0 ⇒ x=(-5/3) и 5x – 2 = 0 ⇒ x = 2/5
Нанесите эти точки на числовую прямую.
Так как данное неравенство отрицательное, то решение (-5/3)< x < (2/5)
Модульные неравенства или абсолютные неравенства
Неравенства вида |ax + b| < k или |ax + b| > k называются модульными или абсолютными неравенствами.
Чтобы решить эти неравенства, помните о следующих правилах:
- Если |x| < а, тогда – а < х < а
- Если |х| > а, то либо х > а, либо х < - а
- Если |х – л| < a, то l – a < x < l + a
- Если |х – л| > a, то либо x > l + a, либо x < l – a.
Давайте попробуем ответить на вопросы о модульном неравенстве:
Иллюстрация 2: Решить |x – 3| < 5.
Решение: Имеем |x – 3| < 5
⇒ — 5 < x – 3 < 5 (Если |x| < a, то – a < x < a)
⇒ 3 – 5 < x < 3 + 5 (Одно и то же число может быть добавлено с обеих сторон неравенство)
⇒ -2 < x < 8, что и является требуемым решением.
Рекомендуемое действие:
Начните подготовку с БЕСПЛАТНОГО доступа к 25+ макетам, 75+ видео и 100+ тестам по главам. Зарегистрируйтесь сейчас
Иллюстрация 3: Решите |8x + 5| < 9.
Решение: Имеем |8x + 5| < 9.
⇒ — 9 < 8x + 5 < 9 (Если |x| < a, то – a < x < a)
⇒ — 14 < 8x < 4
⇒ -14/8 < x < 4/8
⇒ -7/4 < x < 1/2, что и является требуемым решением.
Неравенства абсолютного значения
Горячая математикаАн абсолютная величина неравенство является неравенство который имеет знак абсолютного значения с переменной внутри.
Неравенства абсолютного значения (
< ):Неравенство | Икс | < 4 означает, что расстояние между Икс а также 0 меньше чем 4 .
Так, Икс > − 4 А ТАКЖЕ Икс < 4 . Набор решений { Икс | − 4 < Икс < 4 } .
При решении абсолютных неравенств необходимо учитывать два случая.
Кейс
1
: выражение внутри символов абсолютного значения является положительным.
Кейс 2 : выражение внутри символов абсолютного значения отрицательное.
Решение — это перекресток решений этих двух случаев.
Другими словами, для любых действительных чисел а а также б , если | а | < б , тогда а < б А ТАКЖЕ а > − б .
Пример 1
Решите и нарисуйте.
| Икс − 7 | < 3
Чтобы решить такое неравенство, нам нужно разбить его на составное неравенство .
Икс − 7 < 3 а также Икс − 7 > − 3 .
− 3 < Икс − 7 < 3
Добавлять
7
к каждому выражению.
− 3 + 7 < Икс − 7 + 7 < 3 + 7 4 < Икс < 10
График выглядит так:
Неравенства абсолютного значения ( > ):
Неравенство | Икс | > 4 означает, что расстояние между Икс а также 0 больше, чем 4 .
Так, Икс < − 4 ИЛИ ЖЕ Икс > 4 . Набор решений { Икс | Икс < − 4 или же Икс > 4 } .
При решении абсолютных неравенств необходимо учитывать два случая.
Кейс 1 : выражение внутри символов абсолютного значения является положительным.
Другими словами, для любых действительных чисел а а также б , если | а | > б , тогда а > б А ТАКЖЕ а < − б .
Пример 2 :
Решите и нарисуйте.
| Икс + 2 | ≥ 4
Разбить на два неравенства.
Икс + 2 ≥ 4 ИЛИ ЖЕ Икс + 2 ≤ − 4
Вычесть
2
с каждой стороны каждого неравенства.