Высота треугольника это: Что такое высота треугольника? Ответ на webmath.ru

Высота треугольника. Визуальный гид (ЕГЭ — 2021)

Как и для медиан, и для биссектрис, для высот треугольника верно следующее утверждение:

В любом треугольнике три высоты или их продолжения пересекаются в одной точке.

Доказывать это утверждение мы здесь, пожалуй, не будем.

Давай просто нарисуем, чтобы понять, как это бывает «высоты или их продолжения».

Хотите читать учебник без ограничений? Зарегистрируйтесь:

1. Треугольник остроугольный – тогда пересекаются сами высоты:

2. Треугольник тупоугольный – тогда пересекаются продолжения высот:

Что же полезного мы ещё не обсудили?

Угол между высотами

Давай узнаем, вдруг угол между высотами можно как–то выразить через углы треугольника? Давай рассмотрим остроугольный треугольник.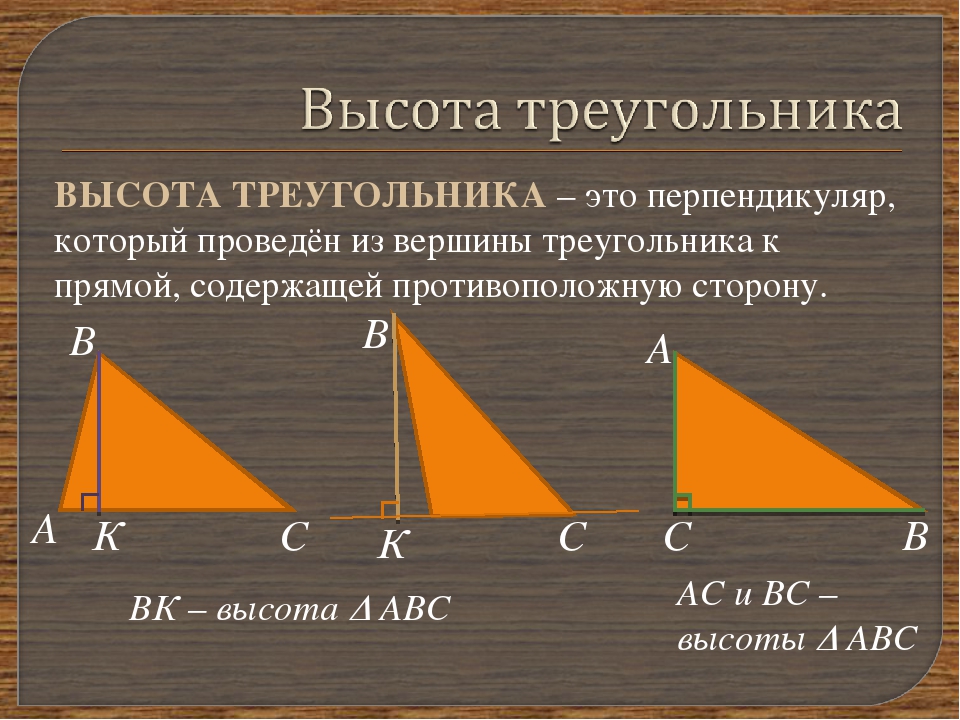

\circ -\angle ~B\).

И ещё кое–что…

Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:

Что видим теперь? Ещё подобные треугольники!

Как от двух линий вообще могут получиться столько подобных треугольников?!

Но тем не менее…

\( \Delta C{{H}_{C}}B\sim \Delta C{{H}_{A}}H\sim \Delta A{{H}_{A}}B\sim \Delta A{{H}_{C}}H\)

Видишь, какое богатство? И всё это может быть использовано в задачах!

Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.

Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…

Главное, ты не старался просто запоминать все эти факты, а осознай, что

их можно очень просто вывести.

И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Высота треугольника. Свойство высоты прямоугольного треугольника

      Определение 1. Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).

Рис.1

      На рисунке 1 изображена высота BD, проведённая из вершины B треугольника ABC. Точка D – основание высоты.

      Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.

      Утверждение. Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).

Рис.2

      Доказательство. Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям

      В силу признака подобия прямоугольных треугольников треугольники BCD и ACD подобны. Следовательно,

      Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD, что и требовалось доказать.

      Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.

Расположение высот у треугольников различных типов

Остроугольный треугольник

Все высоты остроугольного треугольника лежат внутри треугольника.

Прямоугольный треугольник

Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника

Тупоугольный треугольник

Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника

Ортоцентр треугольника

      Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.

      Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).

Рис.3

      Обозначим точки пересечения этих прямых символами A₁, B₁ и C₁, как показано на рисунке 3.

      В силу параллельности прямых AC и C₁A₁, а также BC и C₁B₁ четырёхугольники   AC₁BC   и   ABA₁C – параллелограммыпараллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства

C₁B = AC = BA₁.

      Следовательно, точка B является серединой стороны C₁A₁.

      В силу параллельности прямых BC и C₁B₁, а также AB и B₁A₁ четырёхугольники   AC₁BC   и   ABCB₁ – параллелограммы,параллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства

C₁A = BC = A₁B₁.

      Следовательно, точка A является серединой стороны C₁B₁.

      В силу параллельности прямых AB и B₁A₁, а также AC и C₁A₁ четырёхугольники   ABA₁C   и   ABCB₁ – параллелограммыпараллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства

A₁C = AB = B₁C.

      Следовательно, точка C является серединой стороны B₁A₁.

      Таким образом, высоты треугольника ABC являются серединными перпендикулярами треугольника A₁B₁C₁ (рис. 4),

Рис.4

и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.

      Теорема 1 доказана.

      Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.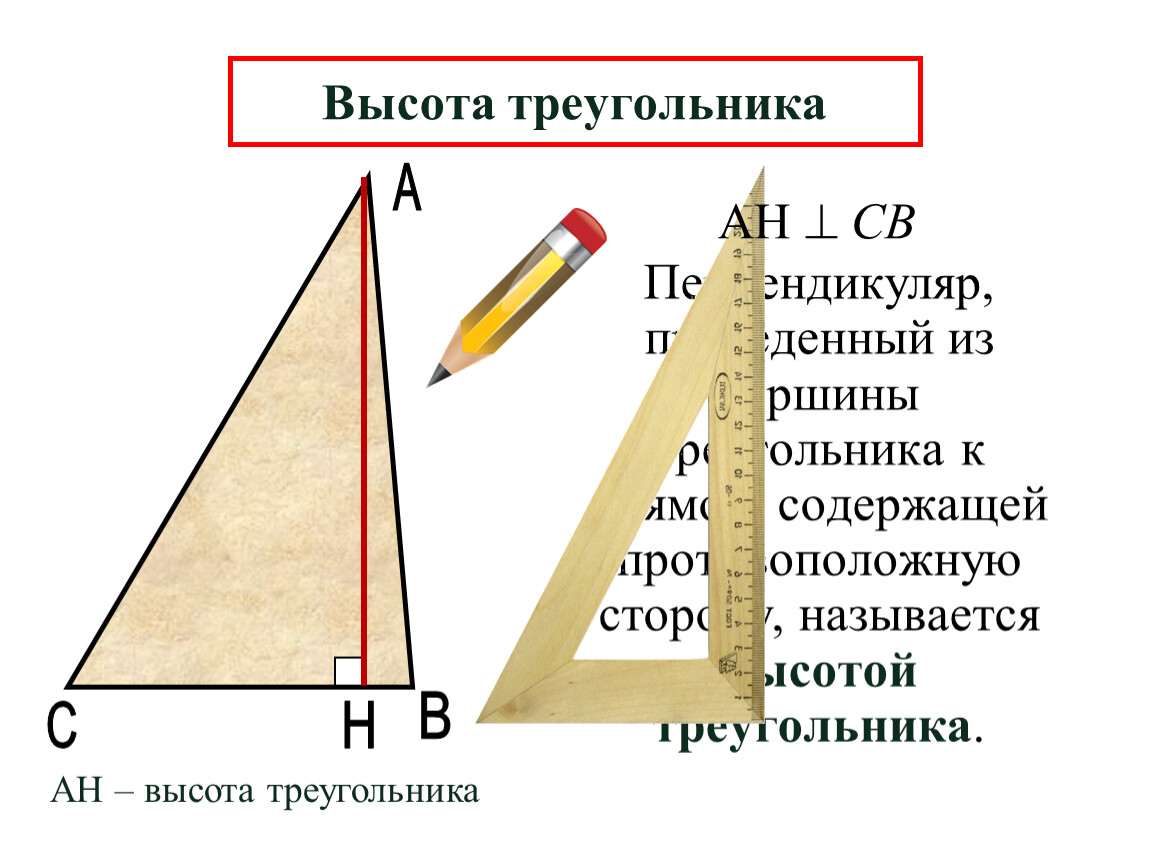

      У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.

Расположение ортоцентров у треугольников различных типов

Фигура	Рисунок	Описание
Остроугольный треугольник		Ортоцентр остроугольного треугольника лежит внутри треугольника.
Прямоугольный треугольник		Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Тупоугольный треугольник		Ортоцентр тупоугольного треугольника лежит вне треугольника. В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.

Ортоцентрический треугольник

      Решим следующую задачу.

      Задача. В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC.

Рис.5

      Решение. Рассмотрим треугольники ADC и BEC. Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство

      Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники   DCE   и   ABC   подобны. Решение задачи завершено.

      Из подобия треугольников   ABC   и   EDC (рис.5) вытекает важное следствие.

      Следствие 1.

      Определение 3. Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).

Рис.6

      Из определения 3 и следствия 1 вытекает следствие 2.

      Следствие 2. Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).

Рис.7

      Тогда справедливы равенства

      Из следствия 2 вытекает теорема 2.

      Теорема  2. Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).

      Доказательство. Воспользовавшись следствием 2, получаем:

что и требовалось доказать.

Задача Фаньяно

      Задача Фаньяно. Рассматриваются всевозможные треугольники   DEF,   вершины    D,   E   и   F   которых лежат на сторонах   BC,   AC и   AB   остроугольного треугольника   ABC   соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника   ABC.

      Решение. Пусть   DEF – один из рассматриваемых треугольников. Обозначим символом   D₁   точку, симметричную точке   D   относительно прямой   AC, и обозначим символом  

D₂   точку, симметричную точке D относительно прямой   AB (рис.8).

Рис.8

      Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D₁D₂. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D₁D₂ с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D₁D₂ (рис. 9).

Рис.9

      Заметим также, что выполнено равенство

AD = AD₁ = AD

₂.

      Кроме того, выполнено равенство

      Поэтому

      Отсюда вытекает, что длина отрезка D₁D₂ будет наименьшей тогда, когда длина отрезка AD  будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF  треугольник с наименьшим периметром является единственным.

      Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:

      Следовательно, наименьший периметр рассматриваемых треугольников DEF равен

      Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.

      Лемма. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).

Рис.10

      В этом случае отрезок D₁D₂  проходит через точки F и E.

      Доказательство. Заметим, что в силу следствия 2 выполняются равенства:

      Кроме того, в силу равенства треугольников DFK и KFD₂, а также в силу равенства треугольников DEL и

LED₁ выполняются равенства:

      Следовательно,

откуда вытекает, что углы AEF и D₁EL , а также AFE и D₂FK являются вертикальными углами. Это означает, что точки D₁, F, E, D₂ лежат на одной прямой. Лемма доказана.

      Доказательство леммы и завершает решение задачи Фаньяно.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Треугольник: вершины, стороны, углы. Высота, биссектриса и медиана

Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами

треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике  ABC  вершины  A,  B  и  C  — это вершины треугольника, звенья  AB,  BC  и  CA  — стороны треугольника. Три угла —  ∠ABC,  ∠BCA  и  ∠CAB  — углы треугольника. Часто углы треугольника обозначаются только одной буквой:  ∠A,  ∠B,  ∠C.

Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник  ABC,  или  BCA,  или  CBA.  Вместо слова треугольник часто используется знак  .  Так, запись  ABC  будет читаться:  треугольник  ABC.

У каждого треугольника 3 вершины, 3 стороны и 3 угла.

Высота

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок  BN  — это высота  ABC. Отрезок  EL  высота  DEF, опущенная на продолжение стороны  DF.

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.

Каждый треугольник имеет три высоты.

Биссектриса

Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок  BN  — это биссектриса  ABC.

Каждый треугольник имеет три биссектрисы.

Медиана

Медиана треугольника

— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок  BN  — это медиана  ABC.

Каждый треугольник имеет три медианы.

Высота треугольника, ортоцентр

Расстояние между вершиной треугольника и противоположной стороной называется высотой. Формально, это самый короткий отрезок между вершиной треугольника и (с возможным продлением) противоположной стороной.

Каждый треугольник имеет 3 высоты которые пересекаются в одной точке — ортоцентре. Если мы используем стандартные обозначения, в треугольнике ABC, есть три высоты: AH_a, BH_b, CH_c. Эти три отрезка пересекаются в одной точке — ортоцентре (точка H на рисунке) треугольника. Для тупого треугольника (имеющего один угол, больше чем 90°), ортоцентр находится за пределами треугольника.

Высоты остроугольного треугольника

Ортоцентр — это точка внутри треугольника.

∠ AHB = 180 — γ = α + β
∠ BHC = 180 — α = β + γ
∠ AHC = 180 — β = α + γ
∠ AHH_c = β, ∠ BHH_c = α, ∠ BHH_a = γ

Высоты тупоугольного треугольника

Ортоцентр находится вне треугольнка.
Две высоты также всегда лежат вне треугольника.
∠ AHH_c = ∠ CBA = β
∠ H_cHB = ∠ CAB = α

Правый треугольник

Высота AH_a совпадает с AC.
Высота BH_b совпадает с BC.
Ортоцентр H совпадает с C.
∠ ACH_c = β, ∠ BCH_c =α

Формулы

$AH_a:BH_b:CH_c=\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$

$\frac{a}{AH_a}=\frac{b}{BH_b}=\frac{c}{\frac{AH_aBH_b}{CH_c}}$

R — радиус описанной окружности
r — радиус вписанной окружности
p — полуперимерт: (a + b + c)/2

$AH_a=b \sin\gamma=c \sin\beta=\frac{a \sin\beta \sin\gamma}{\sin\alpha}=$

$=2R \sin\beta\ \sin\gamma=\frac{bc}{2R}=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{a}$

$BH_b=a\ \sin\gamma=c\ \sin\alpha=\frac{b\ \sin\alpha\ \sin\gamma}{\sin\beta}=$
$=2R\ \sin\alpha \sin \gamma=\frac{ac}{2R}=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{b}$

$CH_c=a\ \sin\beta=b\ \sin\alpha=\frac{c\ \sin\alpha\ \sin\beta}{\sin\gamma}=$
$=2R\ \sin\alpha \sin \beta=\frac{ab}{2R}=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{c}$

$\frac{1}{AH_a}+\frac{1}{BH_b}+\frac{1}{CH_c}=\frac{1}{r}$

Равнобедренный треугольник.

Свойства, Признаки, Высота

Определение равнобедренного треугольника

Определение равнобедренного треугольника звучит проще простого:

Равнобедренным называется треугольник, у которого две стороны равны.

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.

Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!

 

Геометрия в 7 классе полна острых углов. Чтобы ваш ребенок миновал их круглым отличником, запишите его на бесплатный пробный урок математики в онлайн-школу Skysmart.

Наши опытные преподаватели научат с закрытыми глазами отличать равнобедренный треугольник от равностороннего, а интерактивная платформа не даст заскучать на уроках.

 

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.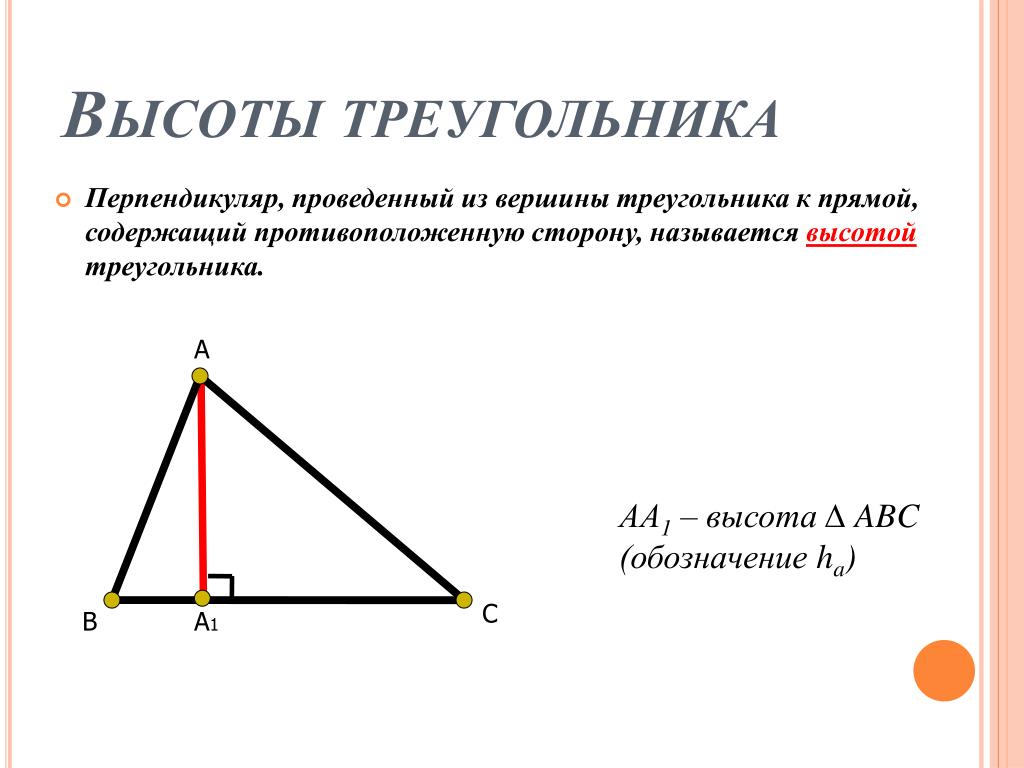

Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.

А вот и доказательство:

• Δ ABC
• Высота BH делит Δ ABC на два прямоугольных треугольника ABH и CBH
• Δ ABH = Δ CBH, поскольку гипотенузы и катет равны по теореме Пифагора
• Согласно теореме 1: в треугольниках ABH и BCH ∠ BАH = ∠ BСH, поскольку углы при основании равнобедренного треугольника равны
• Так как Δ ABC — равнобедренный, то его боковые стороны равны AB = BC
• AH = CH, поскольку точка H делит основание Δ ABC на две равные части
• Δ ABH = Δ BCH
• Значит, отрезок BH одновременно биссектриса, медиана и высота равнобедренного треугольника ABC

Вуаля, сразу три теоремы доказаны.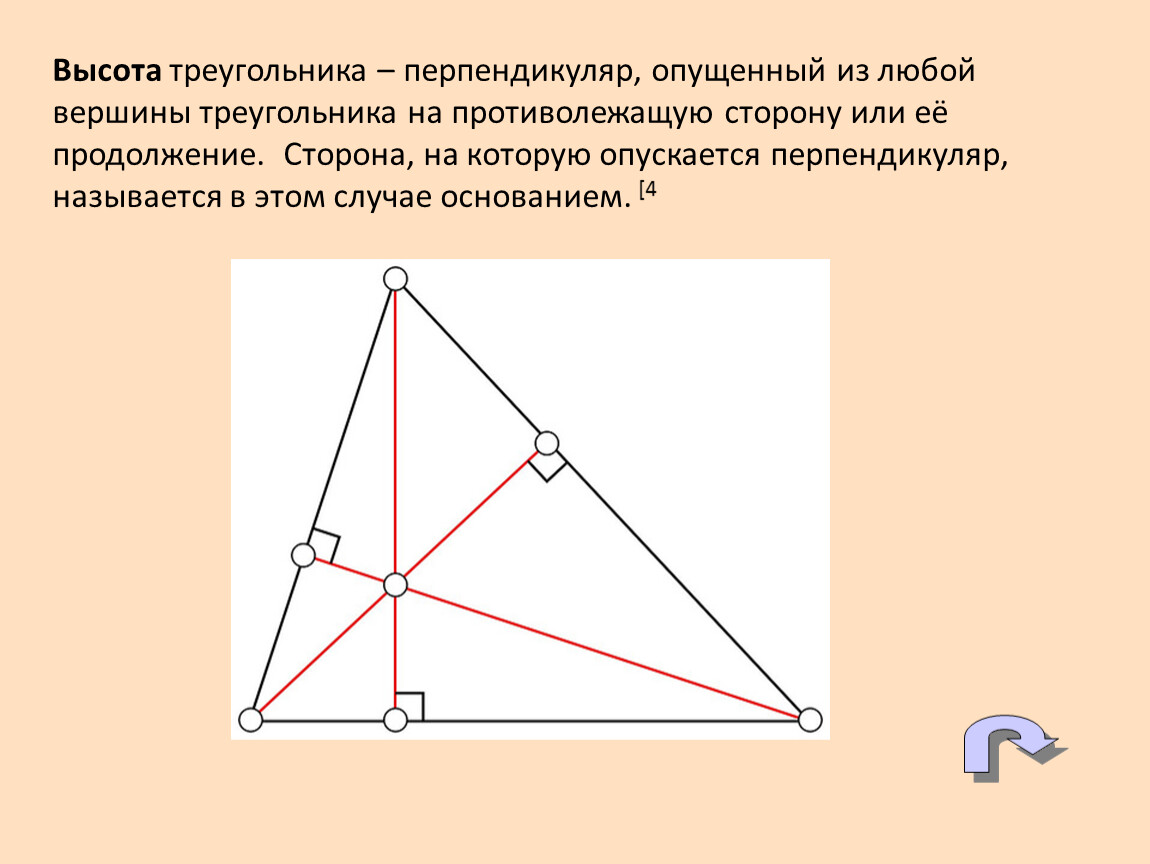

Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).

Доказательство:

Дано два Δ ABC = Δ A1B1C1.

Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.

Если все стороны совпадают — треугольники равны, а теорема доказана.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

 

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.


2. Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.


3. Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.


4. Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!


5. Если два угла треугольника равны, такой треугольник является равнобедренным.

Свойства углов равнобедренного треугольника В равнобедренном треугольнике углы при основании равны. Углы при основании в равнобедренном треугольнике — всегда острые. Сумма углов равнобедренного треугольника равна 180 градусам.

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

Формулы длины стороны (основания b) равнобедренного треугольника

 

Формулы длины равных сторон равнобедренного треугольника (стороны a):

 

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

L — высота, биссектриса и медиана

 

Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)

Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘

Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.

Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘

Еще больше тренировок — в детской школе Skysmart. Записывайте ребенка на бесплатный урок математики и приходите сами: покажем, как все устроено и наметим индивидуальную программу занятий.

Что такое высота треугольника

Геометрия покажется не такой сложной, если знать ее законы. В пространственных построениях есть не только строгая логика, но и своеобразная поэзия. Но сначала нужно запомнить термины и определения.

Треугольник — это плоский многоугольник, ограниченный тремя отрезками прямой. Эти отрезки называются сторонами, а точки пересечения сторон — вершинами.Все три внутренних угла фигуры могут быть разными. Если один угол прямой или тупой, то два других обязательно острые. Три угла треугольника в сумме составляют триста шестьдесят градусов.

Внутри треугольника можно провести разные линии. Свойства некоторых из них изучены и служат для определения геометрических параметров. К таким особым линиям относятся высоты. Высотой треугольника называется перпендикуляр, опущенный из вершины угла на противоположную сторону. Сторона в этом случае является основанием треугольника.

Очевидно, что у данной фигуры может быть не более трех высот. В прямоугольном треугольнике можно провести только одну высоту — из вершины прямого угла на гипотенузу. В тупоугольном треугольнике высоты из вершин острых углов проводятся на продолжение сторон и находятся за пределами площади, но тем не менее это именно высоты треугольника со всеми их свойствами.

Проведите высоту к любой из сторон произвольного треугольника, и исходная фигура будет разделена на два прямоугольных треугольника. Наличие прямого угла облегчает решение геометрических задач. Для прямоугольных треугольников известны многие соотношения, начиная с теоремы Пифагора.

Высота входит в различные формулы решения треугольников. Самая известная — формула площади, которая для треугольника равна половине произведения его основания на высоту.

В правильных многоугольниках случается совпадение высот с другими «замечательными»линиями — медианой, биссектрисой или осью симметрии. В равностороннем треугольнике все три высоты равны между собой и являются одновременно медианами и биссектрисами.

Медианы, биссектрисы и высоты треугольника

Цели.

1) Познакомить с понятиями “перпендикуляр, медиана, биссектриса и высота треугольника”.

2) Научить распознавать в треугольнике медиану, биссектрису и высоту и применять эти понятия при решении задач.

3) Сформировать умение строить медиану, биссектрису и высоту.

4) Воспитывать у учащихся потребность к обоснованию своих высказываний.

5) Развивать эстетические навыки: красоту, точность и аккуратность построения.

6) Развивать интеллектуальные навыки: сравнение, классификация, анализ.

7) Развивать коммуникативные навыки.

8) Воспитывать диалоговую культуру.

9) Воспитывать любовь к предмету.

Оборудование урока: экран, проектор, ноутбук, презентация, чертежные инструменты, раздаточный материал.

План урока.

1. Организационный момент.

2. Геометрический марафон.

3. Изучение нового материала.

4. Закрепление полученных знаний.

5. Итог урока. Задание на дом.

Ход урока

I. Организационный момент

Объявить тему, проверить готовность к уроку, раздать листы контроля, открыть слайд №1.

II. Проверка изученного ранее материала

1. Геометрический марафон.

Задание учащимся: необходимо сопоставить фигуру, появляющуюся на экране, с её названием (слайд № 2) и записать соответствующую букву в клетку листа контроля.

2) Взаимопроверка (слайд №3).

3) На слайде №2 указать термины, которые будут использованы при изучении нового материала: перпендикулярные прямые, отрезок, биссектриса, треугольник, луч, прямой угол, прямая.

Напомнить построение этих фигур.

III. Изучение нового материала

Введение понятия перпендикуляра (слайд № 4).

Вспомнить, что означает запись:

Учитель дает задание классу (одновременно идет иллюстрация слайда).

В тетрадях построить прямую а и точку А, не лежащую на этой прямой.

Построить прямую т, проходящую через точку А, и перпендикулярную прямой а.

Построить отрезок АН (та = Н) – перпендикуляр.

Попытайтесь сформулировать определение перпендикуляра и ответить на вопрос “Сколько перпендикуляров можно провести из данной точки А к данной прямой а?”

2) Введение понятия медианы (слайд № 5).

Уточнить, чем является в треугольнике АВС точки М и В.

Сказать, что отрезок ВМ называют медианой и попросить учащихся попытаться дать определение этому отрезку. Затем открыть формулировку на слайде.

Задать вопрос: “Сколько медиан можно построить в треугольнике?”.

Попросить одного из учащихся прокомментировать построение медианы.

Всем учащимся выполнить построение медиан на листе контроля.

3) Введение понятия биссектрисы треугольника (слайд № 6).

Уточнить, что луч ВК – это биссектриса угла АВС и точка К лежит на стороне, противолежащей углу В треугольника АВС.

Сказать, что отрезок ВК называют биссектрисой треугольника и попросить учащихся попытаться дать определение биссектрисы треугольника. Затем открыть формулировку на слайде. Задать вопрос: “Сколько биссектрис можно построить в треугольнике?”.

Попросить учащихся выполнить построение биссектрис треугольника на листе контроля.

4) Введение понятия высоты треугольника (слайд №7).

а) Учитель показывает построение перпендикуляра из вершины. В на прямую, содержащую сторону АС; говорит, что отрезок ВК называют высотой треугольника АВС и просит учащихся попытаться дать определение высоты треугольника.

Затем открывает формулировку на слайде.

Задает вопрос: “Сколько высот можно построить в треугольнике?”.

Учащиеся выполняют построение высот на листе контроля.

б) Дать задание построить высоты в тупоугольном треугольнике на листе контроля. Здесь возникает проблемная ситуация: как провести высоту из вершины острого угла треугольника.

Показать построение (слайд №8).

в) Дать задание построить высоты в прямоугольном треугольнике.

— Как провести высоты из вершин острых углов треугольника (слайд №9).

5) Рефлексия определений (понятий).

а) Назвать элемент и дать его определение (слайд №10, №11).

б) Проверочная работа (слайд №12 и №13).

IV. Закрепление полученных знаний. (Решение задач)

№105(учебник), №7, №11 (дидактические материалы).

V. Итог урока. Задание на дом. П 17, №114,118,120(б)

Проверочная работа (слайд №12, №13).

Как найти высоту треугольника (правого, равностороннего, равнобедренного …)

Треугольники имеют три высоты, каждый связан с отдельным основанием. Независимо от того, имеется ли до трех разных высот, у одного треугольника всегда будет только одна мера площади. В некоторых треугольниках, таких как прямоугольные, равнобедренные и равносторонние треугольники, определить высоту легко одним из двух способов.

Как найти высоту треугольника

Каждый треугольник имеет три высоты или высоты, потому что у каждого треугольника три стороны.Высота треугольника — это длина перпендикулярного отрезка прямой, начинающегося на одной стороне и пересекающего противоположный угол.

В равностороннем треугольнике, таком как △ СОЛНЦЕ ниже, каждая высота — это отрезок прямой, разделяющий сторону пополам, а также биссектрису противоположного угла. Это произойдет только в равностороннем треугольнике.

По определению равностороннего треугольника вы уже знаете, что все три стороны равны, и все три угла равны 60 °.Если сторона помечена, вы знаете ее длину.

У нашего яркого маленького △ СОЛНЦА одна сторона обозначена 24 см, поэтому все три стороны равны 24 см. Каждый отрезок линии, показывающий высоту с каждой стороны, также делит равносторонний треугольник на два прямоугольных.

Формула высоты треугольника

Ваша способность разделить треугольник на прямоугольные или распознать существующий прямоугольный треугольник — ваш ключ к определению высоты исходного треугольника. Вы можете взять любую сторону нашего великолепного △ СОЛНЦА и увидеть, что отрезок линии, показывающий его высоту, делит сторону пополам, так что каждая короткая ножка только что созданного прямоугольного треугольника составляет 12 см.Мы уже знаем, что гипотенуза равна 24 см.

Зная все три угла и две стороны прямоугольного треугольника, какова длина третьей стороны? Это работа для теоремы Пифагора :

Использование теоремы Пифагора

Ориентируйтесь на длину; углы не важны в теореме Пифагора. Подключите то, что вы знаете:

а2 + Ь2 = с2

122 + b2 = 242

144 + b2 = 576 см2

b2 = 432 см2

b2 = 432 см2

б = 20.7846096908 см

Большинство людей с радостью скажут, что высота (сторона b) приблизительно равна 20,78, или b ≈ 20,78.

Вы можете решить для себя, сколько значащих цифр нужно вашему ответу, поскольку десятичная дробь будет продолжать повторяться. Не забудьте использовать для ответа линейные измерения!

Решение теоремы Пифагора работает с прямоугольными, равнобедренными и равносторонними треугольниками. На разносторонних треугольниках не получится!

Используя формулу площади, чтобы найти высоту

Формула для площади треугольника: 12 основание × высота, или 12 bh.Если вы знаете площадь и длину основания, вы можете рассчитать высоту.

В отличие от метода теоремы Пифагора, если у вас есть две из трех частей, вы можете найти высоту для любого треугольника!

Здесь у нас есть scalene △ ZIG с базой в 56 ярдов и площадью 987 квадратных ярдов, но никаких подсказок об углах и двух других сторонах !:

Вспоминая формулу для площади, где A означает площадь, b — основание, а h — высота, мы вспоминаем

А = 12 ч

Это можно переставить с помощью алгебры:

А = bh3

ч = 2 (Ab)

Введите наши известные значения:

h = 2 (987 квадратных ярдов 56 ярдов)

ч = 2 (17.625 ярдов)

h = 35,25 ярда

Помните, как мы говорили, что у каждого треугольника три высоты? Если мы возьмем ZIG и повернем его по часовой стрелке так, чтобы сторона GZ была горизонтальной, и построим высоту до I, мы сможем получить высоту и для этой стороны.

ч = 2 (Ab)

h = 2 (987 квадратных ярдов 57,255)

ч = 2 (17,2385)

ч = 34,477

Следующий урок:

Гипотенуза: определение и формула

Как определить высоту треугольника в 3 различных ситуациях

В тригонометрии высоту треугольника можно определить разными способами в зависимости от того, прямоугольный ли это треугольник, равнобедренный треугольник (треугольник с двумя равными сторонами) или равносторонний треугольник.

1. Как найти высоту прямоугольного треугольника

Прежде чем мы начнем, вот что вам нужно знать о прямоугольных треугольниках. Прямоугольный треугольник имеет три стороны: гипотенузу, высоту и основание треугольника. Основание и высота прямоугольного треугольника — это всегда стороны, прилегающие к прямому углу, а гипотенуза — самая длинная сторона.

Высоту прямоугольного треугольника можно определить по формуле площади:

Если заданная площадь неизвестна, вы можете использовать теорему Пифагора, чтобы найти высоту прямоугольного треугольника.Вот что утверждает теорема Пифагора, учитывая, что c — гипотенуза, а a и b — две другие стороны:

Давайте возьмем единицы с рисунка выше и подставим длину основания и гипотенузы, чтобы найти недостающую высоту:

2. Определение высоты неправильного треугольника

К сожалению, вы не можете использовать теорему Пифагора, чтобы найти высоту равнобедренного треугольника или высоту равностороннего треугольника (где все стороны треугольника равны).Вместо этого вам придется провести перпендикулярную линию через основание треугольника, чтобы образовался прямой угол:

Эта линия представляет высоту этих неправильных треугольников. После того, как вы сформировали эту линию, вам нужно будет использовать формулу Герона, чтобы найти площадь всего треугольника.

Формула Герона

Первый шаг формулы Герона — вычисление половины периметра треугольника. В этом случае s представляет половину периметра, а a, b, и c — стороны:

После того, как вы определили s , используйте следующую формулу для вычисления площади треугольника.Опять же, две стороны — это a и b , а самая длинная сторона (гипотенуза) — c :

.

Давайте подставим длины сторон этого равнобедренного треугольника, чтобы найти площадь треугольника:

Теперь мы заменим s в формуле площади непрямого треугольника.

Использование площади для определения высоты треугольника

Теперь, когда вы знаете площадь изображенного выше треугольника, вы можете подставить его в формулу треугольника A = 1 / 2bh, чтобы найти высоту треугольника.В этом случае основание будет равно половине расстояния пяти (2,5), так как это самая короткая сторона треугольника.

Формулы высоты главного треугольника

Определение высоты треугольника — это многоэтапный процесс, который может сбивать с толку. Однако его освоение поможет вам изучить различные типы формул площади, такие как формула цапли и A = 1 / 2bh. В нем также показано, как использовать теорему Пифагора и формулы периметра треугольника для определения других величин внутри треугольника.

Дополнительные домашние задания по математике

Как найти высоту прямоугольного треугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Высота треугольника

У нас есть два ответа для вас.

Привет,

Высота может быть любой от 16 дюймов

до почти нулевой высоты

Если треугольник прямоугольный, как на первой диаграмме, но это гипотенуза, имеющая длину 16 дюймов, то вы можете использовать теорему Пифагора, чтобы найти длину третьей стороны, которая в данном случае является высотой.

Пенни

Привет,

При рассмотрении треугольников одним из самых мощных инструментов является теорема Пифагора: a ² + b ² = c ² , где a и b — катеты прямоугольного треугольника, а c — гипотенуза. (сторона, противоположная прямому углу). Однако единственная загвоздка теоремы Пифагора состоит в том, что она верна только для треугольников с прямым углом, а наш треугольник ничего об этом не говорит. В вашем случае нам дан треугольник, и нет информации о том, какой это треугольник.Я предполагаю, что мы говорим о равнобедренном треугольнике (треугольнике с двумя равными сторонами). Итак, аналогично вашему вопросу, допустим, нам дан равнобедренный треугольник с основанием 10 и длиной стороны 13. Что мы можем сделать для начала, так это нарисовать наш треугольник. Затем, когда он будет нарисован, опустите перпендикулярную линию (линии, которые встречаются под углом 90 градусов или прямым углом) от вершины треугольника до стороны 10. Теперь мы превратили наш равнобедренный треугольник в два прямоугольных. треугольников, и, кроме того, мы создали ситуацию, в которой мы можем использовать нашу теорему Пифагора.Поскольку мы имеем дело с равнобедренным треугольником, на какую бы сторону мы ни опускали перпендикуляр, в нашем случае на сторону длиной 10, результат перпендикуляра состоит в том, что он разрезает линию пополам, поэтому наш прямоугольный треугольник имеет основание 5. Вот диаграмма, чтобы помочь проиллюстрировать это

Теперь, используя теорему Пифагора, мы можем подставить числа.

Итак, а ² + b ² = с ²
5 ² + b ² = 13 ²

Причина, по которой мы вставляем 13 вместо c, а не b, заключается в том, что сторона, противоположная прямому углу, переходит в положение c, где 13 находится в нашем треугольнике.Затем мы можем перейти к решению относительно b,

25 + b ² = 169
b ² = 144
√b ² = √144
b = 12

Таким образом, значение b равно 12, поэтому высота треугольника равна 12
Теперь, поскольку b — это длина, мы не включаем значение -12, в данном случае это называется главным квадратным корнем.

Теперь, если ваш треугольник уже был прямоугольным, вам не нужно опускать перпендикуляр, чтобы получить правильный угол, вы можете просто продолжить с теоремой Пифагора и решить для стороны b, которая будет вашим ростом.

Бреннан

Как определить высоту треугольника — Видео и стенограмма урока

Метод площади

Прежде чем мы сможем начать использовать метод площади, мы должны сначала вспомнить формулу площади треугольника:

Теперь мы можем просто взять площадь, предусмотренную для треугольника, и длину его основания и подставить эти числа в нашу формулу, чтобы составить уравнение. В этом случае наша недостающая высота обозначена как х .Получаем:

Используя наши шаги для поиска отсутствующей переменной в уравнении, мы получаем:

Метод теоремы Пифагора

Допустим, вам не указана высота вашего треугольника, но вы работаете с равнобедренным или равносторонним треугольником, и вам даны размеры сторон вашего треугольника. Затем вы можете использовать метод теоремы Пифагора.

Прежде чем мы сможем применить теорему Пифагора для определения неизвестной высоты грани пирамиды, мы должны сначала просмотреть формулу этой теоремы.Теорема Пифагора утверждает, что если сложить квадрат каждого катета (стороны a и b ) прямоугольного треугольника, он будет равен квадрату гипотенузы (сторона c ). Помните, что катеты — это две стороны, которые встречаются под прямым углом, а гипотенуза — это самая длинная сторона треугольника.

Для начала проведите воображаемую линию по центру треугольника. Это наш рост, не так ли? Вспоминая свойства равностороннего или равнобедренного треугольника, вы можете вспомнить, что линия высоты делит основание треугольника пополам.Это означает, что он разрезает базу ровно пополам, создавая две «мини-базы» размером 115 метров. Вы также можете помнить, что эта линия высоты создает угол 90 градусов к нашей основе, образуя два равных прямоугольных треугольника.

Теперь, когда у нас есть прямоугольный треугольник с известными основанием и гипотенузой, мы можем использовать теорему Пифагора, чтобы найти второй отрезок, который, как оказалось, является высотой. Круто, как это сработало, правда?

Подставляя наши числа к теореме Пифагора, мы получаем:

Округляя до ближайшего целого числа, наше решение составляет 146, а поскольку b — это наша высота, высота нашего треугольника составляет 146 метров .Это та же высота, которую мы нашли с помощью нашего метода площади. Отлично, да?

Краткое содержание урока

Хотя я не стал архитектором, вы можете видеть, что существуют реальные приложения для использования геометрии. В этом уроке мы применили наше понимание треугольников и связанных с ними формул, чтобы найти неизвестную высоту существующей конструкции (Великой пирамиды Хуфу). Мы узнали, что существует два метода: метод площади и метод теоремы Пифагора .2 \).

Предположим, вам нужно знать, как найти высоту треугольника △ ABC с учетом трех сторон, {6,7,8}.

Это вопрос, который задают некоторые экзаменуемые на GMAT. Они знают, что им потребуется высота, чтобы найти место, поэтому они беспокоятся: как я найду эту высоту.

Короткий ответ: забудьте об этом!

Высота треугольника: какая высота?

Я не хочу показаться легкомысленным. Просто, прежде всего, «высота» треугольника — это высота.Любой треугольник имеет три высоты и, следовательно, три высоты! Сбивает с толку? Я знаю, извини.

Видите ли, любая сторона может быть базой. Из любой вершины вы можете провести линию, перпендикулярную противоположному основанию — это высота до этого основания.

Любой треугольник имеет три высоты и три основания.

Вы можете использовать любую одну пару высота-база, чтобы найти площадь треугольника по формуле \ (A = \ frac {1} {2} bh \).

На каждой из диаграмм выше треугольник ABC одинаков.Зеленая линия — это высота, «высота», а сторона с красным перпендикулярным квадратом на ней — «основание». Все три стороны треугольника повернуты.

В поисках высоты

Учитывая длину трех сторон треугольника, единственный способ найти высоту и площадь только по сторонам — это тригонометрия , что выходит далеко за рамки GMAT.

Вы на 100% НЕ несете ответственности за знание того, как выполнять эти вычисления.Это несколько уровней продвинутого уровня помимо математики, которые вам нужно знать. Не беспокойся об этом.

На практике, если задача GMAT требует, чтобы вы вычислили площадь треугольника, им придется дать вам высоту .

Единственным исключением может быть прямоугольный треугольник. В прямоугольном треугольнике, если одна из ног является основанием, другая сторона — это высота, высота, поэтому особенно легко найти площадь прямоугольных треугольников.

Что нужно знать

Вам необходимо знать основы геометрии.Да, помимо этого есть еще масса математики и еще много всего, что вы могли бы знать о треугольниках и их свойствах, но вы не несете ответственности ни за что из этого. Вам просто нужно знать основную геометрию треугольников, в том числе формулу:

A = 12bh

Если треугольник не является прямоугольным, вы не несете никакой ответственности за то, чтобы знать, как найти высоту — она ​​всегда будет дана, если вам это нужно.

Вот вам бесплатный вопрос.

Две стороны треугольника имеют длину 6 и 8.Какие из следующих возможных областей треугольника?

2
12
24

Нажмите здесь, чтобы получить ответ и видео-объяснение!

Некоторые предостережения «больше, чем вам нужно знать»

• Если вы не хотите знать по этой теме что-либо, что вам совершенно не нужно для GMAT, пропустите этот раздел !

1. Технически, если вы знаете три стороны треугольника, вы можете найти площадь по так называемой формуле Герона, но это также больше, чем ожидает от вас GMAT.
2. Если один из углов треугольника тупой, то высоты до любого основания, примыкающего к этому тупому углу, находятся за пределами треугольника.
3. Сверхтехнически, высота — это не отрезок, проходящий через вершину, перпендикулярную противоположному основанию, а вместо этого отрезок через вершину, перпендикулярную линии, содержащей противоположное основание.

На диаграмме выше в треугольнике △ DEF одна из трех высот — это DG, которая идет от вершины D к бесконечной прямой, содержащей сторону EF.GMAT не будет проверять это на техническом уровне и не ожидает, что вы его узнаете.

Если все три стороны треугольника представляют собой красивые положительные целые числа, то, по всей вероятности, фактическое математическое значение высот будет уродливым десятичным числом.

Многие специалисты по подготовке к GMAT и учителя в целом не обращают на это внимания и, чтобы облегчить решение задач, также дадут вам хорошее положительное целое число для высоты.

Помните треугольник △ ABC сверху?

Например, реальное значение высоты от C до AB в треугольнике 6-7-8 равно:

Вы не только 100% НЕ ожидаете, что знает, как найти это число, но и большинство составителей практических вопросов GMAT избавят вас от уродливых деталей и просто скажут, например, altitude = 5.

Это позволяет очень легко рассчитать площадь.

Да, технически это ложь во благо, но она избавляет бедных студентов от кучи уродливой десятичной математики, которой им не нужно заниматься.

На самом деле учителя математики всех уровней делают это все время — маленькая белая математическая ложь, чтобы избавить учащихся от деталей, которые им не нужно знать.

Насколько я могу судить, люди, которые пишут сам GMAT, являются приверженцами всевозможной истины и даже не лгут в этом виде «упрощения для учеников».

Они с большей вероятностью обойдут всю проблему, например, сделав все соответствующие длины переменными или что-то в этом роде.

На вынос

Все еще со мной?

Вот что вам нужно знать о треугольниках в день теста GMAT:

• \ (Площадь = \ frac {1} {2} bh \)
• Вам нужно знать только высоту прямоугольных треугольников на GMAT
• Если это не прямоугольный треугольник, вам будет присвоена высота
• Знать все три угла и две стороны? Используйте теорему Пифагора

Если вам нравится больше бесплатных ресурсов (а кто нет?), Или вам просто интересно, каким будет содержание теста GMAT, ознакомьтесь с нашим полным руководством.

Вот это у вас есть.

Если у вас есть вопросы, дайте мне знать в комментариях ниже. И да, я прочитал все до единого!

Готовы получить отличный результат GMAT? Начните здесь.

Самые популярные ресурсы

О Майке MᶜGarry

Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах.Майку нравится разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс.

Площадь треугольника — пояснения и примеры

В этой статье вы узнаете площадь треугольника и определить площадь различных типов треугольников . Площадь треугольника — это пространство внутри треугольника. Он измеряется в квадратных единицах.

Прежде чем перейти к теме , касающейся области треугольника , давайте познакомимся с такими терминами, как основание и высота треугольника.

Основание — это сторона треугольника, которая считается нижней частью, а t Высота треугольника — это перпендикулярная линия, опущенная на его основание из вершины, противоположной основанию.

На приведенном выше рисунке пунктирными линиями показаны возможные значения △ ABC. Обратите внимание, что у каждого треугольника, возможно, есть три высоты или высоты.

• Высота треугольника △ ABC равна h ₁ , когда основание является стороной.
• Высота треугольника △ ABC равна h3 при основании AB.
• Высота треугольника △ ABC равна h ₃ при основании
• Высота треугольника △ ABC может быть вне треугольника ( h ₄ ), что совпадает с высотой h ₁ .

Из иллюстраций выше мы можем сделать следующие наблюдения:

• Высота треугольника зависит от его основания.
• Перпендикуляр к основанию треугольника равен высоте треугольника.
• Высота треугольника может быть вне треугольника.

Обсудив понятие высоты и основания треугольника, давайте теперь приступим к вычислению площади треугольника.

Как найти площадь треугольника?

Площадь прямоугольника нам хорошо известна, т.е. длина * ширина . Что будет, если прямоугольник разделить пополам по диагонали (разрезать пополам)? Какая будет его зона новостей? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц, соответственно, площадь прямоугольника составляет 72 квадратных единицы.

Теперь, если вы разделите на две равные половины (после деления прямоугольника пополам по диагонали), площадь двух новых фигур должна составлять 36 квадратных единиц каждая. Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезан по диагонали на две равные половины, две новые формы образуются треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.

Площадь треугольника — это общее пространство или область, ограниченная определенным треугольником.
Площадь треугольника равна произведению основания и высоты, разделенных на 2.

Стандартная единица измерения площади — квадратные метры (м ² ).

Прочие единицы включают:

• Квадратные миллиметры (мм ² )
• Квадратные дюймы (в ² )
• Квадратных километров (км ² )
• квадратных ярдов.

Формула площади треугольника

Общая формула для вычисления площади треугольника:

Площадь (A) = ½ (b × h) квадратных единиц, где; A — площадь, b — основание, h — высота треугольника.Треугольники могут быть разной природы, но важно отметить, что эта формула применима ко всем треугольникам. Различные типы треугольников имеют разные формулы площади.

Примечание: база и высота должны быть в одних и тех же единицах измерения, то есть в метрах, километрах, сантиметрах и т. Д.

Площадь прямоугольного треугольника

Площадь треугольника = (½ × основание × высота) квадратных единиц.

Пример 1

Найдите площадь прямоугольного треугольника с основанием 9 м и высотой 12 м.

Решение

A = ¹ / ₂ × основание × высота

= ¹ / ₂ × 12 × 9

= 54 см²

Пример 2

Основание и высота прямоугольного треугольника 70 см и 8 м соответственно. Какая площадь у треугольника?

Решение

A = ½ × основание × высота

Здесь 70 см и 8 м. Вы можете работать с cm или m. Давайте работать в метрах, заменив 70 см на метры.

Разделим 70 см на 100.

70/100 = 0,7 м.

⇒ A = (½ × 0,7 × 8) м ²

⇒ A = (½ x 5,6) м ²

⇒ A = 2,8 м ²

Площадь равнобедренного треугольника

Равнобедренный треугольник — это треугольник, у которого две стороны равны, а также два угла равны. Формула площади равнобедренного треугольника:

⇒A = ½ (основание × высота).

Если высота равнобедренного треугольника не указана, для определения высоты используется следующая формула:

Высота = √ (a ² — b ² /4)

Где;

b = основание треугольника

a = Длина двух равных сторон.

Следовательно, площадь равнобедренного треугольника может быть;

⇒A = ½ [√ (a ² — b ² /4) × b]

Также площадь равнобедренного прямоугольного треугольника определяется по формуле:

A = ½ × a ² , где a = длина стороны двух равных сторон

Пример 3

Вычислите площадь равнобедренного треугольника с основанием 12 мм и высотой 17 мм.

Решение

⇒ A = ½ × основание × высота

⇒ 1/2 × 12 × 17

⇒ 1/2 × 204

= 102 мм ²

Пример 4

Найдите площадь равнобедренного треугольника с длинами сторон 5 и 9 м

Решение

Пусть база, b = 9 м и a = 5 м.

⇒ A = ½ [√ (a ² — b ² /4) × b]

⇒ ½ [√ (5 ² — 9 ² /4) × 9]

= 9,81 м ²

Площадь равностороннего треугольника

Равносторонний треугольник — это треугольник, в котором три стороны равны и три внутренних угла равны. Площадь равностороннего треугольника:

A = (a ² √3) / 4

Где a = длина сторон.

Пример 5

Вычислите площадь равностороннего треугольника со стороной 4 см.

Решение

⇒ A = (a ² /4) √3

⇒ (4 ² /4) √3

⇒ (16/4) √3

= 4√3 см ²

Пример 6

Найдите площадь равностороннего треугольника с периметром 84 мм.

Решение

Периметр равностороннего треугольника = 3a.

⇒ 3a = 84 мм

⇒ a = 84/3

⇒ a = 28 мм

Площадь = (a ² /4) √3

⇒ (28 ² /4) √3

= 196√3 мм ²

Площадь разностороннего треугольника

Разносторонний треугольник — это треугольник с 3 разными длинами сторон и 3 разными углами.Площадь разностороннего треугольника можно рассчитать по формуле Герона.