Свойства высоты треугольника — энциклопедический справочник и словарь для студента от А до Я
ОПРЕДЕЛЕНИЕ Высота треугольника, взятого из заданной вершины, называется перпендикуляром, отброшенным от этой вершины к противоположной стороне или ее продолжению. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. 1. В остром треугольнике высоты пересекаются внутри треугольника; в тупой — вне треугольника; в прямоугольном — в верхней части правого угла. 2. В правом треугольнике ноги — это высоты. 3. В прямоугольном треугольнике высота, выведенная из вершины правого угла, разбивает ее на два треугольника, аналогичные исходной. 4. В остром треугольнике его две высоты отключают от него аналогичные треугольники. 5. В равнобедренном треугольнике высота, опущенная на основание, является медианной и биссектрисой. В равностороннем треугольнике все высоты являются медианами и биссектрисами. Примеры решения проблем ПРИМЕР 1 В треугольнике \(\
\mathrm{ABC}
\) со стороной \(\
A B=8 \mathrm{см}
\)и \(\
\angle A=45^{\circ}
\)найдите высоту, опущенную из вершины \(\
B
\). В треугольнике \(\
\mathrm{ABC}
\) из вершины \(\
B
\) мы понижаем высоту \(\
\mathrm{BK}
\). Рассмотрим полученный правый треугольник \(\
\mathrm{ABK}
\) с прямым углом \(\
B
\) и углом \(\
\angle A=45
\) (по условию). Найти \(\
\mathrm{BK}
\): \(\
B K=A B \sin \angle A=8 \cdot \frac{\sqrt{2}}{2}=4 \sqrt{2} \mathrm{cm}
\) \(\
B K=4 \sqrt{2}
\) ПРИМЕР 2 В прямоугольном треугольнике \(\
\mathrm{ABC}
\) высота \(\
\mathrm{BK}
\) делит гипотенузу на сегменты \(\
A K=4 \mathrm{см}
\) и \(\
\mathrm{K}=9 \mathrm{см}
\). Найдите область треугольника \(\
\mathrm{ABC}
\). Треугольники \(\
\mathrm{AKB}
\), \(\
\mathrm{CKB}
\) — аналогичные. Средства \(\
\frac{A K}{B K}=\frac{B K}{K C} \Rightarrow B K^{2}=A K \cdot K C=4 \cdot 9=36 \mathrm{см}
\) отсюда \(\
B K=6 \mathrm{см}
\) Из правых треугольников \(\
\mathrm{AKB}
\) и \(\
\mathrm{CKB}
\) находим \(\
AB
\), \(\
BC
\) (используя теорему Пифагора): \(\
A B=\sqrt{A K^{2}+B K^{2}}=\sqrt{52}=2 \sqrt{13} \mathrm{см}
\), \(\
B C=\sqrt{C K^{2}+B K^{2}}=\sqrt{117} \mathrm{см}
\) Затем мы найдем область треугольника \(\
\mathrm{ABC}
\): \(\
S_{A B C}=\frac{1}{2} A B \cdot B C=\frac{2 \sqrt{13} \sqrt{117}}{2}=\sqrt{1521} \mathrm{см}
\) \(\
S_{A B C}=\sqrt{1521}
\)
sciterm.ru
Высота треугольника — Википедия. Что такое Высота треугольника
Высота в треугольниках различного типа
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
Свойства точки пересечения трех высот треугольника (ортоцентра)
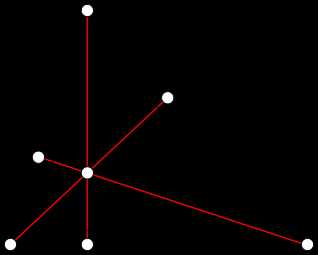Высоты треугольника- Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:
- EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства тождества следует воспользоваться формулами
- AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}
В качестве точки E следует взять пересечение двух высот треугольника.)
- Ортоцентр изогонально сопряжен центру описанной окружности .
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- |OH|=9R2−(a2+b2+c2){\displaystyle |OH|={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}} , где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства высот равнобедренного треугольника
- Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
- У равностороннего треугольника все три высоты равны.
Свойства оснований высот треугольника
- Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
- Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
- Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Другие свойства высот треугольника
Свойства минимальной из высот треугольника
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
Основные соотношения
- ha=b⋅sinγ=c⋅sinβ,{\displaystyle h_{a}=b{\cdot }\sin \gamma =c{\cdot }\sin \beta ,}
- ha=2⋅Sa,{\displaystyle h_{a}={\frac {2{\cdot }S}{a}},} где S{\displaystyle S} — площадь треугольника, a{\displaystyle a} — длина стороны треугольника, на которую опущена высота.
- ha2=12(b2+c2−12(a2+(b2−c2)2a2)){\displaystyle h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))}
- ha=b⋅c2⋅R,{\displaystyle h_{a}={\frac {b{\cdot }c}{2{\cdot }R}},} где b⋅c{\displaystyle b{\cdot }c} — произведение боковых сторон, R−{\displaystyle R-} радиус описанной окружности
- ha:hb:hc=1a:1b:1c=(b⋅c):(a⋅c):(a⋅b).{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=(b{\cdot }c):(a{\cdot }c):(a{\cdot }b).}
- 1ha+1hb+1hc=1r{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}, где r{\displaystyle r} — радиус вписанной окружности.
- S=1(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}, где S{\displaystyle S} — площадь треугольника.
- a=2ha⋅(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}}, a{\displaystyle a} — сторона треугольника к которой опускается высота ha{\displaystyle h_{a}}.
- Высота равнобедренного треугольника, опущенная на основание:
- hc=12⋅4a2−c2,{\displaystyle h_{c}={\frac {1}{2}}{\cdot }{\sqrt {4a^{2}-c^{2}}},}
- где c{\displaystyle c} — основание, a{\displaystyle a} — боковая сторона.
- h=32⋅a{\displaystyle h={\tfrac {\sqrt {3}}{2}}{\cdot }a} — высота в равностороннем треугольнике со стороной a{\displaystyle a}.
Теорема о высоте прямоугольного треугольника
Если высота в прямоугольном треугольнике ABC{\displaystyle ABC} длиной h{\displaystyle h}, проведённая из вершины прямого угла, делит гипотенузу длиной c{\displaystyle c} на отрезки m{\displaystyle m} и n{\displaystyle n}, соответствующие катетам b{\displaystyle b} и a{\displaystyle a}, то верны следующие равенства:
- h3=n⋅m{\displaystyle h^{2}=n{\cdot }m}
- a2=c⋅n{\displaystyle a^{2}=c{\cdot }n}; b2=c⋅m{\displaystyle b^{2}=c{\cdot }m}
- h⋅c=a⋅b{\displaystyle h{\cdot }c=a{\cdot }b}
Теорема о проекциях
См. с. 51, ф. (1.11-4)[2]. Теорема о проекциях: c=acosβ+bcosα; a=bcosγ+ccosβ; b=ccosα+acosγ{\displaystyle c=a\cos \beta +b\cos \alpha ;\ a=b\cos \gamma +c\cos \beta ;\ b=c\cos \alpha +a\cos \gamma }. Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины C{\displaystyle C}, делит противоположную ей сторону c{\displaystyle c} на две части acosβ{\displaystyle a\cos \beta } и bcosα{\displaystyle b\cos \alpha }, считая от вершины A{\displaystyle A} к B{\displaystyle B}.
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.[3]
Вариации по теме. Высоты в четырехугольнике
Теорема[4]. Пусть ABCD{\displaystyle ABCD} – вписанный четырёхугольник, A1{\displaystyle A_{1}} – основание перпендикуляра (высоты), опущенного из вершины A{\displaystyle A} на диагональ BD{\displaystyle BD}; аналогично определяются точки B1,C1,D1{\displaystyle B_{1},C_{1},D_{1}}. Тогда точки A1,B1,C1,D1{\displaystyle A_{1},B_{1},C_{1},D_{1}} лежат на одной окружности.
Примечания
- ↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 137-138, п. 126, теорема, следствия.
- ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
- ↑ Сафронова Вера Николаевна,. Урок геометрии в 7-м классе по теме: «Медиана, биссектриса, высота» (рус.). Открытый урок. Издательский дом «Первое сентября». Проверено 19 июля 2017.
- ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5.
Ссылки
wiki.sc
Высота треугольника — WiKi
Высота в треугольниках различного типа
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
Свойства точки пересечения трех высот треугольника (ортоцентра)
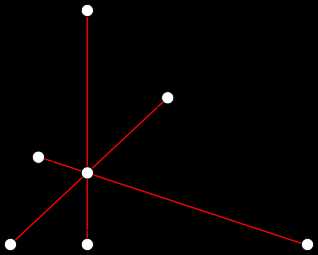Высоты треугольника- Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E} , не обязательно даже лежащих в одной плоскости:
- EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства тождества следует воспользоваться формулами
- AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}
В качестве точки E следует взять пересечение двух высот треугольника.)
- Ортоцентр изогонально сопряжен центру описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} ,
- |OH|=9R2−(a2+b2+c2){\displaystyle |OH|={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}} , где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства высот равнобедренного треугольника
- Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
- У равностороннего треугольника все три высоты равны.
Свойства оснований высот треугольника
- Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
- Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
- Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Другие свойства высот треугольника
Свойства минимальной из высот треугольника
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
Основные соотношения
- ha=bsinγ=csinβ,{\displaystyle h_{a}=b\sin \gamma =c\sin \beta ,}
- ha=2Sa,{\displaystyle h_{a}={\frac {2S}{a}},} где S{\displaystyle S} — площадь треугольника, a{\displaystyle a} — длина стороны треугольника, на которую опущена высота.
- ha2=12(b2+c2−12(a2+(b2−c2)2a2)){\displaystyle h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))}
- ha=bc2R,{\displaystyle h_{a}={\frac {bc}{2R}},} где bc{\displaystyle bc} — произведение боковых сторон, R−{\displaystyle R-} радиус описанной окружности
- ha:hb:hc=1a:1b:1c=bc:ac:ab{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ac:ab}
- 1ha+1hb+1hc=1r{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}} , где r{\displaystyle r} — радиус вписанной окружности.
- S=1(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}} , где S{\displaystyle S} — площадь треугольника.
- a=2ha⋅(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}} , a{\displaystyle a} — сторона треугольника к которой опускается высота ha{\displaystyle h_{a}} .
- Высота равнобедренного треугольника, опущенная на основание:
- hc=124a2−c2,{\displaystyle h_{c}={\frac {1}{2}}{\sqrt {4a^{2}-c^{2}}},}
- где c{\displaystyle c} — основание, a{\displaystyle a} — боковая сторона.
- h=32a{\displaystyle h={\frac {\sqrt {3}}{2}}a} — высота в равностороннем треугольнике со стороной a{\displaystyle a} .
Теорема о высоте прямоугольного треугольника
Теорема о проекциях
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.[3]
Вариации по теме. Высоты в четырехугольнике
Теорема[4]. Пусть ABCD{\displaystyle ABCD} – вписанный четырёхугольник, A1{\displaystyle A_{1}} – основание перпендикуляра (высоты), опущенного из вершины A{\displaystyle A} на диагональ BD{\displaystyle BD} ; аналогично определяются точки B1,C1,D1{\displaystyle B_{1},C_{1},D_{1}} . Тогда точки A1,B1,C1,D1{\displaystyle A_{1},B_{1},C_{1},D_{1}} лежат на одной окружности.
Примечания
- ↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 137-138, п. 126, теорема, следствия.
- ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
- ↑ Сафронова Вера Николаевна,. Урок геометрии в 7-м классе по теме: «Медиана, биссектриса, высота» (рус.). Открытый урок. Издательский дом «Первое сентября». Проверено 19 июля 2017.
- ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5.
Ссылки
ru-wiki.org
высота треугольника — это… Что такое высота треугольника?
- высота треугольника
баландии секунҷа. матем.
Краткий русско-таджикский терминологический словарь по точным, естественным и техническим наукам. Пирмаҳмад Нуров. 2013.
- высота тона
- высота уровня
Смотреть что такое «высота треугольника» в других словарях:
Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав … Википедия
ВЫСОТА — ВЫСОТА, высоты, мн. высоты, высот, жен. 1. только ед. Протяжение снизу вверх, вышина. Высота дома. Башня большой высоты. || (мн. только спец. научн.). Расстояние от земной поверхности, измеряемое по вертикальной линии снизу вверх. Аэроплан летал… … Толковый словарь Ушакова
Высота (геометрия) — У этого термина существуют и другие значения, см. Высота (значения). Высота в элементарной геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на… … Википедия
высота — ы/; мн. высо/ты; ж. см. тж. высотка, высотный 1) Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. Высота/ дома, дерева, горы. Высота/ волны. Плотина высотой в сто пят … Словарь многих выражений
высота — ы; мн. высоты; ж. 1. Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. В. дома, дерева, горы. В. волны. Плотина высотой в сто пятьдесят метров. Измерить, определить высоту чего л. 2. Расстояние от какой л. поверхности до… … Энциклопедический словарь
высота исходного треугольника резьбы — (H) Расстояние между вершиной и основанием исходного треугольника резьбы в направлении, перпендикулярном к оси резьбы. [ГОСТ 11708 82 (СТ СЭВ 2631 80)] Тематики нормы взаимозаменяемости Обобщающие термины основные элементы и параметры резьбы EN… … Справочник технического переводчика
Высота (значения) — Высота размер или расстояние в вертикальном направлении. Другие значения: В астрономии: Высота светила угол между плоскостью математического горизонта и направлением на светило. В военном деле: Высота возвышенность рельефа. В… … Википедия
ВЫСОТА (в геометрии) — ВЫСОТА, в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а… … Энциклопедический словарь
ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь
ВЫСОТА — ВЫСОТА, ы, мн. оты, от, отам, жен. 1. Величина, протяжённость чего н. от нижней точки до верхней. В. кирпичной кладки. В. прибоя. В. циклона. 2. Пространство, расстояние от земли вверх. Смотреть в высоту. Самолёт набирает высоту. Лететь на… … Толковый словарь Ожегова
Высота (геометрич.) — Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя,… … Большая советская энциклопедия
technik_rus_taj.academic.ru
высота треугольника — это… Что такое высота треугольника?
- высота треугольника
гурбанбулантын үндэр гурбанбулантын оройһоо эсэргүү таладань буулгагдалан перпендикуляр
Краткий бурятско-русский словарь математических терминов. 2015.
- высота боковая
- высота плоской фигуры
Смотреть что такое «высота треугольника» в других словарях:
Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав … Википедия
ВЫСОТА — ВЫСОТА, высоты, мн. высоты, высот, жен. 1. только ед. Протяжение снизу вверх, вышина. Высота дома. Башня большой высоты. || (мн. только спец. научн.). Расстояние от земной поверхности, измеряемое по вертикальной линии снизу вверх. Аэроплан летал… … Толковый словарь Ушакова
Высота (геометрия) — У этого термина существуют и другие значения, см. Высота (значения). Высота в элементарной геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на… … Википедия
высота — ы/; мн. высо/ты; ж. см. тж. высотка, высотный 1) Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. Высота/ дома, дерева, горы. Высота/ волны. Плотина высотой в сто пят … Словарь многих выражений
высота — ы; мн. высоты; ж. 1. Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. В. дома, дерева, горы. В. волны. Плотина высотой в сто пятьдесят метров. Измерить, определить высоту чего л. 2. Расстояние от какой л. поверхности до… … Энциклопедический словарь
высота исходного треугольника резьбы — (H) Расстояние между вершиной и основанием исходного треугольника резьбы в направлении, перпендикулярном к оси резьбы. [ГОСТ 11708 82 (СТ СЭВ 2631 80)] Тематики нормы взаимозаменяемости Обобщающие термины основные элементы и параметры резьбы EN… … Справочник технического переводчика
Высота (значения) — Высота размер или расстояние в вертикальном направлении. Другие значения: В астрономии: Высота светила угол между плоскостью математического горизонта и направлением на светило. В военном деле: Высота возвышенность рельефа. В… … Википедия
ВЫСОТА (в геометрии) — ВЫСОТА, в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а… … Энциклопедический словарь
ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь
ВЫСОТА — ВЫСОТА, ы, мн. оты, от, отам, жен. 1. Величина, протяжённость чего н. от нижней точки до верхней. В. кирпичной кладки. В. прибоя. В. циклона. 2. Пространство, расстояние от земли вверх. Смотреть в высоту. Самолёт набирает высоту. Лететь на… … Толковый словарь Ожегова
Высота (геометрич.) — Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя,… … Большая советская энциклопедия
math_bua_rus.academic.ru
высота треугольника — это… Что такое высота треугольника?
- высота треугольника
altitude of a triangle
Русско-английский математический словарь. 2013.
- высота
- выстрел
Смотреть что такое «высота треугольника» в других словарях:
Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав … Википедия
ВЫСОТА — ВЫСОТА, высоты, мн. высоты, высот, жен. 1. только ед. Протяжение снизу вверх, вышина. Высота дома. Башня большой высоты. || (мн. только спец. научн.). Расстояние от земной поверхности, измеряемое по вертикальной линии снизу вверх. Аэроплан летал… … Толковый словарь Ушакова
Высота (геометрия) — У этого термина существуют и другие значения, см. Высота (значения). Высота в элементарной геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на… … Википедия
высота — ы/; мн. высо/ты; ж. см. тж. высотка, высотный 1) Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. Высота/ дома, дерева, горы. Высота/ волны. Плотина высотой в сто пят … Словарь многих выражений
высота — ы; мн. высоты; ж. 1. Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. В. дома, дерева, горы. В. волны. Плотина высотой в сто пятьдесят метров. Измерить, определить высоту чего л. 2. Расстояние от какой л. поверхности до… … Энциклопедический словарь
высота исходного треугольника резьбы — (H) Расстояние между вершиной и основанием исходного треугольника резьбы в направлении, перпендикулярном к оси резьбы. [ГОСТ 11708 82 (СТ СЭВ 2631 80)] Тематики нормы взаимозаменяемости Обобщающие термины основные элементы и параметры резьбы EN… … Справочник технического переводчика
Высота (значения) — Высота размер или расстояние в вертикальном направлении. Другие значения: В астрономии: Высота светила угол между плоскостью математического горизонта и направлением на светило. В военном деле: Высота возвышенность рельефа. В… … Википедия
ВЫСОТА (в геометрии) — ВЫСОТА, в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а… … Энциклопедический словарь
ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь
ВЫСОТА — ВЫСОТА, ы, мн. оты, от, отам, жен. 1. Величина, протяжённость чего н. от нижней точки до верхней. В. кирпичной кладки. В. прибоя. В. циклона. 2. Пространство, расстояние от земли вверх. Смотреть в высоту. Самолёт набирает высоту. Лететь на… … Толковый словарь Ожегова
Высота (геометрич.) — Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя,… … Большая советская энциклопедия
mathematical_ru_en.academic.ru