Метод наименьших квадратов
Программа МНК
Введите данные
Данные и аппроксимация
y = a + b·x
i – номер экспериментальной точки;
xi – значение фиксированного параметра в точке i;
yi – значение измеряемого параметра в точке i;
ωi – вес измерения в точке i;
yi, расч. – разница между измеренным и вычисленным по регрессии значением y в точке i;
Sxi(xi) – оценка погрешности xi при измерении y в точке i.
Кликните по графику,
чтобы добавить значения в таблицу
Данные и аппроксимация
y = k·x| i | xi | yi | ωi | yi, расч. | Δyi | Sxi(xi) |
|---|
чтобы добавить значения в таблицу
Инструкция пользователя онлайн-программы МНК.

В поле данных введите на каждой отдельной строке значения `x` и `y` в одной экспериментальной точке. Значения должны отделяться пробельным символом (пробелом или знаком табуляции).
Третьим значением может быть вес точки `w`. Если вес точки не указан, то он приравнивается единице. В подавляющем большинстве случаев веса экспериментальных точек неизвестны или не вычисляются, т.е. все экспериментальные данные считаются равнозначными. Иногда веса в исследуемом интервале значений совершенно точно не равнозначны и даже могут быть вычислены теоретически. Например, в спектрофотометрии веса можно вычислить по простым формулам, правда в основном этим все пренебрегают для уменьшения трудозатрат.
Данные можно вставить через буфер обмена из электронной таблицы офисных пакетов, например Excel из Майкрософт Офиса или Calc из Оупен Офиса.
Для этого в электронной таблице выделите диапазон копируемых данных, скопируйте в буфер обмена и вставьте данные в поле данных на этой странице.
Для расчета по методу наименьших квадратов необходимо не менее двух точек для определения двух коэффициентов `b` – тангенса угла наклона прямой и `a` – значения, отсекаемого прямой на оси `y`.
Для оценки погрешности расчитываемых коэффициентов регресии нужно задать количество экспериментальных точек больше двух. Чем больше количество экспериментальных точек, тем более точна статистическая оценка коэффицинетов (за счет снижения коэффицинета Стьюдента) и тем более близка оценка к оценке генеральной выборки.
Получение значений в каждой экспериментальной точке часто сопряжено со значительными трудозатратами, поэтому часто проводят компромиссное число экспериментов, которые дает удобоваримую оценку и не привеодит к чрезмерным трудо затратам. Как правило число экспериментах точек для линейной МНК зависимости с двумя коэффицинетами выбирает в районе 5-7 точек.
Краткая теория метода наименьших квадратов для линейной зависимости
Допустим у нас имеется набор экспериментальных данных в виде пар значений [`y_i`, `x_i`], где
`i` – номер одного эксперементального измерения от 1 до `n`;
`y_i` – значение измеренной величины в точке `i`;
`x_i` – значение задаваемого нами параметра в точке `i`.
В качестве примера можно рассмотреть действие закона Ома. Изменяя напряжение (разность потенциалов) между участками электрической цепи, мы замеряем величину тока, проходящего по этому участку. Физика нам дает зависимость, найденную экспериментально:
`I = U / R`,
где `I` – сила тока; `R` – сопротивление; `U` – напряжение.
В этом случае `y_i` у нас имеряемая величина тока, а `x_i` – значение напряжения.
В качестве другого примера рассмотрим поглощение света раствором вещества в растворе. Химия дает нам формулу:
`A = ε l C`,
где `A` – оптическая плотность раствора;
`ε` – коэффициент пропускания растворенного вещества;
`l` – длина пути при прохождении света через кювету с раствором;
`C` – концентрация растворенного вещества.
В этом случае `y_i` у нас имеряемая величина отптической плотности `A`, а `x_i` – значение концентрации вещества, которое мы задаем.
Мы будем рассматривать случай, когда относительная погрешность в задании `x_i` значительно меньше, относительной погрешности измерения `y_i`. Так же мы будем предполагать, что все измеренные величины `y_i` случайные и нормально распределенные, т.е. подчиняются нормальному закону распределения.
В случае линейной зависимости `y` от `x`, мы можем написать теоретическую зависимость:
`y = a + b x`.
С геометрической точки зрения, коэффициент `b` обозначает тангенс угла наклона линии к оси `x`, а коэффициент `a` – значение `y` в точке пересечения линии с осью `y` (при `x = 0`).
Нахождение параметров линии регресии.
В эксперименте измеренные значения `y_i` не могут точно лечь на теоеретическую прямую из-за ошибок измерения, всегда присущих реальной жизни.
Поэтому линейное уравнение, нужно представить системой уравнений:
`y_i = a + b x_i + ε_i` (1),
где `ε_i` – неизвестная ошибка измерения `y` в `i`-ом эксперименте. 2`,
2`,
который сравнивают с табличным коэффициентом Фишера `F(p, n-1, n-2)`.
Если `F > F(P, n-1, n-2)`, считается статистически значимым с вероятностью `P` различие между описанием зависимости `y = f(x)` с помощью уравенения регресии и описанием с помощью среднего. Т.е. регрессия лучше описывает зависимость, чем разброс `y` относительно среднего.
§ 5 Метод наименьших квадратов (мнк).
Помимо двух вышеописанных
способов оценки погрешности результата
при косвенных измерениях, иногда
применяют еще так называемый «метод
наименьших квадратов» или сокращенно
МНК. Этот метод можно использовать, если
известен вид функциональной зависимостимежду измеряемыми физическими величинами,
а требуется определитькоэффициенты,
входящие в эту функцию. В наших лабораторных
работах предлагается применять этот
метод для определения параметров линейной зависимости.
Пусть в
эксперименте можно измерить ряд значений
некоторой величины xи, соответствующие им значения, величины
Как по данным экспериментальных наблюдений наилучшим образом найти коэффициенты aиb? Графически эта задача сводится к построению прямой, ближе всего лежащей ко всем экспериментальным токам, так как прямая однозначно задается этими коэффициентами (рис.4.).
Для аналитического
выражения коэффициентов применяется
метод наименьших квадратов. Утверждается, что наилучшей будет та прямая, сумма квадратов расстояний до которой, от всех экспериментальных точек будет минимальной. Расстояние (вдоль оси y) от точки с координатамиxi,yi до искомой прямой определяется выражением: (axi +b yi), | |
Рис.4 |
тогда сумма квадратов расстояний будет равна:
Решение задачи на нахождение минимума этого выражения (см. приложение, §8) приводит к следующим выражениям для коэффициентовaиb.
(25) | |
(26) |
Дисперсию отклонения экспериментальных точек от прямой S02и дисперсию коэффициентовaиb Sa2 иSb2 можно вычислить по формулам:
S02 = | (27) |
(28) | |
Sb2= | (29) |
Доверительные интервалы для коэффициентов aиb определяются как обычно:
ap = Sabp
= SbЕсли график исследуемой
зависимости проходит через начало
координат, то есть b=0, формулы 25, 27 и 28 существенно упрощаются.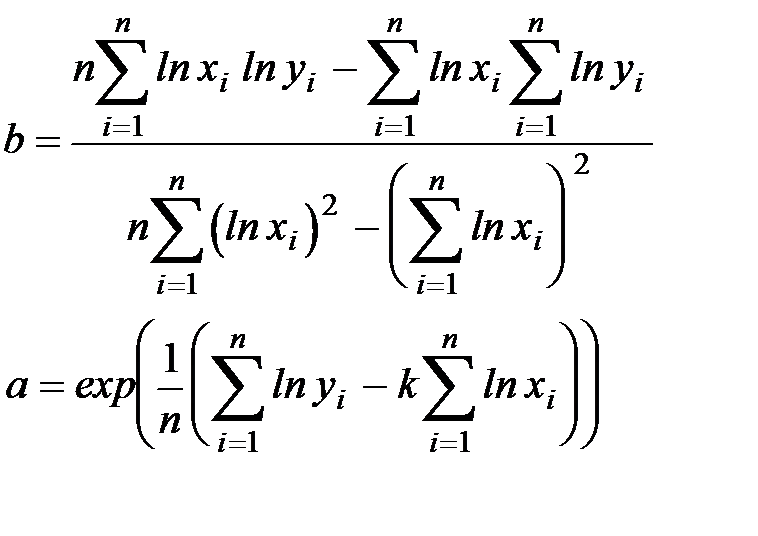 В этом случае коэффициентaи его дисперсию можно рассчитать по
следующим формулам:
В этом случае коэффициентaи его дисперсию можно рассчитать по
следующим формулам:
Однако следует иметь в виду, что формулы 25-28 включают разности больших величин, мало отличающихся друг от друга, что легко может привести к ошибкам при вычислениях, если их проводить с недостаточным числом значащих цифр. Поэтому все промежуточные вычисления следует выполнять с большим числом значащих цифр, без округления. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, а результаты измерений имеют более трех верных знаков, то велика вероятность получить неправильный результат вычислений. В этом случае рекомендуется для вычисления коэффициентов
Во всех случаях
проведения расчетов по МНК для определения
коэффициентов линейной зависимости и
их погрешностей необходимо вычислить
некоторые суммы. Для этого удобно
воспользоваться следующими таблицами
– алгоритмами вычислений. Подсчитав
суммы в каждом столбце и подставив их
в соответствующие формулы, легко
определить и значенияa,b,a иb
Для этого удобно
воспользоваться следующими таблицами
– алгоритмами вычислений. Подсчитав
суммы в каждом столбце и подставив их
в соответствующие формулы, легко
определить и значенияa,b,a иb
Таблица 5
xi | yi | xi2 | yi2 | xi yi |
x1 | y1 | x12 | y12 | x1 y1 |
x2 | y2 | x22 | y22 | x2 y2 |
… | … | … | … | … |
xn | yn | xn2 | yn2 | xn yn |
xi | yi | xi2 | yi2 | x1 y1 |
Или в случае использования формул 33 -37
Таблица 6
xi | yi | xi | (xi )2 | (xi )yi | xi2 | (axi +b yi)2 |
x1 | y1 | x1 | (x1 )2 | (x1 )y1 | x12 | (ax1 +b y1)2 |
x2 | y2 | x2 | (x2 )2 | (x2 )y2 | x22 | (ax2 +b y2)2 |
… | … | … | … | |||
xn | yn | xn | (xn )2 | (xn )yn | xn2 | (axn +b yn)2 |
xi | yi | (xi ) | (xi )2 | (xi )yi | xi2 | (axi +b yi)2 |
Метод наименьших квадратов при решении экспериментальных задач по физике
При решении экспериментальных задач по физике часто возникает необходимость измерения физических величин, находящихся в функциональной зависимости. Как правило, после измерений информация о физическом явлении извлекается из графиков, построенных по данным, полученным экспериментальным путем, а зависимость между двумя физическими величинами — xи yпредставляется в виде таблицы 1.
Как правило, после измерений информация о физическом явлении извлекается из графиков, построенных по данным, полученным экспериментальным путем, а зависимость между двумя физическими величинами — xи yпредставляется в виде таблицы 1.
Таблица 1
|
x |
x1 |
x2 |
x3 |
… |
xn |
|
y |
y1 |
y2 |
y3 |
. |
yn |
В связи с тем, что значения величин xи y измеряются с погрешностью, нанесенные на координатную плоскость точки будут разбросаны относительно предполагаемой кривой.
Если график y = f (x) строить, непосредственно соединяя экспериментально полученные точки, то он будет иметь вид ломаной. Однако в большинстве случаев функции, описывающие процессы в природе, являются гладкими. Значит, необходимо подобрать такую функцию y = f (x), которая наилучшим образом выражала бы экспериментальную зависимость y от x.
Наиболее простым видом функциональной зависимости является прямо пропорциональная зависимость между физическими величинами вида.
Необходимо отыскать такой коэффициент k, а значит, прямую, наилучшим образом согласованную с экспериментальными точками, нанесенными на плоскость (x, y), при котором общее отклонение
минимально (рисунок 1). Для этого необходимо решить уравнение:
или ,
где xi, yi — измеренные значения величин; N — количество пар значений измеренных величин.
Естественно, что для отыскания экстремума дифференцирование ведется по параметру, от которого зависит, как пройдет график. Воспользовавшись правилами дифференцирования суммы и сложной функции, получим
Полученное значение параметра k позволяет наиболее близко к экспериментальным точкам провести прямую, выходящую из начала координат.
Рис. 1. Экспериментальные точки при измерении величин
1. Экспериментальные точки при измерении величин
Погрешность при определении параметра k:
Экспериментальная задача. Измерить сопротивление проводника при помощи амперметра и вольтметра. Оценить погрешность измерений.
Для решения поставленной задачи необходимо собрать электрическую цепь, изображенную на рисунке 2.
Рис. 2. Экспериментальная установка для измерения сопротивления проводника при помощи амперметра и вольтметра
Изменения силы тока и напряжения на резисторе, полученные в результате измерений приведены в таблице 2.
Таблица 2
|
I, А |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
U, В |
0,27 |
0,56 |
0,9 |
1,18 |
1,49 |
1,79 |
2,05 |
2,42 |
2,68 |
3,01 |
|
I, А |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2 |
|
U, В |
3,35 |
3,56 |
3,85 |
4,18 |
4,48 |
4,79 |
5,12 |
5,45 |
5,68 |
5,9 |
Необходимо подобрать такую формулу U = f (I), чтобы она наиболее удачно отражала зависимость между силой тока I и напряжением U. Закон Ома устанавливает эту зависимость в виде U=RI. Это линейная зависимость. Определим величину сопротивления R.
Закон Ома устанавливает эту зависимость в виде U=RI. Это линейная зависимость. Определим величину сопротивления R.
Способ № 1.
- Определим значение сопротивления R каждого из N измерений:
.
- Определим среднее значение сопротивления по формуле:
(Ом).
Погрешность такого косвенного измерения сопротивления можно найти по правилам обработки результатов прямых измерений, рассматривая набор значений Ri как статистический набор данных. Пренебрегая инструментальной погрешностью, получим:
(Ом).
Итак,Ом.
Это самый простой, но не лучший способ выбора коэффициента k в случае, когда сглаживающая зависимость между величинами xи y линейная и имеет вид: y = kx.
Способ № 2 (Метод наименьших квадратов)
- Значение сопротивления R можно найти по формуле:
(Ом).
- Погрешность вычислим по формуле:
(Ом).
В результате получим: (Ом).
Видно, что наиболее вероятные значения сопротивлений, вычисленные двумя рассмотренными способами, попадают в доверительные интервалы друг друга и, следовательно, оба имеют право на существование. Однако погрешность расчета сопротивления при использовании метода наименьших квадратов оказалась вдвое меньше по сравнению с первым способом. Таким образом, результат, полученный методом наименьших квадратов, более точен.
Литература:
-
Тейлор Дж.
 Введение в теорию ошибок / Дж. Тейлор; Пер. с англ. М.: Мир, 1985. 272 с.
Введение в теорию ошибок / Дж. Тейлор; Пер. с англ. М.: Мир, 1985. 272 с.
- Исаков В. А. Физика колебаний. Лабораторный практикум: Методические указания к лабораторным работам по физике / В. А. Исаков, В. П. Нестеров / Омский гос. ун-т путей сообщения. Омск, 2001. 22 с.
- Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений / Ю. В. Линник. Л.: Физматгиз, 1962. 352 с.
Обработка результатов физического эксперимента | Открытые видеолекции учебных курсов МГУ
Курс «Обработка результатов физического эксперимента» читается студентам первого курса физического факультета МГУ имени М. В. Ломоносова в 1 семестре.
В рамках курса «Обработка результатов физического эксперимента» изложены основные понятия и методы, используемые при обработке результатов экспериментальных исследований. Приведена классификация измерений и возникающих при измерениях погрешностей. Дана краткая сводка правил обработки результатов прямых, косвенных и совместных измерений. Уделено большое внимание наиболее часто используемому в практике обработки результатов совместных измерений методу наименьших квадратов.
Дана краткая сводка правил обработки результатов прямых, косвенных и совместных измерений. Уделено большое внимание наиболее часто используемому в практике обработки результатов совместных измерений методу наименьших квадратов.
Курс предназначен в первую очередь для студентов младших курсов, работающих в общем физическом практикуме. Но может быть полезно также для студентов старших курсов, дипломников, аспирантов, проводящих экспериментальные исследования в научных лабораториях.
Список всех тем лекций
Лекция 1. Измерение и погрешность измерений.
Рекомендуемая литература
Физические величины и их измерение
Классификация
Среднее арифметическое
Оценка случайной погрешности прямо измеряемой величины
Правила округления
Лекция 2. Погрешности измерений.
Погрешности измерений.
Суммарная систематическая погрешность
Суммарная погрешность прямо измеряемой величины
Правила округления
Случайная погрешность косвенно измеряемой величины
Погрешность косвенных измерений в случае функции многих переменных
Лекция 3. Метод наименьших квадратов. Часть 1.
Метод наименьших квадратов
Вывод формул МНК для a и b
Формулы МНК для погрешностей a и b
Коэффициент корреляции
Лекция 4. Метод наименьших квадратов. Часть 2.
Коэффициент корреляции
Хи-квадрат
Описание программы МНК
МНК с весами
Лекция 5. Метод наименьших квадратов. Часть 3.
Метод наименьших квадратов. Часть 3.
и y0
Линеаризация
Одновременный учёт погрешностей x и y
Нахождение наилучшей оценки при помощи МНК с весами
Лекция 6. Теория вероятностей.
Проблема случайных и систематических погрешностей МНК
Вероятность события
О проблемах случайных и систематических погрешностей
Несовместные и независимые события
Математическое ожидание и дисперсия случайной величины
Лекция 7. Функции распределения.
Плотность распределения
Расчёт погрешности округления
Центральная предельная теорема
Лекция 8. Распределение Стьюдента и распределение Хи-квадрат.
Распределение Стьюдента и распределение Хи-квадрат.
Доверительный интервал
Коэффициент Чебышёва
Распределение Хи-квадрат
Критерии наилучшей оценки и её нахождение
Поиск наилучшей оценки в виде линейной комбинации результатов измерений
Лекция 9. Наилучшая оценка.
Поиск наилучшей оценки в виде линейной комбинации результатов измерений
Несмещенная оценка дисперсии
Наилучшая оценка и дисперсия косвенно измеряемой величины
Измерение масс двух тел идеальными весами
Расчёт погрешности ускорения шарика, скатывающегося по наклонной плоскости
Лекция 14. Регрессионный анализ. Градуировка.
Проведение количественного анализа, как правило, включает в себя построение градуировки, т. е. находждение градуировочной функции экспериментальным путем. Для этого измеряется аналитический сигнал для серии образцов сравнения, в результате получается массив данных: {xi,yi}, где x — содержание определяемого компонента, y — аналитический сигнал. На плоскости каждое измерение можно представить точкой:
е. находждение градуировочной функции экспериментальным путем. Для этого измеряется аналитический сигнал для серии образцов сравнения, в результате получается массив данных: {xi,yi}, где x — содержание определяемого компонента, y — аналитический сигнал. На плоскости каждое измерение можно представить точкой:
Градуировочная функция y = f(x) определяется методами регрессионного анализа. Прямо через точки проводить ломаную и считать ее градуировочной функцией нельзя, т.к. измеряемый сигнал содержит погрешность.
Т.о. необходимо:
1) доопределить функцию (между точками)
2) минимизировать погрешность и
3) выбрать вид зависимости.
Вид функции зависимости выбирается исходя из внешней информации (расположения точек на плоскости) и из общих соображений относительно физических и химических законов, связывающих аналитический сигнал с содержанием определяемого компонента (например, построение градуировки в спектрофотометрии опирается на закон Бугера-Ламберта-Бера). Наиболее часто используется линейная зависимость.
Наиболее часто используется линейная зависимость.
Обозначим k — число параметров градуировочной функции, n — число измерений. Мы получаем систему уравнений:
Рассмотрим различные варианты соотношений n и k:
1) n — данных недостаточно. Необходимо провести больше измерений или упростить модель — уменьшить число параметров.
2) n = k — у системы единственное точное решение. Однако в этом случае нельзя оценить погрешность измерения
3) n > k — система уравнений несовместна и не имеет точного решения. Существует бесконечное множество приближенных решений, возникает задача аппроксимации.
На практике наиболее распространен 3-й случай. Рассмотрим его более подробно на примере линейного регрессионного анализа (т.е. градуировочная зависимость имеет линейный вид y = ax + b, определяется двумя параметрами a и b, k = 2).
Необходимо найти a и b такие, чтобы погрешность была минимальной.
Один из наиболее распространенных методов нахождения параметров линейной зависимости — метод наименьших квадратов, МНК
Предпосылки МНК:
1) Погрешность аргумента (x) пренебрежимо мала по сравнению с погрешностью y
2) Погрешность y постоянна (не зависит от x) — постулат равноточности (в условиях реального эксперимента погрешность обычно растет с ростом y)
3) Данные подчиняются нормальному закону распределения
4) Данные независимы, коэффициент корреляции r(yi,yj) = 0
5) Отклонение градуировочной функции от экспериментальных данных минимально. В рамках метода наименьших квадратов минимизируется величина , где Yi— величина аналитического сигнала, рассчитанная по уравнению Y = ax + b, yi— экспериментальная величина аналитического сигнала
С учетом всех предпосылок получаются следующие выражения для a и b:
О том, как оценивается погрешность градуировки, а также погрешность связанных с ней вычислений, читайте в следующих лекциях.
лекции читает А.В.Гармаш, химический факультет МГУ
Р 50.2.028-2003 ГСИ. Алгоритмы построения градуировочных характеристик средств измерений состава веществ и материалов и оценивание их погрешностей (неопределенностей). Оценивание погрешности (неопределенности) линейных градуировочных характеристик при использовании метода наименьших квадратов
Р 50.2.028-2003
|
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ |
Государственная система обеспечения единства измерений
АЛГОРИТМЫ ПОСТРОЕНИЯ ГРАДУИРОВОЧНЫХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ СОСТАВА ВЕЩЕСТВ И МАТЕРИАЛОВ И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ (НЕОПРЕДЕЛЕННОСТЕЙ)
Оценивание погрешности (неопределенности) линейных градуировочных характеристик использовании метода наименьших квадратов
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1
РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием «Всероссийский
научно-исследовательский институт метрологии им. Д.И. Менделеева» (ФГУП «ВНИИМ
им. Д.И. Менделеева») Госстандарта России
Д.И. Менделеева» (ФГУП «ВНИИМ
им. Д.И. Менделеева») Госстандарта России
ВНЕСЕНЫ Управлением метрологии Госстандарта России
2 ПРИНЯТЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Госстандарта России от 14 мая 2003 г. № 142-ст
3 ВВЕДЕНЫ ВПЕРВЫЕ
Содержание:
|
1 Область применения 2 Определения и обозначения 3 Построение линейных градуировочных характеристик средств измерений (ГХ СИ) методом наименьших квадратов (МНК) 4 Оценивание характеристик погрешности (неопределенности) построения ГХ СИ* 5 Планирование измерений при построении линейных ГХ СИ 6 Контроль стабильности ГХ СИ ПРИЛОЖЕНИЕ А (рекомендуемое) Пример построения градуировочной характеристики ПРИЛОЖЕНИЕ Б (справочное) Библиография |
|
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ |
|
Государственная система обеспечения единства измерений АЛГОРИТМЫ ПОСТРОЕНИЯ ГРАДУИРОВОЧНЫХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ СОСТАВА ВЕЩЕСТВ И МАТЕРИАЛОВ И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ (НЕОПРЕДЕЛЕННОСТЕЙ) Оценивание погрешности (неопределенности) линейных градуировочных характеристик использовании метода наименьших квадратов |
Дата введения 2004-01-01
Настоящие
рекомендации распространяются на методы планирования измерительного
эксперимента и оценивания характеристик погрешности (неопределенности)
построения линейных градуировочных характеристик средств измерений состава
веществ и материалов (ГХ СИ) методом наименьших квадратов (МНК).
2.1 В настоящих рекомендациях применены следующие термины с соответствующими определениями:
градуировочная характеристика средства измерения состава веществ и материалов: Функциональ ная зависимость между входной (х ) и выходной ( y ) величинами, построенная на основе значений градуировочных смесей и результатов измерений соответствующих выходных величин в N точках диапазона измерений (х i , у ij ), где i = 1,…, N ; j = 1,…, n [ 1], [ 2];
оценка стандартной неопределенности по типу А: Оценка на основании результатов многократных измерений [ 1], [ 2 ];
оценка стандартной неопределенности по типу В: Оценка на основании априорной информации [ 1], [ 2 ].
2.2 В настоящих рекомендациях применены следующие обозначения:
S ( y ) — среднее квадратическое отклонение (СКО) однократного измерения выходной величины;
S ( ) — СКО среднего значения выходной величины;
u A ( ) — стандартная неопределенность среднего значения выходной величины, оцененная по типу А;
u B ( ) — стандартная неопределенность среднего значения выходной величины, оцененная по типу В;
u B ( x ) - стандартная неопределенность градуировочной смеси, оцененная по типу В;
S θ ( х ) — СКО неисключенной систематической погрешности градуировочных смесей;
S Σ (х) — СКО погрешности построения ГХ СИ в точке х ;
u Σ ( х ) — суммарная стандартная неопределенность построения ГХ СИ в точке х
U p ( х ) — расширенная неопределенность построения ГХ СИ в точке х ;
cov ( x i , х j ) — ковариация погрешностей i , j градуировочных смесей;
ГХ - градуировочная характеристика;
СИ — средство
измерения.
3.1 Исходными данными для построения ГХ СИ являются результаты измерений ( х i , у ij ), где i = 1,…, N ; j = 1,…, n .
3.2 ГХ СИ задается в виде:
, (1)
где
. (2)
3.3 Оценки параметров ГХ СИ вычисляют по формулам:
, (3)
, (4)
. (5)
4.1 Источниками погрешности (неопределенности) построения ГХ СИ являются:
— случайные погрешности измерения выходной величины у ij ,
— систематические погрешности градуировочных смесей х i ,
4. 2
Оценивание СКО (стандартной неопределенности) случайной погрешности измерения
выходной величины
2
Оценивание СКО (стандартной неопределенности) случайной погрешности измерения
выходной величины
* В ФГУП «ВНИИМ им. Д.И. Менделеева» разработана программа обработки данных и оценивания характеристик погрешности (неопределенности) построения градуировочных характеристик средств измерений в соответствии с настоящими Рекомендациями.
4.2.1 При многократных равноточных измерениях (независимость СКО от точки диапазона) СКО (стандартную неопределенность) выходной величины у вычисляют на основании экспериментальных данных (оценивание по типу А) по формуле:
. (6)
4.2.2 При однократных измерениях СКО (стандартная неопределенность) выходной величины у может быть рассчитана по типу В, используя паспортные данные средства измерения о сходимости показаний, по формуле:
, (7)
где S сход — СКО случайной погрешности
средства измерения.
4.3 СКО систематической погрешности (стандартную неопределенность) градуировочных смесей обычно оценивают на основании информации о границах допустимых погрешностей градуировочных смесей (по типу В) по формулам:
(8)
если нормируют абсолютные погрешности [Ө( x )] градуировочных смесей;
(9)
если нормируют относительные погрешности [δ( x )] градуировочных смесей.
4.4 Оценивание корреляции между погрешностями градуировочных смесей
4.4.1 Если градуировочные смеси готовились независимо, то в большинстве случаев можно считать их погрешности независимыми, в этом случае коэффициент корреляции равен нулю и ковариацию оценивают по формуле:
.
4. 4.2 Если
градуировочные смеси готовились разбавлением основной смеси или с
использованием одних и тех же стандартных образцов, то корреляция между
погрешностями их приготовления может достичь 1, что соответствует присутствию
постоянной систематической погрешности градуировочных смесей, в этом случае
ковариацию оценивают по формуле:
4.2 Если
градуировочные смеси готовились разбавлением основной смеси или с
использованием одних и тех же стандартных образцов, то корреляция между
погрешностями их приготовления может достичь 1, что соответствует присутствию
постоянной систематической погрешности градуировочных смесей, в этом случае
ковариацию оценивают по формуле:
.
4.5 Оценивание СКО погрешности (суммарной стандартной неопределенности) построения ГХ СИ
4.5.1 Если корреляция погрешностей градуировочных смесей отсутствует и характеристики абсолютных погрешностей градуировочных смесей остаются постоянными на всем диапазоне изменения входной величины, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
, (10)
где θ
— границы абсолютных погрешностей градуировочных смесей.
Если корреляция погрешностей градуировочных смесей отсутствует, а характеристики погрешности градуировочных смесей зависят от точки диапазона, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
, (11)
где θ ( х ) — границы абсолютных погрешностей градуировочных смесей в точке х .
4.5.2 Если корреляция погрешностей градуировочных смесей присутствует и характеристики абсолютных погрешностей градуировочных смесей остаются постоянными на всем диапазоне изменения входной величины, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
(12)
Если присутствует корреляция погрешностей градуировочных смесей, а характеристики погрешностей градуировочных смесей зависят от точки диапазона, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
, (13)
4. 6 При
вычислении доверительных границ погрешности (расширенной неопределенности)
построения ГХ СИ рекомендуется использовать следующие коэффициенты охвата k :
6 При
вычислении доверительных границ погрешности (расширенной неопределенности)
построения ГХ СИ рекомендуется использовать следующие коэффициенты охвата k :
k = 2 — при доверительной вероятности Р = 0,95;
k = 3 — при доверительной вероятности Р = 0,99.
Доверительные границы (расширенную неопределенность) вычисляют по формуле:
. (14)
5.1 Планирование измерений направлено на оптимизацию затрат при проведении измерений для достижения
требуемой точности построения ГХ СИ и проводится на этапе разработки методик
выполнения измерений. Планирование измерений
заключается в выборе числа параллельных
измерений в точке n , числа градуировочных точек N , а также установлении требований к
точности градуировочных смесей, исходя из требуемой точности построения
градуировочной характеристики. Ниже приводится одно из возможных простых
решений задачи планирования измерений. После выбора числа параллельных измерений
в точке n , числа градуировочных точек ( N ),
а также точности градуировочных смесей оценивание характеристик погрешности
(неопределенности) ГХ СИ следует проводить в соответствии с разделом
4.
Ниже приводится одно из возможных простых
решений задачи планирования измерений. После выбора числа параллельных измерений
в точке n , числа градуировочных точек ( N ),
а также точности градуировочных смесей оценивание характеристик погрешности
(неопределенности) ГХ СИ следует проводить в соответствии с разделом
4.
5.2 Число измерений n в точке рационально выбирать из условия незначительного (не более 20 %) роста суммарной погрешности по сравнению с систематической составляющей по формуле:
. (15)
5.3 Если погрешности градуировочных смесей не коррелированы, то требуемая точность построения ГХ СИ может быть достигнута за счет увеличения числа градуировочных смесей и уменьшения их погрешностей в соответствии с формулой:
, (16)
где u Σ доп — допустимая суммарная
стандартная неопределенность построения ГХ СИ (СКО допустимой погрешности).
5.4 Если погрешности градуировочных смесей коррелированы, то при построении линейных ГХ СИ рекомендуется использовать две градуировочные смеси. При этом должны быть обеспечены следующие погрешности градуировочных смесей, исходя из требований к точности построения ГХ СИ:
(17)
6.1 Обычно процедура контроля стабильности ГХ СИ состоит в сравнении измеренного значения выходного сигнала в градуировочных точках с его оценкой по ГХ СИ (данный результат измерения не используется при построении ГХ СИ). Для линейной ГХ СИ число точек контроля должно быть не менее двух.
6.2 Если погрешности градуировочных смесей не коррелированы, то проверяют следующие условия в соответствии с формулами:
при N ≥ 5; (18)
при N ≤ 4, (19)
где yi — измеренное значение выходного сигнала в точке х i ,
— оценка выходного сигнала по
ГХ СИ в точке х i .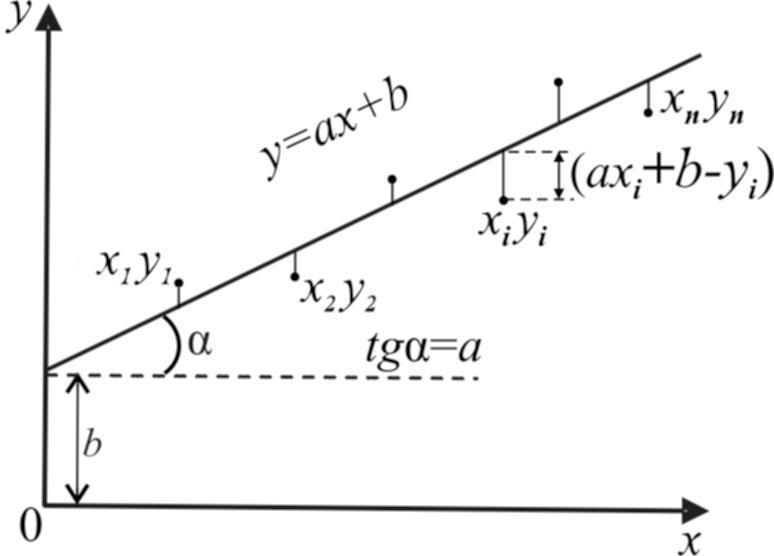
6.3 Если погрешности градуировочных смесей коррелированы, то проверяют следующие условия в соответствии с формулами:
при N ≥ 5; (20)
при N ≤ 4, (21)
А. 1 Исходные данные
Градуировочная характеристика хроматографа строится по стандартным образцам водных растворов этанола массовой концентрации х i (N = 7). Границы относительной погрешности массовой концентрации этанола не превышают 0,5 %. Выполняют по 5 параллельных измерений в каждой точке ( n = 5). Данные для построения градуировочной характеристики приведены в таблице А.1.
Таблица А.1
|
Обозначение параметра |
Значения массовой концентрации (входная величина) |
||||||
|
xi , мг/мл |
0,49 |
0,97 |
2,00 |
2,96 |
4,05 |
5,07 |
6,05 |
|
Результаты измерения |
|||||||
|
yij |
227451 |
439935 |
942200 |
1404433 |
1821194 |
2277460 |
2824679 |
|
221585 |
454170 |
935664 |
1391932 |
1825116 |
2240900 |
2825947 |
|
|
232387 |
444558 |
929875 |
1409124 |
1874371 |
2275484 |
2834183 |
|
|
223216 |
453812 |
933705 |
1385680 |
1834334 |
2319111 |
2816202 |
|
|
233628 |
457800 |
937104 |
1375168 |
1802673 |
2180685 |
2853467 |
|
|
Средние значения выходного сигнала в i-й точке |
|||||||
|
|
227653 |
450055 |
935710 |
1393267 |
1831538 |
2258728 |
2830896 |
|
СКО единичного измерения выходного сигнала в i-й точке |
|||||||
|
Si |
5353,965 |
7477,712 |
4531,355 |
13811,61 |
26208,11 |
51687,29 |
14136,05 |
А. 2
Вычисление коэффициентов градуировочной характеристики
2
Вычисление коэффициентов градуировочной характеристики
Градуировочная характеристика представлена в виде:
; (А.1)
. (А.2)
Оценки градуировочных коэффициентов вычисляют по формулам:
, (А.3)
, (А.4)
. (А.5)
А.3 Оценивание погрешности (неопределенности) построения градуировочной зависимости
Оценку СКО (стандартную неопределенность по типу А) выходного сигнала в предположении равноточности измерений получают по формуле:
, (А. 6)
6)
где
Оценку СКО систематической погрешности (стандартной неопределенности по типу В) градуировочной смеси, которое в данном случае зависит от значения градуировочной смеси, вычисляют по формуле:
, (А.7)
где δ(х) = 0,5 % — границы относительной погрешности массовой концентрации этанола. Оценку СКО суммарной погрешности (суммарной стандартной неопределенности) построения градуировочной характеристики вычисляют по формуле:
, (А.8)
где ;
Доверительные границы погрешности (расширенную неопределенность) построении градуиро вочной характеристики вычисляют по формуле:
. (А.9)
[1] МИ 2175-91 Государственная
система обеспечения единства измерений. Градуировочные характеристики средств
измерений. Методы построения, оценивание погрешностей
Градуировочные характеристики средств
измерений. Методы построения, оценивание погрешностей
[2] РМГ 43-2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»
|
Ключевые слова: средство измерений состава веществ, линейная градуировочная характеристика, построение градуировочной характеристики, метод наименьших квадратов, погрешность, неопределенность, оценивание погрешности (неопределенности), среднее квадратическое отклонение. |
Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y. Занесем их в таблицу.
| i=1 | i=2 | i=3 | i=4 | i=5 | |
| xi | 0 | 1 | 2 | 4 | 5 |
| yi | 2,1 | 2,4 | 2,6 | 2,8 | 3,0 |
После выравнивания получим функцию следующего вида: g(x)=x+13+1.
Мы можем аппроксимировать эти данные с помощью линейной зависимости y=ax+b, вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F(a, b)=∑i=1n(yi-(axi+b))2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F(a, b)=∑i=1n(yi-(axi+b))2 по a и b и приравниваем их к 0.
Для этого мы вычисляем частные производные выражения F(a, b)=∑i=1n(yi-(axi+b))2 по a и b и приравниваем их к 0.
δF(a, b)δa=0δF(a, b)δb=0⇔-2∑i=1n(yi-(axi+b))xi=0-2∑i=1n(yi-(axi+b))=0⇔a∑i=1nxi2+b∑i=1nxi=∑i=1nxiyia∑i=1nxi+∑i=1nb=∑i=1nyi⇔a∑i=1nxi2+b∑i=1nxi=∑i=1nxiyia∑i=1nxi+nb=∑i=1nyi
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n∑i=1nxiyi-∑i=1nxi∑i=1nyin∑i=1n-∑i=1nxi2b=∑i=1nyi-a∑i=1nxin
Мы вычислили значения переменных, при который функция
F(a, b)=∑i=1n(yi-(axi+b))2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a, включает в себя ∑i=1nxi, ∑i=1nyi, ∑i=1nxiyi, ∑i=1nxi2, а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a.
Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a.
Обратимся вновь к исходному примеру.
Пример 1Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i=1 | i=2 | i=3 | i=4 | i=5 | ∑i=15 | |
| xi | 0 | 1 | 2 | 4 | 5 | 12 |
| yi | 2,1 | 2,4 | 2,6 | 2,8 | 3 | 12,9 |
| xiyi | 0 | 2,4 | 5,2 | 11,2 | 15 | 33,8 |
| xi2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i. Пятая строка содержит данные из второй, возведенные в квадрат.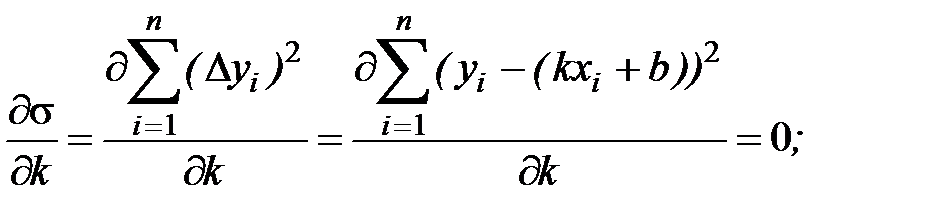 В последнем столбце приводятся суммы значений отдельных строчек.
В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b. Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n∑i=1nxiyi-∑i=1nxi∑i=1nyin∑i=1n-∑i=1nxi2b=∑i=1nyi-a∑i=1nxin⇒a=5·33,8-12·12,95·46-122b=12,9-a·125⇒a≈0,165b≈2,184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y=0,165x+2,184. Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g(x)=x+13+1 или 0,165x+2,184. Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ1=∑i=1n(yi-(axi+bi))2 и σ2=∑i=1n(yi-g(xi))2, минимальное значение будет соответствовать более подходящей линии.
σ1=∑i=1n(yi-(axi+bi))2==∑i=15(yi-(0,165xi+2,184))2≈0,019σ2=∑i=1n(yi-g(xi))2==∑i=15(yi-(xi+13+1))2≈0,096
Ответ: поскольку σ1<σ2, то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y=0,165x+2,184.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеКак изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g(x)=x+13+1, синей – y=0,165x+2,184. Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x=3 или при x=6. Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b, нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F(a, b)=∑i=1n(yi-(axi+b))2 была положительно определенной. Покажем, как это должно выглядеть.
Пример 2У нас есть дифференциал второго порядка следующего вида:
d2F(a; b)=δ2F(a; b)δa2d2a+2δ2F(a; b)δaδbdadb+δ2F(a; b)δb2d2b
Решение
δ2F(a; b)δa2=δδF(a; b)δaδa==δ-2∑i=1n(yi-(axi+b))xiδa=2∑i=1n(xi)2δ2F(a; b)δaδb=δδF(a; b)δaδb==δ-2∑i=1n(yi-(axi+b))xiδb=2∑i=1nxiδ2F(a; b)δb2=δδF(a; b)δbδb=δ-2∑i=1n(yi-(axi+b))δb=2∑i=1n(1)=2n
Иначе говоря, можно записать так: d2F(a; b)=2∑i=1n(xi)2d2a+2·2∑xii=1ndadb+(2n)d2b.
Мы получили матрицу квадратичной формы вида M=2∑i=1n(xi)22∑i=1nxi2∑i=1nxi2n.
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b. Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2∑i=1n(xi)2>0. Поскольку точки xi не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
det(M)=2∑i=1n(xi)22∑i=1nxi2∑i=1nxi2n=4n∑i=1n(xi)2-∑i=1nxi2
После этого переходим к доказательству неравенства n∑i=1n(xi)2-∑i=1nxi2>0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n. Возьмем 2 и подсчитаем:
2∑i=12(xi)2-∑i=12xi2=2×12+x22-x1+x22==x12-2x1x2+x22=x1+x22>0
У нас получилось верное равенство (если значения x1 и x2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n, т.е. n∑i=1n(xi)2-∑i=1nxi2>0 – справедливо.
- Теперь докажем справедливость при n+1, т.е. что (n+1)∑i=1n+1(xi)2-∑i=1n+1xi2>0, если верно n∑i=1n(xi)2-∑i=1nxi2>0.
Вычисляем:
(n+1)∑i=1n+1(xi)2-∑i=1n+1xi2==(n+1)∑i=1n(xi)2+xn+12-∑i=1nxi+xn+12==n∑i=1n(xi)2+n·xn+12+∑i=1n(xi)2+xn+12—∑i=1nxi2+2xn+1∑i=1nxi+xn+12==∑i=1n(xi)2-∑i=1nxi2+n·xn+12-xn+1∑i=1nxi+∑i=1n(xi)2==∑i=1n(xi)2-∑i=1nxi2+xn+12-2xn+1×1+x12++xn+12-2xn+1×2+x22+…+xn+12-2xn+1×1+xn2==n∑i=1n(xi)2-∑i=1nxi2++(xn+1-x1)2+(xn+1-x2)2+…+(xn-1-xn)2>0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2), и остальные слагаемые будут больше 0, поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F(a, b)=∑i=1n(yi-(axi+b))2, значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Автор: Ирина
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
6.15.1 Использование MNC
Далее: 6.15.2 Внутреннее устройство MNC Up: 6.15 Интеграция ввода-вывода NetCDF: Предыдущая: 6.15 Интеграция ввода-вывода NetCDF: Содержание
Подразделы
6.15.1.1 Конфигурация MNC
Как и все пакеты MITgcm, MNC можно включить или выключить во время компиляции. используя файл packages.conf или genmake2 -enable = mnc или -disable = mnc переключатели.
Хотя MNC, скорее всего, будет работать « как есть », есть несколько этапов компиляции. константы, которые, возможно, потребуется увеличить для моделирования, использующего большое количество плиток в каждом процессе.Обратите внимание, что важные количество — максимальное количество плиток на процесс . С Конфигурации MPI имеют тенденцию распределять большое количество плиток по относительно большое количество процессов MPI, эти константы редко нужно увеличить.
Если MNC исчерпывает пространство в его « справочных » таблицах во время симуляции, то он выдаст сообщение об ошибке вместе с рекомендация, какой параметр увеличить. Параметры все находится в пределах pkg / mnc / mnc_common.h и те, которые, возможно, потребуется увеличить:
| Имя | По умолчанию | Описание |
|---|---|---|
| MNC_MAX_ID | 1000 | ID для различных низкоуровневых сущностей |
| MNC_MAX_INFO | 400 | идентификаторов (в основном для размеров объектов) |
| MNC_CW_MAX_I | 150 | ID для слоя « обертка » |
В тех редких случаях, когда появляются сообщения об ошибке MNC « Out-of-memory » встречается, рекомендуется увеличить слишком маленький параметр на коэффициент 2-10 , чтобы не тратить время на итеративная последовательность компиляции-тестирования.
6.15.1.2 Входы MNC
Для конфигурации во время выполнения большинство параметров модели, связанных с MNC содержатся в файле списка имен Fortran с именем data.mnc. Если этот файл не существует, пакет MNC интерпретирует это как указание на то, что его нельзя использовать. Если data.mnc файл существует, то он может содержать следующие параметры:
| Имя | т | По умолчанию | Описание |
|---|---|---|---|
| использоватьMNC | л | .ЛОЖНЫЙ. | общий выключатель MNC ON / OFF |
| mnc_echo_gvtypes | л | .FALSE. | echo предопределенные « типы » (отладка) |
| mnc_use_outdir | л | .FALSE. | создать каталог для вывода |
| mnc_outdir_str | S | ‘mnc_’ | имя выходного каталога |
| mnc_outdir_date | л | .ЛОЖНЫЙ. | вставить дату в имя выходного каталога |
| pickup_write_mnc | л | .FALSE. | использовать MNC для записи (создания) файлов подбора |
| pickup_read_mnc | л | .FALSE. | использовать MNC для чтения файлов подбора |
| mnc_use_indir | л | .FALSE. | использовать каталог (путь) для ввода |
| mnc_indir_str | S | ‘ | входной каталог (или путь) имя |
| snapshot_mnc | л | .ЛОЖНЫЙ. | запись снимка (мгновенная) с MNC |
| monitor_mnc | л | .FALSE. | монитор записи с MNC |
| timeave_mnc | л | .FALSE. | запись timeave с MNC |
| autodiff_mnc | л | .FALSE. | написать автодифф с MNC |
Дополнительные параметры, относящиеся к MNC, содержатся в основном файл списка имен данных и в некоторых файлах списков имен для индивидуальные пакеты.Вот эти варианты:
| Имя | т | По умолчанию | Описание |
|---|---|---|---|
| Основной файл списка имен: « данные » | |||
| snapshot_ioinc | л | .FALSE. | записать снимок « включительно » |
| timeave_ioinc | л | .ЛОЖНЫЙ. | написать timeave « включительно » |
| monitor_ioinc | л | .FALSE. | записать монитор « включительно » |
| the_run_name | С | « имя … » | имя включено во все выходные данные MNC |
| Файл списка имен диагностики: « диагностика данных » | |||
| diag_mnc | л | .ЛОЖНЫЙ. | написать диагностику с MNC |
| diag_ioinc | л | .FALSE. | написать диагностику « включительно » |
По умолчанию включение MNC для определенного типа вывода приведет к отключение всех соответствующих (обычно по умолчанию) MDSIO или STDOUT механизмы вывода. Другими словами, по умолчанию вывод эксклюзивный выбор. Чтобы включить несколько видов одновременного вывода, флаги формы NAME_ioinc были созданы, где NAME соответствует различным выходным флагам MNC.Когда Флаг NAME_ioinc установлен на .TRUE., Затем несколько одновременные формы вывода разрешены для вывода NAME механизм. Этот дизайн предназначен для того, чтобы обычные пользователи могли только требуется один вид вывода, пока люди отлаживают код (особенно процедуры ввода-вывода) могут потребоваться одновременные типы вывода.
Этот « инклюзивный » дизайн по сравнению с « эксклюзивным » легко применяется в случаи, когда могут быть сгенерированы три или более вида вывода. Таким образом, это может быть легко расширен до дополнительных новых типов вывода (например,HDF5).
Типы ввода всегда исключающие.
6.15.1.3 Вывод MNC
Хотя файлы NetCDF должны быть « самоописывающимися », они полезно отметить следующее:
- Ограничения, накладываемые на « неограниченный » (или « рекордный ») размерность, присущая NetCDF v3.x, делает очень неэффективным размещение переменные, записанные с потенциально разными интервалами в одном и том же файл. По этой причине вывод MNC разделен на несколько файлов. имена », которые пытаются отразить характер своего содержания.
- Весь вывод MNC в настоящее время выполняется в режиме « плитка на файл »
поскольку большинство реализаций NetCDF v3.x не могут безопасно писать в MPI
или многопоточные среды. Эта мозаика выполняется в глобальном
мода и номера плиток добавляются к базовым именам
описано выше. Доступны некоторые скрипты для « сборки » вывода
(MITgcm / utils / matlab). Более общие манипуляции можно
выполнено с
Операторы NetCDF (или `` NCO '') на http: //nco.sourceforge.сеть
который представляет собой очень мощный и удобный набор инструментов для работы со всеми файлами NetCDF. - Во многих системах NetCDF имеет практические ограничения на размер файла порядка 2-4 ГБ (максимальная адресуемая память с 32-битной указатели) из-за отсутствия операционной системы, компилятора и / или поддержка библиотеки. В случаях, когда этот предел достигнут, как правило, неплохо уменьшить частоту записи или перезапустить с пикапы.
- MNC (пока) не предоставляет механизм для чтения информации из одного « глобального » файла, как это можно сделать с помощью MDSIO упаковка.Это в процессе.
Далее: 6.15.2 Внутреннее устройство MNC Up: 6.15 Интеграция ввода-вывода NetCDF: Предыдущая: 6.15 Интеграция ввода-вывода NetCDF: Содержание [email protected]
| Авторское право 2002 г. Массачусетский технологический институт |
| Далее: 7.2.3 Внутреннее устройство MNC Up: 7.2 NetCDF I / O: MNC Предыдущее: 7.2.1 Использование MNC Содержание Подразделы 7.2.2.1 Устранение неполадок при сборке:Чтобы собрать MITgcm с включенным MNC, netCDF v3.x Fortran-77 (не Fortran-90) библиотека должна быть доступна.Эта библиотека составная одного файла заголовка (называемого netcdf.inc) и одного файл библиотеки (обычно называется libnetcdf.a), и он должен быть построенный с помощью того же компилятора (или компилятора, совместимого с двоичными кодами) с совместимые параметры компилятора, которые использовались для сборки MITgcm. Для получения более подробной информации о процессе сборки и установки netCDF, посетите домашнюю страницу netCDF по адресу: http://www.unidata.ucar.edu/packages/netcdf/который включает обширный список заведомо хороших конфигураций netCDF для различных платформ 7.2.2.2 Устранение неполадок во время выполнения:Обратите внимание на следующее:
Далее: 7.2.3 Внутреннее устройство MNC Up: 7.2 NetCDF I / O: MNC Предыдущее: 7.2.1 Использование MNC Содержание [email protected]
|
Ошибки параметров.
Ошибки параметров.Далее: Установка Minuit. Up: Основные концепции Minuit Предыдущая: Minuit Strategy. & nbsp Индекс
Подразделы
Minuit обычно используется для поиска « лучших » значений набора параметров, где « лучший » определяется как те значения, которые минимизируют данную функцию FCN. Ширина функционального минимума или, в более общем смысле, форма функция в некоторой окрестности минимума, дает информацию о неопределенность в лучших значениях параметров, часто называемая физики ошибка параметра .Важной особенностью Minuit является то, что он предлагает несколько инструментов для анализа ошибки параметра.
Какой бы метод не использовался для расчета ошибок параметров, они будут зависеть от на общую (мультипликативную) нормализацию FCN в том смысле, что если значение FCN везде умножается на константу, тогда ошибки будет уменьшено в раз . Аддитивные константы не изменяют параметр ошибок, но может означать другой уровень достоверности согласия. Предполагая, что пользователь знает, что означает нормализация его FCN, и также, что его интересуют ошибки параметров, команда SET ERRordef позволяет ему определить, что он имеет в виду под одной « ошибкой », с точки зрения изменение значения FCN, которое должно быть вызвано изменением одного параметра на одна « ошибка ».Если FCN — обычная функция chisquare (определенная ниже), тогда ERRordef должен быть установлен на 1.0 (в любом случае значение по умолчанию), если пользователь требуется обычная ошибка в одно стандартное отклонение. Если FCN является отрицательным логарифмическим правдоподобием функции, то значение одного стандартного отклонения для ERRORDEF — 0,5. Если FCN является точным квадратом, но пользователю нужны ошибки с двумя стандартными отклонениями, тогда ERRORDEF должно быть = 4.0 и т. Д. Обратите внимание, что в обычном случае, когда Minuit используется для выполнения подгонки некоторых экспериментальных данных, ошибки параметров будут пропорциональны неопределенность данных и, следовательно, значимые ошибки параметров не могут быть полученным, если не известны ошибки измерения данных.В общем В случае аппроксимации методом наименьших квадратов FCN обычно определяется как chisquare:где — вектор аппроксимируемых свободных параметров, а в — погрешности отдельных измерений e i . Если эти неопределенности неизвестны и просто не учитываются при расчетах, тогда соответствие может иметь значение, но не количественные значения результирующие ошибки параметров. (Только относительные погрешности разных параметров с уважение друг к другу может иметь смысл.) Если все завышены на фактор, то результирующие погрешности параметров из подгонки будут завышены на тот же коэффициент.
Процессоры Minuit MIGRAD и HESSE обычно формируют матрицу ошибок. Эта матрица является обратной матрицей вторых производных FCN, трансформируется при необходимости во внешнее координатное пространство , г. и умножается на квадратный корень из ERRORDEF. Следовательно, ошибки, основанные на матрице ошибок Minuit, учитывают все корреляции параметров, но не нелинейности.То есть из-за ошибки одна матрица, ошибки двух стандартных отклонений всегда ровно в два раза больше как ошибки в одно стандартное отклонение. Когда матрица ошибок рассчитана (например, по успешному выполнение команды MIGrad или HESse), то параметр errors напечатанные Minuit — квадратные корни из диагональных элементов этого матрица. Команды SHOw COVariance и SHOw CORrelations позволяют пользователю также видеть недиагональные элементы. Команда SHOw EIGenvalues заставляет Minuit вычислить и распечатать из собственных значений матрицы ошибок, которые все должны быть положительно, если матрица положительно определена (см. ниже о Миграде и положительная определенность).Влияние корреляций на ошибки отдельных параметров может быть видно следующим образом. Когда параметр N ФИКСИРОВАН, Minuit инвертирует ошибку матрица, удаляет строку и столбец, соответствующие параметру N, и повторно инвертирует результат. Влияние на погрешности других параметров в общем будет делать их меньше, так как компонент из-за неопределенность в параметре N теперь устранена. (В пределе что данный параметр не коррелирован с параметром N, его ошибка будет не изменяется, когда параметр N фиксирован.) Однако процедура необратима, поскольку Minuit забывает исходная матрица ошибок, поэтому, если параметр N отключен, матрица ошибок считается неизвестной и должна быть пересчитана с соответствующие команды.
Ошибки MINOS.
Процессор Minuit MINOS был, вероятно, первым и, возможно, до сих пор единственным, общедоступная программа для расчета погрешностей параметров с учетом учитывать как корреляции параметров, так и нелинейности. Интервалы ошибок MINOS в целом асимметричны и могут быть дорогостоящими. рассчитывать, особенно если свободных параметров много и проблема очень нелинейная.MINOS может работать только после того, как будет найден хороший минимум, и матрица ошибок рассчитана, поэтому команда MINOS будет обычно следует за командой MIGRAD. Ошибка MINOS для данного параметра определяется как изменение значение этого параметра, которое заставляет F ‘ увеличиваться на величину UP, где F ‘ — это минимум FCN по отношению ко всем другим свободные параметры, а UP — значение ERRordef, заданное параметром пользователь (по умолчанию = 1.). Алгоритм поиска положительных и отрицательных ошибок MINOS для параметр N состоит из изменяющегося параметра N, каждый раз минимизирующего FCN по отношению ко всем остальным параметрам переменной NPAR-1, численно найти два значения параметра N, для которых минимум FCN принимает значения FMIN + UP, где FMIN — это минимум FCN по всем параметрам NPAR.Чтобы сделать процедуру максимально быстрой, MINOS использует матрица ошибок для прогнозирования значений всех параметров на различные субминимумы, которые он должен будет найти в ходе расчет, и в пределе, когда задача близка к линейной, предсказания MINOS будут почти точными, что потребует очень несколько итераций. С другой стороны, когда проблема очень нелинейная (т.е. FCN далека от квадратичной функции своего параметры), это как раз та ситуация, когда нужен MINOS чтобы указать правильные ошибки параметров.
В настоящее время Minuit предлагает две очень разные процедуры поиска Контуры FCN. Они будут обозначены соответствующими имена команд: CONtour и MNContour.
КОНтур
Эта процедура предназначена для линейного принтера или буквенно-цифрового принтера. терминал в качестве устройства вывода и дает статическое изображение FCN как функция двух параметров, указанных пользователем, то есть все остальные переменные параметры (если есть) считаются временно зафиксированы на текущих значениях.Сначала диапазон выбрано, по умолчанию два текущих стандартных отклонения на любом сторона текущего лучшего значения каждого из двух параметров, и выбран размер сетки n, по умолчанию 25 на 25 позиций для полного диапазона каждого параметра. Нулевой контур определяется как текущее лучшее значение функции F мин. (предположительно минимум), а затем i th контур определяется как где FCN имеет значение F мин. + i 2 * UP.Затем процедура просто оценивает FCN в четырех углах каждая из n 2 позиций сетки (что составляет ( n + 1) 2 оценок) чтобы определить, есть ли i th контур проходит через Это. Метод, хотя и не очень эффективный и точный, очень надежен и способен обнаруживать неожиданные множественные долины.
MNContour
Контур, рассчитанный MNContour, является динамическим в том смысле, что что он представляет собой минимум FCN по отношению ко всем другие параметры НПАР-2 (если есть).Статистически это означает, что MNContour учитывает корреляции между два отображаемых параметра и все остальные переменные параметры, используя процедуру, аналогичную MINOS. (Если эта функция не нужна, тогда другая параметры должны быть ИСПРАВЛЕНЫ перед вызовом MNContour.) MNContour предоставляет фактические координаты точек вокруг контур, подходящий для построения графиков или рукой. Очки даются в порядке против часовой стрелки. по контуру.На команду (или вызов Фортрана) рассчитывается только один контур, и уровень F мин + UP. где UP — ERRordef, указанный пользователем, или 1.0 по умолчанию. Количество начисляемых баллов выбирается пользователь (по умолчанию 20 для режима управления данными). В качестве побочного продукта MNContour предоставляет ошибки MINOS два рассматриваемых параметра, так как это как раз крайние точки контура (используйте SHOw MINos, чтобы увидеть их). В командном режиме грубая (буквенно-цифровая, а не графическая) дан график точек (если PRIntlevel 0) и числовые значения координат печатаются (если PRIntlevel 1).В вызываемом Fortran режиме пользователь получает Fortran доступ к вектору координат точки через SUBROUTINE MNCONT.
Далее: Установка Minuit. Up: Основные концепции Minuit Предыдущая: Minuit Strategy. & nbsp Индекс Вернуться к ЦЕРН | ЭТО | РАС | Главная страница программной библиотеки ЦЕРН MG (последняя модификация. 19.08.1998) Код MNC
запускает сбор журнала ошибок
Код ошибкиMNCE запускает сбор записей
В предыдущем блоге были представлены теоретические знания, это вводит некоторые ошибки, возникающие при запуске исходного кода, предоставленного автором, а также неправильное решение.
Предыдущий блог описывает теоретические знания MNC, этот блог посвящен ряду ошибок, возникающих при запуске исходного кода, предоставленного автором, а также неправильному решению.
Адрес проектаMNC: https: //github.com/daijifeng001/MNC
В соответствии с инструкцией по установке github адрес монтирования MNC. Я не был установлен успешно, возникновение различных проблем, ниже приведены некоторые из ошибок, с которыми я столкнулся во время установки, ступенчатый пит-бар.
Код ошибки запускает запись :
1.cudnn Связанные вопросы
из-за того, что MNC основан на более быстром rcnn, из которых caffeAn более ранней версии cudnn Требуется более высокая версия, проблемы несовместимости могут возникнуть при компиляции MNCEngineeringcaffe-mncWhen, которую вам необходимо в besrc / caffe / Layers / Directory oncudnn Заменить все файлы на последнюю версиюcaffeFiles.
2. Ошибка CompilelibFile
Вопрос1.
ImportError: Нет модуля с именем Cython.Distutils
Решение 1.
sudo pip установить cython
Вопрос 2.
x86_64-linux-gnu-gcc: ошибка: utils / bbox.c: нет такого файла или каталога
x86_64-linux-gnu-gcc: fatalerror: нет входных файлов
Решение 2.
компакт-диск MNC / lib / utils
cython bbox.pyx
Вопрос 3.
x86_64-linux-gnu-gcc: ошибка: nms / cpu_nms.c: нет такого файла или каталога
x86_64-linux-gnu-gcc: фатальная ошибка: нет входных файлов
Решение 3.
компакт-диск MNC / lib / nms
cython cpu_nms.pyx
Вопрос 4.
AttributeError: объект ‘модуль’ не имеет атрибута ‘text_format’
Решение 4.
inMNC / train_net.py Добавить файлmport google.protobuf.text_format
Вопрос 5.
AttributeError: объект ‘модуль’ не имеет атрибута ‘text_format’
Решение 5.
inMNC / train_net.py Добавить файл google.protobuf.text_format
Вопрос6.
TypeError: объект numpy.float64 не может быть интерпретирован как индекс
Решение 6.
sudo pip install -U numpy == 1.11.0
Следующее соответствует результатам успешной операции
Работа
Результаты экспериментов
Работа
Результаты экспериментов
Как создаются (и не создаются) локальные и глобальные решения
6
Построение рамок нестандартных проблем.Как только происходит нестандартное событие, менеджеры дочерней компании
должны сформулировать нестандартную проблему: понять и определить ее природу, масштаб и границы
, построив концептуальную интерпретацию (Baer, Dirks, & Nickerson, 2012; Cowan , 1990;
Lyles, 1981; Lyles & Mitroff, 1980; Smith, 1989, 1988; Vaccaro, Brusoni, & Veloso, 2011). Первоначально
из-за двусмысленности, сложности и плохо структурированного характера проблем (Simon, 1973) может быть
трудно понять их точно или инициировать соответствующие действия, чтобы стимулировать разработку решений
.Результаты часто остаются ограниченными, потому что люди склонны к
, полагая, что из любой конкретной проблемной ситуации можно извлечь лишь немногое (Starbuck, 2009). Тем не менее,
менеджеров дочерних компаний, которые берут на себя труд, чтобы лучше понять нестандартные проблемы, и
, интерпретировать различные аспекты таких сложных ситуаций, с большей вероятностью обеспечат организационное обучение
(Beck & Plowman, 2009). Такие задачи предъявляют высокие требования: их локальные
и глобальные сложности необходимо разобрать, а проблему разложить на более или менее
знакомые и взаимозависимые подзадачи (Newell, Shaw, & Simon, 1958; Simon, 1962; Simon &
Баренфельд, 1969).Социальные взаимодействия с коллегами, которые могут опираться на свой собственный опыт, обычно помогают
более точно определить проблемное пространство (Cross & Sproull, 2004; Dunbar & Garud, 2009), и поэтому
способствуют более продуктивному поиску решения.
Действия по поиску решений, включая поиск знаний. Действия по поиску решений — это
действия по поиску и разработке решений, которые включают поиск знаний (Cyert &
March, 1963; Nickerson & Zenger, 2004).Поиск знаний определяется как все действия по поиску
и определению того, какие знания потенциально могут быть доступны (Hansen, 1999), где термин
«знание» относится к ноу-хау, опыту или передовым методам / процедурам (Gupta & Govindarajan, 1991,
,, 2000) и может быть скрытым или кодифицированным (Polanyi, 1966). Поиск предполагает уравновешивание времени и усилий
, затрачиваемых на поиск и оценку знаний (Hansen, Mors, & Løvås, 2005), с шаблоном поиска
в зависимости от того, какое решение предполагается разработать (Gray & Meister, 2006; Haas &
Хансен, 2007).Хотя менеджеры могут предпочесть копировать существующие решения (Spender, 1989), новинка
нестандартных проблем часто требует от них сбора знаний для создания решения путем разработки
новых комбинаций существующих знаний (Galunic & Rodan, 1998; Henderson & Кларк, 1990; Когут
и Зандер, 1993). Если требуется создание решения, менеджеры дочерних компаний должны иметь желание и возможность
Насколько крупные MNC управляют своими большими данными? | автор: Милинд Растоги
В этой статье я расскажу вам, как крупные транснациональные компании, такие как Google, Facebook и Amazon, хранят, управляют и манипулируют своими тысячами терабайт данных или, в частности, как они управляют большими данными.
Прежде чем объяснять управление данными этих компаний, позвольте мне объяснить, что на самом деле означает термин Big Data .
Что ж, большинство людей думают, что большие данные — это технология, используемая для управления большими объемами данных, но на самом деле большие данные — это проблема, с которой сталкиваются многие транснациональные компании, такие как Facebook, Google, Amazon и т. Д. Данные, генерируемые этими компаниями, выходят за рамки объем их хранения и данные настолько велики и сложны, что ни один из традиционных инструментов управления данными не может их эффективно хранить или обрабатывать.Вот почему большие данные являются проблемой для многих ТНК.
Теперь посмотрим, как facebook, google, amazon управляет своими данными.
Facebook генерирует 4 петабайта данных в день — это миллион гигабайт. И эта система производит около 2,5 миллиардов единиц контента каждый день. Все эти данные хранятся в так называемом Hive, который содержит около 300 петабайт данных. Это огромное количество контента, без сомнения, связано с тем фактом, что пользователи Facebook проводят на сайте больше времени, чем пользователи в любой другой социальной сети, тратя на это около часа в день.
Для управления большими данными Facebook разрабатывает собственные серверы и сети. Он проектирует и строит собственные центры обработки данных. Его сотрудники пишут большинство собственных приложений и создают практически все свое собственное промежуточное программное обеспечение. Все, что связано с его операционной ИТ, объединяет его в одну чрезвычайно большую систему, которая используется как внутренними, так и внешними специалистами.
Google — самая «ориентированная на данные» компания в мире. Он входит в число крупнейших разработчиков технологий больших данных.
Отображение всех данных в Интернете.Определите, что используется чаще всего. Больше нажал. Больше взаимодействовали. Что наиболее выгодно? Это основные задачи Google по работе с данными.
На основе службы ПОИСК, своего первого продукта, со временем Google создает множество других продуктов для обработки данных. Google Apps, Google Docs, Google Maps, YouTube, Translator и т. Д.
По некоторым оценкам, размер базы данных Google составляет около 10 эксабайт, что составляет 10 миллионов терабайт.
Итак, вопрос в том, как Google управляет таким огромным объемом данных?
Ответ — внедрение вычислительных инструментов и технологий, аналогичных Hadoop и BigQuery (технология Google NoSQL).
Amazon использует наибольшее количество серверов для размещения своих данных: они размещают около 1 000 000 000 гигабайт данных на более чем 1 400 000 серверов.
Amazon генерирует данные вдвойне. Крупный розничный торговец собирает и обрабатывает данные о своем обычном розничном бизнесе, включая предпочтения клиентов и покупательские привычки. Но также важно помнить, что Amazon предлагает возможности облачного хранения для корпоративного мира.
Amazon S3 — помимо всего прочего, чем занимается компания — предлагает комплексное облачное решение для хранения данных, которое, естественно, облегчает передачу и хранение огромных массивов данных.Из-за этого трудно точно определить, сколько данных Amazon генерирует в целом.
Вместо этого лучше взглянуть на доход компании, который напрямую связан с обработкой и хранением данных. Компания зарабатывает более 258 751,90 долларов США на продажах и обслуживании в минуту.
В этой статье я буду обсуждать две проблемы больших данных
- Объем: Как мы знаем, для хранения больших данных нам нужен больший объем хранилища.И мы можем подумать, что покупка жесткого диска или сервера данных большего размера решит эту проблему. Но проблема этого решения в том, что компании не знают, сколько данных они будут хранить. Поскольку более крупные компании генерируют много данных, они не могут купить один-единственный жесткий диск или сервер данных. Они могут в конечном итоге купить много жесткого диска, но все равно их полные данные не могут быть сохранены.
- Скорость: Обычно данные хранятся на жестком диске, но хранение и извлечение данных на жестком диске занимает много времени.Это хранение и получение данных в хранилище известно как операции Innput / output. Таким образом, хранение большого количества данных на одном жестком диске занимает много времени, и это не может быть решением для хранения больших данных.
Одним из способов решения проблем с большими данными является использование распределенной системы хранения . Эта система следует топологии ведущий-ведомый. В этой системе много ресурсов хранения подключено к одному основному ведущему хранилищу. Этот главный узел известен как узел имени, а подчиненные узлы хранения известны как узел данных.Все эти узлы данных предоставляют свое хранилище одному главному узлу. Это могут быть тысячи узлов данных, предоставляющих свои ресурсы главному узлу или узлу имени.
С помощью этой системы мы можем решить проблему как объема, так и скорости. Теперь нам не требуется неограниченное количество жестких дисков для хранения данных, вместо этого нам нужны тысячи узлов данных, которые могут быть добавлены в зависимости от требований к хранилищу для узла Name. Таким образом, проблема объема решается легко.
Проблема скорости также может быть решена с помощью этой системы, поскольку для выполнения операций ввода / вывода мы можем разделить задачу между различными узлами. Поскольку тысячи узлов данных будут хранить и извлекать данные, скорость операций ввода-вывода будет автоматически увеличиваться.
- Hadoop
- MongoDB
- Cassandra
- Drill
- Elasticsearch
Скорость загрузки (MCC / MNC) Руководство для продавцов (SMS): Поддержка
1. Войдите в свою учетную запись на членах.нейтрафикс.telin.net.
2. Щелкните Маршруты / Мои маршруты
Следующим шагом будет загрузка ставок для маршрута:
- Щелкните значок настроек под столбцом действий, чтобы начать загрузку ваших маршрутов.
- Нажмите кнопку «Обзор» рядом с «Загрузить тариф MCCMNC:»
- Выберите CSV-файл, который вы хотите загрузить.
- Щелкните по обновлению.
- Если в вашем файле есть ошибки, и вы все равно хотите загрузить, вы можете установить флажок рядом с «Обновить MCC / MNC», даже если обнаружены ошибки…) и повторите шаг 4.
Примечание. Платформа не вернет никаких сообщений об ошибках, если используется этот параметр.
В приведенном ниже руководстве объясняются поля для загрузки, или вы можете загрузить прикрепленный образец с этой страницы и отредактировать информацию о своем маршруте.
Вот пример нового листа для загрузки нового маршрута в Пакистан в первый раз:
A = MCC / MNC B = Rate C = Дата вступления в силу
ASAP = Маршруты для загрузки на рынок как как можно скорее, обычно сразу.
Дата выборки: «2015-01-01 01:01:01».
Поддерживается специальное значение: как можно скорее. Если в качестве значения указано ASAP, ставка сразу же станет
Примечание:
1. Чтобы предложить остальную часть страны (RoC) пункта назначения, укажите MCC, за которым следует 0 «как MNC.
Например, MCC Соединенного Королевства — 234. Итак, чтобы предложить RoC Соединенного Королевства в NeuTrafiX, используйте только MCCMNC 2340 (MCC + «0») вместо 234.
2. Чтобы предложить пункт назначения, у которого MNC начинается с 0, оставьте MNC по умолчанию (2 или 3 цифры), не удаляя первый 0.

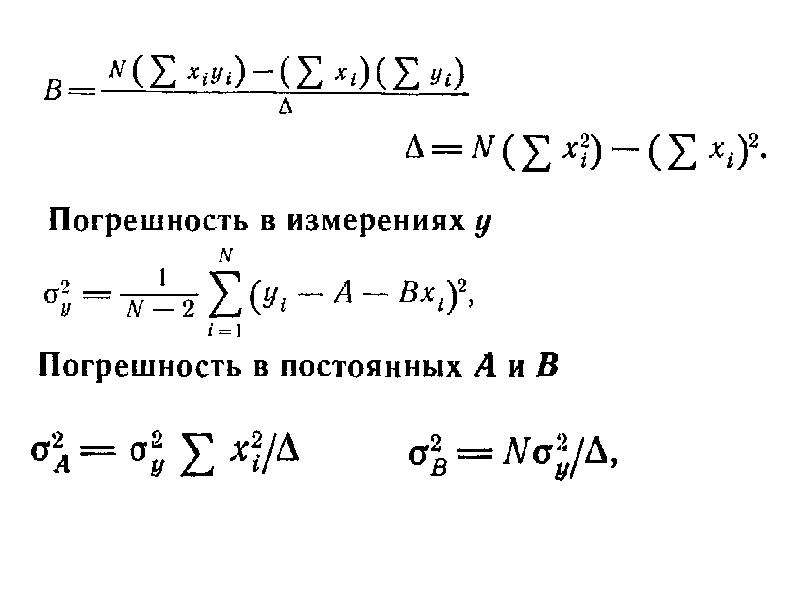
 ..
..
 Введение в теорию ошибок / Дж. Тейлор; Пер. с англ. М.: Мир, 1985. 272 с.
Введение в теорию ошибок / Дж. Тейлор; Пер. с англ. М.: Мир, 1985. 272 с.