9 класс решение систем неравенств – Системы неравенств — урок. Алгебра, 9 класс.

Урок по теме решение систем неравенств. 9 класс

Решение неравенств и систем неравенств с двумя переменными

9 класс.

Цели урока: 1) образовательная: закрепление знаний и умений по данной теме; формирование умения свободно решать системы нера­венств; 2) воспитательная: формирование интереса к решению не­однозначных примеров; воспитание чувства взаимопомощи и мате­матической культуры; 3) развивающая: развитие логического мыш­ления, кругозора, внимания, умения систематизировать и применять полученные знания.

Оборудование: написанные на доске примеры для устной и само­стоятельной работы, листы с заданими (без решений), учебники.

Тип урока: урок применения и совершенствования знаний.

План урока:

1. Понятие решения неравенства и алгоритма решения неравенства с двумя переменными и закреплениеэтой темы.

2. Понятие решения системы неравенств и алгоритма решения системы неравенства с двумя переменными.

3. Самостоятельная работа.

Ход урока:

1. Организационный момент.

2. решения неравенства и алгоритма решения неравенства с двумя переменными.

Решением неравенств с двумя переменными называется пара значений переменных, обращающая данное неравенство в верное числовое неравенство.

Изобразите на координатной плоскости множество решений неравенства:

а) у ≥ |х|; б) у ≤ |х — 2|.

Задание б) все учащиеся выполняют самостоятельно с последующей самопроверкой. Для этого два ученика одновременно выполняют решение на внутренних частях доски. Затем открывают своё решение и все учащиеся проверяют верность выполненного задания.

4. решения системы неравенств и алгоритма решения системы неравенства с двумя переменными и закреплениеэтой темы.

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в неё неравенств. На координатной плоскости множество решений системы неравенств изображается множеством точек, представляющих собой общую часть множеств, задаваемых неравенствами, входящими в систему.

Изобразите на координатной плоскости множество решений системы

.

5. Самостоятельная работа (разноуровневая).

Вариант А 1.

№1. Изобразите на координатной плоскости множество решений неравенства у ≥ |х — 3|.

№2. Изобразите на координатной плоскости множество решений системы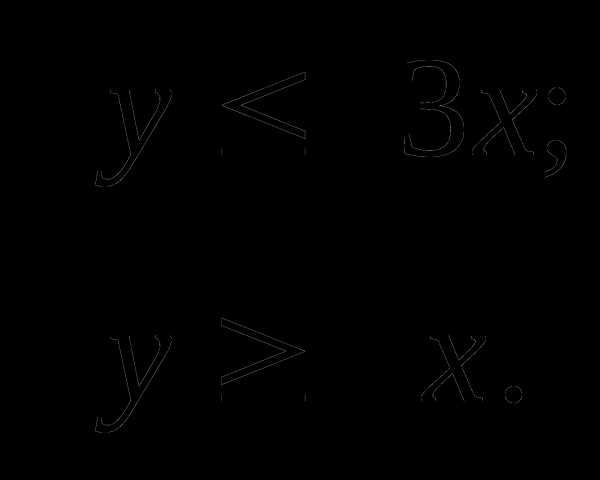

Вариант А 2.

№1. Изобразите на координатной плоскости множество решений неравенства у ≤ |х — 4|. №2. Изобразите на координатной плоскости множество решений системы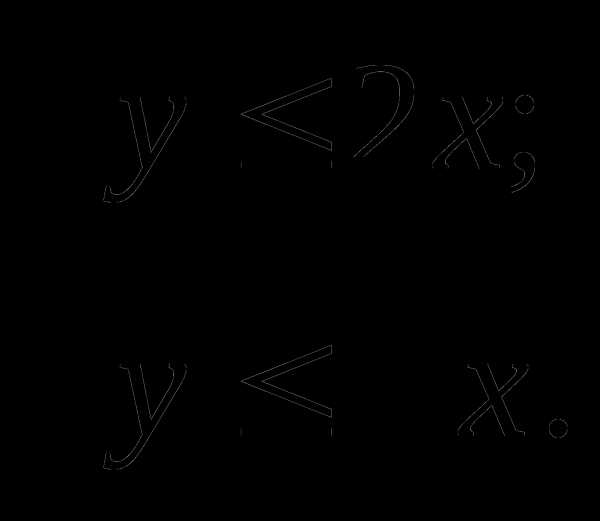

6. Домашнее задание:

№1 Решите неравенства: а) 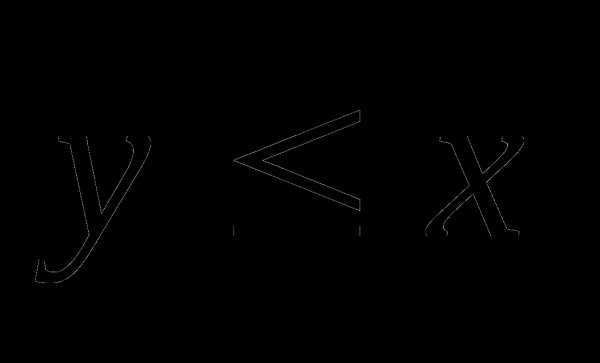, б) .

№2 Изобразите на координатной плоскости множество решений системы

а) 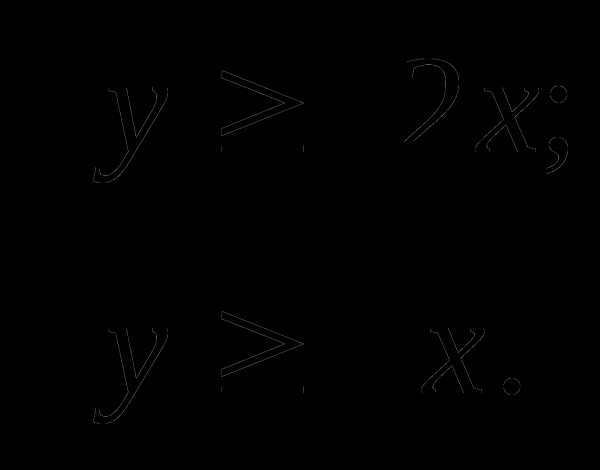б)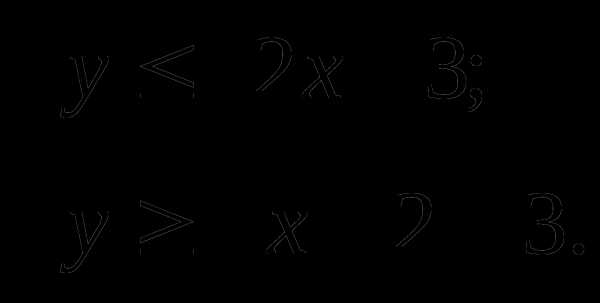

infourok.ru

«Решение неравенств и систем неравенств с двумя переменными»

Методическая разработка урока

по математике

«Решение неравенств и систем неравенств

с двумя переменными»

(9 класс)

Учитель: Супрун А.В.

г. Донецк

2017 г.

Тема: «Решение неравенств и систем неравенств с двумя переменными»

Цели урока:

1. образовательные: систематизация знаний и умений по теме «Решение неравенств с двумя переменными», применение полученных знаний на практике;

2. развивающие: развитие мышления, памяти, самостоятельной творческой деятельности учащихся, графической грамотности;

3. воспитательные: воспитание ответственности за свою учёбу и интереса к изучаемому предмету.

Тип урока: обобщение и систематизация знаний.

Формы, методы, приёмы работы: фронтальная беседа, работа учащихся в парах, индивидуальная работа.

Ресурсы: раздаточный материал.

План урока

I – Организационный момент.

Приветствие учащихся, проверка готовности к уроку. Сообщение темы и цели урока.

II – Проверка домашнего задания.

Работа в парах, взаимопроверка. Проверка по образцу решения домашнего задания. Учитель предлагает проверить и оценить выполнение домашнего задания. Выяснить ошибки, исправить их, используя метод «Пресс». Оценить работу (2 балла).

1. x²+y²>4

3)

III – Актуализация знаний учащихся.

Фронтальная беседа с классом, отработка теории по теме «Неравенства с двумя переменными, уравнения с двумя переменными и их графики».

1.

1. Что называется графиком уравнения с двумя переменными?

2. Что называется решением неравенства с двумя переменными?

3. Что называется графиком неравенства с двумя переменными?

4. Что является графиком неравенства

   x≥2, y≤-3, y>x², x²+y²≤4, y≥|x|, |x|+|y|≤2

2.Практическая работа «Задание на двоих» (работа в парах).

Установить соответствие между графиком неравенства и формулой. Оценить работу (1 задание – 1 балл).

a)

б)

в)

IV – Практическое применение полученных знаний, усовершенство- вание умений и навыков.

Знакомство с заданиями. Установить шаги решения.

Изобразить на координатной плоскости XY множество решений неравенства или системы неравенств:

1. y≤x²-2|x|–3

2. |y-3x|≤4

Индивидуальное задание (повышенной трудности)

|x+1|-|y-1|≤2

V –Рефлексия. Итог урока.

Мы повторили построение и преобразование графиков уравнений с двумя переменными, рассмотрели примеры графического решения неравенств и систем неравенств с двумя переменными.

VI –Домашнее задание:

П. 20, № 20.11 (1), № 20.9 (4)

Дополнительное задание: решить систему уравнений с двумя переменными.

x²+y²=17

x+xy+y=9

VII –Закрепление.

Самостоятельная работа по вариантам

Изобразите на координатной плоскости XY множество решений системы неравенств:

I вариант

1)

3б

2)

4б

II вариант

1)

2)

infourok.ru

Урок алгебры по теме «Системы неравенств с двумя переменными». 9-й класс

Любому учителю известно, что уроки, посвященные изучению графиков функций, требуют построения большого количества графиков. Чем больше будет построено графиков, тем лучше учащиеся освоят данный материал. Но возникает проблема – ограниченное время урока. Перед учителем встает вопрос о выборе средств и методов обучения с целью обеспечения максимальной эффективности изучения математики. В этом случае приходят на помощь компьютерные технологии. В настоящее время существует много программ, с помощью которых можно рисовать графики функций. Они дают возможность проиллюстрировать свойства функций быстро и наглядно, что повышает и активизирует познавательную деятельность учащихся. На представленном уроке используется программа Advanced Grapher.

Класс: 9.

Технологии: Информационно-коммуникативные технологии.

Оборудование

: Компьютер; проектор, интерактивная доска; программа «Advanced Grapher», классная доска; учебник «Алгебра 9 класс». (Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Москва «Просвещение», 2011г.), рабочая тетрадь, карточки-тесты.

Цели:

• Образовательные – ввести понятие решения системы неравенств с двумя переменными; формировать умение решать системы неравенств с двумя переменными, отработать навыки построения множества решений систем неравенств на координатной плоскости;
• Развивающие – формирование графической и функциональной культуры учащихся;
• Воспитательные – воспитание интереса к математике и повышение мотивации учебной деятельности через внедрение компьютерных технологий в процесс обучения, побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.

Ход урока

Актуализация знаний.

Учитель. На доске вы видите два неравенства

х²+3ху –у²<20 и (х-3)²+(у-4)²<2

• Как они называются? [Неравенства с двумя переменными]
• Что является решением такого неравенства? [Пара чисел, которые удовлетворяют неравенству]
• Определите, является ли пара чисел (-2;3) решением какого либо из этих неравенств? [Являются решением только первого неравенства]
• Найдите свою пару чисел которая являлась бы решением второго неравенства [Например 3 и 4, 4 и 4, 3 и 5 и т.д.]

Проверка домашнего задания.

Учитель Давайте вспомним , как решаются такие неравенства.

На примере неравенств х²+2 > у и (x-1)^2+(y+2)^2<4 рассказать о решении неравенств с двумя переменными.

Двое учащихся рассказывают и показывают решение неравенств на доске.

• Чем отличается решение строгого неравенства от нестрогого? [линия функии штриховая]
• Как можно проверить правильно ли вы выбрали множество? [Правило пробной точки]

Проверим решение №484б и г с помощью программы «Advanced Grapher» на интерактивной доске. (Учитель открывает готовый файл Приложение 1.agr. В окне слева выбирает первую и вторую функцию

Чтобы проверить решение второго неравенства отмените построение предыдущих двух и выберите следующие две)

[Учащиеся сравнивают решение в тетрадях с изображением на интерактивной доске.]

Тестовая работа.

на готовых карточках- координатных плоскостях (Приложение 2) показать решения неравенств а) х>2, б) у<-2; в) -3<у<3; г)│х│<у ; д)│ х-2│>у с последующей проверкой на интерактивной доске с помощью программы «Advanced Grapher». (Приложение 1. agr)

Новая тема.

Учитель. Тема сегодняшнего урока «Системы неравенств с двумя переменными»

• Как вы думаете, каковы цели сегодняшнего урока?
• Чему вы должны научиться к концу сегодняшнего урока?

Рассмотрим систему неравенств с двумя переменными.

№496

• Как вы думаете, что же может, является решением такой системы? [Пара чисел]
• Какие из пар (4;2), (-5;1), (-2;-1) являются решением этой системы? [Первая]
• Как по-вашему, сколько решений может иметь такая система? [Множество]
• Что значит решить систему?c[Найти все решения, или доказать, что таких решений нет]

Учитель. Давайте выясним, какое множество точек задает на координатной плоскости система. Как это сделать? [Решить по отдельности каждое неравенство и найти их пересечение решений.]

Пример 1

Ребята в тетрадях рисуют графики функций, а учитель поэтапно показывает графики на интерактивной доске (Приложение 1.agr)

Как можно проверить правильно ли показано множество решений? [Правило пробной точки]

Пример 2. Выполнение в тетради, затем поэтапная проверка на интерактивной доске (Приложение 1.agr)

Пример 3 Выполнение в тетради, затем поэтапная проверка на интерактивной доске (Приложение 1.agr)

Закрепление.

№497 а, в на обычной доске [Одновременное решение на доске и в тетрадях]

Итоги урока.

– Что называется решением системы неравенств с двумя переменными?

– Как решаются системы линейных неравенств с двумя переменными?

– Как проверить верно ли выбрано решение?

Домашнее задание.

№ 497 (б, г), Доп.задание: Изобразите на координатной плоскости множество решений системы неравенств:

Приложение.

urok.1sept.ru

Решение систем неравенств 9 класс

Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:

---

Решение систем неравенств (9 класс) Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной А. Нивен Запомним Решить систему неравенств – это значит найти значение переменной, при котором верно каждое из неравенств системы. Запомним Если надо решить систему неравенств, то:решаем каждое неравенство системы отдельноизображаем полученные решения на числовой прямой и смотрим пересечения этих решений. Эта общая часть и является решением данной системы неравенств. Содержание Решение систем линейных неравенствРешение двойных неравенствРешение систем, содержащих квадратные неравенства Решим систему неравенств(состоящую из линейных неравенств) 5х + 1 > 6 2х – 4 6 2х – 4 6 -1 2х 5 2х 1 х — 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4] Работа в парах: Решить системунеравенств:1) 3х – 2 ≥ х + 1 4 – 2х ≤ х – 2 2) 3х > 12 + 11х 5х – 1 ≥ 0 Проверим ответы:1) [2; +∞)2) Нет решения Примеры двойных неравенств Прочитайте неравенства: -6 0 4х + 2 ≤ 6Решим каждое неравенство системы отдельно: 1) 4х + 2 > 0 2) 4х + 2 ≤ 6 х > — 0,5 х ≤ 1Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5

educontest.net

Презентация к уроку (алгебра, 9 класс) по теме: Презентация «Решение систем уравнений и неравенств» (9 класс)

Слайд 1

Решение систем неравенств (9 класс) Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной

Слайд 2

А. Нивен

Слайд 3

Запомним Решить систему неравенств – это значит найти значение переменной , при котором верно каждое из неравенств системы.

Слайд 4

Запомним Если надо решить систему неравенств, то : решаем каждое неравенство системы отдельно изображаем полученные решения на числовой прямой и смотрим пересечения этих решений. Эта общая часть и является решением данной системы неравенств.

Слайд 5

Содержание Решение систем линейных неравенств Решение двойных неравенств Решение систем, содержащих квадратные неравенства

Слайд 6

Решим систему неравенств (состоящую из линейных неравенств) 5х + 1 > 6 2х – 4 6 2х – 4 6 -1 2х 5 2х 1 х

Слайд 7

Решим систему неравенств 5х + 12 ≤ 3х+ 20 х — 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4 ]

Слайд 8

Работа в парах: Решить систему неравенств: 1) 3х – 2 ≥ х + 1 4 – 2х ≤ х – 2 2) 3х > 12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [ 2; +∞ ) 2) Нет решения

Слайд 9

Примеры двойных неравенств Прочитайте неравенства : -6

Слайд 10

Решение двойных неравенств Решить неравенство: 0 0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 > 0 2) 4х + 2 ≤ 6 х > — 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5

Слайд 11

Решите неравенства, работая в парах Решить неравенства: -6 ≤ — 3х ≤ 3 4

Слайд 12

Решим систему неравенств (в которую входит квадратное неравенство) Решить систему неравенств: х ² — 5х + 4 ≤ 0 9 — 4х 9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; + ∞ ) + — —

Слайд 13

Решить систему неравенств: х ² — 3х + 2 0 Решение: решим каждое неравенство отдельно х ² — 3х + 2 0 Найдем корни соответствующих квадратных уравнений х ² — 3х + 2 = 0 2х ² — 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞) Решим систему неравенств (в которую входит квадратное неравенство) + + + — — —

Слайд 14

Решим системы неравенств, работая вместе 1) 6х ² — 5х + 1 > 0 4х – 1 ≥ 0 2) 4х ² — 1 ≤ 0 х ² > 1 3х ² — 2х – 1 0

Слайд 15

Решите системы неравенств, работая самостоятельно 1) х ² — 10х + 9 ≥ 0 12 – 3х 0 4х – 1 ≥ 3 3) 2х ² — 7х + 5

Слайд 16

http://krasdo.ucoz.ru/ee383358c499.png

nsportal.ru

Конспект урока математики в 9 классе Подготовка к ОГЭ по теме «Неравенства и системы неравенств».

ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ

В 9 КЛАССЕ

по теме

Неравенства

Подготовка к экзамену

Подготовила: Пестрецова Т.Г.,
учитель математики

МБОУ «Чекмаревская ООШ»

Конспект урока математики в 9 классе

Подготовка к ОГЭ   по  теме «Неравенства и системы неравенств».

Цель: обобщить и оценить знания учащихся по теме

образовательная:

-повторить и закрепить учебный материал по теме «Решения линейных неравенств с одной переменной и их систем»; контроль приобретённых знаний;

развивающая:

— развивать приёмы мыслительной деятельности, внимание;

— формировать потребность к приобретению знаний;

-развивать коммуникативную и информационную компетенции учащихся;

воспитательная:

-воспитывать культуру коллективной работы;

-развитие самостоятельности.

Знать и понимать алгебраическую трактовку отношений «больше» и «меньше» между числами; знать и применять свойства числовых неравенств;

Знать и понимать термины «решение неравенства с одной переменной», «решение системы неравенств с одной переменной»;

Решать линейные неравенства с одной переменной и их системы;

Находить множество решений квадратного неравенства с одной переменной, опираясь на графическое изображение.

Место урока: организация повторения при подготовке к ОГЭ  по математике

по темы «Решение неравенств с одной переменной и их систем».

Тип урока: урок обобщения изученного материала

Оборудование: интерактивная доска, компьютер, мультимедийный проектор, презентация.

Ход урока.

1. Организационный момент, мотивация учащихся. Определение темы урока (слайд №1)

Я рада всех вас приветствовать. Мы проводим очередной урок по подготовке к государственной итоговой аттестации. Тему сегодняшнего урока вы сами попробуете ее сформулировать, посмотрев на слайд 2.

Итак, тема урока «Линейные неравенства и системы линейных неравенств».

2. Актуализация знаний

а) устная работа по теории

Чтобы перейти к решению неравенств и систем неравенств, предлагаю вспомнить (Фронтальный опрос) слайды 5 – 7.

1. Когда число а больше числа b,
   если разность а – b – положительное число
   a > b, если а – b > 0
   Число а меньше числа b,
   если разность а – b – отрицательное число
   a < b, если а – b < 0
   Число а равно числу b,
   если а – b = 0,

На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.

Выполним задания:

2. Что такое неравентва?

Это соотношения вида

f(x)>g(x), f(x)

Решения неравенства – это значения переменной, обращающие его в верное числовое неравенство.

Решить неравенство – значит найти все решения или доказать, что их нет.

3. Какие виды неравенств вы знаете?

Числовое: а>b, где a и b- числа
Линейное: ax+b≤0, где a и b- числа, х- переменная
Квадратное: ax2+bx+c>0 (неравенство II степени)
где a, b, c- числа, х- переменная
Неравенство вида: (x-a)(x-b)(x-c)>0
где a, b, c- числа, х- переменная

4. Сформулируйте свойства числовых неравенств

5. Выполним задания

8. Выполним задания:

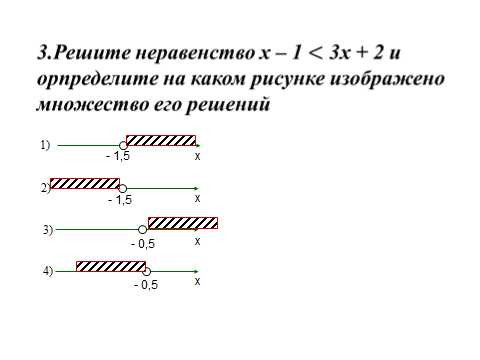
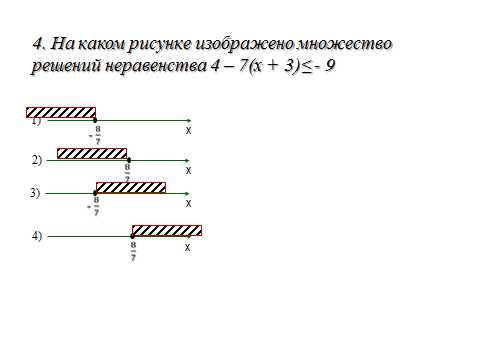
9. Система неравенств — это несколько неравенств с одной переменной.

Решение системы неравенств — это значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство.

Общее решение неравенств — это множество всех решений системы неравенств.

10. Выполним задания:

11. Алгоритм решения квадратных неравенств ax²+bx+c>0

1. Находят дискриминант квадратного трехчлена ах²+вх+с и выясняют, имеет ли трехчлен корни;

D >0, два корня х и х

D=0, один корень х

D<0 корней нет

2. Если трехчлен имеет корни, то отмечают их на оси Х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а < 0; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а > 0 или в нижней при а< 0;

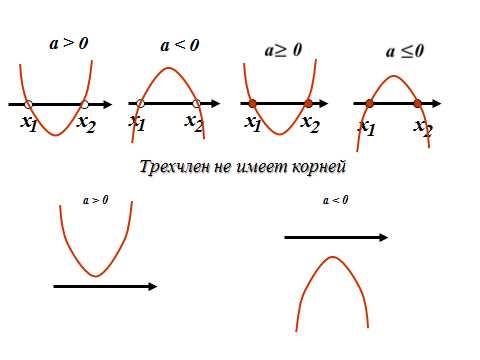
3. Находят на оси Х промежутки, для которых точки параболы расположены выше оси Х (если решают неравенство ах+вх+с>0) или ниже оси Х (если решают неравенство ах+вх+с<0)

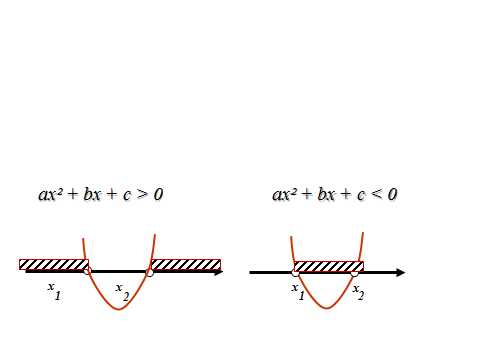
12. Выполним задания:

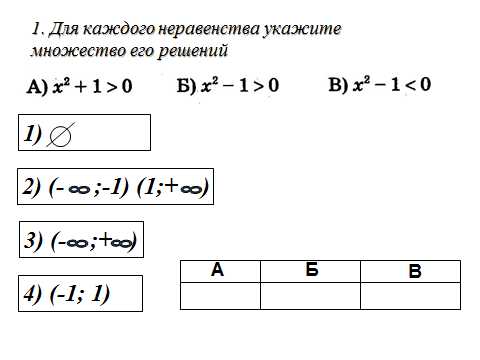
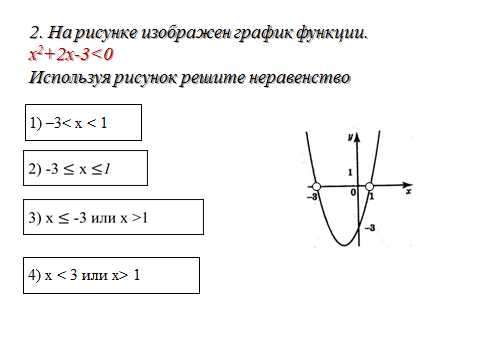
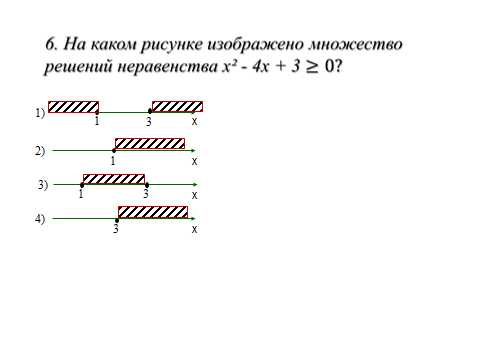
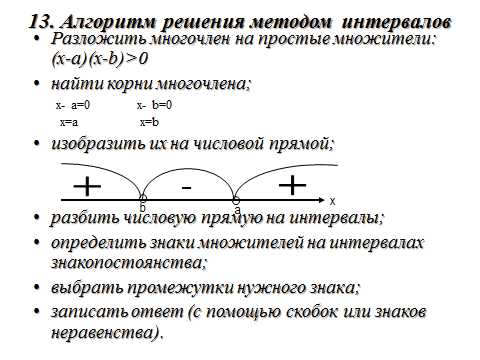
Задание на дом:

1)Решите неравенство:

А)4+12х>7+13х

Б)-(2-3х)+4(6+х)>1

2)Решите систему неравенств:

3х+4≤4х+6,

х-5≤4-2х

3)Решите двойное неравенство (2 способами)

-3<2-5х<1

Задание на дом:

1)Решите неравенство:

А)4+12х>7+13х

Б)-(2-3х)+4(6+х)>1

2)Решите систему неравенств:

3х+4≤4х+6,

х-5≤4-2х

3)Решите двойное неравенство (2 способами)

-3<2-5х<1

infourok.ru

Системы рациональных неравенств. Алгебра, 9 класс: уроки, тесты, задания.

1.	Запись системы неравенств Сложность: лёгкое	2
2.	Решение системы неравенств Сложность: лёгкое	2
3.	Решение более сложной системы неравенств Сложность: среднее	4
4.	Целые ответы системы неравенств, решение Сложность: среднее	4
5.	Дробное неравенство как система, решение системы Сложность: среднее	2
6.	Замена квадратного неравенства системами неравенств Сложность: среднее	2
7.	Система, состоящая из неполного квадратного и линейного неравенств Сложность: сложное	3
8.	Система, состоящая из квадратного и линейного неравенств Сложность: сложное	3
9.	Система, состоящая из квадратных неравенств Сложность: сложное	3
10.	Система, состоящая из квадратного и кубического неравенств Сложность: сложное	4
11.	Система квадратных неравенств Сложность: сложное	3
12.	Система, состоящая из линейного и рационального неравенств Сложность: сложное	3
13.	Система, состоящая из квадратного и рационального неравенств Сложность: сложное	4
14.	Система рациональных неравенств Сложность: сложное	3
15.	Система, состоящая из рационального и квадратного неравенств Сложность: сложное	3

www.yaklass.ru