Матричный метод решения систем линейных уравнений
Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.
Другое условие применимости матричного метода — невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.
Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.
Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .
Пусть нужно решить систему линейных уравнений:
Запишем эту систему уравнений в матричном виде:
Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов
.
Тогда
То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.
Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.
Пример 1. Решить матричным методом систему линейных уравнений:
Решение состоит из следующих шагов.
Шаг 1. Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:
По выведенному выше последнему равенству и будем вычислять решения данной системы.
Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.
Для второго примера выберем систему линейных уравнений третьего порядка.
Пример 2. Решить матричным методом систему линейных уравнений:
Шаг 1. Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.
Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение
Всё по теме «Системы уравнений и неравенств»
Начало темы «Линейная алгебра»
Поделиться с друзьями
Матричный метод решения уравнений онлайн калькулятор
Применение уравнений широко распространено в нашей жизни.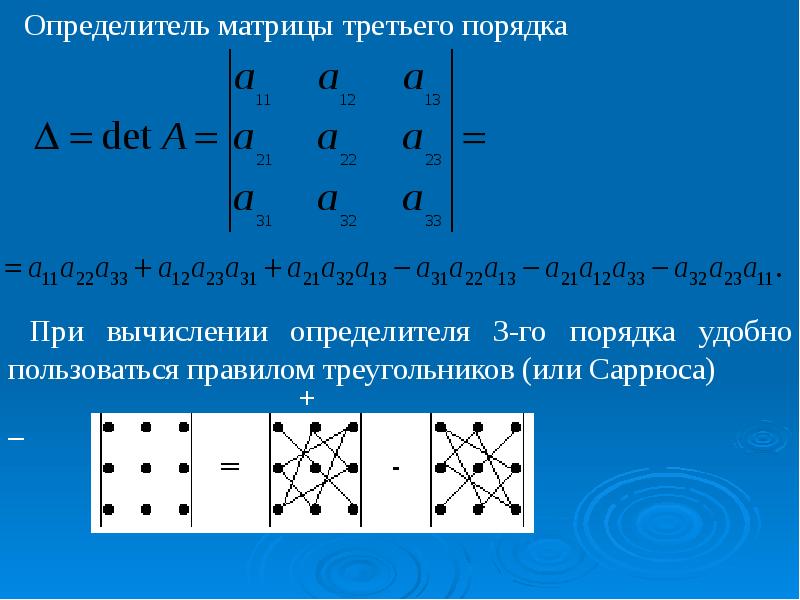
Решения таких систем основано на определенном свойстве обратной матрицы: произведение обратной матрицы (А-1) и исходной матрицы равно единичной матрице.
Так же читайте нашу статью «Решить уравнения методом простой итерации онлайн»
Допустим, нам дана следующая система:
\[ \left\{\begin{matrix} 2x_1-x_2+3x_3=1\\ -2x_2+2x_3=2\\ 3x_1+x_2+x_3=0 \end{matrix}\right.\]
Данную систему можно решить всего за три шага:1 шаг
Составляем матрицу:
Матрица коэффициентов при неизвестных
\[A=\begin{pmatrix} 2 & -1&3\\ 0&-2&2\\ 3&1&1 \end{pmatrix}\]
Матрица неизвестных:
\[x=\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}\]
Матрица свободных членов:
\[ B=\begin{pmatrix} 1\\ 2\\ 0 \end{pmatrix} \]
2 шаг
Все, что мы делали в 1 шаге, было сделано для того, чтобы получить обратную матрицу коэффициентов при неизвестных:
\[ A^{-1}=\frac{1}{4}\cdot \begin{pmatrix} -4&4&4\\ 6&-7&-4\\ 6&-5&-4 \end{pmatrix} \]
3 шаг
Определяем матрицу неизвестных:
\[ x=\frac{1}{4}\cdot \begin{pmatrix} -4&4&4\\ 6&-7&-4\\ 6&-5&-4 \end{pmatrix}\cdot \begin{pmatrix} 1\\ 2\\ 0 \end{pmatrix}=\begin{pmatrix} 1\\ -2\\ -1 \end{pmatrix} \]
Ответ:
\[x_1=1;x_2=-2;x_3=-1\]
Поскольку математика точная наука, нужно быть уверенным в правильности решения. Для этого сделаем стандартную
проверку:
Для этого сделаем стандартную
проверку:
\[\left\{\begin{matrix} 2\cdot1-(-2)+3\cdot (-1)=1\\ -2\cdot(-2)+2\cdot (-1)=2\\ 3\cdot 1+(-2)+(-1)=0 \end{matrix}\right.\]
Проверка подтвердила правильность решения.
Где можно решить уравнение матричным методом онлайн с решением?
Решить уравнение матричным способом онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
определение, теорема и примеры решения задач
Задание. Таким образом, Определитель матрицы $A$ А тогда Отсюда искомая матрица Для
решения произвольной системы линейных
уравнений нужно уметь решать системы,
в которых число уравнений равно числу
неизвестных, — так называемые системы крамеровского типа : a 11
x 1
+
a 12
x 2
+…
+ a 1n
x n
=
b 1 , a 21
x 1
+ a 22
x 2
+…
+ a 2n
x n
=
b 2 ,
(5.3) …
… … …
… … a n1
x 1
+ a n1
x 2
+… + a nn
x n
= b n . Системы (5.3) решаются
одним из следующих способов: 1) методом
Гаусса, или методом исключения неизвестных;
2) по формулам Крамера;
3) матричным
методом. Пример
2.12 . Исследовать
систему уравнений и решить ее, если она
совместна: 5x 1
— x 2
+ 2x 3
+ x 4
= 7, 2x 1
+ x 2
+ 4x 3 —
2x 4
= 1, x 1
— 3x 2
— 6x 3
+ 5x 4
= 0. Решение. Выписываем
расширенную матрицу системы:
. Вычислим
ранг основной матрицы системы. Следовательно,
ранг основной матрицы системы равен 2,
т.е. r(A) = 2. Для вычисления ранга расширенной
матрицы A
рассмотрим окаймляющий минор значит,
ранг расширенной матрицы r(A)
= 3. Поскольку r(A)
r(A),
то система несовместна. Это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица — таблица элементов. О такой таблице, где m строк и n столбцов, говорят, что это матрица имеет размерность m на n . Общий вид матрицы: Для решения матриц необходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы: Основные виды матриц: Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если а 12 =а 21 , а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1 , то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы. Почти все методы решения матрицы заключаются в нахождении ее определителя n -го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы. Для вычисления определителя матрицы А 2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали: Ниже приведены правила для нахождения определителя 3го порядка. Упрощенно правило треугольника, как одного из методов решения матриц , можно изобразить таким образом: Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «+»; так же, для 2го определителя — соответствующие произведения берутся со знаком «-«, то есть по такой схеме: При решении матриц правилом Саррюса , справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком «+»; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком «-«: Разложение определителя по строке или столбцу при решении матриц. Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Приведение определителя к треугольному виду при решении матриц. При решении матриц методом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали. Теорема Лапласа при решении матриц. Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть Δ — это определитель n -го порядка. Выбираем в нем любые k строк (либо столбцов), при условии k ≤ n — 1 . В таком случае сумма произведений всех миноров k -го порядка, содержащихся в выбранных k строках (столбцах), на их алгебраические дополнения будет равна определителю. Последовательность действий для решения обратной матрицы : Для решения систем матриц наиболее часто используют метод Гаусса. Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т. Метод Гаусса является самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом. Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный — метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных. Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу. Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем: Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем): Значит, её легко перевести в матричную форму: AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно: Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B. Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A . detA≠0. Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма. Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 . Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю. Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ. Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ. Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы. Подставляем переменные в формулу: Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов. Итак, x=2; y=1; z=4. При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например : НЕЛЬЗЯ записать как: Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи: Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. в матричной форме записываем так: Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса. Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод
вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». × Очистить все ячейки? Закрыть
Очистить Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Рассмотрим следующую систему линейных уравнений: Учитывая определение обратной матрицы, имеем A −1 A =E , где E — единичная матрица. Следовательно (4) можно записать так: Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b . Пример 1.
Решить следующую систему линейных уравнений матричным методом: Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу: Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно: Исключим элементы 2-го столбца матрицы ниже главной диагонали. Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17: Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A : Матричный вид записи системы линейных уравнений: Ax=b , где Вычислим все алгебраические дополнения матрицы A : Обратная матрица вычисляется из следующего выражения. Калькулятор основан на решении неоднородной системы линейных алгебраических уравнений при помощи матричного метода ( другими словами данный метод еще называют решением через обратную матрицу). Кто еще не знаком с решениями неоднородной системы алгебраических уравнений, то вы можете ознакомится с теорией на данной страничке: The field is not filled. ‘%1’ is not a valid e-mail address. Please fill in this field. The field must contain at least% 1 characters. The value must not be longer than% 1 characters. Field value does not coincide with the field ‘%1’ An invalid character. Valid characters:’%1′. Expected number. It is expected a positive number. Expected integer. It is expected a positive integer. The value should be in the range of [%1 .. %2] The ‘% 1’ is already present in the set of valid characters. The field must be less than 1%. The first character must be a letter of the Latin alphabet. Su Mo Tu We Th Fr Sa January February March April May June July August September October November December century B. %1 century An error occurred while importing data on line% 1.
Value: ‘%2’.
Error:
%3 Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,). %3.%2.%1%4 %3.%2.%1%4 %6:%7 s.sh. u.sh. v.d. z.d. yes no Wrong file format. Only the following formats: %1 Please leave your phone number and / or email. Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений. Пусть задана система линейных уравнений с неизвестными: Эту систему можно записать в виде матричного уравнения , где – матрица системы, – столбец неизвестных, – столбец свободных коэффициентов. Из полученного матричного уравнения необходимо выразить . Для этого умножим обе части матричного уравнения слева на , получим: Так как , то или . Далее находится обратная матрица и умножается на столбец свободных членов . где , , . Выразив из этого уравнения , получим Найдем определитель матрицы : Так как , то система имеет единственное решение, которое можно найти методом обратной матрицы. Найдем обратную матрицу с помощью союзной матрицы. Вычислим алгебраические дополнения к соответствующим элементам матрицы : Запишем союзную матрицу , составленную из алгебраических дополнений элементов матрицы : Далее запишем обратную матрицу согласно формуле . Будем иметь: Умножая обратную матрицу на столбец свободных членов , получим искомое решение исходной системы: Умножение матрицы на вектор Ранг матрицы Вычитание матриц Перемножение матриц Элементарные преобразования матриц Операции над матрицами и их свойства метод Гаусса–Жордана – один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Комментарий к шагу 2 Метода Гаусса. Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей: Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число. Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной. Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце. Комментарий к шагу 3 Метода Гаусса. Рангом матрицы A размера m × n называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы A обозначается через r(A) = rangA = rankA. Основываясь на сравнении полученных значений рангов для основной и расширенной матрицы можно сделать следующие выводы о разрешимости системы: Этот решатель будет складывать, вычитать, умножать, делить и возводить в степень две матрицы с указанными шагами. {3+3}\left|\begin{array}{rr}
2 & 1 \\
1 & -1
\end{array}\right|=-3$$
{3+3}\left|\begin{array}{rr}
2 & 1 \\
1 & -1
\end{array}\right|=-3$$ $$
$$\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.$$
$$
$$\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.$$Матричный метод онлайн калькулятор с подробным решением. Матричный метод онлайн
 Очевидно,
что, например, минор второго порядка в
левом верхнем углу
=
7
0; содержащие его миноры третьего порядка
равны нулю:
Очевидно,
что, например, минор второго порядка в
левом верхнем углу
=
7
0; содержащие его миноры третьего порядка
равны нулю:
Методы решения матриц.
Нахождение определителей 2-го порядка.
Методы нахождения определителей 3го порядка.

 Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.
Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.
Решение обратной матрицы.
Решение систем матриц.
 е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц. Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :
Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :
Пример решения неоднородной СЛАУ.
 К примеру :
К примеру :Предупреждение
 Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.Матричный метод решения систем линейных уравнений
Примеры решения системы линейных уравнений матричным методом
 Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
Для этого сложим строку 3 со строкой 2, умноженной на -24/51:, , , , , , , , . решение неоднородной системы линейных алгебраических уравнений через обратную матрицу

 C.
C.Решение уравнений методом обратной матрицы
Суть метода

Пример решения методом обратной матрицы
ПРИМЕР 1
Читайте также:Задание
Решить систему линейных уравнений методом обратной матрицы
Решение
Данная система уравнений может быть записана матричным уравнением

Ответ
Решение системы линейных уравнений методом Гаусса-Жордана
 Матричный метод и метод Крамера обладают тем недостатком,
Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.Алгоритм метода Гаусса
переменные которые могут принимать произвольные значения; Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.
Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:
 Если a11 отличен от нуля – переходим к следующему шагу;
Если a11 отличен от нуля – переходим к следующему шагу;
После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n – размерность матрицы A
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
Минором M (от латинского “minor” меньший) k-го порядка матрицы A называется определитель некоторой матрицы, составленной из элементов матрицы A, стоящих на пересечении произвольно выбранных k
строк и k столбцов с сохранением их порядка. Если номера столбцов, в которых расположен минор M, совпадают с номерами строк, то этот минор называется главным. Каждая матрица A порядка n имеет
(Ckn)2 миноров k-го порядка. Минорами 1-го порядка являются сами элементы матрицы A.
Калькулятор матрицы — eMathHelp
 Он также найдет определитель, инверсию, rref (сокращенная форма эшелона строк), пустое пространство, ранг, собственные значения и собственные векторы.
Он также найдет определитель, инверсию, rref (сокращенная форма эшелона строк), пустое пространство, ранг, собственные значения и собственные векторы. Ваш ввод
Вычислить $$$ \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 0 & 4 \\ 0 & 1 & 0 \ end {array} \ right] + \ left [\ begin {array} {ccc} 2 & 1 & 4 \\ 5 & 7 & 1 \\ 1 & 2 & 5 \ end {array} \ right].$$$
Решение
$$$ \ left [\ begin {array} {ccc} \ color {Violet} {1} & \ color {Chartreuse} {0} & \ color {DarkBlue} {0} \\\ color {Коричневый} {0} & \ color {Красный} {0} & \ color {Fuchsia} {4} \\\ color {Purple} {0} & \ color {SaddleBrown} {1} & \ color {Зеленый} { 0} \ end {array} \ right] + \ left [\ begin {array} {ccc} \ color {Violet} {2} & \ color {Chartreuse} {1} & \ color {DarkBlue} {4} \\ \ color {Brown} {5} & \ color {Red} {7} & \ color {Fuchsia} {1} \\\ color {Purple} {1} & \ color {SaddleBrown} {2} & \ color {зеленый } {5} \ end {array} \ right] = \ left [\ begin {array} {ccc} \ color {Violet} {\ left (1 \ right)} + \ color {Violet} {\ left (2 \ right)} & \ color {Chartreuse} {\ left (0 \ right)} + \ color {Chartreuse} {\ left (1 \ right)} & \ color {DarkBlue} {\ left (0 \ right)} + \ color {DarkBlue} {\ left (4 \ right)} \\\ color {Brown} {\ left (0 \ right)} + \ color {Brown} {\ left (5 \ right)} & \ color {Красный} {\ left (0 \ right)} + \ color {Red} {\ left (7 \ right)} & \ color {Fuchsia} {\ left (4 \ right)} + \ color {Fuchsia} {\ left (1 \ right)} \\\ color {Purple} {\ left (0 \ right)} + \ color {Purple} {\ left (1 \ right)} & \ color {Садд leBrown} {\ left (1 \ right)} + \ color {SaddleBrown} {\ left (2 \ right)} & \ color {Green} {\ left (0 \ right)} + \ color {Green} {\ left (5 \ right)} \ end {array} \ right] = \ left [\ begin {array} {ccc} 3 & 1 & 4 \\ 5 & 7 & 5 \\ 1 & 3 & 5 \ end {array} \ right] $$$
Ответ
$$$ \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 0 & 4 \\ 0 & 1 & 0 \ end {array} \ right] + \ left [\ begin {array} {ccc} 2 & 1 & 4 \\ 5 & 7 & 1 \\ 1 & 2 & 5 \ end {array} \ right] = \ left [\ begin {array} {ccc} 3 & 1 & 4 \\ 5 & 7 & 5 \\ 1 & 3 & 5 \ end {array} \ right] $$$ A
Простой онлайн-калькулятор матриц
Этот калькулятор матриц позволяет вам вводить ваши собственные матрицы 2 × 2, складывать и вычитать их, находить умножение матриц (в обоих направлениях) и обратное за вас.
Здесь показаны шаги для получения ответов.
В ячейки матрицы можно ввести любое число (не буквы) от –99 до 99.
Выход
Вот результаты с использованием заданных чисел.
Наши две матрицы:
Добавление матрицы
A + B
Вычитание матрицы
A — B
| = | −5 | -2 | ||
| -2 | −3 |
Умножение матриц
В общем, если
, то произведение матриц X и Y равно:
XY
| = | ( a × e + b × g ) | ( a × f + b × h ) | ||
| ( c × e + d × g ) | ( c × f + d × h ) |
Используя этот процесс, мы умножаем наши 2 данные матрицы A и B следующим образом:
AB
| = | (0 × 5 + −4 × 6) | (0 × −2 + −4 × 4) | ||
| (4 × 5 + 1 × 6) | (4 × -2 + 1 × 4) |
| = | −24 | −16 | ||
| 26 | −4 |
Теперь перемножим матрицы в обратном порядке:
BA
| = | (5 × 0 + −2 × 4) | (5 × −4 + −2 × 1) | ||
| (6 × 0 + 4 × 4) | (6 × −4 + 4 × 1) |
| = | −8 | −22 | ||
| 16 | −20 |
Умножение матриц некоммутативное
В общем, когда мы умножаем матрицы, AB не равно BA . -1 млрд
= [(0,125,0,0625), (- 0,1875,0,1563)] [(5, -2), (6,4)] `
-1 млрд
= [(0,125,0,0625), (- 0,1875,0,1563)] [(5, -2), (6,4)] `
`= [(1,0), (0,1)]`
Попробовать другой?
Онлайн калькулятор обратной матрицы
Для любой неособой матрицы (т.е. определитель не равен нулю) существует инверсная матрица , например, его произведение с исходной матрицей дает единичную матрицу:
А ∙ А −1 = А −1 ∙ А = E
Наш онлайн-калькулятор поддерживает два различных метода вычисления обратной матрицы: с помощью метода Гаусса-Жордана и с помощью составления алгебраических добавок к исходной матрице.
Чтобы найти обратную матрицу методом Гаусса-Жордана, нужно прикрепить единичную матрицу справа от исходной матрицы:
(A | E)
Затем с помощью элементарных преобразований преобразуйте исходную матрицу в единичную, применив те же преобразования к единичной матрице, записанной справа. Следовательно, исходная матрица будет преобразована в единичную, а выписанная справа единичная матрица — в обратную:
Следовательно, исходная матрица будет преобразована в единичную, а выписанная справа единичная матрица — в обратную:
(A | E) → (E | A −1 )
Этот способ прост, удобен и не требует больших затрат времени.
Чтобы найти обратную матрицу с помощью метода алгебраических дополнений, можно использовать следующую формулу:
где
| А |
— определитель матрицы
А,
А и Дж — алгебраическое дополнение элемента и матрицы
А.
По определению
A i j = (-1) i + j M i j
где M и J — минор элемента и матрицы А.
По определению — второстепенный элемент и матрицы
А
— определитель, полученный удалением
я
строка,
j
столбец матрицы
А.
Итак, метод алгебраического дополнения для нахождения обратной матрицы исходной матрицы порядка п очень трудоемко, потому что нужно вычислить не только определитель исходной матрицы, но и n 2 детерминанты порядка п-1 .
ПРИЛОЖЕНИЕ ДЛЯ МНОЖЕСТВЕННОГО КАЛЬКУЛЯТОРА ДЕСЯТЬ МАТРИЦ TOP
| Калькуляторы матричного умножения |
Вы ищете лучший калькулятор, который шаг за шагом решает умножение? Конечно, да. Продолжайте читать эту статью, потому что мы подготовили для вас десять лучших приложений-калькуляторов матричного умножения.
Эти приложения для вычисления матриц очень полезны при решении матриц. Следовательно, вы можете выбрать один из них.
Здесь представлены десять лучших матричных калькуляторов.
Это приложение для расчета матриц основано на Android. Это совершенно бесплатно. Приложение калькулятора предназначено только для вычисления матриц, оно решает не только умножение матриц, но также транспонирование матрицы и обратную матрицу.
Это совершенно бесплатно. Приложение калькулятора предназначено только для вычисления матриц, оно решает не только умножение матриц, но также транспонирование матрицы и обратную матрицу.
1. Он выполняет почти все матричные операции: умножение, сложение, вычитание, обратную матрицу, определитель, скалярное умножение и транспонирование матрицы.
2.Он поддерживает целые числа, дроби (десятичные и обычные) и комплексные числа.
3. Это не стоит денег.
4. Очень проста в использовании и понимании.
5. Намного лучше, чем другие.
6. Очень простой и быстрый
7. Выполняет быстрое матричное умножение.
1. Не поддерживает деление.
2. Не могу решить матрицу 6х6.
3. Никакой интеграции и дифференциации.
2.Матричный калькулятор от Softminds
Это проект с открытым исходным кодом. Его слоган — это простая матрица. Приложение работает на базе Android. Доступны как бесплатная, так и платная версия.
Доступны как бесплатная, так и платная версия.
Есть ли в этом калькуляторе умножения матриц переменные?
Да, это калькулятор умножения матриц с переменными. Вы можете добавлять переменные в калькулятор.
1.Выполняет все операции, включая возведение в степень, первую, вторую и бесконечную норму.
2. Может решать матрицу размером до 9×9.
3. Можно изменить имя матрицы.
4. Расширенный, набор настроек и легкий.
5. Может вспомнить результаты.
Минусы:1. Никаких комплексных чисел.
2. В бесплатной версии можно создавать 3 или 4 переменных.
3. Некоторые устройства ниже версии 4.4 не могут создавать переменные.Это еще один простой калькулятор с полными шагами. Хотя в нем есть реклама, это бесплатно.
Плюсы:
1. Решает все основные матричные вычисления.
2. Может транспонировать матрицу.
3. Доступно решение системного линейного уравнения методом Крамера.
Доступно решение системного линейного уравнения методом Крамера.
4. Возможность выполнять возведение в степень в матрице.
Минусы:
1. Бесплатная версия содержит рекламу.
2. Показательные функции нуждаются в исправлении.
Инструмент очень полезен и помогает студентам. Матричный калькулятор решает умножение вместе с определителем и обратным. Кроме того, он решает систему линейных уравнений.
Плюсы:
1. Решает обратную матрицу методом Гаусса-Жордана.
2. Умножает матрицу на шаги.
3. Найти обратную матрицу методом определителя.
4. Вычисляет след матрицы.
Минусы:
1. Вместо десятичной точки используется запятая.2. Есть реклама.
Как работает матричный калькулятор?
Работать с этим калькулятором очень просто. Посмотрите видео, в котором показано, как им пользоваться.
ytimg.com/vi/PMgXsKayzt0/0.jpg» frameborder=»0″ src=»https://www.youtube.com/embed/PMgXsKayzt0?feature=player_embedded»/>
В приложение matrix очень удобно для студентов, которые хотят решить матрицу проблемы. Это очень просто и содержит все необходимые вам операции.
Плюсы:
1. Поддерживает рациональное число. 3. Ночная тема для использования ночью. 4. Вы можете решить как скалярное умножение, так и умножение двух матриц.Минусы:
1. Магазины всего две матрицы.6. Матричный супернаучный калькулятор от NTsoft apps
Этот еще одно бесплатное приложение для Android для матричных вычислений. Он выполняет почти все операции и имеет множество функций. Вы бы хотели его использовать.
Плюсы:
1. Работает с целыми числами, дробями и десятичными знаками. 2. Вы может управлять матричными кофакторами и матричным рангом. 3. По строкам операция исключения матрицы Гаусса.
Минусы:
1. Некоторые ошибки в детерминантных и сопряженных вычислениях. 2. Тема выглядит плохо.Чтобы получить обзор калькулятора матриц Android, просмотрите видео ниже.
Этот калькулятор матриц идеально подходит для студентов, изучающих линейную алгебру и матрицы. Вместе с ответом отображается подробный расчет.
Плюсы:
1. Обеспечивает вычисление нулевого пространства.
2. Поддерживает расчет собственных векторов.
3. Выполняется ли нормализация по Граму-Шмидту.
4. Использует дроби.
Минусы:
1. Слишком много надоедливой рекламы.
2. Для получения результата нужно смотреть рекламу.
Посмотрите видео, чтобы увидеть, как он решает умножение матриц с шагом.
ytimg.com/vi/pEbBpmH_M7A/0.jpg» frameborder=»0″ src=»https://www.youtube.com/embed/pEbBpmH_M7A?feature=player_embedded»/>
Умножить матрицу просто и легко с помощью этого замечательного приложения для работы с матрицами. Вы можете рассчитать все матричные задачи в приложении для расчета.
Плюсы:
1.У него есть опция автоматического преобразования дроби.
2. Представляет вам настраиваемую клавиатуру.
3. Помогает вам в разложении LU.
Минусы:
1. Не поддерживает матрицу 6х6.
2. Вы можете использовать дроби.
3. Требует улучшения.
Калькулятор квадратных матриц — это очень простое приложение для вычисления матриц. Он решает только квадратную матрицу и выполняет сложение, вычитание и умножение.
Плюсы:
1.Очень просто для умножения квадратной матрицы.
2. Легкий и простой интерфейс.
3. Поддерживает матрицу 4х4.
Минусы:
1. Нет матрицы 5х5.
2. Вы не можете выполнять скалярное умножение.
10.Счетчик научных матриц Даниэля Ди Капуа
Калькулятор научных матриц, как следует из названия, — отличное приложение для студентов инженерных специальностей. Выполняет большое количество операций. Калькулятор облегчает написание и редактирование длинных выражений с отличной типографикой.
Плюсы:
1. Возможность хранить выражения.
2. Поддерживает греческие буквы.
3. Возможность увеличения и уменьшения масштаба.
4. Создает пользовательские функции.
5. Предоставляет комплексные числа.
Минусы:
1. На некоторых устройствах возникают проблемы с установкой.
3. Требуется версия Android 8.1 и более.Заключение:
Калькуляторы действительно помогают при изучении математики.Мы обсудили десять лучших приложений для вычисления матриц, которые выполняют умножение.
 Мы узнали, что приложения на базе Android, помимо умножения, выполняют множество операций. Мы рекомендуем вам выбрать один из них в соответствии с вашими потребностями.
Мы узнали, что приложения на базе Android, помимо умножения, выполняют множество операций. Мы рекомендуем вам выбрать один из них в соответствии с вашими потребностями. Если вы хотите научиться умножению матриц, ознакомьтесь с нашей статьей о том, как умножить матрицу на 2. Мы написали подробный пост о умножении скалярных матриц.
Вычислить определитель матрицы Пошаговое решение математических задач
Мы знаем, что не каждая система линейных уравнений имеет единственное решение.Иногда система из n уравнений от n переменных не имеет решения или бесконечное множество решений. В этом разделе мы вводим определитель матрица. В следующем разделе мы увидим, что определитель можно использовать чтобы определить, имеет ли система уравнений единственное решение.
Каждой квадратной матрице A соответствует действительное число, называемое определителем A, написано | A |.
Определитель матрицы 2 x 2 A,
определяется как
ПРИМЕЧАНИЕ Обратите внимание, что матрицы заключены в квадратные скобки, а определители обозначаются вертикальными полосами.Кроме того, матрица представляет собой массив чисел, но ее определитель — это одно число.
ОЦЕНКА A 2 X 2
ДЕТЕРМИНАНТ
Если
, затем
ОПРЕДЕЛИТЕЛЬ А МАТРИЦА 3 X 3
Определитель матрицы 3 x 3 A,
определяется как
Простой метод вычисления определителей 3 X 3 находится путем перестановки и факторинг условий, приведенных выше, чтобы получить
Каждая из величин в скобках представляет определитель 2 X 2 матрица, которая является частью матрицы 3 x 3, остающейся, когда строка и столбец множитель исключается, как показано ниже.
Эти определители матриц 2 X 2 называются минорами элемента в матрица 3 x 3. Обозначение M ij представляет определитель матрица, которая получается при удалении строки i и столбца j. Следующий список дает некоторые из миноров из приведенной выше матрицы.
В матрице 4 x 4 миноры являются определителями матриц 3 X 3, а n x
Матрица n имеет миноры, которые являются определителями (n — 1) X (n — 1) матрицы.
Чтобы найти определитель матрицы 3 X 3 или больше, сначала выберите любую строку или
столбец. Затем необходимо умножить минор каждого элемента в этой строке или столбце.
на + l или — 1, в зависимости от того, сумма номеров строк и столбцов
числа четные или нечетные. Произведение младшего и числа +1 или — l равно
называется кофактором .
КОФАКТОР Пусть M ij будет второстепенным для элемента au в матрице n x n . Кофактор ij , написано A ij , это:
Наконец, определитель матрицы n x n находится следующим образом.
ПОИСК ОПРЕДЕЛЕНИЯ МАТРИЦЫ
Умножьте каждый элемент в любой строке или столбце матрицы на его кофактор. В
сумма этих продуктов дает значение определителя.
эта сумма продуктов называется расширением по данной строке или столбцу.
НАЙТИ
КОФАКТОР ЭЛЕМЕНТА
Для матрицы
найдите кофактор каждого из следующих элементов.
(a) 6
Поскольку 6 находится в первой строке и первом столбце матрицы, i = 1 и j = 1.
Кофактор: (-1) 1 + 1 * (-6) = 1 * (-6) = -6.
(b) 3
Здесь i = 2 и j = 3.
Кофактор (-1) 2 + 3 * 10 = (-1) * 10 = -10.
(c) 8
Имеем i = 2 и j = l.
Кофактор: (-1) 2 + 1 * (-8) = (-1) * (-8) = 8.
ОЦЕНКА ДЕТЕРМИНАНТА 3 X 3
Оценить
во втором столбце.
Чтобы найти этот определитель, сначала получите миноры каждого элемента во втором
столбец.
Теперь найдите сомножитель каждого из этих младших.
Определитель находится путем умножения каждого сомножителя на соответствующий ему элемент в матрице и найти сумму этих произведений.
ВНИМАНИЕ: Будьте очень осторожны, чтобы отслеживать все отрицательные знаки, когда оценка детерминант. Работайте осторожно, записывая каждый шаг, как в Примеры.Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Точно такой же ответ можно найти, используя любую строку или столбец матрицы.
Одна из причин использования столбца 2 в примере 3 заключается в том, что он содержит элемент 0,
так что рассчитывать M 32 и A 32 толком не пришлось
выше. Быстро понять, что нули могут быть очень полезны при работе с
детерминанты.
Вместо вычисления (-1) i + j для данного элемента следующие
можно использовать доски для проверки знаков:
Знаки чередуются для каждой строки и столбца, начиная с + в первом строка, позиция первого столбца.Таким образом, эти массивы знаков можно воспроизвести как нужный. Если мы расширим матрицу 3 X 3 около строки 3, например, первый второстепенный будет иметь знак +, связанный с ним, второй второстепенный знак — и третий минор а + знак. Эти массивы знаков могут быть расширены таким образом для определителей матриц 5 × 5, 6 × 6 и более крупных.
ОЦЕНКА ДЕТЕРМИНАНТА 4 X 4
Оценить
Расширение на младшие около четвертой строки дает
Каждый из четырех определяющих факторов в примере 4 должен быть оценен путем раскрытия трое несовершеннолетних, требующих большой работы для получения окончательного значения.Всегда ищите строка или столбец с наибольшим количеством нулей для упрощения работы. В следующем разделе мы ввести несколько свойств, упрощающих вычисление определителей. К счастью, детерминанты больших матриц можно оценить быстро и легко с помощью компьютера или некоторых калькуляторов.
Матрицыи матричная алгебра — Статистика Как к
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: другие примеры
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрица?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица — это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список вроде этого: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы соблюсти соглашение.
Некоторые из наиболее распространенных терминов, с которыми вы столкнетесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, в которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т.е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерность должна быть точно так же . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одно и то же место (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать местоположение ячейки, например A1 или D2. Для матриц типично использовать обозначение типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Матричное вычитание работает точно так же.
В начало
Матричное дополнение — это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа и запишите сумму в правом верхнем углу.
- Сложите числа в нижнем левом углу и запишите сумму в левом нижнем углу.
- Сложите числа справа внизу и запишите сумму справа внизу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Сложение матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов — прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q представляет собой матрицу размера (m + p) × (n + q):
Например:
К началу
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Не можете посмотреть видео? Кликните сюда.
Вы можете выполнить матричное умножение для двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице. Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете перемножить несколько матриц вместе.
Microsoft Excel также может выполнять матричное умножение с использованием функций «массива». Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
В начало
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет обратного.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица — это квадратная матрица, но не все квадратные матрицы сингулярны.
Матрицы необратимые
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица — это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Определитель нуля
Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы. Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 является сингулярной, потому что ее определитель равен нулю:
К началу
Единичная матрица — это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева вниз справа и нулями в остальных местах. .Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным. Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x.По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n .На главной диагонали всегда будут единицы, а оставшиеся пробелы — нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Матрица аддитивной идентичности
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности. Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули.Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обзор поиска инверсий смотрите в этом коротком видео:
Не можете посмотреть видео? Кликните сюда.
Обратные матрицы — это то же самое, что и обратные. В элементарной алгебре (а, возможно, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение любезно предоставлено LTU
Если вы умножите одну матрицу на обратную, вы получите матричный эквивалент 1: Identity Matrix , которая по сути представляет собой матрицу с единицами и нулями.
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) — (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ умножением матриц.Умножьте свою матрицу ответов на исходную матрицу, и вы должны получить единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
В начало
Собственное значение (λ) — это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем. Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его по вектору x .
Пример собственного значения
В следующем примере 5 — собственное значение A, а (1,2) — собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что, если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в разложении на собственные значения . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) — (3) (3)
Упрощая, получаем:
-5 — 5λ + λ + λ 2 — 9
= λ 2 — 4λ — 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 — 4λ — 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
В начало
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений, и именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Можно поместить в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас не , а , чтобы использовать вертикальную полосу в расширенной матрице. Обычно матрицы вообще не имеют линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, а затем укажите «z.«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y — 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце, поставив перед знаком равенства.
-1x + 7y + 3 = 0
2x + 4y — 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом этапе у вас стоит отрицательный знак, просто сделайте константу отрицательным числом.
В начало
Определитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A — это | A |, который также является тем же символом, который используется для абсолютного значения, хотя эти два символа не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 — ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые находятся в матрице 4 × 4.В виде формулы:
Вернуться к началу
Диагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая содержит все единиц по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е.2,2,2 или 9,9,9), является скалярным кратным единичной матрицы и также может быть классифицировано как диагональное.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n — порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Обозначение, обычно используемое для описания диагональной матрицы, — diag (a, b, c) , где abc представляет числа в ведущей диагонали.Для приведенной выше матрицы это обозначение будет diag (3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. В нижнетреугольной матрице числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица — это матрица с нижней диагональю и матрица с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n . Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
В начало
Транспонирование матрицы (или транспонирование матрицы) — это как раз то место, где вы переключаете все строки матрицы в столбцы.Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица — это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Формально A = A T .
Символы для транспонированной матрицы
Обычный символ для транспонированной матрицы — A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их матриц транспонирования в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
Вернуться к началу
Симметричная матрица — это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа по диагонали). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T — матрица транспонирования.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица — это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбце 2, которая равна 4. Его симметричный аналог — -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = — А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что i, i = −a i, i влечет i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг — убедиться, что все элементы на главной диагонали равны нулю (то, что невозможно «доказать» математически!).Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = — a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и кососимметричный эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) — это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Разница — это мера того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариативной матрицы, потому что, по сути, эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете смотреть в столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Вычислите ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A). На следующей диаграмме показано, где появляются ковариация и дисперсия для каждого варианта.
В начало
См. Также:
Что такое матрица неточностей?
Следующий : Форма эшелона строк / Форма сокращенного эшелона строк
————————————————— —————————-Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Калькулятор обратной матрицы
Добро пожаловать в калькулятор обратной матрицы , где у вас будет возможность узнать все об инвертировании матриц. Эта операция аналогична поиску дроби данного числа, за исключением того, что теперь мы перемножаем матрицы и хотим получить единичную матрицу в результате . Но не волнуйтесь, прежде чем мы дадим, скажем, обратную матрицу 4×4, мы рассмотрим некоторые основные определения, включая сингулярную матрицу и невырожденную матрицу .Затем мы перейдем к общей формуле обратной матрицы с аккуратным упрощением для обратной матрицы 2×2 и некоторыми полезными обратными свойствами матрицы. И последнее, но не менее важное: мы даем пример с подробными вычислениями того, как найти обратную матрицу 3×3.
Так что налейте себе стакан воды и наслаждайтесь поездкой!
Что такое матрица?
В начальной школе вас учат натуральным числам , 1 , 2 или 143 , и они имеют смысл — у вас есть 1 машинка, 2 комиксов и ужасно длинные 143 дней до Рождества.Затем они сообщают вам, что существуют дроби (или рациональных чисел , как они их называют), например, ½ , или десятичные дроби, например, 1,25 , что все еще кажется разумным. В конце концов, вы подарили брату ½ плитки шоколада, а она стоила $ 1,25 . Затем вы встретите отрицательных чисел , таких как -2 или -30 , и их немного сложнее понять. Но если подумать, один парень из вашего класса получил -2 баллов на тесте на читерство, а в Черную пятницу была скидка –30 долларов на джинсы.
Наконец, школа вводит вещественных чисел и некоторые странные символы, похожие на червяков, которые продолжают называть квадратными корнями. Что еще хуже, в то время как √4 — это простое 2 , √3 — это что-то вроде 1.73205 ... , и цифры продолжаются бесконечно. Они убеждают вас, что такие числа описывают, например, диагональ прямоугольника. И еще есть π , который каким-то образом появился из ниоткуда, когда вы говорили о кругах. Достаточно справедливо, может быть, эти числа в каком-то смысле являются реальными .Но это почти все, что может быть , не так ли?
Неправильно. Математики заняты выяснением различных интересных и, не поверите, полезных расширений действительных чисел . Самый важный из них — комплексные числа, которые являются отправной точкой для любого современного физика. К счастью, мы здесь не в этом направлении. Есть еще один.
Матрица — это массив элементов (обычно чисел) , который имеет заданное количество строк и столбцов. Пример матрицы:
| А | = |
|
Более того, мы говорим, что матрица имеет ячеек , или ячеек , в которые мы записываем элементы нашего массива.Например, матрица A выше имеет значение 2 в ячейке, которая равна во второй строке и втором столбце . Отправной точкой здесь являются матрицы с одной ячейкой, которые в основном аналогичны действительным числам.
Как видите, матрицы — это инструмент, используемый для лаконичной записи нескольких чисел и работы со всей партией как с единым объектом . Таким образом, они чрезвычайно полезны при работе с:
Вычисления с матрицами намного сложнее, чем с числами .Например, если мы хотим добавить их, мы сначала должны убедиться, что можем. Но, поскольку мы здесь, на калькуляторе обратной матрицы , мы оставляем сложение на потом. Однако сначала давайте познакомимся с несколькими определениями.
Сингулярная и невырожденная матрица, единичная матрица
Если вы хотите найти обратную матрицу 2×2 или обратную матрицу 4×4, вы должны сначала понять одну вещь: не всегда существует . Придумайте дробь, скажем a / b .Это прекрасно , пока b ненулевое значение . Если это так, выражение не имеет смысла, и то же самое происходит с матрицами.
Сингулярная матрица — это матрица, у которой нет обратной. Неособая матрица (неожиданный сюрприз) справляется. Поэтому всякий раз, когда вы сталкиваетесь с упражнением с обратной матрицей, вам следует начинать с проверки, является ли оно невырожденным. В противном случае нет смысла заниматься расчетами. Это просто невозможно.
По определению, является инверсией матрицы A — это матрица A⁻¹ , для которой
A * A⁻¹ = A⁻¹ * A = I ,
, где I обозначает единичную матрицу , то есть квадратную матрицу, которая имеет 1 с на главной диагонали и 0 с в другом месте. Например, единичная матрица 3x3 равна
| I | = |
|
Другими словами, когда дана произвольная матрица A , мы хотим найти другую, для которой произведение двух (в любом порядке) дает единичную матрицу .Думайте о I как о 1 (элемент идентичности) в мире матриц. В конце концов, для дроби a / b обратная величина будет b / a , но не только потому, что мы « перевернем » (по крайней мере, не по определению). Это из-за аналогичного свойства умножения:
(а / б) * (б / а) = (б / а) * (а / б) = 1 .
Это было достаточно времени, потраченного на чтение определений, вам не кажется? Давайте, наконец, посмотрим , формулу обратной матрицы и узнаем, как найти обратную матрицу 2×2, 3×3 и 4×4.
Как найти обратную матрицу: формула обратной матрицы
Прежде чем мы перейдем к частным случаям, таким как обратная матрица 2×2, давайте взглянем на , общее определение .
Пусть A — квадратная невырожденная матрица размера n . Тогда обратная величина A⁻¹ (если она существует) дается формулой:
| * |
|
| A | — это определитель A (не путать с абсолютным значением числа). Aᵢⱼ обозначает минор i, j A , то есть определитель матрицы, полученной из A , забыв о его i -й строке и j -м столбце (это квадратная матрица размером n-1 ). Что мы получили в названии
матрица кофакторов из A . Наконец, ᵀ вне массива — это транспонирование. Это означает, что как только мы узнаем ячейки внутри, мы должны « перевернуть их на », чтобы строка i стала его столбцом i и наоборот.Это приводит к сопряженной матрице из A .
Уф, это было , много символов и много технической ерунды. , но это то, что нравится математикам. Некоторые из нас заканчивают просмотр ромкомов, другие записывают определения, которые кажутся умными. Кто мы такие, чтобы их судить?
В следующем разделе мы укажем на несколько важных фактов, которые следует учитывать при поиске обратной матрицы 4×4 или любого ее размера.Но прежде, чем мы их увидим, давайте посмотрим на , что приведенная выше формула обратной матрицы превращается в , когда это обратная матрица 2×2, которую мы ищем.
Пусть
Затем младшие ( Aᵢⱼ s выше) возникают в результате вычеркивания одной из строк и одного из столбцов. Но если мы это сделаем, у нас останется на одну ячейку ! И определитель такой вещи (матрица 1×1) — это просто число в этой ячейке. Например, A₁₂ происходит из-за того, что мы забываем первую строку и второй столбец, что означает, что остается только c (или, скорее, [c] , поскольку это матрица).Следовательно,
| A⁻¹ | = | * |
|
Кроме того, в этом частном случае определитель достаточно простой : | A | = а * г - б * с .Итак, после учета минусов и перестановки, мы приходим к — красивой и красивой формуле для обратной матрицы 2×2:
| A⁻¹ | = | * |
|
Возможно, обратную матрицу 4×4 не так просто вычислить, как в случае 2×2. Существует альтернативный способ вычисления обратной матрицы ; метод включает операций с элементарными строками и так называемое исключение по Гауссу (для получения дополнительной информации обязательно ознакомьтесь с калькулятором (сокращенной) эшелонированной формы строк). В качестве примера ниже мы опишем, как найти обратную матрицу 3×3, используя альтернативный алгоритм.
Допустим, вы хотите вычислить обратную матрицу
|
Затем мы строим матрицу с тремя строками и вдвое большим количеством столбцов, как показано ниже:
|
и используйте исключение Гаусса в 6-элементных строках матрицы, чтобы преобразовать его в нечто вроде
|
, где x , y и z получаются в процессе преобразований.Тогда
| A⁻¹ | = |
|
Какой бы метод вы ни предпочли, может быть полезно проверить несколько обратных свойств матрицы , чтобы сделать наши исследования немного проще.
Обратные свойства матрицы
Ниже мы перечисляем несколько наблюдений и обратные свойства матрицы.
Не всегда существует обратная матрица. Давайте подробнее рассмотрим формулу обратной матрицы в раздел выше. Он содержит определитель матрицы. Это означает, что, прежде всего, нам нужно иметь квадратную матрицу даже для того, чтобы задуматься о ее инверсии. Во-вторых, определитель появляется в знаменателе дроби в формуле обратной матрицы.Следовательно, если этот определитель равен
0, тогда это выражение не имеет никакого смысла, и обратное выражение не существует.Матрица, обратная обратной, является исходной матрицей. Другими словами, если вы дважды перевернете матрицу, вы получите то, с чего начали. Символически это свойство можно записать как
(A⁻¹) ⁻¹ = Aдля произвольной невырожденной матрицыA.Обратное произведение — это произведение обратных чисел в обратном порядке. Это означает, что если у вас есть две квадратные матрицы
AиBодинакового размера и вы хотите вычислить обратное их произведение, то, в качестве альтернативы, вы можете найти их отдельные обратные и умножить их, но в обратном порядке. Короче говоря,(A * B) ⁻¹ = B⁻¹ * A⁻¹.Обратное транспонирования — это транспонирование обратного. По сути, не имеет значения, если вы сначала транспонируете матрицу, а затем вычислите ее обратную, или сначала найдете обратную матрицу и только потом ее транспонируете.В символической записи это означает
(Aᵀ) ⁻¹ = (A⁻¹) ᵀ. В частности, обратите внимание, что это основано на том факте, что определитель матрицы остается неизменным после транспонирования .
Мы надеемся, что вы достаточно заинтригованы теорией и не можете дождаться, чтобы рассказать о ней своим друзьям за чашкой кофе. Однако, прежде чем вы начнете распространять знания, давайте вместе рассмотрим пример и посмотрим , как найти на практике обратную матрицу 3×3 .
Пример: использование калькулятора обратной матрицы
Теперь мы рассмотрим шаг за шагом, как найти обратную матрицу 3×3 . Скажите, что вам дан массив
| А | = |
|
Прежде чем мы перейдем к вычислениям, давайте посмотрим, как мы можем использовать калькулятор обратной матрицы , чтобы сделать все это за нас.
Прежде всего, мы имеем дело с матрицей 3×3, поэтому мы должны сообщить калькулятору, что это , выбрав соответствующий вариант в « Размер матрицы ». Это покажет нам символический пример такого массива с ячейками, обозначенными a₁ , a₂ и так далее. Мы должны ввести числа, указанные в нашей матрице, под правильными символами на картинке. Например, a₃ находится в первой строке третьего столбца, поэтому мы находим соответствующую ячейку в нашей матрице и проверяем, что там 5 .Поэтому в вычислителе обратной матрицы мы кладем a₃ = 5 . Аналогично получаем остальные ячейки:
a₁ = 1 , a₂ = 0 , a₃ = 5 ,
b₁ = 2 , b₂ = 1 , b₃ = 6 ,
c₁ = 3 , c₂ = 4 , c₃ = 0 .
В тот момент, когда мы введем последнее число, калькулятор обратной матрицы выдаст ответ или сообщит нам, что обратной матрицы не существует.Но, если вам не нужны спойлеры, мы также можем произвести расчеты вручную .
Априори мы даже не знаем, существует ли A⁻¹ , может это просто сказка про вампиров? Для уверенности вычислим его определитель:
| A | = 1 * 1 * 0 + 0 * 6 * 3 + 5 * 2 * 4-5 * 1 * 3-0 * 2 * 0-1 * 6 * 4 = 0 + 0 + 40-15-0-24 = 1 .
Уф, сегодня нет вампиров , просто невырожденная матрица и старая добрая математика .
Вспомните формулу обратной матрицы и обратите внимание, что теперь пора вычислить Aᵢⱼ с для i и j между 1 и 3 .В качестве примера возьмем, скажем, A и A . Первый из двух является определяющим фактором того, что мы получим, если забудем первую строку и первый столбец A . Это означает, что
Аналогично, A₂₃ получается, если вычеркнуть вторую строку и третий столбец:
Это дает
A₁₁ = 1 * 0 - 6 * 4 = -23 ,
A₂₃ = 1 * 4 - 0 * 3 = 4 915 14.
Итого получаем
A₁₁ = -23 , A₁₂ = -18 , A₁₃ = 5 ,
A₂₁ = -20 , A₂₁ = -15 , A₂₃ = 4 ,
A₃₁ = -5 , A₃₂ = -4 , A₃₃ = 1 .
Остается только использовать формулу обратной матрицы и подставить все числа, которые мы вычислили выше:
| A⁻¹ | = | * |
| = |
| = | * |
| = |
| = | 1 | * |
| = |
| = |
|
Было не так уж плохо, правда? Тем не менее, калькулятор обратной матрицы весьма полезен , поскольку он избавляет нас от лишних хлопот.
