Длины высот треугольника по трем сторонам. Высота треугольника
Вычисление высоты треугольника зависит от самой фигуры (равнобедренный, равносторонний, разносторонний, прямоугольный). В практической геометрии сложные формулы, как правило, не встречаются. Достаточно знать общий принцип вычислений для того, чтобы он мог быть универсально применим для всех треугольников. Сегодня мы познакомим вас с базовыми принципами вычисления высоты фигуры, расчетными формулами, основываясь на свойствах высот треугольников.
Что такое высота?
Высота имеет несколько отличительных свойств
- Точка, где все высоты соединяются, называется ортоцентром. Если треугольник остроконечный, то ортоцентр находится внутри фигуры, если один из углов тупой, то ортоцентр, как правило, находится снаружи.
- В треугольнике, где один угол равен 90°, ортоцентр и вершина совпадают.
- В зависимости от вида треугольника есть несколько формул, как найти высоту треугольника.

Традиционные вычисления
- Если р – это половина периметра, тогда a, b, c являются обозначением сторон требуемой фигуры, h – высота, то первая и самая простая формула будет выглядеть следующим образом: h = 2/a √p(p-a) (p-b) (p-c).
- В школьных учебниках часто можно найти задачи, в которых известно значение одной из сторон треугольника и величина угла между данной стороной и основанием. Тогда формула расчета высоты будет выглядеть так: h = b ∙ sin γ + c ∙ sin β.
- Когда дана площадь треугольника – S, а также длина основания – а, то вычисления будут максимально простыми. Высоту находят по формуле: h = 2S/a.
- Когда дан радиус окружности, описанной вокруг фигуры, вначале вычисляем длины его двух сторон, а затем приступаем к вычислению заданной высоты треугольника. Для этого используем формулу: h = b ∙ c/2R, где b и c – это две стороны треугольника, которые не являются основанием, а R – радиус.
Как найти высоту равнобедренного треугольника?
Все стороны у данной фигуры равнозначны, их длины равны, поэтому и углы при основании тоже будут равными.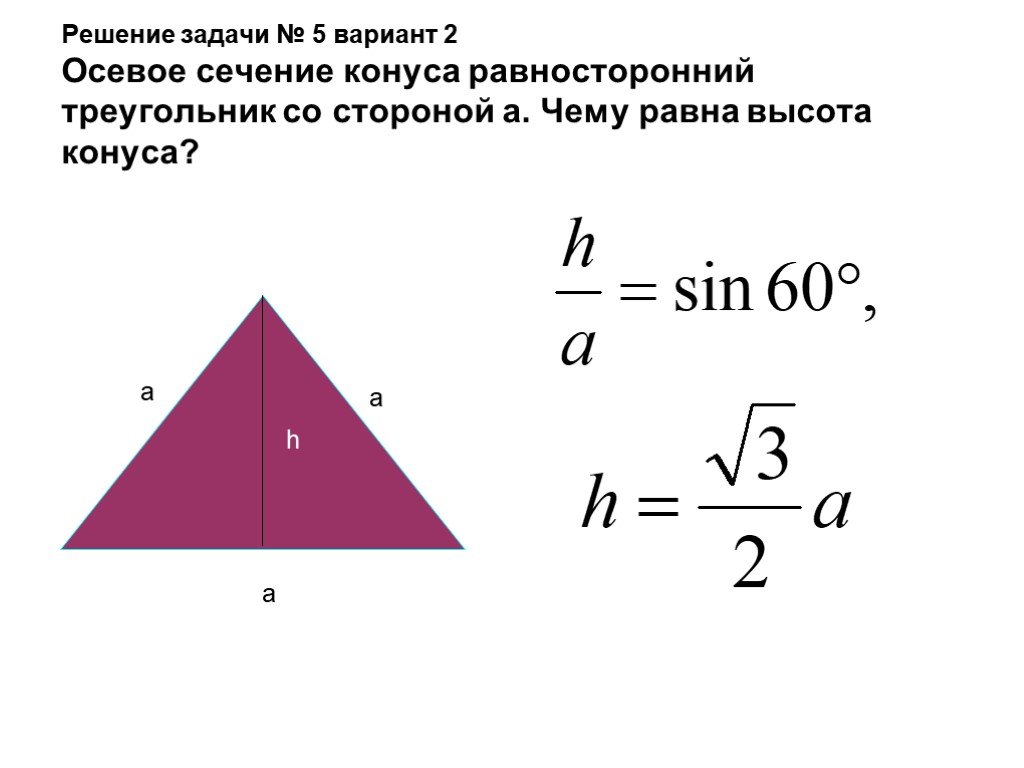 Из этого следует, что высоты, которые проводим на основания, тоже будут равны, они же и медианы, и биссектрисы одновременно. Говоря простым языком, высота в равнобедренном треугольнике делит основание надвое. Треугольник с прямым углом, который получился после проведения высоты, будем рассматривать с помощью теоремы Пифагора. Обозначим боковую сторону как а, а основание как b, тогда высота h = ½ √4 a2 − b2.
Из этого следует, что высоты, которые проводим на основания, тоже будут равны, они же и медианы, и биссектрисы одновременно. Говоря простым языком, высота в равнобедренном треугольнике делит основание надвое. Треугольник с прямым углом, который получился после проведения высоты, будем рассматривать с помощью теоремы Пифагора. Обозначим боковую сторону как а, а основание как b, тогда высота h = ½ √4 a2 − b2.
Как найти высоту равностороннего треугольника?
Формула равностороннего треугольника (фигуры, где все стороны являются равновеликими), можно найти, исходя из предыдущих вычислений. Необходимо только измерить длину одной из сторон треугольника и обозначить её как а. Тогда высота выводится по формуле: h = √3/2 a.
Как известно, угол в прямоугольном треугольнике равен 90°. Высота, опущенная на один катет, одновременно является и вторым катетом. На них и будут лежать высоты треугольника с прямым углом.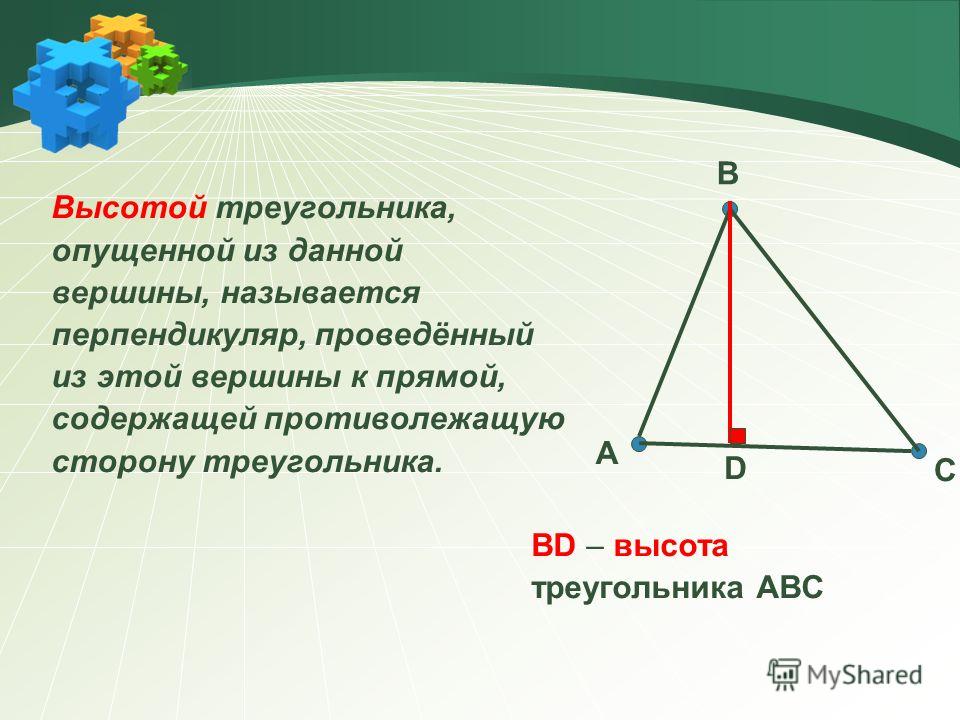 Для получения данных о высоте, нужно немного преобразовать имеющуюся формулу Пифагора, обозначив катеты – а и b, а также измерив длину гипотенузы – с.
Для получения данных о высоте, нужно немного преобразовать имеющуюся формулу Пифагора, обозначив катеты – а и b, а также измерив длину гипотенузы – с.
Найдем длину катета (сторона, которой будет перпендикулярна высота): a = √ (c2 − b2). Длина второго катета находится по точно такой же формуле: b =√ (c2 − b2). После чего можно приступать к вычислению высоты треугольника с прямым углом, предварительно сосчитав площадь фигуры – s. Значение высоты h = 2s/a.
Расчеты с разносторонним треугольником
Когда разносторонний треугольник имеет острые углы, то высота, опускаемая на основание, видна. Если же треугольник с тупым углом, то высота может находиться вне фигуры, и нужно мысленно её продолжить, чтобы получить точку соединения высоты и основания треугольника. Самым простым способом измерить высоту является вычисление её через одну из сторон и величины углов. Формула выглядит следующим образом: h = b sin y + c sin ß.
Высота треугольника это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение (сторона, на которую опускается перпендикуляр, в данном случае называется основанием треугольника).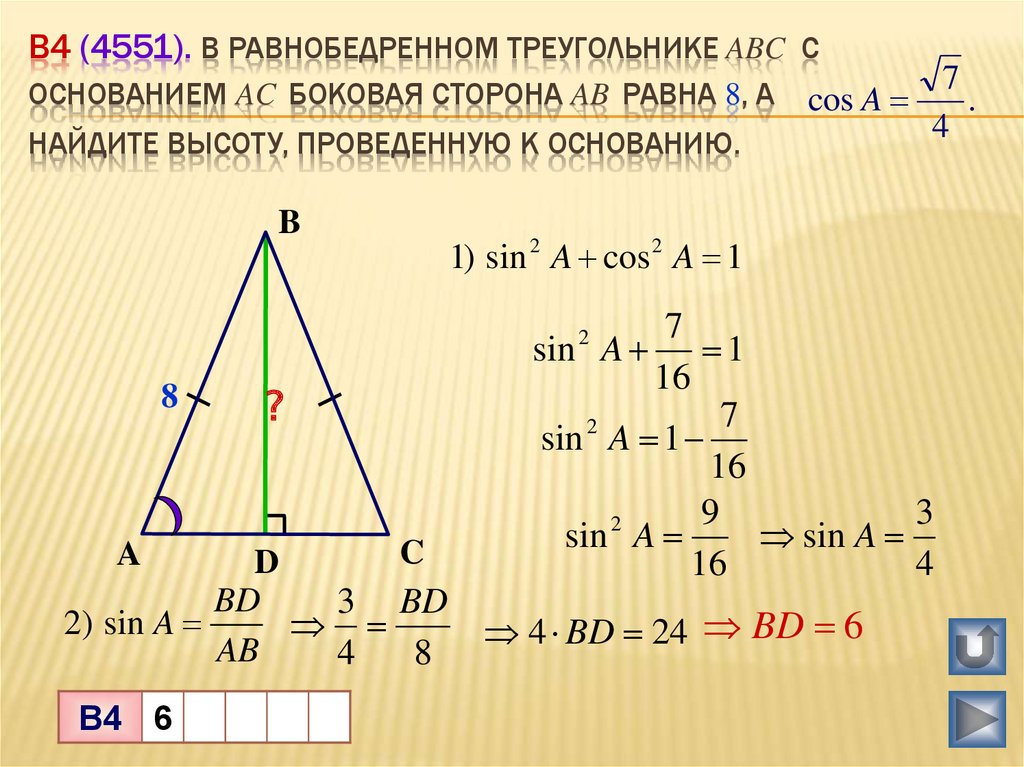
В тупоугольном треугольнике две высоты падают на продолжение сторон и лежат вне треугольника. Третья внутри треугольника.
В остроугольном треугольнике все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты служат высотами.
Как найти высоту по основанию и площади
Напомним формулу для вычисления площади треугольника. Площадь треугольника вычисляется по формуле:
- А — площадь треугольника
- b — сторона треугольника, на которую опущена высота.
- h — высота треугольника
Посмотрите на треугольник и подумайте, какие величины вам уже известны. Если вам дана площадь, обозначьте ее буквой «А» или «S». Вам также должно быть дано значение стороны, обозначьте ее буквой «b». Если вам не дана площадь и не дана сторона, воспользуйтесь другим методом.
Имейте в виду, что основанием треугольника может быть любая его сторона, на которую опущена высота (независимо от того, как расположен треугольник).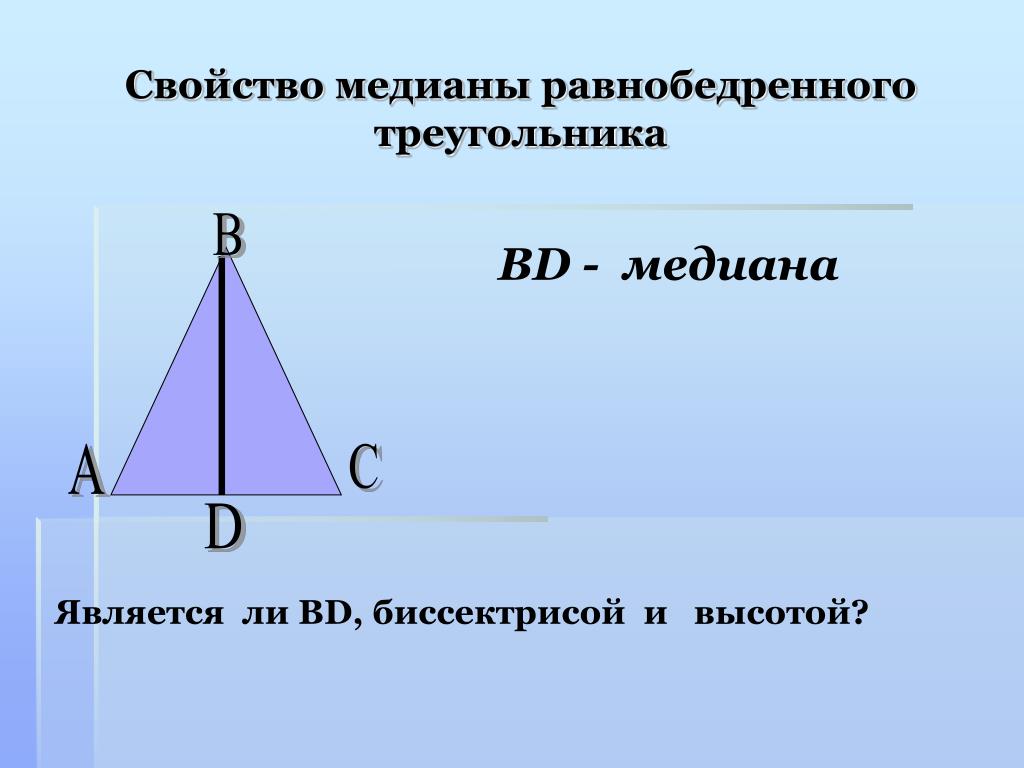 Чтобы лучше понять это, представьте, что вы можете повернуть этот треугольник. Поверните его так, чтобы известная вам сторона была обращена вниз.
Чтобы лучше понять это, представьте, что вы можете повернуть этот треугольник. Поверните его так, чтобы известная вам сторона была обращена вниз.
Например, площадь треугольника равна 20, а одна из его сторон равна 4. В этом случае «‘А = 20″‘, ‘»b = 4′».
Подставьте данные вам значения в формулу для вычисления площади (А = 1/2bh) и найдите высоту. Сначала умножьте сторону (b) на 1/2, а затем разделите площадь (А) на полученное значение. Таким образом, вы найдете высоту треугольника.
В нашем примере: 20 = 1/2(4)h
20 = 2h
10 = h
Вспомните свойства равностороннего треугольника. В равностороннем треугольнике все стороны и все углы равны (каждый угол равен 60˚). Если в таком треугольнике провести высоту, вы получите два равных прямоугольных треугольника.
Например, рассмотрим равносторонний треугольник со стороной 8.
Вспомните теорему Пифагора. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами «а» и «b» гипотенуза «с» равна: a2+b2=c2. Эту теорему можно использовать, чтобы найти высоту равностороннего треугольника!
Эту теорему можно использовать, чтобы найти высоту равностороннего треугольника!
Разделите равносторонний треугольник на два прямоугольных треугольника (для этого проведите высоту). Затем обозначьте стороны одного из прямоугольных треугольников. Боковая сторона равностороннего треугольника – это гипотенуза «с» прямоугольного треугольника. Катет «а» равен 1/2 стороне равностороннего треугольника, а катет «b» – это искомая высота равностороннего треугольника.
Итак, в нашем примере с равносторонним треугольником с известной стороной, равной 8: c = 8 и a = 4.
Подставьте эти значения в теорему Пифагора и вычислите b2. Сначала возведите в квадрат «с» и «а» (умножьте каждое значение само на себя). Затем вычтите a2 из c2.
42 + b2 = 82
16 + b2 = 64
b2 = 48
Извлеките квадратный корень из b2, чтобы найти высоту треугольника. Для этого воспользуйтесь калькулятором. Полученное значение и будет высотой вашего равностороннего треугольника!
b = √48 = 6,93
Как найти высоту с помощью углов и сторон
Подумайте, какие значения вам известны.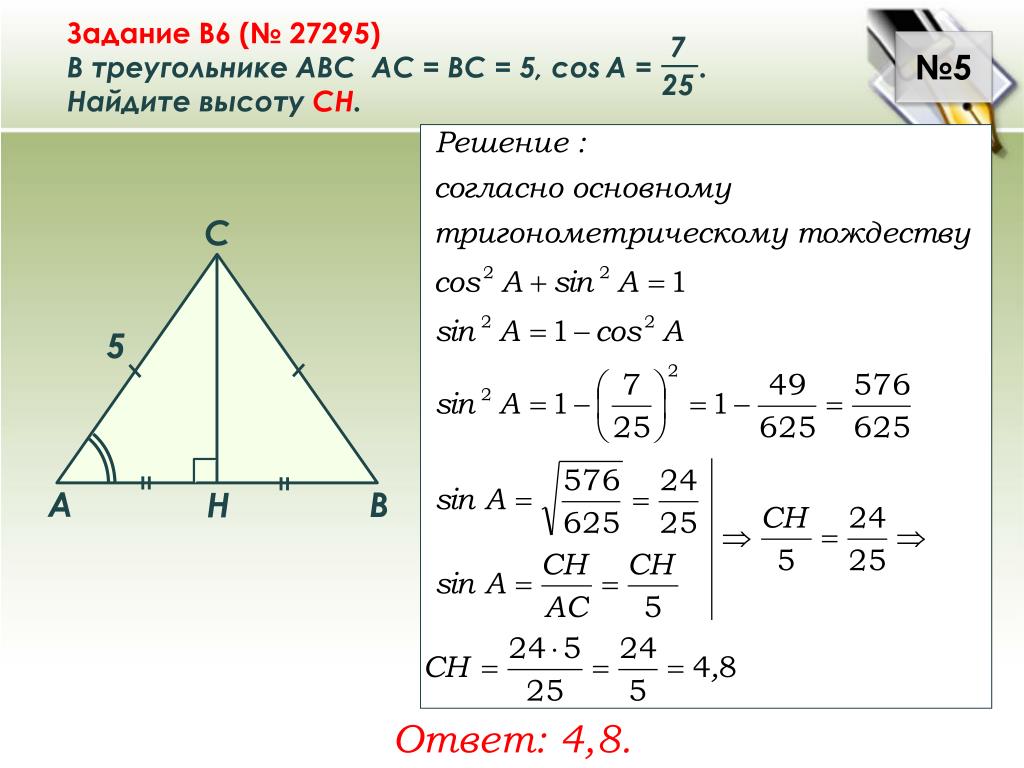 Вы можете найти высоту треугольника, если вам известны значения сторон и углов. Например, если известен угол между основанием и боковой стороной. Или если известны значения всех трех сторон. Итак, обозначим стороны треугольника: «a», «b», «c», углы треугольника: «А», «В», «С», а площадь — буквой «S».
Вы можете найти высоту треугольника, если вам известны значения сторон и углов. Например, если известен угол между основанием и боковой стороной. Или если известны значения всех трех сторон. Итак, обозначим стороны треугольника: «a», «b», «c», углы треугольника: «А», «В», «С», а площадь — буквой «S».
Если вам известны все три стороны, вам понадобится значение площади треугольника и формула Герона.
Если вам известны две стороны и угол между ними, можете использовать следующую формулу для нахождения площади: S=1/2ab(sinC).
Если вам даны значения всех трех сторон, используйте формулу Герона. По этой формуле придется выполнить несколько действий. Сначала нужно найти переменную «s» (мы обозначим этой буквой половину периметра треугольника). Для этого подставьте известные значения в эту формулу: s = (a+b+c)/2.
Для треугольника со сторонами а = 4, b = 3, c = 5, s = (4+3+5)/2. В результате получается: s=12/2, где s=6.
Затем вторым действием мы находим площадь (вторая часть формулы Герона).
Теперь найдите эквивалентное выражение для высоты (h). Для нашего треугольника будет справедливо следующее уравнение: 1/2(3)h = (6(6-4)(6-3)(6-5)). Где 3/2h=√(6(2(3(1))). Получается, 3/2h = √(36). С помощью калькулятора вычислите квадратный корень. В нашем примере: 3/2h = 6. Получается, что высота (h) равна 4, сторона b – основание.
Если по условию задачи известны две стороны и угол, вы можете использовать другую формулу. Замените площадь в формуле эквивалентным выражением: 1/2bh. Таким образом, у вас получится следующая формула: 1/2bh = 1/2ab(sinC). Ее можно упростить до следующего вида: h = a(sin C), чтобы убрать одну неизвестную переменную.
Теперь осталось решить полученное уравнение. Например, пусть «а» = 3, «С» = 40 градусов. Тогда уравнение будет выглядеть так: «h» = 3(sin 40). С помощью калькулятора и таблицы синусов подсчитайте значение «h».
Треугольники.
Основные понятия.
Треугольник — это фигура, состоящая из трех отрезков и трех точек, не лежащих на одной прямой.
Отрезки называются сторонами , а точки — вершинами .
Сумма углов треугольника равна 180 º .
Высота треугольника.
Высота треугольника — это перпендикуляр, проведенный из вершины к противолежащей стороне.
В остроугольном треугольнике высота содержится внутри треугольника (рис.1).
В прямоугольном треугольнике катеты являются высотами треугольника (рис.2).
В тупоугольном треугольнике высота проходит вне треугольника (рис.3).
Свойства высоты треугольника:
Биссектриса треугольника.
Биссектриса треугольника — это отрезок, который делит угол вершины пополам и соединяет вершину с точкой на противолежащей стороне (рис.5).
Свойства биссектрисы:
Медиана треугольника.
Медиана треугольника — это отрезок, соединяющий вершину с серединой противолежащей стороны (рис.9а).
Длину медианы можно вычислить по формуле: 2b 2 + 2c 2 — a 2 где m a — медиана, проведенная к стороне а . В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы: c где m c — медиана, проведенная к гипотенузе c (рис.9в) Медианы треугольника пересекаются в одной точке (в центре масс треугольника) и делятся этой точкой в соотношении 2:1, отсчитывая от вершины. То есть отрезок от вершины к центру в два раза больше отрезка от центра к стороне треугольника (рис.9с). Три медианы треугольника делят его на шесть равновеликих треугольников. |
Средняя линия треугольника.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон (рис.10).
Средняя линия треугольника параллельна третьей стороне и равна ее половине
Внешний угол треугольника.
Внешний угол треугольника равен сумме двух несмежных внутренних углов (рис.11).
Внешний угол треугольника больше любого несмежного угла.
Прямоугольный треугольник.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол (рис.12).
Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой .
Две другие стороны называются катетами .
Пропорциональные отрезки в прямоугольном треугольнике.
1) В прямоугольном треугольнике высота, проведенная из прямого угла, образует три подобных треугольника: ABC, ACH и HCB (рис.14а). Соответственно, углы, образуемые высотой, равны углам А и В.
Рис.14а
Равнобедренный треугольник.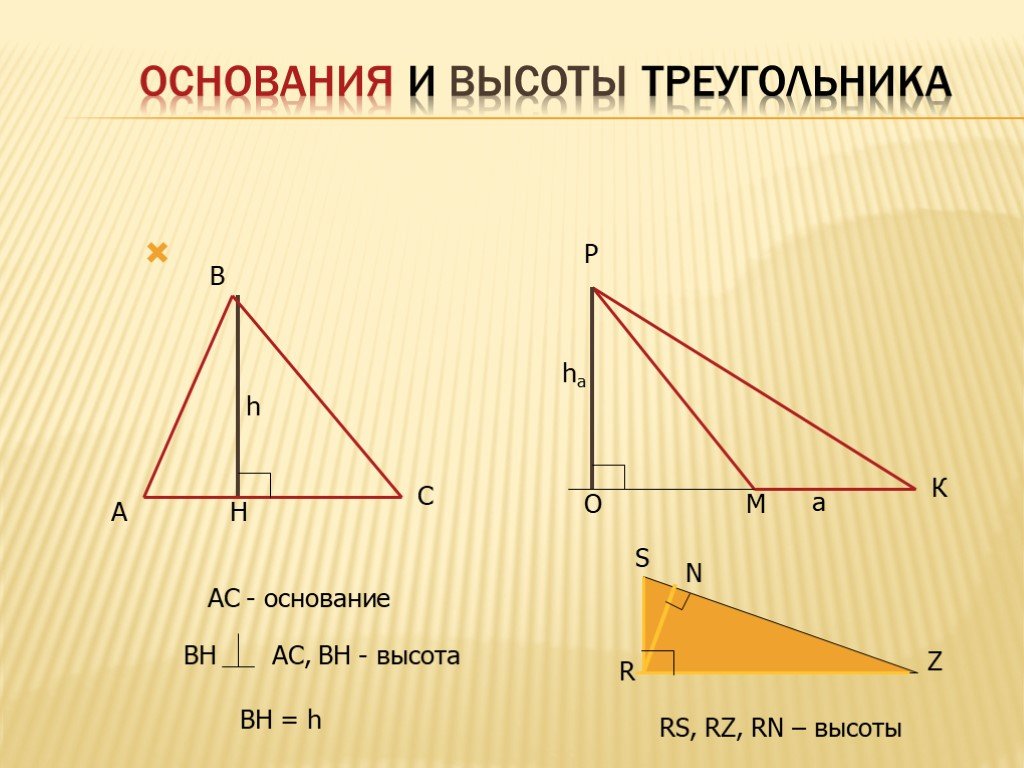
Равнобедренный треугольник — это треугольник, у которого две стороны равны (рис.13).
Эти равные стороны называются боковыми сторонами , а третья — основанием треугольника.
В равнобедренном треугольнике углы при основании равны. (В нашем треугольнике угол А равен углу C).
В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно и биссектрисой, и высотой треугольника.
Равносторонний треугольник.
Равносторонний треугольник — это треугольник, у которого все стороны равны (рис.14).
Свойства равностороннего треугольника:
Замечательные свойства треугольников.
У треугольников есть оригинальные свойства, которые помогут вам успешно решать задачи, связанные с этими фигурами. Некоторые из этих свойств изложены выше. Но повторяем их еще раз, добавив к ним несколько других замечательных особенностей:
1) В прямоугольном треугольнике с углами 90º, 30º и 60º катет b , лежащий напротив угла в 30º, равен половине гипотенузы. 2) В прямоугольном равнобедренном треугольнике с углами 90º, 45º и 45º гипотенуза в √2 раз больше катета (рис.15b ). К примеру, если катеты равны 5, то гипотенуза равна 5√2. 3) Средняя линия треугольника равна половине параллельной стороны (рис.15с ). К примеру, если сторона треугольника равна 10, то параллельная ей средняя линия равна 5. 4) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы (рис.9в): m c = с/2. 5) Медианы треугольника, пересекаясь в одной точке, делятся этой точкой в соотношении 2:1. То есть отрезок от вершины к точке пересечения медиан в два раза больше отрезка от точки пересечения медиан к стороне треугольника (рис.9c) 6) В прямоугольном треугольнике середина гипотенузы является центром описанной окружности (рис. |
Признаки равенства треугольников .
Первый признак равенства : если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства : если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства : если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Неравенство треугольника.
В любом треугольнике каждая сторона меньше суммы двух других сторон.
Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
c 2 = a 2 + b 2 .
Площадь треугольника.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
ah
S = ——
2
2) Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними:
1
S = — AB · AC · sin A
2
Треугольник, описанный около окружности.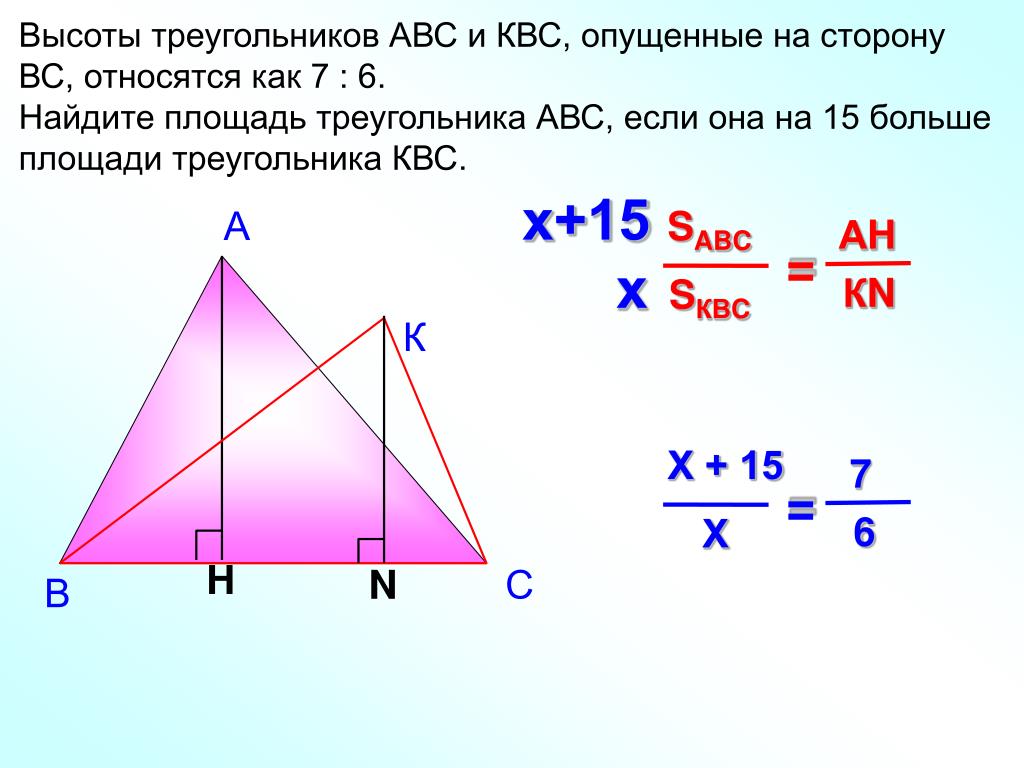
Окружность называется вписанной в треугольник, если она касается всех его сторон (рис.16а ).
Треугольник, вписанный в окружность.
Треугольник называется вписанным в окружность, если он касается ее всеми вершинами (рис.17a ).
Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника (рис.18).
Синус острого угла x противолежащего катета к гипотенузе.
Обозначается так: sin x .
Косинус острого угла x прямоугольного треугольника — это отношение прилежащего катета к гипотенузе.
Обозначается так: cos x .
Тангенс острого угла x — это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg x .
Котангенс острого угла x — это отношение прилежащего катета к противолежащему.
Обозначается так: ctg x .
Правила:
Катет, противолежащий углу x , равен произведению гипотенузы на sin x :
b = c · sin x
Катет, прилежащий к углу x , равен произведению гипотенузы на cos x :
a = c · cos x
Катет, противоположный углу x , равен произведению второго катета на tg x :
b = a · tg x
Катет, прилежащий к углу x , равен произведению второго катета на ctg x :
a = b · ctg x .
Для любого острого угла x :
sin (90° — x ) = cos x
cos (90° — x ) = sin x
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.
Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.
Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя сторонами составляют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, не стандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
Рис. 1. Высота тупоугольного треугольника.
Как правило, высота треугольника имеет обозначение буквой h. Так же обозначается высота и в других фигурах.
Как найти высоту треугольника?
Существует три стандартных способа нахождения высоты треугольника:
Через теорему Пифагора
Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.
Дано : равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.
Рис. 2. Рисунок к задаче.
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.
Свойства высоты равнобедренного треугольника, проведенной к основания:
- Высота совпадает с медианной и биссектрисой
- Делит основание на две равные части.
 2}=\sqrt{25-16}=3$$
2}=\sqrt{25-16}=3$$Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.
Через площадь треугольника
Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.
Формула площади треугольника: $$S={1\over2}*bh$$, где b – это сторона треугольника,а h – высота, проведенная к этой стороне. Выразим из формулы высоту:
$$h=2*{S\over b}$$
Если площадь равна 15, сторона 5, то высота $$h=2*{15\over5}=6$$
Через тригонометрическую функцию
Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.
Рис. 3. Рисунок к задаче.
Угол ВСН=300 , а сторона BC=8.
 У нас все тот же прямоугольный треугольник BCH. Воспользуемся синусом. Синус это отношение противолежащего катета к гипотенузе, значит: BH/BC=cos BCH.
У нас все тот же прямоугольный треугольник BCH. Воспользуемся синусом. Синус это отношение противолежащего катета к гипотенузе, значит: BH/BC=cos BCH.Угол известен, как и сторона. Выразим высоту треугольника:
$$BH=BC*\cos (60\unicode{xb0})=8*{1\over2}=4$$
Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.
Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.6 . Всего получено оценок: 152.
Узнаем как найти высоту треугольника? Формула расчета
Для решения многих геометрических задач требуется найти высоту заданной фигуры. Эти задачи имеют прикладное значение. При проведении строительных работ определение высоты помогает вычислить необходимое количество материалов, а также определить, насколько точно сделаны откосы и проемы.
 Часто для построения выкроек требуется иметь представление о свойствах геометрических фигур.
Часто для построения выкроек требуется иметь представление о свойствах геометрических фигур.У многих людей, несмотря на хорошие оценки в школе, при построении обычных геометрических фигур возникает вопрос о том, как найти высоту треугольника или параллелограмма. Причем определение высоты треугольника является самым сложным. Это происходит потому, что треугольник может быть острым, тупым, равнобедренным или прямоугольным. Для каждого из видов треугольников существуют свои правила построения и расчета.
Как найти высоту треугольника, в котором все углы острые, графическим способом
Если все углы у треугольника острые (каждый угол в треугольнике меньше 90 градусов), то для нахождения высоты необходимо сделать следующее.
- По заданным параметрам выполняем построение треугольника.
- Введем обозначения. А, В и С будут вершинами фигуры. Углы, соответствующие каждой вершине – α, β, γ. Противолежащие этим углам стороны – a, b, c.
- Высотой называется перпендикуляр, опущенный из вершины угла к противоположной стороне треугольника.
 Для нахождения высот треугольника проводим построение перпендикуляров: из вершины угла α к стороне a, из вершины угла β к стороне b и так далее.
Для нахождения высот треугольника проводим построение перпендикуляров: из вершины угла α к стороне a, из вершины угла β к стороне b и так далее. - Точку пересечения высоты и стороны a обозначим h2, а саму высоту h2. Точка пересечения высоты и стороны b будет h3, высота соответственно h3. Для стороны c высота будет h4, а точка пересечения h4.
Далее для каждого вида треугольника будем использовать те же обозначения сторон, углов, высот и вершин треугольников.
Высота в треугольнике с тупым углом
Теперь рассмотрим, как найти высоту треугольника, если один угол тупой (больше 90 градусов). В этом случае высота, проведенная из тупого угла, будет внутри треугольника. Остальные две высоты будут находиться за пределами треугольника.
Пусть в нашем треугольнике углы α и β будут острыми, а угол γ – тупой. Тогда для построения высот, выходящих из углов α и β, надо продолжить противоположные им стороны треугольника, чтобы провести перпендикуляры.

Как найти высоту равнобедренного треугольника
У такой фигуры есть две равные стороны и основание, при этом углы, находящиеся при основании, также являются равными между собой. Это равенство сторон и углов облегчает построение высот и их вычисление.
Сначала нарисуем сам треугольник. Пусть стороны b и c, а также углы β, γ будут соответственно равными.
Теперь проведем высоту из вершины угла α, обозначим ее h2. Для равнобедренного треугольника эта высота будет одновременно биссектрисой и медианой.
Далее построим две другие высоты: h3 для стороны b и угла β, h4 для стороны c и угла γ. Эти высоты будут равными по длине.
Для основания можно сделать только одно построение. Например, провести медиану – отрезок, соединяющий вершину равнобедренного треугольника и противоположную сторону, основание, для нахождения высоты и биссектрисы. А для вычисления длины высоты для двух других сторон можно построить только одну высоту. Таким образом, чтобы графически определить, как вычислить высоту равнобедренного треугольника, достаточно найти две высоты из трех.

Как найти высоту прямоугольного треугольника
У прямоугольного треугольника определить высоты намного проще, чем у других. Это происходит потому, что сами катеты составляют прямой угол, а значит, являются высотами.
Для построения третьей высоты, как обычно, проводится перпендикуляр, соединяющий вершину прямого угла и противоположную сторону. В итоге для того, чтобы узнать, как найти высоту треугольника в данном случае, требуется только одно построение.
Как найти высоту треугольника в 3 разных ситуациях
Как найти высоту треугольника в 3 разных ситуациях
Яна Руссик
03 марта 2021
Онлайн-обучение
6,
9 ГеометрияМатематика
,
Тригонометрия
В тригонометрии высоту треугольника можно определить разными способами в зависимости от того, является ли он прямоугольным, равнобедренным (треугольник с двумя равными сторонами) или равносторонним.

1. Как найти высоту прямоугольного треугольника
Прежде чем мы начнем, вот что вам нужно знать о прямоугольных треугольниках. Прямоугольный треугольник имеет три стороны: гипотенузу, высоту и основание треугольника. Основанием и высотой прямоугольного треугольника всегда являются стороны, примыкающие к прямому углу, а гипотенуза — самая длинная сторона.
Высоту прямоугольного треугольника можно определить по формуле площади:
Если данная площадь неизвестна, вы можете использовать теорему Пифагора, чтобы найти высоту прямоугольного треугольника. Вот что утверждает теорема Пифагора, учитывая c — гипотенуза, а a и b — две другие стороны:
Возьмем единицы измерения с рисунка выше и подставим длину основания и гипотенузу, чтобы найти недостающую высоту. :
2. Нахождение высоты неправильного треугольника
К сожалению, вы не можете использовать теорему Пифагора, чтобы найти высоту равнобедренного треугольника или высоту равностороннего треугольника (где все стороны треугольника равны).
 Вместо этого вам нужно будет провести перпендикулярную линию через основание треугольника, чтобы образовать прямой угол:
Вместо этого вам нужно будет провести перпендикулярную линию через основание треугольника, чтобы образовать прямой угол:Эта линия представляет высоту этих непрямоугольных треугольников. После того, как вы сформировали эту линию, вам нужно будет использовать формулу Герона, чтобы найти площадь всего треугольника.
Формула Герона
Первым шагом формулы Герона является вычисление половины периметра треугольника. В этом случае s представляет собой половину периметра, а a, b, и c являются сторонами:
После того, как вы определили s , используйте следующую формулу для вычисления площади треугольника. . Опять же, две стороны равны a и b , а самая длинная сторона (гипотенуза) равна c :
Подставим длины сторон этого равнобедренного треугольника, чтобы найти площадь треугольника:
5
6 Теперь , мы заменим s в формуле площади для непрямоугольного треугольника.

Использование площади для нахождения высоты треугольника
Теперь, когда вы знаете площадь изображенного выше треугольника, вы можете подставить ее в формулу треугольника A=1/2bh, чтобы найти высоту треугольника. В этом случае основание будет равно половине расстояния пяти (2,5), так как это самая короткая сторона треугольника.
Основные формулы высоты треугольника
Определение высоты треугольника — это многоэтапный процесс, который может привести к путанице. Однако его освоение поможет вам изучить различные типы формул площади, такие как формула Герона и A=1/2bh. Также показано, как использовать теорему Пифагора и формулы периметра треугольника для определения других величин внутри треугольника.
Дополнительная помощь с домашним заданием по математике
- Вот как найти гипотенузу прямоугольного треугольника
- Узнайте, как найти площадь неправильного треугольника
- Как найти основание треугольника четырьмя различными способами
Высота равностороннего треугольника – формула, метод, часто задаваемые вопросы
Высота равностороннего треугольника – это прямая линия, проведенная из вершины к противоположной стороне треугольника таким образом, что она делит треугольник на две равные -угольные треугольники.
 Это также известно как высота треугольника, который начинается с вершины и является серединным перпендикуляром к противоположной стороне. Равносторонний треугольник – это треугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. Давайте узнаем больше о высоте равностороннего треугольника в этой статье.
Это также известно как высота треугольника, который начинается с вершины и является серединным перпендикуляром к противоположной стороне. Равносторонний треугольник – это треугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. Давайте узнаем больше о высоте равностороннего треугольника в этой статье.1. Какова высота равностороннего треугольника? 2. Формула высоты равностороннего треугольника 3. Часто задаваемые вопросы о высоте равностороннего треугольника Какова высота равностороннего треугольника?
Высота равностороннего треугольника — это линия, проведенная из любой вершины треугольника на противоположной стороне. Эта линия является биссектрисой противоположной стороны. Это означает, что он делит противоположную сторону пополам на две равные части и образует угол 90° на нем.
 Высота равностороннего треугольника также известна как высота, которая делит треугольник на два конгруэнтных прямоугольных треугольника, как показано на следующем рисунке.
Высота равностороннего треугольника также известна как высота, которая делит треугольник на два конгруэнтных прямоугольных треугольника, как показано на следующем рисунке.Определение равностороннего треугольника
Равносторонний треугольник определяется как треугольник, у которого все три стороны и углы равны. Значение каждого угла составляет 60 градусов, поэтому он также известен как равноугольный треугольник. Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы и стороны равны.
Формула высоты равностороннего треугольника
Высоту равностороннего треугольника можно вычислить по теореме Пифагора. Формула, используемая для нахождения высоты равностороннего треугольника, выглядит следующим образом:
Высота равностороннего треугольника (h) = ½(√3a) или (a√3)/2
, где «a» — сторона равностороннего треугольника. равносторонний треугольник. Это означает, что если известна длина стороны равностороннего треугольника, мы можем легко найти высоту треугольника.

Пример: Если одна сторона равностороннего треугольника равна 12 единицам, какова его высота?
Решение: Дано, длина стороны а = 12 единиц.
Воспользуемся формулой высоты равностороннего треугольника, h = (a√3)/2. Подставляя значение «а», получаем h = (12√3)/2 = 6√3 = 10,39 единиц. Следовательно, высота равностороннего треугольника равна 10,39 ед.
Формула высоты равностороннего треугольника Доказательство
Мы знаем, что высота делит равносторонний треугольник на два прямоугольных треугольника. Поэтому применим теорему Пифагора, которая гласит: Гипотенуза 2 = Основание 2 + Высота 2
Если мы посмотрим на рисунок, приведенный выше, каждая сторона равностороннего треугольника представлена буквой «а», поскольку все стороны равны, поэтому основание равно также обозначается буквой «а», а высота = h. Также известно, что высота делит треугольник на два равных прямоугольных треугольника, а основание делится на две равные части.
 Это означает, что если мы воспользуемся теоремой Пифагора для одного из прямоугольных треугольников, это можно выразить как
Это означает, что если мы воспользуемся теоремой Пифагора для одного из прямоугольных треугольников, это можно выразить какA 2 = H 2 + (A /2) 2
⇒ H 2 = A 2 — (A 2 /4) 9000
6674 — (A 2 /4)
6666666674. 3a 2 )/4
Или, h = ½(√3a)
Таким образом, формула для высоты равностороннего треугольника: h = ½(√3a), которая также может быть записана как, h = ( a√3)/2
Высота равностороннего треугольника, если известна сторона
Высоту равностороннего треугольника можно легко вычислить, если известна сторона. Поскольку все стороны равностороннего треугольника равны, и мы знаем, что высота делит треугольник на конгруэнтные прямоугольные треугольники, мы можем применить теорему Пифагора и найти высоту, как описано в разделе, данном выше. Следовательно, если дана одна сторона равностороннего треугольника, формула для нахождения высоты равностороннего треугольника будет следующей: h = ½ (√3a), где «a» представляет собой длину стороны равностороннего треугольника.

Высота равностороннего треугольника при заданной площади
Высоту равностороннего треугольника можно вычислить, зная площадь треугольника. Мы знаем, что площадь равностороннего треугольника можно рассчитать по формуле Площадь равностороннего треугольника = √3/4 × (сторона) 2 . Итак, если мы знаем площадь, мы можем подставить ее значение в эту формулу, чтобы получить длину стороны. Зная длину стороны, мы можем использовать следующую формулу, чтобы найти высоту. Высота равностороннего треугольника, h = ½(√3a).
Пример: Найдите высоту равностороннего треугольника, если его площадь равна 24 кв.
Решение: Дано, площадь равностороннего треугольника = 24 ед.
24 = √3/4 × (сторона) 2
(сторона) 2 = (24 × 4)/√3
сторона = 7,4 единицы
Теперь, когда мы знаем длину стороны, мы можно вычислить высоту равностороннего треугольника по формуле h = ½(√3a), где h — высота, а a — длина стороны.
 Здесь «а» = 7,4 единицы
Здесь «а» = 7,4 единицыч = ½(√3a)
ч = ½(√3 × 7,4) = 6,4 единицы.
Высота равностороннего треугольника при заданном периметре
Высоту равностороннего треугольника можно вычислить, если известен периметр треугольника. Мы знаем, что периметр равностороннего треугольника вычисляется по формуле, периметр равностороннего треугольника = 3а. Также известно, что все стороны равностороннего треугольника равны по длине, поэтому, если известен периметр, мы можем вычислить длину стороны по этой формуле. После вычисления длины стороны можно найти высоту по формуле высота равностороннего треугольника = ½(√3a).
Пример: Найдите высоту равностороннего треугольника, если его периметр равен 21 единице.
Решение: Дан периметр равностороннего треугольника = 21 единица
Сначала найдем длину стороны по формуле Периметр равностороннего треугольника = 3a
21 = 3a
a = 7 единиц
Теперь мы можем рассчитать высоту равностороннего треугольника по формуле h = ½(√3a), где h — высота, а a — длина стороны.
 Мы рассчитали длину стороны как «а» = 7 единиц
Мы рассчитали длину стороны как «а» = 7 единицч = ½(√3a)
ч = ½(√3 × 7) = 6,06 единиц.
Похожие темы
- Гипотенуза
- Площадь равностороннего треугольника
Часто задаваемые вопросы о высоте равностороннего треугольника
Какова высота равностороннего треугольника в математике?
Высота равностороннего треугольника — это прямая линия, проведенная из вершины к противоположной стороне треугольника таким образом, что она делит треугольник на два равных прямоугольных треугольника. Это также известно как высота треугольника, который начинается с вершины и является серединным перпендикуляром к противоположной стороне.
Какая формула высоты равностороннего треугольника?
Высоту равностороннего треугольника можно вычислить по теореме Пифагора. Формула, которая используется для нахождения высоты равностороннего треугольника: Высота равностороннего треугольника (h) = (a√3)/2; где «а» — сторона равностороннего треугольника.
 Это означает, что если известна длина стороны равностороннего треугольника, мы можем легко найти высоту треугольника.
Это означает, что если известна длина стороны равностороннего треугольника, мы можем легко найти высоту треугольника.Как найти высоту равностороннего треугольника, если дана сторона?
Высоту равностороннего треугольника можно легко вычислить, если известна его сторона. Мы знаем, что все стороны равностороннего треугольника равны, а высота делит треугольник на два конгруэнтных прямоугольных треугольника. Следовательно, мы можем применить теорему Пифагора и найти высоту. Формула для нахождения высоты равностороннего треугольника: h = (a√3)/2, где «a» представляет собой длину стороны равностороннего треугольника.
Как найти высоту равностороннего треугольника, зная площадь?
Высоту равностороннего треугольника можно вычислить, если известна площадь треугольника. Мы знаем, что площадь равностороннего треугольника можно рассчитать по формуле Площадь равностороннего треугольника = √3/4 × (сторона) 2 . Итак, если мы знаем площадь, мы можем подставить ее значение в эту формулу, чтобы получить длину стороны.
 Зная длину стороны, мы можем использовать следующую формулу, чтобы найти высоту. Высота равностороннего треугольника, h = ½(√3a).
Зная длину стороны, мы можем использовать следующую формулу, чтобы найти высоту. Высота равностороннего треугольника, h = ½(√3a).Как найти высоту равностороннего треугольника, зная периметр?
Зная периметр равностороннего треугольника, мы можем легко найти его высоту. Формула, которая используется для нахождения периметра равностороннего треугольника: периметр = 3а, где «а» представляет длину стороны. Используя эту формулу, мы можем найти длину стороны после подстановки значения периметра. После того, как длина стороны вычислена, мы можем использовать формулу Высота равностороннего треугольника, h = ½ (√3a), чтобы найти высоту равностороннего треугольника.
Как найти высоту равностороннего треугольника с помощью теоремы Пифагора?
Мы знаем, что высота делит равносторонний треугольник на два прямоугольных треугольника. Следовательно, мы можем использовать теорему Пифагора, чтобы найти высоту равностороннего треугольника. Теорема Пифагора гласит: Гипотенуза 2 = Основание 2 + Высота 2
Поэтому возьмем один из прямоугольных треугольников, в котором длина стороны (в данном случае гипотенуза) = a, h = высота треугольника, а а/2 — третья сторона.


 А катет a больше катета b в √3 раз (рис.15а ). К примеру, если катет b равен 5, то гипотенуза c обязательно равна 10, а катет а равен 5√3.
А катет a больше катета b в √3 раз (рис.15а ). К примеру, если катет b равен 5, то гипотенуза c обязательно равна 10, а катет а равен 5√3.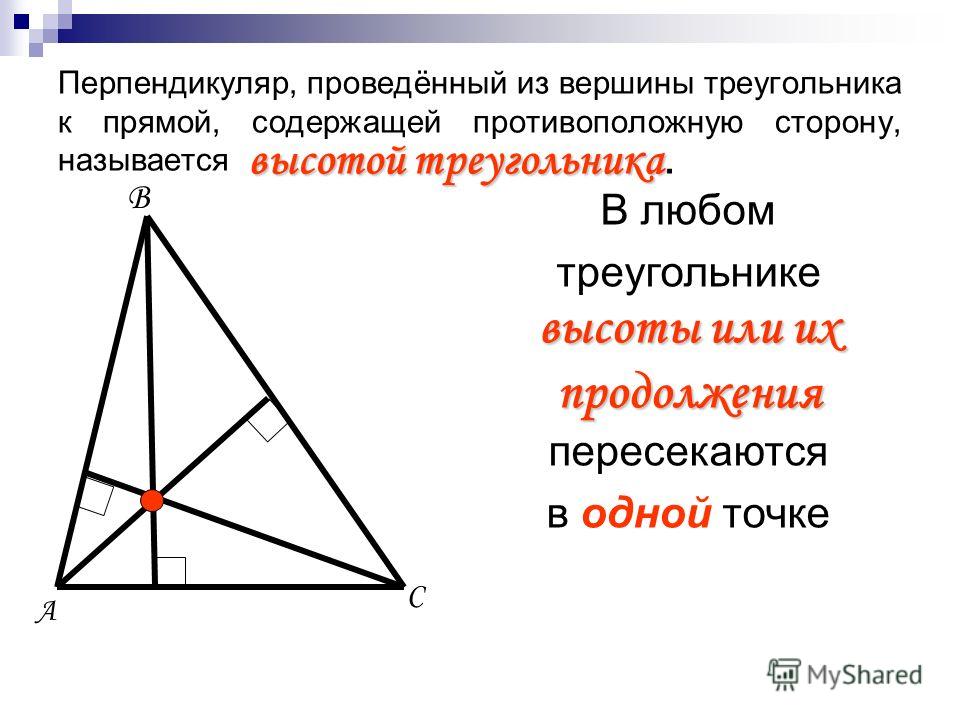 15d ).
15d ).