Выведите уравнение окружности данного радиуса с центром в данной точке,заданной координатами.2. Найдите координаты середины отрезка АВ,если даны координаты его концов А(-3;4) и В(3;-6).Только пожалуйста понятный ответ!)))
Русский язык
3 минуты назад
. Употребите данные словосочетания в единственном числе.Биология
12 минут назад
пресноводная рыба теряет больше воды с мочой чем морская рыба. почему? срочноАнглийский язык
12 минут назад
AMMAR B ose A, B, or C to complete the sentences. mple: My name is Robert. am B is Care What time do B does C is He’s going to bed. He is B has C does your father normally get home? A Do you like shopping? B — Yes, I like B Yes, I love it C No, I do Fiona hates up early. C geting getting B get She doesn’t like Alive B liveing I don’t like A her B him C them The children are very quiet. I can’t hear A they B them C their very tired. alone. C living . I think she’s a terrible actress. A Do you want a mineral water? B No, thanks. I thirsty. A don’t have B haven’t C’m not Where the Red Hot Chili Peppers from? A are B do C come C September 6 June, VOCABULARY What is the missing word? Choose A, B, or C. Example: one, two, three, four A seven B four C five 1 first, second, fourth A third B three C thirty 2 tenth, twelfth, thirteenth A fourteenth B ninth C eleventh 3 nineteenth, twentieth, A twenty-first B twentieth-one C thirty-first 4 January, February, A May B April C March 5 October, November, A January B December August A July B September C October 7 My birthday’s June. A in B at Con 8 The party’s A in B at Con Saturday 3rd October. b Choose A, B, or C to complete the sentences. Example: Steve plays in a band A rock B band C reggae 9 Can you the phone? A speak B ask C answer III-My-school teacher.
C geting getting B get She doesn’t like Alive B liveing I don’t like A her B him C them The children are very quiet. I can’t hear A they B them C their very tired. alone. C living . I think she’s a terrible actress. A Do you want a mineral water? B No, thanks. I thirsty. A don’t have B haven’t C’m not Where the Red Hot Chili Peppers from? A are B do C come C September 6 June, VOCABULARY What is the missing word? Choose A, B, or C. Example: one, two, three, four A seven B four C five 1 first, second, fourth A third B three C thirty 2 tenth, twelfth, thirteenth A fourteenth B ninth C eleventh 3 nineteenth, twentieth, A twenty-first B twentieth-one C thirty-first 4 January, February, A May B April C March 5 October, November, A January B December August A July B September C October 7 My birthday’s June. A in B at Con 8 The party’s A in B at Con Saturday 3rd October. b Choose A, B, or C to complete the sentences. Example: Steve plays in a band A rock B band C reggae 9 Can you the phone? A speak B ask C answer III-My-school teacher.

Кыргыз тили
12 минут назад
43. Жөнөкөй толуктоочторду бөлүп көрсөткүлө. СИЛЕР БИЛЕСИНЕРБИ? А. С. Пушкин 20 жашында «Руслан менен Людмила» поэмасын жаз- ган. Ал эми М. А. Шолохов 23 жашында атактуу «Тынч Дон» романынын биринчи китебин жазып бүтүргөн. К. Маркс 29 жашында, ал эми Ф. Энгельс 27 жашында «Коммунисттик партиянын манифестин» жазган. Ф. Энгельс 18 жашында латын, эски грек, англис, италия, испан, португал, француз, голланд жана немис тилдерин билген. Ф. Энгельс 68 жашында румын, норвег тилдерин үйрөнгөн. Бардыгы болуп 20дан ашык тил билген.
Ф. Энгельс 68 жашында румын, норвег тилдерин үйрөнгөн. Бардыгы болуп 20дан ашык тил билген.Математика
12 минут назад
Из школы домой Айдос пришел в 2 ч дня. Саша пришел на 10 мин раньше, а Валя пришла на 0,5 ч позже Айдоса. Какое время пока- когда пришла зывали часы, когда пришел домой Саша, а какое Валя? использую — + пример: -18, +1, т.д.
Все предметы
Выберите язык и регион
Русский
Россия
English
How much to ban the user?
1 hour 1 day
Уравнение оси y. Напишите уравнение движения твердого тела вокруг неподвижной оси
1.AB=2j-3j. 2 — 5х +6.
2 — 5х +6.
Помогите Пожалуйста с вопросами по геометрии(9 класс)! 1)Сформулируйте и докажите лемму о коллинеарных векторах. 2)Что значит разложить вектор по двум
данным векторам. 3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам. 4)Объясните, как вводится прямоугольная системы координат. 5)Что такое координатные векторы? 6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам. 7)Что такое координаты вектора? 8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.9)Что такое радиус-вектора точки?Докажите, что координаты точки равны соответствующим координатам векторов. 10)Выведите формулы для вычисления координат вектора по координатам его начала и конца. 11)Выведите формулы для вычисления координат вектора по координатам его концов. 12) Выведите формулу для вычисления длины вектора по его координатам.
1)Сформулируйте и докажите лемму о коллинеарных векторах.
2)Что значит разложить вектор по двум данным векторам.
3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4)Объясните, как вводится прямоугольная системы координат.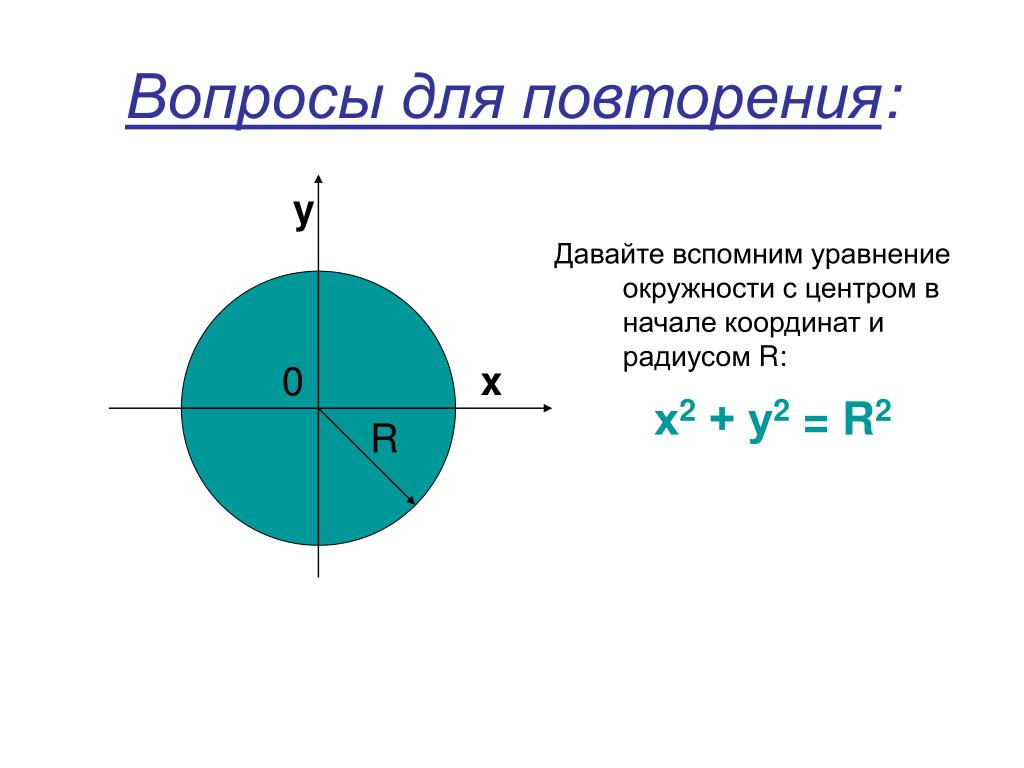
5)Что такое координатные векторы?
6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
7)Что такое координаты вектора?
8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
9)Что такое радиус-вектора точки? Докажите, что координаты точки равны соответствующим координатам векторов.
10)Выведите формулы для вычисления координат вектора по координатам его начала и конца.
12) Выведите формулу для вычисления длины вектора по его координатам.
13)Выведите формулу для вычисления расстояния между двумя точками по их координатам.
14)Приведите пример решения геометрической задачи с применением метода координат.
15)Какое уравнение называется уравнением данной линии? Приведите пример.
16)Выведите уравнение окружности данного радиуса с центром в данной точке.
17)Напишите уравнение окружности данного радиуса с центром в начале координат.
18)Выведите уравнение данной прямой в прямоугольной системе координат.
19)Напишите уравнение прямых, проходящих через данную точку M0 (X0: Y0) и параллельных осям координат.
20)Напишите уравнение осей координат.
21)Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.
Пожалуйста очень надо! Желательно с рисунками(где надо)!
ОПРЕДЕЛЕНИЕ СКОРОСТИ МОНТАЖНОГО ПАТРОНА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО КРУТИЛЬНОГО МАЯТНИКА
Цель работы: изучение законов сохранения на примере баллистического крутильного маятника.
Приборы и принадлежности: баллистический крутильный маятник, комплект монтажных патронов, блок миллисекундомера.
Описание экспериментальной установки
Общий вид баллистического маятника показан на рисунке. Основание 1 оснащено регулируемыми ножками 2 , позволяющими выровнять прибор. В основании закреплена колонка 3 , на которой закреплены верхний 4 , нижний 5 и средний 6 кронштейны. К среднему кронштейну прикреплено стреляющее устройство 7 , а также прозрачный экран, с нанесенной на него угловой шкалой 8 и фотоэлектрический датчик 9 . Кронштейны 4 и 5 имеют зажимы для крепления стальной проволоки 10 , на которой подвешен маятник, состоящий из двух мисочек, наполненных пластилином 11 , двух перемещаемых грузов 12 , двух стержней 13 , водилки 14 .
В основании закреплена колонка 3 , на которой закреплены верхний 4 , нижний 5 и средний 6 кронштейны. К среднему кронштейну прикреплено стреляющее устройство 7 , а также прозрачный экран, с нанесенной на него угловой шкалой 8 и фотоэлектрический датчик 9 . Кронштейны 4 и 5 имеют зажимы для крепления стальной проволоки 10 , на которой подвешен маятник, состоящий из двух мисочек, наполненных пластилином 11 , двух перемещаемых грузов 12 , двух стержней 13 , водилки 14 .
Порядок выполнения работы
1. Сняв прозрачный экран, установить грузы на расстоянии r1 от оси вращения.
3. Вложить патрон в пружинное устройство.
4. Вытолкнуть патрон из пружинного устройства.
6. Включить счетчик времени (на панели индикаторы измерителя высвечивают «0»).
7. Отклонить маятник на угол φ1, и затем пустить его.
8. Нажать кнопку «СТОП», когда счетчик покажет девять колебаний, записать время десяти полных колебаний t1. Вычислить период колебаний Т1. Данные занести в таблицу №1, пункты 7,8 повторить еще четыре раза.
Вычислить период колебаний Т1. Данные занести в таблицу №1, пункты 7,8 повторить еще четыре раза.
9. Установить грузы на расстоянии r2. Выполнить пункты 2-8 для расстояний r2.
10. Вычислить по формуле скорость для пяти измерений:
11. Оценить абсолютную погрешность вычисления скорости по разбору пяти значений скорости (табл. №1).
r = 0,12 м, m = 3,5 г., М = 0,193 кг.
Таблица №1
| № опыта | r1 = 0,09 м | r2 = 0,02 м | |||||||
| φ1 | t1 | Т1 | φ2 | t2 | Т2 | V | |||
| град. | рад. | с | град. | рад. | с | м/с | |||
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
4. | |||||||||
| 5. |
Расчетная часть
Контрольные вопросы
Сформулируйте закон сохранения момента импульса.
Момент импульса системы «патрон-маятник» относительно оси сохраняется:
Сформулируйте закон сохранения энергии.
При колебании маятника кинетическая энергия вращательного движения системы превращается в потенциальную упругодеформированной проволоки при кручении:
Напишите уравнение движения твердого тела вокруг неподвижной оси
4. Что такое крутильный маятник и как определяется период его колебаний?
Крутильный маятник представляет собой массивный стальной стержень, жестко прикрепленный к вертикальной проволоке. На концах стержня закреплены мисочки с пластилином, который позволяет патрону «прилипать» к маятнику. Также на стержне имеются два одинаковых груза, которые могут перемещаться по стержню относительно его оси вращения. Это дает возможность менять момент инерции маятника. С маятником жестко закреплена «водилка», позволяющая фотоэлектрическим датчикам отсчитывать число его полных колебаний. Крутильные колебания обусловлены упругими силами, возникающими в проволоке при ее кручении. При этом период колебаний маятника:
Также на стержне имеются два одинаковых груза, которые могут перемещаться по стержню относительно его оси вращения. Это дает возможность менять момент инерции маятника. С маятником жестко закреплена «водилка», позволяющая фотоэлектрическим датчикам отсчитывать число его полных колебаний. Крутильные колебания обусловлены упругими силами, возникающими в проволоке при ее кручении. При этом период колебаний маятника:
5. Как по-другому можно определить в данной работе скорость монтажного патрона?
Эта статья является частью темы уравнение прямой на плоскости . Здесь мы разберем со всех сторон: начнем с доказательства теоремы, которая задает вид общего уравнения прямой, далее рассмотрим неполное общее уравнение прямой, приведем примеры неполных уравнений прямой с графическими иллюстрациями, в заключении остановимся на переходе от общего уравнения прямой к другим видам уравнения этой прямой и приведем подробные решения характерных задач на составление общего уравнения прямой.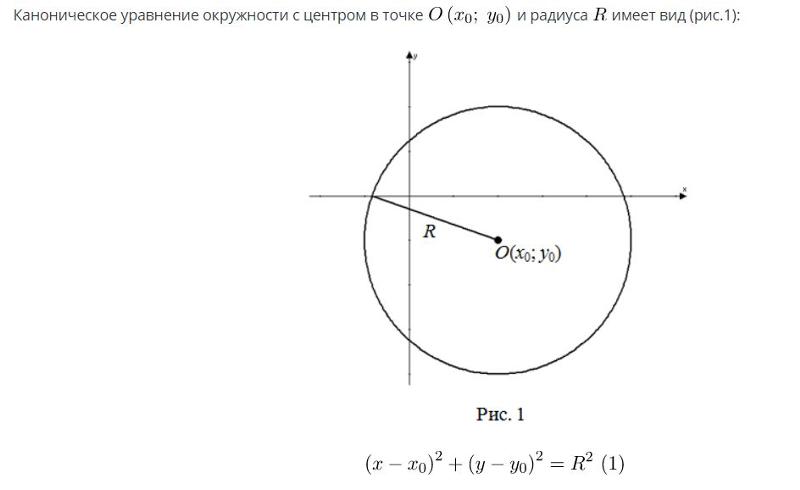
Навигация по странице.
Разберем этот алгоритм при решении примера.
Пример.
Напишите параметрические уравнения прямой, которая задана общим уравнение прямой .
Решение.
Сначала приведем исходное общее уравнение прямой к каноническому уравнению прямой:
Теперь принимаем левую и правую части полученного уравнения равными параметру . Имеем
Ответ:
Из общего уравнения прямой вида получить уравнение прямой с угловым коэффициентом возможно лишь тогда, когда . Что нужно сделать для перехода? Во-первых, в левой общего уравнения прямой оставить только слагаемое , остальные слагаемые нужно перенести в правую часть с противоположным знаком: . Во-вторых, разделить обе части полученного равенства на число B , которое отлично от нуля, . И все.
Пример.
Прямую в прямоугольной системе координат Oxy задает общее уравнение прямой . Получите уравнение этой прямой с угловым коэффициентом.
Решение.
Проведем необходимые действия: .
Ответ:
Когда прямая задана полным общим уравнением прямой, то легко получить уравнение прямой в отрезках вида . Для этого переносим число С
в правую часть равенства с противоположным знаком, делим обе части полученного равенства на –С
, и в заключении переносим в знаменатели коэффициенты при переменных x
и y
:
Уравнение линии. Определение уравнения линии, примеры линии на плоскости Что называется уравнением линии
Давайте повторим * Какое уравнение называется квадратным? * Какие уравнения называются неполными квадратными уравнениями? * Какое квадратное уравнение называется приведенным? * Что называют корнем квадратного уравнения? * Что значит решить квадратное уравнение? Какое уравнение называется квадратным? Какие уравнения называются неполными квадратными уравнениями? Какое квадратное уравнение называется приведенным? Что называют корнем квадратного уравнения? Что значит решить квадратное уравнение? Какое уравнение называется квадратным? Какие уравнения называются неполными квадратными уравнениями? Какое квадратное уравнение называется приведенным? Что называют корнем квадратного уравнения? Что значит решить квадратное уравнение?
Алгоритм решения квадратного уравнения: 1. Опредилить каким способом рациональней решить квадратное уравнение 2. Выбрать наиболее рациональный способ решения 3. Определение количества корней квадратного уравнения 4. Нахождение корней квадратного уравнения Для лучшего запоминания заполним таблицу… Для лучшего запоминания заполним таблицу… Для лучшего запоминания заполним таблицу…
Опредилить каким способом рациональней решить квадратное уравнение 2. Выбрать наиболее рациональный способ решения 3. Определение количества корней квадратного уравнения 4. Нахождение корней квадратного уравнения Для лучшего запоминания заполним таблицу… Для лучшего запоминания заполним таблицу… Для лучшего запоминания заполним таблицу…
Дополнительное условие Уравнение Корни Примеры 1. в = с = 0, а 0 ах 2 = 0 х 1 = 0 2. с = 0, а 0, в 0 ах 2 + bх = 0 х 1 = 0, х 2 =-b/а 3. в = 0, а 0, в 0 ах 2 + с = 0 а) х 1,2 = ±(c/а), где с/а 0. б) если с/а 0, то решений нет 4. а 0 ах 2 + bх + с = 0 x 1,2 =(-b±D)/2 а, где D = в 2 – 4 ас, D0 5. в – четное число (в = 2k), а 0, в 0, с 0 ах 2 + 2kx + c = 0 х 1,2 =(-b±D)/а, D 1 = k 2 – ac, где k = 6. Теорема обратная теореме Виета x 2 + px + q = 0x 1 + x 2 = — p x 1 x 2 = q
II. Специальные методы 7. Метод выделения квадрата двучлена. Цель: Привести уравнение общего вида к неполному квадратному уравнению.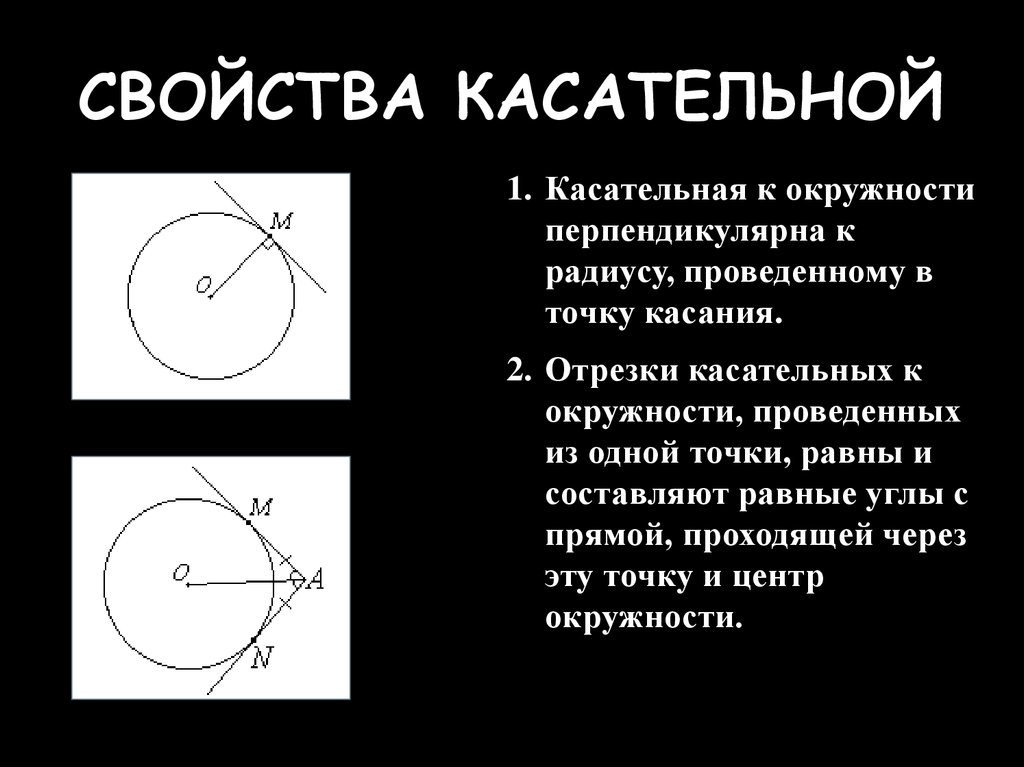 Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения. Пример: решите уравнение х 2 -6 х+8=0 8. Метод «переброски» старшего коэффициента. Корни квадратных уравнений ax 2 + bx + c = 0 и y 2 +by+ac=0 связаны соотношениями: и Замечание: метод хорош для квадратных уравнений с «удобными» коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно. Пример: решите уравнение 2 х 2 -9 х-5=0 На основании теорем:Пример: решите уравнение 157 х х-177=0 9. Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета равен с /а 10. Если в квадратном уравнении a+c=b, то один из корней равен -1, а второй по теореме Виета равен –с/а Пример: решите уравнение 203 х х+17=0 х 1 =у 1 /а, х 2 =у 2 /а
Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения. Пример: решите уравнение х 2 -6 х+8=0 8. Метод «переброски» старшего коэффициента. Корни квадратных уравнений ax 2 + bx + c = 0 и y 2 +by+ac=0 связаны соотношениями: и Замечание: метод хорош для квадратных уравнений с «удобными» коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно. Пример: решите уравнение 2 х 2 -9 х-5=0 На основании теорем:Пример: решите уравнение 157 х х-177=0 9. Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета равен с /а 10. Если в квадратном уравнении a+c=b, то один из корней равен -1, а второй по теореме Виета равен –с/а Пример: решите уравнение 203 х х+17=0 х 1 =у 1 /а, х 2 =у 2 /а
III. Общие методы решения уравнений 11. Метод разложения на множители. Цель: Привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х) – многочлены относительно х.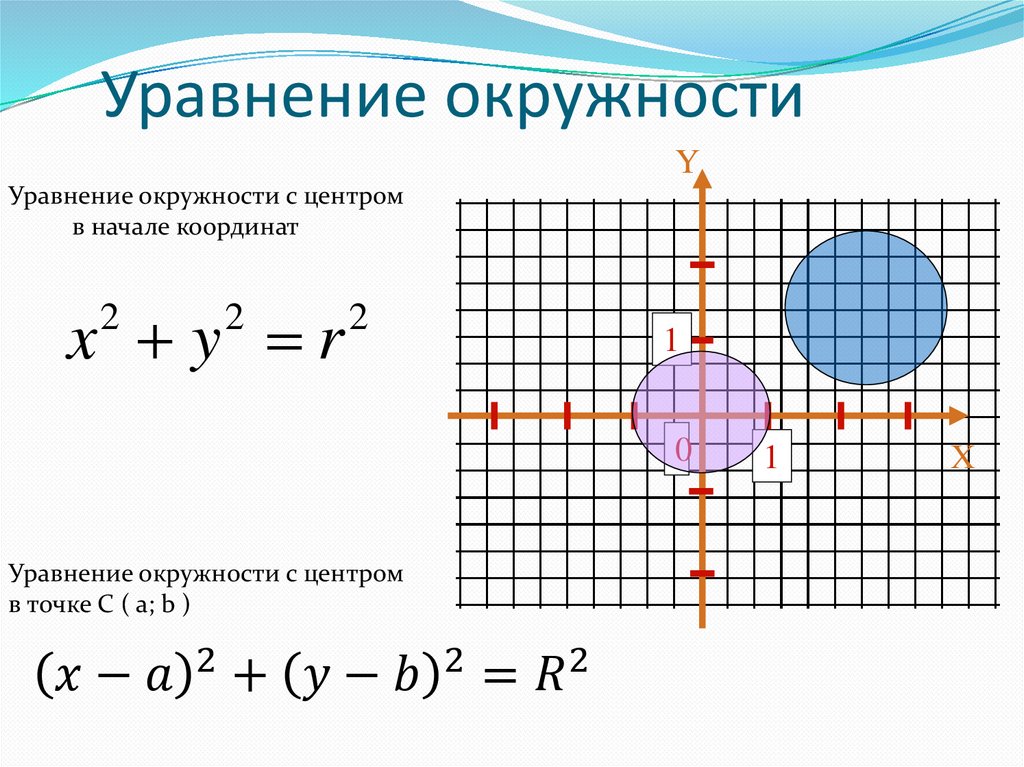 Способы: Вынесение общего множителя за скобки; Использование формул сокращенного умножения; Способ группировки. Пример: решите уравнение 3 х 2 +2 х-1=0 12. Метод введения новой переменной. Удачный выбор новой переменной делает структуру уравнения более прозрачной Пример: решите уравнение (х 2 +3 х-25) 2 -6(х 2 +3 х-25)= — 8
Способы: Вынесение общего множителя за скобки; Использование формул сокращенного умножения; Способ группировки. Пример: решите уравнение 3 х 2 +2 х-1=0 12. Метод введения новой переменной. Удачный выбор новой переменной делает структуру уравнения более прозрачной Пример: решите уравнение (х 2 +3 х-25) 2 -6(х 2 +3 х-25)= — 8
Скачать с Depositfiles
Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
1.1. Линии и их уравнения в декартовой системе координат
В аналитической геометрии линии на плоскости рассматриваются как геометрическое место точек (г.м.т.), обладающих одинаковым свойством, общим для всех точек линии.
Определение.
Уравнение линии
– это уравнение с двумя переменными х и у , которому удовлетворяют координаты любой точки линии и не удовлетворяют координаты никакой другой точки, не лежащей на данной линии.
Верно и обратное, т.е. любое уравнение у
вида , вообще говоря, в декартовой
системе координат (ДСК) определяет линию
как г. м.т., координаты которых удовлетворяют
м.т., координаты которых удовлетворяют
этому уравнению. О х
Замечание 1.
Не всякое уравнение вида определяет линию. Например, для уравнения
не существует точек, координаты, которых удовлетворяли бы этому уравнению. Такие случаи в дальнейшем рассматривать не будем.
Это случай так называемых мнимых линий.
Пример 1.
Составить уравнение окружности радиуса R с центром в точке
.
Для любой точки , лежащей у М
на окружности, в силу определения R
окружности как г.м.т., равноудаленных
от точки , получаем уравнение х
1.2. Параметрические уравнения линий
Существует ещё один способ задавать линию на плоскости при помощи уравнений, которые называются параметрическими :
Пример 1.
Линия задана параметрическими уравнениями
Требуется получить уравнение этой линии в ДСК.
Исключим параметр t . Для этого возведём обе части этих уравнений в квадрат и сложим
Пример 2. Линия задана параметрическими уравнениями
Линия задана параметрическими уравнениями
а
Требуется получить уравнение
этой линии в ДСК. — а а
Поступим аналогично, тогда получим
— а
Замечание 2. Следует отметить, что параметром t в механике явля-ется время.
1.3. Уравнение линии в полярной системе координат
ДСК является не единственным способом определять положение точки и, следовательно, задавать уравнение линии. На плоскости часто целесо-образно использовать так называемую полярную систему координат (ПСК).
ПСК будет определена, если задать точку
О – полюс и луч
ОР, исхо-дящий из этой точки, который называется полярной осью. Тогда положение любой точки определяется двумя числами: полярным радиусом
и полярным углом – угол между
полярной осью и полярным радиусом.
Положительное направление отсчета
полярного угла от полярной оси
считается против часовой стрелки.
Для всех точек плоскости
,
О Р
а для однозначности полярного угла считается
.
Если начало ДСК совместить с
полюсом, а ось Ох направить по
полярной оси, то легко убедиться у
в связи между полярными и
декартовыми координатами:
О х Р
Обратно,
(1)
Если уравнение линии в ДСК имеет вид , то в ПСК — Тогда из этого уравнения можно получить урав-нение в виде
Пример 3. Составить уравнение окружности в ПСК, если центр окружности находится в полюсе.
Используя формулы перехода (1) от ДСК к ПСК, получим
Пример 4. Составить уравнение окружности,
если полюс на окружности, а полярная ось у
проходит через диаметр.
Поступим аналогично
О 2 R х
R
Данное уравнение можно получить и
из геометрических представлений (см. рис.).
Пример 5. Построить график линии
Перейдём к ПСК. Уравнение
примет вид
О
График линии построим с а
учётом его симметрии и ОДЗ
функции:
Данная линия называется
лемнискатой Бернулли
.
1.4. Преобразование системы координат.
Уравнение линии в новой системе координат
1. Параллельный перенос ДСК. у
Рассмотрим две ДСК, имеющие М
одинаковое направление осей, но
различные начала координат.
В системе координат Оху точка
относительно системы
О х
имеет координаты
. Тогда имеем
и
В координатной форме полученное векторное равенство имеет вид
или
. (2)
Формулы (2) представляют собой формулы перехода от «старой» системы координат Оху к «новой» системе координат и наоборот.
Пример 5. Получить уравнение окружности выполнив параллельный перенос системы координат в центр окружности.
Из формул (2) следует
у О
Решение уравнения
Иллюстрация графического метода нахождения корней уравнения
Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).
На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).
При подстановке другого корня получается неправильное утверждение:
.
Таким образом, второй корень нужно отбросить, как посторонний.
Виды уравнений
Различают алгебраические , параметрические , трансцендентные , функциональные , дифференциальные и другие виды уравнений.
Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.
К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение , квадратное уравнение , кубическое уравнение и уравнение четвёртой степени . Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.
Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.
Уравнение, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.
В общем случае, когда аналитического решения найти не удается, применяют численные методы . Численные методы не дают точного решения, а только позволяют сузить интервал , в котором лежит корень, до определенного заранее заданного значения.
Примеры уравнений
См. также
Литература
- Бекаревич, А. Б. Уравнения в школьном курсе математики / А. Б. Бекаревич. — М., 1968.
- Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.
- Каплан Я. В. Рівняння.
 — Киев: Радянська школа, 1968.
— Киев: Радянська школа, 1968. - Уравнение — статья из Большой советской энциклопедии
- Уравнения // Энциклопедия Кольера. — Открытое общество. 2000.
- Уравнение // Энциклопедия Кругосвет
- Уравнение // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977-1985.
Ссылки
- EqWorld — Мир математических уравнений — содержит обширную информацию о математических уравнениях и системах уравнений.
Wikimedia Foundation . 2010 .
Синонимы :
Антонимы :
- Хаджимба, Рауль Джумкович
- ЕС ЭВМ
Смотреть что такое «Уравнение» в других словарях:
УРАВНЕНИЕ — (1) математическая запись задачи о разыскании таких значений аргументов (см. (2)), при которых значения двух данных (см.) равны. Аргументы, от которых зависят эти функции, называют неизвестными, а значения неизвестных, при которых значения… … Большая политехническая энциклопедия
УРАВНЕНИЕ — УРАВНЕНИЕ, уравнения, ср. 1. Действие по гл. уравнять уравнивать и состояние по гл. уравняться уравниваться. Уравнение в правах. Уравнение времени (перевод истинного солнечного времени в среднее солнечное время, принятое в общежитии и в науке;… … Толковый словарь Ушакова
1. Действие по гл. уравнять уравнивать и состояние по гл. уравняться уравниваться. Уравнение в правах. Уравнение времени (перевод истинного солнечного времени в среднее солнечное время, принятое в общежитии и в науке;… … Толковый словарь Ушакова
УРАВНЕНИЕ — (equation) Требование того, чтобы математическое выражение принимало определенное значение. Например, квадратное уравнение записывается в виде: ах2+bх+с=0. Решением является такие значения х, при котором данное уравнение становится тождеством. В… … Экономический словарь
УРАВНЕНИЕ — математическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются неизвестными, а значения неизвестных, при которых значения функций равны,… … Большой Энциклопедический словарь
УРАВНЕНИЕ — УРАВНЕНИЕ, два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными. Решить уравнение значит найти все значения неизвестных, при которых оно обращается в тождество, или установить … Современная энциклопедия
Решить уравнение значит найти все значения неизвестных, при которых оно обращается в тождество, или установить … Современная энциклопедия
1. Какое утверждение называется следствием? Докажите, что прямая, пересекающая одну из двух параллельных прямых, пересекает и другую.2.Докажите, что ес
ли две прямые параллельны третьей прямой, то они параллельны.3. Какая теорема называется обратной данной теореме?Приведите примеры теорем, обратных данным.4.Докажите, что при пересечении двух параллельных прямых секущей накрест лежащие углы равны.5.Докажите, что если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.6.Докажите, что при пересечении двух параллельных прямых секущей: а) соответственные углы равны; б) сумма односторонних углов равна 180°.
Помогите Пожалуйста с вопросами по геометрии(9 класс)! 2)Что значит разложить вектор по двум
данным векторам. 9)Что такое радиус-вектора точки?Докажите, что координаты точки равны соответствующим координатам векторов. 10)Выведите формулы для вычисления координат вектора по координатам его начала и конца. 11)Выведите формулы для вычисления координат вектора по координатам его концов. 12) Выведите формулу для вычисления длины вектора по его координатам. 13)Выведите формулу для вычисления расстояния между двумя точками по их координатам. 15)Какое уравнение называется уравнением данной линии?Приведите пример. 16)Выведите уравнение окружности данного радиуса с центром в данной точке.
9)Что такое радиус-вектора точки?Докажите, что координаты точки равны соответствующим координатам векторов. 10)Выведите формулы для вычисления координат вектора по координатам его начала и конца. 11)Выведите формулы для вычисления координат вектора по координатам его концов. 12) Выведите формулу для вычисления длины вектора по его координатам. 13)Выведите формулу для вычисления расстояния между двумя точками по их координатам. 15)Какое уравнение называется уравнением данной линии?Приведите пример. 16)Выведите уравнение окружности данного радиуса с центром в данной точке.
1)Сформулируйте и докажите лемму о коллинеарных векторах.
3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4)Объясните, как вводится прямоугольная системы координат.
5)Что такое координатные векторы?
6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
7)Что такое координаты вектора?
8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
10)Выведите формулы для вычисления координат вектора по координатам его начала и конца.
11)Выведите формулы для вычисления координат вектора по координатам его концов.
12) Выведите формулу для вычисления длины вектора по его координатам.
13)Выведите формулу для вычисления расстояния между двумя точками по их координатам.
14)Приведите пример решения геометрической задачи с применением метода координат.
16)Выведите уравнение окружности данного радиуса с центром в данной точке.
17)Напишите уравнение окружности данного радиуса с центром в начале координат.
18)Выведите уравнение данной прямой в прямоугольной системе координат.
19)Напишите уравнение прямых, проходящих через данную точку M0 (X0: Y0) и параллельных осям координат.
20)Напишите уравнение осей координат.
21)Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.
Пожалуйста очень надо! Желательно с рисунками(где надо)!
ГЕОМЕТРИЯ 9 КЛАСС.
1)Сформулируйте и докажите лемму о коллинеарных векторах.
2)Что значит разложить вектор по двум данным векторам.
3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4)Объясните, как вводится прямоугольная системы координат.
5)Что такое координатные векторы?
6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
7)Что такое координаты вектора?
8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
9)Что такое радиус-вектора точки? Докажите, что координаты точки равны соответствующим координатам векторов.
14)Приведите пример решения геометрической задачи с применением метода координат.
15)Какое уравнение называется уравнением данной линии? Приведите пример.
17)Напишите уравнение окружности данного радиуса с центром в начале координат.
18)Выведите уравнение данной прямой в прямоугольной системе координат.
19)Напишите уравнение прямых, проходящих через данную точку M0 (X0: Y0) и параллельных осям координат.
20)Напишите уравнение осей координат.
21)Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.
Линию на плоскости можно задать при помощи двух уравнений
где х и у — координаты произвольной точки М (х ; у ), лежащей на данной линии, а t — переменная, называемая параметром .
Параметр t определяет положение точки (х ; у ) на плоскости.
Так, если
то значению параметра t = 2 соответствует на плоскости точка (4; 1), т.к. х = 2 + 2 = 4, y = 2 · 2 – 3 = 1.
Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания кривой называется параметрическим , а уравнения (1) — параметрическими уравнениями линии .
Рассмотрим примерыизвестных кривых, заданных в параметрическом виде.
1) Астроида:
где а > 0 – постоянная величина.
При а = 2 имеет вид:
Рис.4. Астроида
2) Циклоида: где а > 0 – постоянная.
При а = 2 имеет вид:
Рис.5. Циклоида
Векторное уравнение линии
Линию на плоскости можно задать векторным уравнением
где t – скалярный переменный параметр.
Каждому значению параметра t 0 соответствует определённый вектор плоскости. При изменении параметра t конец вектора опишет некоторую линию (рис. 6).
Векторному уравнению линии в системе координат Оху
соответствуют два скалярных уравнения (4), т.е. уравнения проекций
на оси координат векторного уравнения линии есть её параметрические уравнения.
| |
Рис.6. Векторное уравнение линии
Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения , линия – траекторией точки, параметр t — время .
Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения , линия – траекторией точки, параметр t — время .
6.4.1: Окружности с центром в начале координат
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14764
Окружности с центром в начале координат
Вы рисуете круг с центром в начале координат. Вы измеряете диаметр круга должен быть 32 ед. Точка \(\ (14,8)\) лежит на окружности?
Круги с центром в начале координат
До сих пор вы только ссылались на круги из геометрии. Окружность — это множество точек, которые равноудалены ( радиус ) от заданной точки ( центр ). Отрезок линии, который проходит через центр и имеет конечные точки на окружности, имеет диаметр .
Отрезок линии, который проходит через центр и имеет конечные точки на окружности, имеет диаметр .
Теперь мы возьмем круг и поместим его на плоскость x-y, чтобы посмотреть, сможем ли мы найти его уравнение. В этой концепции мы собираемся поместить центр круга в начало координат.
Нахождение уравнения окружности
Шаг 1: На листе миллиметровой бумаги начертите плоскость x-y. Используя циркуль, нарисуйте окружность с центром в начале координат и радиусом 5. Найдите точку (3,4) на окружности и нарисуйте прямоугольный треугольник с радиусом в качестве гипотенузы.
Шаг 2: Используя длину каждой стороны прямоугольного треугольника, докажите, что теорема Пифагора верна. 9{2} &=225 \\
81+121 & \stackrel{?}{=} 225 \\
202 & \neq 225
\end{выровнено}\)
Точка не на окружности.
Примеры
Пример 1
Ранее вас попросили определить, лежит ли точка (14 ,8) на окружности с центром в начале координат и диаметром 32 единицы.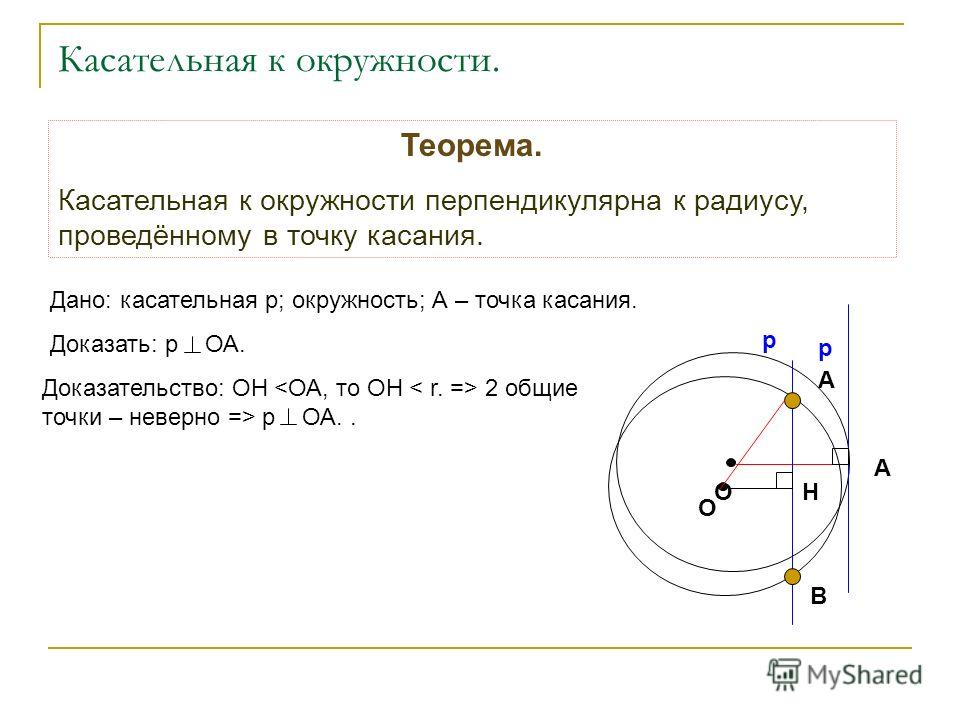 {2}=74\). 9{2}=34\) с точкой касания \(\ (3,5)\).
{2}=74\). 9{2}=34\) с точкой касания \(\ (3,5)\).
Ответы на проблемы с обзором
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 10.3.
Словарь
| Срок | Определение |
|---|---|
| центр | Центр круга — это точка, определяющая положение круга. Все точки окружности равноудалены от центра окружности. |
| Круг | Окружность — это набор всех точек на определенном расстоянии от данной точки в двух измерениях. |
| Диаметр | Диаметр — это мера расстояния через центр окружности. Диаметр равен удвоенной мере радиуса. |
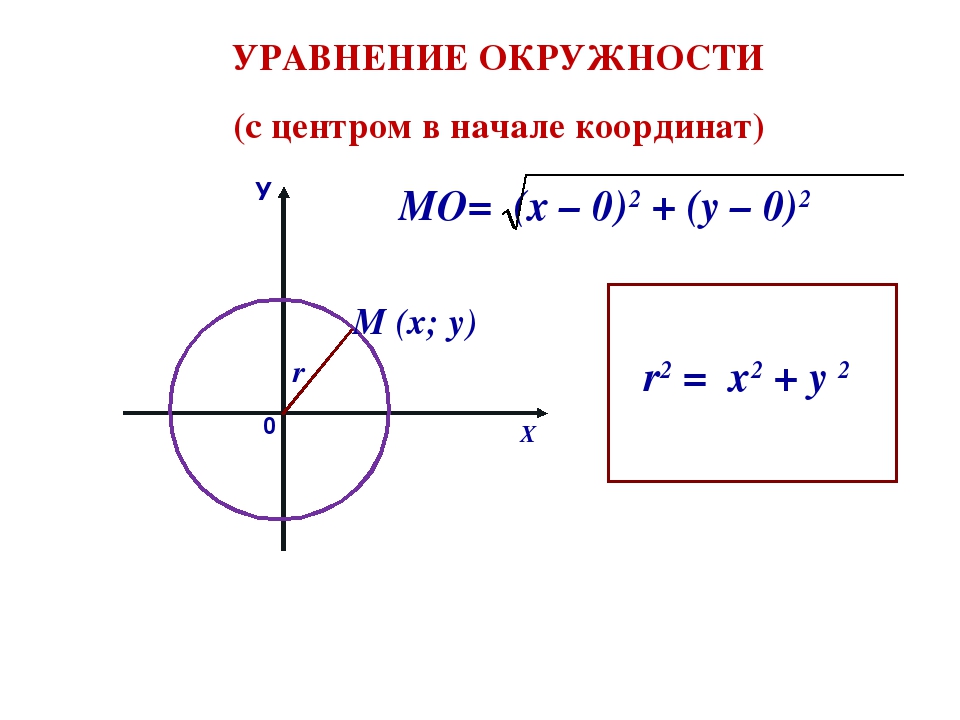
| Уравнение окружности | Если центр окружности равен (0, 0), то уравнение окружности имеет вид \(\ x^{2}+y^{2}=r^{2}\), где \( \r\) — радиус. |
| Радиус | Радиус круга — это расстояние от центра круга до края круга. |
Атрибуции изображений
- [Рисунок 1]
Кредит: Тони Вебстер; Роберт Пернетт
Source: Htttps.gmonlys/° С.Г. 20216869960).jpg;https://flic.kr/p/nQD1fo
Эта страница под названием 6.4.1: Circles Centered at the Origin распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Теги
- источник@https://www.
 ck12.org/c/analysis
ck12.org/c/analysis
- источник@https://www.
Как начертить круг
Начертить круг
Начертить круги требуется две вещи: координаты центральной точки и радиус круга. Окружность – это множество всех точек, находящихся на одинаковом расстоянии от данной точки, центра окружности. Радиус r — это расстояние от этой центральной точки до самой окружности.
На графике все эти точки на окружности могут быть определены и нанесены на график с использованием координат (x, y).
Содержание
- Рисование круга
- Уравнения окружности
- Форма центр-радиус
- Стандартное уравнение окружности
- Использование формы центр-радиус
- Как построить уравнение окружности
- Как нарисовать круг, используя стандартную форму
Уравнения окружности
Два выражения показывают, как построить окружность: центр-радиус формы и стандартная форма . Где x и y — координаты всех точек окружности, h и k — значения x и y центральной точки, а r — радиус окружности.
Где x и y — координаты всех точек окружности, h и k — значения x и y центральной точки, а r — радиус окружности.
x — h3 + y — k2 = r2
Стандартное уравнение окружности
Стандартная, или общая, форма требует немного больше усилий, чем форма центр-радиус, для получения и построения графика. Уравнение стандартной формы выглядит так:
x2 + y2 + Dx + Ey + F = 0
В общем виде D, E и F — заданные значения, подобные целым числам, которые являются коэффициентами значений x и y.
Использование формы «Центр-радиус»
Если вы не уверены, что предполагаемая формула является уравнением, необходимым для построения круга, вы можете проверить ее. Он должен иметь четыре атрибута:
- Члены x и y должны быть возведены в квадрат
- Все элементы в выражении должны быть положительными (что достигается возведением в квадрат значений в скобках)
- Центральная точка задается как (h, k), координаты x и y
- Значение r, радиуса, должно быть задано и должно быть положительным числом (что имеет здравый смысл, у вас не может быть отрицательной меры радиуса)
Форма с центральным радиусом дает тренированному глазу много информации. Группируя значение h с x x – h3, форма сообщает вам координату x центра круга. То же самое относится и к значению k; это должна быть координата y для центра вашего круга.
Группируя значение h с x x – h3, форма сообщает вам координату x центра круга. То же самое относится и к значению k; это должна быть координата y для центра вашего круга.
После того, как вы узнали координаты центральной точки круга, вы можете определить радиус круга, r. В уравнении вы можете увидеть не r2, а число, квадратный корень из которого и есть фактический радиус. Если повезет, квадрат значения r будет целым числом, но вы все равно можете найти квадратный корень из десятичных дробей с помощью калькулятора.
Какие центрально-радиальные формы?
Попробуйте эти семь уравнений, чтобы узнать, сможете ли вы распознать форму центра и радиуса. Какие из них являются уравнениями центра и радиуса, а какие просто уравнениями линий или кривых?
- х — 22 + у — 32 = 16
- 5x + 3y = 6
- х + 12 + у + 12 = 25
- г = 6x + 2
- х + 42 + у — 62 = 49
- х — 52 + у + 92 = 8,1
- г = x2 + -6x + 3
Только уравнения 1, 3, 5 и 6 являются формами центр-радиус. Второе уравнение изображает прямую линию; четвертое уравнение представляет собой известную форму пересечения наклона; последнее уравнение изображает параболу.
Второе уравнение изображает прямую линию; четвертое уравнение представляет собой известную форму пересечения наклона; последнее уравнение изображает параболу.
Как нарисовать уравнение окружности
Окружность можно рассматривать как нарисованную линию, которая изгибается по своим значениям x и y. Это может показаться очевидным, но рассмотрим следующее уравнение:
y = x2 + 4
Здесь только значение x возводится в квадрат, что означает, что мы получим кривую, но только кривую, идущую вверх и вниз, а не замыкающуюся на себя. Мы получаем параболическую кривую, так что она проходит мимо вершины нашей сетки, два ее конца никогда не встречаются и не видны снова.
Введем вторую экспоненту x-значения, и мы получим более живые кривые, но они, опять же, не поворачиваются вспять.
Кривые могут извиваться вверх и вниз по оси Y по мере того, как линия перемещается по оси X, но линия на графике по-прежнему не возвращается сама на себя, как змея, кусающая себя за хвост.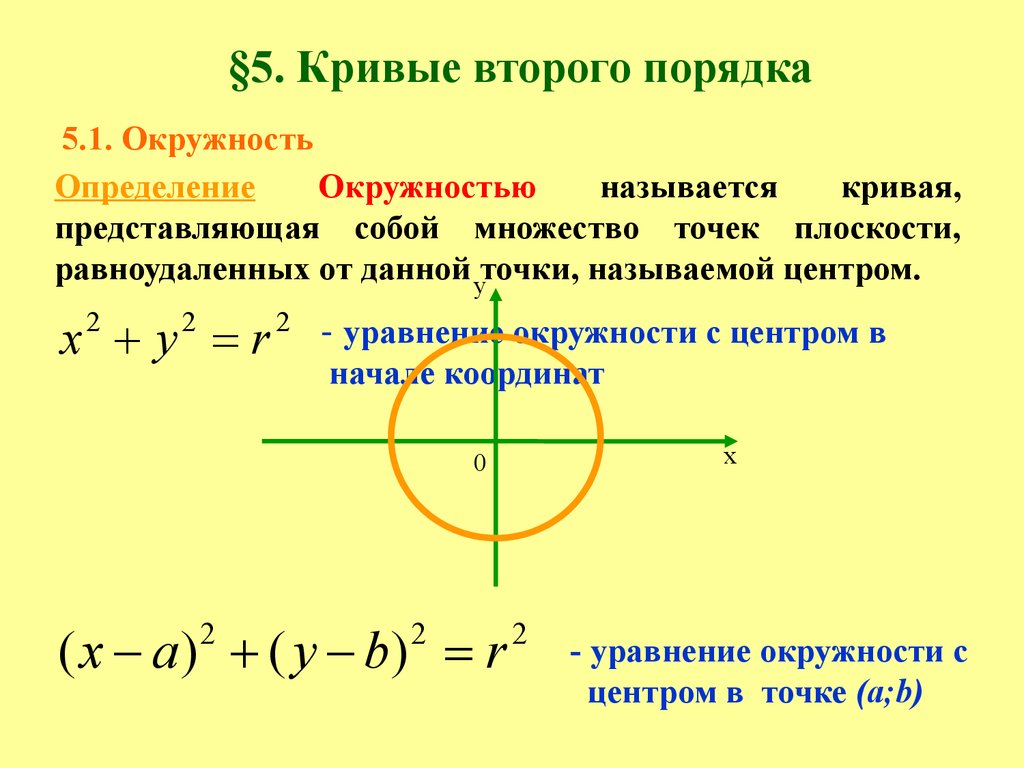
Чтобы кривая отображалась в виде круга, вам нужно изменить как , так и , показатель x, и , показатель y. Как только вы возьмете квадрат значений x и y, вы получите круг, возвращающийся к самому себе!
Часто форма центра-радиуса не содержит ссылок на такие единицы измерения, как мм, м, дюймы, футы или ярды. В этом случае просто используйте одиночные поля сетки при подсчете единиц радиуса.
Центр в начале координат
Когда центральной точкой является начало координат (0, 0) графика, форма центра-радиуса сильно упрощена:
x2 + y2 = r2
Например, круг с радиус 7 единиц и центр в точке (0, 0) выглядит следующим образом в виде формулы и графика:
x2 + y2 = 49
в стандартной форме
или общей форме вы должны сначала завершить квадрат, а затем обработать его в форме центра и радиуса. Предположим, у вас есть это уравнение:x2 + y2 — 8x + 6y — 4 = 0
Перепишите уравнение так, чтобы все x-члены были в первых скобках, а y-члены — во вторых:
x2 — 8x + ?1 + y2 + 6y + ?2 = 4 + ?1 + ?2
Вы изолировали константу справа и добавили значения ?1 и ?2 к обеим сторонам.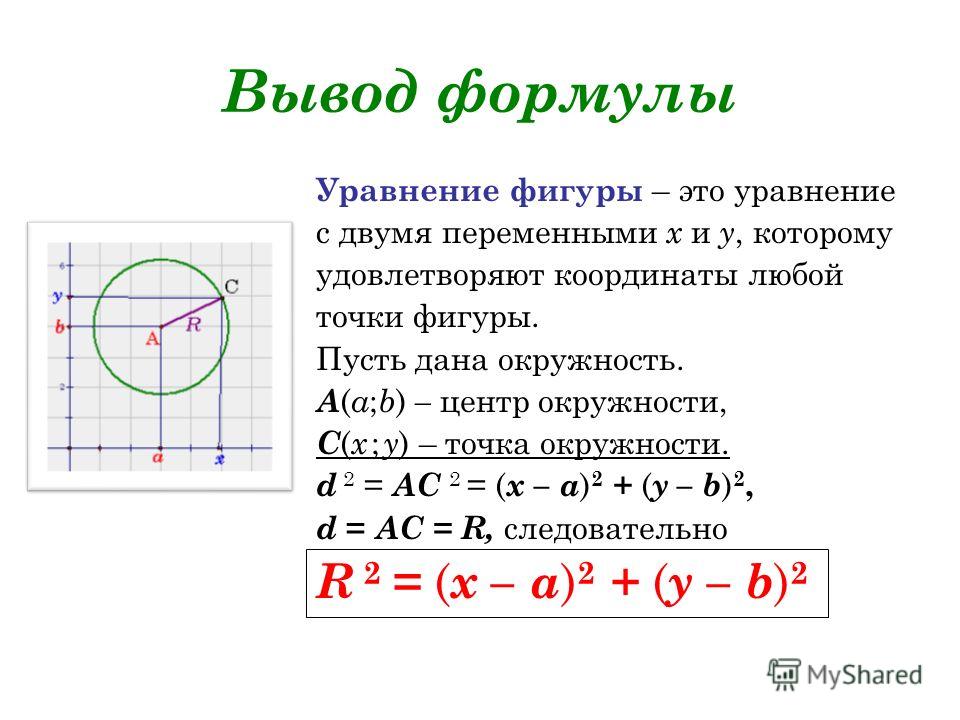 Значения ?1 и ?2 — это числа, которые вам нужны в каждой группе для завершения квадрата.
Значения ?1 и ?2 — это числа, которые вам нужны в каждой группе для завершения квадрата.
Возьмите коэффициент при x и разделите на 2. Возведите его в квадрат. Это ваше новое значение для ?1:
-82 = -4
-42 = 16
?1 = 16
Повторите это для значения, которое нужно найти с y-терминами:
62 = 3
2002 ? 9
Замените неизвестные значения ?1 и ?2 в уравнении новыми рассчитанными значениями:
x2 — 8x + 16 + y2 + 6y + 9 = 4 + 16 + 9
Упрощение:
x2
8x + 16 + y2 + 6y + 9 = 29
x — 42 + y + 32 = 29
Теперь у вас есть форма центра-радиуса для графика. Вы можете подставить значения, чтобы найти этот круг с центральной точкой -4, 3 и радиусом 5,385 единиц (квадратный корень из 29):
Предостережения, на которые следует обратить внимание
С практической точки зрения помните, что центральная точка, хотя и необходима, на самом деле не является частью круга. Итак, когда вы рисуете свой круг, очень легко отметьте центральную точку. Разместите легко подсчитываемые значения по осям x и y, просто посчитав длину радиуса по горизонтальной и вертикальной линиям.
Итак, когда вы рисуете свой круг, очень легко отметьте центральную точку. Разместите легко подсчитываемые значения по осям x и y, просто посчитав длину радиуса по горизонтальной и вертикальной линиям.
Если точность не важна, вы можете нарисовать остальную часть круга. Если точность имеет значение, используйте линейку, чтобы сделать дополнительные отметки, или чертежный циркуль, чтобы выполнить полный круг.
Не забывайте также о своих негативах. Внимательно следите за своими отрицательными значениями, помня, что, в конечном счете, все выражения должны быть положительными (поскольку ваши значения x и y возводятся в квадрат).
Следующий урок:
Завершение квадрата
Раздел 1.2: Круги | Предварительное исчисление
Результаты обучения
- Написать уравнение окружности в стандартной форме
- Нарисуйте круг
ОПРЕДЕЛЕНИЕ КРУГА
A окружность — это все точки плоскости, находящиеся на фиксированном расстоянии от данной точки плоскости. Данная точка называется центром, [латекс](h,k)[/латекс], а фиксированное расстояние называется радиусом , [латекс]r[/латекс] окружности.
Данная точка называется центром, [латекс](h,k)[/латекс], а фиксированное расстояние называется радиусом , [латекс]r[/латекс] окружности.
ВЫВОД СТАНДАРТНОЙ ФОРМЫ КРУГА
Чтобы вывести уравнение окружности, мы можем использовать формулу расстояния с точками [латекс](h,k)[/латекс], [латекс](х,у)[ /latex] и расстояние [latex]r[/latex].
9{2}+8y=0[/латекс].Показать решение
Пример 7: ПРИМЕНЕНИЕ ФОРМУЛ РАССТОЯНИЯ И СЕРЕДИНЫ К УРАВНЕНИЮ КРУГА
Диаметр окружности имеет конечные точки [латекс](-1,-4)[/латекс] и [латекс](7,2)[/латекс ]. Найдите центр и радиус круга, а также напишите уравнение стандартной формы.
Центром круга является центр или середина его диаметра. Таким образом, формула средней точки даст центральную точку.
[латекс]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_ {2}}{2}\справа)[/латекс] 9{2}=25[/latex]
Пример 8.
 Нахождение центра окружности
Нахождение центра окружностиДиаметр окружности имеет конечные точки [латекс]\влево(-1,-4\вправо)[/латекс ] и [латекс]\влево(5,-4\вправо)[/латекс]. Найдите центр круга.
Показать решение
Ключевые понятия
- Окружность — это все точки плоскости, находящиеся на фиксированном расстоянии от данной точки плоскости. Данная точка называется центром, а фиксированное расстояние называется радиусом. 9{2}[/латекс]
Раздел 1.2. Домашнее задание. Упражнения
Для следующих упражнений напишите стандартную форму уравнения окружности с заданным радиусом и центром [латекс](0,0)[/латекс].
1. Радиус: [латекс]7[/латекс]
2. Радиус: [латекс]9[/латекс]
3. Радиус: [латекс]\sqrt{2}[/латекс]
4. Радиус: [латекс]\sqrt{5}[/латекс]
В следующих упражнениях напишите стандартную форму уравнения окружности с заданными радиусом и центром.
5. Радиус: [латекс]1[/латекс], центр: [латекс](3,5)[/латекс]
6.

 C geting getting B get She doesn’t like Alive B liveing I don’t like A her B him C them The children are very quiet. I can’t hear A they B them C their very tired. alone. C living . I think she’s a terrible actress. A Do you want a mineral water? B No, thanks. I thirsty. A don’t have B haven’t C’m not Where the Red Hot Chili Peppers from? A are B do C come C September 6 June, VOCABULARY What is the missing word? Choose A, B, or C. Example: one, two, three, four A seven B four C five 1 first, second, fourth A third B three C thirty 2 tenth, twelfth, thirteenth A fourteenth B ninth C eleventh 3 nineteenth, twentieth, A twenty-first B twentieth-one C thirty-first 4 January, February, A May B April C March 5 October, November, A January B December August A July B September C October 7 My birthday’s June. A in B at Con 8 The party’s A in B at Con Saturday 3rd October. b Choose A, B, or C to complete the sentences. Example: Steve plays in a band A rock B band C reggae 9 Can you the phone? A speak B ask C answer III-My-school teacher.
C geting getting B get She doesn’t like Alive B liveing I don’t like A her B him C them The children are very quiet. I can’t hear A they B them C their very tired. alone. C living . I think she’s a terrible actress. A Do you want a mineral water? B No, thanks. I thirsty. A don’t have B haven’t C’m not Where the Red Hot Chili Peppers from? A are B do C come C September 6 June, VOCABULARY What is the missing word? Choose A, B, or C. Example: one, two, three, four A seven B four C five 1 first, second, fourth A third B three C thirty 2 tenth, twelfth, thirteenth A fourteenth B ninth C eleventh 3 nineteenth, twentieth, A twenty-first B twentieth-one C thirty-first 4 January, February, A May B April C March 5 October, November, A January B December August A July B September C October 7 My birthday’s June. A in B at Con 8 The party’s A in B at Con Saturday 3rd October. b Choose A, B, or C to complete the sentences. Example: Steve plays in a band A rock B band C reggae 9 Can you the phone? A speak B ask C answer III-My-school teacher.

 Ф. Энгельс 68 жашында румын, норвег тилдерин үйрөнгөн. Бардыгы болуп 20дан ашык тил билген.
Ф. Энгельс 68 жашында румын, норвег тилдерин үйрөнгөн. Бардыгы болуп 20дан ашык тил билген. — Киев: Радянська школа, 1968.
— Киев: Радянська школа, 1968.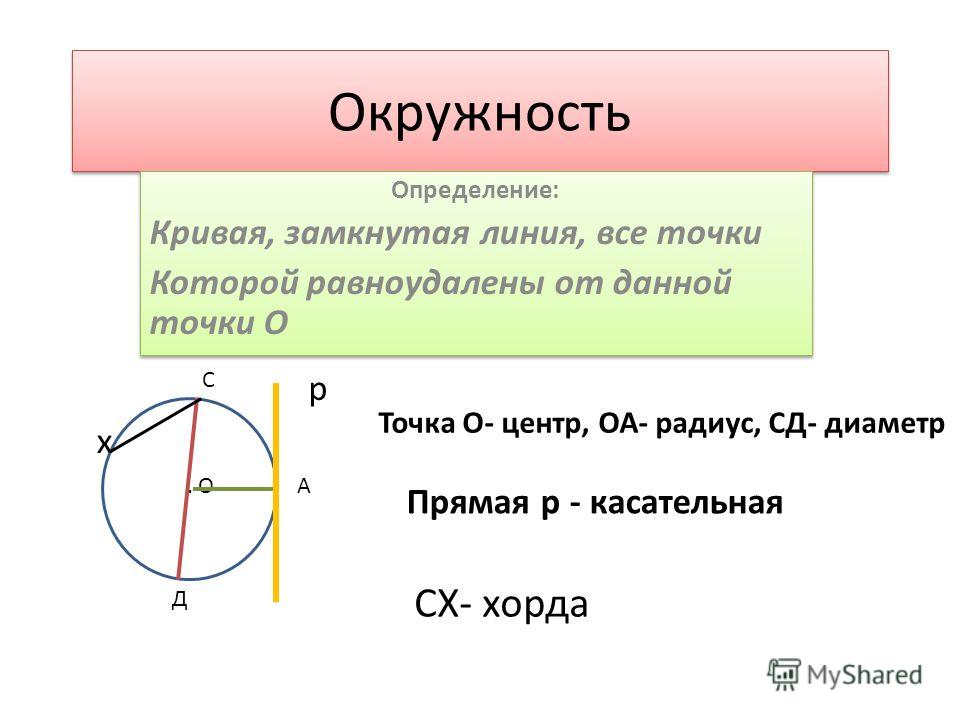 ck12.org/c/analysis
ck12.org/c/analysis