Вывод формулы лапласа давление: 21. Формула Лапласа

21. Формула Лапласа

С тремление поверхности жидкости к сокращению приводит к тому, что давление под выпуклой поверхностью жидкости оказывается больше, а под вогнутой меньше, чем под плоской (рис. 54). Силы дополнительного давление р направлено к центру кривизны поверхности.

Вычислим это добавочное давление р для пузырька газа, находящегося в жидкости (рис. 55). Пусть под действием давления р объем шара уменьшился на dV, а поверхность уменьшилась на dS.

Объем шара равен

Площадь поверхности равна S = 4R²  dS = 8R dR.

Работа сжатия внешних сил

отрицательна и равна

dA = – p dV = – p 4R² dR.

Другая формула для работы: dA = –  dS = –  8R dR.

Приравняем уравнения для работ и получим формулу Лапласа для сферической поверхности:

p 4R² dR =  8R dR 

В общем случае формула Лапласа имеет вид:

, (86)

где R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных нормальных сечений. (Нормальным сечением поверхности в некоторой точке называется линия пересечения этой поверхности с плоскостью, проходящей через нормаль к поверхности в рассматриваемой точке. Для сферы нормальные сечения – это окружности радиуса R.)

В формуле (86) радиус кривизны R считают положительным (рис. 54 б), если центр кривизны находится внутри жидкости (при несмачивании). Радиус кривизны считают отрицательным (рис. 54 в), если центр кривизны лежит над поверхностью (смачиваемость).

Ч астные случаи формулы Лапласа:

1. для сферы R₁ = R

   2 = R и p = 2/R;

2. для плоскости R₁ = R₂ =  и р = 0;

3. для цилиндрической поверхности (рис. 56) – жидкость находится между двумя параллельными пластинками: R₁ = R, R₂ =  и p = /R;

4. мыльный пузырь имеет две сферические поверхности мыльной пленки, избыточное давление которых направлено к центру мыльного пузыря, поэтому p = 4/R.

И з формулы Лапласа следует, что, чем меньше радиус поверхности жидкости, тем больше избыточное давление. Это легко можно продемонстрировать на опыте с двумя мыльными пузырями, соединенными трубкой (рис. 57): маленький пузырь будет уменьшаться, а большой – увеличиваться.

Капиллярные явления

Можно взять такой узкий сосуд (трубка или узкая щель), что искривленной оказывается вся поверхность жидкости (плоской поверхности нет). Если расстояние между стенками сосуда сравнимо с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярами, а происходящие в них явления – капиллярными явлениями.

Используем формулу Лапласа для расчета высоты поднятия жидкости в цилиндрическом капилляре радиуса r (рис. 58). Пусть жидкость смачивает капилляр. Тогда жидкость образует вогнутый мениск.

Если   краевой угол жидкости, то из рис. 58 следует, что радиус кривизны мениска равен

.

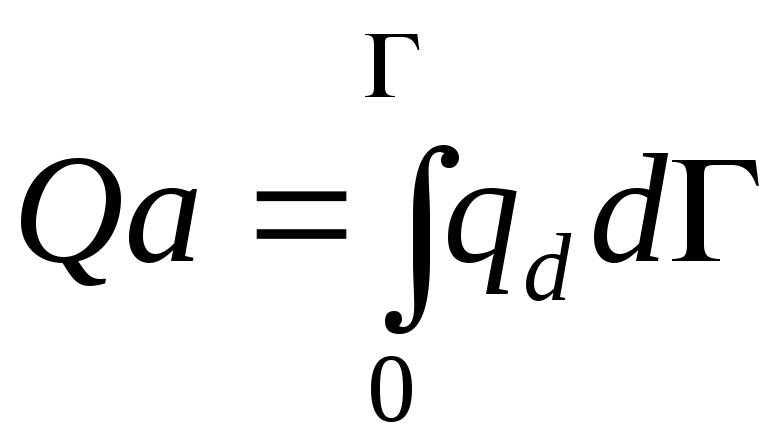
Силы давления р направлено к центру кривизны, т.е. вверх, и жидкость поднимается до высоты h, на которой давление Лапласа уравновешивает гидростатическое давление:

, , . (87)

Для полного смачивания ( = 0, cos  = 1) получаем:

.

Если жидкость не смачивает капилляр (рис. 59), мениск будет выпуклый, центр кривизны находится внутри жидкости, силы давления Лапласа направлены вниз. Глубину опускания жидкости («отрицательную высоту») находят по тем же формулам. Знак «минус» перед высотой h появляется автоматически, так как косинус тупого угла – отрицателен. Для полного несмачивания  = .

Если рассматривать рис. 58 как вид поверхности жидкости между двумя параллельными пластинками, то путем аналогичных рассуждений можно получить формулу для расчета высоты поднятия жидкости между ними: , где d – расстояние между пластинами.

19. Капиллярное давление. Закон Лапласа . Коллоидная химия.

Шпаргалка

Поверхность раздела фаз на практике довольно часто оказывается не плоской, а искривленной. Поверхность раздела фаз может быть выпуклой или вогнутой. Молекула жидкости, находящаяся на выпуклой поверхности, будет испытывать равнодействующую силу, меньшую, чем на плоской поверхности и направленную в глубь жидкости.

На вогнутой поверхности эта сила больше. Вследствие изменения поверхностных взаимодействий происходит изменение условий равновесия фаз, разделенных искривленной поверхностью.

На искривленной поверхности, помимо общего давления в обеих сосуществующих фазах, возникает добавочное давление, направленное в сторону той фазы, по отношению к которой поверхность вогнута, т. е. давление в фазе, отделенной от другой фазы вогнутой поверхностью, больше. Разность давлений, возникающая по обе стороны искривленной поверхности жидкости, получила название капиллярного давления, иначе его называют лапласовым давлением.

Величина капиллярного давления зависит от кривизны поверхности и поверхностного натяжения и выражается уравнением Лапласа

. Рассмотрим вывод данного уравнения. Пусть нам дан элементарный участок искривленной поверхности площадью

s = L₁L₂,

где L₁ и L₂ – криволинейные отрезки, ограничивающие искомый участок.

Радиусы кривизны криволинейных отрезков равны r₁, r₂, следовательно, площадь s равна:

s = L₁L₂ = r₁?₁ … r₂?₂,

где ?₁ и ?₂ – соответствующие центральные углы.

Если под действием силы, вызванной разностью давлений ?р по обе стороны поверхности, произошло смещение поверхности на величину dr без изменения кривизны, то имеет место увеличение этой поверхности на величину ds.

Затраченная работа dW может быть вычислена как произведение силы на путь или как произведение поверхностного натяжения на прирост поверхности следовательно,

dW = ?ds = ?рsdr = r₁r ₂?₁?₂?рdr.

Таким образом, величина ds будет определена как

ds = (r₁ + dr) x (r₂ + dr)?₁?₂ – r₁r₂?₁?₂.

Преобразовав данное уравнение, пренебрегая бесконечно малыми величинами, получим:

ds = ?₁?₂r₁dr – ?₁?₂r₂dr.

Пользуясь полученными уравнениями, получим уравнение Лапласа, выражающее избыток давления со стороны вогнутой поверхности:

?р = ?(r₁^–1 + r₂^—1).

Если поверхность сферическая, то r ₁ = r ₂, а уравнение Лапласа примет вид:

Величина давления насыщенного пара жидкости при данной температуре зависит от формы поверхности. Капиллярные явления – это явления физического свойства. Действие поверхностного натяжения происходит на границе раздела несмешивающихся сред. К капиллярным явлениям относят явления в жидких средах, вызванные искривлением их поверхности, граничащей с состояниями сред. Искривление поверхности ведет к появлению в жидкости дополнительного капиллярного давления, оно обозначается ?p, величина которого связана со средней кривизной r поверхности уравнением Лапласа.

Данный текст является ознакомительным фрагментом.

Вывод уравнения Юнга-Лапласа

Капиллярность 2021, 4(2): 23-30 https://doi. org/10.46690/capi.2021.02.01

Оригинальная статья | Открытый доступ | Проблема | Опубликовано: 28 апреля 2021 г.

Показать информацию об авторе Скрыть информацию об авторе Лейв Магне Сиквеланд, Свейн Магне Скьявеланд (англ. )

Кафедра энергетических ресурсов, Университет Ставангера, 4036 Ставангер, Норвегия

Ключевые слова:

Юнг-Лаплас, пространственные кривые, основные радиусы, линейная алгебра

Цитируйте эту статью:

Siqveland LM, Skjæveland SM. Вывод уравнения Юнга-Лапласа. капиллярность, 2021, 4(2): 23-30. https://doi.org/10.46690/capi.2021.02.01

Скачать цитату

EndNote(RIS)

БибТекс

377

Просмотры

101

Загрузки

Цитаты

7

CrossRef

N/A

WOS

7

Scopus

Аннотация Полный текст Об этой статье

Abstract

Классическое уравнение Юнга-Лапласа связывает капиллярное давление с поверхностным натяжением и главными радиусами кривизны границы раздела двух несмешивающихся жидкостей. В этой статье требуемые свойства пространственных кривых и гладких поверхностей описываются дифференциальной геометрией и линейной алгеброй. Условие равновесия формулируется балансом сил и минимизацией поверхностной энергии.

Полный текст

Меню

Резюме

Полный текст

Схема

Об этой статье

Показать информацию об авторе Скрыть информацию об авторе Лейв Магне Сиквеланд, Свейн Магне Скьявеланд ( )

Департамент энергетических ресурсов, Университет Ставангера, 4036 Ставангер, Норвегия

Abstract

Классическое уравнение Юнга-Лапласа связывает капиллярное давление с поверхностным натяжением и главными радиусами кривизны границы раздела двух несмешивающихся жидкостей. В этой статье требуемые свойства пространственных кривых и гладких поверхностей описываются дифференциальной геометрией и линейной алгеброй. Условие равновесия формулируется балансом сил и минимизацией поверхностной энергии.

Ключевые слова:

Юнг-Лаплас, пространственные кривые, основные радиусы, линейная алгебра

Получено: 10 апреля 2021 г. Пересмотрено: 25 апреля 2021 г. Принято: 26 апреля 2021 г. Опубликовано: 28 апреля 2021 г. Дата выпуска: июнь 2021 г.

Список литературы(9)

Дефай Р., Пригожин И. Поверхностное натяжение и адсорбция. Лондон, Великобритания, Longmans, Green & Co. Ltd., 1966.

Ховард А. Элементарная линейная алгебра. John Wiley and Sons, 1984.

Ландау Л., Лифшиц Э. Гидромеханика. Оксфорд, Великобритания, Pergamon Press, 1987.

Лаплас, П. Дополнение к десятому изданию. Méchanique Céleste 10, 1806.

Папацакос, П. Математическое моделирование. Kompendium ved Høgskolen i Stavanger, 1989. (на норвежском языке)

Шифрин, Т. Дифференциальная геометрия: первый курс кривых и поверхностей. Университет Джорджии, 2013.

Google Scholar

Тамбс Лич, Р. Математический анализ II. Gyldendal Norsk Forlag, Oslo, 1962. (на норвежском языке)

Weatherburn, CE Дифференциальная геометрия трех измерений. Кембридж, Великобритания, Cambridge University Press, 2016.

Янг, Т. III. Очерк о сцеплении жидкостей. Философские труды Лондонского королевского общества, 1805 г., 95: 65–87.

ДОИ Google Scholar

Об этой статье

История публикаций

Copyright

Благодарности

Права и разрешения

История публикаций

Получено: 10 апреля 2021 г.

Пересмотрено: 25 апреля 2021 г.

Принято: 26 апреля 2021 г. 28 апреля 2021 г.

Дата выпуска: июнь 2021 г.

Авторское право

© Автор(ы) 2021

Благодарности

Обсуждения с Полом Папацакосом и Пером Амундом Амундсеном подтверждены.

Права и разрешения

Эта статья распространяется в соответствии с положениями и условиями лицензии Creative Commons Attribution (CC BY-NC-ND), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа надлежащим образом цитируется.

Пример: Закон Лапласа о пузыре

Понимание ситуации

При обсуждении поверхностного натяжения мы показали, что поверхность жидкости притягивает сама себя. Это также работает для натянутой мембраны. Применение идеи поверхностного натяжения к изогнутой мембране дает интересный результат; тот, который имеет важные биологические последствия. Чтобы понять, как это работает, рассмотрим простую модель: тонкая сферическая мембрана, удерживаемая жидкостью (газом или жидкостью) под давлением.

Представление примера задачи

Предположим, что сферическая мембрана содержит жидкость под давлением. (Представьте себе воздушный шар, наполненный воздухом.) Если поверхностное натяжение в мембране равно $\gamma$, как перепад давления на мембране связан с размером пузырька? Не обращайте внимания на гравитацию.

Решение этой задачи

Итак, вот наша картина: у нас есть сферический пузырь, содержащий жидкость. Давление снаружи равно $p_{outside}$, а давление внутри равно $p_{inside}$. Насколько большой пузырь? Если внутреннее давление больше, чем внешнее, пузырь пытается увеличиться. Это уравновешивается поверхностным натяжением удерживающей его мембраны. Посмотрим, что говорит нам баланс. 92 Δp = γ 2πR$ или 

$$Δp = 2γ/R$$

Это то, что мы называем законом пузыря Лапласа .

Физические последствия

Закон Пузыря кажется довольно неинтуитивным. В нем говорится, что если поверхностное натяжение остается постоянным, то меньший пузырь будет иметь большее давление внутри. Хотя не совсем верно, что по мере того, как воздушный шар становится больше, поверхностное натяжение не меняется, это неплохое приближение. Взгляните на видео на YouTube слева. На нем показаны два шара разного размера, соединенные открытой трубкой. Открытая трубка имеет запорный кран, который позволяет закрывать и открывать трубку. Когда запорный кран открыт, воздух будет течь в трубке от высокого давления к низкому. Как вы думаете, в какую сторону она будет течь? Станет ли меньший из них больше, чтобы шарики стали более ровными? Или больший станет еще больше? Почему? Решите, прежде чем смотреть!

Закон Лапласа

Медицинские последствия

Закон пузыря Лапласа имеет медицинские последствия. Сердце похоже на мышечный пузырь, создающий напряжение жидкости внутри него (крови). Увеличенное сердце (большой $R$) потребует большего напряжения (большего $\gamma$) для создания той же разницы давлений.