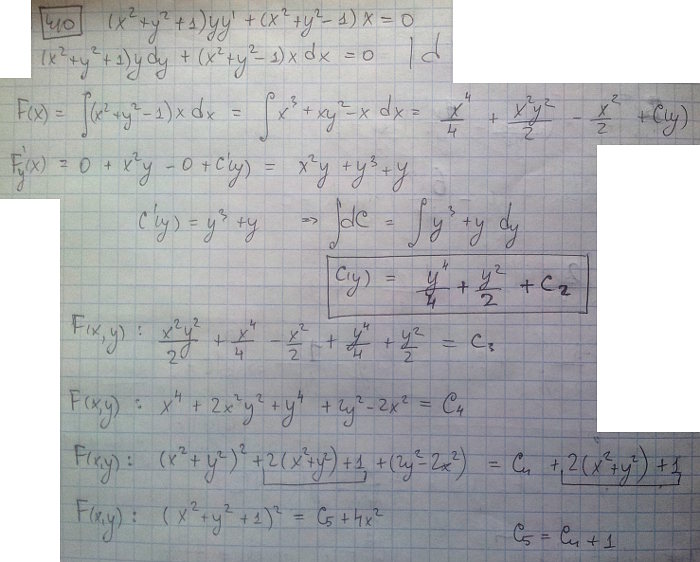X 2 y 2 1 решение: Сколько решений имеет система уравнений x^2+y^2=1 y=x

2

Филиппов § 10. Уравнения, допускающие понижение порядка

 

Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.

§ 10. Уравнения, допускающие понижение порядка

421. Решить уравнение: x2y» = y’2.

422. Решить уравнение: 2xy’y» = y’2 — 1.

423. Решить уравнение: y3y» = 1.

424. Решить уравнение: y’2 + 2yy» = 0.

425. Решить уравнение: y» = 2yy’.

426. Решить уравнение: yy» + 1 = y’2.

427. Решить уравнение: y»(ex + 1) + y’ = 0.

428. Решить уравнение: y»’ = y»2.

429. Решить уравнение: yy» = y’2 — y’3.

430. Решить уравнение: y»’ = 2(y» — 1) ctg x.

432.  Решить уравнение: y»3 + xy» = 2y’.

433. Решить уравнение: y»2 + y’ = xy».

434. Решить уравнение: y» + y’2 = 2e-y.

435. Решить уравнение: xy»’ = y» — xy».

436. Решить уравнение: y»2 = y’2 + 1.

438. Решить уравнение: y» — xy»’ + y»’3 = 0.

439. Решить уравнение: 2y'(y» + 2) = xy»2.

441. Решить уравнение: y’2 = (3y — 2y’)y».

442. Решить уравнение: y»(2y’ + x) = 1.

443. Решить уравнение: y»2 — 2y’y»’ + 1 = 0.

444. Решить уравнение: (1 -x2)y» + xy’ = 2.

445. Решить уравнение: yy» — 2yy’ ln y = y’2.

446. Решить уравнение: (y’ + 2y)y» = y’2.

447. Решить уравнение: xy» = y’ + x sin(y’/x).

448. Решить уравнение: y»’y’2 = y»3.

449. Решить уравнение: yy» + y = y’2.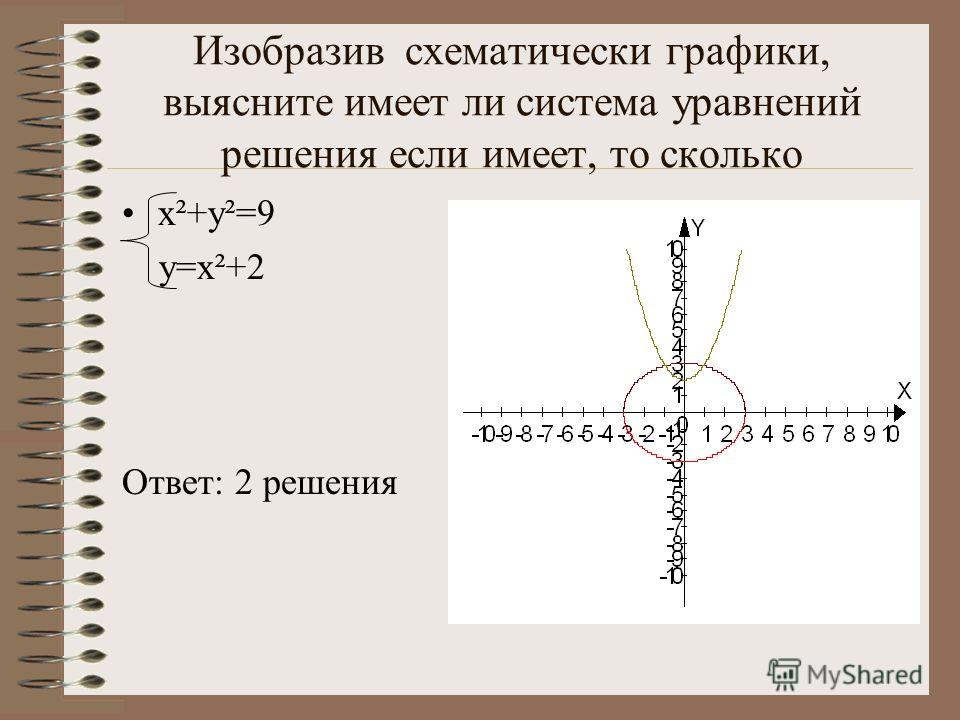

450. Решить уравнение: xy» = y’ + x(y’2 + x2).

452. Решить дифференциальное уравнение, воспользовавшись формулой, сводящей многократное интегрирование к однократному. 
xy» = sin x.

455. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
yy»’ + 3y’y» = 0.

456. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
y’y»’ = 2y»2.

457. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
yy» = y'(y’ + 1).

458. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
5y»’2 — 3y»yIV = 0.

459. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными.  
yy» + y’2 = 1.

460. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
y» = xy’ + y + 1.

461. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
xy» = 2yy’ — y’.

462. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
xy» — y’ = x2yy’.

463. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
xyy» — xy’2 = yy’.

464. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 

yy» = y’2 + 15y2 sqrt(x).

465. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
(x2 + 1)(y’2 — yy») = xyy’.

466.  Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
xyy» + xy’2 = 2yy’.

467. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2yy» = (y — xy’)2.

468. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y» + y’/x + y/x2 = y’2/y.

469. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y(xy» + y’) = xy’2(1 — x).

470.

 Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2yy» + y’2 = 0.

471. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2(y’2 — 2yy») = y2.

472. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение.  
xyy» = y'(y + y’).

473. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
4x2y3y» = x2 — y4.

474. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x3y» = (y — xy’)(y — xy’ — x).

475. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y2/x2 + y’2 = 3xy» + 2yy’/x.

476. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y» = (2xy — 5/x)y’ + 4y2 — 4y/x2.

477. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2(2yy» — y’2) = 1 — 2xyy’.

478. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2(yy» — y’2) + xyy’ = (2xy’ — 3y)x3/2.

479.  Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x4(y’2 — 2yy») = 4x3yy’ + 1.

480. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
yy’ + xyy» — xy’2 = x3.

482. Понизив порядок данного дифференциального уравнения, свести его к уравнению первого порядка. 

y»2 — y’y»’ = (y’/x)2.

487. Понизив порядок данного дифференциального уравнения, свести его к уравнению первого порядка. 
y2(y’y»’ — 2y»2) = y’4.

500. Понизив порядок данного дифференциального уравнения, свести его к уравнению первого порядка. 
x2(y2y»’ — y’3) = 2y2y’ — 3xyy’2…

501. Найти решение, удовлетворяющие заданным начальным условиям. 
yy» = 2xy’2; y(2) = 2, y'(2) = 0,5.

502. Найти решение, удовлетворяющие заданным начальным условиям.  
2y»’ — 3y’2 = 0; y(0) = -3, y'(0) = 1, y»(0) = -1.

503. Найти решение, удовлетворяющие заданным начальным условиям. 
x2y» — 3xy’ = 6y2/x2 — 4y; y(1) = 1, y'(1) = 4.

505.

 Найти решение, удовлетворяющие заданным начальным условиям. 
y» cos y + y’2 sin y = y’; y(-1) = π/6, y'(-1) = 2.

507. Найти кривые, у которых радиус кривизны обратно пропорционален косинусу угла между касательной и осью абсцисс.

508. Определить форму равновесия нерастяжимой нити с закрепленными концами, на которую действует нагрузка так, что на каждую единицу длины горизонтальной проекции нагрузка одинакова (цепи…

509. Найти форму равновесия однородной нерастяжимой нити (с закрепленными концами) под действием ее веса.

510. Доказать, что уравнение движения маятника у» + sin у = 0 имеет частное решение y(x), стремящееся к π при x → +∞.

 

   

2=1$$ есть решение $(x,y)$ в натуральных числах? Если мы предположим, что натуральные числа не включают в себя $0$, может ли выполняться это равенство? Я предположил, что это неверно, так как только $1$, $-1$ и $0$ дают это решение, но $0$ и $-1$ использовать нельзя. 2)}$ из первого квадранта и, следовательно, добавить еще одно условие $x\geq 0$ и $y \geq 0$. 92 \geq 0 \\ \ подразумевает & -1 \leq y \leq 1 \end{align}

Пересечение этого условия с $y\geq 0$ дает $y \leq 0 \leq 1$.

Аналогично, $0 \leq x \leq 1$. Следовательно, если $x$ и $y$ должны принимать натуральные значения, то $x$ и $y$ должны быть равны 1, но тогда они не будут лежать на нашей окружности.

Следовательно, утверждение ложно.

$\endgroup$

2

$\begingroup$ 92=1$ описывает множество точек единичного круга на плоскости. Нарисовав круг, вы легко найдете все натуральные (или даже целые) решения.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 9{-1}{2}$.

После этого я застрял, так как не могу найти различные наборы $x,y$ из этих отношений. Может ли кто-нибудь дать мне подсказку?

• абстрактная алгебра
• теория чисел
• теория полей
• алгебраическая теория чисел
• конечные поля

$\endgroup$

6

$\begingroup$

Если вам нужно что-то еще более явное, чем упоминание Андре об этом факте, обратите внимание, что у нас есть 92 = 1$. Все точки на такой кривой степени 2 легко параметризуются с помощью теоремы Безу, неформально говоря, что количество точек пересечения равно произведению степени. Следовательно, мы можем рассмотреть возможность использования семейства прямых (степень 1) для пересечения этой кривой степени 2, что по теореме Безу должно дать нам две точки пересечения. Теперь, если мы выберем эту линию более тщательно, в частности, зафиксировав заранее определенную точку на кривой и рассмотрев линии, проходящие через эту точку, она пересечет конику ровно в одной другой точке (здесь необходимо соблюдать некоторую осторожность).