X 2y xy 1: заказ решений на аукционе за минимальную цену с максимальным качеством

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например,

уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).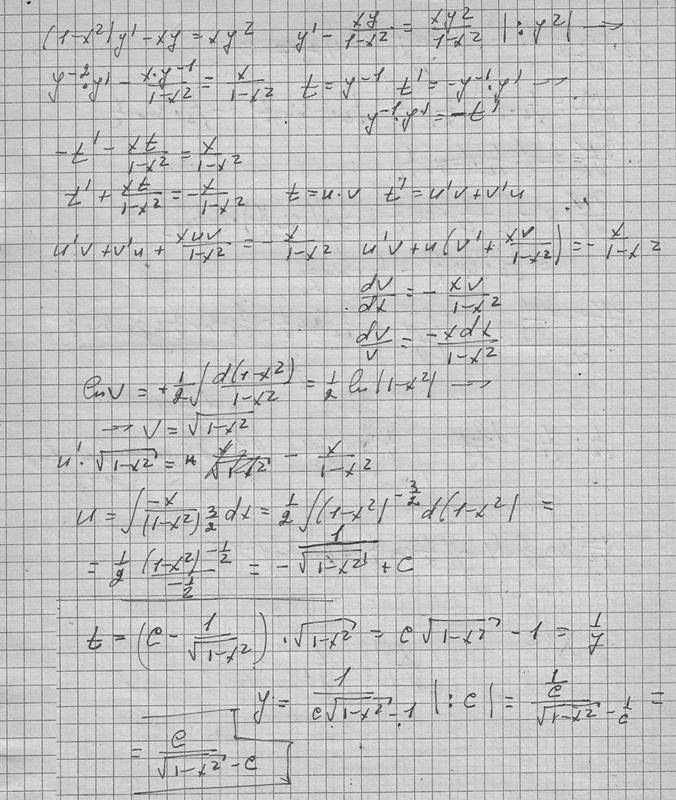 Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.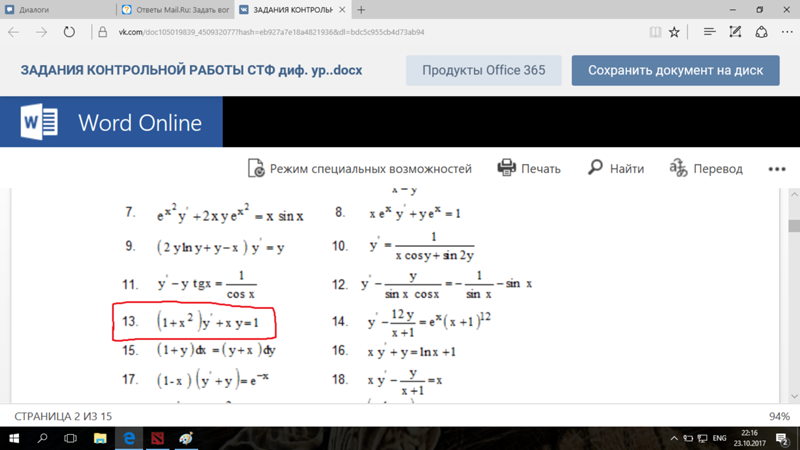

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.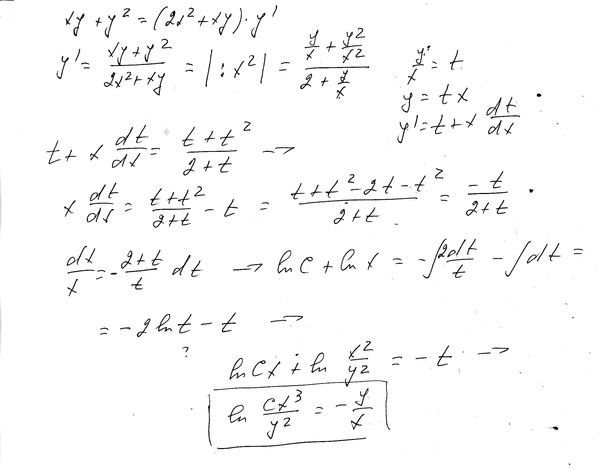 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

---

Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai

Решить {l}{x-y=1}{x+2y=7} | Microsoft Math Solver

x=3

y=2

Викторина

Simultaneous Equation

5 задач, подобных этой:

\left. \begin{array} { l } { x — y = 1 } \\ { x + 2 y = 7 } \end{array} \right.

Подобные задачи из результатов поиска в Интернете

Поделиться

Скопировано в буфер обмена

x-y=1,x+2y=7

Чтобы решить два уравнения методом подстановки, сначала решите одно из уравнений для одной из переменных. Затем подставьте результат для этой переменной в другое уравнение.

x-y=1

Выберите один из уравнений и решите его для x, изолируя x в левой части знака равенства.

x=y+1

Прибавьте y к обеим частям уравнения.

y+1+2y=7

Подставьте y+1 вместо x в другом уравнении x+2y=7.

3y+1=7

Прибавьте y к 2y.

3y=6

Вычтите 1 из обеих частей уравнения.

y=2

Разделите обе части на 3.

x=2+1

Подставьте 2 вместо y в x=y+1. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.

x=3

Прибавьте 1 к 2.

x=3,y=2

Система решена.

x-y=1,x+2y=7

Приведите уравнения к стандартному виду, а затем решите систему уравнений с помощью матриц.

\left(\begin{matrix}1&-1\\1&2\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}1\\7\end{matrix}\right)

Запишите уравнения в матричном виде.

inverse(\left(\begin{matrix}1&-1\\1&2\end{matrix}\right))\left(\begin{matrix}1&-1\\1&2\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&-1\\1&2\end{matrix}\right))\left(\begin{matrix}1\\7\end{matrix}\right)

Левое произведение с матрицей, обратной \left(\begin{matrix}1&-1\\1&2\end{matrix}\right).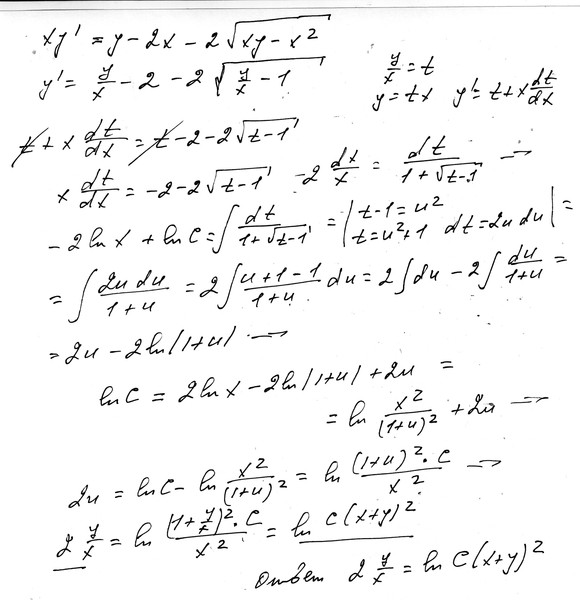

\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&-1\\1&2\end{matrix}\right))\left(\begin{matrix}1\\7\end{matrix}\right)

Произведение матрицы на обратную ей является единичной матрицей.

\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&-1\\1&2\end{matrix}\right))\left(\begin{matrix}1\\7\end{matrix}\right)

Перемножение матриц слева от знака равенства.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{2}{2-\left(-1\right)}&-\frac{-1}{2-\left(-1\right)}\\-\frac{1}{2-\left(-1\right)}&\frac{1}{2-\left(-1\right)}\end{matrix}\right)\left(\begin{matrix}1\\7\end{matrix}\right)

Для матрицы \left(\begin{matrix}a&b\\c&d\end{matrix}\right) с размерностью 2\times 2 обратная матрица имеет вид \left(\begin{matrix}\frac{d}{ad-bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матричное уравнение можно переписать в виде задачи умножения матриц.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{2}{3}&\frac{1}{3}\\-\frac{1}{3}&\frac{1}{3}\end{matrix}\right)\left(\begin{matrix}1\\7\end{matrix}\right)

Выполните арифметические операции.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{2}{3}+\frac{1}{3}\times 7\\-\frac{1}{3}+\frac{1}{3}\times 7\end{matrix}\right)

Перемножьте матрицы.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}3\\2\end{matrix}\right)

Выполните арифметические операции.

x=3,y=2

Извлеките элементы матрицы x и y.

x-y=1,x+2y=7

Для решения методом исключения коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сократилась при вычитании одного уравнения из другого.

x-x-y-2y=1-7

Вычтите x+2y=7 из x-y=1 путем вычитания подобных членов в обеих частях уравнения.

-y-2y=1-7

Прибавьте x к -x. Члены x и -x сокращаются, после чего в уравнении остается только одна переменная, и его можно решить.